CHAPTER 14
Science, mathematics, and computing
14.1 General principles
14.1.1 Official guidelines
Authors and editors involved in publishing scientific material must be aware of the intended readership and its level of expertise when considering what specialist terminology and stylistic conventions to adopt. Authors of texts involving the ‘harder’ sciences, such as astronomy, biology, chemistry, computing, mathematics, and technology, commonly employ practices different from those in the humanities and social sciences, particularly in those texts aimed at a specialist readership. Authors should follow the standards common in their discipline, as well as any set out for specific contexts, such as series or journal articles. In general, authors and editors should follow the recommendations of the Royal Society and the Système International d’Unités (SI), particularly those for styling symbols and units, which can vary between disciplines. Internal consistency is vital where more than one standard is acceptable, or where recommendations conflict.
If an author has good reason for using a convention different from the norm, they should mention this to the editor early on. As common usage changes more frequently in the sciences than in other disciplines, it is particularly important to clarify variations before editing begins. Many scientific journals have developed their own house style: this will vary according to the subject’s conventions and the readership’s requirements. Authors should be aware that, for reasons of efficiency and speed, this style may be imposed—often automatically by computer software—without the author being consulted.
Authors should avoid introducing a novel notation or non-standard symbols. If non-standard terms are essential to the notation system, authors should consider including a list of symbols in the preliminary matter and supplying the editor with printed examples or a PDF, so that there is no danger of misunderstanding what is intended.
As a requirement of submission, journal authors in particular may need to write in a template downloaded from a publisher’s website. This framework ensures that the document is structured in such a way that encoding for output as print or digital product can be achieved without manual intervention.
14.1.2 Clarity
Clarity in the presentation and explanation of difficult scientific concepts is to be valued. The principle of maximum clarity underpins most scientific style guidance and should be used to discriminate between alternative solutions to presentational problems.
Authors and editors should take care that hard copy, if used, is clear and unambiguous, and any handwritten notation is kept to a minimum. Whether hard copy or on-screen, ensure the correct character is used for special sorts (accented characters, Greek letters, mathematical symbols). For example, distinguish between:
Do not underline the inequality signs < and > to create less-than/greater-than or equal to symbols ≤ and ≥, and degree symbols should not be typed as lower-case superscript ‘o’s. See Table 14.4 for the corresponding Unicode code points.
Likewise, in electronic documents do not underline text to be set in italic. On hard copy, ensure that any hand-drawn rules above or below letters or whole expressions are not mistaken for underlining for italic.
There are particular issues of clarity involved in typesetting mathematics which affect the choice of typeface (see 14.6.1).
Scientific illustrations should adhere to the principle of maximum clarity: all unnecessary graphic effects should be eschewed. As far as possible, illustrations and their captions should be self-contained and require no reference to text material to make interpretation of them possible. See Chapter 16.
14.1.3 Numerals
Numbers in general are dealt with in Chapter 11. In science and mathematics figures are set close up, without a comma, in numbers up to 9999. In larger numbers thin spaces (see 14.1.5) are introduced after each group of three digits to the right or left of a decimal point (1 234 567.891 011 12); to permit alignment, spaces can also be introduced into four-figure numbers in columnar and tabular work. Decimal points are set on the baseline, not medially. Numbers less than one must be preceded by a zero (0.75), except where specific style guidance allows quantities that never exceed unity (such as probabilities) to be typeset without.
The SI guidelines state that it is preferable to use only numbers between 0.1 and 1000. It is better, therefore, to write 22 km rather than 22 000 metres, or 3 mm3 rather than 0.003 cubic centimetres. Powers of units can be represented exponentially, for example m2 for square metre and cm3 for cubic centimetre.
14.1.4 Units
There are internationally agreed abbreviations for many units (unit symbols), including all those in the SI. When used in full, a unit takes lower case (kilogram, nanometre), even eponymous ones (newton, tesla); when assigned a value, the unit symbol is used, standardly followed by a space (10 kg, 1.435 m), preferably a non-breaking or thin space (see 14.1.5). Unit symbols must not be pluralized (not cms). Table 14.1 shows SI units, prefixes, and their symbols.
Table 14.1 SI units
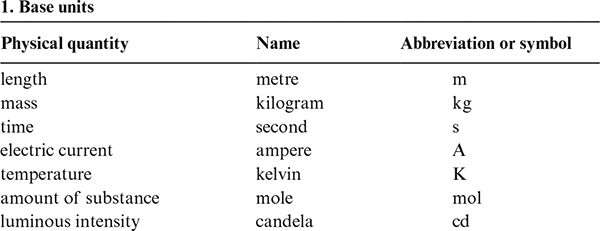
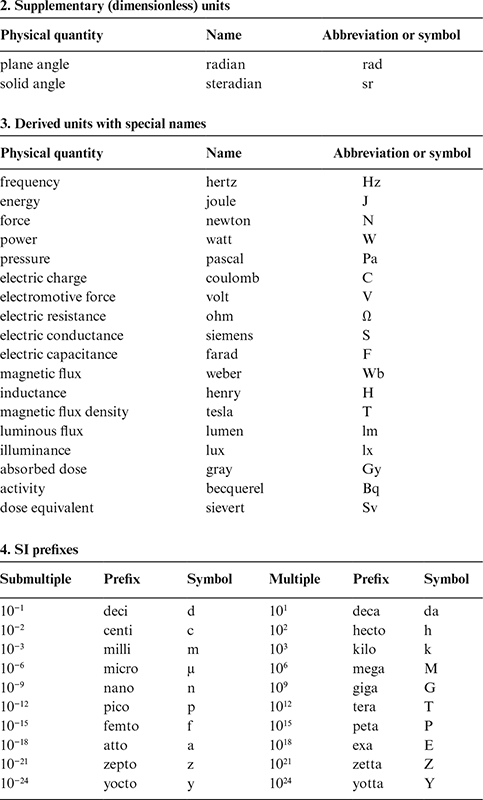
Some units not defined by SI are still compatible with SI units, such as hours, minutes, days, litres. The unit symbol for hour is h not hr and either L or l is acceptable for litre; if L is preferred it should also be used with prefixes such as mL for millilitres.
The unit symbol does not need to be repeated when en rules (dashes) are used to indicate a range (45.6–50.2 kg) unless the unit symbol is closed up (14°–18° [of angle]; see also 14.1.8).
Units are derived from other units by multiplication or division (m2, m/s). A product of two or more different units may be separated with a fixed thin or hair space (narrower than a thin space; see 2.5.1), for example N m, or with a medial dot (N⋅m, set closed up; U+22C5 DOT OPERATOR) but not Nm. Use a solidus or negative index (m/s or ms−1) for division but no more than one solidus in the same expression, to avoid ambiguity (instead of J/K/mol use J K−1 mol−1 or spell out the final expression, J/K per mole).
14.1.5 Punctuation and spaces
Oxford style is to omit full points at the end of a displayed formula or equation, and internal punctuation is limited to that in or following any interpolated text. Other styles treat formulas and equations as an integral part of the sentence and punctuate accordingly. Text set on the same line as a displayed equation that qualifies some aspect of the equation should be spaced off from the equation by at least one em.
The presence or absence of spaces can alter the meaning of scientific text so care must be taken that they are used appropriately: +5 is a positive integer; + 5 indicates an addition. Spaces come in various widths, either breaking or non-breaking; Unicode fonts have a variety of spaces between 2000 to 200A (hexadecimal) but the two that are used most frequently in technical texts, other than the word space, are the non-breaking space (U+00A0) and the thin space (U+2009) (see also 2.5.1).
14.1.6 Notes
It is good practice in scientific writing for all important information to be worked into the text, leaving only matter of secondary interest in notes, such as references, interpretations, and corrections. Since authors in many technical subjects choose to use an author–date (Harvard) style of references (see Chapter 17), notes occur infrequently. If a note is needed, however, make every effort to avoid adding the cue to a formula or equation, where it may be mistaken for part of the notation. For this reason superscript numerical note cues are not used except in contexts where equations are sparse. Where non-numerical note cues are required, the cue should be one of the marks of reference († ‡ § ¶ ||) in that order, repeated as necessary (††, ‡‡, etc.) throughout the chapter. The asterisk (*) reference mark used in other disciplines is not found in scientific or mathematical contexts, where that symbol may be assigned special uses. For more on notes and references see Chapter 17.
14.1.7 Eponymic designations
Names identified with specific individuals may be treated in several ways. Traditionally a disease, equation, formula, hypothesis, law, principle, rule, syndrome, theorem, or theory named after a person is preceded by the person’s name followed by an apostrophe and s:
| Alzheimer’s disease | Bragg’s law | Caro’s acid |
| Gödel’s proof | Newton’s rings |
Any variation follows the normal rules governing possessives (see 4.2.1):
| Charles’s law | Descartes’s rule of signs |
| Archimedes’ principle | Chagas’s disease |
An apparatus, coefficient angle, constant, cycle, effect, function, number, phenomenon, process, reagent, synthesis, or field of study named after a person is usually preceded by the name alone or its adjectival form:
| Leclanché cell | Salk vaccine |
| Cartesian coordinates | Newtonian telescope |
Eponymic anatomical or botanical parts may incorporate the name either as a possessive (Cowper’s glands, Bartholin’s gland, Wernicke’s area) or adjectivally (Casparian strip, Eustachian tube, fallopian tube). Something named after two or more people is known by the bare surnames, joined by an en rule:
| Cheyne–Stokes respiration | Epstein–Barr virus |
| Stefan–Boltzmann law | Haber–Bosch process |
| Creutzfeldt–Jakob disease |
although the en rule is often erroneously replaced by a hyphen, especially in digital text—internet usage is an unreliable indicator in this regard.
Particularly in medical use, British technical practice increasingly is to use bare surnames, so as to avoid the possessive’s proprietary effect:
| Angelman syndrome | Kawasaki disease |
| Rous sarcoma |
This is the typical form for toponymic designations:For guidance on capitalization of words derived from proper nouns, see 5.14.
| Borna disease | Coxsackie virus | East Coast fever |
| Ebola fever | Lyme disease |
14.1.8 Degrees
Degrees are of three types: degrees of inclination or angle, abbr. d. or deg.; degrees of temperature, symbol ° (U+00B0 DEGREE SIGN); and degrees of latitude and longitude, abbr. lat. and long. (no points in scientific work). For degrees of temperature see 14.1.9.
14.1.9 Temperature and calories
The various common scales of temperature are Celsius (or centigrade), kelvin, and Fahrenheit; in scientific work only the Celsius and kelvin scales are used. Generally, use Arabic numerals for degrees of temperature, but words for degrees of inclination and in ordinary contexts for temperature. SI guidelines stipulate a space between the value and the degree symbol used with the scale abbreviation (10 °C) but it is commonly closed up (10°C). The degree symbol itself is printed close up to its scale abbreviation (°C not ° C); alternatively use Unicode code point U+2103 for the glyph degree Celsius (°C). For a range of temperatures repeat the unit if closed up but not if a space is normally used (15°C–17°C or 15–17 °C). Do not use the degree symbol with the kelvin scale.
14.2 Biological nomenclature
14.2.1 Capitalization of English names
In general contexts the English names of animal or plant species should not be capitalized, unless one of the words is a proper name:
| red deer | greater spotted woodpecker | lemon balm |
| mock orange | Pallas’s cat | Camberwell beauty |
In specialized contexts such as field guides and handbooks capitalization is more usual, especially in ornithology. A third style is to capitalize only the first word of the compound. In most contexts, however, the use of lower case is still preferable. This could give rise to ambiguities—a little gull could be a particular species or just ‘a small gull’—but these are avoidable by careful wording.
14.2.2 Structure of taxonomic groups
In descending order, the hierarchy of taxonomic groups is:
kingdom
phylum (in botany, division)
class
order
family
genus
species
All organisms are placed in categories of these ranks: the domesticated cat, for example, is described in full as Carnivora (order), Felidae (family), Felis (genus), Felis catus (species). In addition, intermediate ranks may be added using the prefixes super, sub, and infra, and sub-families may be further divided into tribes. All taxonomic names are Latin in form, though often Greek in origin, except for the individual names of cultivated varieties of plant.
Rules for naming taxonomic groups are published in the following guides: for animals, the International Code of Zoological Nomenclature (ICZN); for wild plants and fungi, the International Code of Botanical Nomenclature (ICBN); for cultivated plants, the International Code of Nomenclature for Cultivated Plants (ICNCP); for bacteria, the International Codes of Nomenclature of Bacteria (ICNB); for viruses, the International Committee on Taxonomy of Viruses (ICTV).
14.2.3 Groups above generic level
Names of groups from kingdom to family are plural and printed in roman with initial capitals (Bacillariophyceae, Carnivora, Curculionidae). The level of the taxon is usually indicated by the ending: the names of botanical or bacteriological families and orders, for example, end in -aceae and -ales, while zoological families and sub-families end in -idae and -inae respectively. (Ligatures such as æ and œ are not now used in printing biological nomenclature.)
14.2.4 The binomial system
Living organisms are classified by genus and species according to the system originally devised by Linnaeus. This two-part name—called the binomial or binomen—is printed in italic, and usually consists of the capitalized name of a genus followed by the lower-case specific name. Thus the forget-me-not is Myosotis alpestris, with Myosotis as its generic name and alpestris as its specific epithet; similarly the bottlenose dolphin is Tursiops (generic name) truncatus (specific name). Specific names are not capitalized even when derived from a person’s name: Clossiana freija nabokovi (Nabokov’s fritillary), Gazella thomsoni (Thomson’s gazelle).
A genus name is printed in italic with an initial capital when used alone to refer to the genus. If, however, it also has become a common term in English for the organism concerned it is printed in roman and lower case (rhododendron, dahlia, tradescantia, stegosaurus); thus ‘Rhododendron is a widespread genus’ but ‘the rhododendron is a common plant’. Specific epithets are never used in isolation except in the rare cases where they have become popular names ( japonica), when they are printed in roman.
Latin binomials or generic names alone may be followed by the surname of the person who first classified the organism. These surnames and their standardized abbreviations are called ‘authorities’ and are printed in roman with an initial capital: ‘Primula vulgaris Huds.’ shows that this name for the primrose was first used by William Hudson; ‘Homo sapiens L.’ shows that Linnaeus was the first to use this specific name for human beings. If a species is transferred to a different genus, the authority will be printed in parentheses. For example, the greenfinch, Carduelis chloris (L.), was described by Linnaeus but placed by him in the genus Loxia.
14.2.5 Abbreviation
After the first full mention of a species, later references may be shortened by abbreviating the generic name to its initial capital, followed by a full point: P. vulgaris, E. caballus. If two organisms with the same single-letter abbreviation occur in the same sentence or paragraph, a multiple-letter abbreviation is sometimes used (Staphylococcus and Streptococcus may become Staph. and Strep. for example) but is best avoided as there are very few ‘official’ multiple-letter abbreviations so inconsistencies between publications can occur. The species names are usually sufficient to avoid confusion, or use the full version.
14.2.6 Subspecies and hybrids
Names of animal subspecies have a third term added in italic to the binomial, for example Motacilla alba alba (white wagtail), M. alba yarrelli (pied wagtail). Plant categories below the species level may also have a third term added to their names, but only after an abbreviated form of a word indicating their rank, which is printed in roman:
subspecies (Latin subspecies, abbreviation subsp.)
variety (Latin varietas, abbreviation var.)
subvariety (Latin subvarietas, abbreviation subvar.)
form (Latin forma, abbreviation f.)
subform (Latin subforma, abbreviation subf.)
So ‘Salix repens var. fusca’ indicates a variety of the creeping willow, and ‘Myrtus communis subsp. tarentina’ a subspecies of the common myrtle.
Other abbreviations are occasionally printed in roman after Latin names, such as ‘agg.’ for an aggregate species, ‘sp.’ (plural ‘spp.’) after a genus name for an unidentified species, ‘gen. nov.’ or ‘sp. nov.’ indicating a newly described genus or species, and ‘auctt.’ indicating a name used by many authors but without authority.
The names attached to cultivated varieties of plants follow the binomial, printed in roman within single quotation marks (Rosa wichuraiana ‘Dorothy Perkins’). The cultivar name may be preceded by the abbreviation ‘cv.’, in which case the quotation marks are not used (Rosa wichuraiana cv. Dorothy Perkins). The names of cultivated varieties may also appear after variety or subspecies names, or after a genus name alone: for example, the ornamental maple Acer palmatum var. heptalobum ‘Rubrum’, and the rose Rosa ‘Queen Elizabeth’. Names of hybrid plants are indicated by a roman multiplication sign (×): Cytisus × kewensis is a hybrid species, × Odontonia is a hybrid genus. Horticultural graft hybrids are indicated by a plus sign (+Laburnocytisus adami).
14.2.7 Bacteria and viruses
Bacteria
Genera used adjectivally are lower case roman (salmonella poisoning, streptococcal infection); plural noun forms can add -s or take the Latin form (rickettsias, salmonellae, staphylococci). Bacterial strains are usually designated by capitals and numbers in roman (Escherichia coli K12) but consult the relevant authority as nomenclature changes.
Viruses
The International Committee on Taxonomy of Viruses (ICTV) has developed a system of classifying and naming viruses. The ranks employed for animal, fungal, and bacterial viruses are order, family, subfamily, genus, and species. Wherever possible, Latinized names are used for the taxa; hence names of genera end in the suffix -virus, subfamilies end in -virinae, families end in -viridae, and orders end in -virales. Latinized specific epithets are not used, so binomial nomenclature does not obtain. The ICTV recommends italicizing and capitalizing the first word of all Latinized names when used in a taxonomic sense, but not in vernacular usage.
taxonomic: a newly acquired virulence of several bee viruses belonging to the family Dicistroviridae has been observed worldwide
vernacular: measuring the impact of herpes zoster and post-herpetic neuralgia on quality of life
However, not all publishers (including OUP) follow this guidance, italicizing only genera and species, so check which style is used. Those genera or higher groups that do not yet have approved Latinized names are referred to by their English vernacular names. Capitalization is used only for proper nouns:
We have focused our interest on acute bee paralysis virus, which shares some antigenic and sequence similarities with Kashmir bee virus and Israeli acute paralysis virus.
The ranks of genus and species are not used in the taxonomy of plant viruses, which are classified in groups—not families—with the approved group name ending in -virus. Existing names employ various combinations of Roman or Greek letters, Arabic or Roman numerals, and superscript and subscript characters. Many names are prefixed with a capital P or lower-case phi (PM2, ɸ6, ɸX, Pf1). It is important therefore to follow carefully the conventions employed in the original name.
14.2.8 Enzymes
Enzyme nomenclature has several forms, depending on context. Most enzyme trivial names are based on the name of the type of reaction they catalyse and the name of the substrate or product they are associated with. Most end in -ase, though some do not.
A systematic nomenclature has been devised by the International Union of Biochemistry and Molecular Biology. Each enzyme has a systematic name incorporating its type designation (i.e. group name), the name of its substrate(s), and a unique four-digit numerical designation called the EC (Enzyme Commission) number. For example, the systematic name of glutamate dehydrogenase is L-glutamate:NAD+ oxidoreductase (deaminating), EC 1.4.1.2.
Because systematic names are so unwieldy, they tend to supplement or clarify trivial names rather than replace them. In most contexts trivial names alone suffice, though the EC number and full systematic name should follow at first occurrence in formal usage.
Although restriction endonucleases also have EC classifications, they have additional nomenclature that is based on the genus, species, and strain from which they are derived (such as BamHI from Bacillus amyloliquefaciens strain HI).
14.2.9 Genes and chromosomes
Conventions for naming genes and gene products (the proteins they code for) vary widely among species or type of organism, and also change rapidly. Authors and editors are advised to check the website of the relevant nomenclature committee or other authority for current guidelines—many organisms now have dedicated online databases containing a searchable catalogue of genes with annotated gene sequence data, plus descriptions of gene functions. The New Oxford Dictionary for Scientific Writers and Editors has a helpful summary of the basic rules of gene nomenclature for selected groups of organisms or species.
The following is some general guidance but there are many exceptions so editors with limited knowledge of the subject should not be tempted to standardize capitalization, hyphenation, and italicization for example, without checking the relevant authority. As an example, acute myeloid leukaemia genes in humans and mice are AML1 and Aml1, respectively, and their protein products are AML1 and Aml1.
Each community also has its own convention for designation of genetic markers and transgenic strains.
Chromosomes are designated by a roman letter or number (in humans 1 to 22, X, Y); different regions and bands on the short (p) or long (q) chromosome arms are specified with Arabic numbers and letters, in roman, for example 14q32.2. Duplicated, deleted, or translocated regions are designated dup, del, or t respectively; for example t(9;22)(q34;q11.2) refers to a reciprocal translocation between bands 34 and 11.2 of the long arms of chromosomes 9 and 22. Gain or loss of a chromosome is indicated by a plus or minus sign, so +21 indicates an extra chromosome 21. The length of DNA sequences is cited in base pairs (bp), kilobases (kb), or megabases (Mb); the centiMorgan (cM) is a measure of genetic distance and relates to recombination frequency.
14.3 Medical terminology
14.3.1 Abbreviations
Abbreviations should be defined when first used. Avoid using clinical-style shorthand in formal writing (US for ultrasound; Hb for haemoglobin unless referring to specific types; see 14.3.3).
Abbreviations of Latin terms are now discouraged, particularly in pharmacology, where clarity of meaning is paramount. In addition, British and US usage differs in some cases (see Table 14.2).
The same abbreviations may be used for different terms: CSF may be cerebrospinal fluid or colony-stimulating factor. Which of these abbreviations should be employed in a text depends on the type of work and its expected readership.
Some abbreviations will be so familiar to the readership that they do not need to be defined (DNA, HIV) but be aware that some well-known English abbreviations may be known by a different abbreviation in other languages (AIDS, SIDA in French). It is useful to have a house style list of those that do not need to be defined for a particular specialty but, if in doubt, it is best to define it at some point.
Table 14.2 Dosage abbreviations
| British | US | |
| a.c | ante cibum (before food) | |
| b.d | b.i.d. | bis die (twice daily) |
| o.d | q.d | omni die (every day) |
| o.m | omni mane (every morning) | |
| o.n | q.h.s | omni nocte (every night) |
| p.c | post cibum (after food) | |
| p.r.n. | pro re nata (when required) | |
| q.d.s. | q.i.d. | quater die sumendum (to be taken four times daily) |
| q.q.h. | quarta quaque hora (every four hours) | |
| stat | statim (immediately) | |
| t.d.s. | t.i.d. | ter die sumendum (to be taken three times daily) |
| t.i.d. | ter in die (three times daily) |
14.3.2 Blood groups
Blood-group antigens are designated by capital letters, sometimes combined with a lower-case letter or letters, such as A, B, AB, O, Rh. Note that while A, for example, is defined as a blood group, not blood type, blood is described as being type A, not group A.
14.3.3 Haemoglobin
The types of normal human haemoglobin are designated Hb A, Hb A2, and Hb F. Their component globin chains are designated by a Greek letter (α, β, γ, or δ); subscript numerals indicate the number of chains. Abnormal haemoglobins are designated either by letters (C–Q, S) or by the name of the place where they were first identified (e.g. Hb Bart’s, Hb Chad).
14.3.4 Vitamins
The group of organic compounds that form vitamins may be known by their chemical names or by a single capital letter; those forming part of a group are identified further by subscript Arabic figures (e.g. vitamin B1). (Dietary minerals are known only by their chemical names.)
14.3.5 Immunology
Symbols for human histocompatibility leukocyte antigens are HLA followed by a letter to designate the class (e.g. HLA-A). Classification is complex and ongoing; consult the website of the World Health Organization Nomenclature Committee for Factors of the HLA System, which changed the way HLA alleles are designated and named in 2010. Symbols for human immunoglobulins are Ig also followed by a class letter (e.g. IgA); do not use Ig as an abbreviation for immunoglobulin. T cell is not hyphenated unless used adjectivally (T-cell receptor). The gene symbols for immunoglobulins and T-cell receptors are assigned by the ImMunoGeneTics (IMGT) Nomenclature Committee; lists of human and murine gene names can be found on their website. Symbols for many other molecules such as interferons consist of capital letters to designate the molecule, prefixed by the source, and followed by other designations (rhIFN-α1, recombinant human interferon-α1).
14.3.6 Diseases
Disease names may be descriptive or eponymic (e.g. Parkinson’s disease). Derived words do not take a capital letter (e.g. parkinsonism). See also 14.1.7 on eponymic designations. Note that descriptive names are now preferred (reactive arthritis over Reiter’s disease). Avoid using nouns derived from disease names to describe patients (diabetics, epileptics); use people with diabetes or epileptic patients for example.
14.3.7 Drug nomenclature
In professional or technical contexts, prefer a drug’s generic name (in lower case) to its proprietary name (with an initial capital), which may differ over time and between countries. Even generic names can vary, however, and there are several conventions worldwide, chiefly British Approved Names (BANs), Recommended International Non-Proprietary Name (rINNs), US Adopted Names (USANs), and Japanese Approved Names (JANs). European legislation requires the use of rINNs for medicinal product labelling and in 2003 all British Approved Names (BANs) were harmonized with rINNs with the exception of adrenaline (in rINN epinephrine) and noradrenaline (norepinephrine). Publishers should therefore impose rINNs/new BANs as a matter of policy. In a historical context, and for lidocaine (lignocaine) where changeover has been slower, it may be useful to add the original BAN as a gloss. The British National Formulary retains original BANs as synonyms and the Medicines and Healthcare Products Regulatory Agency (MHRA) website has a complete list of the BANs changed. A dictionary that includes all the international systems is published annually by the US Pharmacopeial Convention.
14.4 Chemistry
14.4.1 Introduction
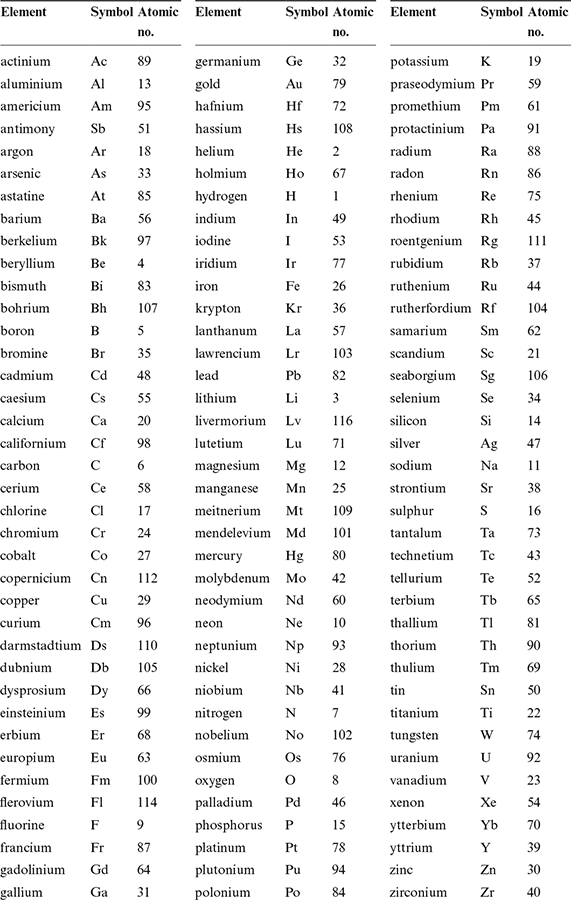
The International Union of Pure and Applied Chemistry (IUPAC) generates comprehensive advice on chemical nomenclature, terminology, standardized methods for measurement, and atomic weights. By their recommendations, symbols for the elements are set in roman with an initial capital, no point at the end; spelled-out names of chemical compounds are in lower-case roman; and symbols for the elements in formulas are printed in roman without spaces:
H2SO4 Cu(CrO2)2
Table 14.3 lists the IUPAC-accepted names and abbreviations of chemical elements.
14.4.2 Roman and italic
In certain kinds of name, symbols are printed in italic (O-methylhydroxylamine, fac-triamine-trinitrosylcobalt(III)). Italic is also used for certain prefixes, of which the commonest are o-, m-, p-, cis-, and trans- (o-tolidine, p-diethylbenzene, cis-but-2-ene). Retain the italic, but not
| the cis isomer | position a is ortho to the methyl group |
the hyphen, when the prefix is used as a separate word:
The prefixes d-, l-, and dl- are no longer used for labelling stereoisomers, which are expressed either by small capitals or by symbols: D-(+), L-(−), and DL-(±) respectively; for example ‘DL-lactic acid’, ‘(+)-tartaric acid’. In each case the hyphens must be retained, although not when expressing their absolute configuration.
14.4.3 Formulas and structural drawings
A chemical formula shows the elements present in a compound and their relative proportions (H2O, C2H6O); a chemical equation represents the changes that occur in a chemical reaction, in words or symbols:
glucose + oxygen→carbon dioxide + water
C6H12O6(aq) + O2(g)→CO2(g) + H2O(g)
Formulas and reaction schemes may be numbered separately from figures, often with a sequence of bold numbers or letters in square brackets or parentheses, ranged right.
Table 14.3 Chemical elements
When expressing formulas, the order of brackets normally follows that in mathematics: {[( )]}. Parentheses are used to define the extent of a chemical group, as in (C2H5)3N; square brackets are used to denote, for example, chemical concentration in complex formulas: [H2SO4]. This sequence will vary in certain circumstances, for example in the use of square brackets in denoting coordination compounds:
| K3[Fe(CN)6] | [Ni(CO)4] |
In organic chemical nomenclature, it is usual to write a formula as a series of groups (known as a structural formula):
| CH3COC2H5 | RCH2COOCH3 |
Medial dots can be used to divide off the groups, if clarification of a formula is needed (usually in textbooks). Unicode code point U+00B7 MIDDLE DOT is acceptable.
| (CH3CO·C2H5; | R·CH2·COOCH3) |
In most other contexts they can be dispensed with, although dots are required in formulas of addition compounds (Na2CO3·10H2O). Indicate a single bond with a closed-up en rule or a minus sign (C–H), a double bond by an equals sign (CH3CH=CH2), and a triple bond by an equivalence sign (U+2261 IDENTICAL TO) (CH3C≡CH).
In chemical equations, different types of arrows are used to represent reactions or electron movement; arrows may be single or double barbed—each has significance. For example, a long double-barbed arrow is used to indicate the direction of a reaction
CO2 + 2H2O →CH4 + 2O2
and two single-barbed arrows pointing in opposite directions indicate a reversible reaction, which may be in balanced equilibrium (same length arrows)
N2 + 3H2 ⇌ 2NH3
or favour either the reactants or products (different length arrows).
Equations and displayed or skeletal formulas can be created in dedicated chemistry drawing packages; anything other than simple, single-line formulas that can be word processed will be treated as artwork (for details see Chapter 16). There are also TeX macro packages that can be used for creating chemistry graphics or typesetting chemistry according to a publisher’s style (see 14.6.1).
14.4.4 Superscripts and subscripts
Superscripts and subscripts need not occur only singly, and need not follow what they modify. In specifying a particular nuclide, the atomic (proton) number is printed as a left subscript (12Mg). Similarly, the mass (nucleon) number of an element is shown with its symbol and printed as a left superscript (235U, 14C)—not to the right, as formerly. If it is given with the name of the element no hyphen is necessary (uranium 235, carbon 14).
In inorganic chemical nomenclature the relationship between the superscripts and subscripts surrounding a chemical symbol is important: superscript expresses the electrical charge and subscript the number of atoms for each molecule. These should be staggered so as to indicate the ions present (Na+2CO32– (sodium carbonate) but Hg22+Cl2– (dimercury(I) chloride)). A medial dot is used to indicate coordinated species (CuSO4.5H2O). Ionic charge is shown by a right superscript (SO42–). Indicate complex ions by square brackets: K+3[FeCl6]3–.
Indicate oxidation states by a small-capital Roman numeral, set in parentheses close up to the spelled-out name, for example ‘manganese(IV)’; or by a superscript Roman numeral set in capitals to the right of the abbreviated name, for example ‘MnIV’.
Atomic orbitals, designated s, p, d, f, g, are roman, and can have subscript letters with superscript numbers attached (dz2, dx2–dy2).
14.5 Computing
14.5.1 Terminology
The influence of the US on the computing field has resulted in US spelling being adopted for much of the standard vocabulary, such as analog, disk, and program rather than analogue, disc, programme (but note compact disc, digital versatile disc). Phrases such as object-oriented should not be changed to British usage (orientated). Other spellings not forming part of computing terminology should be normalized to British spelling for texts intended wholly or mostly for the UK market.
In the main, the names of programming languages, including acronyms, are styled in upper and lower case (Unix (trademark UNIX), Java, Python, Lisp); capitals are used for abbreviations (PHP, SQL). The plus signs in C++ are styled on the line, not superscripted, and C# (pronounced C sharp) uses a hash on the line, not a sharp sign. While it is acceptable to style different language names differently, ensure that the same style is adopted for the same language throughout a work. Styling of programming language names and many of the other computing abbreviations and terms can be found in the New Oxford Dictionary for Scientific Writers and Editors or the New Oxford Dictionary for Writers and Editors.
Data storage is measured in bytes (symbol B), which is usually defined as 8 bits (b); multiples may appear to use the same prefixes as the SI, including K (not k) for kilo-, M for mega-, G for giga-, T for tera-, but they are in fact binary so a kilobyte (1 KB) is 1024 bytes, a megabyte (1 MB) is 1024 × 1024 bytes, and so on. Note that this usage is confined to data storage—other measurements such as data transmission rates take the standard SI prefixes. Linux and open-source communities often use the International Electrotechnical Commission standard, which uses the prefixes
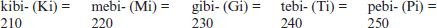
14.5.2 Representation
The text of a computer program or textual data file such as an XML file may be presented in a work in several ways: in whole or in part, displayed or run into text. Not being a prose extract in the traditional sense, any such material is treated rather like an equation, with no minimum size and no small type needed for display.
Where the features of the program or mark-up language require character-literal syntax and precise line breaks, display, indentation, spacing, or special sorts, these must be reproduced exactly. It is wise to insert any lengthy code directly from the source rather than retype it, which can introduce error. It is useful to set any selected material in a distinctive typeface—a sans-serif font, or a monospace typeface such as Courier—one advantage of the latter being that fixed-width fonts preserve alignment of code elements, such as end-of-line comments, as they would appear on-screen in a text editor.
<body bgcolor = "#000033" text = "#000033"link = "#FF0000" vlink = "#66CC33" alink = "#FFFF00" onLoad = "MM_displayStatusMsg('welcome'); return document:MM_returnValue">
If the font chosen to indicate programming or mark-up language text is sufficiently different from the font used for normal text, it is unnecessary to delimit it further by quotation marks, even when run into text. If, however, quotation marks are needed, note that computing practice matches standard British usage in the relative placement of punctuation and quotation marks. The punctuation falls outside the closing quotation mark, so that in citing parts of
x=0;
for (i-0;i++;i < n)
x+=V[i];
in text, the punctuation does not interfere with the syntax: ‘x = 0;’, and ‘x += V[i]’. This style, which would be imposed naturally in British publishing, should also be imposed in US computing texts, though not extended to normal quotations. US computing books can also reserve British-style single quotation marks for programming and mark-up language text, using double quotes for normal quotations.
In-text or displayed formulas and equations are best described and set so far as possible according to the rules governing mathematics. Any visual representations of structures or hierarchical classifications (use-case and activity diagrams, screen shots, tree grammars, Venn diagrams) will be treated as artwork (see Chapter 16).
14.5.3 Computing symbols
Mathematical material in computing contexts is usually treated in the same way as in other texts, although the sense of, for example, some logic symbols may differ from standard practice. In programming, the different types of bracket have various specific uses and order, depending on the language. In computing, the slash (/) is used as a separator, as with URLs for example. When a backslash (\) separator is used, the slash can be called a forward slash to differentiate it further.
Code tags in SGML-based languages are enclosed by angle brackets < >: note that the narrow angle brackets 〈 〉 generally employed in technical contexts should not be used here (see 14.6.5 for mathematical brackets).
Other symbols have various context-specific functions: the asterisk, for example, is a Kleene star in BNF, a multiplication operator in C, and a wildcard character in various command-line shells. In some computing languages multi-symbol operators are used—for example, a combined colon and equals sign := is used as the assignment symbol (‘gets’ or ‘becomes’); in others ::= means ‘is defined as’ and :- means ‘if’. These symbols constitute a single unit and are set close up, with space either side:
{A[x] := y, B[u, v] := w}.
〈decimal fraction〉 ∷= 〈unsigned integer〉
but not all languages require space around operators. It is important to be aware of the specific rules regarding spaces, indentation, commenting, spelling and capitalization, and the meanings of symbols used alone or in combinations in programming and mark-up languages—if working in an unfamiliar language, find out the rules online or raise a query with the originator.
14.6 Mathematics
14.6.1 Introduction
The de facto standard for mathematical typesetting is TEX (usually reproduced as TeX), a mark-up language available for many computing platforms, which consists of a coded, plain-text file that can be output to a device-independent file for printing or to PDF to produce high-quality results in terms of the complex layout, formatting, and special characters often demanded in mathematical work. LaTeX is the most popular TeX-based system. Some mathematical societies and publishers have their own plain TeX or LaTeX style files to help authors prepare their submissions according to the required specifications. Mathematical mark-up languages such as MathML and TeXML can be used to embed formulas in webpages, ebooks, and apps.
As a result, former constraints in setting ‘difficult’ material such as embellishments, fractions, fences, and overbars have been overcome, and digital product has removed the necessity to minimize displayed matter to reduce page extents and production costs.
When mathematical notation is required in text that is not created in a TeX-based system, authors should prepare their files using a word-processor equation editor or a stand-alone WYSIWYG (graphical) application for creating mathematical notation based on MathML.
In a mathematical equation each letter represents a quantity or operation, but the style (bold, italic, script, sans serif) and the relative positioning and sizes of the symbols (subscript, superscript) also convey important information.
Some typefaces are not suited to setting mathematics and should be avoided: sans-serif faces often suffer from indistinguishable characters (l, I, 1 are common examples). Subscripts and sub-subscripts must be legible and the distinction between roman, italic, bold, and sans serif clear even in one isolated character. Plain serifed faces such as Times, Computer Modern, and Lucida Math are generally to be favoured for mathematical work. The choice of typeface should be carried through to headings and labelling of figures where maths may occur. The typography of equations should not be altered to conform with design specifications for headings and labels.
14.6.2 Notation
The established style is to use roman type for operators and certain numerical constants, and to label points in a diagram. Italic is used for letters expressing a variable, and bold is used for vectors and matrices. Each description should be represented by a single symbol: avoid using abbreviated words. Here are some specific points:
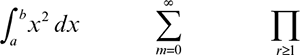
14.6.3 Symbols
Operational signs are of two types: those representing a verb (e.g. = ≈ ≢ ≥) and those representing a conjunction (e.g. + − ⊃ ×). All operational signs take a space on either side, consistently either a thin space or a word space. (If setting in TeX, such spaces are built in, so there is no need to add any.) They are not closed up unless they are being used to modify a value, for example, a difference of ±2; magnification ×200.
Set a multiplication point as a medial point (⋅) (U+22C5 DOT OPERATOR) but it should be used only to avoid ambiguity and is not needed between letters, unless a vector product is intended (e.g. a∙b), in which case U+2219 BULLET OPERATOR should be used; there are no spaces either side of a medial point.
In print product where space-saving is desirable, any symbol that involves setting a separate line of type should be avoided when an alternative form is available. So, for angle ABC, prefer ∠ ABC to
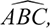
and for vector r, prefer r (in bold) to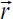 
to prevent uneven line spacing, unless using TeX, which can handle this.
The space around a colon used as a ratio sign (mixed in the proportion 1: 2) is narrower than that used around an operational sign, so when using either word or thin spaces around operators, use a thin or hair space respectively on either side of the colon; some styles set the colon closed up. A colon in a set or function such as {x: x > 0} is closed up to the preceding letter with a non-breaking space after.
A solidus is set closed up to the characters either side (12/28, a/b) and there is no space before a factorial (12!). In TeX-based systems there is no constraint in using the vinculum or overbar—the horizontal rule above the square-root sign (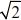
), although it is still best avoided in tightly leaded text, in which case √2 is sufficient or the extent covered by the rule may be shown by parentheses:
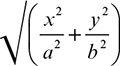
is sufficient for
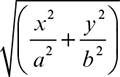
14.6.4 Superscripts and subscripts
Reserve superscript letters for variable quantities (set in italic); reserve subscript letters for descriptive notation (set in roman). Asterisks and primes are not strictly superscripts and so should always follow immediately after the term to which they are attached, in the normal way.
When first a subscript and then a superscript are attached to the same symbol or number, mark the subscript to align with the superscript in a ‘stack’.
If it is necessary to have multiple levels of superscripts or subscripts, the relationships must be made clear for the typesetter if rekeying is necessary.
Wherever possible, it is customary—and a kindness to the reader’s eyesight—to represent each superscript or subscript description by a symbol rather than an abbreviated word. Those subscript descriptions that are standardly made up of one or more initial letters of the word they represent are set in roman type.
14.6.5 Brackets
The preferred order for brackets is {[( )]}. When a single pair of brackets has a specific meaning, such as [n] to denote the integral part of n, they can, of course, be used out of sequence. The vertical bars used to signify a modulus— │x│ —should not be used as brackets.
Two further sorts of mathematical brackets may be used: double square brackets 〚 〛 and ‘narrow’ angle brackets 〈 〉. Angle brackets are used singly in Dirac bra and ket notation and in pairs they may be used to indicate the value of a quantity over a period of time, but they can also be used generally. Note that in mathematical work, the inequality signs < and > are not used as brackets. Double square brackets can be placed outside, and narrow angle brackets inside, the bracket sequence, and are handy for avoiding the re-arrangement of brackets throughout a formula or, especially, a series of formulas. Thus for comparison’s sake the formula
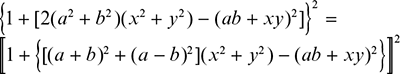
is perhaps better put
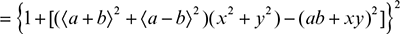
14.6.6 Fractions, formulas, and equations
Definitions
The terms equation, formula, and expression are sometimes confused by non-mathematicians; the following explanations may help to clarify usage.
An equation is a statement in which two mathematical expressions are linked by an equals sign:
y = 12a + b or 10 ÷ 5 = 2
A mathematical expression does not have an equals sign—
v2 + f or 3 − 7i
—or can be a single term such as exponential e.
A formula is a mathematical rule expressed in words or symbols:
(in words) the circumference of a circle is equal to twice the radius multiplied by pi
(in symbols) c = 2πr
Layout
As discussed in 14.6.1, digital product has fewer constraints on space than the printed page, so displaying equations where it helps clarity of meaning is desirable; even inline expressions can be satisfactorily presented in TeX, which subtly adjusts interline spacing and character size and spacing. If not set in TeX, simplification remains desirable for equations embedded in text material that would otherwise require extra leading to be introduced. For example,
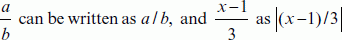
and simple fractions such as 
can be written as ½π, ⅓x, ¼(a+b).
But just because the equations can have complex formatting, it does not necessarily mean that they should: work can be reduced and appearance improved by writing such a formula as
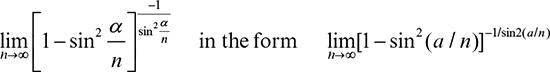
In printed product, displayed formulas three or four lines deep can thus be reduced to a space-saving, neater, and more manageable two-line form in almost all instances.
Displayed formulas are usually centred on the page. If there are many long ones, or a wide discrepancy in their length, it may be better to range them all left with a 1- or 2-em indent.
If it is necessary to break a formula—whether displayed or run-in—at the end of a line, it should be done at an operational sign, with the sign carried over to the next line. If an equation takes up two or more lines it should be displayed, with turnover lines aligned on the operational sign (preferably =):
(2.1)
Any equation referred to at another point in the text should be numbered; any numbered equation should be displayed. It is usually better to include the chapter number in front of the sequence number, such as 2.1 for the first equation in Chapter 2. If, however, the total number of equations is very small, it is possible to use a single sequence of numbers throughout the text. As illustrated above, these numbers are enclosed in parentheses and set full right, aligned on the same line as the final line of the equation.
14.6.7 Mathematical symbols
Table 14.4 Some mathematical symbols and corresponding Unicode code points
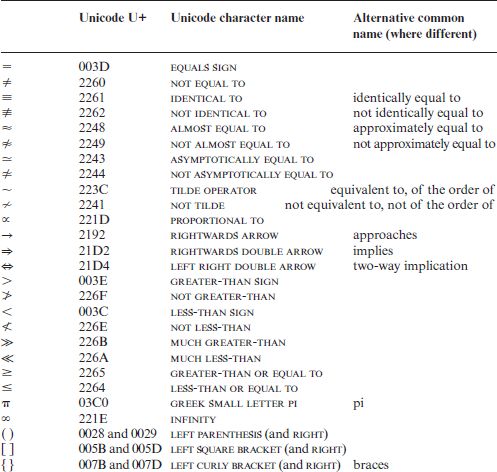
14.7 Astronomy
14.7.1 Conventions
Most current astronomy texts follow those recommendations for style set out by the International Astronomical Union (IAU), though other styles may be found, especially in older works. Ensure consistency within a given work, preferring modern to older styles except when reproducing earlier texts.
Capitalize Earth, Moon, and Sun in astronomical contexts but not in general text; the definite article is omitted before Earth in technical texts:
On Earth, valleys occur both on dry land and beneath the sea; there are also valleys on the Moon, Mars, and Venus.
The members organise turtle walks everyday and during full moon and new moon days, intensify the patrols.
Common sense seems to be disappearing off the face of the earth.
Use lower case for suns and moons. Capitalize Galaxy and Solar System when it refers to the Milky Way and our planetary system, but galactic and solar is lower case in all other contexts. While minor planet is preferable to asteroid in technical usage, asteroid belt is an accepted astronomical term.
14.7.2 Units
One-letter abbreviations for time units (second, minute, hour, day, year) are acceptable (s, m, h, d, y) if the context makes them clear. Time units can be written on the line with spaces (5h 35m 45s) or superscripted and closed up (5h35m45s); aim for consistency. Dates are commonly written in the form 1954 March 31. A year stated in the form 2000.0 represents an epoch; the ‘.0’ is significant and should not be deleted. Angles are often written with the angle symbol immediately before the decimal point (0″.001). Conventional notation is also acceptable but be consistent.
Note light year is a unit of distance, not time, is abbreviated with points, l.y., and is used in non-specialist texts. The distance unit parsec, symbol pc, is preferred in academic texts. SI prefixes (see 14.1.4) can be used with parsec (e.g. 5 Mpc), unlike the light year. Within the Solar System, distances are measured in astronomical units, symbol AU.
14.7.3 Stellar nomenclature
Galaxies, nebulae, and bright star clusters can be designated by names (Crab Nebula, Beehive Cluster, Sombrero Galaxy) or by numbers in a catalogue such as that of Messier (M1, M104) or the New General Catalogue (NGC 1952, NGC 4594). Note the prefix M is closed up, whereas a space is inserted after NGC.
The eighty-eight constellations have been assigned official names by the IAU. Many bright stars within these constellations have traditional names (Sirius, Canopus, Castor, and Pollux), though astronomers tend to favour the Bayer letter system, in which Greek letters are allotted in alphabetical order by brightness as seen from Earth. The letter can be written in full or using the Greek character, and is used in combination with a three-letter roman abbreviation (no point) assigned by the IAU, so in the constellation Centaurus, for example, the brightest star is written as Alpha Centauri, Centauri, or Cen. The genitive form of the constellation name is used (Orionis not Orion), both capitalized when in full form (Beta Crucis). An alternative designation is the Flamsteed system, which uses a number and the constellation abbreviation (61 Cyg, 58 Ori).