Information Theory
Pascal Wallisch
We used the assumption that a neuron encodes any relevant stimulus parameters by modifying its firing rate to construct tuning curves describing this stimulus encoding. But a neuron could also encode a stimulus by changing the relative timing of its spikes. In this chapter we will introduce the methodology used in a series of papers by Richmond and Optican exploring temporal encoding in a primate visual area. They used principal components analysis and information theory to argue that a temporal code provided more information about the stimulus than a rate code did. You will apply similar methodology to data recorded from the primate motor cortex. Note that this chapter assumes familiarity with principal components analysis.
Keywords
motor cortical data; spike density; probability distribution; joint probability distribution; bias; shuffle correction
20.1 Goals of this Chapter
Thus far, we have assumed that a neuron encodes any relevant stimulus parameters by modifying its firing rate. We used this assumption to construct tuning curves describing this stimulus encoding. But a neuron could also encode a stimulus by changing the relative timing of its spikes. In this chapter we will introduce the methodology used in a series of papers by Richmond and Optican exploring temporal encoding in a primate visual area. They used principal components analysis and information theory to argue that a temporal code provided more information about the stimulus than a rate code did. You will apply similar methodology to data recorded from the primate motor cortex. Note that this chapter assumes familiarity with principal components analysis introduced in Chapter 19.
20.2 Background
Richmond and Optican studied pattern discrimination in a primate visual area, the inferior temporal (IT) cortex. They addressed the question of temporal coding in IT in a well-known series of papers in the Journal of Neurophysiology (Optican and Richmond, 1987; Richmond and Optican, 1987; Richmond et al., 1987). They found that the firing rate of IT neurons modulated in response to the presentation of one of 64 two-dimensional visual stimuli. They also saw evidence of temporal modulation that was not captured by the firing rate.
To quantify the relevance of this temporal modulation, Richmond and Optican converted the raster plot for each trial into a spike density function (defined later in Section 20.2.2). They then computed principal components (PCs) of these functions. They computed the mutual information between the stimulus and either the firing rates (rate code) or the first three PCs (temporal code). Their results indicated that the temporal code carried on average twice the information as the rate code.
20.2.1 Motor Cortical Data
In this chapter you will use a similar approach to examine encoding of movement direction in the primate motor cortex. You have already seen that motor neurons modulate their firing rate systematically depending on the direction of motion during a center-out task and that this modulation can be fit to a cosine-tuning curve. However, this analysis computed the firing rate over a coarse time bin (1 second). A tuning curve might predict a firing rate of 30 spikes per second for a preferred stimulus, but there are a lot of ways to arrange 30 spikes (each lasting 1–2 ms) over a 1-second time period.
When you use a rate code, you are implicitly assuming that there is no additional information contained in the relative timing of the spikes. This does not mean you assume there is no temporal variation. Instead, a rate code assumes this temporal variation is uninformative about the stimulus. For example, when you calculated a peri-stimulus time histogram (PSTH) centered on movement time in the preceding chapter, you saw the firing rate ramp up slowly 500 ms before movement initiation and ramp back down to baseline by 500 ms later. If each direction elicits this same temporal response scaled up or down, then the coarse rate code is appropriate. However, if the temporal response varies systematically across movement directions, then the rate code will ignore potentially useful information.
Figure 20.1 contains the raster plots (left) and PETHs (right) for unit #16 in the center-out dataset from Chapter 17 (available on the companion web site) recorded on electrode #19. The spike times are relative to the beginning of the instructed delay, where the peripheral target is visible but the animal is still holding on the center target. The responses to a preferred stimulus (135° or 180°) are similar; both show an increase in the firing rate about 500 ms after the target appears. However, the responses to an antipreferred stimulus (0° or 315°) are different; both show a transient increase in the firing rate in the first 100 ms followed by a marked depression for the following 900 ms. A rate code is unlikely to capture all the information in these responses.
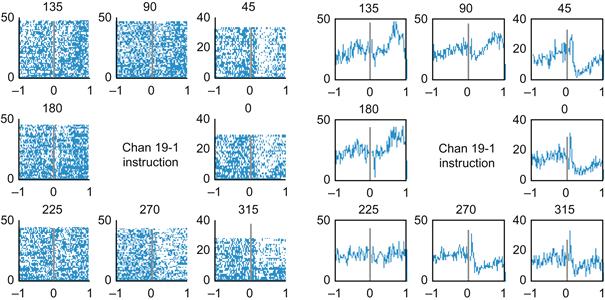
Figure 20.1 Left: A raster plot of the sample neuron. The x-axis is time in seconds, the y-axis is the trial number, and the title reflects the movement direction. Right: A peri-event time histogram for the same neuron. Here, the y-axis reflects the number of spikes in a 10 ms bin across all trials.
How do you quantify such temporal information? Principal components analysis might work. However, you first need to think about how to format the spike times. Binning the data seems natural, but choosing the proper bin size can be tricky. If the bin is too small (1 ms), then you may make your potential response space huge (21000 possible responses) compared to the number of trials. If the bin is too large (1 second), then you lose potentially useful temporal variations within the time bin. The best bin size is close to the order of the temporal dynamics you are interested in. If you observed consistent variations on a 50–100 ms time scale, a 50–100 ms time bin would probably work.
20.2.2 Spike Density Functions
Another problem with binning spike times is that binning can introduce artifacts into the data. Suppose a response to a stimulus always consists of a single spike around time t, and the variability from trial to trial follows a Gaussian distribution around t. If t sits right on an edge between two bins, then sometimes it will be counted in the first bin, and other times it will be counted in the second bin. This produces the illusion of a bimodal response when, in fact, there is only a single response.
An elegant solution to this problem is to convert each raster plot into a continuous spike density function. You first bin the spike times at a fine time resolution (1 ms) so that each bin has a 0 or 1. You then convolve this data with another function, called the kernel. The kernel captures how precise you think the spike times are: a wide kernel implies high variability, whereas a narrow kernel implies high precision.
You explored 2D convolution in Chapter 16; the 1D convolution function in the MATLAB® software is conv. Pay attention to the length of the resulting vector because conv(a,b) results in a function whose length is length(a)+length(b)-1. Suppose the kernel is a Gaussian function with a standard deviation of 15 ms. This is equivalent to putting a confidence interval on the spike times. This kernel means you believe that a neuron that wants to fire at 0 ms will actually fire at between −30 and 30 ms 95% of the time. To use this kernel in MATLAB, you need to evaluate the Gaussian over a range of time values (every 1 ms from −45 ms to 45 ms). If you convolve this function with 1 second of spike data (binned every 1 ms), the resulting vector will contain 1090 values. The corresponding time axis is −44 ms to 1045 ms. If you don’t want values outside the 1-second time period of interest, you just select the middle section. Load the dataset for this chapter, which contains data from the sample neuron in the variable trial. In the following code, binned spike data from the first trial are stored in binned and the spike density function is stored in s:
An example of a spike density function is shown in Figure 20.2, along with the original raster plot.
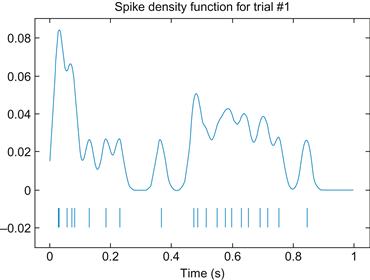
Figure 20.2 Top: An example of a spike density function using a Gaussian kernel with a standard deviation of 15 ms. Bottom: the original raster plot.
Once you compute spike density functions for each neuron, you can compute the principal components of the spike density functions. However, to avoid computing a 1000×1000 dimensional covariance matrix, you should first sample the spike density functions every 10 or 20 ms and then apply principal components analysis.
20.2.3 Joint, Marginal, and Conditional Distributions
The goal here is to compute the amount of information contained in a firing rate code compared to a temporal code (as captured by principal components). However, before defining “information” precisely, we need to review the concept of joint, marginal, and conditional probability distributions. For a discrete variable (which is all we will consider here), a probability distribution is simply a function that assigns a probability between 0 and 1 to all possible outcomes such that all the probabilities sum to 1. A joint probability distribution is the same, except it involves more than one variable and thus assigns probabilities to combinations of variables.
In this example, you have a stimulus S, which can take on one of eight discrete values. Suppose you divide the firing rates R of the same sample neuron from earlier into three bins (low, medium, and high firing rate). If you use the code below to count how many times each of 24 possible combinations shows up in the data, you end up with something like Table 20.1.
for ii=1:8 %Loop over all directions.
ind=find(direction==ii); %Find trials in same direction
%Bin firing rate R into low, medium, high
table(:,ii)=histc(R(ind),[0 19.5 30 100]);
end
From Table 20.1, it is clear that there is a relationship between the firing rate and stimulus direction. A high firing rate corresponds to a stimulus of 3, 4, or 5, while a low firing rate corresponds to a stimulus of 7, 8, 1, or 2. Remember that S=1 corresponds to a movement direction of 0°, S=2 to 45°, and so on. You can determine the observed joint probability distribution P(S,R) simply by dividing each count by the total number of counts (here, this is 315). In addition, you can compute the marginal probability distributions, which are the probability distributions of one variable computed by summing the joint probability distribution over the other variable:
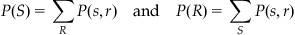(20.1)
Note that in these equations, S and R refer to all possible stimuli or responses, respectively, and that s and r refer to a particular stimulus or response.
Table 20.2 shows the values of P(S,R). The marginal distributions are listed in the last row and far right column because they are the sum taken across rows and across columns of the joint distribution.
Table 20.2
The Joint Probability Distribution P(S,R) and the Marginal Distributions P(R) and P(S) for the Sample Neuron
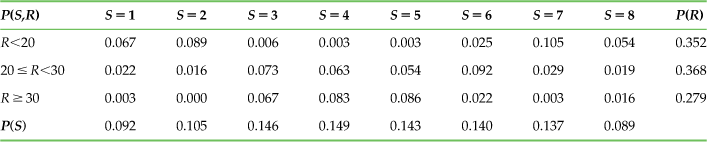
The last concept we need to address is the conditional distribution. The distribution of the response R given knowledge of the stimulus S is written P(R|S) and is defined as P(R|S)=P(S,R)/P(S). Likewise, the conditional distribution of S given R is P(S|R)=P(S,R)/P(R). As an example, what is the probability distribution of firing rates given a movement direction of 0° (S=1)? To find the answer, simply take the first column of values in Table 20.2, P(S=1, R), and divide by P(S=1) to get P(R|S=1). Hence, the probably of a low firing rate given S=1 is 0.067/0.092=0.73 and so on.
20.2.4 Information Theory
The foundation of information theory was laid in a 1948 paper by Shannon titled, “A Mathematical Theory of Communication.” Shannon was interested in how much information a given communication channel could transmit. In neuroscience, you are interested in how much information the neuron’s response can communicate about the experimental stimulus.
Information theory is based on a measure of uncertainty known as entropy (designated “H”). For example, the entropy of the stimulus S is written H(S) and is defined as follows:
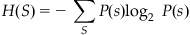(20.2)
The subscript S underneath the summation simply means to sum over all possible stimuli S=[1, 2 … 8]. This expression is called “entropy” because it is similar to the definition of entropy in thermodynamics. Thus, the preceding expression is sometimes referred to as “Shannon entropy.” The entropy of the stimulus can be intuitively understood as “how long of a message (in bits) do I need to convey the value of the stimulus?” For example, suppose the center-out task had only two peripheral targets (“left” and “right”), which appeared with an equal probability. It would take only one bit (a 0 or a 1) to convey which target appeared; hence, you would expect the entropy of this stimulus to be 1 bit. That is what the preceding expression gives you, as P(S)=0.5 and log2(0.5)=−1. The center-out stimulus in the dataset can take on eight possible values with equal probability, so you expect its entropy to be 3 bits. However, the entropy of the observed stimuli will actually be slightly less than 3 bits because the observed probabilities are not exactly uniform.
Next, you want to measure the entropy of the stimulus given the response, H(S|R). For one particular stimulus, the entropy is defined similarly to the previous equation:
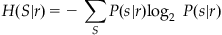(20.3)
To get the entropy H(S|R), you just average over all possible responses:
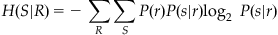(20.4)
Now you can define the information that the response contains about the stimulus. This is known as mutual information (designated I), and it is the difference between the two entropy values just defined:
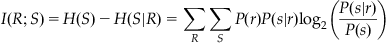(20.5)
Why does this make sense? Imagine you divide the response into eight bins and that each stimulus is perfectly paired with one response. In this case, the entropy H(S|R) would be 0 bits, because given the response, there is no uncertainty about what the stimulus was. You already decided the H(S) was theoretically 3 bits, so the mutual information I(R;S) would be 3 bits – 0 bits=3 bits. This confirms that the response has perfect information about the stimulus.
Suppose instead that you divide the response into two bins, and that one bin corresponds to stimuli 1–4 and the other bin corresponds to stimuli 5–8. Each bin has four equally likely choices, so the entropy H(R|S) will be 2 bits. Now the mutual information is I(R;S)=3 bits – 2 bits=1 bit. This means that response allows you to reduce the uncertainty about the stimulus by a factor of 2. This makes sense because the response divides the stimuli into two equally likely groups. This also emphasizes that the choice of bins affects the value of the mutual information.
Note that you can use the definition of conditional probability to rearrange the expression for mutual information. The following version is easier to use with the table of joint and marginal probabilities computed earlier. Mutual information can also be defined as follows:
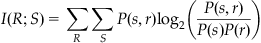(20.6)
Applying this equation to the joint distribution of the sample neuron gives a mutual information of 0.50 bits for a rate code.
20.2.5 Understanding Bias
Now we will try estimating the mutual information of an uninformative neuron. “Uninformative” means that the firing rate probabilities are independent of the stimulus probabilities. By the definition of independence, the joint probability distribution of two independent variables is the product of their marginal distributions P(R,S)=P(S)P(R). If you substitute this into the previous expression for mutual information, you will see the quantity inside the logarithm is always 1. Since log2(1)=0, this means the mutual information of two independent variables is also 0.
To make things easy, assume that each of the three responses is equally likely and that each of the eight stimuli is equally likely. Thus, P(R)=1/3 and P(S)=1/8, and each value of the joint probability distribution is the same: P(S,R)=1/24. The mutual information of this distribution is still 0 bits.
However, even if this is the true probability distribution, the observed probabilities would likely be different. You can simulate the values of observed probabilities with the following code. Here, you will simulate 24 random trials, so the expected count for each cell is 1:
| edges=[0:24]/24; | %Bin edges for each table entry |
| data=rand(24,1); | %Generate 24 random values between 0 and 1 |
| count = histc(data,edges); | %Count how many fall in the bin edges |
| count=count(1:24); | %Ignore the last value (counts values equal to 1). |
| count=reshape(count,3,8); | %Reformat the table. |
This might lead to the counts shown in Table 20.3.
Table 20.3
The Observed Counts of the Stimulus-Response Pairs for 24 Random Trials of an Uninformative Neuron
If you calculate the mutual information of the associated joint distribution (divide each count by 24 for the joint distribution), you get 0.50 bits, which is much higher than the 0.00 bits you expect. In fact, this is the same information as the sample neuron found previously. How can you now trust this earlier calculation?
Calculating mutual information directly from the observed probability distribution (as done here) leads to a biased estimate. A biased estimate is one that will not equal the true value, even if the estimate is averaged over many repetitions. The estimate of mutual information becomes unbiased only when you have infinite data. Such datasets are hard to come by.
However, all hope is not lost, because you can reduce the size of this bias. To start with, note that the number of trials is the same as the number of bins in the joint distribution. The sample data had 315 trials, which should reduce the chance of spurious counts. Repeating the previous exercise with 315 random trials might give the counts shown in Table 20.4.
Table 20.4
The Observed Counts of the Stimulus-Response Pairs for 315 Random Trials of an Uninformative Neuron
The mutual information calculating from this table’s joint distribution is now just 0.03 bits, which is much closer to the expectation (0 bits). This gives you more confidence in the 0.50 bits you estimated for the sample neuron. However, these numbers are each generated from a single random experiment. In the exercises you will see that repeated experiments confirm this trend: increasing the number of trials does decrease the bias of the estimate of mutual information.
Note that the relevant parameter is actually the number of trials per bin. This means that if you have 315 trials but you also have 315 bins, you will still have a significant bias. Therefore, you must choose the number of bins carefully. It seems that large bins throw away information (shouldn’t a spike count of 4 be treated differently than 16?), but smaller bins introduce a larger bias.
20.2.6 Shuffle Correction
These simulations are similar to a simple method (called shuffle correction) that corrects for the bias in the mutual information estimate. Suppose you store the stimulus values in a vector direction. You are interested in determining what the estimated mutual information would be if the firing rates were independent of the stimulus values. To do this, you randomly rearrange (or “shuffle”) the stimulus vector and then compute a new joint distribution and estimate mutual information from that. If you repeat this operation many times, you can derive a “null distribution” of mutual information estimates of a firing rate which carries no information. Thus, you can conclude that any neuron whose mutual information value that is significantly different from this null distribution is informative. You can also calculate a “shuffle corrected” mutual information estimate by subtracting the mean of this null distribution. The following code shows how you can shuffle the stimulus values in MATLAB:
| x=rand(315,1); | %Vector of 315 random numbers between 0 and 1 |
| [temp ind]=sort(x); | %Sort random numbers and keep the indices in vector "ind" |
| dirSh=direction(ind); | %Use "ind" to randomly shuffle the vector of stimuli |
Now you can compute a table counting combinations of the original firing rate and the shuffled stimulus. One example might be the one shown in Table 20.5.
Table 20.5
The Observed Counts of the Stimulus-Response Pairs for the “Shuffled” Version of the Sample Neuron
The mutual information of the associated joint distribution is 0.03 bits. Repeating the shuffling 30 times gives a mean information of 0.03 bits and a standard deviation of 0.01 bits for the null distribution. Hence, the “shuffle corrected” mutual information of the original neuron is 0.50 bits – 0.03 bits=0.47 bits. Thus, you can be confident that a rate code contains significant information about the stimulus direction.
Bias correction is particularly important when you are comparing mutual information of joint distributions that have different numbers of bins. In the project for this chapter, you will compare a rate code to a temporal code. Comparing a rate code to the first principal component is straightforward because you could use the same number of bins for each variable. However, if you use the n bins to look at the first principal components, you would have to use n2 bins to look at the first two principal components together using the same bin widths. As you know, increasing the number of bins increases the bias. If you compared uncorrected estimates, it would by easy to assume the second principal component provides additional information when it actually doesn’t.
It should also be noted that accurate estimation of information measures is an active research field and that shuffle correction is perhaps the simplest of available techniques. Refer to Panzeri et al. (2007) for a more recent review of bias correction techniques and to Hatsopoulos et al. (1998) for another example of the use of shuffle correction.
20.4 Project
Choose at least five active neurons from the dataset from Chapter 17, “Neural Data Analysis I: Encoding” (the sample neuron here is unit #16) available at the companion web site to analyze. Convert each raster plot into a spike density function. Report the details of the kernel you used. Calculate principal components (PCs) of the spike density functions. Calculate the shuffle-correction mutual information between the stimuli and, in turn, the firing rate, first PC score, and first and second PC score considered together.