Bioeconomics of Invasive Species

6
Estimating Dispersal and Predicting Spread of Nonindigenous Species

Jim R. Muirhead, Angela M. Bobeldyk, Jonathan M. Bossenbroek, Kevin J. Egan, and Christopher L. Jerde

In a Clamshell

The ability to estimate dispersal and the subsequent spread of nonindigenous species is important because preventative methods most readily apply to these stages of the invasion sequence. We address several methods used to calculate dispersal kernels for nonindigenous species, including natural movement, hydrological, aerial, and anthropogenic dispersal. In particular, we focus on gravity and random-utility models because they are suitable for modeling anthropogenic dispersal among spatially discrete habitat such as freshwater systems. We then address mechanisms of population spread and link dispersal kernels to models forecasting spread. We compare the merits and data requirements for different models of dispersal and population spread, and illustrate which models are best suited to deal with long-distance dispersal and heterogeneous habitat according to model assumptions. We also highlight the role of Allee effects on management strategies for invasive population spread where controlling population spread may be more effective when individuals in an invading population experience difficulty in finding mates, for example. Finally, we show how some of these models may be used as tools in making bioeconomic and management decisions in terms of risk assessment and risk management.

Invasions of aquatic ecosystems by nonindigenous species (NIS) are occurring at increasing rates in terms of both the number of novel species entering a system (Ricciardi 2006) and the cumulative number of systems or geographic areas that have been invaded (e.g., Veit and Lewis 1996; MacIsaac et al. 2004; Gilbert et al. 2005). NIS are also becoming increasingly important agents in altering ecosystem processes and contributing to the global homogenization of biodiversity (Crooks 2002; Rahel 2002; Olden et al. 2004). The best way to reduce the impacts of many species is to prevent their movement into uninvaded areas. Thus, the ability to accurately forecast spread enables prediction of high-risk areas and may lead to management strategies that contain or reduce spread.

NIS movement occurs during two stages of the invasion sequence: the initial transport of propagules from the native region, and secondary spread once populations become established in novel habitats (Kolar and Lodge 2001). Management efforts focusing on the initial transport of propagules (see chapter 1) are potentially easier and less costly than mitigation after the invasion has occurred because curbing species dispersal will likely have the greatest influence in determining establishment of the species (Leung et al. 2002; Jeschke and Strayer 2005). Through the identification of mechanisms, pathways, and spatially explicit invasion “hotspots,” management efforts become more feasible and cost-effective. For example, by distinguishing high-risk sites, forecasts can guide prevention or rapid response efforts that do not waste resources on low-risk sites. In addition, focusing on dispersal vectors allows for a management strategy applicable to multiple species transported by similar mechanisms as opposed to a strategy specific to each new NIS.

This chapter is divided into three sections: dispersal, spread, and risk management. Here, dispersal is defined as the process that describes the movement or redistribution of individuals from one place to another (e.g., Wiens 2001), and spread as the change in population density as a function of space and time. It is important to make this distinction between dispersal and population spread, because models of population spread implicitly address the additional invasion “filters” of habitat suitability and biotic integration into the recipient community (chapters 4 and 5). That is, at each step of the invasion sequence, only a subset of propagules are able to make the transition from the previous stage. First, we address methods used to collect data and to calculate dispersal kernels for different mechanisms such as animal movement or hydrological or anthropogenic dispersal. We define the dispersal kernel as the probability of an individual moving a specified distance from its last location per unit time, or the proportion of the population dispersed a specified distance within a time interval. In particular, we focus on two methods to describe the dispersal kernel for the anthropogenic transport of NIS, gravity and random-utility models, because they are suitable for modeling dispersal among spatially discrete habitat. Second, we address mechanisms of population spread and link dispersal kernels to models forecasting spread. For each section, we also compare the merits of different modeling approaches and data requirements for dispersal models and models of population spread. Finally, we highlight applications of these models for bioeconomic and management decisions in terms of risk assessment and risk management.

DISPERSAL

Dispersal is an essential component in organismal biology, affecting individual survival and reproduction as well as population- and ecosystem-level dynamics (Turchin 1998). Dispersal continues to be one of the most studied aspects of ecology and has been fundamental to works on island biogeography, metapopulations, and more recently, metacommunities (e.g., MacArthur and Wilson 1963; Hanski 1999; Leibold et al. 2004). Depending on the transport mechanism, dispersal patterns are often characterized by two overlapping modes: local and long-distance dispersal. Patterns of local dispersal are frequently observed when the organism disperses under its own power (e.g., walking). Here, range expansion proceeds continuously from the periphery of the population (Shigesada and Kawasaki 2002). Long-distance dispersal, on the other hand, is more of a passive process where the organism is transported by vectors such as water currents or wind or through interaction with human movement. In recent years, studies have recognized the importance of longdistance dispersal and have focused on its role in determining rates of spread and persistence of populations, the genetic structure of populations, and natural versus human-mediated vectors (e.g., Okubo 1980; Avise 1994; Suarez et al. 2001; Trakhtenbrot et al. 2005). Understanding long-distance dispersal of NIS is important because in both theoretical and empirical examples, long-distance dispersal events result in a change from linear to exponential rates of population spread (Lewis 1997). As a consequence, characterizing long-distance dispersal and predicting the location of future “satellite” colonies become increasingly difficult (Nathan et al. 2003).

Mechanisms involved in the introduction and subsequent dispersal of NIS can be divided into two major categories: natural and anthropogenic. An understanding of this distinction is necessary when addressing preventative measures of further spread or applying appropriate educational or legislative management efforts. However, several dispersal mechanisms may be operating simultaneously and interactively for many NIS, thus increasing the number of vectors that need to be assessed and the level of uncertainty involved when forecasting spread. In addition, dispersal mechanisms may have indirect effects that alter habitat invasibility. For example, as a byproduct of anthropogenic activity, the quality of habitat may also become stressed resulting in increased invasibility.

Natural Dispersal

Without human intervention, species may spread under their own power and by the aid of abiotic factors. Life history characteristics of NIS, such as individual mobility, pelagic larval stages, or the production of resistant resting eggs, lend themselves to natural dispersal. Chance abiotic events, such as wind storms or floods, also contribute to the natural dispersal of species across distances far greater than would be possible under individual mobility. Finally, the loss of a restrictive barrier (e.g., glacial ice sheet, waterfall) may allow species to invade a new environment.

Hydrologic Dispersal

Hydrologic pathways, such as rivers and streams (i.e., lotic systems), provide a natural mechanism for aquatic species to disperse into connected systems. For example, the veliger stage (planktonic larval stage) of zebra mussels (Dreissena polymorpha) has been widely recognized as a key factor in the invasion of entire river systems. After primary introductions, zebra mussel veligers drift through outflowing streams, colonizing downstream reaches and lakes (Horvath et al. 1996; Stoeckel et al. 1997; Bobeldyk et al. 2005). Similar dispersal has been documented for the waterflea (Daphnia lumholtzi) drifting downstream from invaded reservoirs (Shurin and Havel 2002). Even species without planktonic larval stages, such as rusty cray-fish (Orconectes rusticus), can spread naturally through lakes and stream corridors to invade other systems (Puth and Allen 2005).

In these systems, dispersal data can be obtained through mark-recapture studies or radiotelemetry tracking of individuals (table 6.1). Under the assumption that populations in lotic systems form along a one-dimensional strip of habitat, the dispersal kernel can then be fitted from the dispersal data of the tracked individuals (Lewis et al. 2006). Movements of the invasive signal crayfish (Pacifastacus leniusculus), for example, were tracked by radiotelemetry every 2 days (Bubb et al. 2004). The frequency distribution of movements upstream and downstream from the release location, as well as the total distance dispersed, was described by inverse power laws:

where m is the probability of a movement, x is the displacement from the release point, and c and n are fitted constants.

However, if the underlying shape of the dispersal kernel is unknown, the moment-generating function for the kernel is estimated from one-dimensional dispersal data:

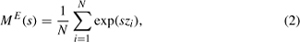
where s is the unknown slope, z_i is the observed individual dispersal, N is the number of individuals, and the superscript E refers to the empirical estimate of the moment-generating function (Lewis et al. 2006). A moment-generating function is unique to each dispersal kernel and is used to describe characteristics (i.e., moments) of the dispersal kernel such as the mean and variance in dispersal distance.

Alternatively, data on the movement of organisms may be collected such that the density of organisms (number per unit area) is recorded at distance intervals from the putative source. Horvath et al. (1996) recorded the density of zebra mussels in two streams in the St. Joseph River basin (Indiana and Michigan, USA) and found that density within the streams decreased exponentially with distance from invaded upstream lakes. In order to avoid bias due to the width of the stream or river when fitting the dispersal kernel, the density of organisms should be multiplied by the width of the stream and the dispersal kernel constrained so that the integrand is equal to 1 (Lewis et al. 2006).

Occasionally, data are in the form of frequency distributions, and the dispersal kernels are fit to histograms. Care should be taken with this approach because the width of the distance intervals may bias the shape of the dispersal kernel. More formally, the associated moment-generating function M^H(s) is represented as

TABLE 6.1. Examples of natural and human-mediated dispersal, and methods to collect data and estimate dispersal kernels.

where f_i is the bin height of the histogram for bin i, b_i and b_i−1 are the end points of bin i, L is the maximum number of bins in the histogram, and s as the unknown slope (Lewis et al. 2006).

Within a lake, diffusion of species through water currents will increase colonization rates of the entire lake. Hydrologic pathways can also assist in spreading aquatic plants, especially those with free-floating life forms, such as water hyacinth (Eichhornia crassipes) and aquarium water moss (Salvinia molesta). Even for submerged macrophytes such as water milfoil (Myriophyllum spicatum), dispersal occurs via advective transport of vegetative fragments (Madsen et al. 1988).

Animal-mediated Dispersal

Animal-mediated dispersal has been shown to spread several taxonomic groups over long distances. Plant seeds, for example, have the potential to be transported in the digestive tract of animals such as white-tailed deer and waterfowl (DeVlaming and Proctor 1968; Myers et al. 2004). Waterfowl have also been shown to carry species such as snails and zooplankton on their feathers and feet (Boag 1986; Green and Figuerola 2005). Fish may also act as dispersal agents by moving to a new environment after consuming species that can withstand gut passage. For example, the diapausing eggs of the invasive spiny waterflea (Bythotrephes longimanus) have been shown to survive passage through fish guts (Jarnagin et al. 2000). As with hydrological dispersal, models of animal-mediated dispersal may be parameterized by collecting data through mark-recapture or radiotelemetry (table 6.1).

Aerial Dispersal

Advective transport by air currents or gusts of wind is another dispersal mechanism for some NIS, even aquatic ones. Unlike dispersal via water currents, species that disperse aerially can move outside of closed systems and into new environments and are thus not limited to downstream movement. For example, small species such as zooplankton that have desiccation-tolerant resting stages can be carried by the wind outside of isolated aquatic environments. Although ample anecdotal evidence exists for wind-mediated species dispersal, manipulative studies necessary to calculate dispersal rates are rare (but see Cáceres and Soluk 2002; Skarpaas et al. 2005). Most studies have shown that zooplankton, especially rotifers, are capable of aerial transport but that dispersal events are infrequent and limited to a few species and that dispersal and colonization potential differ among different zooplankton species (Cáceres and Soluk 2002). As an example, in all samples of a year-long study, only four species of rotifers from regionally available zooplankton species were collected from rain and wind samples, and all were within 1 km of the source body of water (Jenkins and Underwood 1998). For aquatic species, one consequence of wind dispersal is that lower densities of species disperse and colonize new systems than if dispersed through hydrologic pathways. Seeds from aquatic macrophytes carried by the wind, for example, have a lower chance of successfully colonizing new habitats than if dispersed through streams (Soons 2006).

Aerial dispersal of organisms is frequently estimated by collecting data on the density of individuals or on measured dispersal of propagules. For insects, mark-recapture methods based on pheromone traps provide an empirical measure of the mean number of recaptures as a function of distance from release (table 6.1). For example, Turchin and Thoeny (1993) fit a two-parameter exponential distance decay function to the number of insects as a function of distance from the release source:

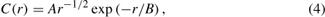
where C(r) is the number of recaptures as a function of the radial distance from the point of release, r, and A and B are the fitted parameters.

Greene and Johnson (1989) were able to describe the dispersal of winged seeds based on a ballistic formulation. The resultant dispersal from a point source using the geometric mean and variance of wind speed in the downwind direction, u_g and σ_x, release height H, and falling speed W_s is described by

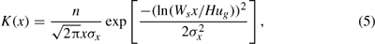
where n is total seed production. Jung and Croft (2001) used this model to parameterize mite dispersal with measurements of falling speeds in a greenhouse.

Anthropogenic Dispersal

Anthropogenic dispersal of NIS can result in the transport of propagules at a faster rate and greater distance beyond their native range than they could otherwise achieve (Wonham et al. 2000; Mack and Lonsdale 2001; Hebert and Cristescu 2002). As a result of this rapid transport, propagules often have a greater chance of surviving the trip. For example, both transoceanic ships and ships that remain in the Laurentian Great Lakes make multiple stops for unloading and loading cargo at several ports within the Great Lakes. Many of these ships unload cargo in Lake Erie and Lake Ontario and take on ballast water at these locations for stability. These ships then proceed to Lake Superior ports, where ballast water is pumped out and cargo is picked up for the return trip. As a result, biotic exchange of NIS among the Great Lakes occurs on the order of days, orders of magnitude faster than would be possible under the intrinsic dispersal abilities of the species.

The spread of the pathogen Phytophthora ramorum, which causes sudden oak death, is a well-documented example of human-mediated dispersal. This pathogen was first reported in central California in 1995 (Garbelotto et al. 2001) and has since been transported long distances from infested nurseries via commercially important hosts susceptible to disease (e.g., oak saplings, rhododendrons), in addition to local dispersal.

FIGURE 6.1.
Exponential dispersal kernel fitted to distances recreationalists traveled in Ontario (z) after visiting a lake invaded by the spiny water flea (Bythotrephes longimanus). The histogram and fitted dispersal kernel, k(z) = 0.005 exp (−0.005 z), have been scaled so that ∫ k(z)dz = 1.

Two methods well suited for modeling human-mediated dispersal of propagules are gravity models and random-utility models. In both cases, the dispersal kernel is modeled on overland human-mediated transport and describes the distribution of trip distances across a landscape or a road-based network (figure 6.1). Both methods are applicable for modeling dispersal of aquatic NIS, because lakes may be considered to be discrete patches in a heterogeneous landscape. Like advective flow through rivers or streams, overland human-mediated dispersal is constrained to a network composed of one-dimensional segments.

Gravity Models

A common tool for modeling spatial interaction is a gravity model, which is used to describe how the influences of distances and the “mass” or attraction of origins and/or destinations affect the flow of people (Thomas and Huggett 1980; Roy and Thill 2004). The attractiveness of a location can be described as the property that creates an incentive for trips to be made to that location. The simplest formulation of a gravity model is

where T_ij is the interaction between locations i and j, k is a constant, A_i and B_j define the propulsion from the origin and the attraction to the destination, respectively, c_ij is the distance between i and j, and α is a distance coefficient, or distance-decay parameter, which defines how much of a deterrent distance is to interaction. In a transportation context, A_i and B_j can be described as the number of individuals leaving and arriving at particular locations.

Gravity models can be used in heterogeneous landscapes, can incorporate various dispersal kernels, and are based on known transport mechanisms. The cognitive process of humans in making decision about where they travel is incorporated into gravity models. These models are also spatially explicit because they model flow from specific origins to destinations and thus enable the incorporation of large GIS databases as data sources for model parameterization and prediction. In addition, gravity models are created with an assumption that the specific perception of what is attractive to humans is correct and is the dominant driving force in destination choice.

Although gravity models were initially developed for use in economics (Reilly 1931; Linneman 1966) and other social sciences (Zipf 1946), they have more recently been used to predict the spread of diseases such as influenza (Viboud et al. 2006), plant pathogens (Ferrari et al. 2006), and NIS. The first published use of a gravity model to successfully assess the risk of human-mediated transport of an NIS was by Schneider et al. (1998), who used a doubly constrained gravity model to predict the rank order in which inland lakes and reservoirs of Illinois were expected to become invaded. Their concern was to predict the threat posed by zebra mussels to the native mussel communities of these water bodies. A doubly-constrained gravity model is used when information is known about the number of individuals leaving and arriving at each destination. In general, Schneider et al. (1998) predicted that those water bodies with high boat use and close to sources of zebra mussels were the most likely to become invaded with zebra mussels. An assessment of the predictions from this study shows that only 2 of the 55 lakes that were assessed are now invaded by zebra mussels. These lakes were predicted to be the first and the 52nd lakes to become invaded, suggesting a re-evaluation of the risk to these lakes is necessary. Since this publication, several additional lakes have become infested in Illinois, but most are in the greater Chicago area and close to Lake Michigan—a major source of zebra mussels.

Gravity models have been successfully used to model rare, long distance disperal events. For example, the discovery of the zebra mussel congener, the quagga mussel (Dreissena bugensis (= D. rostriformis bugensis [Andrusov (1897)])), in Lake Mead identifies the relevance of this type of modeling and the likelihood of such events since it is almost certain that human-mediated transport was responsible for its introduction and not transport through connected waterways.

Gravity models have also been used to assess human-mediated movement of terrestrial NIS such as the emerald ash borer (Agrilus planipennis) (Muirhead et al. 2006; Iverson et al. in press). The emerald ash borer is an invasive beetle from China that rapidly kills the native ash tree species of North America. It was first discovered in North America in the summer of 2002 and since has spread from its point of introduction, Detroit, Michigan, to much of the lower peninsula of Michigan, and to southwestern Ontario and northern Ohio. This species can disperse by flight, but most movement is less than 1 km and only 1% travel farther than 4 km in a 24-h period (Taylor et al. 2004). Thus, the rapid spread of the emerald ash borer suggests that human-mediated dispersal, such as the movement of firewood by campers, or the movement of ash products for use in landscaping, has been important (figure 6.2). Both Muirhead et al. (2006) and Iverson et al. (in press) demonstrate the importance of considering long-distance spread when predicting the overall dispersal rate of the emerald ash borer. Additionally, Iverson et al. (in press) specifically predict the relative risk of campers moving wood from the core area of emerald ash borer infestation to campgrounds across Ohio (figure 6.2).

The initial uses of gravity models were either untested in their predictions (e.g., Schneider et al. 1998) or parameterized based on their ability to recreate known patterns or distributions of an invasion (e.g., Bossenbroek et al. 2001). These analyses, however, did not assess whether the model predictions were accurately simulating the mechanism behind the patterns. Leung et al. (2006) compared the results of a production-constrained gravity model to four different metrics of human movement behavior based on angler activity records and a mailed survey developed specifically for that project. Leung et al. (2006) found that gravity models were able to simulate the mechanism of long-distance zebra mussel transport, i.e. the movement of recreational boaters.

Gravity models used in invasion biology have mostly been used to assess the likelihood that an NIS will be transported to a particular location. These models have not included biological attributes of the NIS, such as colonization or reproduction potential. Leung et al. (2004), however, were able to use the gravity model framework to demonstrate that zebra mussels are subject to Allee effects within their invaded range in North America. Likewise, Leung and Delaney (2006) demonstrated that spread can be estimated with limited data sets, particularly when propagule pressure is accounted for. Leung et al. (2004) and Leung and Delaney (2006) show the importance of accounting for population dynamics at early stages of an invasion when modeling patterns of dispersal.

FIGURE 6.2.
Relative risk of an introduction of emerald ash borer to Ohio campgrounds due to higher attractiveness and/or travel from the core area in southern Michigan infested with emerald ash borer, based on a gravity model.

The next steps in the development of gravity models for use in risk assessment require the inclusion of NIS population dynamics such as growth rate and mortality and more rigorous assessments of uncertainty (see chapter 7). This would enable gravity models to serve as a bridge from describing dispersal of individual propagules to describing population spread of NIS at a landscape level (Jerde and Lewis 2007). For example, models describing population growth can be coupled with gravity models describing immigration and emigration among systems, in a manner analogous to metapopulation models.

Random-Utility Models

An alternative to the gravity model for estimating the human-mediated movement of organisms is the random-utility maximization (RUM) model. This is the most widely used modeling framework for economists estimating the recreation demand of various sites. An advantage of RUM models over gravity models is that they explain more fully the individual economic behavior driving decisions by humans of where to recreate. The primary reason for moving away from gravity models is the necessity to include travel costs so that a demand function can be estimated and utilized in the calculation of benefit values for cost-benefit analysis. Travel costs in a RUM model (and all other models in recreation demand) incorporate road infrastructure, population centers, and varying attainable speeds. Included are out-of-pocket expenses from traveling to the site, such as the cost of gasoline and vehicle value deprecation, and the value of time during transit (i.e., opportunity cost of time).

Once travel costs are estimated for each individual to each site in the choice set, a demand function for each site is recoverable, where the number of trips taken to the site and travel costs are inversely related (i.e., individuals choose fewer trips to a site as it becomes more expensive per trip). Benefit values are easily recoverable from the demand functions (for an overview, see Corrigan et al. in press). For example, if one wanted to estimate the benefits from the reduced spread of an NIS by human-mediated movement, a RUM model is suited to this task, whereas the gravity model is a statistical allocation model that does not include estimates of individual economic benefits (Bockstael et al. 1986). Moreover, even if the goal is only the prediction of spread, the RUM model will most likely be superior, due to the more complete modeling of the individual’s decision making.

One particular advantage of RUMs is that they model individual-level trips instead of aggregate zonal trips. With the current state-of-the-art RUM, the repeated mixed logit model, the individual makes repeated choices of which sites to visit. In economics, utility is a measure of the relative satisfaction or desiredness from the consumption of goods. Given this measure, one may speak meaningfully of increasing or decreasing utility and thereby explain economic behavior in terms of attempts to increase one’s utility. The assumption is that individuals visit the sites that give them the most utility, constrained by their income and time to recreate. The RUM model assumes the utility of individual i choosing site j on choice occasion t is of the form

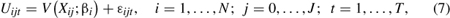
where V represents the observed portion of utility, and from the perspective of the researcher, ε_ijt represents the random, unobserved portion of utility (hence the name “random-utility model”). The observed portion of utility is a function of explanatory variables, X_ij, such as travel costs, site characteristics (e.g., lake size), and household characteristics; and β_i is the estimated parameters on the explanatory variables, where these parameters are routinely allowed to vary across the population of individuals, allowing for substantial heterogeneous trip-taking behavior (hence the random effect leading to the mixed model).

Conditional on knowing β_i, the probability that individual i chooses alternative j on choice occasion t is defined as

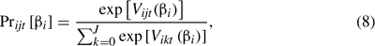
and the unconditional probability can be obtained by integrating the conditional probability over all possible values of β_i and then using maximum simulated likelihood to estimate the parameters (Train 2003). For the modeling of the human-mediated movement of organisms, it is convenient that RUM models estimate a trip probability (i.e., dispersal kernel) for each individual to each site. These estimated trip probabilities can easily be augmented with additional data on the biological attributes of the destination site concerning their candidacy for the accidentally transported NIS (Macpherson et al. 2006), as well as including biological attributes of NIS that may facilitate dispersal, such as the production of resistant resting stages by zooplankton or vegetative reproduction in plants.

While Macpherson et al. (2006) discuss a simulation exercise with a dynamic RUM model, no papers to date have applied the RUM model to the spread of invasive species with actual data, not even a simpler static model. This emphasizes the downside of utilizing RUM models—the more intensive data requirements, because individuals must be surveyed about which sites they visit and how often, along with other information such as their income. However, in the case of zebra mussels, Leung et al.’s (2002) high estimates of the partial economic costs from the spread of zebra mussels indicates the extra data collection costs would be worth undertaking to better predict NIS spread based on a more accurate modeling of boaters’ recreation activity.

POPULATION SPREAD

The development of spatial models for the spread of NIS has a long history starting with diffusion theory and gas kinetics in physics and chemistry. In the biological literature, dispersal models have been developed for a wide range of applications, including gene flow (Fisher 1937), spread of and susceptibility to infectious diseases (Kendall 1957; Noble 1974), predator–prey dynamics (Okubo 1980), and aerial dispersal of fungal spores (Aylor 2003; see also reviews in Higgins and Richardson 1996; Hastings et al. 2005).

The application of these modeling approaches to forecasting NIS spread is a logical extension, and the choice of a particular model depends on the type of information available (Shigesada and Kawasaki 1997). For many invasions, species presence/absence data may be the only information available from historical records. With this scenario, pattern-based, or spatial-phenomenological, models (using the terminology of Higgins and Richardson 1996) can be used to forecast range expansion (or, in economic terms, expanding the extensive margin). These types of models assume that the location of the invasion wavefront corresponds to the location of first recording, and forecast rates of spread are generally equivalent to past spread rates. These models are more applicable to terrestrial systems at regional spatial scales than to the discrete habitat of aquatic systems, and do not incorporate the ecology of the species or recipient habitat in predictions. As with many dispersal models, there is also the assumption that sampling effort is sufficient to detect the species if present beyond the invasion wavefront—otherwise, rates of spread would be underestimated. An example of a phenomenological invasion model is the spread of Mimosa pigra in Australia (Lonsdale 1993). Mimosa pigra is an invasive shrub that has been identified as one of the 100 worst invaders in the world by the Global Invasive Species Programme. The area invaded by M. pigra was positively related to the time of occurrence extracted from historical records and aerial photographs. Future spread was then predicted assuming that the rate of spread remains constant and expansion occurs similarly in all directions.

In contrast to the spatial-phenomenological class of models, patterns of spread from process-based or mechanistic models can be forecast using information on the ecology of NIS or properties of the transport mechanism. One of the first forms of a process-based approach is a reaction-diffusion (RD) model that predicts population density as a function of space and time. Reaction-diffusion models describe exponential or logistic population growth that diffuses randomly across homogeneous space (Okubo 1980). Population spread assuming exponential growth in a two-dimensional environment is represented as

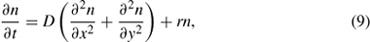
where n is the population size, r is the intrinsic per capita population growth rate, and D is the diffusion coefficient (distance²/time) for propagules dispersing in x and y directions. Here, distances that individuals disperse from a source are assumed normally distributed, with corresponding directions uniformly distributed from 0 to 360° (i.e., isotropic). The resulting pattern of population spread forms a series of concentric circles spreading away from the source through time. The diffusion coefficient D is often measured using mark-recapture data, for example, and can be estimated by

where x is the distance from the marking site, m is the number of marked individuals released, and t is the time since marking (Lockwood et al. 2007).

For marine or aerial dispersers, the basic diffusion model may be modified to include advective flow due to water or air currents. Two-dimensional spread in these systems is described by

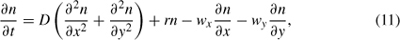
where w_x and w_y describe velocity down x- and y-axes, and other terms in the model are as in equation 9 (Holmes et al. 1994). Here, dispersal distances are also assumed to follow a normal distribution, but spread is not isotropic.

In one-dimensional RD models, the location of the invasion wavefront is expected to travel away from the epicenter at a constant rate of 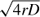, where r is the intrinsic rate of population increase and D is the diffusivity coefficient, providing population density is sufficient for detection. This, however, holds true only when the dispersal kernels reach an asymptote at large distances (e.g., exponential decay). For fat-tailed dispersal kernels, the velocity of the wavefront increases through time.

In addition to assumptions about the homogeneity of space and random dispersal, this class of models assumes continuous reproduction and dispersal through time and that there is no finite border limiting geographic spread.

Reaction-diffusion models have been successfully applied to describing secondary spread for a number of species. Skellam’s (1951) assertion that the European range expansion of muskrats followed a linear rate of increase as predicted from an RD model is generally supported by the observed spread of this species. Predicted rates of range expansion of the small cabbage white butterfly, Pieris rapae, based on estimates of intrinsic rates of increase and survivorship fit with observed expansion rates in North America (Andow et al. 1990). However, in the same study, predicted rates of spread of the cereal leaf beetle, Oulema melanopus, from diffusion models were underestimated by at least two orders of magnitude. The authors suggested that other mechanisms, such as human-mediated dispersal or advection in air currents, were responsible for long-distance transport. Current patterns of O. melanopus spread in the United States are consistent with “stratified diffusion” (Hengeveld 1989), in which spread proceeds by a combination of local and long-distance dispersal events (Shigesada et al. 1995). These long-distance dispersal events appear to be important in determining both the speed of the invasion and the variability in population density at the invasion wavefront.

Although RD models that assume a continuous landscape have been successful for predicting geographic range extensions (e.g., Hengeveld 1989), they are limited in their applicability to heterogeneous systems. Consequently, spatially discrete RD models have been developed that convert a continuous landscape into a lattice of grid cells representing suitable and unsuitable habitat (e.g., Flather and Bevers 2002). In the Flather and Bevers (2002) model, individuals of a hypothetical species dispersed from one habitat cell to another with distances according to a Weibull distribution and with uniformly distributed directions. Habitat amount relative to habitat arrangement was key to the overall regional population size. No studies to date, however, have applied this method to predict NIS spread, although it seems like a promising approach for terrestrial species.

The limitations of RD models for predicting the spread of aquatic invasive species were first highlighted with zebra mussels. Buchan and Padilla (1999) attempted to fit an RD model to the spread of zebra mussels in the State of Wisconsin. They determined that due to the heterogeneous nature of the landscape and the need to understand the mechanism of dispersal (in this case, recreational boaters), RD models were not sufficient for this system. Due to the limitations of RD models, researchers have developed more sophisticated statistical methods for dealing with long-distance dispersal (see below) and have adapted techniques from geography and economics to model different mechanisms of dispersal (see “Dispersal,” above).

Several modeling approaches have been developed to forecast range expansion without the restrictive assumptions underlying RD models. Integrodifference (ID) models (e.g., Kot et al. 1996; Veit and Lewis 1996; Krkošek et al. 2007) have two primary advantages over RD models: (1) they estimate dispersal of individuals according to their life stage at discrete time intervals, and (2) they are flexible due to their use of non-Gaussian dispersal kernels. The shape of the dispersal kernel can be fitted to data from mark-recapture experiments and include rare, long-distance dispersal events observed with invasive spread (i.e., leptokurtic, or “fat-tailed” dispersal kernels; Kot et al. 1996). With flowering plants, for example, seeds are the primary dispersing stage transported by vectors such as wind, water, and animals. Sensitivity analysis on the contribution that each life stage provides to the overall rate of spread may then guide management efforts (Neubert and Caswell 2000). Like their RD counterparts, basic ID models assume a homogeneous landscape and that population growth and dispersal are the same at each point in space. Consequently, they are better suited for aerial or terrestrial invasions than for aquatic invasions, which occur across a matrix of habitat suitability. In ID models, population density at time t + 1 and location x is represented as

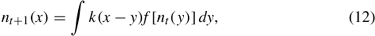
where n is population size, t is time interval, k is the dispersal kernel for displacement from y to x, and f (n_t) describes population growth as a function of population size in the previous time step at location y.

Population-based models such as the RD or ID equations have been adapted for scenarios when propagules of the NIS are first introduced into a novel habitat and mate location is difficult due to low population size. As a result, the population experiences reduced or negative growth rates at low density, called Allee effects, which then translate to fewer individuals able to undergo secondary spread. In theory, Allee effects may serve as an alternate mechanism to explain increasing rates of spread as a contrast to long-distance dispersal events, because Allee effects may cause a lag in the initial stages of secondary dispersal (Kot et al. 1996). Allee effects have been shown to be present for the invasive weed smooth cordgrass (Spartina alterniflora; Davis et al. 2004) and zebra mussels (Leung et al. 2004) and have been modeled for several organisms, including the plant pathogen Tilletia indica (Garrett and Bowden 2002), the house finch (Carpodacus mexicanus; Veit and Lewis 1996), and the gypsy moth (Lymantria dispar; Liebhold and Bascompte 2003). In the latter study, the authors suggest that 100% eradication of the species may not be necessary as long as the population density is reduced to a threshold below which Allee effects will cause the population to crash.

MANAGEMENT GUIDANCE

Historically, dispersal models have been used to describe the patterns and processes by which organisms colonize novel habitat (Shigesada and Kawasaki 1997), but these models are increasingly being used to predict locations likely to become invaded (e.g., Leung et al. 2004; Bossenbroek et al. 2007) so that monitoring and control actions can be implemented. However, success in predicting biological invasions has been limited, and Gilpin (1990) advocates a probabilistic approach for predicting biological invasions. That is, the probability of a prescribed undesired effect (i.e., biological invasions) is by definition risk (Suter 1993). Risk analysis involves estimating probabilities of invasion, while management activities involve deciding how to respond to each risk. Together, risk analysis and risk management form a risk assessment approach to biological invasions (Suter 1993). The development of spread and dispersal models provides a useful framework in estimating the risk of invasion and evaluating management decisions (Leung et al. 2002).

Risk analysis has a variety of modeling approaches (Suter 1993). Each of the models discussed in this chapter represent a different approach that is more or less suited for predicting the dispersal of an NIS, depending on the mechanisms of dispersal, the environment the organism is being introduced into, the life history of the organism, the risk assessor’s understanding of these processes, and the data available to parameterize the models (Stohlgren and Schnase 2006). In general, the goal of risk analysis for a single species is to predict when and where the species is likely to invade (MacIsaac et al. 2004; Bossenbroek et al. 2007) and report the probability associated with an invasion event (Jerde and Lewis 2007).

Management efforts will change depending on whether the goal is to stop the initial dispersal of propagules into a new habitat or to contain a spreading population. In the first scenario, risk management involves a preventative approach and relies on some knowledge of the dispersal mechanisms. In this chapter, we have shown that it is possible to assess the risk of one destination being invaded relative to another. The models discussed can thus be used to prioritize the location of investments in NIS prevention. For containing a spreading population, transport mechanisms also should be considered, but management efforts may be focused on restricting the outbound flow of propagules through quarantine or other methods. Modeling the patterns of population spread also may indicate that novel management decisions are optimal. Sharov and Liebhold’s (1998) model for spread reduction of the gypsy moth (Lymantria dispar), for example, suggests that the optimal method for reducing the rate of spread is to eliminate satellite colonies outside the expanding population front.

Leung et al. (2002) provide a general risk management framework that links risk analysis to an economic model and uses stochastic dynamic programming to evaluate the costs and benefits of management actions (chapter 9). This framework requires estimating the probability of invasion, evaluating the costs of an invasion and management actions, and measuring the reduction in the probability of invasion from the different management actions (Stohlgren and Schnase 2006). An overview of the process of valuing market and nonmarket costs of invasion is discussed in chapter 8. From the management framework, connecting models of dispersal and spread to risk management rests on the risk analysis and the potential changes in the probability of invasion due to management actions (Leung et al. 2002).

Although predicting invasions through modeling is gaining popularity, more attention should be paid to communicating results, and especially to connecting risk analyses to management (Bossenbroek et al. 2005). The main problems are the lack of reporting probabilities, and failure to report the type of model used to estimate the probabilities (Nelson et al. 2007). One common approach to communicating risk is to rank order locations from greatest risk to least risk for invasion (e.g., Schneider et al. 1998; location A is more likely to be invaded than location B under the assumption that the sites are independent). Alternatively, it may be possible to estimate the relative risk of invasion, where the relative risk is a ratio of invasion probabilities for two locations (e.g., Herborg et al. 2007; location A is 10 times more likely to be invaded than location B). While both rank orders and relative risk measures are formulated from probabilities and represent a risk analysis, they do not directly communicate the probability of invasion needed to apply risk management as proposed by Leung et al. (2002). Therefore, it is unclear if ranked and relative risk measurements provide sufficient information to make risk management decisions (Nelson et al. 2007; see also chapter 7). For some systems, it may be necessary, due to data limitations, and reasonable, given simplifying assumptions, to apply relative risk estimators to perform a risk analysis (Jerde and Lewis 2007), and the use of ranks and relative measures may be useful for sampling design and monitoring. As discussed, however, this needs further development and careful interpretation.

Risk management includes evaluating the potential influence of management actions on reducing the invasion probability (Suter 1993; Leung et al. 2002). Experiments that estimate this influence are undoubtedly useful but may be costly. Alternatively, models of dispersal and spread can be analyzed using sensitivity analysis. Sensitivity analysis evaluates how perturbations of model parameters influence the probability of invasion (Suter 1993). Small changes in model parameters may substantially change the calculated probability of invasion. Identifying which parameters contribute most to reductions in the probability of invasion may provide insights into the effectiveness of management actions that aim to reduce invasion risk.

CONCLUSIONS

The ability to quantify dispersal and population spread is a key component in NIS management because reductions in species dispersal can reduce the likelihood of species establishment. A strength of dispersal models such as gravity and RUM models is their flexible modeling framework. Both of these model types are well suited for anthropogenic dispersal and can provide a mechanistic basis for multiple dispersal vectors, in general. RUM models are further refined than are gravity models, because RUM models take into consideration an individual’s behavior in terms of minimizing economic costs. Current challenges for gravity and RUM models are to quantify the actual propagule pressure of NIS for various dispersal mechanisms and to tie in NIS dispersal with models of habitat suitability and biological resistance to invasions.

For models of population spread, strengths of ID models include being able to incorporate non-Gaussian distribution kernels and being able to be tailored for species in which particular life stages are dispersed. One challenge is to apply models of NIS spread to heterogeneous environments such as networks of lakes and streams, islands, or corridors in a terrestrial landscape.

Models of dispersal or population spread are able to guide management depending on whether the goal is to predict and prevent new invasions or to control established NIS populations. For predicting and preventing new invasions, model predictions, when developed using historical abundance or presence/absence data, can then be cast into a probabilistic framework for use in risk analysis. For curtailing the spread of established populations, these models can be used to identify an optimal management strategy when used as a basis for what-if scenarios.

Acknowledgments This chapter was substantially improved by the editors of this book and three reviewers. This material is based on work supported by the Integrated Systems for Invasive Species project (D. M. Lodge, principal investigator) funded by the National Science Foundation (DEB 02-13698). Support was provided by Ontario Graduate Fellowships (J.R.M.), the University of Notre Dame Center for Aquatic Conservation (A.M.B.), the U.S. Department of Agriculture Program of Research on the Economics of Invasive Species Management (J.M.B.), and a National Sciences and Engineering Research Council of Canada collaborative research grant to H. J. MacIsaac and M. A. Lewis (C.L.J.). This is publication 2009-02 from the University of Toledo Lake Erie Center.

References

Andow, D. A., P. M. Kareiva, S. A. Levin, and A. Okubo. 1990. Spread of invading organisms. Landscape Ecology 4:177–188.

Avise, J. C. 1994. Molecular markers, natural history and evolution. Chapman and Hall, New York.

Aylor, D. E. 2003. Spread of plant disease on a continental scale: role of aerial dispersal of pathogens. Ecology 84:1989–1997.

Boag, D. A. 1986. Dispersal in pond snails: potential role of waterfowl. Canadian Journal of Zoology 64:904–909.

Bobeldyk, A. M., J. M. Bossenbroek, M. A. Evans-White, D. M. Lodge, and G. A. Lamberti. 2005. Secondary spread of zebra mussels (Dreissena polymorpha) in coupled lake-stream systems. Ecoscience 12:339–346.

Bockstael, N. E., W. M. Hanemann, and I. E. Strand. 1986. Measuring the benefits of water quality improvements using recreation demand models. Report presented to the Environmental Protection Agency under cooperative agreement CR-811043-01-0. Washington, DC.

Bossenbroek, J. M., L. E. Johnson, B. Peters, and D. M. Lodge. 2007. Forecasting the expansion of zebra mussels in the United States. Conservation Biology 21:800–810.

Bossenbroek, J. M., C. E. Kraft, and J. C. Nekola. 2001. Prediction of long-distance dispersal using gravity models: zebra mussel invasion of inland lakes. Ecological Applications 11:1778–1788.

Bossenbroek, J., J. McNulty, and R. Keller. 2005. Can ecologists heat up the discussion on invasive species risk? Risk Analysis 25:1595–1597.

Bubb, D. H., T. J. Thom, and M. C. Lucas. 2004. Movement and dispersal of the invasive signal crayfish Pacifastacus leniusculus in upland rivers. Freshwater Biology 49:357–368.

Buchan, L. A. J., and D. K. Padilla. 1999. Estimating the probability of long-distance overland dispersal of invading aquatic species. Ecological Applications 9:254–265.

Cáceres, C. E., and D. A. Soluk. 2002. Blowing in the wind: a field test of overland dispersal and colonization by aquatic invertebrates. Oecologia 131:1432–1939.

Corrigan, J. R., K. J. Egan, and J. A. Downing. In Press. Aesthetic values of lakes and rivers. In G. Likens, editor. The encyclopedia of inland waters. Elsevier Science, London.

Crooks, J. A. 2002. Characterizing ecosystem-level consequences of biological invasions: the role of ecosystem engineers. Oikos 97:153–166.

Davis, H. G., C. M. Taylor, J. C. Civille, and D. R. Strong. 2004. An Allee effect at the front of a plant invasion: Spartina in a Pacific estuary. Journal of Ecology 92:321–327.

DeVlaming, V., and V. W. Proctor. 1968. Dispersal of aquatic organisms: viability of seeds recovered from the droppings of captive killdeer and mallard ducks. American Journal of Botany 55: 20–26.

Ferrari, M. J., O. N. Bjornstad, J. L. Partain, and J. Antonovics. 2006. A gravity model for the spread of a pollinator-borne plant pathogen. American Naturalist 168:294–303.

Fisher, R. A. 1937. The wave of advance of advantageous genes. Annals of Eugenics 7:355–369.

Flather, C. H., and M. Bevers. 2002. Patchy reaction-diffusion and population abundance: the relative importance of habitat amount and arrangement. American Naturalist 159:40–56.

Garbelotto, M., P. Svihra, and D. M. Rizzo. 2001. Sudden oak death syndrome fells 3 oak species. California Agriculture 55:9–19.

Garrett, K. A., and R. L. Bowden. 2002. An Allee effect reduces the invasive potential of Tilletia indica. Phytopathology 92:1152–1159.

Gilbert, M., S. Guichard, J. Freise, J. C. Gregoire, W. Heitland, N. Straw, C. Tilbury, and S. Augustin. 2005. Forecasting Cameraria ohridella invasion dynamics in recently invaded countries: from validation to prediction. Journal of Applied Ecology 42:805–813.

Gilpin, M. 1990. Ecological prediction. Science 248:88–89.

Green, A. J., and Figuerola, J. 2005. Recent advances in the study of long-distance dispersal of aquatic invertebrates via birds. Diversity and Distributions 11:149–156.

Greene, D. F., and E. A. Johnson. 1989. A model of wind dispersal of winged or plumed seeds. Ecology 70:339–347.

Hanski, I. 1999. Metapopulation ecology. Oxford University Press, New York.

Hastings, A., K. Cuddington, K. F. Davies, C. J. Dugaw, S. Elmendorf, A. Freestone, S. Harrison, M. Holland, J. Lambrinos, U. Malvadkar, B. A. Melbourne, K. Moore, C. Taylor, and D. Thomson. 2005. The spatial spread of invasions: new developments in theory and evidence. Ecology Letters 8:91–101.

Hebert, P. D. N., and M. E. A. Cristescu. 2002. Genetic perspectives on invasions: the case of the Cladocera. Canadian Journal of Fisheries and Aquatic Sciences 59:1229–1234.

Hengeveld, R. 1989. Dynamics of biological invasions. Chapman and Hall, New York.

Herborg, L.-M., C. L. Jerde, D. M. Lodge, G. M. Ruiz, and H. J. MacIsaac. 2007. Predicting invasion risk using measures of introduction effort and environmental niche models. Ecological Applications 17:663–674.

Higgins, S. I., and D. M. Richardson. 1996. A review of models of alien plant spread. Ecological Modelling 87:249–265.

Holmes, E. E., M. A. Lewis, J. E. Banks, and R. R. Veit. 1994. Partial differential equations in ecology: spatial interactions and population dynamics. Ecology 74:17–29.

Horvath, T. G., G. A. Lamberti, D. M. Lodge, and W. L. Perry. 1996. Zebra mussel dispersal in lake-stream systems: source-sink dynamics. Journal of the North American Benthological Society 15:564–575.

Iverson, L. R., A. Prasad, J. Bossenbroek, D. Sydnor, and M. W. Schwartz. In press. Modeling potential movements of an ash threat: the emerald ash borer. In J. Pye and M. Raucher, editors. Advances in threat assessment and their application to forest and rangeland management.

Jarnagin, S. T., B. K. Swan, and W. C. Kerfoot. 2000. Fish as vectors in the dispersal of Bythotrephes cederstroemi : diapausing eggs survive passage through the gut. Freshwater Biology 43:579–589.

Jenkins, D. G., and M. O. Underwood. 1998. Zooplankton may not disperse readily in wind, rain, or waterfowl. Hydrobiologia 338:15–21.

Jerde, C. L., and M. A. Lewis. 2007. Waiting for invasions: a framework for the arrival of non-indigenous species. American Naturalist 170:1–9.

Jeschke, J. M., and D. L. Strayer. 2005. Invasion success of vertebrates in Europe and North America. Proceedings of the National Academy of Sciences of the United States of America 102:7198–7202.

Jung, C. L., and B.A. Croft. 2001. Aerial dispersal of phytoseiid mites (Acari: Phytoseiidae): estimating falling speed and dispersal distance of adult females. Oikos 94:182–190.

Kendall, D. G. 1957. In discussion on Bartlett, M. S.: measles periodicity and community size. Journal of the Royal Statistical Society Series A (General) 120:48–70.

Kolar, C. S., and D. M. Lodge. 2001. Progress in invasion biology: predicting invaders. Trends in Ecology and Evolution 16:199–204.

Kot, M., M. A. Lewis, and P. van den Driessche. 1996. Dispersal data and the spread of invading organisms. Ecology 77:2027–2042.

Krkošek, M., J. S. Lauzon-Guay, and M. A. Lewis. 2007. Relating dispersal and range expansion of California sea otters. Theoretical Population Biology 71:401–407.

Leibold, M. A., M. Holyoak, N. Mouquet, P. Amarasekare, J. M. Chase, M. F. Hoopes, R. D. Holt, J. B. Shurin, R. Law, D. Tilman, M. Loreau, and A. Gonzalez. 2004. The metacommunity concept: a framework for multi-scale community ecology. Ecology Letters 7:601–613.

Leung, B., J. M. Bossenbroek, and D. M. Lodge. 2006. Boats, pathways, and aquatic biological invasions, estimating dispersal potential with gravity models. Biological Invasions 8: 241–254.

Leung, B., and D. G. Delaney. 2006. Managing sparse data in biological invasions: a simulation study. Ecological Modelling 198:229–239.

Leung, B., J. M. Drake, and D. M. Lodge. 2004. Predicting invasions: propagule pressure and the gravity of Allee effects. Ecology 85:1651–1660.

Leung, B., D. M. Lodge, D. Finnoff, J. F. Shogren, M. A. Lewis, and G. A. Lamberti. 2002. An ounce of prevention or a pound of cure: bioeconomic risk analysis of invasive species. Proceedings of the Royal Society of London Series B Biological Sciences 269:2407–2413.

Lewis, M. A. 1997. Variability, patchiness, and jump dispersal in the spread of an invading population. Pages 46–69 in D. Tilman and P. M. Kareiva, editors. Spatial ecology: the role of space in population dynamics and interspecific interactions. Princeton University Press, Princeton, NJ.

Lewis, M. A., M. G. Neubert, H. Caswell, J. S. Clark, and K. Shea. 2006. A guide to calculating discrete-time invasion rates from data. Pages 169–192 in M. W. Cadotte, S. M. McMahon, and T. Fukami, editors. Conceptual ecology and invasion biology: reciprocal approaches to nature. Springer, Dordrecht, The Netherlands.

Liebhold, A. M., and J. Bascompte. 2003. The Allee effect, stochastic dynamics and the eradication of alien species. Ecology Letters 6:133–140.

Linneman, H. V. 1966. An econometric study of international trade flows. North-Holland, Amsterdam.

Lockwood, J. L., M. F. Hoopes, and M. P. Marchetti. 2007. Invasion Ecology. Blackwell, Oxford.

Lonsdale, W. M. 1993. Rates of spread of an invading species—Mimosa pigra in Northern Australia. Journal of Ecology 81:513–521.

MacArthur, R. H., and E. O. Wilson. 1963. The Theory of Island Biogeography. Princeton University Press, Princeton, NJ.

MacIsaac, H. J., J. Borbely, J. R. Muirhead, and P. Graniero. 2004. Backcasting and forecasting biological invasions of inland lakes. Ecological Applications 14:773–783.

Mack, R. N., and W. M. Lonsdale. 2001. Humans as global plant dispersers: getting more than we bargained for. BioScience 51:95–102.

Macpherson, A. J., R. Moore, and B. Provencher. 2006. A dynamic principal-agent model of human-mediated aquatic species invasions. Agricultural and Resource Economics Review 35: 144–154.

Madsen, J. D., L. W. Eichler, and C. W. Boylen. 1988. Vegetative spread of Eurasian watermilfoil in Lake George, New York. Journal of Aquatic Plant Management 26:47–50.

Muirhead, J. R., B. Leung, C. van Overdijk, D. W. Kelly, K. Nandakumar, K. R. Marchant, and H. J. MacIsaac. 2006. Modelling local and long-distance dispersal of invasive emerald ash borer Agrilus planipennis (Coleoptera) in North America. Diversity and Distributions 12:71–79.

Murray, J. D., E. A. Stanley, and D. L. Brown. 1986. On the spatial spread of rabies among foxes. Proceedings of the Royal Society of London Series B Biological Sciences 229:111–150.

Myers, J. A., M. Vellend, S. Gardescu, and P. L. Marks. 2004. Seed dispersal by white-tailed deer: implications for long-distance dispersal, invasion, and migration of plants in eastern NorthAmerica. Oecologia 139:35–44.

Nathan, R., G. Perry, J. T. Cronin, A. E. Strand, and M. L. Cain. 2003. Methods for estimating long-distance dispersal. Oikos 103:261–273.

Nelson, W., A. Potapov, M. A. Lewis, A. Hundsdorfer, and F. He. 2007. Balancing ecological complexity in predictive models: a reassessment of risk models in the mountain pine beetle system. Journal of Applied Ecology doi:10.1111/j.1365-2664.2007.01374.x.

Neubert, M. G., and H. Caswell. 2000. Demography and dispersal: calculation and sensitivity analysis of invasion speed for structured populations. Ecology 81:1613–1628.

Noble, J. V. 1974. Geographic and temporal development of plagues. Nature 250:726–729.

Okubo, A. 1980. Diffusion and ecological problems: mathematical models. Springer-Verlag, Berlin.

Olden, J. D., N. L. Poff, M. R. Douglas, M. E. Douglas, and K. D. Fausch. 2004. Ecological and evolutionary consequences of biotic homogenization. Trends in Ecology and Evolution 19:18–24.

Puth, L. M., and T. F. H. Allen. 2005. Potential corridors for the rusty crayfish, Orconectes rusticus, in northern Wisconsin (USA) lakes: lessons for exotic invasions. Landscape Ecology 20:567–577.

Rahel, F. J. 2002. Homogenization of freshwater faunas. Annual Review of Ecology and Systematics 33:291–315.

Reilly, W. J. 1931. The law of retail gravitation. Knickerbocker Press, New York.

Ricciardi, A. 2006. Patterns of invasion in the Laurentian Great Lakes in relation to changes in vector activity. Diversity and Distributions 12:425–433.

Roy, J. R., and J. C. Thill. 2004. Spatial interaction modelling. Papers in Regional Science 83:339–361.

Schneider, D. W., C. D. Ellis, and K. S. Cummings. 1998. A transportation model assessment of the risk to native mussel communities from zebra mussel spread. Conservation Biology 12:788–800.

Sharov, A. A., and A. M. Liebhold. 1998. Bioeconomics of managing the spread of exotic species with barrier zones. Ecological Applications 8:833–845.

Shigesada, N., and K. Kawasaki. 1997. Biological invasions: theory and practice. Oxford University Press, New York.

Shigesada, N., and K. Kawasaki. 2002. Invasion and the range expansion of species: effects of longdistance dispersal. Pages 350–373 in J. M. Bullock, R. E. Kenward, and R. S. Hails, editors. Dispersal ecology. Blackwell, Oxford.

Shigesada, N., K. Kawasaki, and Y. Takeda. 1995. Modeling stratified diffusion in biological invasions. American Naturalist 146:229–251.

Shurin, J. B., and J. E. Havel. 2002. Hydrologic connections and overland dispersal in an exotic freshwater crustacean. Biological Invasions 4:431–439.

Skarpaas, O., K. Shea, and J. M. Bullock. 2005. Optimizing dispersal study design by Monte Carlo simulation. Journal of Applied Ecology 42:731–739.

Skellam, J. G. 1951. Random dispersal in theoretical populations. Biometrika 38:196–218.

Soons, M. B. 2006. Wind dispersal in freshwater wetlands: knowledge for conservation and restoration. Applied Vegetative Science 9:271–278.

Stoeckel, J. A., D. W. Schneider, L. A. Soeken, K. D. Blodgett, and R. E. Sparks. 1997. Larval dynamics of a riverine metapopulation: implications for zebra mussel recruitment, dispersal, and control in a large-river system. Journal of the North American Benthological Society 16:586–601.

Stohlgren, T., and J. Schnase. 2006. Risk Analysis for biological hazards: what we need to know about invasive species. Risk Analysis 26:163–173.

Suarez, A. V., D. A. Holway, and T. J. Case. 2001. Patterns of spread in biological invasions dominated by long-distance jump dispersal: insights from Argentine ants. Proceedings of the National Academy of Sciences of the United States of America 98:1095–1100.

Suter, G. W. 1993. Ecological risk assessment. Lewis Publishers, Chelsea, MI.

Taylor, R. A. J., L. S. Bauer, D. L. Miller, and R. A. Haack. 2004. Emerald ash borer flight potential. Research and Technology Development Meeting, Romulus, Michigan.

Thomas, R. W., and R. J. Huggett. 1980. Modeling in geography: a mathematical approach. Harper and Row, London.

Train, K. 2003. Discrete choice methods with simulation. Cambridge University Press, Cambridge, UK.

Trakhtenbrot, A., R. Nathan, G. Perry, and D. M. Richardson. 2005. The importance of long-distance dispersal in biodiversity conservation. Diversity and Distributions 11:173–181.

Turchin, P. 1998. Quantitative analysis of movement. Sinauer Associates, Sunderland, MA.

Turchin, P., and W. T. Thoeny. 1993. Quantifying dispersal of southern pine beetles with mark-recapture experiments and a diffusion model. Ecological Applications 3:187–198.

Veit, R. R., and M. A. Lewis. 1996. Dispersal, population growth, and the Allee effect: dynamics of the house finch invasion of eastern North America. American Naturalist 148:255–274.

Viboud, C., O. N. Bjornstad, D. L. Smith, L. Simonsen, M. A. Miller, and B. T. Grenfell. 2006. Synchrony, waves, and spatial hierarchies in the spread of influenza. Science 312:447–451.

Wiens, J. A. 2001. The landscape concept of dispersal. Pages 96–109 in Clobert, J., E. Danchin, A. A. Shondt, and J. D. Nichols, editors. Dispersal. Oxford University Press, New York.

Wonham, M. J., J. T. Carlton, G. M. Ruiz, and L. D. Smith. 2000. Fish and ships: relating dispersal frequency to success in biological invasions. Marine Biology 136:1111–1121.

Zipf, G. K. 1946. The P1P2/D hypothesis: on the intercity movement of persons. American Sociological Review 11:677–686.

6Estimating Dispersal and Predicting Spread of Nonindigenous Species