In a Clamshell
When there is variability in predictions or when mechanisms of how systems or processes work are unknown, there is uncertainty. From medicine to engineering, and biology to economics, uncertainty is an important consideration when testing hypotheses and predicting outcomes. In this chapter, we explore the role of uncertainty on explaining and predicting invasions from a biological perspective. We begin by reviewing a classification of uncertainty that conforms to how many biologists and statisticians perceive the role of uncertainty in their scientific explorations. We then narrow our focus by evaluating the uncertainty in explanations and predictions from a gravity model of zebra mussel invasion into the western United States. This includes providing bootstrapped confidence intervals on parameter estimates from survey data and evaluating the predictive performance of the gravity model on a subset of economically and ecologically valuable lakes using probability theory and receiver operator characteristic curves. Many of these evaluations of uncertainty are uncommon in current gravity model applications to invasive species and are generalizable to other modeling approaches and the larger concern of predicting successful invasions.
In the absence of perfect knowledge about how a system or process works, there is unexplained variability in observations and predictions, or uncertainty. Uncertainty is the reason biologists experience difficulty identifying the properties of successful invaders and predicting invasions (Kolar and Lodge 2001). Prior to and following Elton’s (1958) treatise, invasion biology received mainly disparate scientific interest, and it has only recently gained general ecological popularity (Davis et al. 2001; Puth and Post 2005) because of threats to biodiversity and financial losses (Pimentel et al. 2000, 2005). Now scientists are faced with the challenge of predicting and ideally preventing invasions without fully understanding the mechanisms that lead to successful invasion. Some have argued that predicting invasions in light of such uncertainty is futile (Gilpin 1990). Nevertheless, there has been considerable progress in predictive methods to identify species likely to invade and the locations likely to become invaded, which have emerged from the study of biological invasions (Reichard and Hamilton 1997; Schneider et al. 1998; Kolar and Lodge 2001; Rouget et al. 2004) and the uncertainty of invasions has been reduced.
Uncertainty is an interdisciplinary subject and consequently has varied usage. In economics, uncertainty is regularly mentioned in the same context of risk, where risk is a product of the probability of an event occurring and the impact of that event (Knight 1921). As long as the probability of the event is not zero or one, there is uncertainty. Biologists generally associate uncertainty with unexplained processes and mechanisms by which variability in observations arise (Taper and Lele 2004). This uncertainty is often presented as confidence intervals, standard errors, or posterior distributions on model parameters (Lewin-Koh et al. 2004; Cumming et al. 2007). However, there is considerable overlap between these two generalized perspectives of uncertainty (e.g., Dovers and Norton 1996). With an interdisciplinary approach to biological invasions, it is therefore unsurprising to find multiple perspectives regarding the importance and role of uncertainty. Because of the breadth of perspectives regarding uncertainty, in this chapter we provide a biological perspective of uncertainty and invasions.
Our biological perspective of uncertainty begins by reviewing a general taxonomy of uncertainty (Regan et al. 2002) and applying this taxonomy to biological invasions. Our list of sources of uncertainty is not comprehensive, but we believe it highlights some areas of invasion biology that, if emphasized in future studies, will strengthen our explanatory and predictive capabilities. We then focus our study of uncertainty and biological invasions to deconstructing a national gravity model of zebra mussel invasion. Specifically, we demonstrate a bootstrapping method of survey data used to parameterize a gravity model of the United States and assess the influence of uncertainty on the risk of invasion for two environmentally and economically valuable lakes, Lake Mead (Arizona and Nevada, USA) and Lake Roosevelt (Washington State, USA). We then evaluate the risk of invasion for 13 uninvaded lakes and evaluate the predictive performance of the gravity model on 15 lakes recently invaded. In closing, we discuss the challenges of prediction and validation of predictions in the face of uncertain invasions.
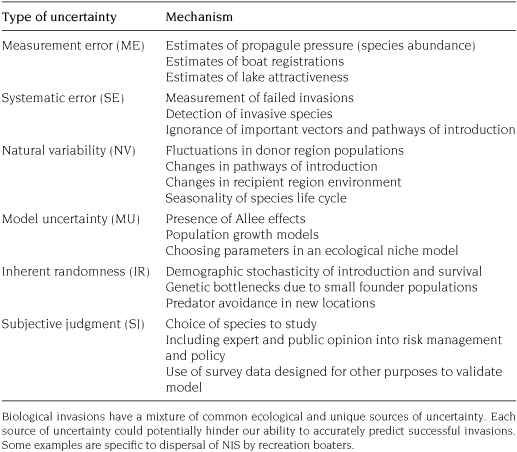
Even in the discipline of biology there are multiple perspectives on sources of uncertainty (e.g., Shaffer 1981; Burnham and Anderson 2002). Many of these treatments focus on a particular type of uncertainty (e.g., measurement error: Thomas et al. 1993) or a particular methodology of assessing uncertainty (e.g., natural variability: Harwood and Stokes 2003; Cumming et al. 2007). However, a broad perspective of classifying uncertainty was taken by Regan et al. (2002) and is generally consistent with biological and statistical perspectives of sources of uncertainty. We adopt this classification for its completeness as a taxonomy with which to discuss the uncertainty related to biological invasions.
The general classification system starts by separating uncertainty into linguistic and epistemic uncertainty (Regan et al. 2002). Linguistic uncertainty is associated with communicating ideas and definitions. Chapter 5 contains a discussion about the linguistic uncertainty associated with defining when an invader is said to have established. Establishment is defined both by an abundance of the invader and by a persistence of the invader in a new landscape. In theoretical treatments of the invasion process, establishment is rarely defined with precise, numerical thresholds, but for empirical applications, these thresholds are required to define whether a species has established in a system and are necessary to perform statistical analyses. The variability in thresholds used to define establishment represents one form of linguistic uncertainty.
Within invasion biology, linguistic uncertainty has received some attention. Richardson et al. (2000) discuss the vagueness of the terms “naturalized” and “invasive.” They also attempt to provide a clear vocabulary for discussing the invasion process. The vagueness, context dependence, and ambiguity (Regan et al. 2002) of invasion biology terms is pervasive throughout the entire invasion process from transport and arrival of invaders to the establishment, spread, and impact of those invasions (Sakai et al. 2001; Colautti and MacIsaac 2004).
Another example of linguistic uncertainty is in the assessment of whether an invasive species has had an impact. Invasion biologists have variably defined impact as the presence of any nonindigenous species (NIS), an NIS that has spread, and an NIS that has produced harmful environmental changes, particularly to native species (Ricciardi and Cohen 2007). Although attempts have been made to provide clear working definitions, such as the Parker et al. (1999) formulation stating that impact is the product of species range (area), abundance, and per-unit (or biomass) effect. These formulations may be entirely appropriate for considering impact in an ecological context, but this ignores the economic impact.
The simplest solution to linguistic uncertainty is to provide precise definitions that can be agreed upon by the scientific community (Richardson et al. 2000; Regan et al. 2002). However, finding consistent terminology has been, and continues to be, a problem for exploring the patterns and processes of biological invasion (Shrader-Frechette 2001) and also for communicating invasion biology and risk to the public and policy makers (Bossenbroek et al. 2005; Hodges 2008). The evolution of invasion biology into an objective discipline will likely be tied to the preciseness of the definitions employed in its description and application (Colautti and MacIsaac 2004). Another solution to the linguistic uncertainty of invasion biology is to provide syntheses of work on a particular subject, such as propagule pressure (Lockwood et al. 2005), that makes connections across multiple definitions and inferences.
Epistemic uncertainty is more closely related to data, models, and the methods of scientific inquiry, which can be secondarily separated into uncertainty due to measurement error, systematic error, natural variation, inherent randomness, and subjective judgment (Regan et al. 2002). Epistemic uncertainty is often accounted for by reporting quantitative measures such as confidence intervals, prediction intervals, probability distributions, or p-values.
Measurement error and systematic error are associated with errors in the recording of data by either human observation or errors from measurement devices, where measurement error is an unbiased measurement and systematic error is a biased measurement (Thomas et al. 1993). Natural variation is uncertainty due to spatial or temporal differences in the values of model parameters (e.g., Lele et al. 1998). Even when model parameters are accurately and precisely estimated, some ecological processes are inherently (effectively) random because it is infeasible to account for all the processes that influence model outcomes, nor is it possible to know the initial conditions with such precision as to make deterministic predictions (Gilpin 1990). Model uncertainty occurs when a biological process is described using a mathematical representation (Jonzen et al. 2002), and model uncertainty applies to not only variability in approaches (e.g., deterministic and stochastic modeling) but also to interpolation and extrapolation of model results beyond the coverage of the data that can be used to support such modeling-based inferences. An example of the variability in approaches for modeling the dispersal of invasive species is discussed in chapter 6. Lastly, subjective judgment emerges as a form of uncertainty throughout scientific inquiry, from evaluating the quality of data and choosing a modeling approach, to interpreting results and making decisions (Harwood and Stokes 2003). Table 7.1 provides the taxonomy of epistemic uncertainty with examples from biological invasions.
Many of the epistemic uncertainty issues in invasion biology are common problems in general ecology. For example, some species are able to invade at low population densities and remain undetected at low densities, only later experiencing population growth and spread (Christian and Wilson 1999). Detecting species at low abundance is the same problem community ecologists face when attempting to detect the presence of rare species (Longino and Colwell 1997; Costello and Solow 2003). Similarly, in conservation biology, demographic stochasticity and minimum viable population size (Lande 1993) are directly related to propagule pressure in invasion biology (Lockwood et al. 2005; Drake and Lodge 2006).
Invasion biology, however, faces some unique sources of uncertainty. In community ecology, the rare species are usually known to occur within the area being searched, and the observer has some search recognition pattern. This is often not true in invasion biology, where many invaders are surprise discoveries (Solow and Costello 2004). Similarly, population parameters such as growth rate, survivorship, fecundity, and reproductive value may be known for a species in its native range, but unless the destination has very similar habitat characteristics, these parameters will be different and will remain unknown until the invasion has occurred and population data collected. As a consequence, and in part to sidestep added uncertainty due to population dynamics, there has been a call to develop robust methods and models of invasive species risk assessment that do not require specific details regarding population dynamics (Simberloff 2003).
TABLE 7.1. Uncertainty in biological invasions.

One solution to both epistemic and linguistic uncertainty is through mathematical modeling of biological (Taper and Lele 2004) and economic processes (Leung et al. 2002). For epistemic uncertainty, the modeling solution is straightforward. Models represent hypotheses about how a system or process works. Confronting models with data allows us to perform hypothesis testing and model selection among competing hypotheses (Hilborn and Mangel 1997; Burnham and Anderson 2002; Lewin-Koh et al. 2004). Alternatively, models of these processes can be evaluated on their predictive performance. Both strategies require accounting for uncertainty, that is, quantifying the explanatory (e.g., goodness of fit) and predictive (e.g., receiver operating characteristic [ROC] curves) capabilities (Hosmer and Lemeshow 2000). Methods to assess the explanatory and predictive performance of models are demonstrated in the following section.
Less obvious is the role mathematical modeling plays in reducing linguistic uncertainty. When theory and experimentation meet, there is necessarily a measurable quantity to evaluate from a model that is evaluated with data (hypothesis testing or model selection: Lewin-Koh et al. 2004). Returning to the example of defining establishment (chapter 5), empiricists must specify thresholds of abundance and/or persistence above which establishment is said to have occurred. It is possible, although not likely, that invasion biologist, mathematical modelers, and economists could reach an agreement regarding the threshold of establishment. It is more likely that we will continue to have a variety of thresholds. Arguably, the most common thresholds will be determined by the data available (e.g., presence or absence vs. count data) and the models used (chapter 6) to assess the process of establishment. Although some linguistic uncertainty will remain, depending on the data collected and modeling approach, mathematical models will force clearly delineated (at least mathematically) definitions of establishment that theory likely would not evolve to if left in a conceptual form. Byers and Goldwasser (2001) provide one such example where thresholds are defined in order to assess a variety of invasion biology issues.
We now transition to an example of estimating the risk of invasion and accounting for uncertainty by modeling the transport of zebra mussels through the use of a gravity model produced by Bossenbroek et al. (2007). The purpose of this specific example is to demonstrate how uncertainty in explanation and prediction can be accounted for. While gravity models are regularly applied to aquatic invasions, particularly zebra mussels, previous studies have only haphazardly quantified uncertainty (but see Bossenbroek et al. 2001; Leung et al. 2006). Here we show a bootstrapping routine that accounts for uncertainty in parameter estimates used in the gravity model, and we evaluate the predictive power of the gravity model on the order of lake invasions.
The dreissenid mussel invasion of the Great Lakes began about 1986, with the successful establishment of the zebra mussel, Dreissena polymorpha, in Lake St. Clair via ships’ ballast water (Hebert et al. 1989), causing extensive ecological and economic impacts. The present North American range of D. polymorpha includes much of northeastern and north central North America, including more than 400 inland lakes. In 2008, zebra mussels were also discovered in one reservoir in Colorado and one in California. A second species of dreissenid, the quagga mussel (D. bugensis (=D. rostriformis bugensis [Andrusov (1897)])), was found in the Erie Canal and Lake Ontario in 1991 (May and Marsden 1992) and is now common in lakes Erie and Ontario (Diggins et al. 2004). This species was also discovered in Lake Mead on the Colorado River in January 2007 and now extends to several other reservoirs up and downstream of Lake Mead. The range expansion of dreissenid mussels in North America to date has resulted from a combination of processes, involving the dispersal within and between water bodies. The primary pathways of dreissenid dispersal include shipping routes in the United States, natural downstream dispersal, and overland dispersal by human vectors, such as recreational boaters (see chapter 12 for a more thorough discussion of these processes). Gravity models of recreational boater movement patterns have been used to forecast the overland dispersal of D. polymorpha (Schneider et al. 1998; Bossenbroek et al. 2001, 2007; Leung et al. 2006).
Gravity models use formulations, analogous to Newton’s laws of attraction, to estimate the arrival of invaders into discrete patches. The variables and parameters susceptible to epistemic uncertainty are listed in table 7.2, and an overview of the mathematics of gravity models can be found in Bossenbroek et al. (2001) or Leung et al. (2006). The formulation used here follows the national gravity model for zebra mussel dispersal (Bossenbroek et al. 2007). The critical result useful for predicting invasions from the gravity model is the number of arriving boaters that previously visited waters infected with zebra mussel (Q). Bossenbroek et al. (2007) report Q as the proportion of all boaters traveling to a destination from a zebra mussel source. Here Q is the number of infested boaters arriving into a destination.
Estimating the number of arriving boaters starts by first modeling the distribution of all boaters from watershed, i, to destination, j, between N watersheds,
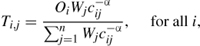
where Oi is the number of licensed boaters in their watershed of origin, Wj is the area of lakes in the destination watershed, cij is the Euclidean distance between the source and destination watersheds, and
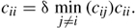
The sum in the denominator is a balancing factor that ensures all boaters that leave a source arrive at a destination. The national gravity model for zebra mussels (Bossenbroek et al. 2007) has two notable differences from previous zebra mussel studies (Bossenbroek et al. 2001; Leung et al. 2006). First, the locations are delineated by watersheds (figure 7.1) rather than counties, and second, it is possible for boaters to redistribute themselves within the same watershed (i = j). This leads to a need to define how far boaters travel within their own watershed, because a distance value of 0 would render a gravity model useless. A typical convention is to have the distance traveled within a watershed be some proportion (δ) of the distance to the next nearest possible destination (Thomas and Hugget 1980). The parameter α is a distance coefficient that describes the deterrent effect of distance upon a boater. The variables O, W, and c are properties of each watershed, while the parameters α and δ are estimated from data.
TABLE 7.2. Uncertainty in gravity models.
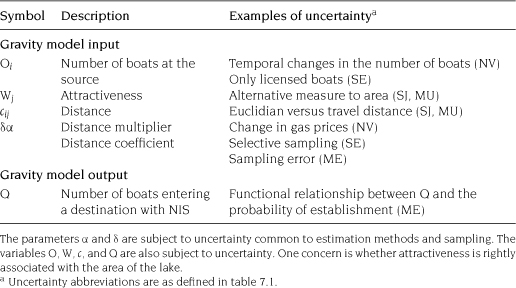
FIGURE 7.1.
Reservoirs and watersheds. Lakes Roosevelt and Mead receive boater traffic from watersheds east of the 100th meridian (dashed line) that have zebra mussels present. These lakes have been the focus of managers as likely locations for zebra mussels to be introduced in the western United States. Each watershed is shaded based the number of licensed boats found within the watershed. The Great Lakes region, which has the highest density of waters invaded by zebra mussels, also has a high density of licensed recreational boaters. Adapted from Bossenbroek et al. (2007), with permission of the Society for Conservation Biology.
Survey data for the 100th Meridian Initiative were used to parameterize the national gravity model. The 100th Meridian Initiative is a cooperative effort by state, federal, and provincial agencies to prevent the spread of zebra mussels and other aquatic nuisance species into western North America. Surveys were conducted at 20 reservoirs throughout the Great Plains region (i.e., roughly along the 100th meridian) that recorded the distance traveled by recreational boaters between sources and destinations. The 13 reservoirs that had more than 50 completed surveys were used for the parameterization, and this procedure is consistent with the analysis performed in Bossenbroek et al. (2007). Using boater survey data from only reservoirs in the Great Plains states is subject to several sources of uncertainty, including systematic error, because only a portion of the country is used to parameterize a national model, and subjective judgment, because the surveyors may be specifically targeting boaters from long distances.
In the national gravity model, the number of boaters carrying zebra mussels (Zi) is assumed to be proportional to the area of lakes infested with zebra mussels found within watershed i. This results in the redistribution of infested boaters,
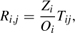
where Zi/Oi is the proportion of boaters carrying zebra mussels. The number of infested boaters arriving to a watershed j is
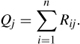
The number of boaters visiting a watershed that previously visited watersheds with invaded lakes (Q) is purportedly an indicator of invasion risk and can be interpreted as the dose in a dose–response application of biological invasions (chapter 5; Bossenbroek et al. 2001; Leung et al. 2004; Lockwood et al. 2005).
The 100th Meridian Initiative was initially established to stop or slow the spread of zebra mussels into the western United States, but the funding was grossly inadequate relative to what would be required to meet this goal. No guidance currently exists about how best to allocate funding to alternative methods of prevention and control. The national gravity model was developed in part to inform this management dilemma (see chapter 12). We focus our analysis hereafter on accounting for the uncertainty in the gravity model, because this is a necessary component for implementing management actions (Leung et al. 2002). How the measured uncertainty, dealt with here, feeds into economic considerations and resulting management decisions is more thoroughly treated in chapter 8. We begin our treatment of uncertainty in gravity models by first considering the invasion of two popular destinations for boaters across the United States, lakes Mead and Roosevelt.
So which of these two lakes is most likely to be invaded first? Jerde and Lewis (2007), using invasion waiting times (chapter 5), formulated the order of invasion for two locations. This ordering, applied to outputs from gravity models, requires three assumptions: the survivorship of individuals is small, the survivorship at both locations is approximately the same, and the gravity scores (Qm, Lake Mead; Qr, Lake Roosevelt) are proportional to the actual propagule pressure. Under these conditions, the probability of Lake Mead being invaded before Lake Roosevelt is (1 + Qr/Qm)−1, and the probability of Lake Roosevelt being invaded before Lake Mead is the complement, (1 + Qm/Qr)−1.
Based on Bossenbroek et al. (2007), the probability of Lake Mead being invaded before Lake Roosevelt is 0.797, and the probability of Lake Roosevelt being invaded before Lake Mead is 0.203. These probabilities are based on the gravity model structure, the measured variables, the estimated parameters, and the model assumptions—all of which are subject to the influences of uncertainty. We now turn to quantifying the uncertainty in the parameters α and δ that are estimated from the survey data regarding the distance boaters traveled to get to reservoirs in the Midwest of the United States.
To investigate the change in the probabilities of ordered invasion, due to uncertainty in the estimates of α and δ, we performed a Monte Carlo simulation by the following:
1. For a single reservoir, we estimated the probability an arriving boater would be from a specific watershed using the survey data used to parameterize the gravity model.
2. We then drew from a multinomial distribution with these probabilities as parameters and recorded the distance this boater traveled to arrive at the destination (cij).
3. This was repeated at a single reservoir for the number of surveys recorded at that reservoir.
4. Steps 1–3 were then repeated for each reservoir.
5. From steps 1–4, the parameters δ and α were estimated following Bossenbroek et al. (2007) and recorded.
6. Qm, Qr, and the estimated probabilities of ordered invasion were recorded.
7. Lastly, steps 2–6 were repeated 1,000 times.
This procedure is a bootstrapping routine that accounts for the uncertainty in and from the survey samples. The uncertainty arises not from the number of boaters arriving to the reservoir but from the variability in the contribution of observed sources to the estimates. The list of replicates resulting from the bootstrapping routine can be used to build 95% confidence intervals on α, δ, and the resulting uncertainty in the ordered probabilities of invasion (Efron and Tibshirani 1993).
The distance coefficient (α) estimate has fairly tight confidence intervals, while the distance multiplier (δ) has broader confidence intervals (table 7.3). This is expected after inspecting the sums-of-squares surface provided in figure 1 of Bossenbroek et al. (2007). The relatively small range of the confidence intervals on the parameters and minimal change in the probabilities of ordered invasion indicate that the uncertainty in the boater surveys due to variability in the source of boater movements is negligible. A subsequent sensitivity analysis (Bossenbroek et al. 2007) indicated that a 25% reduction in α could lead to approximately an 8% decrease in the proportion of boats arriving to a location. However, as demonstrated here, this does little to change the predicted ordered probabilities of invasion. Taken together, the reduction in α would likely increase the expected invasion waiting time for both lakes but does not change the order in which the invasion would likely occur (Jerde and Lewis 2007).
TABLE 7.3. Confidence intervals (CIs) on parameters and probability estimates.

Bootstrapped confidence intervals account for uncertainty in the parameters that can be quantified from the survey data, and this encompasses many of the common sources of uncertainty surrounding surveys, such as sample size, randomness, and completeness (Barnett 2002). Bootstrapping does not account for any bias, such as interviewing boaters with only out-of-state plates, nor does this bootstrapping account for any temporal variability in the values of α or δ.
Uncertainty may also influence the variables in a model (e.g., the gravity variables O, W, and c) and the model structure. Assessing model structure and the inclusion or exclusion of different variables is generally referred to as model selection. In statistical practice, there are multiple ways to perform model selection, such as likelihood ratio tests and Akaike’s information criterion (Burnham and Anderson 2002). But these methods have yet to be applied to invasion gravity models because the data are insufficient and, due to the expenses involved in continuously monitoring boater traffic at multiple uninvaded locations, unlikely to ever be collected.
As an alternative to directly applying a model selection approach on Q, the estimated number of boaters arriving is used as an explanatory variable and then the probability of establishment is modeled from presence or absence of an invasion into a lake. This may be accomplished using logistic regression or a functional form of the response curve (Bossenbroek et al. 2001; Leung et al. 2004, 2006). Statistically, this approach is problematic because the explanatory variable, in this case Q, is usually assumed fixed and known (Hosmer and Lemeshow 2000), but here the number of arriving boaters is an estimate from the gravity model and therefore contains some variability, or uncertainty. Specifically, there is measurement error and/or systematic error in the explanatory variable. Measurement error can change the observed mean structure, the variance structure, and obscure significant covariates (Thomas et al. 1993). This in turn will lead to poor predictions and model fit from a dose-response curve. Proper model selection using this approach would require accounting for the measurement error. Assessing the gravity model structure and accounting for measurement error in gravity scores are important future directions for invasion biology research. In the following section, we offer a few prescriptions for where gravity model research may proceed in order to account for uncertainty as it relates to predictive performance.
Predicting establishment with accuracy is an aspiration of invasion biology (Kolar and Lodge 2001), and of gravity models in particular (Bossenbroek et al. 2001; Leung et al. 2006). Predictive accuracy is critical for proactive management to prevent invasions (chapter 1). However, it is still unclear whether models of species arrival and spread (chapter 6) developed thus far are sufficient to offer reliable guidance about when and where to intervene against invasive species (Gilpin 1990; but see chapter 9). Here, we demonstrate three related predictive insights related to gravity models. First, we look at the pairwise probabilities of 13 uninvaded lakes. Second, we estimate the pairwise probabilities of 15 recently invaded lakes and show graphically the relationship between Q and the pairwise probabilities of invasion given the distribution of Q from the invaded lakes. Third, we apply logistic regression, knowing full well there is uncertainty in the explanatory variable Q, to demonstrate how uncertainty confounds predictive performance.
Gravity scores, Q, are known to be positively correlated with successful invasions (MacIsaac et al. 2004). Moreover, invasion order probability, as demonstrated for lakes Mead and Roosevelt, can be calculated. For the 13 lakes of interest presented in Bossenbroek et al. (2007), the pairwise probabilities are provided in table 7.4. All lakes in the table were uninvaded by zebra mussels at the onset of this project. Since then, however, the Lake of the Ozarks, just downstream from H. S. Truman Reservoir, was reported to contain zebra mussels in June 2006, Lake Mead was reported to contain quagga mussels in January 2007, and Lake Perry in Kansas was reported to contain zebra mussels in October 2007.
As apparent from gravity score, Q, H. S. Truman Reservoir is the most likely to become invaded, and each paired probability is greater than 0.75. This later result indicates that we should not expect many, if any, lakes in this group to become invaded before H. S. Truman Reservoir. Analytically, the probability of r lakes becoming invaded before some time, t, while H. S. Truman Reservoir remains uninvaded is
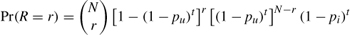
TABLE 7.4. Pairwise order of invasion for currently uninvaded lakes.
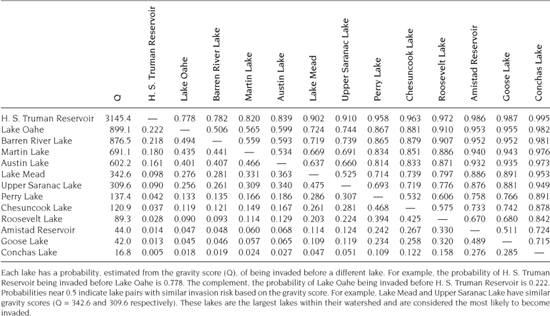
where there are N lakes in the group of uninvaded lakes (table 7.4; N = 12 when excluding H. S. Truman Reservoir). The parameter pu is the probability at each discrete time step that an uninvaded lake transitions to become invaded, and pi is the probability that H. S. Truman Reservoir becomes invaded; [1 −(1 − pu)t]r is the probability of r invaded lakes, [1 −(1 − pu)t]N − r is the probability of N − r invaded lakes, and (1 − pi)t is the probability of H. S. Truman Reservoir remaining uninvaded. This formulation rests on the assumptions that each lake in the group has the same pu and that both pi and pu are known. Unfortunately, neither of these assumptions is easily justified or met for the gravity scores presented in table 7.3. We know the gravity scores, Q, are very different between the group of uninvaded lakes, and this can reflect different probabilities of invasion (Von Holle and Simberloff 2005; see table 7.4). The pairwise probabilities (table 7.4) of Lake Oahe, Barren River Lake, Martin Lake, and Austin Lake all have order pairings close to 0.5, implying that either lake could be invaded before the other, and these lakes form a group with similar likelihoods of invasion. Given a larger sample than just four lakes with similar pairing, scores may be more useful for producing the group of reference lakes.
For an example, we could assume that the group of uninvaded lakes were similar to Lake Oahe, the next most likely invaded lake based on the gravity scores. Then, using the relative probability formulation (presented in Jerde and Lewis 2007), the relative probability of H. S. Truman Reservoir transitioning to invaded is pi = (QH.S.Truman)(QOahe)−1(pu) = 3.5pu. This can be inserted into the equation above, and we are left with one parameter to estimate, pu. Alternatively, we can insert (899.1/3145.4)pi for pu, and then we are similarly left with pi to estimate. However, neither of these parameters is known.
Figure 7.2A is a plot of the probability of observing one or more of the 12 reference lakes becoming invaded (given pu = (899.1/3145.4)pi) as a function of probability that H. S. Truman Reservoir becomes invaded, and figure 7.2B is a plot of the probability of observing five or more of the 12 reference lakes becoming invaded under the same conditions. The probability of observing one or more lakes invaded ranges from zero to approximately 0.5 for the possible values of pi and for t = 1, 5, and 10 time step periods of observation. With almost no better than a fair coin’s chance of one or more of the reference lakes becoming invaded and the uncertainty due to pi being unknown, observing a few of the reference lakes becoming invaded before H. S. Truman would not invalidate the predictions of the gravity model. However, observing five or more lakes invaded before H. S. Truman (figure 7.2B) has only a 0.1 or less probability of being observed by chance for all time periods and all values of pi. This observation provides a robust rule of thumb for evaluating the performance of predictions gleaned from the gravity scores. If we observe five or more lakes in the reference group become invaded before H. S. Truman Reservoir becomes invaded, we should be skeptical of the gravity model’s predictive capabilities.
Validating gravity models through testing of predictions is desperately needed. Gravity models for invasive species have a relatively young history compared to other models of species spread (Schneider et al. 1998; Bossenbroek et al. 2001, 2007; Leung et al. 2004, 2006; MacIsaac et al. 2004). One evaluation of predictive performance is to compare the gravity scores of recently invaded locations to uninvaded locations (Leung et al. 2004, 2006; MacIsaac et al. 2004). As mentioned above, logistic regression is used with presence/absence data to test the significance of the gravity score. In the studies thus far, the gravity score is shown to be positively correlated with successful invasions and is a significant explanatory variable. This is the usual extent to which diagnostics of model fit and predictive power are performed (but see MacIsaac et al. 2004). However, more diagnostics exist, and some of these diagnostics are more useful for evaluating the predictive capability of logistic regression models.
FIGURE 7.2.
The probability that one or more (A) or five or more (B) of the reference lakes (n = 12) becoming invaded by time t as a function of the probability that H. S. Truman Reservoir becomes invaded, pi. Uncertainty is captured in the range of probability values (height of the curves). Because pi is unknown, there is considerable uncertainty about the probability of one or more lakes becoming invaded while H. S. Truman remains uninvaded, even over 10 time steps. However, for all values of pi and t = 1, 5, and 10, the probability of observing five or more lakes invaded is low [Pr(r ≥ 5) < 0.1].
The receiver operating characteristic (ROC) curve and the resulting area under the curve (AUC) are one such diagnostic. The purpose of such curves is to evaluate how well the logistic model is able to discriminate invaded lakes and uninvaded lakes based on the gravity score. The curve is a reflection of the sensitivity and specificity. Sensitivity accounts for the correct discrimination of successful invasions—meaning it is a proportion of lakes that are predicted and observed to be invaded. Similarly, specificity accounts for correctly discriminating lakes predicted and observed to be uninvaded. Both sensitivity and specificity are proportions and range from 0 to 1. The ROC uses 1-specificity. This reflects the proportion of misclassified lakes that are predicted to be invaded but are actually uninvaded. A more thorough discussion of ROC curves, sensitivity, and specificity can be found in Hosmer and Lemeshow (2000).
The heuristic measure of the ROC is the AUC. When the AUC is between 0.9 and 1, the model does an excellent job of discriminating between invaded and uninvaded. In contrast, when the AUC is close to 0.5, discriminating between invaded and uninvaded lakes is really no better than flipping a fair coin to predict whether it is invaded.
Table 7.5 provides the gravity scores for 15 lakes invaded just prior to construction of the national gravity model (Bossenbroek et al. 2007). Applying logistic regression to these lakes and the gravity scores of the uninvaded lakes found in table 7.4 produces the ROC and AUC shown in figure 7.3. With an AUC of 0.63, we can conclude the logistic regression model with the gravity score as an explanatory variable does a relatively poor job of discriminating, and hence predicting, successful invasions. However, a few caveats are in order. First, this is a small subsample of the lakes in the national gravity model, and it would be unfair to say that the failure of this subset to provide a larger AUC is evidence for a failure of the entire system of lakes and the gravity model. Second, the logistic regression showed that Q was not a significant explanatory variable. Using a likelihood ratio test between a constant only and constant with parameter for the Q variable, the p-value was 0.57. This leads us to select the constant-only model even though we used the model with the added parameter for estimating the AUC. Poor model fit is often, although not necessarily, associated with poor discrimination (Hosmer and Lemeshow 2000). As mentioned above, one of the consequences of measurement error is the failure to detect significant covariates (Thomas et al. 1993). Future studies may consider the approach and subsequent improvements on this concern suggested by Wacholder et al. (1993) or Lele and Allen (2006).
The purpose of discussing ROC and AUC as diagnostics is not to call into question the national gravity model for zebra mussels. Rather, ROC and AUC diagnostics represent a tool to evaluate the predictive performance of the model. ROC and AUC are not exclusive to logistic regression and may be useful with other applications, and therefore should be the subject of future studies that seek to demonstrate the predictive capabilities of invasion models.
Pairwise probabilities can also be used as a visual diagnostic to assess uncertainty in model predictions. Table 7.5 contains the pairwise probabilities of invaded (rows) and uninvaded (columns) lakes. The table itself is difficult to decipher, as would be the ROC and AUC diagnostics without some familiarity. However, figure 7.4 contains 13 box plots, one for each uninvaded lake, that show the distribution of the pairwise probabilities to the group of invaded lakes. The box plots are ordered by the gravity score, Q, such that H. S. Truman Reservoir, with the largest gravity score, is the rightmost box plot and Conchas Lake, with the smallest gravity score, is the leftmost plot. The spread of each box represents the uncertainty associated with each uninvaded lake given the observed group of invaded lakes. Interestingly, 10 of the 13 uninvaded lakes have means greater than 0.5, indicating that relative to the values of Q for the recently invaded lakes, there is a reasonable chance of invasion. Of the three remaining uninvaded lakes, there is considerable variability, as demonstrated by the whiskers of the box plots. We may conclude, similarly to the ROC and AUC plots, but by visual inspection, that there is considerable uncertainty in the likelihood of invasion and that the predictive power resulting from the gravity model is questionable, again, with the same caveats.
TABLE 7.5. Probabilities of invaded lakes being invaded before currently uninvaded lakes.
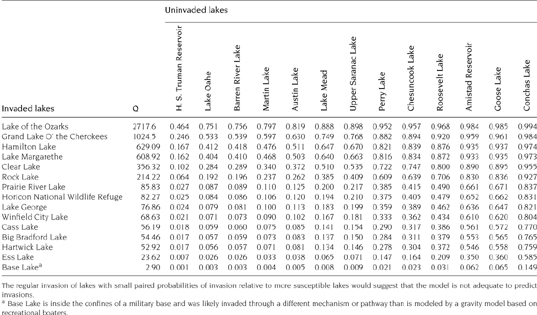
FIGURE 7.3.
Receiver operating characteristic (ROC) curve for the logistic regression of invaded (n = 13) and uninvaded lakes (n = 15) based on the gravity scores. The AUC is 0.63 and indicates there is poor discrimination between invaded and uninvaded lakes. As a diagnostic, the ROC and resulting AUC indicate that the gravity score for this subsample of lakes has poor predictive capabilities.
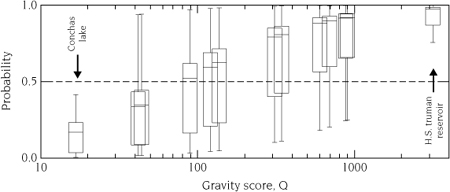
FIGURE 7.4.
The pairwise probability distributions of invaded lakes for each uninvaded lake. Each box plot is one of the uninvaded lakes from table 7.4, positioned at its respective gravity score, Q. The distribution of the box plot is all of the pairwise probabilities with invaded lakes. Most uninvaded lakes have expectations greater than 0.5, which implies they are more susceptible, based on the gravity score, to invasion than are lakes already invaded.
We have offered a few prescriptions to account for uncertainty in gravity models, including building and reporting confidence intervals on parameter estimates, applying probability theory to the order of invasions, ROC plots and AUC metrics, and building box plots of relative probabilities. Undoubtedly, other diagnostics exist and should be explored. We very much encourage the development of diagnostics for gravity models of invasive species dispersal, and believe this will be an avenue of future invasive species research.
From the small collection of invaded and uninvaded lakes and the analyses performed here, one may conclude that gravity models are left wanting. We believe this is not a fair conclusion. Indeed, there appears to be predictive performance issues with gravity models. However, this is less an indictment of gravity models and more of a guidepost of where our research needs to go. For example, there are likely groups of lakes with similar susceptibility of being invaded where there are substantial differences in susceptibility between groups. This phenomenon was observe in the suitability of U.S. shipping ports to the potential invasion of Chinese mitten crab (Eriocheir sinensis) when coupling a relative measure of propagule pressure and habitat suitability mapping (Herborg et al. 2007). The result of comparing two locations with different susceptibility is that the probability of invasion will be different even though the gravity scores are similar (Jerde and Lewis 2007). A likely next objective in gravity model research will be to include susceptibility in evaluating the model predictions (Muirhead 2007). In the case of the uninvaded lakes listed in table 7.4, only lakes Mead and Roosevelt have been evaluated for susceptibility of zebra mussel invasion (Bossenbroek et al. 2007).
The study of biological invasions is plagued by uncertainty. From identifying the characteristics of successful invaders (Goodwin et al. 1999) or detecting new invaders at a location (Costello et al. 2007), to predicting when and where the next lake in the western United States is going to be invaded by zebra mussels (Bossenbroek et al. 2007), there are few topics that are deterministic (Gilpin 1990). This includes not only the epistemic uncertainty emphasized in this chapter, but also the linguistic uncertainty of the terminology used in the biological and bioeconomic research of invasive species (Colautti and MacIsaac 2004; Shrader-Frechette 2001). Here, we have provided a biological and statistical perspective of uncertainty with emphasis on the role of making and evaluating predictions, in particular, to a subset of invaded and uninvaded lakes with scores from a gravity model of zebra mussel dispersal (Bossenbroek et al. 2007). We have offered a few specific prescriptions for evaluating the predictive capability of gravity models, but much more needs to be done to account for the uncertainty in invasion biology. Listing all the ways we may account for uncertainty would be an arduous task indeed. Instead, we offer examples from the literature, following the order of the sections of this chapter, that we hope will guide researchers in future studies and investigations of biological invasions.
Identifying sources of uncertainty for any biological process is a critical step that should be done in concert with formulating hypotheses and models (Hilborn and Mangel 1997; Lewin-Koh et al. 2004). Carlton (1996) provides an exemplary overview of the sources of uncertainty for predicting the arrival of invasive species into new locations. He identified six important sources of uncertainty: changes in donor regions, new donor regions, changes in recipient region, invasion windows, stochastic inoculation events, and dispersal vector changes. These processes have become the subject of empirical investigations (e.g., Wonham et al. 2000) and theoretical frameworks (e.g., Jerde and Lewis 2007). More generally, overviews of the study of biological invasions (e.g., Vermeij 1996; Puth and Post 2005) highlight areas in the field that need more attention, due in large part to the uncertainty of specific processes, such as predicting invasions (Kolar and Lodge 2001).
Reducing linguistic uncertainty has been accomplished, so far, by evaluating the terminology used in the literature. To this end, there are many notable examples of how to proceed (e.g., Colautti and MacIsaac 2004; Hodges 2008). When recognizable differences between definitions for the same term are detected, it may be time for a critical review that attempts to bridge and clarify the discrepancy. One such term, from a bioeconomic perspective, is the term “risk.” For biologists, risk is often associated with a probability of some unwanted event occurring, such as invasion (Suter 1993; Jerde and Lewis 2007). However, economists generally associate risk with the probability of an event occurring times the loss accrued because of that event occurring. Undoubtedly interdisciplinary approaches to biological invasions will uncover similar disparities and will require some attention.
Reporting parameters with some measure of variability is a common method for dealing with uncertainty (Cumming et al. 2007). One approach to mathematical modeling is to produce a model and then search the literature for the parameter values of a particular species and/or system from which to make predictions. This is actually quite difficult because often only point estimates (i.e., means), and not measures of variability, are reported, especially for parameters such as growth and predation rates. A measure of variability in parameter estimates can be used to analyze qualitative differences between model predictions (e.g., Wonham et al. 2006) from perturbation analysis (Caswell 2001). This problem can easily be overcome with diligence in the reporting of descriptive statistics for point estimates (e.g., the variance or standard deviation) in future empirical studies of biological invasions. A good review of the appropriate error bars to produce for point estimates is presented by Cumming et al. (2007).
Assessing gravity model structure and the variables to include in a gravity model has received limited attention. The differences in models are usually determined by the available data, such as production constrained or doubly constrained gravity models (Leung et al. 2006; see also chapter 6). That said, Leung et al. (2004) provided an example of how to detect Allee effects from gravity scores. Yet many questions remain for gravity model research. For example, the attraction coefficient, Wj (table 7.2), the area of the destination lake or the area of lakes within a water shed (Bossenbroek et al. 2007), has been shown to be a reasonable measure of how attractive a lake is to boaters (e.g., Reed-Andersen et al. 2000). But should measures of recreational fishing opportunities, or distance to population centers, or availability of facilities (see Reed-Andersen et al. 2000), or water quality, or water skiing also be used? Similarly, watersheds that have big reservoirs, such as lakes Mead, Roosevelt, and Oahe, can probably be assumed to be the main attractor of these watersheds, and it seems reasonable that the proportion of boaters coming to these big reservoirs is related to the overall proportion of water in the watershed. For watersheds in Michigan, for example, with a lot of small lakes, the spatial interactions within the watershed, including the distribution of people living within the watershed, may be a critical consideration not currently captured in the gravity model dynamics. With the predictive performance observed within this chapter, it is likely that assessing the model structure of gravity models will be a fruitful area for reducing the uncertainty of invasions.
Likely the most pressing issue for invasion biologists with respect to epistemic uncertainty is that of predicting successful invasions—successfully. This is why we focused much of our attention here on gravity model diagnostics of predictive performance. To date, little has been presented regarding the predictive performance of gravity models other than to show significant correlation between the gravity scores and observed invasions (Leung et al. 2004; MacIsaac et al. 2004). But it bears repeating that correlation is not necessarily an indicator of good predictive performance (Hosmer and Lemeshow 2000).
Applying the probability theory of waiting times (Drake et al. 2005; Jerde and Lewis 2007) appears to be one avenue for evaluating predictions from gravity models with a lot of potential. With the specific question, “what is the probability of observing r lakes invaded before H. S. Truman Reservoir,” we were able to find a robust threshold; that is to say, there is a probability of less than 0.1 of observing five lakes invaded within 1-, 5-, and 10-year time periods. Similarly, there appears to be some usefulness of formulating relative waiting times (Jerde and Lewis 2007), but this likely needs to be expanded into formulations that include multiple lakes or groups of lakes with similar invasion susceptibility (Herborg et al. 2007).
One of the drawbacks of predictive formulations based on waiting times is that in order to validate or invalidate the predictions, we must wait for invasions to occur. This is likely a problem for the impatient and, more important, for managing the spread of invasive species. Alternatively, there are diagnostics such as ROC and AUC that assess predictive performance based on the model’s ability to discriminate between invaded and uninvaded lakes based on the gravity score and can be conducted on existing data without having to wait for future invasions. However, the ability to discriminate between invaded and uninvaded can be sensitive to measurement error (Thomas et al. 1993). Therefore, it appears that gravity scores will need to be calibrated with census data about the number of boaters arriving to lakes that are infested with zebra mussels, but some of the necessary information may already be available (e.g., Johnson et al. 2001).
We have focused on the biological processes of invasive species and the uncertainty in our understanding of these processes. The next step is to translate these measures into decision-making frameworks based on the economic realities of managing invasive species. In transition to chapter 8, which deals with some of the bioeconomic issues of uncertainty, one last uncertainty issue should be raised, and that is the uncertainty of uncertainty. As mentioned above, risk, in economics, is the product of the probability of an event occurring and the loss accrued due to that event occurring. Certainty is defined by the probability of an event occurring and is equal to 0 or 1, and uncertainty in the outcome occurs everywhere in between. Much of the uncertainty we have been emphasizing is in the estimate of the probability of that event occurring. As a result, the biological uncertainty we have in a processes will in large part also influence our ability to make any economic decision.
Acknowledgments This chapter was substantially improved by the editors of this book and reviews by A. Potapov, J. Rothlisberger, and three anonymous reviewers. This material is based on work supported by the Integrated Systems for Invasive Species project (D. M. Lodge, principle investigator) funded by the National Science Foundation (DEB 02-13698). C.L.J. was supported by a National Sciences and Engineering Research Council of Canada Collaborative Research Opportunities Grant to M. A. Lewis and the Canadian Aquatic Invasive Species Network. J.M.B. was supported by a National Sea Grant and U.S. Fish and Wildlife Service award to D. M. Lodge. This is publication 2009-03 from the University of Toledo Lake Erie Center.
Barnett, V. 2002. Sample survey: principles and methods, 3rd edition. Hodder Arnold Press, London.
Bossenbroek, J., C. Kraft, and J. Nekola. 2001. Prediction of long-distance dispersal using gravity models: zebra mussel invasion of inland lakes. Ecological Applications 11:1778–1788.
Bossenbroek, J., J. Ladd, B. Peter, and D. Lodge. 2007. Forecasting the expansion of zebra mussels in the United States. Conservation Biology 21:800–810.
Bossenbroek, J., J. McNulty, and R. Keller. 2005. Can ecologists heat up the discussion on invasive species risk? Risk Analysis 25:1595–1597.
Burnham, K., and D. Anderson. 2002. Model selection and multimodel inference: a practical information-theoretic approach, 2nd edition. Springer, New York.
Byers, J., and L. Goldwasser. 2001. Exposing the mechanism and timing of impact of nonindigenous species on native species. Ecology 82:1330–1343.
Carlton, J. 1996. Pattern, process, and prediction in marine invasion ecology. Biological Conservation 78:97–106.
Caswell, H. 2001. Matrix population models, 2nd edition. Sinauer, Sunderland, MA.
Christian, J., and S. Wilson. 1999. Long-term ecosystem impacts of an introduced grass in the northern Great Plains. Ecology 80:2397–2407.
Colautti, R., and H. MacIsaac. 2004. A neutral terminology to define invasive species. Diversity and Distributions 10:135–141.
Costello, C., J. Drake, and D. Lodge. 2007. Evaluating an invasive species policy: ballast water exchange in the Great Lakes. Ecological Applications 17:655–662.
Costello, C., and A. Solow. 2003. On the pattern of discovery of introduced species. Proceedings of the National Academy of Sciences of the United States of America 100:3321–3323.
Cumming, G., F. Fidler, and D. Vaux. 2007. Error bars in experimental biology. Cell Biology 177:7–11.
Davis, M., K. Thompson, and J. Grime. 2001. Charles S. Elton and the dissociation of invasion ecology from the rest of ecology. Diversity and Distributions 7:97–102.
Diggins, T., M. Weimer, K. Stewart, R. Baier, A. Meyer, R. Forsberg, and M. Goehle. 2004. Epiphytic refugium: are two species of invading freshwater bivalves partitioning spatial resources? Biological Invasions 6:83–88.
Dovers, S., and T. Norton. 1996. Uncertainty, ecology, sustainability and policy. Biodiversity and Conservation 5:1143–1167.
Drake, J., P. Baggenstos, and D. Lodge. 2005. Propagule pressure and persistence in experimental populations. Biology Letters 1:480–483.
Drake, J., and D. Lodge. 2006. Allee effects, propagule pressure and the probability of establishment: risk analysis for biological invasions. Biological Invasions 8:365–375.
Efron, B., and R. Tibshirani. 1993. An introduction to the bootstrap. Chapman and Hall/CRC, Boca Raton, FL.
Elton, C. 1958. The ecology of invasion by animals and plants. Methuen, London.
Gilpin, M. 1990. Review: ecological prediction. Science 248:88–89.
Goodwin, B., A. McAllister, and L. Fahrig. 1999. Predicting invasiveness of plant species based on biological information. Conservation Biology 13:422–426.
Harwood, J., and K. Stokes. 2003. Coping with uncertainty in ecological advice: lessons from fisheries. Trends in Ecology and Evolution 18:617–622.
Hebert, P., B. Muncaster, and G. Mackie. 1989. Ecological and genetic studies on Dreissena polymorpha (Pallas): a new mollusc in the Great Lakes. Canadian Journal of Fisheries and Aquatic Sciences 46:1587–1591.
Herborg, L., C. Jerde, D. Lodge, G. Ruiz, and H. MacIsaac. 2007. Predicting the North American distribution of Chinese mitten crabs (Eriocheir sinensis) using measures of propagule pressure and environmental niche models. Ecological Applications 17:663–674.
Hilborn, R., and M. Mangel. 1997. The ecological detective: confronting models with data. Princeton University Press, Princeton, NJ.
Hodges, K. 2008. Defining the problem: terminology and progress in ecology. Frontiers in Ecology and the Environment 6:35–42.
Hosmer, D., and S. Lemeshow. 2000. Applied logistic regression, 2nd edition. Wiley Interscience, New York.
Jerde, C., and M. Lewis. 2007. Waiting for invasions: a framework for the arrival of non-indigenous species. American Naturalist 170:1–9.
Johnson, L., A. Ricciardi, and J. Carlton. 2001. Overland dispersal of aquatic invasive species: a risk assessment of transient recreational boating. Ecological Applications 11:1789–1799.
Jonzen, N., P. Lundberg, E. Ranta, and V. Kaitala. 2002. The irreducible uncertainty of the demography-environment interaction in ecology. Proceedings of the Royal Society of London Series B Biological Sciences 269:221–225.
Knight, F. 1921. Risk, uncertainty, and profit. Houghton Mifflin, Boston.
Kolar, C., and D. Lodge. 2001. Progress in invasion biology: predicting invaders. Trends in Ecology and Evolution 16:199–204.
Lande, R. 1993. Risks of population extinction from demographic and environmental stochasticity and random catastrophes. American Naturalist 142:911–927.
Lele, S., and K. Allen. 2006. On using expert opinion in ecological analyses: a frequentist approach. Environmetrics 17:683–704.
Lele, S., M. Taper, and S. Gage. 1998. Statistical analysis of population dynamics in space and time using estimating functions. Ecology 79:1489–1502.
Leung, B., J. Bossenbroek, and D. Lodge. 2006. Boats, pathways, and aquatic biological invasions: estimating dispersal potential with gravity models. Biological Invasions 8:241–254.
Leung, B., J. Drake, and D. Lodge. 2004. Predicting invasions: propagule pressure and the gravity of Allee effects. Ecology 85:1651–1660.
Leung, B., D. Lodge, D. Finnoff, J. Shogren, M. Lewis, and G. Lamberti. 2002. An ounce of prevention or a pound of cure: bioeconomic risk analysis of invasive species. Proceedings of the Royal Society of London Series B Biological Sciences 269:2407–2413.
Lewin-Koh, N., M. Taper, and S. Lele. 2004. A brief tour of statistical concepts. Pages 3–16 in M. L. Taper and S. R. Lele, editors. The nature of scientific evidence: statistical, philosophical, and empirical considerations. University of Chicago Press, Chicago.
Lockwood, J., P. Cassey, and T. Blackburn. 2005. The role of propagule pressure in explaining species invasions. Trends in Ecology and Evolution 20:223–228.
Longino, J., and R. Colwell. 1997. Biodiversity assessment using structured inventory: capturing the ant fauna of a tropical rain forest. Ecological Applications 7:1263–1277.
MacIsaac, H., J. Borbely, J. Muirhead, and P. Graniero. 2004. Backcasting and forecasting biological invasions of inland lakes. Ecological Applications 14:773–783.
May, B., and J. Marsden. 1992. Genetic identification and implications of another invasive species of dreissenid mussel in the Great Lakes. Canadian Journal of Fisheries and Aquatic Science 49: 1501–1506.
Muirhead, J. 2007. Forecasting and validating the establishment of aquatic nonindigenous species. Ph.D. thesis, University of Windsor.
Parker, I., D. Simberloff, W. Lonsdale, K. Goodell, M. Wonham, P. Kareiva, M. Williamson, B. Von Holle, P. Moyle, J. Byers, and L. Goldwasser. 1999. Impact: toward a framework for understanding the ecological effects of invaders. Biological Invasions 1:3–19.
Pimentel, D., L. Lach, R. Zunign, and D. Morrison. 2000. Environmental and economic costs of non-indigenous species in the United States. BioScience 50:53–67.
Pimentel, D., R. Zuniga, and D. Morrison. 2005. Update on the environmental and economic costs associated with alien-invasive species in the United States. Ecological Economics 52:273–288.
Puth, L., and D. Post. 2005. Studying invasion: have we missed the boat? Ecology Letters 8:715–721.
Reed-Andersen, T., E. Bennett, B. Jorgensen, G. Lauster, D. Lewis, D. Nowacek, J. Riera, B. Sanderson, and R. Stedman. 2000. Distribution of recreational boating across lakes: do landscape variables affect recreational use? Freshwater Biology 43:439–448.
Regan, H., M. Colyvan, and M. Burgman. 2002. A taxonomy and treatment of uncertainty for ecology and conservation biology. Ecological Applications 12:618–628.
Reichard, S., and C. Hamilton. 1997. Predicting invasions of woody plants introduced into North America. Conservation Biology 11:193–203.
Ricciardi, A., and J. Cohen. 2007. The invasiveness of an introduced species does not predict its impact. Biological Invasions 9:309–315.
Richardson, D., M. Pysek, M. Rejmanek, M. Barbour, F. Panetta, and C. West. 2000. Naturalization and invasion of alien plants: concepts and definitions. Diversity and Distributions 6:93–107.
Rouget, M., D. Richardson, S. Milton, and D. Polakow. 2004. Predicting invasion dynamics of four alien Pinus species in a highly fragmented semi-arid shrubland in South Africa. Plant Ecology 152:79–92.
Sakai, A., F. Allendorf, J. Holt, D. Lodge, J. Molofsky, K. With, S. Baughman, R. Cabin, J. Cohen, N. Ellstrand, D. McCauley, P. O’Neil, I. Parker, J. Thompson, and S. Weller. 2001. The population biology of invasive species. Annual Reviews of Ecology and Systematics 32:305–332.
Schneider, D., C. Ellis, and K. Cummings. 1998. A transportation model assessment of the risk to native mussel communities from Zebra Mussel spread. Conservation Biology 12:788–800.
Shaffer, M. 1981. Minimum population sizes for species conservation. BioScience 31:131–134.
Shrader-Frechette, K. 2001. Non-indigenous species and ecological explanation. Biology and Philosophy 16:507–519.
Simberloff, D. 2003. How much population biology is needed to manage introduced species? Conservation Biology 17:83–92.
Solow, A., and C. Costello. 2004. Estimating the rate of species introductions from the discovery record. Ecology 85:1822–1825.
Suter, G. 1993. Ecological risk assessment. Lewis Publishers, Chelsea, Michigan.
Taper, M., and S. Lele. 2004. Dynamical models as paths to evidence in ecology. Pages 275–297 in M. L. Taper and S. R. Lele, editors. The nature of scientific evidence: statistical, philosophical, and empirical considerations. University of Chicago Press, Chicago.
Thomas, D., D. Stram, and J. Dwyer. 1993. Exposure measurement error: influence on exposure disease relationships and methods for correction. Annual Reviews of Public Health 14:69–93.
Thomas, R. W., and R. J. Hugget. 1980. Modeling in geography. Barnes and Noble Books, Totowa, New Jersey.
Vermeij, G. 1996. An agenda for invasion biology. Biological Conservation 78:3–9.
Von Holle, B., and D. Simberloff. 2005. Ecological resistance to biological invasion overwhelmed by propagule pressure. Ecology 86:3212–3218.
Wacholder, S., B. Armstrong, and P. Hartge. 1993. Validation studies using an alloyed gold standard. American Journal of Epidemiology 137:1251–1258.
Wonham, M., J. Carlton, G. Ruiz, and L. Smith. 2000. Fish and ships: relating dispersal frequency to success in biological invasions. Marine Biology 136:1111–1121.
Wonham, M., M. Lewis, J. Renclawowicz, and P. van den Driessche. 2006. Transmission assumptions generate conflicting predictions in hostvector disease models: a case study in West Nile virus. Ecology Letters 9:706–725.