The Princeton Guide to Evolution

V.14

Searching for Adaptation in the Genome

Dmitri A. Petrov

OUTLINE

1. Evolution as mutation and change in allele frequencies

2. The neutral theory of molecular evolution

3. The McDonald-Kreitman test

4. Population genomics approaches for detecting and quantifying adaptation

5. Remaining challenges

The study of adaptation lies at the heart of evolutionary biology; despite 150 years of intense study, however, many foundational questions about the mode and tempo of adaptation remain unanswered. The development of population genetics theory and the rise of genomics are bringing a promise of new types of data that are able to provide insight into these long-standing issues. This chapter discusses some of the key conceptual underpinnings of methods that use population and comparative genomics data to study adaptation, and it underscores some of the remaining difficulties and challenges.

GLOSSARY

Adaptation. The process by which a population evolves to having greater fitness in a given environment.

Effective Population Size. One common attempt to simplify the modeling of the evolutionary process is to assert that evolutionary dynamics in a real population N(t) (where t stands for time in generations) can be modeled faithfully in an idealized population of a different, constant effective size N_e. N_e is generally smaller than the census population size. Rapid adaptation should be sensitive to fluctuations in N only over short periods of time (short-term N_e) while slower neutral processes should be sensitive to the fluctuations over much longer periods of time (long-term N_e). Short- and long-term N_e can be different by many orders of magnitude from each other.

Fixation. The process in which a new mutation that is present in some individuals in a species becomes present in all individuals in a species.

Hitchhiking. The process of change of the allele frequency of a particular polymorphism allele as a result of its linkage to selected alleles in the genomic vicinity.

Indel. Insertion/deletion mutation, polymorphism, or substitution.

Mutation. A change in the DNA sequence in the genome of the individual. Can range from a change of a single nucleotide to much larger structural changes such as insertions, deletions, translocations, and inversions all the way to whole genome polyploidization.

Polymorphism. A genetic variant (an allele) that is present in some but not all individuals in a species.

Replacement. Mutation, polymorphism, or substitution in the protein-coding sequence that does change the amino acid sequence of the encoded protein. Also often called nonsynonymous.

SNP. Single nucleotide polymorphism.

Substitution. The outcome of fixation of new mutation. It is often observed by comparing DNA sequences from different species in which the majority of differences are due to fixations during the long-term evolution of independent lineages.

Synonymous. Mutation, polymorphism, or substitution in the protein-coding sequence that does not change the amino acid sequence of the encoded protein.

Adaptation is the primary process in evolution, yet after a century and a half of intensive study, most key questions about the mode and tempo of adaptation remain largely unanswered. This is troubling but also understandable given the extreme difficulty of (1) identifying individual adaptive genetic changes in a convincing way, (2) understanding their phenotypic effects, and (3) identifying the adaptive nature of these phenotypes in ecological and functional contexts. One approach is to start at the level of phenotype and work down to genes (see chapters V.12 and V.13). Another is to look for the signatures left by adaptation in the patterns of genetic (genomic) variation and then to work from candidate genetic regions to their phenotypic and possibly adaptive effects. Neither approach is foolproof, but much promise rests on the genomes-first, phenotype-second approach. This is because recent technological developments are allowing researchers to ever more quickly and efficiently document genetic variation on a genome-wide scale in multiple organisms and whole populations. The great promise of these approaches is that they can be applied to most organisms in a way that is virtually agnostic to their specific biology and in a way that is not biased by assumptions of which phenotypes are adaptive and which are not.

This chapter will focus only on the study of adaptation using population genomic data. The chapter will not be able to cover all or even a sizable fraction of the methods that have been developed—the ambition is to elucidate the main logic of several key approaches, highlight a few classical, popular, or most logically transparent methods, discuss the key caveats, and present some of the main insights into the adaptive process that have been gathered using population genomics to date.

1. EVOLUTION AS MUTATION AND CHANGE IN ALLELE FREQUENCIES

From the point of view of a population geneticist, evolution can be separated into two key phases: (1) origination of new alleles by mutation and (2) change of allele frequencies within populations. The first phase can involve mutations of varying magnitude, from single nucleotide changes all the way to chromosomal rearrangements and even whole genome duplications (see chapter IV.2); however, no matter how small or large these mutations are in physical scope or phenotypic and fitness effects, they always appear in a single individual or at most in a few siblings at once. For these new genetic variants to become established as differences between species (substitutions) or even be detectable as genetic variants (polymorphisms) within species, they need to increase in frequency very substantially. Hence the central importance to evolution of the second phase: the change in allele frequencies.

The process of allele frequency change is also the place where natural selection acts. Natural selection acts against new deleterious alleles, purging them from the population. Such natural selection is called purifying as it keeps the population “pure,” preserving the ancestral state and slowing down evolutionary change. This is likely the most common form of natural selection; in contrast, natural selection promotes increase in frequency and even eventual fixation of advantageous alleles. Such “positive” selection speeds up evolution and divergence between species.

The way natural selection affects allele frequencies is at times counterintuitive (see chapters III.1 and III.3). For example, even though the naive expectation is that all advantageous mutations should be fixed (i.e., reach 100% frequency) by natural selection, the reality is that the vast majority are lost almost immediately after they are generated by mutation. The probability that a strongly beneficial mutation escapes loss is roughly equal to its selective advantage, such that only 5 percent of mutations with 5 percent selective benefit are expected to fix, and 95 percent of them are expected to be lost. The main intuition here is that even adaptive mutations are very vulnerable to loss when they are extremely rare, because even a small fluctuation in frequency resulting from random events can remove them from the population and because natural selection is inefficient when allele frequencies are low (see chapter IV.1). Similarly, even the selectively neutral (i.e., natural selection does not favor one over any other) alleles can change in frequency, and one can become fixed as a result of purely stochastic fluctuations that are inevitable in finite populations. These stochastic fluctuations at neutral sites are further exacerbated by selection, both purifying and positive, at sites that are located nearby on a chromosome to a site with a neutral polymorphism. This latter phenomenon is known as hitchhiking because neutral or weakly selected polymorphisms can hitchhike on more selectively substantial mutations to which they are physically linked. Hitchhiking has recently received much attention and will be described in greater detail later in this chapter. These stochastic fluctuations also mean that not all deleterious mutations are lost as one might expect. Although the probability of loss of an even moderately deleterious mutation is much higher than loss of a neutral or advantageous mutation, it is not a certainty and some deleterious mutations can even fix in populations.

These considerations make it clear that the mere observation of an allele that reached high frequencies or of a substitution between species is not sufficient to argue that positive selection was involved. Indeed, the mutation in question could have been neutral or even weakly deleterious. Similarly, just because an allele was lost does not mean it was deleterious, because the vast majority of all new mutations, be they deleterious, neutral, or adaptive, are lost and lost quickly.

2. THE NEUTRAL THEORY OF MOLECULAR EVOLUTION

To detect adaptation with confidence, much more specific, quantitative expectations under the null model of no adaptation must be generated. The neutral theory, most commonly associated with Motoo Kimura, provides a good example of such expectations (see chapter V.1). The neutral theory postulates that practically all mutations are either deleterious or neutral and that practically all detectable polymorphisms and all substitutions are due to neutral mutations. Note that the second postulate is much more restrictive than the first. Even if the adaptive mutations are vanishingly rare compared with neutral or deleterious mutations, they still could easily contribute to the majority of substitutions. This is because the probability of fixation of a new neutral mutation is the reciprocal of the population size (N) (technically of the long-term effective population size N_e), while the probability of fixation of a strongly advantageous mutation is roughly equal to its selective benefit (as mentioned above) and the latter can be much, much larger. For instance, in Drosophila melanogaster, where the (long-term effective) population size is roughly 1 million, a mutation that provides 1 percent benefit has a 10,000 times greater chance of fixation than a neutral mutation. This implies that if adaptive mutations of 1 percent advantage were even 1000 times less frequent than neutral ones, they would still correspond to about 90 percent of all substitutions. The neutral theory thus claims that the increased chance of fixation of adaptive mutations does not compensate for their relative rarity.

Whether or not one agrees with the neutral theory as a description of empirical reality—and as a disclaimer, this author does not—it is indisputable that the neutral theory provides a useful null model for the study of adaptation. The next sections discuss some of the key approaches that employ the neutral theory as a null model for the detection and quantification of adaptive evolution.

3. THE MCDONALD-KREITMAN TEST

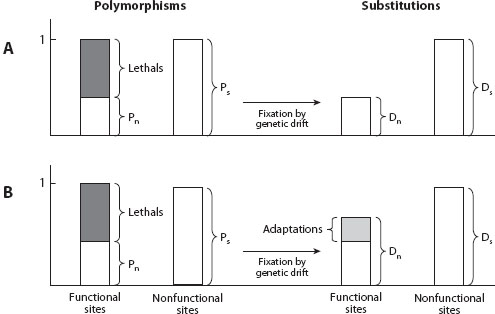
Consider the process of molecular evolution as envisioned by the neutral theory (figure 1A). Imagine you could classify all positions in the genome into functional (some mutations at these positions alter the functioning of the gene) and nonfunctional (all mutations at such positions have no effect on function at all). For simplicity, consider only protein-coding regions and assume that all synonymous mutations have no functional significance and that some nonsynonymous mutations have functional effects. Synonymous mutations contribute to the synonymous polymorphism (P_s) within species and synonymous divergence (D_s) between species, whereas nonsynonymous mutations contribute to the nonsynonymous polymorphism (P_n) within species and nonsynonymous divergence (D_n) between species (figure 1A).

Figure 1. Expected patterns of polymorphism (P) and divergence (D) and functional (subscript n) and neutral (subscript s) sites. (A) The expectation under the neutral theory. Mutations at functional sites come in two classes, either lethal or neutral. Lethals are eliminated right away; the remaining neutral mutations, at both functional and neutral sites, being identical in fitness, fix in the population and turn into divergent sites at identical rates. As a result, the ratio of the number of polymorphisms at functional and neutral sites (Pn/Ps) is expected to be equal to the ratio of the same ratio at divergent sites (Dn/Ds). (B) If some mutations are adaptive and happen rarely, the approximate expectation is that they are never seen as polymorphisms but do accumulate at a high rate as divergent sites. They reveal themselves as the excess of divergent sites at functional sites (Dn) relative to the neutral expectation (i.e., Dn > Ds × [Pn/Ps]).

Imagine that you then take the same number of both types of sites and carefully ensure that mutation rates are the same at both types of positions. Some mutations at functional sites will be deleterious, and according to the neutral theory, they are immediately eliminated from the population. In fact, they are eliminated so quickly that they can never reach frequencies at which they can be detected even as rare polymorphisms in samples of reasonable size. This assumption is equivalent to saying that all deleterious mutations are very strongly deleterious. Furthermore, because the neutral theory postulates that there are no adaptive mutations, the remaining mutations are all neutral at both functional and nonfunctional sites. Thus all observable polymorphisms at both types of sites should be due to neutral mutations, with the number of polymorphisms at functional sites reduced by the immediate elimination of the deleterious mutations. The next insight is that because all polymorphisms are neutral, polymorphisms at both types of sites should be fixing at the same rate such that the ratio of the numbers of functional and nonfunctional polymorphisms should be equal to the ratio of functional and nonfunctional substitutions (figure 1A). This equality is one of the key predictions of the neutral theory.

Now consider a modification of the neutral theory in which adaptive mutations are allowed to occur at some rate (figure 1B), but slightly deleterious mutations are still not permitted. How would this change the picture? The adaptive mutations must have a functional effect and so can take place only at functional sites. They have a much higher probability of fixation and fix much, much more quickly than neutral mutations; indeed, population-genetic theory suggests that the number of generations that a neutral mutation destined for fixation spends as a polymorphism is on the order of the (long-term effective) population size. For instance, in D. melanogaster, with the long-term effective population size of about 1 million, it takes on the order of 1 million generations for a neutral mutation to reach fixation. In contrast, an adaptive mutation of 1 percent advantage takes about 1000 generations—approximately 1000-fold less time. Because adaptive mutations fix so fast and the time they spent as polymorphisms is so fleeting, it is hard to detect them as segregating polymorphisms in populations. The adaptive mutations should thus contribute disproportionately to the number of substitutions between species and less so to the polymorphism within species.

These considerations immediately suggest a way both to test the neutral theory and to estimate the number of adaptive substitutions. Figure 1B illustrates that adaptive substitutions should constitute simply the excess of divergence at functional sites compared with what you would expect given the number of substitutions at nonfunctional sites (Ds) and the amounts of polymorphism at functional (Pn) and nonfunctional sites (Ps). Specifically, given that Pn/Ps is the proportion of the mutations at functional sites that are neutral, Ds × (Pn/Ps) becomes the estimate of the number of neutral substitutions at functional sites, and Dn – Ds × (Pn/Ps) is the estimate of the excess of substitutions at functional sites compared to the neutral theory expectations and thus also an estimate of the number of adaptive substitutions.

The test of the equality of Pn/Ps and Dn/Ds ratios can be formalized as the test of the neutral theory. This test was proposed in the seminal 1991 paper of McDonald and Kreitman and is now known as the McDonald-Kreitman (MK) test. They used their test with the polymorphisms and substitutions in a single gene (Adh in D. melanogaster and D. yakuba) and showed that the number of nonsynonymous substitutions was much larger than expected under the neutral theory, with practically all substitutions appearing to have been driven by positive selection.

Since its inception, the MK test has proved extremely popular, and it has been extended to other types of functional sites and applied to many individual genes and also genome-wide in a number of species, from yeast to humans and to nonprotein-coding functional sites. The results have been surprisingly mixed. At one extreme, all tested Drosophila species showed extremely high rates of adaptation, with about 50 percent of all amino acid substitutions (and similar rates at noncoding sites) in the genome appearing to be driven by positive selection. Similarly, substitutions in putative regulatory regions show high rates of adaptation. High rates of positive selection were also detected in some vertebrates such as house mouse (Mus musculus; ~50%) and chicken (Gallus gallus; ~25%), but not in humans (0–10%) or some plants (Helianthus, Capsella, and Populus). No evidence of positive selection at the protein level could be detected in Saccharomyces and in many species of plants (from Arabidopsis to Oryza to Zea). At first glance, there is no obvious population size or phylogenetic or ecological pattern to which organisms show high and low levels of adaptation according to the MK test.

One possibility is that the rate of positive selection really does vary substantially across different lineages and that there is now an opportunity to understand why. The other, less interesting but important possibility is that the MK test can be substantially biased in some situations, and that the type and direction of the bias varies in different organisms.

Let’s consider how the MK test can be biased. What are the fragile points? First, are the counts of the polymorphisms and substitutions that go into the MK test likely to be correct? MK tests generally employ closely related organisms; thus, not many errors are expected to result from multiple events happening at the same position and obscuring each other. The principal error, if it does occur, must come from incorrectly estimating the number of nonadaptive (neutral or slightly deleterious), nonsynonymous substitutions that are subtracted from the total number of nonsynonymous substitutions to arrive at the number of specifically adaptive ones (figure 1B).

A number of ways in which this can happen have been proposed; most of these depend on the existence of slightly deleterious mutations. Slightly deleterious mutations are a class ignored by the neutral theory (they were later considered by the nearly neutral theory), but they might turn out to be of great consequence both for the evolutionary process and also for the ability to estimate the rate of adaptive evolution. Slightly deleterious mutations have such a small deleterious effect that they are not efficiently removed from the population by purifying selection and can segregate in the population at appreciable frequencies. These polymorphisms, however, do feel the effect of purifying natural selection that pushes their frequency down; thus, they have substantially lower probabilities of fixation compared with the similarly frequent truly neutral polymorphisms. If the slightly deleterious nonsynonymous (or other functional) polymorphisms are mistakenly considered neutral, the rate of neutral amino acid (functional) substitutions will be overestimated, and the rate of adaptive evolution will be underestimated. On the other hand, slightly deleterious polymorphisms can also segregate at synonymous sites—by treating these as neutral polymorphisms, estimates of the rate of adaptive evolution will be too high.

To complicate these matters further, the fate of slightly deleterious mutations depends strongly on the population size variation and on the rate and strength of adaptive evolution. The same mutations should behave as strongly deleterious mutations during population booms and as virtually neutral mutations during population busts. This is because the effect of natural selection must be compared to the amount of stochastic noise generated by random genetic drift that in turn is stronger in small populations; thus, selection strong enough to significantly affect the fate of a polymorphism in a large population would have virtually no discernable effect in smaller populations. If the population size during evolution of the two species since their divergence was systematically different from the recent times over which the sampled polymorphisms have been segregating, then the effect that slightly deleterious polymorphisms have on divergence and polymorphism might be over- or underestimated. In addition, some deleterious mutations might happen to be linked to new adaptive mutations and reach unusually high frequencies through this linkage (see below for the description of hitchhiking). These moderately frequent polymorphisms can be easily mistaken for neutral ones even though they have virtually no chance of fixation and thus no chance to contribute to functional divergence.

Overall, it is likely that slightly deleterious mutations are more likely to mask effects of adaptation because most slightly deleterious mutations are found at nonsynonymous sites. A number of approaches have been proposed to deal with this problem, but none of them are likely to be foolproof. These approaches generally involve a way to estimate the proportion and selective effect of segregating slightly deleterious polymorphisms and then statistically adjusting the estimate of the neutral and slightly deleterious functional substitutions. It is still not known whether such approaches are reliable in practice, especially because most of them assume that all sites are evolving independently from each other (although it is possible that interactions between adaptive substitutions and slightly deleterious polymorphisms can be highly consequential) and thus that the fates of different polymorphisms really cannot be modeled independently of each other.

The uncertainty over the veracity of MK tests spurred search for additional signatures of adaptation that would complement MK tests, and that even if not foolproof themselves, would hopefully be immune to the problems that potentially plague the MK tests and thus provide an independent way to verify MK estimates. Approaches that rely on the search for patterns of hitchhiking and selective sweeps are described below.

4. POPULATION GENOMICS APPROACHES FOR DETECTING AND QUANTIFYING ADAPTATION

Selective Sweeps

Some of the most promising approaches to the detection and quantification of adaptation focus on the effects of adaptive alleles on linked neutral variation. Consider a new strongly adaptive mutation that is destined to become fixed in the population. When it has just arisen, it is present on a particular chromosome (figure 2A). Because it is destined to reach fixation, it will increase quickly in frequency.

Figure 2. A cartoon representation of expected patterns of selective sweeps driven by adaptation generated by de novo mutation. (A) Pattern expected in the mutation-limited regime. A new adaptive mutation appears (lightning); if it is not quickly lost through stochastic fluctuations near the absorbing boundary and can reach establishment frequency, it quickly starts increasing in frequency and drags with it linked neutral polymorphisms. At the end, a single haplotype reaches high frequencies and ultimately fixation. Not shown are mutations and recombination events taking place during the rise to high frequency. These should generate relatively rare additional haplotypes. (B) Adaptation in the non-mutation-limited regime can proceed differently. Here a second adaptive mutation at the same locus takes place and reaches establishment frequency before the first one reaches very high frequencies. At the end, multiple independent adaptive mutations rise to high frequencies and drag multiple haplotypes with them, generating the signature of a soft sweep.

What about the neutral variants initially present on the same chromosome? At the beginning, all of them start increasing in frequency as well, as a result of the physical linkage with the adaptive variant. With time, recombination will separate neutral variants located along the chromosome far away from the adaptive mutation frequently enough that the dynamics of the neutral variants will not be affected by the dynamics at the adaptive locus. By contrast, neutral variants located close to the adaptive substitution would not be separated by recombination from the adaptive mutation frequently, and thus might be driven to high frequency or even fixation along with the adaptive mutation itself.

This process (termed adaptive hitchhiking by Maynard-Smith and Haigh) should perturb the pattern of neutral polymorphism right next to the adaptive mutation that is increasing in frequency and ultimately around the adaptive substitution. The key expectation is that there should be a dearth of polymorphism next to the adaptive substitution because the allele linked to the new adaptive mutation should fix and the rest should be lost. This pattern of variation reduction by an adaptive mutation was termed a selective sweep.

The key expectations of selective sweeps are outlined in figure 2. First, during the sweep itself, the sweeping adaptive mutation and the linked region next to it are generating a pattern of a partial sweep (figure 2A), with the pattern of unusually long and unusually frequent haplotypes being its key feature. Note that a partial sweep does not lead to a substantial reduction of the overall levels of polymorphism. Only when the sweep reaches completion or near completion are regions of reduced variability observed. The range over which partial or complete selective sweeps extend are proportional to the strength of selection acting on the adaptive mutation and inversely proportional to the rate of local recombination. The rule of thumb is that the distance over which a sweep can be detected is about 0.1 s/r, such that an adaptive substitution of 1 percent advantage in the region with the recombination rate of 1 cM/Mb (cM or centimorgan is a unit of recombination such that two markers located 1 cm apart from each other will generate on average 1% of recombinant progeny) will generate sweeps of about 100 kb. With time, selective sweeps dissipate as new mutations in the swept region rise in frequency and the level of polymorphism eventually increases to its background level. Individual sweeps become almost impossible to detect within the length of time equal to the (long-term) N_e generations. For some statistics, the time is even shorter if the generated patterns are rapidly broken up by recombination.

Common Statistics for the Detection of Sweeps

Different statistical approaches have been designed to detect partial and complete selective sweeps. This section briefly outlines some of the most instructive and popular approaches. One of the most commonly used and powerful methods for the detection of partial sweep was proposed by Pardis Sabeti and colleagues. The original statistic (that has since been refined) is called EHH (extended haplotype homozygosity), and it is based on the comparison of the lengths of haplotypes that are linked to the two alternative states of a single nucelotide polymorphism, or SNP. SNPs that are linked to unusually long haplotypes might be associated with a sweeping adaptive mutation. A comparison of the length of the unbroken haplotypes linked to the alternative versions of the same SNP is very powerful as it allows one to control for the variation of recombination rate in the genome.

The statistics designed to detect complete sweeps, in contrast, cannot rely on the haplotype structure and must instead use other signatures. As mentioned above, the first and most obvious signature of a complete sweep is the local loss of variation. Although this signature is used commonly, it suffers from the possibility that detected regions are devoid of polymorphism simply because of regionally low mutation rates. To avoid this possibility, several other approaches have been developed that look for additional deviations from the expectations under the neutral theory.

Consider a complete sweep that removes all variation from the population in a region. After some time, additional neutral mutations will arise and start increasing in frequency. For a period after the sweep, their frequencies will tend to be low as it takes some time (on the order of long-term N_e generations) for the neutral alleles to drift to intermediate frequencies. This means that selective sweeps can be detected for a period of time by the paucity of intermediate frequency variants compared to the low-frequency ones. One of the earliest and most popular such tests was developed by Fumio Tajima. Tajima’s D, as it is known, is negative if the pattern of polymorphisms shows a bias in favor of rare variants compared with the expectations of the neutral theory. Thus, a lack of polymorphism in the region combined with negative values of Tajima’s D (or similar such tests) is often treated as a hallmark of a selective sweep.

Unfortunately, negative values of Tajima’s D are also expected under many demographic scenarios, and specifically in populations experiencing recent population growth. Given that many organisms of interest such as humans, D. melanogaster, and house mice have experienced sharp recent population growth, this presents a serious problem. One solution is to use genome-average values of Tajima’s D and look for regions both devoid of variation and having more negative values of Tajima’s D than shown by the genome on average.

Many other statistics have been developed that summarize the allele frequency distribution in different ways and attempt to be sensitive to specific perturbations of the spectrum expected under adaptation. All of them suffer from the same problems: they can be strongly affected by demographic scenarios, fluctuations in recombination rate, and other phenomena that cannot be easily ascertained. Assessing the expected values under refined demographic models and neutrality and defining empirical cutoffs based on the genome-wide assessments of these statistics are both common though imperfect means of dealing with these difficulties.

Soft Sweeps: Single and Multiple-Origin Soft Sweeps

The discussion of sweeps in the previous section represents the classical view of a selective sweep with a single de novo mutation rapidly increasing in frequency. Such classical sweeps are also known as “hard sweeps” (figure 2A). However, sweeps driven by multiple adaptive mutations on multiple haplotypes simultaneously rising in frequency might be even more common than hard sweeps. Such multiple adaptive allele sweeps were first systematically discussed by Hermisson and Pennings, who termed them “soft sweeps” (figure 2B).

What are the scenarios under which adaptive mutations on multiple haplotypes should be present at the same time in the population? There are two key possibilities: adaptation from standing variation and adaptation from de novo mutation in large populations. The first possibility is one in which a neutral or even slightly deleterious allele becomes adaptive as a result of a change in the environment. Because such an allele has been present in the population for a while, it should be present on multiple haplotypes. The second possibility is that multiple independently generated adaptive mutations should be generated roughly at the same time and roughly at the same chromosomal location site; thus multiple-origin de novo adaptive mutations on multiple haplotypes should be spreading through the population at the same time.

The notion of standing variation being the source of adaptation is a very natural one. What about the second, multiple-origin scenario? At first, this scenario appears far-fetched unless the mutational target is very large; indeed, most organisms have been assumed to have effective population size at most in the millions, while the mutation rate per site is on the order of one in a billion. This suggests that unless the same adaptation can be generated by mutations at multiple sites (for instance, a gene loss can be brought about by multiple stop codon generating point mutations and indels), most single-site adaptations generated by de novo mutations should generate hard sweeps. Surprisingly, however, recent analysis of dynamics of adaptation in D. melanogaster to pesticide resistance at the Ace locus revealed that even point mutations generating specific individual amino acid changes occur multiple times per generation in the population. This suggests that the relevant, short-term effective population size in D. melanogaster is more than 100-fold larger than previously thought. In many ways, this makes sense as the short-term N_e relevant to adaptation should be closer to the nominal population size, which is often going to be much, much larger than the long-term N_e. This is because the long-term but not the short-term N_e is very sensitive to any significant population decline occurring at any time over the past hundreds of thousands or even millions of generations. The same pattern can be seen even in humans, where population sizes have increased to an extent that adaptations such as lactase persistence arose in large enough populations to produce soft sweeps.

One can see immediately that soft sweeps should generate very different signatures compared with those generated by hard sweeps (figure 2). For instance, a complete soft sweep is not expected to lead to the complete loss of variation. Because multiple haplotypes increase in frequency simultaneously, the polymorphisms that distinguish these haplotypes from each other would not be eliminated; however, this does not mean that soft sweeps are indistinguishable from neutrality. Even though soft sweeps do not strongly perturb the total amounts of variability per site, they do generate very unusual haplotype patterns that can be detected as regions of high linkage disequilibrium. Tests based on these signatures are only now being designed; thus it is not yet known how prevalent soft sweeps are in comparison to hard sweeps.

5. REMAINING CHALLENGES

The genome-first approach discussed in this chapter clearly holds much promise, especially now that the ability to generate genome-level polymorphism and divergence data is growing by leaps and bounds, and experiments unthinkable even a few years ago are suddenly within reach of even individual investigators. While 10 years ago, barely enough data existed to reject the simplest and most clearly incorrect null hypotheses, it is now conceivable to estimate demography, distribution of fitness, and heterozygous effects of new mutations, and assess the rate of adaptation in different regions of the genome, genes, and pathways. At the same time, much remains to be done.

One of the most difficult questions in the study of adaptation is that of assessment of the rate of generation and the selective advantage of new adaptive mutations. Even more difficult is to assess the way in which the selective advantage of a new allele may vary through time and space and as a function of the genetic background (epistasis). One key question is how often adaptive alleles are advantageous only when rare (frequency-dependent selection or fitness overdominance leading to balancing selection) and how often they are unconditionally advantageous. This is a big question, partly because the answer will determine whether adaptation will increase genetic variation by driving adaptive alleles into the populations but not fixing them. Another important question is the prevalence of multistep adaptation and the number of steps that single adaptive bouts take should they be common. Such multistep adaptation will generate correlations in the fixation of individual adaptive events in space, time, and genomic location and thus could in principle be detectable. Failure to acknowledge this possibility could lead to incorrect inference.

Answers to these questions are not yet known, but the ease with which data can now be obtained should allow time-series studies of populations (natural and experimental) that will provide information about trajectories of adaptive mutations. These time-series data are not commonly available yet but should prove instrumental in further understanding of the adaptive process.

Finally, it is important to reemphasize that however powerful these approaches are, they will never be sufficient by themselves. The hard work of understanding the action of natural selection at the ecological, physiological, and molecular levels will remain. Population genetics can provide candidate loci and estimates of timing and strength of positive selection, but full understanding of the adaptive process must come from comprehensive inquiry that combines population genomics with all the biological levels that lie above the genotype.