This chapter is included to provide the reader with a brief introduction to some of the approximate techniques commonly employed in applied mathematics.†
The need for approximate methods arises from many diverse circumstances. One such case is experimental work where data is accumulated and there is no a priori knowledge of an analytical representation of the physical system; at most there is only a general idea of a mathematical model with undefined parameters. In order to obtain an analytical representation or a satisfactory evaluation of the parameters, curve-fitting techniques of various types are employed.
Another situation in which approximate methods must be resorted to is that in which the mathematical model of the system is known but exact solutions cannot be obtained for various reasons. In these situations when solutions must be obtained, the only recourse is to resort to some approximate method. It should be pointed out that this chapter deals with approximate methods of solving mathematical models of physical systems which are themselves only approximate descriptions of physical systems. The problem the analyst must always concern himself with, regardless of whether he is using exact or approximate solutions, is that he must be always on guard to be sure that his basic model is consistent with the physical problem he is dealing with. In other words, he must always check to see that the underlying postulates of the mathematical model are indeed applicable to the problem at hand.
As an illustration, let us consider fluid flow. If we postulate inviscid and incompressible flow, it may be shown that the fluid potential functions satisfy Laplace’s equation (see Appendix E, Sec. 13). With Laplace’s equation as the mathematical model, it may be further shown that the drag coefficient varies inversely with the square root of 1 minus the mach number. This result predicts that the drag will become infinite when the speed of sound is approached. We know this is not true; however, many people were quite certain of this in the not too far distant past. The fallacy lay in the fact that the postulates are no longer valid at speeds near the speed of sound. Those investigators who knew the very close fit of this model with experimental data for low velocities and failed to check the postulates against the physical problem for near-sonic conditions were greatly disappointed.
In reading this chapter the reader should also remember that the material presented is only an introduction to a few of the many approximate techniques that have been developed to date. Those desiring further information should consult the references at the end of this chapter.
Quite frequently in experimental work there arises a need to generate a curve to fit a set of given data points whose trend might be linear, quadratic, or of higher order. The method of least squares is a method of computing a curve in such a way that it minimizes the error of the fit at the data points.
To begin, let us assume that we have a set of n data points (xi,yi) through which we desire to pass a straight line. This line is to represent the “best fit” in the least-squares sense. As we know, a straight line may be expressed in the form
The formulas we are about to derive will be a set of simultaneous equations for the arbitrary parameters a0 and a1.
To assist in visualizing the process, the reader may refer to Fig. 2.1, which depicts the data points as well as the line to be fitted. Also shown are other quantities to be defined later.
Unless the data fall in a straight line, the general curve will not pass through all of the data points. For convenience, let us consider the kth point. The ordinate of the point is given as yk. The ordinate at xk as given
Fig. 2.1
by the general curve is a0 + a1xk. The difference between these two values is the error of fit at the kth point:
![]()
If we now sum the squares of all the errors at the data points, we will obtain the total error of fit:
The errors have been squared to eliminate possible cancellation.
The total error is a function of how well the line “fits” the data points: that is, it is a function of the parameters a0 and a1 which control the positioning of the line in xy space. It should be fairly evident that the “best” fit is that position which minimizes the total error. To find this position we consider E as a function of a0 and a1 and require that its derivatives vanish. Performing this operation, we have
Dividing each of these equations by – 2 and rearranging terms yields
Equations (2.5) and (2.6) are two simultaneous algebraic equations for the two parameters a0 and a1. If we introduce matrix notation, (2.5) and (2.6) may be combined to give
where
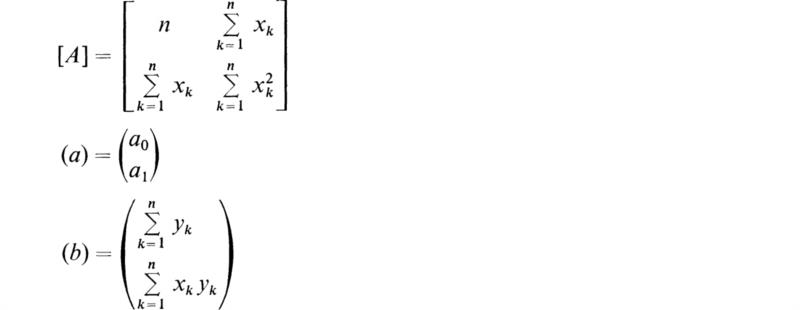
The solution to (2.7) is
Thus, knowing the data points, all the terms in [A] and (b) may be computed, and hence (a) is determined.
This is the method of least squares, and it may be extended to fit a polynomial of any order. In the general case, one may desire to fit an mth-order curve to the n given data points (xk,yk); that is,
Following the same derivation procedure, it may be shown that the general result is again (2.7) where
Thus, given a set of data points for which it is desired to fit a curve with minimum error, one only needs to compute the elements of the matrices [A] and (b).
As an example let us consider the following set of data:

If we examine this data, we may observe that it follows a somewhat linear relation. From this observation we seek to determine the coefficients of
by the method of least squares. Following the indicated procedure, we find that
It is of interest to note what happens when a higher-order polynomial is fitted to the above data. Again if we apply the method of least squares to find the coefficients for
we find that
Going one step further and attempting to fit
yields the result
If we compare the results for the coefficients in each of these three cases, we can readily see that the coefficients of the second- and third-order terms are small compared to the constant and linear coefficients. This shows that the linear character of the data strongly influences the results. The implication is that even though a higher-order polynomial is fitted to a set of data, the method of least squares adjusts the coefficients of the dominate terms to reflect the dominate trend of the data.
From the above derivation, it should be clear that any set of n data points may be fitted exactly with an n – lst-order polynomial. There are, however, a few precautions that the user should be aware of. One of these is that when the number of data points becomes large, the equations for the coefficients may
Fig. 2.2
become ill-conditioned.† When this situation arises, the procedure is to fit a series of orthogonal polynomials such as Legendre’s or Chebyshev’s.‡
Another problem arises when one attempts to fit a set of data exactly with a polynomial of order one less than the number of given points. In this case the curve is forced to pass exactly through every data point, and hence the total error is zero. However, the resulting curve may be far from the desired result. A simple example of this is illustrated in Fig. 2.2, where a third-order polynomial has been fitted through four data points. These points seem to indicate a linear trend, but the curve does not respond.
The advantage of using a larger number of data points than the order of the polynomial is that the curve tends to smooth out the data; that is, it is not sensitive to high-order fluctuations.
An interesting alternative derivation of the method of least squares may be developed from the use of matrices without the requirement of taking partial derivatives to obtain the minimum error. This method of formulation is convenient because of the fact that most digital computing facilities have built-in subroutines for handling matrix manipulations. However, if a computer facility is available, it would be wise to first check to see if a least-squares routine is supplied before looking into the matrix subroutines.
To present this formulation, let us consider a situation in which we have a set of n data points (xi,yi) for which it is desired to determine the coefficients of
for a “best” fit. We begin by writing this equation for every data point; that is,
Obviously all of these equations would be satisfied only when all the data points fall exactly on the desired curve. However, satisfied or not, let us consider the set of Eqs. (3.2) and rewrite them in matrix notation. If we define the following matrices
Eq. (3.2) may be written in terms of the single matrix equation
At first glance one might jump at the conclusion that (3.4) could be solved directly by premultiplying through by the inverse of the matrix [C]’. This operation is not possible since [C]’ is not a square matrix. Only in the special case when there are only three data points can this be done; that is, only when the number of data points is one greater than the order of the degree of the polynomial to be fitted. We can, however, reduce (3.4) to a square system by premultiplying through by [C]:
From (3.5) it can be seen that the order of the system is 3 × 3. If we introduce the notation
![]()
the solution to (3.5) may be expressed as
If the matrix [D] is examined carefully along with [C]{y}, it should be seen that the former is exactly the matrix [A] and the latter the matrix{b} from the previous section [see Eq. (2.7)]. Thus, the procedure followed here has generated the equations for a least-squares fit. For large problems this approach is recommended because the use of matrices greatly increases the efficiency of the process as a result of the systematic notation.
It happens very frequently in practical applications that one encounters a differential equation describing some physical system which cannot be readily solved by analytical methods. The reason is that it is usually either too complex or nonlinear and cannot be solved. At this point the only recourse left to the analyst is to integrate the equation numerically. With the advent of high-speed digital computers, this procedure has become a straightforward task.
The methods available for numerical integration are numerous, and we shall only attempt to illustrate a few of the classical ones. However, the reader should not forget the fact that an analytical solution is usually more desirable whenever it can be obtained.
As an introduction to the numerical integration of a differential equation, let us consider the ordinary first-order equation
Since we are going to integrate this equation numerically, we must have a specific initial condition given:
Assuming that we are seeking continuous solutions, we may apply Taylor’s expansion to obtain a relation which gives a value for y at a point x + Δx as follows:
If Δx is small, we may neglect all the terms of order Δx2 and higher to obtain
In further considerations we will replace the incremental step Δx with the term h which is called the step size.
To apply this result to obtain a solution to (4.1), we may proceed as follows. From (4.2) we know a value of y at a specified point x0. Using (4.4) a value of y can be computed at a neighboring point a distance h away:
where y’ has been replaced by (4.1). This process of projecting from a known point to a neighboring point is illustrated in Fig. 4.1.
Now, knowing y1 we may compute another value for y a step away from y1, or two steps away from y0:
By continuing this procedure we may extend the solution stepwise, with the general relation
Equation (4.7) is known as the Euler-Cauchy formula. It essentially is a second-order formula since terms of order h2 and higher were neglected in its derivation.
Fig. 4.1
It should be evident that the accuracy of this method is highly dependent upon the step size h. Even with a modern digital computer, a very small step size can result in long run times to integrate (4.1) to a desired final value with small error. To improve this situation, several higher-order methods have been devised so that acceptable accuracies may be obtained with reasonable step sizes and run times.
One of the most widely used higher-order methods is that of Runge-Kutta, which is a fourth-order system. Those readers who are interested in the derivation of this procedure are referred to the excellent book by Kuo.† The basic equations for this method are
where k0 =f(xn,yn)

This procedure essentially yields a more accurate estimate of the average slope. As a result, the Runge-Kutta method is sensitive to the higher-order derivatives and tracts the function closer. One of the advantages is that at each computation point the error can be predicted for the next step. This
feature permits the step size to be adjusted as the integration proceeds so that a constant accuracy can be maintained.
To illustrate both the Euler-Cauchy and the Runge-Kutta methods, we will consider a simple example so that the results may be compared with the exact solution. The problem to be considered is the following linear first-order differential equation and associated initial condition:
The exact solution of (4.9) is
In the example we shall solve (4.9) over the interval 0 to 1. Comparing (4.9) to (4.1), it can be seen that
and hence the general Euler-Cauchy formula (4.7) becomes
Also, the constants in the Runge-Kutta equations are
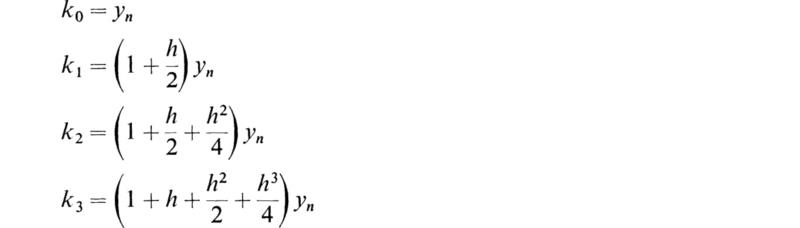
In order to obtain a fair comparison of these two methods, it is suggested† that the step size in the Euler-Cauchy formula be set approximately four times smaller than the step size in the Runge-Kutta procedure. The reason for this method of comparison lies in the fact that four terms must be computed in the Runge-Kutta method, as opposed to one in the Euler-Cauchy method. With the inclusion of this modification, both methods will require approximately the same amount of computer time. Thus the comparison is based on equal computations or computer time as opposed to equal step size.
In this specific example, the step size for the Euler-Cauchy method has been set at 0.025 and at 0.1 for the Runge-Kutta method. Figure 4.2 presents the tabulated results of both of these methods along with the exact solution. The absolute discrepancies have also been included for easier comparison.
Fig. 4.2
It should be of interest to note that the Runge-Kutta solution is far more accurate even with the modified step size discussed above.
One of the great values of these numerical methods is that the operation is identical whether the differential equation is linear or nonlinear. Also, almost every computer facility now has several standard subroutines based on one or more of the standard higher-order methods which provide for fast and efficient solution of differential equations with a minimum of programming effort.
The methods of Sec. 4 may be extended to apply to equations of the second order or higher as the case may be. However, rather than have a modified method for equations of different order, the most common approach at present is to reduce higher-order differential equations to a set of simultaneous first-order equations. The reason for this is that systems of simultaneous first-order equations can be handled with nearly the same degree of ease as a single equation on a digital computer.
To illustrate this approach, let us consider the following second-order equation and its associated initial conditions:
It may be seen that the exact solution to this problem is y = sin x, which will be used for checking the numerical results.
To reduce (5.1) to a first-order system, we introduce the variable
Substituting this variable into (5.1) gives
Thus, the set of simultaneous first-order differential equations representing (5.1) and its initial conditions is
If we convert (5.4) into the standard form for the Euler-Cauchy method, we have
where h is the step size. These equations have been solved for a step size of 0.025, and the results are tabulated in Fig. 5.1. Also shown are the results obtained by using the Runge-Kutta technique with a step size of 0.1.
As previously stated, numerical methods are particularly useful due to the existence of modern high-speed digital computers. Perhaps the greatest value is realized when one must obtain solutions to nonlinear differential equations for which exact solutions do not exist in closed form. When handling problems of this type, one must be careful to maintain a check on the growth of errors which usually implies the need for smaller step sizes and
Fig. 5.1
hence longer computation times. Another advantage is that the procedure is exactly the same for linear and nonlinear equations.
Sometimes the basic nature of a problem makes it difficult to formulate for numerical solutions in the previously described manner. In cases such as these the Monte Carlo method can sometimes be applied to obtain approximate solutions. Perhaps one of the greatest areas of application of this method is in the solution of boundary value problems. In these applications the name random walk is common terminology.
Basically, Monte Carlo is a probabilistic method for which the high-speed digital computer is ideally suited. To illustrate this method we will begin with a simple example.† Let us set out to determine the area under the curve y = x3 over the interval ![]() The answer is
The answer is ![]() however, we will attempt to obtain this answer by the Monte Carlo procedure. Figure 6.1 shows the curve and the desired area.
however, we will attempt to obtain this answer by the Monte Carlo procedure. Figure 6.1 shows the curve and the desired area.
Basically the method proceeds as follows: We may consider the desired area to lie entirely within the square bounded by the axes and the lines x = 1, y = 1. The actual area is bounded by the x axis, the line x = 1, and the curve itself. The method is to arbitrarily select points lying within the square in a random fashion. Once an arbitrary point has been selected, a decision is made as to whether or not it falls within the area of interest. If it does not, then it is simply counted in the total count. If it does fall within the area, then it is counted as a “hit” and also in the total count. As the number of points becomes large, the ratio of total hits to the total count will converge to the actual area. The result is actually a fraction of the total “target” area,
Fig. 6.1
so that if this area is known, then the desired area is simply the resulting fraction times the total area. In our problem the total area is one; hence the resulting fraction should converge to the answer of ![]()
The digital computer program for this problem used the following pattern. Using a standard random number generator, a random number between 0 and 1 was selected. This number was assumed to be the abscissa of the first point. Another random number was selected which was interpreted to be the ordinate of the random point. The point was considered to fall within the desired area if the random ordinate was less than the value for the ordinate computed for the random abscissa using the equation of the curve.
If the random point happens to fall exactly on the curve, then some policy must be established to decide how the point is to be counted. The alternatives are to consider such a point as a hit or a miss or some fraction of a hit. In this example problem, the policy was set to consider these points as one-half a hit. Actually if the number of trials is large, then any decision policy will have little consequence on the result.
The digital computer repeats the above process several thousand times so that a large number of points is obtained. In the example problem an approximate value for the area was printed out every 500 trials for a total of 5,000 samples. Figure 6.2 shows the results in graphical form. It is probably of interest to know that the time required to run this problem on an IBM/1130 computer was something less than three seconds, excluding printing time.
Fig. 6.2
The second example to be presented in this section illustrates the application of the Monte Carlo method to a steady-state boundary value problem. Consider a homogeneous uniform plate of length l and width w. The sides are insulated, and one end is held at 0°F while the other is at 250°F. The problem is to determine the steady-state temperature distribution. This problem is two-dimensional since variations normal to the plate will be neglected. The analytical solution for this problem is easily determined to be a linear temperature distribution along the bar. It may seem that we are killing a moth with a cannon in this problem, but it is useful in illustrating the method. Specifically the procedure to be used is commonly known as a random walk method.
Before we continue with the example, a few comments should be made about the method in general. At the discretion of the investigators, the region comprising the problem is subdivided into a square mesh, as indicated in Fig. 6.3. Rather than show the rectangular region representing the plate problem, an arbitrarily shaped region has been illustrated. Each intersection point of the mesh inside the region of interest is a point at which the temperature may be determined by the random walk method. From each point there are four possible paths or steps to a neighboring point. It should be evident that the finer the mesh, the more detailed the resulting temperature distribution will be. However, as will become apparent, the finer the mesh, the longer the computation time required to solve the problem. As a result the investigator is faced with the ever-present problem of deciding between increased accuracy and computation time.
Once the mesh is established, the procedure is to select one of the mesh nodes as a starting point. One of the four possible steps from that node is selected in a random manner which moves the point to the new position. From the new position another random step is made in any of the four possible directions. This process is repeated many times, and the path from the starting point will wander randomly over the region, thus the name random walk. The random walk continues until the path meets a boundary of the region. If the boundary condition at this point is one of an insulated wall, then the point is reflected back into the region and the walk continues. If the boundary condition prescribes a fixed temperature, then this temperature is recorded as a score and another walk is started from the same initial point. The walk is also terminated whenever another point is hit for which the temperature has already been calculated. The temperature of this point is included in the calculations as a score in the same way as the temperature of boundaries.
Fig. 6.3
Fig. 6.4
After a large number of walks have been made from a single starting point, the temperature is computed by dividing the total score by the total number of walks. This method is repeated for each mesh point until the entire region has been covered.
Fig. 6.5
Returning to the example described earlier, the problem was set up using a 10 × 20 mesh to describe the plate. The problem is shown schematically in Fig. 6.4. Using the random walk method, the temperature at the central mesh point was computed. The results are shown in Fig. 6.5, which presents the computed temperature for every 100 random walks, so that the convergence of the method may be visualized.
One of the primary difficulties with this method is the excessive time required for the computations. However, a new approach has been recently devised which reduces the computer run times by nearly an order of magnitude. This method is the floating random walk† procedure and appears to be an extremely valuable innovation.
Throughout the history of applied mathematics, approximate methods for solving differential equations have received considerable attention. At present most of the widely known procedures have been unified into one standardized procedure termed the method of weighted residuals.‡ Essentially the above-mentioned methods are based on a procedure of selecting a series of standard functions with arbitrary coefficients. This series is used as an approximate solution to the differential equation. These solutions are then forced to satisfy the differential equation by any one of several methods which are based on minimizing the error of the “fit.” This procedure leads to a set of equations for the arbitrary or undetermined coefficients.
With regard to boundary conditions, the approximate solution should preferably satisfy them completely; however, this is not an absolute requirement. It should be clear that if all the boundary conditions are satisfied, the approximate solution will give a more reasonable fit. One convenient method of selecting functions which satisfy the boundary conditions of a problem is to choose them so that each one satisfies one or more of the conditions and is homogeneous at the other boundary points. When all of these functions are combined to form the complete approximate solution, all of the boundary conditions may be satisfied. Another common approach is to use the boundary conditions themselves to generate additional equations for the arbitrary coefficients.
Lord Rayleigh† has given an approximate method for finding the lowest natural frequency of a vibrating system. The method depends upon the energy considerations of the oscillating system.
From mechanics it is known that, if a conservative system (one that does not undergo loss of energy throughout its oscillation) is vibrating freely, then when the system is at its maximum displacement the kinetic energy is instantaneously zero, since the system is at rest at this instant. At this same instant the potential of the system is at its maximum value. This is evident since the potential energy is the work done against the elastic restoring forces, and this is clearly a maximum at the maximum displacement.
In the same manner, when the system passes through its mean position, the kinetic energy is a maximum and the potential energy is zero. By realizing these facts it is possible to compute the natural frequencies of conservative systems.
To illustrate the general procedure, consider the simple mass-and-spring system shown in Fig. 8.1. Let V be the potential energy and T be the kinetic energy of the system at any instant. We then have
since the spring force is given by Kx, where K is the spring constant. The kinetic energy is
Let the system be executing free harmonic vibrations of the type
Now at the maximum displacement
Fig. 8.1
Hence, from (8.1) and (8.2), we have
where VM denotes the maximum potential energy.
Now, when the system is passing through its equilibrium position, we have
Hence we have
Now the total energy in the system is the sum of the kinetic and potential energies. In the absence of damping forces this total remains constant (conservative system). It is thus evident that the maximum kinetic energy is equal to the maximum potential energy, and hence
or
We thus find
for the natural frequency of the harmonic oscillations. The above illustrative example shows the essence of Rayleigh's method of computing natural frequencies. The method is particularly useful in determining the lowest natural frequency of continuous systems in the absence of frictional forces.
The method will now be applied to determine the natural frequencies of uniform beams.
Consider a section of length dx of a uniform beam having a mass m per unit length. The kinetic energy of this element of beam is given by
since ∂y/∂t is the velocity of the element and mdx is its mass. The entire kinetic energy is given by
where s is the length of the beam.
Consider an element of beam of length dx as shown in Fig. 8.2.
If the left-hand end of the section is fixed, the bending moment M turns the right-hand end through the angle ϕ and the bending moment is proportional to ϕ; that is, we have
where k is a constant of proportionality. If now the section is bent so that the right-hand end is turned through an angle θ, the amount of work done is given by
Now the slope of the displacement curve at the left end of the section is ∂y/∂x, and the slope at the right-hand end is
by Taylor’s expansion in the neighborhood of x.
Hence, neglecting higher-order terms, we have
Substituting this into (8.14), we have
for the potential energy of the section of the beam. However, we have
Hence, substituting this into (8.17), we obtain
Fig. 8.2
The potential energy of the whole beam is
If now the beam is executing harmonic vibrations of the type
we have, on substituting this into (8.12),
for the maximum kinetic energy, and, substituting into (8.20), we obtain
for the maximum potential energy.
The natural angular frequency ω can be found if the deformation curve υ(x) is known by equating the two expressions (8.22) and (8.23). The procedure is to guess a certain function υ(x) that satisfies the boundary conditions at the ends of the beam and then equate expressions (8.22) and (8.23) to determine ω.
As an example of the general procedure, consider the system of Fig. 8.3. This system consists of a heavy uniform beam simply supported at each end and carrying a concentrated mass M at the center of the span. The boundary conditions at the ends are
This expresses the fact that the displacement and bending moments at each end are zero. To determine the fundamental frequency, let us assume the curve
where A is the maximum deflection at the center. This assumed curve satisfies the boundary conditions and approximates the first mode of oscillation.
Fig. 8.3
From (8.22) the maximum kinetic energy of the beam is
where
is the mass of the beam. The maximum kinetic energy of the central load is
Hence, for the whole system, the total maximum kinetic energy is
From (8.23) the maximum potential energy of the system is
We have
Hence
Equating expressions (8.29) and (8.32), we obtain
This gives the fundamental angular frequency ω. There are two interesting special cases:
1. If the central load is zero, then M = 0 and we have
This turns out to be the exact expression which would be obtained by the use of the differential equations of Chap. 13, Sec. 12.
2. If the beam is light compared with the central load, then ![]() and we have
and we have
Rayleigh’s method is very useful in the computation of the lowest natural frequencies of systems having distributed mass and elasticity. The success of the method depends on the fact that a large error in the assumed mode υ(x) produces a small error in the frequency ω. If it happens that we choose υ(x) to be one of the true modes, then Rayleigh’s method will give the exact value for ω. In general it may be shown that Rayleigh’s method gives values of the fundamental frequency ω that are somewhat greater than the true values.
Consider the general linear differential equation of motion for a one-dimensional‡ continuous system, that is,
where L = linear differential spatial operator
u(x,t) = dependent variable
If we were considering the transverse motion of a string, the operator L would be
whereas if we wanted to describe the transverse oscillations of a beam, we would have
To simplify this discussion we will limit ourselves to harmonic solutions of (9.1) only; that is, we are assuming that
Thus, with this assumption, Eq. (9.1) reduces to
Even with this reduction, Eq. (9.5) is difficult to solve exactly in many two-dimensional cases. That is particularly true in those cases where the spatial region is nonseparable.†
To proceed with the collocation method, a solution to (9.5) is assumed as follows:
where the ai are arbitrary constants and the ϕi(x) are known functions selected by the user which should be constructed in dimensionless form. It is desirable that these functions satisfy the boundary conditions imposed on (9.1). At this point (9.6) is substituted into (9.5) to yield
where E is the error resulting from the fact that the assumed solution is only an approximate solution. The collocation procedure is to force the error to be zero at N points xk lying within the region over which the solution is desired. These points are usually equally spaced, and the result of this procedure is a system of N equations for the N arbitrary coefficients ai. If the exact solution were used, the error would be identically zero over the entire interval.
Thus if we set (9.7) to zero at the N points xk we have
If we utilize matrix notation, we may write (9.8) in the form
where [Aij] = [Lϕj(xi)]
[Bij] = [ϕj(xi)]
(a) = vector of unknown coefficients, ak
By matrix manipulations, we can write (9.9) in the form
where [c] = [A]–1[B]
λ=–1/ω2
which indicates that the problem has been reduced to a standard eigenvalue problem. In terms of the physical system, each eigenvalue of (9.10) represents the reciprocal of a natural frequency, and each eigenvector represents a mode shape. We have set up the eigenvalue problem of (9.10) so that the largest eigenvalue will correspond to the lowest natural or fundamental frequency. This formulation was chosen since most iteration procedures for determining eigenvalues converge to the one with the largest magnitude first (see Chap. 3, Sec. 34, or Chap. 6, Sec. 7). It is also usually true that as the smaller eigenvalues are computed, many routines lose accuracy. Since an analyst is usually concerned with the fundamental and first few overtones, the problem should be structured as above so that these values are determined first.
As for eigenvectors, we mentioned that they are associated with the modes of the various vibrations. In the case of a vibrating-string problem, the largest eigenvalue should yield an approximate value for the fundamental frequency; the corresponding eigenvector should yield the coefficients for the ϕi which will combine to approximate the fundamental mode which is a sine function.
To illustrate this method, consider a vibrating string of length l and L is given by (9.2). The problem to be solved is
where u(x,t) = displacement from equilibrium.
Equation (9.11) is reduced to
by the substitution
which assumes harmonic vibrations. The boundary conditions are for fixed ends; that is,
![]()
Applying these to (9.13) gives
At this point we assume an approximate function of the form
with
both of which satisfy (9.14). The functions have been chosen in dimensionless form to conform with the basic requirements of this method. Following the collocation procedure, Eq. (9.15) is substituted into (9.12) to obtain the error term
Since we have used two functions to form the approximate solution, two points in the interval ![]() must be chosen at which E will be set to zero. For convenience the points x1= l/3 and x2= 2l/3 will be used. Evaluating the coefficient matrices in (9.9) gives
must be chosen at which E will be set to zero. For convenience the points x1= l/3 and x2= 2l/3 will be used. Evaluating the coefficient matrices in (9.9) gives

At this point we may write (9.9) as
Rearranging terms, (9.18) becomes
Now if we let
and premultiply by [A]–1, we have the eigenvalue problem
The eigenvalues and associated eigenvectors are

From (9.20) we see that
Fig. 9.1
Fig. 9.2
where a′ = arbitrary amplitude for the fundamental

which indicates an error of 4.5 percent in the natural frequency as predicted by the approximate solution (9.16). Figures 9.1 and 9.2 show the approximate and exact solutions in dimensionless form for the fundamental and first harmonic. As shown by these figures, the two-term approximation yields a very reasonable fit to the exact solution.
This approximate technique is generally approached from energy considerations. For purposes of illustration we will concern ourselves with the specific example of the vibrations of a cantilever beam of length l. The total kinetic and potential energy are
where m(x) = mass per unit length
u(x,t) = deflection from equilibrium
EI(x) = flexural rigidity
As in the collocation method, we assume an approximate solution in the form
where ϕk are the approximate functions and qk are general time functions. Substituting this into (10.1) gives
Now, to obtain the equation of motion, we make use of Lagrange’s equation in the form
From (10.3) we see that
Likewise from (10.3) we find
Computing the first term for (10.4) from (10.5) gives
Combining all these results into (10.4) yields
If we now restrict ourselves to periodic time functions
then (10.8) reduces to
The system of equations given by (10.10) represents n linear algebraic equations in the n unknowns ak. If we now introduce the following matrices
the system of (10.10) becomes
which is a standard eigenvalue problem of the form (9.10).
As an example of this method, consider a cantilever beam for which the mass per unit length and the flexural rigidity are constant. If the beam is mounted at x = 0 with x = l being the free end, the boundary conditions are

For an approximate solution, let us use a two-term expansion for (10.2) in which
It should be noted that these functions do not satisfy all the boundary conditions; however, this is not an absolute requirement. Substituting these functions into (10.11), we have
In the form of the standard eigenvalue problem (9.10), our problem reduces to
where
Using standard procedures to find the eigenvalues and eigenvectors yields
From the largest eigenvalue we find that the fundamental frequency is
Comparing this with the exact solution from Chap. 13, Sec. 7, indicates an error of 0.85 percent. Substituting into (10.2) gives the modal solution
where A, ψ = arbitrary constants.
This method was developed by B. Galerkin in 1915† and is perhaps the most widely used approximate method today. The procedure is similar to the collocation method, and we shall use the same approach to illustrate its derivation.
Again, for convenience, we shall assume only one spatial dimension since the extension to more dimensions is a straightforward procedure. We assume that the system under consideration may be described by the equation
where L and u are the same as for (9.1). This equation reduces to
under the assumption of harmonic solutions [cf. (9.4)]. We continue along the same lines and construct an approximate solution
Substituting this into (11.2) yields the error
At this point the procedure differs from the collocation method in that the Galerkin method requires the error to be orthogonal with all the approximating functions ϕk. Specifically this requirement is
where a and b are the limits of the interval of x over which the problem is defined. Equation (11.5) represents n linear algebraic equations for the n unknowns ak.
Substituting (11.4) into (11.5) and rearranging terms gives
Introducing matrix notation

we have
which again may be reduced to the eigenvalue problem
where [C] and λ are defined in (9.10).
To illustrate this method, let us consider the same problem used in Sec. 9. In that problem we were attempting to solve the wave equation for the vibrating string of length l. In this problem

and it was assumed that
The interval for x is 0 to l. Evaluating the coefficient matrices, we have

and converting into the form of (11.8) we have
The eigenvalues and their associated eigenvectors for this problem are
At this point it is interesting to note that the eigenvectors are identical with those obtained in the collocation method. From the largest eigenvalue, we obtain the following approximation for the fundamental frequency:
indicating an error of only 0.6 percent, which is nearly an order-of-magnitude improvement over the result using the collocation method. The error in the first harmonic is 3.0 percent.
1. Repeat the steps of Sec. 2 to obtain the formula for a least-squares fit for a second-order equation.
2. Using the least-squares method, find the coefficients for the best-fit second-order equation for the following data:

3. Integrate y′ = –0.5y, y(0) = 1 from 0 to 2 by the Euler-Cauchy method using a step size of 0.5.
4. Repeat Prob. 3 with h = 0.2.
5. Assume that you have access to a digital computer that has a random number generator which will generate random numbers over the interval 0 to 1. Discuss how you would set up the following problems for solution by the Monte Carlo method:
![]()
6. A string of length s under a tension t carries a mass M at its midpoint. Using Rayleigh’s method, determine the fundamental frequency of oscillation. (HINT: Obtain the total potential and kinetic energies, etc.)
7. A uniform beam is built in at one end and carries a mass M at its other end. Use Rayleigh’s method to determine the fundamental angular frequency of oscillation.
8. A uniform beam is hinged at x = 0 and is elastically supported by a spring whose constant is K at x = 5. Apply Rayleigh’s method to determine the fundamental frequency.
9. Find an approximate value for the fundamental frequency of a vibrating string using the collocation method. Use the same two approximating functions introduced in the text as well as the third function ϕ3 = x(l – x)2/l3. For the collocating points use ![]() .
.
10. Solve Prob. 9 by using Galerkin’s method and the same approximating functions.
11. Solve the sample beam problem of Sec. 10 by the collocation method.
12. Solve Prob. 11 using Galerkin’s method.
13. Use the Rayleigh-Ritz method to solve for the fundamental frequency of the vibrating string of Sec. 9 with the same approximating functions. Compare your answer with those obtained by the collocation and Galerkin methods.
1915. Galerkin, B. G.: Sterzhni i plastiny. Ryady v nekotorykh voprosakh uprogogo ravnovesiya sterzhnei i plastin (Rods and Plates. Series Occurring in Some Problems of Elastic Equilibrium of Rods and Plates), Tekh. Petrograd, vol. 19, pp. 897–908; Translation 63–18924, Clearinghouse for Federal Scientific and Technical Information.
1933. Temple, G., and W. G. Bickley: “Rayleigh’s Principle,” Oxford University Press, New York.
1937. Timoshenko, S.: “Vibration Problems in Engineering,” D. Van Nostrand Company, Inc., Princeton, N.J.
1938. Duncan, W. J.: “The Principles of Galerkin’s Method,” Gt. Brit. Aero. Res. Council Rept. and Memo. No. 1848; reprinted in Gt. Brit. Air Ministry Aero Res. Comm. Tech. Rept., vol. 2, pp. 589–612.
1951. “Monte Carlo Method,” National Bureau of Standards Applied Mathematics Series, vol. 12.
1956. Brown, G. W.: Monte Carlo Method, in E. F. Bechenbach (ed.), “Modern Mathematics for the Engineer,” McGraw-Hill Book Company, New York, pp. 279–306.
1956. Sokolnikoff, I. S.: “Mathematical Theory of Elasticity,” 2d ed., Chap. 7, McGraw-Hill Book Company, New York.
1965. Kuo, S. S.: “Numerical Methods and Computers,” Addison-Wesley Publishing Company, Inc., Reading, Mass.
1966. Finlayson, B. A., and L. E. Scriven: The Method of Weighted Residuals—A Review, Applied Mechanics Reviews, vol. 19, no. 9, September, pp. 735 ff.
† All numerical computations presented in this chapter were made on an IBM/1130 computer located at the University of Redlands, Redlands, Calif.
† The term ill-conditioned is used to denote the condition that the determinant of coefficients becomes very small.
‡ For a more complete discussion, the reader is referred to Kuo, 1965 (see References).
† Kuo, 1965, Chap. 7 (see References).
† This suggestion was made by Robert D. Engel, Assistant Professor of Engineering Science at the University of Redlands, Redlands, Calif.
† This example and the following one were worked out in detail by Bruce Sinclair, an undergraduate engineering major at the University of Redlands, Redlands, Calif.
† A. Haji-Sheikh and E. M. Sparrow, The Floating Random Walk and Its Applications to Monte Carlo Solutions of Heat Equations, SIAM Journal of Applied Mathematics, vol. 14, no. 2, pp. 370–389, March, 1966.
‡ An excellent review of this procedure is given in B. A. Finlayson and L. E. Scriven, The Method of Weighted Residuals—A Review, Applied Mechanics Reviews, vol. 19, no. 9, September, 1966.
† Lord Rayleigh, “Theory of Sound,” 2d ed., vol. I, pp. Ill, 287, Dover Publications, Inc., New York, 1945.
† The material in this section and in Sec. 10 was organized with the assistance of Michael Gollong, a graduate of the Mathematics Department of the University of Redlands, Redlands, Calif.
‡ This method is equally applicable to two- and three-dimensional systems.
† For an excellent example of applying approximate techniques to nonseparable domains, see Daniel Dicker, Solutions of Heat Conduction Problems with Nonseparable Domains, Journal of Applied Mechanics, vol. 30, no. 1, December, 1963.
† Cf. Galerkin, 1915 (see References).