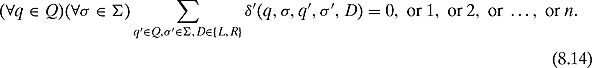Quantum Computing for Computer Scientists

8 Theoretical Computer Science

The meaning of the world is the separation of wish and fact.

Kurt Gödel, quoted in Hao Wang’s A Logical Journey: From Gödel to Philosophy, page 309 ¹

In a sense, theoretical computer science is uniquely qualified to study quantum computing. After all, Alan Turing and the other founders of theoretical computer science studied formal computation long before engineers actually produced a real-life computer. At present, large-scale quantum computers are not a reality yet. Nevertheless, the theoretical analysis of quantum computability and complexity is well on its way.

In Section 8.1, we start with a quick review of some of the basics of deterministic and nondeterministic Turing machines and the complexity classes that they engender. However, we shall discuss them in a way that is easily generalizable for our purposes. Section 8.2 moves on to probabilistic Turing machines and their zoo of complexity classes. Our main objective is found in Section 8.3, where we meet quantum Turing machines and their complexity classes. We shall also state some basic theorems and ideas about quantum computation.

8.1 DETERMINISTIC AND NONDETERMINISTIC COMPUTATIONS

Theoretical computer science deals with the question, “What is computable?” We must immediately qualify the question: “computable according to which model of computation?” It turns out that if we omit the question of efficiency, all sufficiently complicated formal models of computation can simulate each other. However, in order to fix our ideas and notation, we have to stick with one and work with it. For historical reasons, we choose the Turing machine model.

We are going to assume that our reader already knows the basic “yoga” of Turing machines (see Figure 8.1). The simple facts are that a Turing machine is a device with a two-way infinite tape that serves as a place to read input, write output, do scrap work, and to store a potentially infinite amount of information. The tape is split into a one-dimensional infinite array of boxes, each of which can hold exactly one symbol at a time. The machine can be in one of a finite set of states at any given moment and “see” one box at a time. It can move along the tape in any of two directions: left (L) or right (R). At each time step, the machine can read one box on the tape, write on that box, move, and change states.

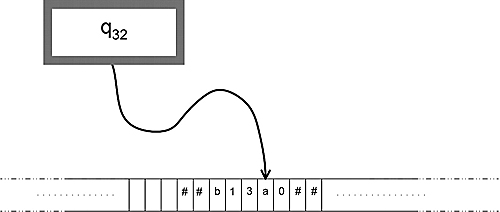
Figure 8.1. Turing machine.

Formally, a deterministic Turing machine M is a 6-tuple

where Q is a finite set of states, ∑ is a nonempty finite alphabet that includes a symbol # which we call “blank”; q_start, q_accept, q_reject are all elements of Q; and a transition function δ,

For a given and if δ(q, σ) = (q′, σ′, D), we mean that

If Turing machine M is in state q and the eye encounters symbol σ, then the machine should exchange symbol σ for σ′, move one box in the direction , and enter state .

Equivalently, we can write the function δ as

where

Because for every and , δ has exactly one output , our (deterministic) transition functions must satisfy the following requirement:

It is not hard to see that any δ is equivalent to a δ′ that satisfies Equation (8.5).

The set of all words in ∑ without blanks is denoted (∑ −{#})*. An input string from this set is placed on the tape at a specific starting place. The rest of boxes on the tape are assumed to have blanks. The Turing machine is then “let loose” from state q_start and follows the rules that are described by δ′. There are three possibilities that can occur to such a machine: (1) the Turing machine can reach state q_accept, (2) the Turing machine can reach state q_reject, or (3) the Turing machine can enter an infinite loop and never reach q_accept or q_reject. Think of a Turing machine as solving a decision problem by being presented with an input and then examining which state the machine will enter. Each such machine determines a language of those words that the machine accepts.

Although there are many other models of computation, we are comfortable with the deterministic Turing machine because of the following thesis:

Thesis. The Classical Church–Turing Thesis states that any problem that is intuitively computable can be computed by a deterministic Turing machine.

This thesis cannot be proved because it is impossible to give an exact definition of what is meant by “intuitively computable.” However, most researchers agree that the thesis is a true statement.

In this chapter, we work through several examples and present some exercises involving Turing machines that follow the same theme. These machines are build up to a crescendo until we reach a Turing machine version of the double-slit experiment.

Example 8.1.1 Consider the following problem: a word of odd length in the alphabet ∑ ={0, 1, #} is given as input and we are asked if this string contains a “1.” Words that have at least one “1” are accepted and words that are all “0’s” are rejected. We are deciding the language

The usual convention is that the head of the Turing machine is at the leftmost letter of the input, but we shall be slightly unconventional and assume that the head is reading the center symbol of the odd-length string.

Let us describe a deterministic Turing machine to solve this problem. The machine should start with its head in the center.² The head should move to the left looking for a “1.” If the left end of the word is reached, then the head should move to the right searching for a “1.” If a “1” is found, then the computer should enter q_accept. If the head reaches the right end of the word without finding a “1,” then the machine goes into state q_reject. By convention, if the machine enters a halting state, then the head just stays there. This Turing machine will not change anything on the tape.³

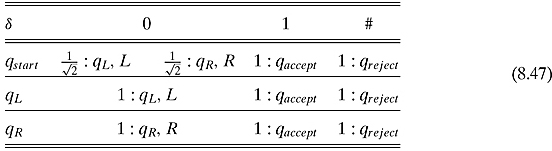
Formally, the set of states will be Q = {q_start, q_accept, q_reject, q_L, q_R}and δ is defined by the following table:

Each row tells what should be done in that state. The columns describe which symbol is seen. The entry tells us which state to enter and in which direction to move. In words, the search begins by going to q_L that continually moves to the left. When the machine hits #, the state enters q_R that always moves to the right. At any time, if a “1” is found, the machine enters q_accept. A configuration (also called a snapshot,or instantaneous description) of a Turing machine contains the complete information of the machine at a particular time step. There are three pieces of information that have to be described:

the tape’s contents,

the state of the machine, and

the position of the head of the Turing machine.

We shall summarize all three pieces of information by writing the contents of the tape and the state exactly to the left of the position that the machine is reading. An example of a configuration is

which means that #000010010010101# is on the tape, the state is q₄₅, and the head is reading the ninth symbol which is a “0.” (We will later need the obvious fact that all the configurations can be put in lexicographical order.)

A typical computation, i.e., a sequence of configurations, might look like this:

In the worst-case scenario, for an input of size n, the machine will have to perform operations before a “1” is found or before it realizes that no “1” is in the word. We shall revisit this example in the next section.

Exercise 8.1.1 Write a deterministic Turing machine that determines if the input string has a substring “101.” You might have to begin by moving off the center a little. For an input of size n, how many moves does the Turing machine have to make in the worst case?

What can and cannot be computed is not our exclusive interest. Another important issue is what can be computed efficiently. We shall be looking at different sets of problems of various degrees of difficulty. A complexity class is a set of problems that can all be solved by a certain model of computation within certain efficiency bounds. By examining and comparing different complexity classes, we shall derive principles about different models of computation.

The number of computational time steps that a machine must undergo before it enters an accepting or rejecting state is the number of steps for the computation. The number will usually depend on the size of the input. Hence we describe a function from the size of an input to the number of steps in the computation. Such a function might be a polynomial. If every input to a problem can be solved within a polynomial number of steps, then the problem is said to be solvable in a polynomial number of steps.

Complexity Class. P is the set of problems that can be solved by a deterministic Turing machine in a Polynomial number of steps.

This complexity class is important because of the following thesis:

Thesis. The Cook–Karp Thesis states that problems that are “tractably computable” can be computed by a deterministic Turing machine in polynomial time, i.e., are in P.

This thesis also cannot be proved because it is impossible to give an exact definition of what we informally mean by “tractably computable.” In fact, one would be hard-pressed to argue that a problem that demands n¹⁰⁰ steps for an input of size n is tractable. Nevertheless, n¹⁰⁰ is a function that grows slower than any nontrivial exponential function (including 1.001ⁿ).

Exercise 8.1.2 Find the least n such that 1.001ⁿ ≥ n¹⁰⁰.

There are other interesting models of computation. A nondeterministic Turing machine is similar to a deterministic Turing machine, but we eliminate the requirement that at every step of the computation, the machine proceeds to exactly one subsequent step. In other words, for a given and , the machine can enter into a subset (possibly empty) of Q× ∑ ×{L, R}. Formally, a nondeterministic Turing machine M is a 6-tuple

where Q, ∑, q_start, q_accept, q_rejectare as before and δ is a function

where is the powerset function. For a given and if , we mean that

If Turing machine M is in state q and the eye encounters symbol σ, then one of the actions that the machine could perform is to exchange symbol σ for σ′, move one box in the direction , and enter state .

Just as we rewrote function (8.2), we might also rewrite function (8.11) as

where {0, 1}^{Q×∑×{L,R}} is the set of functions from Q× ∑ × {L, R} to {0, 1}. Whereas δ in function (8.11) chooses a subset of Q× ∑ ×{L, R}, in function (8.12) chooses the characteristic function of the same subset. We may write this similar to function (8.3):

but this time we do not insist on the requirement that δ′ must satisfy Equation (8.5). In other words,

The largest n is |Q× ∑ ×{L, R}|.

Exercise 8.1.3 Show that every nondeterministic Turing machine is equivalent to a nondeterministic Turing machine that bifurcates into exactly two states at every time step. Another way of stating this is that the summation in Equation (8.14) is exactly 2.

In nondeterministic Turing machines, a computation can perform one of several different tasks at each time step. We say that a word is accepted by such a machine M if there exists a computational path that ends in q_accept.

Complexity Class. NP is the set of problems that can be solved by Nondeterministic Turing machines in a Polynomial number of steps.

Because every deterministic Turing machine is also a nondeterministic Turing machine (i.e., any δ′ that satisfies Equation (8.5) also satisfies Equation (8.14)), every problem that can be solved in polynomial time by a deterministic Turing machine can also be solved by a nondeterministic Turing machine in polynomial time. Hence, . The million-dollar question is whether P = NP. Alas, this question shall not be answered in this text.

If a problem has a “yes” answer, then the complement of the problem has a “no” answer, and vice versa. Hence, we define the following:

Complexity Class. coP is the set of problems whose complements can be solved by a deterministic Turing machine in a Polynomial number of steps.

Complexity Class. coNP is the set of problems whose complements can be solved by a Nondeterministic Turing machine in a Polynomial number of steps.

If we can solve a problem with a deterministic Turing machine, then by swapping the q_accept and the q_reject states, we can solve the complement of the problem. From this we know that P = coP. Notice that this trick does not work for nondeterministic Turing machines: a nondeterministic Turing machine accepts a word if there exists at least one computational path that ends with an accepting state. If a computation has all but one path ending with an accepting state, then the word would be accepted. If we swapped the accepting and rejecting states, then all but one path would end in a rejecting state and exactly one path would end in an accepting state. Because of the single accepting state, the computation would also be accepted. So a word would be accepted by both a problem in NP and its corresponding problem in coNP. This cannot be. In conclusion, although it is known that P = coP, we do not know if NP = coNP. In fact, most researchers believe that NP≠ coNP. For the same reason that , we have that

We are interested in not only how much time a computation uses but also how much of the Turing machine’s infinite tape is used.

Complexity Class. PSPACE is the set of problems that can be solved by deterministic Turing machines using a Polynomial number of SPACEs on the tape.

We could have written the same definition using a nondeterministic Turing machine. It is a consequence of Savitch’s theorem ⁴ that when looking at space (as opposed to time), the distinction between deterministic polynomial space and nondeterministic polynomial space is not essential.

Because a (nondeterministic) Turing machine can change only one box per time step, machines that use p(n) time steps to solve a problem cannot use more than p(n) spaces of its infinite tape. Hence, we have . For similar reasons, .

We may summarize the inclusions of the complexity classes that we have defined so far as follows:

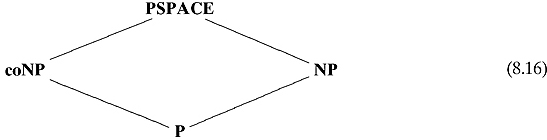
A line between one complexity class and another means that the lower one is included in the higher one. It must be stressed that it is unknown if any of these inclusions are proper inclusions.

8.2 PROBABILISTIC COMPUTATIONS

Probabilistic computations occur when there is a random choice among several possible transitions during a computation. Probabilities can be described with real numbers in the interval . No computer’s memory can hold an arbitrary real number,⁵ and so this set is beyond our bounds. Some tractable computable subset of [0, 1] is needed. Consider the set of tractably computable real numbers. These are real numbers such that a deterministic Turing machine can calculate their nth digit in polynomial time. We shall be concerned with

A probabilistic Turing machine is a Turing machine that randomly performs one of several tasks at each time step. Formally, a probabilistic Turing machine is a 6-tuple

where everything is as before except the transition function δ. δ is now a function

where is the set of functions from the set of all possible actions, Q× ∑ × {L, R} . For a given state and symbol, δ will describe the probabilities of the moves that the machine can make. An arbitrary function from Q× ∑ × {L, R} to is not good enough. We must also restrict δ so that the sum of all the probabilities is equal to 1. δ is restricted as follows: as an analogy to functions (8.3) and (8.13), we define

where

if and only if

It is not hard to see that for every δ there is a unique δ′ that performs the same job. However, we insist that δ′ satisfy the following requirement (analogous to Equations (8.5) and (8.14)):

This means that at every state and when viewing every symbol, the sum of all the probabilities of possible moves is equal to 1.

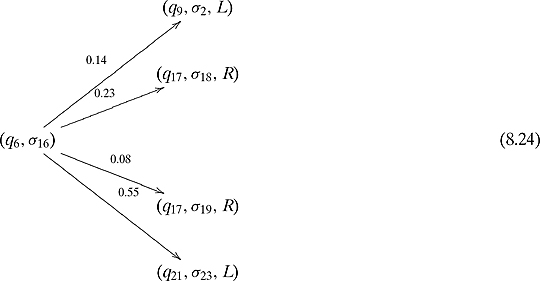
How does this machine work? At every time step, the machine will be in a certain state, say q₆, and will be looking at a certain symbol, say σ₁₆, on the tape. The function δ gives the nonzero probabilities where we list all possibilities in lexicographical order using the ordering of Q, ∑, and{L, R}.

A real number between 0 and 1 is randomly chosen. This real number will determine which operation the Turing machine should perform. For example, if the real number is 0.12, which is between 0.0 and 0.14, then the machine will perform the (q₉, σ₂, L) operation. If the real number is 0.39, which is between 0.14 + 0.23 and 0.14 + 0.23 + 0.08, then the machine will perform the (q₁₇, σ₁₉, R) operation.

Exercise 8.2.1 Following the spirit of Exercise 8.1.3, show that every probabilistic Turing machine is equivalent to a Turing machine that can enter one of exactly two configurations. The machine can choose one of these two configurations by flipping a fair coin or by looking at a tape with a random sequence of “0’s” and “1’s.” The machine will choose one operation if there is a “0” and the other one if there is a “1.” (Hint: Write the probability r as a finite binary sequence.)

As with a regular Turing machine, the input will be placed on the tape, the computer will be put in the q_start state, and then the machine will “run.” At each time step, an arbitrary real number is randomly chosen and the Turing machine performs the appropriate next action. At some point, the computer might enter a halting state and stop.

Exercise 8.2.1 Following Example 8.1.1, let us describe a probabilistic Turing machine that solves the same problem. Because we are dealing with probabilistic algorithms, we shall permit false negatives, i.e., the machine might report that there is no “1” when, in fact, there is one.

We place the probability of performing a given action to the left of the action.

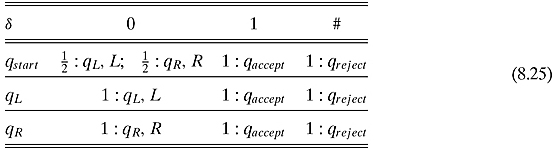
How does this work? When the computer starts, 50% of the time the head moves to the left and 50% of the time it moves to the right. The machine will examine boxes and hence will give a correct answer more than half the time. The machine will have to go through time steps in the worst case.

Exercise 8.2.2 Describe a probabilistic Turing machine that does not generate any false negatives. The machine should start by randomly moving to the left or to the right. However, regardless of direction, if it hits the left end or the right end of the word without finding a “1,” it should reverse itself. Make sure that the machine does not end up in an infinite loop! Show that in the worst case, there will have to be time steps.

Exercise 8.2.3 Describe a probabilistic Turing machine that determines if there is a substring “101” in the input string. Do the same for a solution that permits false negatives and one that does not permit false negatives.

Let us look at the different complexity classes that are defined for probabilistic Turing machines. Because of the probabilistic nature of the execution of such a Turing machine, there is a chance that when you execute the same program on the same input, there will be a different final state, i.e., there is a chance that the Turing machine will produce an error. An input should be accepted by a Turing machine, but the machine rejects it (false negative), or an input should be rejected and the machine accepts it (false positive).

We shall also restrict our attention to those probabilistic Turing machines that stop within a polynomial number of time steps in the length of the input.

In terms of permitting errors, the largest class of problems that we will be interested in are those that can be solved by probabilistic Turing machines that allow some false negatives and some false positives.

Complexity Class. BPP is the set of problems that can be solved by a Probabilistic Turing machine in Polynomial time with the possibility of some errors. To be precise, if M is a probabilistic Turing machine that decides and if x is a word, then

and

We shall discuss the use of the fraction presently.

A smaller set of problems are those that can be solved with a probabilistic Turing machine that permits false positives but does not permit false negatives.

Complexity Class. RP is the set of problems that can be solved by a probabilistic (i.e. Random) Turing machine in Polynomial time with only the possibility of false negatives. In other words, if M is a probabilistic Turing machine that decides and if x is a word, then

and

We can also consider problems that can be solved by probabilistic Turing machines that permit only false positives.

Complexity Class. coRP is the set of problems that can be solved by a Probabilistic Turing machine in Polynomial time with only the possibility of false positives. In other words, if M is a probabilistic Turing machine that decides and if x is a word, then

and

The easiest problems are those that can be solved by probabilistic Turing machines in which no errors are permitted.

Complexity Class. ZPP is the set of problems that can be solved by a Probabilistic Turing machine in Polynomial time with Zero error. In other words, if M is a probabilistic Turing machine that decides and if x is a word, then there is a less than 50% chance that the machine will finish in a “do not know” state, otherwise if the machine does know

and

It is a fact that .⁶

If we can solve a problem with no errors (ZPP), then we can definitely solve the problem permitting false negatives (RP) and we can definitely solve the problem permitting false positives (coRP). Furthermore, if we can solve a problem permitting only false negatives (RP), then we can definitely solve the problem permitting both false negatives and false positives (BPP). A similar argument can be made for coRP. Thus we have the following inclusion diagram:

It must be stressed that it is unknown if any of these inclusions are proper inclusions.

One might wonder why the fraction plays such an important role here. In fact, we could have used any fraction greater than and the classes of problems would have been the same. The reason for this is the amplification lemma.⁷ The idea is that one can execute the Turing machine a polynomial amount of times and accept or reject the input depending on the results of the majority of executions. This method provides exponential growth in the likelihood of excluding false positives and false negatives.

Let us relate the complexity classes of this section with those of Section 8.1. One can consider a deterministic Turing machine a probabilistic Turing machine that does not make any guesses and always comes up with the right answer. From this, we have that . Another way of thinking about is that if , then at least two-thirds of the computational paths end in q_accept, and if , then all the computational paths end in q_reject. Similarly, one can think of as stating that if , then at least one of the computational paths ends in q_accept, and if , then all the computational paths end in q_reject. Because two-thirds of the computational paths (of an RP computation) are greater than one computational path (of an NP computation), it is not hard to see that . Similarly, .

For every , we can create a machine that traverses all the computational paths and keeps track of the paths ending in q_accept and q_reject. There is no reason to save the path once it is calculated, so we might as well reuse the space. Such a machine will take a very long time to calculate an answer, but it will use only a polynomial amount of space. From this, it can be seen that . By a similar analysis, it can be seen that and .

We can sum up our results with the following diagram.

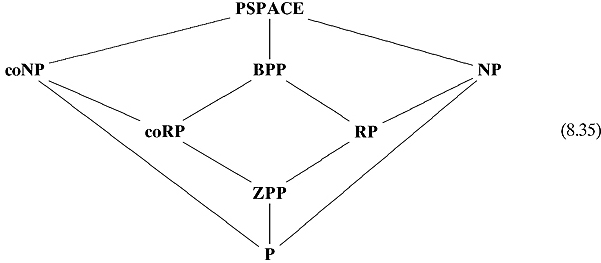
Again, it must be stressed that it is unknown if any of these inclusions are proper inclusions. The relationship between BPP and NP is also unknown.

Because probabilistic Turing machines are so general and because they permit some error (“noise”), we have the following thesis:

Thesis. The Strong Church–Turing Thesis states that any efficient computation that can be performed by any physical machine can be simulated by a probabilistic Turing machine in polynomial time, i.e., in BPP.

We reexamine this thesis at the end of the next section.

8.3 QUANTUM COMPUTATIONS

As you have probably guessed, quantum Turing machines will have something to do with complex numbers. As in the last section, general complex numbers are beyond the reach of a finite machine. Thus, we are in need of the subset of all tractably computable complex numbers consists of those complex numbers such that the nth digit of their real and imaginary parts can be deterministically computed in polynomial time.⁸

At last, we come to the definition of a quantum Turing machine. A quantum Turing machine is a 6-tuple

where everything is as before except the transition function δ′ (analogous to functions (8.3), (8.13), and (8.20))

We require ⁹ that δ′ satisfy (analogous to Equations (8.5), (8.14), and (8.23))

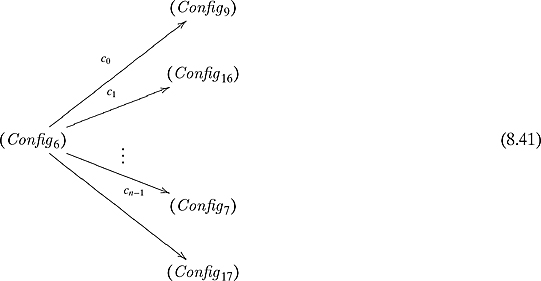
In plain English, a quantum Turing machine is like a probabilistic Turing machine but the probabilities are given as complex number amplitudes.¹⁰ And we require that for any particular and , the sum of those squared norms of the amplitudes equals 1. This can be visualized by a diagram similar to diagram (8.24) but with complex numbers. Another way of thinking about it is to consider what configuration the machine is in and what configurations it will enter with the actions. The complex numbers determine the probabilities of which configuration it will change as follows:

A quantum Turing machine works differently than a probabilistic Turing machine. Rather than carrying out one of the possibilities, it performs all the operations and enters a superposition of all the resulting states. The quantum Turing machine will collapse to a single configuration only when it is measured. In fact, if we observe the state and the contents of the tape of the quantum Turing machine after each step, then a quantum Turing machine will be the same as a probabilistic Turing machine. The difference is that when we do not observe the state and the contents of the tape, the probabilities of performing one operation followed by another sum up as complex numbers (a short review of Section 3.3 would be in order). Hence when we do not observe, there will be interference and superposition of contents of the tape.

Bernstein and Vazirani (1997) have many conventions that they insist their quantum Turing machine follow. There are many different reasons for this. Although these conventions are important for their work, we shall ignore most of them because we want to show only the basic workings of a quantum Turing machine.

There are, of course, many variants of quantum Turing machines, such as machines with many tapes and many tracks. It was shown in Yao (1993) that many of these are polynomially equivalent to the quantum Turing machine described earlier.

Many of the properties that one would want in a Turing machine, such as iteration, subroutines, and looping, are shown to exist with a quantum Turing machine in Bernstein and Vazirani (1997). Some of them are done with great effort. All these different properties are combined to show that one can actually construct a universal quantum Turing machine, i.e., a quantum Turing machine that can simulate¹¹ every other quantum Turing machine. With such a universal quantum Turing machine, we acquire many results similar to those of classical recursion theory.

There is another way of thinking about quantum Turing machines. For a given machine, there is the set of all possible configurations of that machine. We can form a countably infinite dimensional complex vector space from these configurations. The vectors in this vector space will be finite complex linear combinations of configurations.¹² One can think of a vector as a countably infinite sequence of complex numbers indexed by the configurations of the Turing machine, where all but a finite number of the complex numbers are 0.

A classical state of a quantum Turing machine will be a vector for which all but one complex number is 0 and the unique nonzero C_i is 1. This states that the configuration of the Turing machine is Config,. An arbitrary vector in will correspond to a superposition of classical configurations that can be written as

where the sum is over a finite set.

This is fine for states of the system. How does the system itself change? We shall make a countably infinite “matrix” U_M

Every row and column of this matrix will correspond to a possible configuration of the machine.

The entries of the matrix will be the complex numbers that describe the amplitude of going from one configuration to another. That is, c_i, _j will be the amplitude described by δ′ that would change configuration j into configuration i as depicted in diagram (8.41). Obviously, most of the entries of this matrix will be 0.

Definition 8.3.1 A quantum Turing machine is well formed if the constructed U_M preserves the inner product (is an isometry) in .

With a well-formed quantum Turing machine, one is back into the familiar world of unitary matrices. If we let be the initial configuration, then will be a configuration or a superposition of configurations after one time step. will be the (superposition of) configuration(s) after two steps. If the Turing machine runs in time t(n), then we would have to observe the state

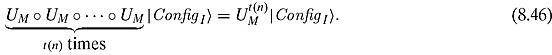
Example 8.3.1 There is nothing particularly quantum about the set of configurations and the matrix acting upon it. In fact, the same can be done for a deterministic Turing machine. In the deterministic case, we will only be concerned with vectors that have exactly one entry as 1 and all others as 0 (note that this is not a subvector space of because it is not closed under addition). The U_M will be such that every column has exactly one 1 and the remaining entries 0.

Exercise 8.3.1 Do a similar analysis to the one in Example 8.3.1 for a reversible deterministic Turing machine and for a probabilistic Turing machine.

Example 8.3.2 In the spirit of Examples 8.1.1 and 8.2.1, let us describe a quantum Turing machine that solves the same problem.

This quantum Turing machine does not start by moving either to the right or to the left. Rather it moves both to the right and to the left simultaneously.

A typical computation might look like this:

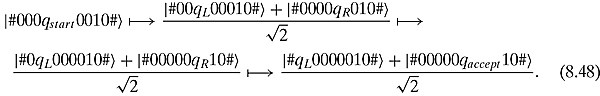
It is obvious that the machine will solve this problem without false positives or false negatives in steps. Again, we want to stress that this is not really a quantum Turing machine because it does not satisfy all the conventions laid down in Bernstein and Vazirani (1997).

We feel confident in identifying this as “a Turing machine version of the double-slit experiment.” The double-slit experiment is performed by physicists who are interested in where a photon lands. A photon exhibits the superposition phenomenon, and hence the photon passes through both slits simultaneously. We are computer scientists and solve searching problems. This problem is solved in time by splitting into a simultaneous superposition of two computational paths. (Of course, it is not really the double-split experiment because there is no interference, only superposition.)

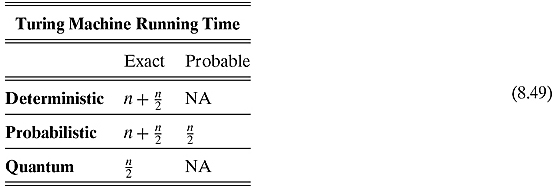
Let us summarize what we have done in Examples 8.1.1, 8.2.1, and 8.3.2 and in Exercise 8.2.2. For the same problem, i.e., given a string to determine if it contains a “1,” we formulated deterministic, probabilistic, and quantum Turing machines. Some of these machines solved the problem without error and some of them gave us probabilistic solutions. The problems were solved in the following time.¹³

Exercise 8.3.2 Write a quantum Turing machine that determines if there is a substring “101” on the tape.

A quantum Turing machine is just one model of quantum computation. In Chapters 5 and 6 we dealt with another one, namely, quantum circuits. (The QRAM model, dealt with in Chapter 7, is yet another way of describing quantum computations.) In the classical case, logical circuits and deterministic Turing machines are polynomially equivalent. That means that each model can implement the other with only polynomial amount of “overhead.” Yao (1993) proved a similar result for the quantum case. That is, quantum circuits and quantum Turing machines are polynomially equivalent.

The following simple example shows how a quantum Turing machine would implement a common quantum circuit:

Example 8.3.3 Many of the algorithms in Chapter 6 required that we apply to a string of qubits. Let us show how one would do this with a quantum Turing machine. Suppose that a string of n “0’s” and “1’s” are on a tape and that the head is pointing to the leftmost symbol of the string.

Basically, the quantum Turing machine will go through the string and change the “0’s” or “1’s” the way a Hadamard matrix would. (This is a simplification of Theorem 8.4.1 of Bernstein and Vazirani (1997). Ours is simpler because we have not followed all their conventions.)

Let us have a look at complexity classes for quantum Turing machines. As in Section 8.2, because of the probabilistic nature of the computations, there is the possibility of false positives and false negatives. We are led to the following three definitions:

Complexity Class. BQP is the set of problems that can be solved by a Quantum Turing machine in Polynomial time with Bounded error on both sides. In other words, if M is a quantum Turing machine that decides and if x is a word, then

and

It was proven in Bennett et al. (1997) that the same amplification lemma that worked for probabilistic complexity classes also works for BQP. Hence, the fraction is not of major significance.

Complexity Class. ZQP is the set of problems that can be solved by a Quantum Turing machine in Polynomial time with Bounded error on both sides. In other words, if M is a quantum Turing machine that decides and if x is a word, then there is a less than 50% chance that the machine will finish in a “do not know” state, otherwise if the machine does know then

and

Complexity Class. EQP is the set of problems that can be solved with a Quantum Turing machine in Polynomial time Exactly (without error). In other words, if M is a quantum Turing machine that decides and if x is a word, then

and

It should be obvious that

Now relate these complexity classes with those of Sections 8.1 and 8.2. Because a deterministic Turing machine can be seen as a type of quantum Turing machine, we have that . Given that we can have a quantum Turing machine simulate a probabilistic Turing machine by using the Hadamard matrix as a fair coin toss, we have that . Also, for the same reason that BPP can be mimicked by a machine that uses only polynomial amount of space, so too BQP can be mimicked by such a machine. Such a machine is the theoretical version of a quantum emulator. The fact that every problem in BQP can be simulated by something in PSPACE shows that every quantum computation can be simulated by a classical computer. Of course, the simulation will probably use exponential time if it was to be exact.¹⁴ Summing up, we have the following:

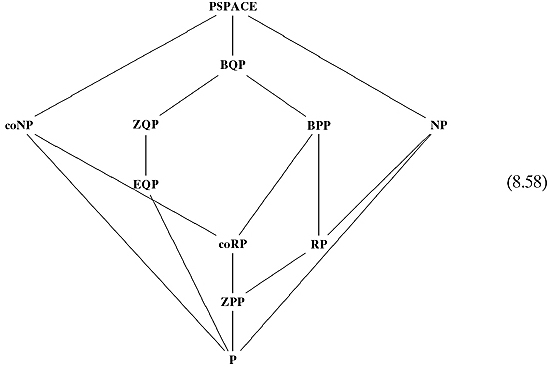
It is unknown if any of these inclusions are proper inclusions. There is much still open about the relationships among these complexity classes.

Because of Shor’s algorithm and the belief that there is no polynomial probabilistic algorithm to factor numbers, it is strongly believed that . It should be noticed that if it were to be proved that BPP≠ BQP, then we would know that P≠ PSPACE, which has been an open problem for a very long time.

It should be noted that Shor’s algorithm is not the only algorithm that we saw that has an exponential speedup. As we saw in Chapter 6, the Deutsch–Jozsa algorithm and Simon’s algorithm also had exponential speedups over any known classical algorithm.

If a large-scale quantum computer is ever built, then there would be evidence that the strong Church–Turing Thesis would be invalidated. Such a quantum computer will be a physical machine that can perform a computation (e.g., factoring large numbers) for which there are no known polynomial time probabilistic machines. (Of course, someone might create such a probabilistic machine in the future.)

It is to be stressed that although Shor’s algorithm solves the factoring problem, factoring is not believed to be an NP-complete problem. The factoring problem, as a decision problem, is an NP problem (and a coNP problem) but has never been shown to be harder than any known NP-complete problem. In terms of quantum computers, this means that even if there were a large-scale quantum computer, we would not be able to use Shor’s algorithm to solve all known NP-complete problems.

Some researchers believe that the fact that there is a quantum algorithm for the factoring problem is a “fluke” and not something that should be expected for many problems. They believe that methods similar to Shor’s algorithm will not be very helpful for other hard problems.

In contrast to Shor’s algorithm, Grover’s algorithm can be very interesting in terms of NP problems. Although the speedup using Grover’s algorithm is from n to , which is quadratic and not exponential, it is still significant. Consider your favorite NP problem. The search space for such a problem is, in general, either n!or 2ⁿ. One can set up Grover’s algorithm to search through the problem’s search space. So if the problem is SAT, we can use Grover’s algorithm to search through all 2ⁿ possible valuations of the n variables in the formula. If the problem is HAMILTONIAN GRAPH, then search through all n! paths on the graph to find one that is hamiltonian. In fact, we are solving a search problem rather than a decision problem.¹⁵

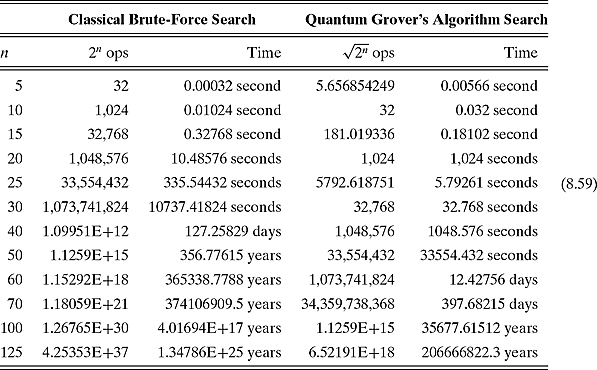
Let us perform some calculations to show how significant Grover’s speedup can be. Say, we would like to solve some NP problem whose search space is 2ⁿ. Imagine a quantum computer running Grover’s algorithm that can perform 1,000 function evaluations per second. This quantum computer will have to perform function evaluations. Contrast this with a classical computer running a brute-force search through all 2ⁿ possible members of the search space. We shall assume that this classical computer is 100 times faster than the quantum computer, i.e., it can perform 100,000 function evaluations per second. The following table shows how these two algorithms compare on different values of n:

We can see that for n = 15, the quantum computer will run faster than the classical computer. We conclude that Grover’s algorithm might have major significance when dealing with “hard” computer problems.

Exercise 8.3.3 Write a short program or use either MATLAB or Microsoft Excel to determine the exact n when the slower quantum computer running Grover’s algorithm runs faster than the classical computer running a brute-force algorithm.

Exercise 8.3.4 Perform a similar analysis to that shown in table (8.59) for an NP problem whose search space is n!.

References: For general Turing machines, see Davis, Weyuker, and Sigal (1994) or Garey and Johnson (1979). Another excellent text is Sipser (2005).

For probabilistic Turing machines, see Section 10.2 of Sipser (2005) or Chapter 11 of Papadimitriou (1994). For general complexity theory, see Papadimitriou (1994).

For Section 8.3, we mostly followed Bernstein and Vazirani (1997). Their definition of a quantum Turing machine is a variant of the one formulated in Deutsch (1985). Much was gained from the following survey papers: Cleve (1999), Fortnow (2003), and Vazirani (2002).

Scott Aaronson has a very interesting blog “Shtetl-Optimized” that looks at current issues in quantum computability and complexity theory: http://www.scottaaronson.com/blog/. Well worth the read. He is also the “Zookeeper” at a Web page (http://qwiki.caltech.edu/wiki/Complexity_Zoo) that has more than 400 different complexity classes. These are great places to start learning more about this topic.

¹ We are indebted to John D. Barrow for the source of this quote.

² We have the adopted the convention that if the word is empty it is rejected.

³ In fact, what we have described is a two-way finite automaton. This example does not require the full definition of a Turing machine.

⁴ Savitch’s theorem states that any nondeterministic computation that uses f(n) space can be simulated by a deterministic computation that uses at most ( f(n))² space. If f(n) is a polynomial, then ( f(n))² is also a polynomial. See, e.g., page 306 of Sipser (2005) or page 149 of Papadimitriou (1994).

⁵ An arbitrary real number might have an infinite expansion. One could encode any language in that expansion.

⁶ See, e.g., page 256 of Papadimitriou (1994).

⁷ E.g., see Zachos (1982), page 369 of Sipser (2005), or page 259 of Papadimitriou (1994).

⁸ We do this for the reasons given in the last section. It was proven in Adleman, DeMarrais, and Huang (1997) that any quantum Turing machine can be simulated by a machine that uses only the numbers

or, if irrationals are permitted,

⁹ This requirement is not strictly needed because we are going to impose a much stronger requirement presently. (It is left in the text to make the connection between classic probabilistic Turing machines and quantum Turing machines.) Furthermore, we can permit arbitrary tractably computable complex numbers and then calculate probabilities with a normalization trick as we did in Section 4.1 on page 103.

¹⁰ The clever reader will notice the progression of δ′s in this chapter. They were all the same functions, except they take values in different sets. We went from{0,1}to real numbers (of the appropriate type) to complex numbers (of the appropriate type.) This progression is exactly the same as the progression of entries in the adjacency matrices of the weighted graphs discussed in Chapter 3. That makes sense; after all, the different systems discussed in Chapter 3 were introduced to bring to light the different types of computational power. However, the analogy highlights a problem with Chapter 3. Just as we restricted the values of the real and complex numbers in this chapter to tractably computable real and complex numbers, so too we should have restricted the values of the entries in the matrices of classical probabilistic systems and quantum systems. However, we wrote it as is for simplicity’s sake.

¹¹ The notion of simulation has to be suitably adjusted because of the probabilistic nature of the computation. We cannot simply state that one machine outputs as the other. There must be a statement about “how far away” the simulated output is from the real one.

¹² This complex vector space is an inner product space but not a Hilbert space because of the finiteness in the definition. If we relax the finiteness requirement, then the inner product space is, in fact, complete and thus a Hilbert space.

¹³ We have deliberately omitted the nondeterministic case from our chart. The reason is that a nondeterministic Turing machine can also solve the problem in steps. This is just as fast as the quantum Turing machine and would have “stolen its thunder.” We should remind the reader that nondeterminism is a mathematical fiction whereas the laws of quantum mechanics are a physical fact.

¹⁴ We can also make the obvious definition of QSPACE. It was shown in Watrous (1999) that . This is analogous to Savitch’s theorem about nondeterministic computation.

¹⁵ We showed that we can solve an NP problem in time using Grover’s algorithm. We are led to the obvious question of whether we can do better. It has been shown in Bennett (1997) that relative to an oracle chosen uniformly at random with probability 1, the class of NP cannot be solved by quantum Turing machines in time.