9

Cryptography

---

 

 

 

 

We dance round in a ring and suppose,
But the Secret sits in the middle and knows.

Robert Frost, The Secret Sits (1942)

In this chapter we explore the merging of quantum computation and classical cryptography. This is a new and exciting field of pure and applied research known as quantum cryptography.

We begin with the basics of classical cryptography in Section 9.1. Section 9.2 demonstrates a quantum cryptographic protocol that uses two different bases. We improve on this in Section 9.3, where a protocol with one basis is employed. Section 9.4 shows how to use entanglement to secretly send a message. We conclude with Section 9.5, in which teleportation is demonstrated.

9.1 CLASSICAL CRYPTOGRAPHY

Before delving into quantum cryptography, we need to familiarize ourselves with the core ideas of classical cryptography. A good place to start is the following definition.

Definition 9.1.1 Cryptography is the art of concealing messages.

Indeed, this is precisely what the etymology reveals: “Cryptography” is a compound of two Greek words, crypton¹ and graphein, which mean, respectively, hidden and writing.

Turning an ordinary message into an indecipherable one is called encryption. The opposite action, i.e., restoring the original message, is decryption. The original message is generally referred to as the plaintext, and the encrypted message is the ciphertext. A method for encryption is often referred to as an encryption protocol.

Figure 9.1. A basic communication scheme.

The history of cryptography is a very long one. As soon as people started sending messages to each other that were not intended for the public, the need for privacy arose. At the very moment encryption ideas and techniques were devised by some smart individual, another one, just as smart set out to break them. Thus, cryptology was born.

To present encryption and decryption methods, we need to set the scene. First, we need two characters – the sender of messages and the receiver. In the standard cryptology literature, these two are named Alice and Bob. Alice wants to send a message to Bob, say, a string of plaintext T. We assume that Alice and Bob are physically separated and that they can communicate with each other over some kind of insecure channel.²

Alice uses an encryption algorithm – let’s call it ENC – that turns T into some encrypted text E. We can think of ENC as some computable function, taking T and an additional parameter K_E, known as the encryption key, as inputs. ENC computes the encrypted message E, which is transmitted to Bob.

Bob receives E (assuming there is no noise involved) and applies a decryption algorithm, DEC, to the encrypted message to reconstruct T. DEC requires a decryption key K_D as input.

The entire scheme is shown in Figure 9.1.

Summing up, ENC(−, K_E) and DEC(−, K_D) are a pair of computable functions such that for every message T, the following equation holds:

What does this equation tell us? It states that as long as we use the right keys, we can always retrieve the original message intact without any loss of information.

Exercise 9.1.1 Does Equation (9.3) imply that ENC(−, K_E) and DEC(−, K_D)are a pair of bijective functions that are inverse to each other?

Let us now examine a concrete example of an encryption protocol, a method known as the Caesar’s protocol.³ Arrange the letters of the English alphabet on a

Figure 9.2. A children’s encryption toy.

circle, so that the order is

Let ENC = DEC = shift(–, –), where shift(T, n) = T′, the string obtained from T by shifting each character n steps clockwise if n is positive, or counterclockwise if it is negative (for instance, shift(“MOM,” 3) = “PRP”). Children actually make a helpful toy for this encryption protocol as depicted in Figure 9.2. This toy consists of two concentric circles with the alphabet written clockwise on each circle. The circles can be turned until the desired letters are matched up. With this encryption protocol, the decryption key is just the encryption key with the sign changed: K_D = −K_E.

Exercise 9.1.2 Decipher the following message “JNTGMNF VKRIMHZKTIAR BL YNG.” (Hint: Use Figure 9.2.)

Programming Drill 9.1.1 Implement the encryption and decryption of text with the Caesar’s protocol. Using ASCII makes this particularly easy.

To make our story a bit more exciting, we need a third character, Eve, the eavesdropper, who can intercept the encrypted message and try to decode it. As previously noted, Alice is using an insecure channel (such as a public telephone wire) to transmit messages to Bob. Eve can thus tap into the channel and eavesdrop on its content. The protocol we have just presented is quite primitive and would not stand Eve’s scrutiny for too long.

Imagine that you are Eve and that by tapping into the insecure channel you can save fairly long encrypted messages from Alice. How would you discover the encryption mechanism? If you were Eve, you might have a hunch about the weak side of the simple-minded protocol we have just introduced. The weakness lies in the fact that the original message and the encrypted one are highly correlated. By calculating simple statistics on the encrypted text, Eve may easily find her way back to the original text. Aside from her malicious purposes, Eve works exactly like an archeologist decoding an ancient unknown language.

To counter Eve’s insight, Alice and Bob change their protocol. Their ideal strategy is to create an encrypted message E that bears no statistical correlation with the original message T. How can this be accomplished? Here is a surprisingly simple answer: a straightforward protocol known as the One-Time-Pad protocol or Vernam cipher.

As we are computer scientists, for the rest of this chapter, we shall refer to T as a binary string of length n. Alice tosses a coin n times and generates a sequence of random bits that she uses as her random key K. Assuming Alice and Bob both share K, they can exchange messages by means of the following protocol:

Step 1. Alice calculates , where stands for the bitwise XOR operation.⁴

Step 2. Alice sends E along a public insecure channel.

Step 3. Bob retrieves E and calculates T from .

In this notation that we have introduced,

and

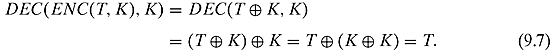
Example 9.1.1 The following table shows an example of an implementation of the One-Time-Pad protocol:

Exercise 9.1.3 Find a friend and flip a coin to get an encryption key K. Then use K to send a message. See if it works.

Programming Drill 9.1.2 Implement the One-Time-Pad protocol.

Exercise 9.1.4 Suppose Alice generates only one pad key K, and uses it to encrypt two messages T₁ and T₂ (we are assuming they have exactly the same length). Show that by intercepting E₁ and E₂, Eve can get and hence is closer to the original text.

There are a couple of issues with the One-Time-Pad protocol:

1. As Exercise 9.1.4 shows, the generation of a new key K is required each time a new message is sent. If the same key is used twice, the text can be discovered through statistical analysis, and hence the name “One-Time-Pad.”

2. The protocol is secure only insofar as the key K is not intercepted by Eve (remember, Alice and Bob must share the same pad in order to communicate). We see in the next section that quantum computing comes to the rescue for this crucial issue.

So far, we have assumed that the pair of keys K_E and K_D are kept secret. In fact, only one key was needed because knowledge of the first key implies knowledge of the second and vice versa.⁵ A cryptographic protocol where the two keys are computable from one another, thus requiring that both keys be kept secret, is said to be private key.

There is yet another game in town: in the 1970s, Ronald Rivest, Adi Shamir, and Leonard Adleman introduced one of the first examples of public-key cryptography, now simply known as RSA (Rivest, Shamir, and Adleman, 1978). In public-key protocols, the knowledge of one key does not enable us to calculate the second one. To be precise, the requirement is that the computation of the second key from the first should be hard.⁶

Now, suppose that Bob has computed such a pair of keys K_E and K_D. Furthermore, suppose that brute force trial and error to find K_D given K_E is totally infeasible by Eve or anyone else (for instance, there could be an endless list of candidate keys). Bob’s course of action is as follows: he places the encryption key K_E, in some public domain, where anyone can get it. He can safely advertise his protocol, i.e., the knowledge of ENC(−, −) and DEC(−, −). At the same time, he guards the decryption key for himself. When Alice wants to send a message to Bob, she simply uses K_E on her message. Even if Eve intercepts the encrypted text, she cannot retrieve Bob’s decryption key, and so the message is safe. This scheme is shown in Figure 9.3.

Let us rephrase the foregoing: once Bob has his magic pair of keys, he finds himself with two computable functions

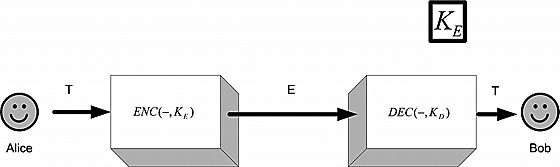
Figure 9.3. A cryptographic communication scheme with a public K_E.

such that F_D is the inverse of F_E but cannot easily be calculated from knowledge of F_E. A function like F_E, which is easy to compute yet hard to invert without extra information, is known as a trapdoor function. The name is quite suggestive: like a trapdoor in an old-fashioned Gothic castle, it opens under your feet but does not let you come back easily. So a trapdoor function is what Bob needs.⁷

Public-key cryptography has pros and cons. On the plus side, it solves the key distribution problem that hinders private-key protocols. If Alice wants to send a message to Bob, she does not need to know Bob’s private key. On the minus side, all public-key protocols to date rely on the fact that the computation of the private key from the public key appears to be hard. This just means that as of yet, there are no known algorithms that do the job. The possibility is still open for some breakthrough result in computational complexity that would put all existing public-key cryptographic schemes out of business.⁸ Finally, public-key protocols tend to be considerably slower than their private-key peers.

In light of the aforementioned, cryptographers devised a marriage of the two approaches to achieve the best of both worlds: public-key cryptography is used only to distribute a key K_E of some private-key protocol, rather than an entire text message. Once Alice and Bob safely share K_E, they can continue their conversation using the faster private-key scheme. Therefore, for the rest of this chapter, our only concern is to communicate a binary K_E of the appropriate length.

Before ending this section, we must expand on the picture of cryptography we have sketched so far. Secure communication of messages is only one of the issues at stake. Here are two others:

Intrusion Detection. Alice and Bob would like to determine whether Eve is, in fact, eavesdropping.

Authentication. We would like to ensure that nobody is impersonating Alice and sending false messages.

We shall show how to implement protocols that include the first of these features. The second feature is also discussed within the context of quantum cryptography but is outside the purview of this text.

Exercise 9.1.5 Suppose Alice and Bob communicate using some kind of public-key protocol. Alice has a pair of keys (one public, one private), and so does Bob. Devise a way in which Alice and Bob can communicate simultaneously while authenticating their messages. (Hint: Think of encoding one message “inside” another.)

9.2 QUANTUM KEY EXCHANGE I: THE BB84 PROTOCOL

While discussing the One-Time-Pad protocol, we pointed out that the problem of securely transmitting the key is a serious one. During the 1980s, two authors came up with a clever idea that exploits quantum mechanics. This idea formed the basis of the first quantum key exchange (QKE) protocol.

Before presenting QKE in some detail, let us first see if we can guess which features of the quantum world are appealing to cryptographers. In the classical case, Eve is somewhere along the insecure channel listening for some bits of information. What can she do?

1. She can make copies of arbitrary portions of the encrypted bit stream and store them somewhere to be used for later analysis and investigations.

2. Eve can listen without affecting the bitstream, i.e., her eavesdropping does not leave traces.

Now, assume that Alice sends qubits, rather than bits, over some channel.⁹

1′. Eve cannot make perfect copies of the qubit stream: the no-cloning theorem discussed in Section 5.4 prevents this from happening.

2′. The very act of measuring the qubit stream alters it.

At first sight, the points raised above seem like limitations, but from the point of view of Alice and Bob, they actually turn out to be great opportunities. How? For one thing, the no-cloning theorem hampers Eve’s ability to use past messages to conduct her analysis. Even more important, each time she measures the qubit stream, she disturbs it, allowing Alice and Bob to detect her presence along the channel.

The first quantum key exchange protocol was introduced by Charles Bennett and Gilles Brassard in 1984, and hence the name BB84. This section describes this important protocol.

Alice’s goal is to send Bob a key via a quantum channel. Just as in the One-Time-Pad protocol, her key is a sequence of random (classical) bits obtained, perhaps, by tossing a coin. Alice will send a qubit each time she generates a new bit of her key. But which qubit should she send?

In this protocol, Alice will employ two different orthogonal bases shown in Figure 9.4:

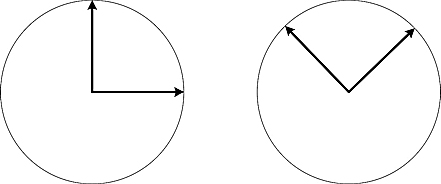
Figure 9.4. Two bases used for BB84.

and

We shall refer to the first basis as the “plus” basis and the second as the “times” basis. Essentially, they are two alternative vocabularies that Alice and Bob will use to communicate.

In these vocabularies, the states and shall be described by the following table:

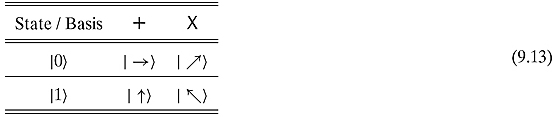
For example, in the + basis, will correspond to . If Alice wants to work in the X basis and wants to convey , she will send . Similarly, if Alice sends and Bob measures in the + basis, he should record .

This is fine for basic states, but what about superpositions? If Bob measures photons using the + basis, he will only see photons as or . What if Alice sends a and Bob measures it in the + basis? Then it will be in a superposition of states

In other words, after measurement, there is a 50–50 chance of Bob’s recording a or a . Again, Alice could use the X basis, intending to send a , and Bob has a 50–50 chance of recording a and a 50–50 chance of recording a . In all, there are four possible superpositions:

with respect to + will be .

with respect to +, will be .

with respect to X, will be .

with respect to X, will be .

Exercise 9.2.1 Work out what , , , and would be in terms of the two bases.

Armed with this vocabulary and the inherent indeterminacy of the two bases, Alice and Bob are ready to start communicating. Here are the steps of the protocol:

Step 1. Alice flips a coin n times to determine which classical bits to send. She then flips the coin another n times to determine in which of the two bases to send those bits. She then sends the bits in their appropriate basis. For example, if n is 12, we might have something like this:

Step 2. As the sequence of qubits reaches Bob, he does not know which basis Alice used to send them, so to determine the basis by which to measure them he also tosses a coin n times. He then goes on to measure the qubit in those random bases.

In our example, we might have something like this:

Here is the catch: for about half of the time, Bob’s basis will be the same as Alice’s, in which case his result after measuring the qubit will be identical to Alice’s original bit. The other half of the time, though, Bob’s basis will differ from Alice’s. In that case, the result of Bob’s measurement will agree with Alice’s original bit about 50% of the time.

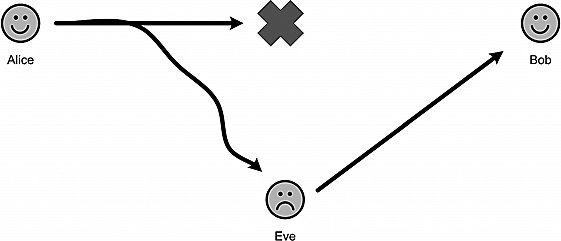
Figure 9.5. Eve “cutting” the quantum wire and transmitting her own message.

Programming Drill 9.2.1 Write functions that mimic Alice, Bob, and their interactions. Alice should generate two random bit strings of the same length. Call one BitSent and the other SendingBasis.

Bob will be a function that generates a random bit string of the same length called ReceivingBasis.

All three of these bit strings should be sent to an “all-knowing” function named Knuth. This function must look at all three and create a fourth bit string named BitReceived. This is defined by the following instruction:

This random{0, 1} is the classical analog of a qubit collapsing to a bit.

Knuth must furthermore evaluate the percentage of bits that Bob receives accurately.

Let us continue with the protocol: If evil Eve is eavesdropping, she must be reading the information that Alice transmits and sending that information onward to Bob, as shown in Figure 9.5.

Eve also does not know in which basis Alice sent each qubit, so she must act like Bob. She will also toss a coin each time. If Eve’s basis is identical to Alice’s, her measure will be accurate and she will, in turn, send accurate information on to Bob. If, on the other hand, her basis is different from Alice’s, her bit will be in agreement with Alice’s only 50% of the time. However, here’s the rub: the qubit has now collapsed to one of the two elements of Eve’s basis. Because of the no-cloning theorem, Eve does not have the luxury of making a copy of the original qubit and then sending it on (after her probe), so she just sends the qubit after her observation. Now Bob will receive it in the wrong basis. What are his chances of getting the same bit Alice has? Answer: His chances are 50-50.¹⁰

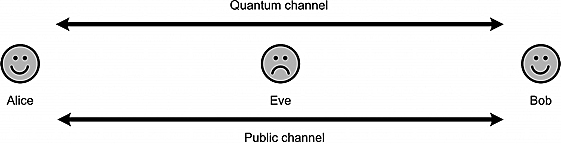
Figure 9.6. Alice and Bob communicating on quantum and public channels, with Eve eavesdropping.

Therefore if Eve intercepts and measures each qubit sent, she will negatively affect Bob’s chances of agreement with Alice.

Exercise 9.2.2 Give an estimate of how frequently Bob’s bit will agree with Alice’s if Eve is constantly eavesdropping.

By computing some simple statistics, a potential intrusion by Eve would be detected. This suggests how to complete BB84. Let us examine the details.

After Bob has finished decoding the qubit stream, he has in his hands a bit stream of length n. Bob and Alice will discuss which of the n bits were sent and received in the same basis. They can do this on a public channel, such as a telephone line. Figure 9.6 is helpful.

Step 3. Bob and Alice publicly compare which basis they used chose at each step. For instance, he can tell her X, +, X, X,… . Alice replies by telling him when he was right, and when he was not. Each time they disagreed, Alice and Bob scratch out the corresponding bit. Proceeding this way until the end, they are each left with a subsequence of bits that were sent and received in the same basis. If Eve was not listening to the quantum channel, this subsequence should be exactly identical. On average, this subsequence is of length .

Programming Drill 9.2.2 Continuing with the last programming drill, write a function named Knuth2 that accepts all three-bit strings and creates a bit string (of possibly shorter length) called AgreedBits, which is a substring of both BitSent and BitReceived.

But what if Eve was eavesdropping? Alice and Bob would also like to engage in some intrusion detection. They want to know if Eve (or anyone else) was listening in. They do this by comparing some of the bits of the subsequence.

Step 4. Bob randomly chooses half of the bits and publicly compares them with Alice. If they disagree by more than a tiny percentage (that could be attributed to noise), they know that Eve was listening in and then sending what she received. In that case, they scratch the whole sequence and try something else. If the exposed sequence is mostly similar, it means that either Eve has great guessing ability (improbable) or Eve was not listening in. In that case, they simply scratch out the revealed test subsequence and what remains is the unrevealed secret private key.

In this protocol, Step 3 has eliminated half of the original qubits sent. So if we begin with n qubits, only qubits will be available after Step 3. Furthermore, Alice and Bob publicly display half of the resulting qubits in Step 4. This leaves us with of the original qubits. Do not be disturbed about this, as Alice can make her qubit stream as large as she needs. Hence, if Alice is interested in sending an m bit key, she simply starts with a 4m qubit stream.

9.3 QUANTUM KEY EXCHANGE II: THE B92 PROTOCOL

In the previous section, we introduced the first quantum key exchange protocol. Alice had two distinct orthogonal bases at her disposal. It turns out that the use of two different bases is redundant, provided one employs a slightly slicker means of measuring. This simplification results in another quantum key distribution protocol, known as B92.B stands for its inventor, Charles Bennett, and 1992 is the year it was published.

The main idea in B92 is that Alice uses only one nonorthogonal basis. Let us work out the protocol with the following example:

Exercise 9.3.1 Verify that these two vectors are, in fact, not orthogonal.

Before going into detail, we need to pause and reflect a little. We know that all observables have an orthogonal basis of eigenvectors. This means that if we consider a nonorthogonal basis, there is no observable whose basis of eigenvectors is the one we have chosen. In turn, this means that there is no single experiment whose resulting states are precisely the members of our basis. Stated differently, no single experiment can be set up for the specific purpose of discriminating unambiguously between the nonorthogonal states of the basis.

Alice takes to be 0 and to be 1. Using this language, we can begin the protocol.

Step 1. Alice flips a coin n times and transmits to Bob the n random bits in the appropriate polarization with a quantum channel.

Here is an example.

Step 2. For each of the n qubits, Bob measures the received qubits in either the + basis or the basis. He flips a coin to determine which basis to use. There are several possible scenarios that can occur:

If Bob uses the + basis and observes a , then he knows that Alice must have sent a because if Alice had sent a , Bob would have received a .

If Bob uses the + basis and observes a , then it is not clear to him which qubit Alice sent. She could have sent a but she could also have sent a that collapsed to a . Because Bob is in doubt, he will omit this bit.

If Bob uses the basis and observes a , then he knows that Alice must have sent a because if Alice had sent a , Bob would have received a .

If Bob uses the basis and observes a , then it is not clear to him which qubit Alice sent. She could have sent a but she could also have sent a that collapsed to a . Because Bob is in doubt, he will omit this bit.

Continuing the example, we have the following:

There are two possible bases that Bob could have used to measure. For each basis, there are two types of results. For half of those four results, the bit sent is certain. For the other half, there is uncertainty. Bob must omit the uncertain ones and keep the others hidden. He must inform Alice of this.

Step 3. Bob publicly tells Alice which bits were uncertain and they both omit them.

At this point, Alice and Bob know which bits are secret, so they may use those. But there is one more step if they want to detect whether or not Eve was listening in. They can, as in Step 4 of BB84, sacrifice half their hidden bits and publicly compare them. If they do not agree for a significant number, then they know that evil Eve has been doing her wicked deeds and the entire bit string should be ignored.

Programming Drill 9.3.1 Write three functions that mimic Alice, Bob, and their interactions. Use functions named Alice92, Bob92, and Knuth92. They should create bit strings that perform the B92 protocol.

9.4 QUANTUM KEY EXCHANGE III: THE EPR PROTOCOL

In 1991, Artur K. Ekert proposed a completely different type of quantum key distribution protocol based on entanglement (Ekert, 1991). We shall present a simplified version of the protocol and then point to the original version.

We remind the reader that it is possible to place two qubits in the following entangled state¹¹:

We saw in Section 4.5 that when one of the qubits is measured, they both will collapse to the same value.

Suppose Alice wants to send Bob a secret key. A sequence of entangled pairs of qubits can be generated and each of our communicators can be sent one of the pairs. When Alice and Bob are ready to communicate, they can measure their respective qubits. It does not matter who measures first, because whoever does it first will collapse the other qubit to the same random value. We are done! Alice and Bob now have a sequence of random bits that no one else has.

There are more sophisticated protocols that will be useful to detect eavesdroppers or if the qubits fell out of entanglement. As in BB84, rather than measure a qubit in one basis, we can measure it in two different bases, say and +.

Following the vocabulary of and + of Section 9.2, we present the protocol.

Step 1. Alice and Bob are each assigned one of each of the pairs of a sequence of entangled qubits.

When they are ready to communicate, they move on to Step 2.

Step 2. Alice and Bob separately choose a random sequence of bases to measure their particles. They then measure their qubits in their chosen basis.

An example might look like this:

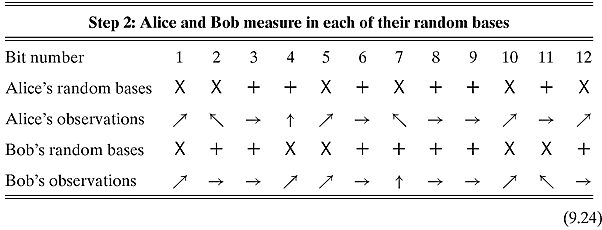
Step 3. Alice and Bob publicly compare what bases were used and keep only those bits that were measured in the same basis.

If everything worked fine, Alice and Bob share a totally random secret key. But problems could have occurred. The entangled pairs could have been exposed to the environment and become disentangled,¹² or wicked Eve could have taken hold of one of the pairs, measured them, and sent along disentangled qubits.

We solve this problem by doing what we did in Step 4 of BB84. Alice or Bob randomly choose half of the remaining qubits and publicly compare the bits (not the bases). If they agree, then the last quarter of hidden qubits are probably good. If more than a small part disagree (from noise), then we must suspect Eve is up to her evil ways and our friendly communicators must throw away the entire sequence.

Ekert’s original protocol is even more sophisticated. For Step 4, rather than measuring the qubits in two different bases, they will be measured in three different bases. As in BB84, Alice and Bob will publicly compare the results of half of their measured sequences to detect if the qubits are still entangled. They will then perform certain tests on the results to determine if they were still entangled. If not, then they throw away the entire sequence.

The test that they will perform is based on John Bell’s famous Bell’s inequality,¹³ which is central to the foundations of quantum mechanics.

Bell’s inequality is a way of describing the results of measurements of three different bases on two particles. If the particles are independent of each other, like classical objects, then the measurements will satisfy the inequality. If the particles are not independent of each other, i.e., they are entangled particles, then Bell’s inequality fails.

Ekert proposed to use Bell’s inequality to test Alice and Bob’s bit sequences to make sure that when they were measured they were, in fact, entangled. This is done by publicly comparing a randomly chosen part of the sequences. We are going to look at one of three possible directions x, y, and z of spin of particles. If the revealed part of the sequence respects Bell’s inequality, then we know that the qubits are not entangled (i.e., not independent) and they are acting like classical objects. In such a case, we throw away the entire sequence and start over. If the revealed portion fails Bell’s inequality, then we can assume that the whole sequence was measured when it was in a quantum entangled state, and hence the sequence is still private.

9.5 QUANTUM TELEPORTATION

In the last section, we became experts at dealing with entangled qubits. We would like to use this expertise to perform quantum teleportation.

Definition 9.5.1 Quantum teleportation is the process by which the state of an arbitrary qubit is transferred from one location to another.

It is important to realize that what we describe in this section is not science fiction. Quantum teleportation has already been performed in the laboratory. The future of teleportation is, indeed, something to look forward to.

Recall that in Section 5.4 we met the no-cloning theorem, which states that we are not able to make a copy of the state of an arbitrary qubit. That means that when the state of the original qubit is teleported to another location, the state of the original will necessarily be destroyed. As stated on page 166, “Move is possible. Copy is impossible.”

Before moving on to the protocol, some preliminaries must be dealt with. In our journey, we have found that working with a cleverly chosen noncanonical basis and switching between the canonical basis and the noncanonical basis is helpful. When working with a single qubit, we worked with the canonical basis

and the noncanonical basis

The teleportation algorithm will work with two entangled qubits, one held by Alice and one held by Bob. The obvious canonical basis for this four-dimensional space is

A noncanonical basis, called the Bell basis in honor of John Bell, consists of the following four vectors:

Every vector in this basis is entangled.

In order to show that these vectors form a basis, we must show that they are linearly independent (we leave this to the reader) and that every vector in can be written as a linear combination of vectors from the Bell basis. Rather than showing it for every vector in , we show it is true for every vector in the canonical basis of .

Because every vector in is a linear combination of canonical basis vectors and every canonical basis vector is a linear combination of Bell basis vectors, we have that the Bell basis is, in fact, a basis.

How are the Bell basis vectors formed? In the two-dimensional case, we saw that the elements of the noncanonical basis can be formed using the Hadamard matrix. Remember that H does the following:

In the four-dimensional case, we need something a little more complicated:

It can easily be seen that this quantum circuit with the appropriate inputs creates the elements of the Bell basis:

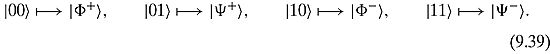
We now have enough tool in our toolbox to move ahead with the quantum teleportation protocol. Alice has a qubit in an arbitrary state that she would like to teleport to Bob.

Step 1. Two entangled qubits are formed as . One is given to Alice and one is given to Bob.

We may envision these three qubits as three lines.

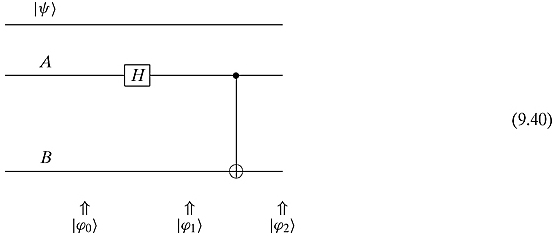
The top two lines are in Alice’s possession and the bottom line is in Bob’s possession. The states are as follows:

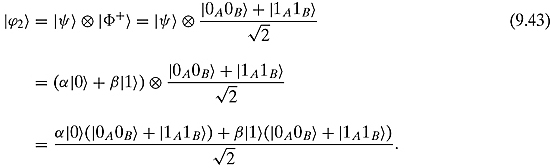
Step 2. Alice lets her interact with her entangled qubit.

Steps 1, 2, and 3 can be seen in the following diagram:

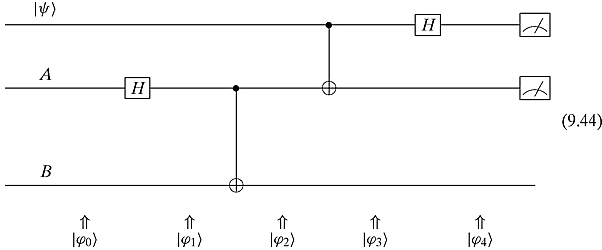
We have

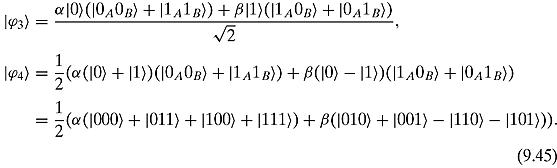
Regrouping these triplets in terms of , which is in Alice’s possession, we have

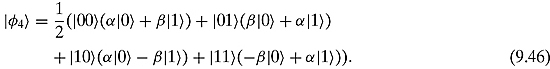
So the system of three qubits is now in a superposition of four possible states.

Step 3. Alice measures her two qubits and determines to which of the four possible states the system collapses.

At the moment Alice measures her two qubits; all three qubits collapse to one of four possibilities. So if she measures then the third qubit is in state .

There are two problems to deal with:

(a) Alice knows this state but Bob does not; and

(b) Bob has , not the desired . Both problems are solved by Step 4.

Step 4. Alice sends copies of her two bits (not qubits) to Bob who uses that information to achieve the desired state .

In other words, if Bob receives from Alice, he then knows that his qubit is in state

hence he should act on his qubit with the following matrix:

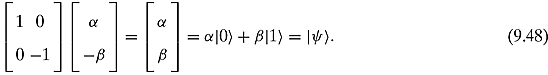
In detail, Bob must apply the following matrices upon receiving information from Alice:

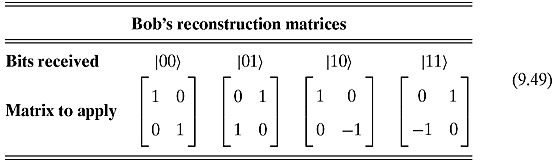
After applying the matrix, Bob will have the same qubit that Alice had.

The following space–time diagram might be helpful. We use the convention that straight arrows correspond to the movement of bits and curvy arrows correspond to qubits on the move.

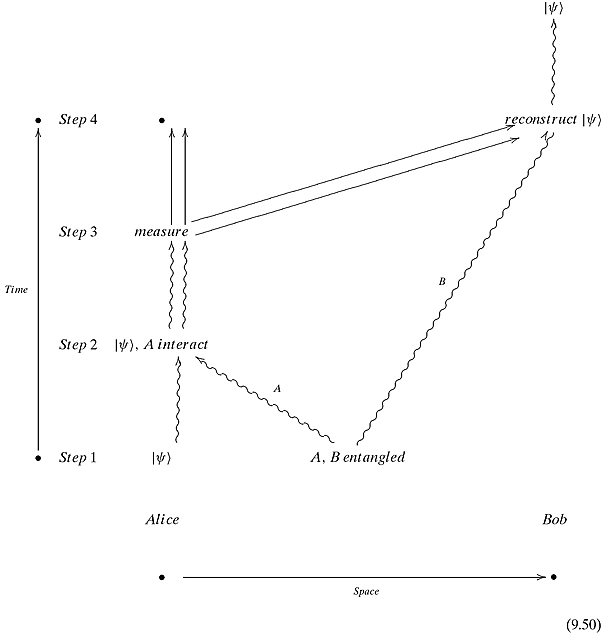
Notice that moves from the lower-left corner in Alice’s possession to the upper-right corner in Bob’s possession. Mission accomplished!

Several points should be made about this protocol:

Alice is no longer in possession of . She has only two classical bits.

As we have seen, to “teleport” a single quantum particle, Alice has to send two classical bits. Without receiving them, there is no way that Bob can know what he has. These classical bits travel along a classical channel and thus they propagate at finite speed (less than the speed of light). Entanglement, in spite of its undisputable magic, does not allow you to communicate faster than the speed of light. Einstein’s theory of relativity would not permit such communication.

α and β were arbitrary complex numbers satisfying |α|² +|β|² = 1. They could have had an infinite decimal expansion. And yet, this potentially infinite amount of information has gone from Alice to Bob across the universe by passing only two bits. However, it is important to realize that this potentially infinite amount of information is passed as a qubit and useless to Bob. As soon as he measures the qubit, it will collapse to a bit.

Someone might argue that calling all the foregoing teleportation is a bit of a stretch. Indeed, no particle has been moved at all. However, from the point of view of quantum mechanics, two particles having exactly the same quantum state are, from the standpoint of physics, indistinguishable and can therefore be treated as the same particle. If you are configured like Captain Kirk down to the minutest details, you are Captain Kirk!

Exercise 9.5.1 What about Eve? She can certainly tap into the classical channel and snatch the two bits. But will it be useful to her?

Exercise 9.5.2 There was nothing special about Alice using to entangle her . She could have just as easily used any of the other three Bell vectors. Work out the result if she had used .

 

---

References: A comprehensive text on classical cryptography is Schneier (1995). For a more mathematical treatment, see Koblitz (1994). A general introduction to quantum cryptography is Lomonaco (2001).

BB84 was first described in Bennett and Brassard (1984). B92 was the first presentation of Bennett (1992). The EPR protocol was first described in Ekert (1991).

A short history of quantum cryptography can be found in Brassard and Créepeau (1993), and a bibliography in Brassard (1993).

Quantum teleportation was first presented in Bennett et al. (1993).

¹ Now you know where the Kryptonite got its name. It is rare to find and hence is “hidden.” It usually stays concealed unless Lex Luthor gets hold of it!

² Why insecure? First of all, if the channel were foolproof beyond any reasonable doubt, we would have no story. Why bother with cryptography if no one else can spy on the message? Second, in the context of secure message transmission, every channel must be assumed insecure unless proven safe.

³ Julius Caesar apparently used an encryption technique like this one to communicate with his generals during his military campaigns. See Suetonius’ Life of Julius Caesar, Paragraph 56.

⁴ A quick reminder on XOR: it is simply bitwise addition modulo two. .

⁵ In Caesar’s protocol, the decryption key is just the encryption key with changed sign, whereas in the One-Time-Pad protocol, the two keys are exactly the same.

⁶ By “hard,” we mean that the number of computational steps to get from the first key to the second key is more than polynomial in the length of the first key.

⁷ Where can Bob find trapdoor functions? There are, at present, quite a few public-key protocols about, drawing their techniques from advanced mathematics such as number theory (prime factorization) or algebraic curves theory (elliptic curves). We invite you to read about them in Koblitz (1994). (Caution: be prepared to perform some calculations!)

⁸ Quantum computing itself offers unprecedented opportunities for breaking codes, as the celebrated result by Shor amply shows (see Section 6.5). For a discussion of the relationship between quantum computing and computational complexity, see Section 8.3.

⁹ This chapter is not concerned with hardware implementation of quantum cryptography. That topic is tackled in Chapter 11. For the time being, suffice it to note that any two-dimensional quantum system (like spin or photon polarization) could be employed for transmission.

¹⁰ Eve does, in fact, have other options. For example, she can “listen in” with a third basis. However, such considerations would take us too far afield.

¹¹ In the real world, the entangled pairs will probably be in a state

    as explained on page 136 of Chapter 4. When one is measured, they will both collapse to opposite values. We shall deal with the slightly easier version given in Equation (9.22). It will become apparent that if we use Equation (9.23), then Alice and Bob will have inverted bit strings. But if we use the simplified one given in Equation (9.22), they will share the exact same bit string.

¹² Entanglement is indeed a volatile property. See Chapter 11 for a further discussion of entanglement and what happens when it is exposed to the environment.

¹³ In fact, a similar inequality that describes classical independent objects was noticed in the nineteenth century by one of the forefathers of computer science, George Boole. Boole called them “conditions of possible experience.” See Pitowsky (1994).