
You’re trying to complete an orienteering course as fast as possible, but it’s a long course (at least given your current level of fitness). Is it better to walk quickly, run, or use a combination of both?

By the end of this chapter you should be able to:
•Describe the kinematics and kinetics of walking and running
•Explain how work is done during walking and running, including the cycle of energy exchange between potential (gravitational and elastic) and kinetic energy
•Understand energetic principles in order to determine the factors that influence our decision to walk versus run
In order to answer this question, we first have to understand how we walk and run (it’s not simple!) and then determine the benefits and costs of each form of locomotion. Let’s start by examining the walking gait, and then move on to running a little later.
Walking
Walking is a form of gait, which is a person’s method of locomotion or ambulation. Humans use several modes of gait, including walking and running in addition to hopping and skipping. Quadrupeds (four-legged animals) have different methods of gait, including galloping and trotting. As shown in Figure 18.1, there are several phases of the walking gait, including:
1. Initial ground contact – initial contact is made between the foot (heel) and the ground, with both vertical and horizontal forces being applied to the ground, and thus ground reaction forces being directed back to the body. The vertical ground reaction forces slow the descent of the body and reaccelerate it upwards. The horizontal ground reaction force is initially directed back toward the body causing a braking action. This acts to slow the body (so an excessive force may be problematic) but also prevents the body from falling forwards and therefore helps in its upward redirection; that is, the braking force is necessary for stable walking. At this point, both feet will be in contact with the ground, and this is referred to as the double support phase. This is also the first point at which we ‘stand’ on the leg that has just made contact with the ground, initiating the stance phase.
2. Loading response – the foot rolls as the body moves forward over the foot, with loading of the stance leg occurring largely in this phase.
3. Midstance – this is the middle of the stance phase of the gait cycle. The opposite foot will have lifted from the ground and therefore the body’s mass is supported solely by the stance leg. This also represents the time in which the forces applied to the ground move from braking (slowing and stabilising) the body to accelerating it.
4. Heel-off or heel lift – this phase commences as the heel is lifted from the ground and the non-stance (swing) leg progresses ahead of the stance leg; the body is in a single-stance phase. This is also called the terminal stance phase.
5. Toe-off or pre-swing – immediately before the heel of the opposite (swing) leg touches the ground, the foot of the current stance leg rolls towards the toes. This is therefore a double support phase where the body’s weight is transferred to the opposite leg.
6. Swing phase – this phase is characterised by the non-stance leg swinging forward to recommence ground contact. It is often described as three separate phases, including early (initial) swing, midswing and late (terminal) swing, each approximately constituting a third of the whole swing phase. The knee normally flexes in early swing and then extends during mid and late swing. At the end of the terminal phase there is a brief retraction of the leg (i.e. it swings back briefly toward the body) before initial ground contact, which among other things is important for bringing the foot closer to zero speed relative to the ground to reduce the chance of slip. The swing phase lasts approximately 40% of the total gait cycle, whereas the stance phase lasts approximately 60%.
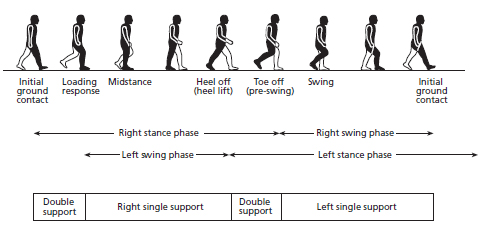
FIG. 18.1 Phases of the walking gait in humans.
Changes in potential and kinetic energy during walking
It is generally accepted that humans evolved to expand our food capture territories, escape predators or hunt. We have therefore developed strategies for fast and efficient movement. So in order to determine whether walking is the best gait pattern to choose, we will have to reflect on its energy cost.
The push-off from one step to another during walking is largely accomplished through ankle joint extension (plantarflexion), with some contribution from the hip and knee extensors. This raises the body’s centre of mass and pushes it forward, and therefore increases gravitational potential energy (PEgrav) as well as both vertical and horizontal kinetic energy (KEv and KEh, respectively), as you know from Chapter 9. In the middle of this process PEgrav is at its maximum, KEh is least, and KEv becomes zero. The body then ‘falls’ forward with PEgrav being converted to KE (positive horizontal KE and negative, or downward, vertical KE).
This forward acceleration of the body occurs as the swing leg makes first contact with the ground (heel strike) in front of the centre of mass. A negative, or braking, force is therefore applied by the ground to us as we push forward into the ground on landing (remember, this braking force is necessary for stable walking, although a very large force will slow the body dramatically). As you might have guessed after reading Chapter 11, some energy will be lost in the collision of the foot with the ground (actually, energy loss is associated with the rapid acceleration of the centre of mass [COM]) and this energy will have to be added by muscles, which do work in order for us to continue walking (Bertram & Hasaneini, 2013). Some energy is also lost as the opposite muscles (that dorsiflex the foot) are lengthened and dissipate energy as the heel strikes the ground (Underwood et al., 2012). The combination of the remaining energy plus the new energy from muscles propels the body upwards and forwards into the next step. Because of this process, walking efficiency, defined as the ratio of energy in (work of the muscles, Wmus) versus energy out (KEh) will be minimised when less energy is lost in the collision between foot and ground (i.e. in redirection of the COM).
In fact, muscle work isn’t only needed to offset the energy lost when the foot collides with the ground. It is also needed to swing the arms and legs to help us maintain balance as we walk (remember, conservation of angular momentum from Chapter 8). This work is called ‘internal work’ because it’s produced internally by our own muscles, whereas the work done on the ground to propel the body upwards and forwards during walking is called ‘external work’ because the ground reaction force is external to us.
Our muscles lose a lot of energy as heat when they do work; in fact, only ~25% of the energy generated in the muscle ends up producing mechanical work. So minimising energy losses during ground contact is vital so that less muscle work is needed. One intelligent strategy that we use is to allow the leg to flex in a spring-like manner during the early stance phase. This reduces the speed of the foot-ground collision and, as you will have guessed after reading Chapter 11, reduces the energy lost in the collision. This spring-like behaviour also allows energy that would otherwise be dissipated to be stored in elastic elements within the muscle-tendon units (this includes the muscles’ contractile elements, but largely occurs in the tendons themselves), as you read in Chapter 17; essentially we store the energy for use later in the gait cycle. During the latter stance phase (midstance to toe-off) the leg extends and the stored elastic energy is recovered to help propel our body upwards and forwards into the next step. Because some of the work for propulsion comes from this energy recovery mechanism, there is a reduced need for muscle work and therefore a reduced total energy cost.
Importantly, under these conditions the muscles may maintain a near-constant length while the tendons stretch and recoil, allowing for a reduction in energy use because muscle energy consumption increases when length change increases; i.e. as mechanical work increases (Roberts et al., 1997; Lichtwark & Wilson, 2006).
The complex transfer of energy was historically (and metaphorically) described as a rolling egg, with the body’s centre of mass rising and falling as a rolling egg’s centre of mass would (see Figure 18.2); although while it’s conceptually appealing, it is not a complete description of the dynamics of walking. Another metaphor was also classically taught – the inverted pendulum. In the early stance phase (initial ground contact and midstance) the vertical ground reaction force is relatively high as we propel our body over our leg (sometimes referred to as a ‘vault’). During midstance, however, the body’s centre of mass moves horizontally and not vertically, so the vertical reaction force is minimal. During propulsion toward heel-off (terminal stance) the vertical force is also relatively high to propel the body into the next step. This creates a U-shaped vertical ground reaction force profile, as shown in Figure 18.3. Because the body is projected over the leg during the support phase, walking gait is sometimes metaphorically described as an inverted pendulum (Figure 18.2).
Both the rolling egg and inverted pendulum metaphors describe the walking gait reasonably accurately, but in fact may be incorrect in explaining exactly why we are so efficient when we move. This is partly because it neglects the double stance part of the stride where much of the energy loss (and therefore opportunity for the implementation economic movement strategy) occurs; e.g. Figure 18.3. Furthermore, paying closer attention to the storage and release of elastic energy during gait (i.e. the leg’s spring-like nature; described in more detail below) is important when using the models to optimise human gait or to build robotic walkers and walking assistants. For this reason, the spring-loaded inverted pendulum (or SLIP) model is now popular because it includes the effects of elastic energy storage and recovery within the standard inverted pendulum model.
FIG. 18.2 During walking the centre of mass oscillates in the vertical direction such that potential (gravitational) and kinetic energy change out of phase. In a classic model, often described as the rolling egg or inverted pendulum model, the ability to exchange potential and kinetic energies was considered to allow for a high walking efficiency. These analogies are still very useful, although more recent theories better explain the energy cost of walking. In particular, the spring-loaded inverted pendulum (or SLIP) model is currently popular because it includes the effects of elastic energy storage and recovery within the standard inverted pendulum model.
FIG. 18.3 During walking the centre of mass rises and falls slightly within each step (top graph), so gravitational potential energy rises and falls accordingly. This oscillation of the centre of mass results a bimodal vertical force production by each leg, shown in the middle graph as recorded by force platform. The velocity of the body’s centre of gravity is not consistent throughout the cycle, with propulsion and braking forces causing acceleration and deceleration of the body (see boxes at bottom). Importantly, in the double-support phase (at approximately 50% of stride in the figure; after ‘Peak 2’) a brief ‘spike’ in total vertical force would be observed, which results from the summing of forces from the right and left legs. This force rise is often forgotten when forces from only a single leg are observed, even though this ‘collision’ force is important for reducing the fall of the body and redirecting the body’s centre of mass into the next step. x-axis values = percent of stride cycle (i.e. left and right steps).
Role of the ankle extensor muscles (plantarflexors)
Knee flexion occurs early in the stance phase (as the joints flex to absorb the energy of foot-ground collision to minimise the centre of mass velocity changes) and extension follows later in the stance phase during propulsion. It might therefore be considered that knee function is a vital aspect of successful walking. However, the ability to produce propulsion at the ankle later in the stance phase (from midstance to heel-off) appears to be of much greater importance.
During the midstance and heel-off phases the ankle joint flexes (called dorsiflexion) and the ankle extensor tendons, especially the long Achilles tendon, are stretched and store energy. The muscles are activated, yet they undergo minimal length change (i.e. they contract almost isometrically). Later in the ground contact phase between heel-off and toe-off the tendons recoil, releasing their stored energy rapidly as the ankle rapidly extends (plantarflexion), i.e. with a high power output (Lichtwark et al., 2007; Cronin et al., 2013).
There appears to be three potential benefits of this muscle-tendon action. First, the ankle extension force provides kinetic energy to the body to push it upwards and forwards into the next step (e.g. Neptune et al., 2001). In this case, strong ankle plantarflexion is thought to provide much of the energy that is lost during the foot’s collision with the ground, through the actions of muscles that move the limbs (internal work), or lost as heat by the muscles as they perform work. Second, an appropriately timed upwards (and forwards) acceleration of the body as the swing leg first contacts the ground (initial contact) reduces vertical collision forces; rather than the body ‘falling’ towards the collision, an upward force is simultaneously provided which reduces the body’s vertical velocity at contact (Kuo et al., 2005). This will minimise energy loss during the collision, and therefore increase walking efficiency. Third, the propulsive force launches the leg into the subsequent swing phase, with the knee flexion and ankle dorsiflexion (i.e. ankle flexion) allowing the leg to then swing freely forwards (Lipfert et al., 2014). This reduces the need for active hip flexion forces to generate the required joint torque for leg swing. Indeed, some of this variability in the tasks achieved by the plantar flexor muscle-tendon unit may come from its complexity, having both mono- and bi-articular muscles acting in synergy but with independent neural control (e.g. Neptune et al., 2001).
There is currently debate surrounding the relative importance of each of these potential benefits of strong ankle plantarflexion, however, it is clear that optimum functioning of the ankle joint is required in order for efficient walking to be achieved. Issues associated with ankle function, such as those from muscle weakness, spasticity, etc., will negatively affect walking speed and efficiency, and exercise training programmes that target plantarflexion strength and power will result in improvements in walking capacity in individuals who currently have a weakness of some level. Additionally, ensuring that the timing of ankle plantarflexion is optimised is also critically important, and will be an important goal of exercise and rehabilitation plans in athletes returning from significant injury or in clinical and/or elderly populations.
What happens when we walk quickly?
Walking is a very efficient form of locomotion for humans. As we walk faster, large muscle forces are required to provide the required propulsion during ground contact (i.e. external work). We also have to swing our limbs faster, that is, we have to do more muscle work because we need larger forces to accelerate the limbs through a greater range of motion (i.e. internal work; remember W = F × d, so if F and d increase, work will also increase). Because we walk with our arms and legs relatively straight, the mass of our limbs is located at quite a distance from the joint centres of rotation and their moments of inertia are large. Swinging the limbs becomes very costly when we walk faster because the torque required to accelerate them becomes greater. In fact, the energy cost of walking on level ground can be quite accurately estimated from an individual’s body mass (which influences the forces of ground support and also the energy required for limb movement; external and internal work, respectively), standing body height (influencing limb length and therefore their moments of inertia; internal work) and walking speed (which influences the forces of ground support and propulsion as well as limb acceleration; external and internal work) (Weyand et al., 2013).
Because of this, the energy cost of walking, defined as the amount of energy needed to travel a given distance, is at a minimum at about 1.3 m·s-1 (4.7 km·h-1) and we almost always choose to walk (rather than run) at speeds less than about 1.5 m·s-1 (5.4 km·h-1; Long & Srinivasan, 2013). But at speeds above about 2.5 m·s-1, locomotion becomes very expensive and we have to change the way we go about it. Certainly if we’re in a hurry to complete our orienteering course, we’ll have to make a change.
Running
Running is a form of gait that we use to move quickly. This pattern of gait has the same characteristics as walking and therefore the terminology for describing the pattern is similar (e.g. initial ground contact, midstance, heel-off, swing phase, stance phase are the same; bringing the leg toward the front of the body is often referred to as the ‘recovery phase’). During running we flex our elbow and knee joints for much of the stride cycle so that the limb moments of inertia are reduced, with only the ground support leg being extended, as shown in Figure 18.4. This allows for much faster limb movement speeds to be achieved with a lower cost than for walking. In fact, it is estimated that only about 7% of the energy of running is used to swing the limbs (i.e. internal work) while body weight support and forward propulsion account for about 80% of the energy cost (Arellano & Kram, 2014).
FIG. 18.4 During much of the running cycle, the arms (e.g. at the elbows) and legs (e.g. at the knees) are flexed to reduce the working length of the limbs. This decreases the moment of inertia of the limbs, and therefore reduces the requirement for torque (muscle force) production and the energy cost of locomotion. At faster speeds, running requires less energy than walking.
In addition to the differences in limb configurations, there are several other important differences between walking and running. In running there is no double-support phase, where both feet are on the ground simultaneously. So enough upwards and forwards propulsion is required in each step to ‘jump’ onto the next leg. Also, while knee flexion during ground contact is minimal in walking (often we consider the leg to be straight when passing under the body), it flexes significantly during running. During the flight phase of running, when no foot is in contact with the ground, air resistance slows the body (albeit slightly) and gravity pulls the body towards the ground. So the body bounces along with significant changes in velocity.
These differences also result in a different exchange of energy during the cycle than walking. In running, PEgrav, KEv and KEh are decreasing at and after initial ground contact towards midstance, whereas they increase simultaneously during the propulsive phase towards toe-off. Therefore, instead of PE and KE changing out of phase with one another as in walking (Figure 18.2) they change in concert with one another, as shown in Figure 18.5. This theoretically prevents the exchange of PE and KE and increases the energy cost of locomotion. The resulting movement of the body’s centre of mass resembles a bouncing ball, which has historically been used as a metaphor.
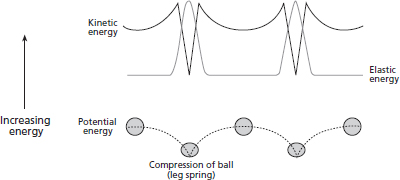
FIG. 18.5 During running the gravitational and kinetic energies change in phase with each other (compare to the out-of-phase exchange in walking in Figure 18.2), which has historically been thought to reduce the economy of the running gait. Although the energy exchange in running is complicated, it is thought that the storage and then release of elastic potential energy in the muscle and tendons in each step can minimise the energy loss and improve running economy. This gait looks similar to a bouncing ball (or a pogo stick; not pictured), with the compression and restitution of the ball (or the leg acting as a spring) allowing for energy storage and recovery.
Because the muscle-tendon units store and release elastic energy as the leg (which acts as a spring) compresses and extends during the ground support phase, another common metaphor is the pogo stick. This action allows for an improvement in movement efficiency by storing PEgrav (and some KEv and KEh) to aid propulsion into the next step as KE and PEgrav increase again. The compliant leg spring also reduces the loss of energy during the foot-ground collision, as described above for walking. Finally, because the tendons typically stretch and recoil significantly (especially the Achilles tendon at the ankle and patellar tendon at the knee), the muscles can produce forces without significant length change (i.e. with minimal work), which costs less energy. While there is some debate as to the true benefit of this leg spring behaviour in running (e.g. Fletcher & MacIntosh, 2015; Holt et al., 2014), it has been estimated that the reuse of stored elastic energy provides for more than half of the energy of propulsion during running (Alexander, 1991; Cavagna et al., 1964).
While running is typically a more costly form of locomotion than walking, the reduction in limb inertia ensures that it becomes less costly than walking when travelling at faster speeds. In fact, humans will choose to run around the speed at which running becomes less energetically costly than walking (probably a little faster than 2 m·s-1, or 7 km·h-1). This is commonly referred to as the gait transition point – interestingly, if we slow from a run to a walk the gait transition occurs at a slightly lower speed than if we accelerate from a walk to a run (called gait hysteresis). Therefore, we will have to use a running gait if we want to move rapidly around our orienteering course.
BOX 18.1 MEASUREMENT OF FORCE APPLICATION DURING GAIT IN HEALTHY AND CLINICAL PATIENT POPULATIONS
We often want to ‘describe’ how a person walks or runs so that we might understand how they’re applying forces to the ground. From this we can determine ways to improve the effectiveness of that force application, and therefore improve that person’s movement capacity. One way to characterise this force application is by graphing the forces produced during walking or running, which can be measured using a force platform. In the example below (Fig. 1) the traces of two individuals can be seen. The bottom graph shows the force application of a young, healthy adult walking at 1.11 m·s-1 (4.0 km·h-1) across a force platform. In the vertical direction, there is a smooth loading of the force, a slight unloading of force around midstance, then a propulsive force produced to launch the body into the next step. In the medio-lateral (side-to-side) direction the forces are much smaller and the body’s centre of mass would therefore translate little in these directions (i.e. the individual remains balanced during walking).
In the top graph, however, which was obtained from a person who suffered a traumatic brain injury six months prior, force application while walking at 1.05 m·s-1 (3.8 km·h-1) is altered. In the vertical direction there is an impact ‘spike’, indicating that the transition into this step was less smooth than for the healthy individual; this foot-ground collision may cause a loss of energy that has to be replaced by (energy costly) muscle work. The ‘bounce-like’ force application in the vertical direction seen in the healthy individual (bottom graph) is also attenuated in the person recovering from brain injury (top graph) and the rate of force production in the push-off phase is slower than in the healthy person. This may account partly for the slower walking velocity, even though the individual was instructed to walk briskly. Differences between the medio-lateral force records can also be observed between these individuals. In the top graph there is more notable medio-lateral force production, indicating that this individual produces more force to maintain stability. This extra work would also increase the energy cost of walking.
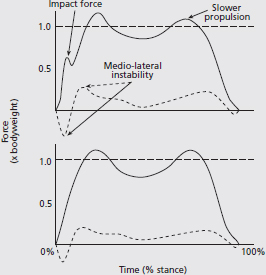
FIG. 1 Vertical (solid line) and medio-lateral (side-to-side; dashed line) ground reaction forces measured by force platform for a young, healthy adult (bottom graph) and an adult recovering from traumatic brain injury (top graph). In the top graph there are several departures from ‘normal’ force production, including a notable foot-ground impact peak (impact force), slower force application during the propulsive phase, and greater medio-lateral force production (indicating difficulty with maintaining stability). Force traces similar to these can also be observed in other populations, including very elderly, motor-impaired (e.g. cerebral palsy) and toddler/child-aged individuals. Measurement of ground reaction forces can be a useful in order to characterise and monitor changes movement performance in sporting and clinical populations.
From this comparison, it would be reasonable to assume that the energy cost of walking (i.e. walking economy) would be much greater for the person recovering from brain injury (top graph) compared to the uninjured adult. By implementing a multi-factorial exercise training programme, a clinician would hope to improve force production during gait and therefore reduce the energy cost of walking. This will be a primary goal of the rehabilitation programme. A method by which a programme might be developed and implemented is provided in the next chapter.
So the simple answer is that we should use a running gait if we want to complete our orienteering course as fast as possible. However, it was also noted at the start of this chapter that the course is very long, at least relative to your current fitness level. In that case, it might not be possible to run the entire distance using the energy-costly running gait. Instead, we might have to walk … at least part of the way.
In fact, most humans use a combination of walking and running when travelling long distances when there is a need to reduce travel time; otherwise we would choose to walk the entire distance. For example, most humans complete a marathon in 4.5–5.0 h and use average speeds of 2.3–2.6 m·s-1 (~8.3–9.4 km·h-1) achieved through walk-run variations. It turns out that when we are asked to cover a distance without time pressure we will almost exclusively walk at speeds <1.5 m·s-1 (5.4 km·h-1), but we choose a walk-run mixture if we are forced to move at an average speed of ~3.0 m·s-1 (10.8 km·h-1) and mostly run if we have so little time that the average speed required is >3.0 m·s-1 (Long & Srinivasan, 2013). This relates somewhat to the important concept of ‘critical power’ (or critical speed), which is the highest power (or speed) that can be sustained almost indefinitely. Once we produce a greater power (or speed) than the critical power then we cannot sustain it and must therefore slow down or change gait (e.g. switch from a run to a walk).
We should also consider what would happen if we had to move over hilly terrain. When running uphill, in which case there is a continual need to increase the body’s gravitational potential energy, much more muscle work is required. This must largely come from muscle activation because the lesser downward fall of the body prior to foot-ground contact ensures that less PEgrav can be stored in the muscle-tendon units for later use in propulsion. As the gradient increases, the speed of locomotion will decrease because we have to rely on muscle work rather than rapid recoil of tendons, and the more efficient walking gait becomes favoured. In fact, on steep gradients it may not be possible to bounce at all during running, in which case walking is obligatory.
During downhill locomotion, it is quite easy to run so we will always choose it if we need to move quickly (although it can be fatiguing because of the intrinsic muscle damage that it can cause, but consideration of such factors is beyond the scope of this chapter). Walking is typically more economical when moving slowly downhill. However, for both running and walking downhill, the cost of locomotion starts to increase when the gradient passes about 10–20% (Minetti et al., 2002). This is because the active, negative work being done by the muscles absorbs and then dissipates mechanical energy to keep us from moving too rapidly down the hill; so we use energy to maintain control over our movement. Ultimately, it can be relatively costly to move down very steep hills.
If we have the choice between an undulating path and a flat one, we should choose the flat one because we don’t save as much energy running downhill (compared to the energy cost of running on the flat) as it costs us to run uphill (DeVita et al., 2007; measured using 5% incline/decline), and this difference becomes greater as the gradients increase (Minetti et al., 2002). This possibly occurs because of the loss of energy caused by muscle (and other soft tissue) oscillations during landing in downhill running, which is caused by vibrations that occur on ground contact. It may also result from the fact that there is still some requirement to project the body upwards relative to the running surface into the next step. All told, we are unexpectedly inefficient when running downhill.
HOW ELSE CAN WE USE THIS INFORMATION?
A detailed understanding of how we walk and run is important in order to detect kinetic and kinematic problems during walking, as might occur in children with developmental delay or in those with muscle weakness, spasticity, etc. By understanding how we move, we will be better able to implement training strategies to improve locomotion, such as training that increases muscle-tendon efficiency. The greater compliance of tendons of older individuals reduces the capacity to store and recover elastic potential energy, and slows the possible rate of recovery (remember, the recoil speed of a tendon that carries a load will be proportional to its stiffness because acceleration is governed by the magnitude of force, and the recoil force of a tendon is influenced by its stiffness). Given that we know that the storage and release of elastic energy is important for efficient walking and running, we might develop strategies to improve this. For example, heavy strength training has been shown to increase tendon stiffness in older individuals, and would thus be an important strategy for improving locomotor function into older age (Reeves et al., 2003); such a strategy is clearly useful for the wide variety of individuals who are relatively inactive and may not have optimum tendon stiffness or muscle strength and power.
Useful Equations
total energy = PE + KE
energy (elastic potential) = ½kx²
moment of inertia (H) = Iω or mk²ω
total moment of inertia (parallel axes theorem) (Itot) = ICM + md²
Alexander, R.M. (1991). ‘Energy-saving mechanisms in walking and running’. Journal of Experimental Biology, 160: 55-69.
Arellano, C.J. & Kram, R. (2014). ‘Partitioning the metabolic cost of human running: A task-by-task approach’. Integrative and Comparative Biology, 54(6): 1084-1098.
Bertram, J.E.A. & Hasaneini, S.J. (2013). ‘Neglected losses and key costs: tracking the energetics of walking and running’. Journal of Experimental Biology, 216: 933-938.
Cavagna, G.A., Saibene, F.P. & Margaria, R. (1964). ‘Mechanical work in running’. Journal of Applied Physiology, 19(2): 2, 249-256.
Cronin, N.J., Avela, J., Finni, T. & Peltonen, J. (2013). ‘Differences in contractile behaviour between the soleus and medial gastrocnemius muscles during human walking’. Journal of Experimental Biology, 216: 909-914.
DeVita, P., Helseth, J. & Hortobagyi, T. (2007). ‘Muscles do more positive than negative work in human locomotion’. Journal of Experimental Biology, 210: 3361-3373.
Fletcher, J.R. & MacIntosh, B.R. (2015). ‘Achilles tendon strain energy in distance running: consider the muscle energy cost’. Journal of Applied Physiology, 118: 193-199.
Holt, N.C., Roberts, T.J. & Askew, G.N. (2014). ‘The energetic benefits of tendon springs in running: is the reduction in muscle work important?’ Journal of Experimental Biology, 217: 4365-4371.
Kuo, A.D., Donelan, J.M. & Ruina, A. ‘Energetic consequences of walking like an inverted pendulum: step-to-step transitions’. Exercise and Sport Sciences Reviews, 33(2): 88-97.
Lichtwark, G.A., Bougoulias, K. & Wilson, A.M. (2007). ‘Muscle fascicle and series elastic element length changes along the length of the human gastrocnemius during walking and running’. Journal of Biomechanics, 40(1): 157-164.
Lichtwark, G.A. & Wilson, A.M. (2006). ‘Interactions between the human gastrocnemius muscle and the Achilles tendon during incline, level and decline locomotion’. Journal of Experimental Biology, 209: 4379-4388.
Lipfert, S.W., Gunther, M., Renjewski, D. & Seyfarth, A. (2014). ‘Impulsive ankle push-off powers leg swing in human walking’. Journal of Experimental Biology, 217: 1218-1228.
Long, L.L. & Srinivasan, M. (2013). ‘Walking, running, and resting under time, distance and average speed constraints: optimality of walk-run-rest mixtures’. Journal of the Royal Society Interface, 10: 20120980.
Minetti, A.E., Moia, C., Roi, G.S., Susta, D. & Ferretti, G. (2002). ‘Energy cost of walking and running at extreme uphill and downhill slopes’. Journal of Applied Physiology, 93: 1039-1046.
Neptune, R.R., Kautz, S.A. & Zajac, F.E. (2001). ‘Contributions of the individual ankle plantar flexors to support, forward progression and swing initiation during walking’. Journal of Biomechanics, 34: 1387-1398.
Reeves, N.D., Maganaris, C.N. & Narici, M.V. (2003). ‘Effect of strength training on human patella tendon mechanical properties of older individuals’. Journal of Physiology, 548(3): 971-981.
Roberts, T.J., Marsh, R.L., Weyand, P.G. & Taylor, C.R. (1997). ‘Muscular force in running turkeys: the economy of minimizing work’. Nature, 275:1113-1115.
Usherwood, J.R., Channon, A.J., Myatt, J.P., Rankin, J.W. & Hubel, T.Y. (2012). ‘The human foot and heel-sole-toe walking strategy: a mechanism enabling an inverted pendular gait with low isometric muscle force?’ Journal of the Royal Society Interface, (9): 2396-2402.
Weyand, P.G., Smith, B.R., Schultz, N.S., Ludlow, L.W., Puyau, M.R. & Butte, N.F. (2013). ‘Predicting metabolic rate across walking speed: one size fit for all body sizes?’ Journal of Applied Physiology, 115: 1332-1342.
Related Websites
The Physics of Sports (http://www.topendsports.com/biomechanics/physics.htm). Website investigating the applications of physics in sports.
The Physics Classroom – Tutorials (http://www.physicsclassroom.com/Class/). Lessons on basic physics concepts.
Smithsonian Museum of Natural History (http://humanorigins.si.edu/human-characteristics/walking). Website detailing the evolution of human walking.