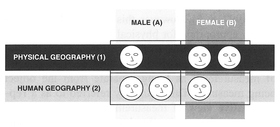
Figure 3.1 Geography students organised into categories.
Within every group of students to whom we have taught basic statistical analysis, at least one-third profess to be 'stato-phobic' and are petrified by the thought of doing anything with numbers. Whilst some statistical tests can be very complicated, those dealt with over the next two chapters are generally basic in nature. At first glance, an equation may look daunting, but as you will see when we work through the examples - particularly the tests in Chapter 5 calculating a statistic simply involves following a number of steps in a particular sequence. When the computer does all the work for you, using statistics becomes even easier: all you need to do is input the data, run the program and interpret the results. As long as you understand the simple mathematical operators +, -, ÷, ×, √,2 and σ, using the statistics in this book should be relatively straightforward. We have come to the conclusion that many of our students find statistics difficult to use because they think they ought to be. Many students think there is a catch, that they are missing something obvious. Statistics are, however, relatively straightforward to use. To carry out the analysis you just need to understand the language or 'jargon' being used, and then follow the set of accompanying rules. In our opinion, qualitative data are often much harder to generate and analyse. Ironically, many of our students choose qualitative studies, not because they think that geographic studies should be qualitative in nature but because they think that qualitative analysis will be easier. As you will see in Chapters 7 and 8, this myth needs to be firmly quashed.
The quantitative analysis methods discussed in Chapters 4 and 5 require the collection of measured data. Such data represent one type of information which we can collect about phenomena in our environment. Here, measurements relate both to the fundamental properties of objects, where quantities like length extend through space, and to measurement operations performed on individual objects. In the former, measurements are known as extensive properties which form the basis of standard measuring systems such as the SI system in use by most scientists today (Chrisman, 1997: 8-9). However, this view of measurement is only appropriate for physical properties, and is not really applicable to the subject matter of most social scientists. The alternative latter view sees the process of measurement as being separate from the object being measured. This is usually referred to as a representative view of measurement. It was this view that was adopted in the levels of measurement developed by Stevens (1946) and listed in Box 3.1. He identified four levels of measurement: nominal,
| Nominal | Observations are placed in categories, symbolised by numerals or symbols (e.g., A, B, C, D). |
| Ordinal | Observations can be placed in a rank order, where certain observations are greater than others. Assigned numerals cannot be taken literally (e.g., first, second, third, fourth). |
| Interval | Each observation is in the form of a number in relation to a scale which possesses a fixed but arbitrary interval and an arbitrary origin. Addition or multiplication by a constant will not alter the interval nature of the observations (e.g., 1°C, 2°C, 3°C, 4°C). |
| Ratio | Similar to the interval scale, except that the scale possesses a true zero origin, and only multiplication by a constant will not alter the ratio nature of the observations (e.g., 0%, 5%, 10% as an exam mark). |
ordinal, interval and ratio, each of which creates data of a different form. As a consequence, the type of quantitative analysis appropriate to each level of measurement also differs. The choice of a level of measurement is important since it will determine what the generated data will tell you.
Nominal measurement (also known as categorical measurement) is based on mathematical set theory, and is concerned with the assignment of objects into categories often signified by numerals or symbols. Each category is homogeneous and mutually exclusive and the overall categorisation is exhaustive (Reynolds, 1984). For example, we might divide a group of geography students sitting an exam into two groups based on gender, and put these into the categories 'A' and 'B'. We could further subdivide each of these groups into a group who were predominantly interested in physical geography (group 1) and a group predominantly interested in human geography (group 2). We have thus categorised the students into four distinct groups (Figure 3.1).
Although we have assigned those in the physical geography group as '1' and those in the human geography group as '2', we could have chosen any two different codes to differentiate the groups. Although we seem to have developed an ordering system - 1A, 1B, 2A, 2B - this is not meaningful, since we could

Figure 3.1 Geography students organised into categories.
Table 3.1 Ordinal ranking scale.
| 1 | Very interesting |
| 2 | Interesting |
| 3 | Neither interesting nor boring |
| 4 | Boring |
| 5 | Mind-bendingly boring |
just as easily categorise each physical geographer as a 2 and each human geographer as a 1. In addition, we cannot say that 1 + 1 = 2 (i.e., two physical geographers = a human geographer), as arithmetic operations make no sense on nominal data.
Ordinal measurement, in contrast, can convey more information since we are able to place objects in some sort of rank order, as the name suggests. For example, the results of an exam will place the above-mentioned students in a rank order. The student with the highest mark will be first, the next highest second, and so on. In this case we can say that the student who came first has a mark which is greater than that of the student who came second, who has a mark greater than that of the student who came third, although the actual mark differential may be less between first and second than between second and third. Another example of ordinal measurement is the use of ranking scales which might be used in a questionnaire analysis. For example, an ordinal ranking scale similar to that in Table 3.1 might be used to rank responses received from each student about how interesting they find their statistics class.
The results of questioning our six students according to Table 3.1 might produce the results seen in Figure 3.2. Numbers are assigned to each ordinal category only to assist analysis (Weisberg, 1992) and they convey information only about rank order: we cannot assume that the intervals between the ranks are equal, or that the quantities ranked are in any way

Figure 3.2 Ordinal ranks of student responses.
absolute (Frankfort-Nachmias and Nachmias, 1996). Even though the difference between the codes for the categories 'Very interesting' and 'Interesting' (1 and 2) is 1, the same as the difference between the codes 'Boring' and 'Mind-bendingly boring' (4 and 5), we cannot treat this numeric interval as being meaningful. We could have chosen other codes, for example 10, 20, 30, 40 and 50, to replace the existing 1-5 codes.
In contrast to nominal and ordinal measurement, interval and ratio measurement are inextricably concerned with quantitative data (also termed metric data). In this case, an observation will usually be in the form of a meaningful number. These can either take on any value within a given range (continuous variables, e.g., length in metres) or be restricted to a number of distinct values within a given range (discrete variables, e.g., counts of people in a sample category). For an interval measurement this number relates to both an arbitrary interval scale and an arbitrary origin, though we do know precisely what the interval is between two measurements. For example, consider the Roman calendar system: 1998 is exactly 100 years greater than 1898, but the origin chosen on the scale is arbitrary - in this case 0 AD. Taking the numbers on such a scale and either multiplying by a constant or adding a constant will not destroy the interval nature of the data (Weisberg, 1992).
For a ratio measurement, which is the highest level of measurement, this number is in relation to a scale of an arbitrary interval, similar to interval data, but with a true zero origin. If we return to the example of students in the exam, each student will have obtained a certain number of marks. It is possible for a student to obtain zero marks in the exam, and the ratio of marks between two students might be 3:2, hence the different scores for each student are measured on a ratio scale. The key point here is that we can multiply ratio variables by a constant, but adding a constant will destroy their ratio nature (Weisberg, 1992). For example, our six students may have obtained the set of exam results displayed in Figure 3.3. Two of the
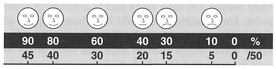
Figure 3.3 Ratio measurement of student exam results.
students have scored 30 and 20 respectively out of a total of 50. Multiplying by 2 gives the mark out of 100, i.e., 60 and 40, which maintains the ratio, but adding an extra 5 marks to each score changes the ratio to 7:5. Ratio measurement more commonly applies to metric quantities such as distance and mass, which possess a zero origin.
As noted above, the level of measurement determines the type of analysis we can perform on the data generated. Nominal and ordinal data can only be analysed using non-parametric tests. Interval and ratio data are generally analysed using parametric statistics, although it is possible to convert data from an interval/ratio measurement scale to an ordinal or nominal scale if required. As a rule, properties measured at a higher level of measurement can be converted (measured) at lower levels (Frankfort-Nachmias and Nachmias, 1996). For example, we can convert the student grades displayed in Figure 3.3 to an ordinal scale, simply by placing them in rank order. This is particularly useful if we wish to use a non-parametric statistical technique for analysis of data which, although interval or ratio in nature, do not fit the assumptions of an appropriate test (see Section 4.7). We will return to describe further parametric and non-parametric methods of analysing data, and the differences between them, in Chapter 5.
Whatever the specific research questions you have established from Chapter 2, you may wish to generate/collect your own data: a process we have termed primary data collection. Primary data generated for quantitative data analysis, as discussed above, do not need to be interval in format. However, such data need to be generated in such a way that they can easily be described and analysed using quantitative techniques. We often use surveys to obtain such data. A survey is a study which seeks to generate and analyse data on a specific subject from a particular sample population. Most people will have taken part in a survey at some point. For example, you could have been stopped in the street, questioned on the doorstep, or phoned at home about things such as who you were going to vote for and why? Or, which washing powder you use or chocolate you eat? Consumer and market research rely almost exclusively upon large-scale surveys to generate data about all aspects of our daily lives. As indicated, surveys can take a number of forms ranging from postal surveys to telephone surveys, and can use a number of different sampling strategies. In general, surveys use questionnaires to generate quantitative data from which they can calculate statistical information (e.g., 39% of males aged 21-30 smoke regularly), and it is this type of survey we will concentrate on below.
When designing any survey there a number of factors you need to consider (see Box 3.2). How you resolve each of these will determine the nature of the data you generate and what they will tell you. You will need some sort of purpose or objective, usually generated by your research problem, in order to motivate your survey. This could be a simple question, for example: 'What motivates people to make intraurban residential moves?'. The sample population are the respondents taking part in the study, which you will have sampled to try and answer your question. You need to decide upon your sample population carefully. There is no point in including people whose opinions and thoughts are not relevant to what you are researching. The characteristics of your sample are usually delineated by factors such as age, occupation and economic status. For example, a survey concerning voting patterns will usually include only people of voting age (18+). Similarly, if you are interested in the behavioural processes underlying intra-urban residential mobility (mobility within a city), there is no point in including people in the survey who are making an inter-urban move (mobility between cities).
After deciding upon who you want to survey, you need to decide how your data will be generated. There are two options. First, you can interview your respondents using a discussion situation aimed at generating qualitative data (see Chapter 7). Second, you can interview your respondents using a more formal, structured questionnaire aimed at generating quantitative data. These two data generation methods are not mutually exclusive and many surveys mix discussion-style open questions with more rigid closed questions, which we will examine in the next section.
Before designing the questionnaire, you will need to decide on the medium in which your questionnaire will be conducted. There are a number of options open to you, each with merits and limitations. The most common questionnaire medium is face-to-face meeting. Unlike an interview, where the discussion may need an informal, comfortable setting due to its length and nature, a questionnaire can be conducted in a variety of settings, for example on the doorstep or in the street. This is because a questionnaire usually takes less time to complete and the relationship between researcher and researched is more formal. Face-to-face meetings have the advantage of personal contact and a higher response rate (especially when administered on the doorstep). However, they can also be quite time-consuming. A second option is to use a postal questionnaire. Here, the questionnaire is sent to all the potential respondents for self-completion. The postal questionnaire increases the potential sample size and can reach those respondents who are geographically dispersed, but has some distinct disadvantages: the response rate can be much lower (especially if return postage is not included), the costs of administration are higher (postal costs), questionnaires are often returned incomplete, and the method provides no opportunity to clear up misunderstandings. It is essential, with a postal questionnaire, that you send a covering letter stating explicitly the reasons for the survey and thanking the respondents in advance. A third option might be to administer the questionnaire using the telephone. Telephone questionnaires
tend to be quicker to complete and increase the potential sample size. They can also limit the sample as respondents must have a telephone. Refusal rates are generally much higher and phone bills can be expensive. A final option might be to distribute the questionnaire via e-mail. Several studies have utilised e-mail as a questionnaire medium, posting their forms to members of a relevant mailing list. The sample population for these questionnaires usually have specialised interests. As with postal administered questionnaires, the response rate can be variable, especially if the questionnaire has been posted to people who have no relevant interest in the topic.
There is more to designing a questionnaire than just assembling a series of questions. The type, wording and order of the questions need to be carefully planned. The questions you ask will be determined by what you want to do with the data. There are generally four types of variables that need to be generated by questions so that they can be statistically analysed (see Box 3.3). When constructing your questionnaire you must be careful to ask questions that will generate these variables to enable subsequent statistical analysis.
There are nine basic types of questions which can be used in a questionnaire, and examples of these are given in Box 3.4. In general, questionnaires usually seek a mix of descriptive and analytical answers. Descriptive questions tell us 'what' and analytical questions tell us 'why'. These aim to generate both factual and subjective data relating to people and their circumstances, the behaviour of people, and attitudes, opinions and beliefs. Questionnaire data to be analysed quantitatively are usually generated using what are termed closed questions (also known as closed-ended questions).
A closed question is one where the respondent is given a set number of answers, one of which they must choose as the most representative of their facts/views. In Box 3.4 questions 2-8 are all different forms of closed questions. Categories are useful mechanisms to obtain factual information, but the options offered to the interviewee must reflect the likely pattern of variation in the sample. For example, if we asked question 2 to a sample of households who lived in new suburban subdivisions, we might find that the bulk of the responses occur in categories 1 or 2. This characteristic, termed heaping (Bourque and Clark, 1992), may occur at either end of a category
Box 3.3 Questionnaire variables for analysis
Source: Adapted from Oppenheim 1992.
scale. Again, if we sampled households comprised of retired people, we might find that the upper limit '5+' heaps respondents in this category. Lists, scales and ranks are also useful devices for closed question construction. A scale allows respondents to qualify their feelings or thoughts on a fixed scale ranging from negative to positive reactions. Questions 4, 5 and 7 are all types of scale. The bipolar scale used in Question 5 is usually referred to as a semantic differential scale (Frankfort-Nachmias and Nachmias, 1996). Ranking questions require the respondent to place a series of choices into an order of importance/preference. Which of these question types you choose to adopt depends upon exactly what you want to know, determined ultimately by your research problem. There is no point asking respondents to rank all choices if all you want to know is which variable is
most important. Finally, contingency questions (e.g., if answered 'yes' to Question 5) are asked only to respondents who gave specific answers. They act as filters to probe a particular issue further. These types of question create skip patterns within a questionnaire, where certain questions are skipped if a respondent gives a certain answer.
The other main type of question is the open question (or open-ended question) where the respondent is given no set of possible answers. Although this type of question is generally easier to put into a questionnaire, and avoids the problem of suggesting potential answers to the respondent, it is harder to analyse quantitatively, requiring some form of content analysis.
Once you have thought about the types of question, and the variables which you need, it is worth considering the various options available for the design of your questionnaire so that the surveyed data can be used for computer-based quantitative analysis with a minimum of difficulty. Bourque and Clark (1992) give many helpful suggestions in this regard, and recommend the use of both closed and pre-coded questions where possible. In Box 3.4 we have deliberately used different styles for several of the closed-ended questions. For example, in ques tions 2 and 3 we have pre-coded the appropriate number to circle guided by dotted lines, but for ques tions 4-8 we have chosen boxes to tick or number. Both are acceptable styles to use, but information entered into the boxes will require subsequent cod ing, and the pre-coded questions are considerably easier for taking the data and entering into a compu ter. Bourque and Clark (1992) advise that when designing questionnaires with closed and pre-coded questions, the researcher should be very careful to ensure that the categories offered in each question are exhaustive (or if not, an 'other' category is included to catch other answers, as in question 3 in Box 3.4), are mutually exclusive, and use consistent coding across different questions for common replies (e.g., no = 1, yes = 2, don't know = 3, missing data = 999). Finally, some thought should be given as to whether alternative answers are read aloud to the respondent. Doing so may suggest potential answers which the respondent may not have thought of.
Taking care over question wording is crucial. Questions should be concise and clear, so that they cannot be misinterpreted or misunderstood. Some general rules concerning question construction are detailed in Box 3.5. Questions should be divided into appropriate sections and ordered in a progressive manner. Respondents should feel that the questionnaire has a logical order so that there is a purpose to their answers. A general guide is to start by providing a set of instructions and a preamble. The instructions should tell the respondent how long the questionnaire will take to complete, and if appropriate, provide a return date and details of how to return the completed questionnaire. The preamble should provide a brief explanatory statement of the purpose of the research. Keep the statement short but as informative as possible. Remember that you are relying on the goodwill of the respondents to complete your questionnaire. You should also explain whether the responses will be treated confidentially. After the preamble, it is usual to seek factual background information (e.g., age, sex, etc.). This is followed by the main sections of the questionnaire. At the end always thank the respondent for their answers and time.
However the questionnaire is worded and ordered, it should not be too long. Respondents will soon become bored when answering closed questions as there is little discussion and interaction. We recommend that you ensure that your questionnaire takes less than ten minutes to complete and consists of only a few pages. If your questionnaire consists of reams of paper then many people will be put off, especially if it is a postal questionnaire. As well as length, presentation is important. Your questionnaire should be presented in a professional manner with appropriate spacing and boxing. A poorly presented questionnaire does not place confidence in the respondent and can be difficult to complete and code. Finally, you may well encounter problems with respect to administering the questionnaire in person. Sometimes people can overreact to someone knocking at their door. Indeed, the father of one of the authors recalls an instance whilst surveying where he was greeted by a man with a revolver who was determined he wasn't going to come into that particular house! This is an extreme example, and is unlikely to happen to you. However, if you are administering the questionnaire in person, it is useful to have an official covering letter - ideally on headed notepaper from your department - which describes who you are and the purpose of your survey.
As with all methodologies your questionnaire should be piloted to determine whether the questions work well and produce the data that you require for your research. Even if this is just a case of trying out the intended questionnaire on your family and friends, feedback received at this stage can be very useful in clarifying the questions you are trying to ask. Some of the key things to look for in inspecting the results of a pilot test are listed in Box 3.6.
Box 3.5 General guidelines for asking questions
Sources: Barrat and Cole 1991; Mikkelsen 1995; Robson 1993.
When you administer your questionnaire, it is possible to introduce error due to non-response, which we term non-response error. As a rule, it is hoped that all respondents in a selected sample will answer all questions. In this case, there will be no nonresponse error. However, in most surveys there is a degree of non-response because of reasons such as refusal to answer questions, absences or lost forms. The concern is that those who do not participate in a survey may well differ from those that do. In general, the larger the non-response error the larger the biasing effects are within the data caused by certain portions of the sample population being missing. One of the largest non-response errors recorded was by the Literary Digest in the poll for the 1936 US election between Roosevelt and Landon (Frankfort-Nachmias and Nachmias, 1996). The Digest conducted a poll of 2.4 million individuals (then the largest in history). The method they used was to mail 10 million questionnaires to people whose names and addresses were taken from sources such as telephone directories and club membership lists. From their sample, they predicted a victory for Landon with 57% of the votes. Roosevelt in fact won the election with 62% of the vote! Despite the large sample size, the error was enormous. This occurred because the sampling scheme failed to recognise that many poor people did not have a telephone or belong to clubs, so they were
missing from the sample framework. In general, poor people voted for Roosevelt. A common non-response error occurs if you try to sample your data between 9 am and 5 pm, as many people are at work and therefore unable to answer your questions.
We can calculate the proportion of responses to non-responses (R) as follows:
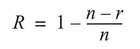
where n is the original sample size and r is the response rate. For example, if the original sample was 500, and 400 responses are obtained, the response rate is 1 - (500- 400)/500 = 0.80, and the non-response rate is 0.20, or 20%.
The proportion of responses to non-responses depends upon such factors as the nature of the population, the method of data generation, the kinds of questions being asked, and the skill of the interviewer, and if a postal questionnaire is used, whether return postage has been paid for, and the number of call-backs (Frankfort-Nachmias and Nachmias, 1996). To try to minimise non-response error we suggest that you design your survey carefully and sensitively; thoroughly pilot your survey; use a strategy of calling back to survey respondents who may have been out or busy when you first called; check the response rate for certain groups against what you might expect (e.g., if you have a response rate of only 20% for women, when an equal proportion of men and women were meant to be sampled, then there may be a problem that needs to be addressed/considered); and consider drawing a sample larger than needed to ensure that a certain sample size is achieved. The final point should be used with care as non-response usually affects certain sections of the population more than others (e.g., older people, immigrants, disabled people), so increasing the sample size might not mean that they will necessarily be included. We will now turn our attention to taking a sample from a population.
Once you have designed and piloted your questionnaire, the next step is to determine how you will sample your respondents. Why sample? The answer to this is straightforward and will be illustrated with a simple example. Suppose you are interested in the decision-making process underlying intra-urban residential mobility, and have decided to interview households to investigate the motivation behind their decision to move. You will normally have a variety of candidate towns and cities in the part of the world in which you live. Even if you could identify all those people who are currently moving house, constraints on time and resources would make it impractical for you to interview all candidate households in all cities. You will clearly have to select a subset of households, perhaps restricting your focus to one urban area, or even a part of one urban area. We term the total of all possible people who display the characteristic we are interested in, a population. The size/extent of a population is determined by the size of the group that we wish to make generalisations about. In the above case the population could be the total of all people in UK cities who are desiring to move within the urban area of their city, or it could be restricted to all the people in one city or part of a city. Once we have identified a population we are now in a position to select a subset of that population. This subset is termed a sample, and in the example above this would constitute households selected from a list of those in the process of moving or wishing to make such a move. Whilst nearly everyone can identify a population and select a sample, it should be noted that different methods of selection exist, some of which may be more valid tham others. As a rule, we want our sample to be free of bias and as representative of the larger population as possible.
There are many different sampling methods (also known as sampling designs) available for the collection of data, and these are described in Table 3.2, with examples given in the context of selecting a sample of households moving house within Belfast to investigate the decision-making process underlying intra-urban residential mobility. The choice of which sampling method to use depends on a variety of questions which we are usually faced with when designing a sampling strategy:
We shall consider each of these questions in turn, and provide some answers which will guide you towards the setting up and execution of a sampling strategy in your own research project.
We often sample for the purpose of generalising about the larger population from which the sample was drawn. The need for some sort of representative sample is most clear in the polling process prior to elections, where polling organisations such as Gallup and Harris want to obtain a sample about voting intentions which is as representative as possible of the larger voting population. As an example of an unrepresentative sample, consider the following case (taken from Chatfield, 1995). Several years ago, Puerto Rico was hit by a hurricane and suffered considerable damage, resulting in 10,000 claims for hurricane damage. The US government initially decided to base its total grant aid on the first 100 claims received, and then multiply this by 100. Clearly, the first 100 applications need not necessarily constitute a representative sample (i.e., small claims requiring less work would be likely to come in first). A more representative sampling scheme was needed, and was eventually applied. There are a variety of methods by which we can produce a representative sample. These include non-probability-based methods such as quota sampling and probability-based methods based on random sampling (see Section 4.6 for details on probability concepts).
The judgemental sample (also known as a purposive sample) is the most subjective sampling method. Here, sample elements are selected based on judgement derived from prior experience. In an interview situation, individuals may be selected on the basis of the sort of response that they are likely to give, and the responses the interviewer is looking for. The quota sample selects those elements to be included in the sample on the basis of satisfying a predefined quota. For example, an interviewer might have a quota to fill of 30 men in the age-group 20-25, who are in an income bracket of high income earners, or as in the example in Table 3.2 homeowners aged 20-40 years. The interviewer has the choice of selecting certain people who might be included in the quota, and therefore introduces bias into the sample. Quota sampling has advantages in that it is easier, generally costs less to perform and does not require a sampling frame, but the key point to emphasise is that it should be used only in those limited situations where experience has shown it to work with minimal interviewer/sample bias (Ehrenberg, 1978). This is usually only when we know enough about the population being sampled to say that any sample bias introduced by the method or interviewer is in fact minimal. Another non-random sampling method which is used with the selection of people, is the snowball sample. This is based on a number of initial contacts who are asked for the names and addresses of any other people who might fulfil the sampling requirements.
The sampling designs considered so far are only really appropriate if you wish to use very simple non-probability-based descriptive techniques such
as raw counts and proportions. If you want to use a probability-based statistical method such as those considered in Chapter 5, then designs where we can estimate the probability of each unit being included in the sample are required. The simplest is the systematic sample. Such a sample involves the sys tematic selection of cases from a sampling frame. Although the initial start point in the sampling frame is random, the subsequent selection of points is usually selected with a regular interval, and can be subject to selection bias. This aside, since we can determine the probability of each unit being included in the sample, the method is probability-based. How ever, usually those methods more firmly based on a random sample are more useful, as they avoid any interviewer/sample bias. At the simplest level, the simple random sample occurs when each unit of the population is given the same probability of independent selection. There are a variety of other designs based on the simple random sample, which include the stratified random sample, the multistage random sample and the clustered random sample, which are described in Table 3.2. All these methods possess several key elements in common (Ehrenberg, 1978):
Other sampling designs can be obtained from combinations of those described above, such as combining quota sampling with a random route, or modifying the systematic sample by implementing a randomly varying interval. All the random sampling methods are based on the use of random numbers. These can be read off from a convenient table of random numbers, or generated using the random number generator of a spreadsheet package such as Microsoft Excel, or a statistical package such as MINITAB. Table 3.3 displays an extract from a random number table - in this case the last three lines from the table which appears in the appendices of Silk (1979).
There are various methods for obtaining numbers from such a table, but the simplest is to choose a start point somewhere on the table, and then to move along either the rows or columns, selecting groups of numbers which fall within the range of numbers in which we are interested. For example, if we wanted a sample of ten numbers coded from 1 to 450, and we had selected the middle '1' of the 71118 as our start point, we could then extract the following three-digit numbers moving along the first row:

We omit the 983 and 454 since they exceed our range (which has an upper limit of 450), and stop once we have obtained ten numbers. If we were to use instead the example given for the simple random sample in Table 3.2, since our codes range from 1 to 600, we would have included all the numbers listed above (except 983), with the addition of a further 18 numbers to bring the sample up to the desired size of 30. For further details on the sampling methods discussed above, you should consult a text such as Cochran (1977) or Dixon and Leach (1978) for a more geographical perspective.
If we take several random samples of the same size from the same population, we would not expect the statistics of each sample, such as the mean, to be the same. This is most clearly demonstrated in Table 3.4 and Figure 3.4 which displays data taken from Ehrenberg (1978). Although not geographic, this example is most helpful in the understanding of some of the characteristics of sampling distributions.
The data in Table 3.4 detail the consumption of Corn Flakes packets in a period of six months by a set of 49 1 households, where the known mean of this population was 3.4 packets. This population is sampled repeatedly using sample sizes of l, 2, 10 and 40 to produce an empirical distribution of sample means which are displayed in histogram form in Figure 3.4. The distribution of means at each sample size is termed a sampling distribution. We can make four useful observations from this table (Ehrenberg, 1978):
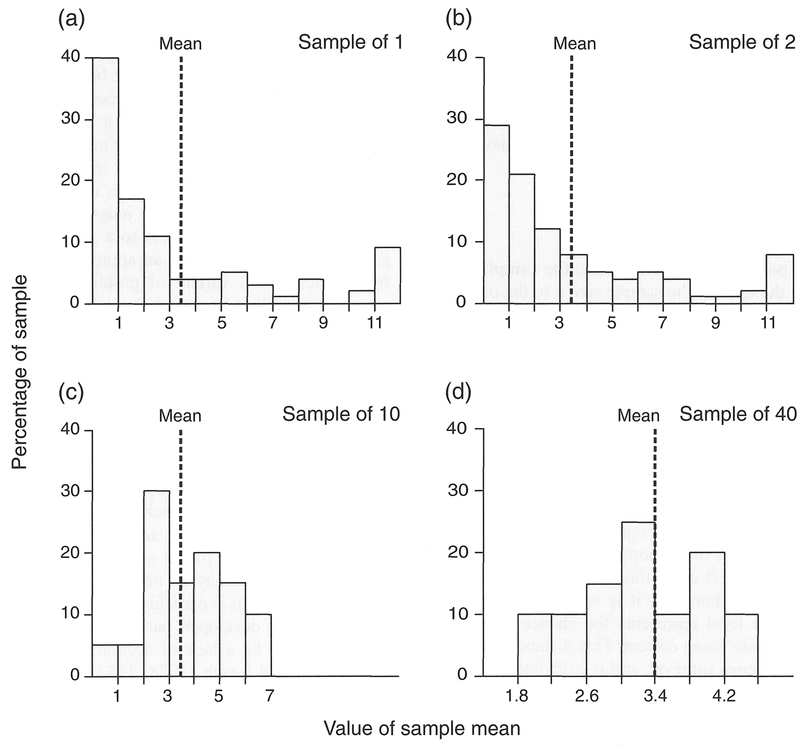
Figure 3.4 Cornflakes sampling distributions for different sample sizes, from Table 3.4
In general, the form of the sampling distribution follows the Student's t-distribution for small samples, but for samples greater than 30 follows a normal distribution (see Section 4.6). The standard deviation of the sampling distribution is termed the standard error of the mean (SE) and is found by:
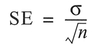
where sigma (σ) is the standard deviation of the population and n the size of the sample. Since we rarely know enough about our population to define sigma, we make use of s, which is the standard deviation of the sample, to give:
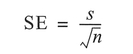
If the population is small, where the sampling fraction - the ratio of the sample size n to the population size N - is 0.2 or greater, a correction factor known as the finite population correction is usually incorporated into the above equation (Malec, 1993):

This SE estimate is useful as it allows us to determine, for a given confidence level, the distance by which a sample mean is within a stated range of its true value, i.e., how accurate an estimate such as the sample mean is of the population mean. We will consider the subject of confidence levels in more detail in Chapter 5. For now, it is sufficient to say that a confidence level represents the chance of our sampled estimate being correct. This distance c is termed the confidence interval, and is calculated as follows:

where z is the standard error unit measure for the desired confidence level (Dixon and Leach, 1978). For example, if we adopt a 95% confidence level (i.e., we allow a 95% chance of being correct that the true population mean is within this range), then for a normal distribution we know that 95% of the values lie within ±1.96SE of the mean. The above equation therefore becomes:
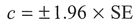
So, the advantage of using a simple random sample in experimental design is that sampling distributions for a variety of summary statistics such as the mean, variance and correlation coefficients can be estimated from the sample data, and corresponding confidence intervals calculated around such statistics.
Once you have identified a method of sampling, the next step is to consider whether or not a convenient sampling frame exists. An example of a sampling frame is a list of names, as might be found in a register of voters, an organisation's membership list, or a membership directory. If such a frame does not exist, or cannot easily be created, it may be costly and impractical or even impossible to implement a random sampling method. In this case, it might be more appropriate to use a quota or judgemental method which does not require access to a sampling frame. Even if you have access to an appropriate sampling frame, there are a variety of problems which may exist. The sampling frame may be incomplete, particularly if compiled several years in the past. Elements in the sampling frame may be clustered together and require considerable effort to extract individuals. Finally, the sampling frame may also contain elements which are ineligible for inclusion in the sample (Frankfort-Nachmias and Nachmias, 1996, after Kish, 1965). However, these problems can be overcome or at least ameliorated. With respect to the omission of eligible elements, and the inclusion of ineligible elements, supplementary lists can be used to make the sampling frame more robust and up to date.
In some cases it may be necessary to construct a sampling frame. This is particularly so for questionnaire surveys in less developed parts of the world where there may well be a lack of accurate and/or official lists. Dixon and Leach (1978, 1984) provide useful introductions to some of the problems and suitable techniques for researchers attempting to undertake such surveys, which includes advice on sampling frame construction that is appropriate in all survey research contexts. It is important that care is taken in this part of the sampling design. Dixon and Leach (1984: 25) note that:
The nature of the sampling frame, how it was compiled ... its discovery or possible defects are essential components of the research report; no frame is perfect, and the validity of the findings will be strengthened rather than undermined by such an appraisal.
With regard to sample size, it is often thought that 'more is better'. We have seen from the example displayed above in Figure 3.4 that larger samples will more accurately estimate the population mean than small samples. Indeed, as a general rule of thumb we can say that the larger the sample, the more confident we can be that the statistics derived from it will be similar to the population parameters. However, a large sample with a poor sampling design will probably contain less information than a smaller but more carefully designed sample (Chatfield, 1995). We have seen from the equations above that the standard error of the mean will clearly decrease as the sample size n increases. With measured variables, a sample size of between 20 and 30 is usually recommended as a minimum to conform to a normal distribution. However, sample size also depends on the variability of the population you are sampling. If you already know something about this variability, you can estimate the size of sample needed to estimate population values with a certain degree of confidence. Rearranging the equation used above to calculate the standard error of the mean gives us:
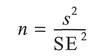
which can be adjusted if n is too large relative to N by incorporating the finite population correction:

The important point from looking at calculations of n' using the SE in this fashion, is that it takes a considerable increase in sample size to make a significant decrease in the SE. It is salutary to look at an example. If we take s = 10 and SE = 2, then substituting in the last-but-one equation above gives us:

If we wanted to decrease the SE by 50%, then the required sample size would be:
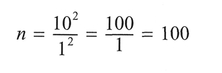
In other words, we need to quadruple the size of n. If we incorporate desired confidence limits at a selected confidence level, we can make a more precise estimate of n. Table 3.5 is taken from Dixon and Leach (1978) and gives the sample size needed to estimate the population values for continuous variables to within a certain percentage, with a probability of being right, when the sample standard deviation is 50% of the mean.
It is worth stressing that the most elegant sample design may be impractical due to logistical considerations. This is particularly so for research projects undertaken by students. In the context of the example given above, the collection of a simple random sample of 600 households in Belfast may be impractical with the time and resources at your disposal. All too often logistical considerations are cited in student research as being the main constraint on sampling and the collection of a data set, when very often the data collection task which has been set by the student (or indeed the supervisor) is over-ambitious. In these situations direct experience of the costs in both time and money for sampling the data is hard to beat. You may have neither of these if you are undertaking an analysis for the first time, and in this situation the only answer is to seek advice, either from the published literature, or from your supervisor or other staff/faculty in your department.
The quantitative data which you might collect in a questionnaire survey is a form of primary data collection. However, there are a number of secondary sources of data which can be used for what is termed secondary data analysis. These can consist of survey data collected by governments in the form of national censuses which provide data at a variety of different spatial scales, or other archives of socioeconomic data which may be available to the researcher. Some of these are produced by government agencies, others by independent surveys. We will consider some of the sources of secondary data of interest to the human geographer, concentrating on digital data available from archives, and census data. However, as a useful preliminary step, it is useful to consider why you might want to use such data in the first place, and some of the pitfalls of so doing.
There are three main justifications for the use of secondary data: conceptual, methodological and economic. These points are largely taken from FrankfortNachmias and Nachmias (1996) and Kiecolt and Nathan (1985). From the conceptual perspective, the data which you are wanting to use may simply not be available in any other form. For example, historical geographers rely almost exclusively on the secondary data available in record offices and other archives to examine historical trends. Methodologically, secondary data can enable the replication of analysis, allowing different researchers to corroborate analytical findings, allowing the possibility of longitudinal and trend analysis, broadening both the scope and dynamism of variables, and the size of the data sets used in a piece of research. The economic justification is perhaps the easiest to appreciate: collecting raw data is a time-consuming and costly process, particularly for the undergraduate or postgraduate student! The availability of suitable secondary data represents a considerable saving on the expenses which would otherwise be incurred to do your research. In some cases, the data collection task would be impossible for one researcher alone: data surveyed at the national scale, for example. The costs that you are likely to face with secondary data are likely to be restricted to data purchase, preparation and costs incurred in undertaking the analysis. However, even these costs, particularly for data purchase, can be prohibitive for student research.
Although there might be considerable savings through, in effect, getting someone else to collect your data, there are many drawbacks. All secondary data are cultural products produced by organisations and individuals with views of the world which may be incompatible with the view adopted in your research (Clark, 1997). Other limitations are summarised in Box 3.7.
Box 3.7 Limitations of secondary data
| Dated | The data were collected some years/decades previously (e.g., census data, which are collected in many countries only every ten years). |
| Too specific | The data were unlikely to have been collected with the goals of your own research project in mind (e.g., census data) and may have been subject to changes in the collection procedures if collected over time. |
| Inaccessible | The data may be available in a digital form, perhaps over the Internet, but may only be held in a restricted access government archive in a remote geographic location, and any data, if supplied at all, may take time and cost money to be accessed. |
| Inaccurate | The data originally collected may be inaccurate, sampled using a non-random method, and of generally poor quality. |
| Poorly documented | Existing data sets may have little or poor documentation to describe the nature and quality of the data or any pre-processing which may have taken place. |
Of course, the degree to which these problems are important in your research will be determined by the nature of your research problem. The availability of census data collected in 1981 and 1991 may be a problem if you wish to analyse contemporary geodemographic characteristics, though the dated nature of these data is an essential component of an historical perspective on geodemography.
Of all the problems listed above, the most critical concern those of data quality, and adequate data documentation, which is increasingly being referred to by the term metadata, particularly in relation to digital databases and data archives. Some statement or feel for the quality of the data in secondary sources is essential, since errors which might have been made in the original data collection exercise are effectively hidden. Errors due to inappropriate sampling methods, or mistakes in the administration of the sample, may be magnified by the use that you might intend for the data. Indeed, data sets generated from nationally representative samples, with carefully designed questionnaires and well-designed coding and pre-processing, do not always exist (Kiecolt and Nathan, 1985). It is therefore wise to be cautious whenever you are using published, secondary data. Indeed, Jacob (1984: 45) recommends that:
Perhaps the most important attribute for the user of published data is a large dose of scepticism. Whether data are found in libraries or data archives, they should not be viewed simply as providing grand opportunities for cheap analyses: they should be seen as problematic. In every case the analyst should ask: Are these data valid? In what ways might they have been contaminated so that they are unreliable?
Metadata is usually defined as 'data about data':
'All the things that surround the actual content of the data to give a person an understanding of how it was created and how it is maintained'.
(Rubenstrank 1996: 1)
This includes not only the description of the data, including quality, but also information about the location of the data. The term has come to subsume what we might previously have referred to as 'data documentation'. The increasing quantity of information in digital databases has led to efforts to develop standards of metadata description. This is particularly so for digital geographic data, with the establishment of a metadata standard for geospatial data by the Federal Geographic Data Committee of the United States in 1994. This requires all federal agencies in the US to document all new and existing geospatial data sets, and make such documentation available to a National Geospatial Data Clearinghouse (NGDC) (FGDC, 1994). In this form, metadata contains information relating to data availability, fitness for use, data access and data transfer (FGDC, 1994). Efforts to improve the quality of metadata are also being made by those involved in developing a National Geospatial Data Framework for the UK. The practical implication for your research is that the increasing standards of data documentation will make it considerably easier for you to obtain secondary data with higher levels of supporting documentation for your research.
In this section we will identify some general sources of data for geographic research. We would like to stress that it is impossible to give an exhaustive overview of all the various types of secondary data which you can obtain for your research. Some of the data sets available in digital form that have been derived from official government statistics and other independent surveys are listed in the section on data archives below. General sources of data on various aspects of human geography in a UK context are listed in Box 3.8.
In addition to those data listed in Box 3.8, it may be possible to obtain various types of health data at a county/state or local level from a city or local authority. Many regional, national and international agencies collect epidemiological data which might be used in the context of your research project. Details of other official and unofficial data sets can also be obtained by searching publications which list available data sets. Clark (1997) provides a useful starting point for such material, and suggests reference to various publications which include Guide to Official Statist ics (Office for National Statistics, 1996), Sources of Unofficial UK Statistics (Mort, 1990), UK Statistics: A Guide for Business Users (Mort, 1992), European Statistics: Official Sources (EUROSTAT, 1993) and ECO Directory of Environmental Databases in the UK 1995/6 (Barlow and Button, 1995). With the advent of the Internet and the World Wide Web (WWW) it is now possible to use one of the standard Web search engines to look online for useful data for your research.
There are an increasing number of national social science data archives available to the human geography researcher which can supply all types of quantitative and non-quantitative data. We will restrict our concern for the moment to quantitative data, and leave the consideration of non-quantitative archival data (e.g., letters, diaries and autobiographies) to Chapter 7. Many of these archives either offer data sets which are restricted to certain categories such as health or crime, or encompass a wide variety of different data sets amenable to quantitative analysis. Archives will generally supply data files either free or by purchase - but often in a digital form by CD-ROM, or increasingly over the Internet via the WWW. Some of the larger archives will offer assistance in the search for appropriate data sets, and some may well be able to help with customised data extraction (Kiecolt and Nathan, 1985). There are a variety of national archives which can supply data, and a useful survey of these has been provided by Kiecolt and Nathan (1985). A current listing, a WWW-clickable map access to a variety of European and North American archives (Figure 3.5) and an Integrated Data Catalogue (IDC) covering ten international archives are provided on the WWW site of CESSDA (Council of European Social Science Data Archives) at http://www.nsd.uib.no/cessda.
We will use two examples, one from the UK and one from the United States, to illustrate some of the data products which can be obtained for quantitative analysis in the context of your research project. Many of the larger data archives, including the examples below, can be found on the WWW. We include the WWW addresses below which contain further information and links to other national and international archives.
The Data Archive at the University of Essex (formerly known as the ESRC Data Archive) was set up in 1967 to act as a repository of quantitative information for use by social scientists, and consists mainly of data collected in the UK. There are a wide number of different categories of data available in this archive, with well over 7,000 data sets in total. Some of the largest data sets are listed in Box 3.9. The data holdings of The Data Archive can be searched using a WWW interface to BIRON: 'Bibliographic Information Retrieval Online', or as part ofthe CESSDA's IDC. The Data Archive also provides access to quantitative data sets held further afield within Europe: the Data Archive is a member of CESSDA and the International Federation of Data Organisations (IFDO). Of particular note is the service the archive provides to postgraduate students (see Figure 3.6). Data sets are disseminated to authorised users in a variety of formats and media including CD-ROM, network file transfer, tape (8 mm and DAT), and floppy disk. In the higher education community in the UK, data are charged at the cost of the media.
Some of the larger data sets can be accessed at the University of Manchester's Information Datasets and Associated Services (MIDAS) service, which is a JISC-funded national data centre. This service provides online access for authorised users in the UK higher education community across the Internet using Telnet and Web-based interfaces (http://midas.ac.uk/) to data for teaching and research purposes. The current data holdings of MIDAS (as of 1998) are listed in Box 3.10 (on p. 65).
The Inter-University Consortium for Political and Social Research (ICPSR) is located at the University of Michigan, in the United States. Formed in 1962, this archive is the largest repository of social science data accessible by computer. A selection of some of
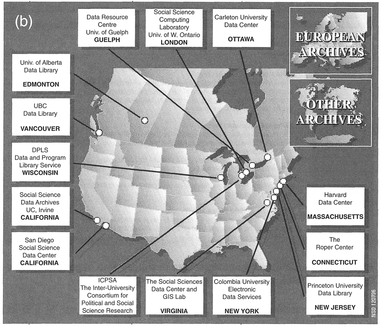
Figure 3.5 CESSDA clickable maps for data archives in (a) Europe and (b) North America (source: CESSDA 1998).
Box 3.9 A selection of the larger data holdings of the ESRC data archive
Source: The Data Archive 1998a.
Figure 3.6 The Data Archive postgraduate resources Web page (source: The Data Archive 1998b).
the data sets available from this archive are listed in Box 3.11. Although your university must belong to the consortium to obtain the full range of services and data sets, it is possible to obtain access to data sets for an appropriate fee. In the UK, data from the ICPSR can be obtained via The Data Archive covered above. Similar to the UK's Data Archive, the main routes of data supply are by CD-ROM, by floppy disk or downloaded across the Internet by FTP or the WWW. Of particular use for research students is the ICPSR Summer Program in Quantitative Methods of Social Research. This offers a wide set of courses in research design, statistics and data analysis of relevance to the social scientist.
Box 3.10 Data sets available at MIDAS
Source: MIDAS 1998.
Box 3.11 Main data holdings of the ICPSR
Source: Adapted from Kiecolt and Nathan 1985 and ICPSR 1998.
The source of secondary data you are most likely to encounter is that based on the census of population which is carried out regularly in most industrialised countries. For example, in the United States, decennial (every 10 years) censuses of population have taken place since 1790, with the last in 1990 and the next planned for 2000. In the UK, similar decennial censuses have taken place since 1841, with the last in 1991 and the next planned for 2001. In Canada, a national decennial census was in place by 1851, which by 1971 had become quinquennial (every five years), with the next planned for 2001.
Confidentiality requirements usually result in the individual census returns being unavailable to the public. For example, in the UK the individual census return information is confidential for 100 years. Census information is usually available in the form of statistics aggregated to various geographic areas which vary in size from roughly 100 people to several thousands and larger. Neither is all the information collected by the questionnaires included in these aggregated statistics. For both the US and UK census, although many variables are sampled at 100%, some variables reflect only a certain percentage (usually 10%) of houses sampled; these are listed in Box 3.12.
The basic census geography for the UK is given at the top of Box 3.13 and is depicted in Figure 3.7. The Enumeration District (ED)/OutputArea (OA) is at the lowest level of aggregation, containing in the region of 400 people, although census data can be obtained aggregated to a variety of other (usually larger) zones, including postcode sectors. In the UK, two main sets of census statistics are available: Local Base Statistics
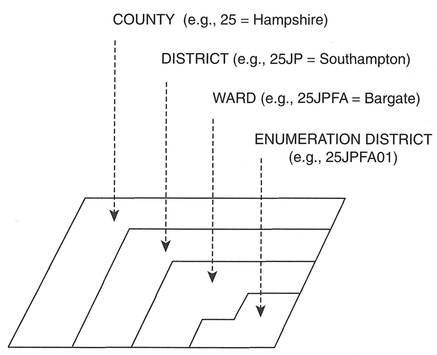
Figure 3.7 UK census geography (source: redrawn from Martin 1996: 74).
(LBS) which for the 1991 census consisted of 99 tables of information, and Small Area Statistics (SAS) which consist of some 86 tables of information. The LBS are unavailable for the lowest levels of aggregation. Both the LBS and SAS data sets are available to authorised users over the Internet from the Census Dissemination Unit at MIDAS, or via CD-ROM from the Data Archive. For access to these data over the Internet, users must make use of either the SASPAC91 software package to extract and output the required datasets as they relate to the census geography outlined above, or the SURPOP (V.2) software package to output selected SAS variables at a 200 m grid resolution.
In the UK, although census SAS are available for small areal units such as unit postcodes and EDs, users of these data should be aware of the 'suppression procedures' which operate if an ED contains fewer than 50 people, to avoid the possibility of disclosing individual information. The counts from such zones are frequently merged with those from adjacent zones, and a zero count will be coded to the zone in question. Similar procedures are followed for wards with the LBS, which are suppressed if they contain fewer than 1,000 people or 320 households. Various other data sets are also available, including census microdata in the form of the Sample of Anonymised Records (SAR), Special Migration Statistics (SMS), Special Workplace Statistics (SWS) and Longitudinal Study (LS) data. Further details of the 1991 UK census can be found in the volumes edited by Dale and Marsh (1993) and Openshaw (1995 - particularly the chapter by Rees) and the monograph by Martin (1993) which also contains an overview of the census geography in the UK. Details of the 1981 census can be found in Rhind (1983) and Dewdney (1985).
In the US, the 1990 census of population provides information on a set of sample and 100% categories similar to the UK census, which are listed in Box 3.14.
The census geography for the US is displayed in Box 3.15 and Figure 3.8, with the lowest level of aggregation being the census block (US Census Bureau, 1996).
In metropolitan areas, blocks contain information on approximately 100 people; block groups on about 800 people; and tracts on about 4,000 people. There are about six million block records, about 300,000 block group records, and about 60,000 tract records. The 1990 US Census data are primarily released as Summary Tape Files (STF) in the form of printed reports, microfiche and digital data files that may be obtained online from the Internet, on tape, on CD-ROMs, or in diskette form. US census data can be supplied aggregated by ZIP code (post code) areas of various sizes, although often by third-party commercial data suppliers.
For both the UK and US census there are an increasing number of locations providing both Internet and Web-based access to census products. For the US census, of particular note is the archive of several past censuses held at the Lawrence Berkeley National Laboratory (http://parep2.lbl.gov/mdocs/LBL_census.html). If you are interested in using US census data in your research you should look at the Web home page for the census, which contains much useful information (http://www.census.gov/). The Census Dissemination Unit at MIDAS in Manchester is probably the most useful means of obtaining census data over the Internet/WWW in the UK, and contains many online help documents as well as census data in a variety of formats (see Box 3.10 above).
After reading this chapter you should:
You should now have a basic understanding of quantitative data and their generation. As we have illustrated, there are a number of issues that you need to consider when designing and implementing a study which aims to generate primary quantitative data. You should consider each of these issues carefully to ensure a valid piece of research. Of particular note is how you construct your questions and the sampling frame
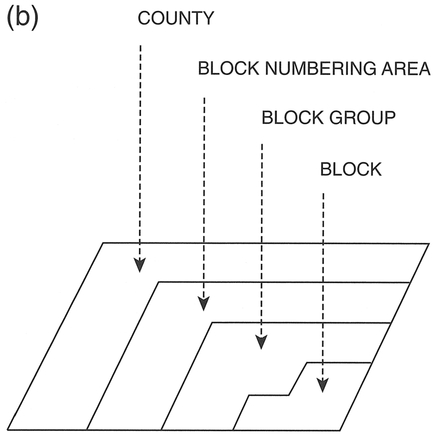
Figure 3.8 US census geography: (a) metropolitan areas; (b) non-metropolitan areas.
adopted. These are important decisions which should not be taken lightly. There are many different sources of secondary quantitative data, a few of which have been detailed above. These data sets can provide a useful source of information for your study, but you must be careful to assess their merits and limitations prior to use to ensure that they are suitable for your purpose. In the following chapter, we introduce the subject of how to prepare quantitative data for analysis and the initial steps of such analysis.
Bourque, L.B. and Clark, VA. (1992) Processing Data: The Survey Example. Sage University Papers Series on Quantitative Applications in the Social Sciences 07-085. Sage, Newbury Park, CA.
Clark, G. (1997) Secondary data sources. In Flowerdew, R. and Martin, D. (eds), Methods in Human Geography: A Guide for Students Doing a Research Project. Longman, Harlow, pp. 57-69.
Dixon, C. and Leach, B. (1978) Sampling Methods for Geographical Research. Concepts and Techniques in Modern Geography 17, Invicta Press, London.
Ehrenberg, A. S.C. (1975) Data Reduction: Analysing and Interpreting Statistical Data. Wiley, Chichester.
Frankfort-Nachmias, C. and Nachmias, D. (1996) Research Methods in the Social Sciences. Edward Arnold, London.
Martin, D. (1993) The UK Census of Population 1991. Concepts and Techniques in Modern Geography 56, Geo Books, Norwich.
Openshaw, S. (1995) Census Users' Handbook. GeoInformation International, Cambridge.