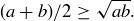
As we mentioned in the Preface, solving the in-text exercises as you encounter them in the text is an essential task. Make earnest attempts on your own to solve each problem that shows up in the text before reading any further or consulting the material in this appendix. Use the solutions, answers, and comments below to check your work or assist your progress if you get stuck.
Chapter 1
Exercise 1.1 Here’s one way to show that if a and b are two non-negative real numbers, then 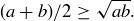
First,
![]()
because the square of any real number is non-negative. Expanding the left-hand side yields
![]()
Adding 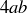 to both sides gives
to both sides gives
![]()
Since ab is non-negative, we know further that
![]()
This can be rewritten as
![]()
The conclusion we desire now follows from taking square roots.

Take a look at your scratch work and attempts on this problem. You might have started with  , squared both sides, and then followed a series of calculations and deductions that are similar to the steps just given, but in reverse. That is certainly a correct approach to first understand the problem. However, the proof should end with
, squared both sides, and then followed a series of calculations and deductions that are similar to the steps just given, but in reverse. That is certainly a correct approach to first understand the problem. However, the proof should end with  as the conclusion, not the first step. “If …, then …” statements and their proofs are studied in Chapter 2.
as the conclusion, not the first step. “If …, then …” statements and their proofs are studied in Chapter 2.
Exercise 1.2 In the sixth month, the original pair and their first and second offspring each create offspring, bringing the total number of pairs to 8.
In the seventh month, the original pair; their first, second, and third offspring; and their first offspring’s offspring each create offspring, bringing the total number of pairs to 13.
Now things are getting quite complicated – there must be a better way to keep track of things …
Exercise 1.3 They are
Exercise 1.4 The key here is to make sure that 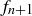 counts all of the rabbit pairs that exist in month
counts all of the rabbit pairs that exist in month 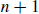 in a way that doesn’t count any pair twice. Every rabbit pair in month
in a way that doesn’t count any pair twice. Every rabbit pair in month 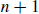 is exactly one of two types:
is exactly one of two types:
(a) It already existed in month n.
(b) It did not exist in month n.
How many pairs are in case (a)? That’s 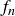 . How many pairs are in case (b)? That’s
. How many pairs are in case (b)? That’s 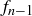 , because we can count their parents, pairs that must have existed two months prior to month
, because we can count their parents, pairs that must have existed two months prior to month 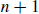 . Add these two numbers together to get
. Add these two numbers together to get 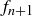 .
.
Notice that, in order to justify that 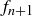 is the correct count for the number of rabbit pairs in month
is the correct count for the number of rabbit pairs in month 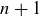 , we are tacitly assuming that
, we are tacitly assuming that 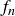 is the correct count for month n and
is the correct count for month n and 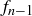 is the correct count for month
is the correct count for month  . This type of reasoning lies at the heart of proofs by mathematical induction, a topic we preview in this chapter and study in Section 2.6.
. This type of reasoning lies at the heart of proofs by mathematical induction, a topic we preview in this chapter and study in Section 2.6.
Exercise 1.5 Let  give the number of different ways to make sums of 1s and 2s that equal n. Then the displayed equalities show that
give the number of different ways to make sums of 1s and 2s that equal n. Then the displayed equalities show that  ,
, 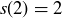 ,
, 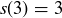 , and
, and 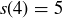 . You might now guess that
. You might now guess that 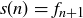 for
for 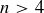 as well. How could you make yourself feel more confident about this guess? And if the equality indeed holds in general, how might you prove it?
as well. How could you make yourself feel more confident about this guess? And if the equality indeed holds in general, how might you prove it?
Exercise 1.6 The correct value for P should certainly be greater than 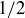 . If
. If 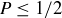 , then
, then 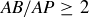 , while
, while  causes
causes 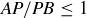 .
.
Exercise 1.7 The calculations are
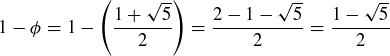
and

Exercise 1.8 The first verification is the calculation
![]()
For the second one, first rewrite
![]()
as
![]()
While it would be easy enough to continue from here by substituting the numerical formulas for ϕ and 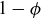 , let’s instead foreshadow the proof technique of Proposition 1.4 by rearranging the terms in the numerator to give
, let’s instead foreshadow the proof technique of Proposition 1.4 by rearranging the terms in the numerator to give
![]()
Since you already know that
![]()
and
![]()
it must be the case that
![]()
Exercise 1.9 First use Lemma 1.5 to rewrite
![]()
as
![]()
Then rearrange the terms in the numerator to give
![]()
Exercise 1.10 (a) If  ,
, 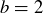 , and
, and 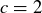 , then
, then 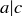 and
and 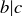 , but
, but 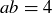 and so
and so 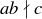 . Thus, the statement is false.
. Thus, the statement is false.
This is only one of many different counterexample sets of values for a, b, and c; another one is  ,
, 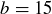 , and
, and 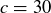 . You only need one counterexample to prove that the statement is false.
. You only need one counterexample to prove that the statement is false.
(b) All of your experimentation should have led you to guess that the statement must be true. For instance, if you tried 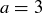 ,
, 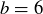 , and
, and 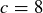 , then that particular instance is true because
, then that particular instance is true because 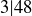 .
.
Here’s a proof that the statement is true in general.
PROOF. Since you are assuming that 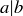 , you know that there is a natural number m such that
, you know that there is a natural number m such that 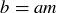 . Multiplying both sides of this equation by c gives
. Multiplying both sides of this equation by c gives
![]()
But now look: bc is a times the natural number mc. This means that 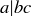 by the definition of divisibility.
by the definition of divisibility.

(c) This statement is true and is called the “transitive” property of divisibility. In Chapter 6 you will study the transitive law in several different contexts.
PROOF. Since 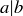 , there is some natural number m such that
, there is some natural number m such that 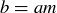 . Since
. Since 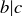 , there is some natural number n such that
, there is some natural number n such that 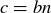 . Since
. Since 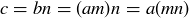 and mn is a natural number, we conclude that
and mn is a natural number, we conclude that 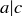 .
.

(d) This proof will follow the proof of Proposition 1.7 very closely. Be sure that you understand how the numbers 2 and 3 can be inserted into that proof with little difficulty.
PROOF. Since 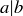 , there is a natural number m such that
, there is a natural number m such that 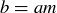 . Similarly, since
. Similarly, since 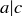 , there is a natural number n such that
, there is a natural number n such that 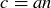 . This means that
. This means that
![]()
where 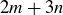 is a natural number, which shows that
is a natural number, which shows that 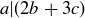 .
.

(e) Look ahead to Lemma 1.10!
Exercise 1.11 (a) Here’s one way to prove that this statement is true.
PROOF. If 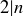 , then there exists a natural number c such that
, then there exists a natural number c such that 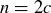 . Multiplying both sides of this equation by n gives
. Multiplying both sides of this equation by n gives
![]()
which shows that 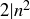 (because nc is a natural number).
(because nc is a natural number).

Another way is to use the result of part (b) in Exercise 1.10. Can you see how to do this?
(b) This statement is not the same as the one in (a) because the hypothesis and conclusion have switched places, so don’t expect a proof of (b) to be similar to a proof of (a).
PROOF. Natural numbers are either odd or even. If n were odd, then 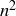 would also be odd, which would imply that
would also be odd, which would imply that 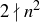 . So the only cases when
. So the only cases when  must have n even, which means that
must have n even, which means that 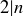 .
.

(c) This statement is false: for a counterexample, simply let 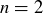 .
.
Exercise 1.12 Since 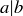 , there is a natural number c such that
, there is a natural number c such that 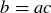 . Since
. Since
![]()
and both a and  are non-negative, we know that
are non-negative, we know that 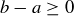 . Thus
. Thus 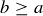 .
.
Exercise 1.13 The only way to factor 1 is 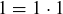 , and those two factors aren’t distinct.
, and those two factors aren’t distinct.
Exercise 1.14 There are 25 primes less than 100:
![]()
Notice that the proportion of natural numbers between 1 and n that are prime seems to decrease as n gets larger. If this fascinates you, research the “prime number theorem.”
Exercise 1.15 They are
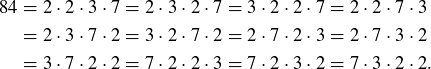
Do you see the systematic way we enumerated them? Maybe you found a better way to do this.
Exercise 1.16 If a is any integer, then 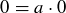 . This means that
. This means that 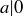 .
.
If a is any non-zero integer, then there’s no  such that
such that 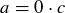 . This means that
. This means that 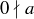 . However, given our definition of divisibility,
. However, given our definition of divisibility, 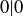 seems to be true, since any integer c satisfies
seems to be true, since any integer c satisfies 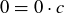 . But you’ve likely heard that it’s never good to divide by 0, so we should really modify our definition of divisibility for
. But you’ve likely heard that it’s never good to divide by 0, so we should really modify our definition of divisibility for  to exclude this possibility. If you need convincing, see Zero: The Biography of a Dangerous Idea by Charles Seife [Sei00].
to exclude this possibility. If you need convincing, see Zero: The Biography of a Dangerous Idea by Charles Seife [Sei00].
Exercise 1.17
Proposition 1.7 If a, b, and c are any integers such that both 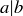 and
and 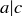 , then
, then 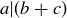 .
.
PROOF. Since 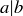 , there is an integer m such that
, there is an integer m such that 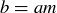 . Similarly, since
. Similarly, since 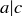 , there is an integer n such that
, there is an integer n such that 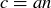 . This means that
. This means that
![]()
which shows that 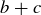 is an integer multiple of a. In other words,
is an integer multiple of a. In other words, 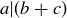 .
.

Lemma 1.10 If a, b, and c are any integers such that both 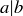 and
and 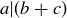 , then
, then 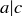 .
.
PROOF. Since 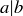 , there is an integer m such that
, there is an integer m such that 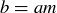 . Similarly, since
. Similarly, since 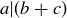 , there is an integer n such that
, there is an integer n such that 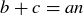 . Thus
. Thus
![]()
which shows that c is an integer multiple of a, so we conclude that 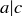 .
.

Exercise 1.18 In view of

we see that 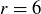 .
.
Similarly,
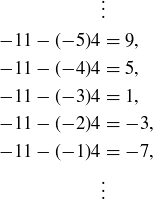
shows that 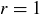 .
.
Exercise 1.19 The Division Algorithm says that, given a natural number b, every integer can be written in the form  , where r is an integer between 0 and
, where r is an integer between 0 and  (inclusive). So if
(inclusive). So if 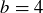 , every number can be written as
, every number can be written as  , which is just a small variation on the statement that every integer can be expressed as
, which is just a small variation on the statement that every integer can be expressed as 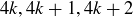 , or
, or 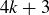 .
.
Exercise 1.20
(a) 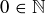 is not true. Natural numbers are positive.
is not true. Natural numbers are positive.
(b) 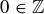 is true from the definition of
is true from the definition of  .
.
(c) 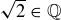 is not true, as was proved in Proposition 1.14.
is not true, as was proved in Proposition 1.14.
(d) Since 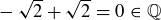 , the statement is true.
, the statement is true.
(e)  is not true. We can prove this with a short proof by contradiction.
is not true. We can prove this with a short proof by contradiction.
PROOF. Assume for the moment that the statement 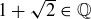 is true. Then
is true. Then  , where
, where 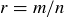 is a rational number. That implies that
is a rational number. That implies that 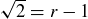 , where
, where  is another rational number, namely
is another rational number, namely  . This contradicts the fact that
. This contradicts the fact that 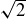 is not a rational number.
is not a rational number.

(f) 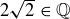 is also not true. Try a short proof by contradiction, like the one just given above.
is also not true. Try a short proof by contradiction, like the one just given above.
(g) 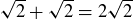 , so the previous result applies.
, so the previous result applies.
(h) 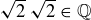 is true, because
is true, because 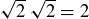 .
.
One of the take-aways from this exercise is that while the sum (or product, or difference) of two rational numbers is rational, the same can’t be said for irrational numbers.
Chapter 2
Exercise 2.1 As in Example 2.1, let C be the proposition “Cecelia is a knight” and let D be “Desmond is a knight.” Then the truth of Cecelia’s statement is determined by the fourth column of the table at the top of the next page.
Since Cecelia is making the statement, we are looking for any rows where the first and final entries agree. This only happens in the final row, so both Cecelia and Desmond are knaves.
| C | D |  |
 |
| T | T | F | F |
| T | F | F | F |
| F | T | T | T |
| F | F | T | F |
Exercise 2.2 P is true and Q is false, hence 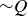 is true. This means
is true. This means 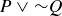 is true. One way to express this statement is “4 is a divisor of
is true. One way to express this statement is “4 is a divisor of 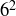 or 4 is not a divisor of 6.”
or 4 is not a divisor of 6.”
Exercise 2.3 They are
| P | Q | 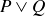 |
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
and
| P | Q | 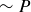 |
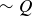 |
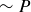  |
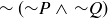 |
| T | T | F | F | F | T |
| T | F | F | T | F | T |
| F | T | T | F | F | T |
| F | F | T | T | T | F |
Notice that the first, second, and last columns of the two tables agree. This means that whatever statements you might use to replace P and Q, the truth values of 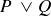 and
and 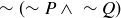 will be the same. Later we will say that these two statements are “logically equivalent.”
will be the same. Later we will say that these two statements are “logically equivalent.”
Exercise 2.4 There will be 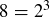 rows for each table because there are 3 statements (P, Q, and R) and 2 possible values for each variable (T and F). Here are the tables:
rows for each table because there are 3 statements (P, Q, and R) and 2 possible values for each variable (T and F). Here are the tables:
| P | Q | R | 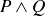 |
 |
| T | T | T | T | T |
| T | T | F | T | F |
| T | F | T | F | T |
| T | F | F | F | T |
| F | T | T | F | T |
| F | T | F | F | T |
| F | F | T | F | T |
| F | F | F | F | T |
and
| P | Q | R | 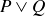 |
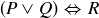 |
| T | T | T | T | T |
| T | T | F | T | F |
| T | F | T | T | T |
| T | F | F | T | F |
| F | T | T | T | T |
| F | T | F | T | F |
| F | F | T | F | F |
| F | F | F | F | T |
Exercise 2.5 Observe that the final column of
| P | Q | 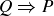 |
 |
| T | T | T | T |
| T | F | T | T |
| F | T | F | T |
| F | F | T | T |
is all Ts.
Exercise 2.6 Truth tables show that the statements in Exercise 2.3 are logically equivalent, while the statements in Exercise 2.4 are not.
Exercise 2.7 The third and sixth columns are the same in this truth table:
| P | Q |  |
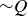 |
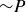 |
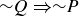 |
| T | T | T | F | F | T |
| T | F | F | T | F | F |
| F | T | T | F | T | T |
| F | F | T | T | T | T |
Exercise 2.8 You can verify this claim by comparing the truth tables for 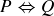 and
and 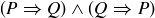 .
.
Exercise 2.9 You can visualize the sum 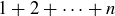 as a sequence of stacked squares, the first stack being of height 1, the second of height 2, and so on. Add n squares to the top of the first stack, and then
as a sequence of stacked squares, the first stack being of height 1, the second of height 2, and so on. Add n squares to the top of the first stack, and then  squares to the second stack, and so forth. The result is a rectangular array of boxes that is
squares to the second stack, and so forth. The result is a rectangular array of boxes that is 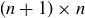 . Thus, as before,
. Thus, as before,  . Can you think of a way to draw a diagram illustrating the general case?
. Can you think of a way to draw a diagram illustrating the general case?
Exercise 2.10
(a) 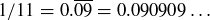
(b) This might require some insight. Since
![]()
and
![]()
we have
![]()
Thus 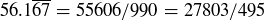 .
.
Exercise 2.11 Let a be a natural number and let x be an irrational number. Assume to the contrary that the product ax is rational, so that 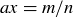 for some integer m and some natural number n. Then
for some integer m and some natural number n. Then  , where an is a natural number, contradicting the fact that x is irrational.
, where an is a natural number, contradicting the fact that x is irrational.
What happens if you try the argument above with 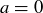 ?
?
Exercise 2.12 No, because 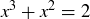 has a rational solution of
has a rational solution of  .
.
Exercise 2.13
(a) Original implication: “If 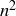 is even, then n is even.”
is even, then n is even.”
Contrapositive: “If n is not even, then 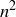 is not even.” Because the contrapositive is logically equivalent to the original implication, either both statements are true or both statements are false. In this case, the contrapositive is probably in the best form to prove that they are true: if n is not even, then
is not even.” Because the contrapositive is logically equivalent to the original implication, either both statements are true or both statements are false. In this case, the contrapositive is probably in the best form to prove that they are true: if n is not even, then 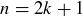 for some integer k, and so
for some integer k, and so 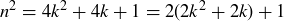 , which is certainly not even.
, which is certainly not even.
Converse: “If n is even, then 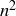 is even.” This is also true, but for a reason that is completely independent of the other two cases (see Exercise 1.11).
is even.” This is also true, but for a reason that is completely independent of the other two cases (see Exercise 1.11).
(b) Original implication: “If 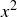 is rational, then x is rational.” This is false: a counterexample is
is rational, then x is rational.” This is false: a counterexample is 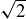 .
.
Contrapositive: “If x is not rational, then 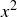 is not rational.”
is not rational.”
Converse: “If x is rational, then 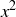 is rational.” This is true. The proof is direct: if x is rational, then
is rational.” This is true. The proof is direct: if x is rational, then 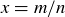 for some
for some 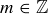 and
and  , and so
, and so 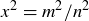 , which is also a rational number.
, which is also a rational number.
(c) Original implication: “If  , then
, then 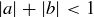 .” This is false: a counterexample has
.” This is false: a counterexample has 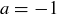 and
and 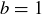 .
.
Contrapositive: “If 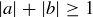 , then
, then 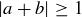 .” Notice how negating
.” Notice how negating 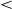 leads to
leads to 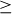 .
.
Converse: “If 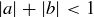 , then
, then 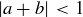 .” This is true. Can you prove it?
.” This is true. Can you prove it?
(d) Original implication: “If the professor is 5 minutes late, then class is cancelled.” This is likely false; consult your instructor for the correct answer.
Contrapositive: “If class is not cancelled, then the professor is not 5 minutes late.” Be sure you understand why this statement must have the same truth status as the original implication.
Converse: “If class is cancelled, then the professor is 5 minutes late.” This is almost certainly false. Class could be cancelled for lots of reasons that have nothing to do with your instructor being late. For example, if she happens to walk by some pygmy marmosets just before class, she will probably not make it to class that day: she’ll just keep petting them.
Exercise 2.14 We hope you can do these types of problems quite well by now …
Exercise 2.15 …including this one!
Exercise 2.16 After rewriting the inequality as 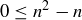 , we can factor the right-hand side as
, we can factor the right-hand side as 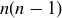 . If n is greater than 1, both n and
. If n is greater than 1, both n and  are positive, so
are positive, so 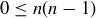 . Also, if n is less than 0, both n and
. Also, if n is less than 0, both n and  are negative, so
are negative, so 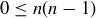 . The only integer values of n we haven’t yet considered are
. The only integer values of n we haven’t yet considered are 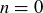 and
and 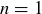 , and each one makes
, and each one makes 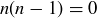 . Thus,
. Thus, 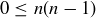 for all integers n.
for all integers n.
Exercise 2.17 Replace n with q in the preceding proof, and all is fine until you get to the sentence that starts with “The only …”. For a specific counterexample, try 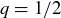 .
.
Exercise 2.18 Two of the four statements are true – which ones?
Exercise 2.19 Part (a) shows that a solution exists, while part (b) shows that the solution is unique. Proving the truth of a  statement usually requires two arguments like these.
statement usually requires two arguments like these.
Exercise 2.20
(a) 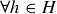 , h is mortal.
, h is mortal.
(b) 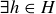 , h scored higher than me on the test.
, h scored higher than me on the test.
(c) 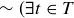 , t is better than apple pie).
, t is better than apple pie).
For practice, rewrite part (c) starting with 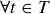 .
.
Exercise 2.21 The first one can be “For every real number y there is a real number x such that  .” The second can be “There is a real number x such that, for all real numbers y,
.” The second can be “There is a real number x such that, for all real numbers y,  .”
.”
Exercise 2.22 She said 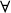 persons,
persons,  true soul mate; in this order, the soul mate can depend on the person. Dilbert stupidly thought
true soul mate; in this order, the soul mate can depend on the person. Dilbert stupidly thought  true soul mate for all persons. His question about the monkey is a good one.
true soul mate for all persons. His question about the monkey is a good one.
Exercise 2.23 Only one of the statements is false – which one?
Exercise 2.24
(a) 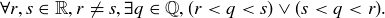
(b) 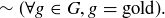 Now try to write this with an
Now try to write this with an 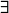 but no ~.
but no ~.
(c) 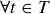 , t can’t stop the Sandman!
, t can’t stop the Sandman!
(d) 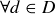 , d will not open. One wonders why they bother to make the stop! What is a more accurate statement as the train approaches the station?
, d will not open. One wonders why they bother to make the stop! What is a more accurate statement as the train approaches the station?
Notice that in part (a), the statement accommodates either 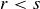 or
or 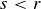 . Another possible statement would be
. Another possible statement would be
(a) 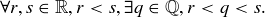
The reason this statement also works is that for any two distinct real numbers, one of them must be less than the other, and so we might as well call the smaller one r.
Exercise 2.25 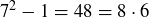 and
and 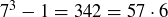 .
.
Exercise 2.26 The inductive assumption lets us know that expression B is a multiple of 6.
Exercise 2.27 The only modification necessary to the template is replacing “Assuming that 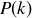 is true for all values of k with
is true for all values of k with 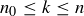 ” with “Assuming that
” with “Assuming that 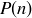 is true.” Now revisit Theorem 2.12 with 9 and 10 in place of 6 and 7.
is true.” Now revisit Theorem 2.12 with 9 and 10 in place of 6 and 7.
Exercise 2.28
(a) 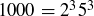
(b) 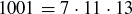
(c) 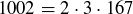
(d) 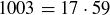
It is pretty clear that simple induction will not be helpful, as there is no apparent way to relate the factorization of 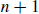 to the factorization of n.
to the factorization of n.
Exercise 2.29 In the final presentation of your proof, five base cases might be acceptable but are certainly unnecessary and possibly distracting: only two bases are needed. In your initial work on the problem you might have directly verified that the statement holds for five cases like these, and that’s totally fine.
Exercise 2.30 The proof uses strong induction because both 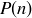 and
and 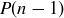 , which are the respective formulas
, which are the respective formulas
![]()
and
![]()
are assumed to be true to prove that 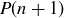 is true.
is true.
Exercise 2.31 Despite the fact that Exercises 1.45 and 1.46 involve the Fibonacci numbers, neither requires consideration of only the two previous cases: Exercise 1.45 can be proved using simple induction and a single base case, while Exercise 1.46 is probably best proved with a single base case and a strong induction step that assumes the truth of the statement over a wide range of previous cases.
Exercise 1.47 might best be proved directly: consider the expression
![]()
after writing n in terms of powers of 10.
Exercise 1.48 is probably best proved using strong induction, by letting 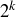 be the highest power of 2 less than or equal to
be the highest power of 2 less than or equal to  and using the inductive assumption to tell you something about
and using the inductive assumption to tell you something about  . The argument is similar to one you might use for Exercise 1.46.
. The argument is similar to one you might use for Exercise 1.46.
Exercise 2.32 Start by declaring at the outset that x is a real number such that 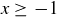 . The proof uses simple induction on the natural number n.
. The proof uses simple induction on the natural number n.
Base Case: If 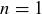 ,
, 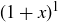 and
and 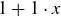 both equal
both equal 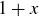 , so the inequality holds (as an equality).
, so the inequality holds (as an equality).
Inductive Step: We assume that the inequality is true for 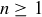 . Then to prove that the inequality is true for
. Then to prove that the inequality is true for 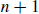 , consider
, consider
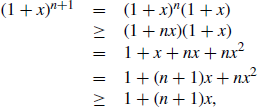
where the first inequality in the derivation uses the inductive assumption, and the final inequality holds because 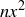 can’t be negative. Once you have also said where it is important in the derivation that
can’t be negative. Once you have also said where it is important in the derivation that 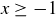 , you will have a complete proof.
, you will have a complete proof.
Exercise 2.33 Look for them!
Exercise 2.34 There is no absolute minimum number of examples that are needed to provide the basis for a conjecture, and it is sometimes the case that more examples are better. Using data for only the first four positive integers might not be enough for this problem. On the other hand, you can waste a lot of time checking cases when an attempted proof might highlight the sort of cases that could be problematic.
Exercise 2.35 Before you play, be kind and wish your friend good luck.
Exercise 2.36 Among other things, be sure that you explain why the second player always has a move to make.
Exercise 2.37 The case of 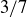 is handled in the paragraph that follows this exercise.
is handled in the paragraph that follows this exercise.
Exercise 2.38 If four cases aren’t enough, try eight or more.
Exercise 2.39 For example,
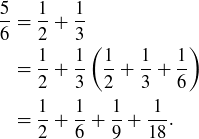
Exercise 2.40 Here’s an easy question to ask: “Can you always avoid using 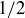 ?”
?”
Exercise 2.41 In part (b), you need to point out that  so that you avoid dividing by 0.
so that you avoid dividing by 0.
Exercise 2.42 Using no lines leaves the plane whole, so  seems best.
seems best.
Chapter 3
Exercise 3.1 Try “ ” or “
” or “ .”
.”
Exercise 3.2 When  , the element
, the element  is an integer, so it’s already in the set in the form
is an integer, so it’s already in the set in the form  .
.
Exercise 3.3 We know that 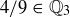 because setting
because setting 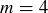 and
and 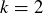 in the definition of
in the definition of 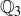 gives
gives 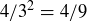 .
.
We also know that 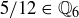 because taking
because taking  and
and 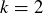 in the definition of
in the definition of 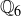 gives
gives  . Note that there is no requirement in the definition of
. Note that there is no requirement in the definition of 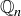 that
that 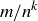 be in lowest terms when
be in lowest terms when 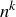 is an integer.
is an integer.
Now let’s show that 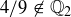 , using a proof by contradiction. Suppose for the moment that
, using a proof by contradiction. Suppose for the moment that 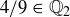 . Then Exercise 3.2 implies that
. Then Exercise 3.2 implies that
![]()
Cross-multiplying gives 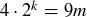 , but the right-hand side is divisible by 3 while the left-hand side is not. This is a contradiction, so we conclude that
, but the right-hand side is divisible by 3 while the left-hand side is not. This is a contradiction, so we conclude that 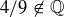 .
.
Exercise 3.4 Regarding the existential quantifier, the assertion that 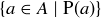 is non-empty means that there is at least one element x in that set; and, by the definition of the set,
is non-empty means that there is at least one element x in that set; and, by the definition of the set, 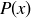 is true, so
is true, so 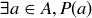 is true as well. Conversely, if
is true as well. Conversely, if 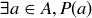 is true, then
is true, then 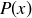 is true for some
is true for some 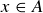 . This means that x is in the set
. This means that x is in the set  , so the set is non-empty.
, so the set is non-empty.
Exercise 3.5 If 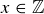 , then
, then 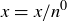 for integers x and 0, so
for integers x and 0, so 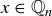 .
.
Here’s one reason  is a proper subset of
is a proper subset of 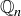 if
if 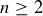 :
:  , but
, but 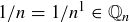 .
.
Exercise 3.6
(a) 4 is not equal to 1, 2, 3, or 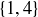 , so
, so 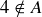 .
.
(b) Since 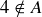 ,
, 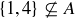 .
.
(c)  is not equal to 1, 2, 3, or
is not equal to 1, 2, 3, or 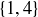 , so
, so 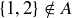 .
.
(d)  , but
, but 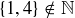 .
.
Exercise 3.7 We can put them in a line: 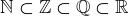 . They are proper subsets owing to numbers like
. They are proper subsets owing to numbers like 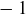 ,
, 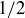 , and
, and 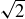 , respectively.
, respectively.
Exercise 3.8 They are  ,
,  ,
, 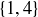 ,
, 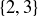 ,
,  , and
, and 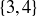 .
.
Exercise 3.9 This requires two arguments: one to show that 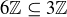 , and one to show that
, and one to show that 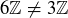 .
.
For the first, let 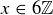 . Then
. Then 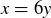 for some
for some 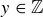 , so that
, so that 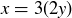 with
with  . This means that
. This means that 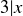 , so
, so 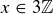 .
.
The second argument is easy: 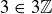 , but
, but 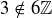 .
.
Exercise 3.10 The sets are as follows.
(a) 
(b) 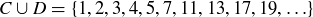
(c) 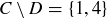
(d) 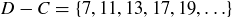
(e) 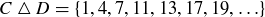
Exercise 3.11 Both statements are logically equivalent to  .
.
For the first statement, 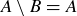 implies that B contains no elements of A, and
implies that B contains no elements of A, and 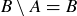 implies that A contains no elements of B; thus A and B have no common elements. Conversely, if A and B have no common elements, then we must also have
implies that A contains no elements of B; thus A and B have no common elements. Conversely, if A and B have no common elements, then we must also have 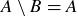 and
and 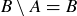 .
.
Exercise 3.12 Remember that 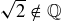 .
.
Exercise 3.13 (a) In Figure 2 on page 71, both  and
and 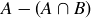 can be seen as the crescent-shaped region on the left.
can be seen as the crescent-shaped region on the left.
(b) First, let 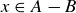 . This means that
. This means that 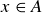 and
and 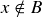 . Since x is not an element of B, it can’t be an element of both A and B, so
. Since x is not an element of B, it can’t be an element of both A and B, so 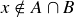 . Thus,
. Thus, 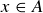 and
and  , so
, so 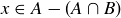 .
.
Second, let 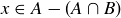 . This means that
. This means that 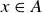 and
and 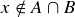 . Since
. Since 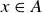 , the only way that x is not in
, the only way that x is not in  is if
is if 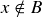 . Since
. Since 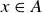 and
and 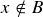 ,
, 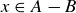 .
.
Exercise 3.14 The proof is similar to the first half. Let 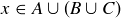 . By the definition of the union of two sets, this implies that
. By the definition of the union of two sets, this implies that 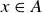 or
or 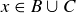 , which (again by the definition of union) means that
, which (again by the definition of union) means that 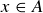 or
or 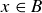 or
or 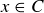 . This in turn means that
. This in turn means that 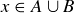 or
or 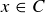 , which implies that
, which implies that 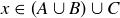 . Thus, we have shown that
. Thus, we have shown that 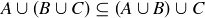 .
.
Exercise 3.15 Let 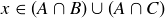 . Then it must be the case that
. Then it must be the case that 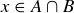 or
or 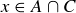 . Either way, we know
. Either way, we know 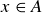 . We also know that
. We also know that 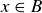 or
or 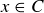 , and so
, and so 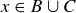 . Thus,
. Thus, 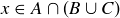 .
.
Exercise 3.16 Begin by assuming that 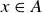 , and use the assumption that
, and use the assumption that 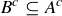 to prove that
to prove that 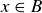 .
.
Exercise 3.17 Both expressions describe the shaded region in Figure 1. This should be a sufficient hint for leading you to a proof (or a radioactive safe room).
Exercise 3.18 Looking at a 2-set Venn diagram, we see that enumerating all of the elements of A plus all of the elements of B double-counts the elements in  . So, to get the correct size of
. So, to get the correct size of 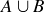 , we must subtract the number of elements in
, we must subtract the number of elements in  from
from 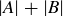 .
.
A similar formula for  accounts for double- and triple-counting certain elements:
accounts for double- and triple-counting certain elements:
![]()
Exercise 3.19 There are many good ways to do this. Our attempt at a picture is shown in Figure 2. The intervals are nested, as each sits inside the previous interval, like a matryoshka doll.
Exercise 3.20 The key is that “for some” expresses the same concept as “or,” and “for all” corresponds to “and.”
Exercise 3.21 The union consists of all of the points on the curves in Figure 3. The intersection contains four points:
![]()
Exercise 3.22 There are no ordered pairs because there is no element available for the first entry, so 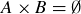 .
.
Exercise 3.23 Suppose that A and B are both finite. Since an ordered pair is just a short sequence of length 2, Proposition 2.13 tells us that
![]()
because there are 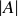 choices for the first term and
choices for the first term and 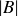 choices for the second term. If at least one of A and B is empty, then either Exercise 3.22 or Proposition 2.13 shows that the formula still holds. The only other case is if at least one of A and B is infinite and the other is non-empty, and it shouldn’t be too hard to see that
choices for the second term. If at least one of A and B is empty, then either Exercise 3.22 or Proposition 2.13 shows that the formula still holds. The only other case is if at least one of A and B is infinite and the other is non-empty, and it shouldn’t be too hard to see that 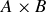 must be infinite in this case.
must be infinite in this case.
Exercise 3.24 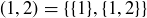 , whereas
, whereas  .
.
Exercise 3.25
(a) Any set A with 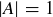 can be expressed as
can be expressed as  for some element a, so
for some element a, so  .
.
(b) Similarly, if 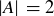 , then
, then 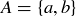 for some distinct elements a and b, so
for some distinct elements a and b, so 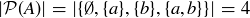 .
.
(c) 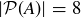 if
if 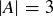 . Can you write down all eight elements of
. Can you write down all eight elements of  ?
?
Exercise 3.26 Since 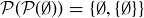 ,
,  is equal to the 4-element set
is equal to the 4-element set
![]()
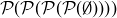 contains 16 elements – can you find all of them?
contains 16 elements – can you find all of them?
Exercise 3.27 The first case requires  , so the eight possible subsets B are
, so the eight possible subsets B are
![]()
The second case requires 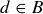 . The subsets B are listed below, and the corresponding sets
. The subsets B are listed below, and the corresponding sets 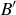 are obtained by simply removing the element d:
are obtained by simply removing the element d:
![]()
Exercise 3.28 In no particular order, they are
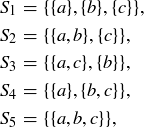
Exercise 3.29 For the partition into three blocks, note that
![]()
Exercise 3.30 Since there are n options for the ith term of the sample, the total number of samples is
![]()
Exercise 3.31 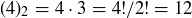 counts the number of ordered samples of size 2, without replacement:
counts the number of ordered samples of size 2, without replacement:
![]()
Exercise 3.32 The empty set is the first set in any path. Regardless of the choices made along the way, it is clear from the number of edges directly above each subset in the diagram that there are 4 options for the second set on the path, 3 options for the third, 2 options for the fourth, and the path ends with 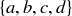 . By Proposition 2.13, there are
. By Proposition 2.13, there are 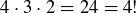 such paths.
such paths.
Now see if you can arrive at 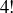 in a different way, by having a permutation of
in a different way, by having a permutation of 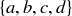 determine the four edges of the path.
determine the four edges of the path.
Exercise 3.33 Notice that each 2-combination of 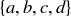 is represented by exactly
is represented by exactly  of the
of the  ordered samples in Exercise 3.31, so the number of 2-combinations is
ordered samples in Exercise 3.31, so the number of 2-combinations is
![]()
Exercise 3.34 Every subset of an n-element set contains either 0 elements, or 1 element, or 2 elements, …
Exercise 3.35 You will get the same partition by choosing  to be a subset of S or its complement in S. And you had better not let
to be a subset of S or its complement in S. And you had better not let  equal either S or its complement,
equal either S or its complement, 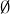 .
.
Exercise 3.36 The number of blocks can be  only if all of the blocks contain a single element of S, except for one block containing two elements. In how many ways can you choose these two elements?
only if all of the blocks contain a single element of S, except for one block containing two elements. In how many ways can you choose these two elements?
Chapter 4
Exercise 4.1 No. If you thought q was it, consider 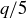 .
.
Exercise 4.2 After some experimentation, and deciding that “0 cents postage” doesn’t make much sense, we know that we can create the following values using only 10 and 4 cent stamps.
![]()
We can prove that all of these values are possible by considering numbers of the form  and
and 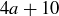 .
.
We conjecture that this is a complete list. To prove this conjecture, assume to the contrary that there are counterexamples. By the Well-Ordering Principle there must be a minimal counterexample, m, which we know by our earlier computations must be at least 20. We also know that m must be even, since 4 and 10 are even. Because  , it must be the case that
, it must be the case that 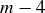 is an even integer that is at least 16. Thus
is an even integer that is at least 16. Thus  for some non-negative integers a and b. But then
for some non-negative integers a and b. But then 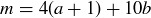 , which contradicts the claim that m is the minimal counterexample.
, which contradicts the claim that m is the minimal counterexample.
Exercise 4.3 Finding an integer combination that equals 1 isn’t hard to do: 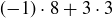 is one, as is
is one, as is 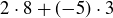 . How many different possibilities are there? Finding a combination of 8 and 3 that equals 0 might help.
. How many different possibilities are there? Finding a combination of 8 and 3 that equals 0 might help.
On the other hand, 8 and 6 are both even, so any integer combination of them must be even, too.
Exercise 4.4 The pairs are 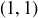 ,
, 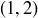 ,
, 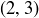 ,
, 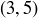 ,
, 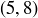 ,
, 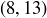 ,
, 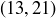 ,
, 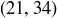 ; no pair shares a common integer divisor greater than 1. But
; no pair shares a common integer divisor greater than 1. But  and
and  , as you might also recall from Section 2.9.2.
, as you might also recall from Section 2.9.2.
Exercise 4.5 There are only two integers relatively prime to 0, and 0 isn’t one of them.
Exercise 4.6
(a) False: For example, let 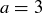 and
and 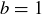 .
.
(b) True: A proof very similar to the one given in Lemma 4.7 works here, although you’ll need to tweak Exercise 1.17.
(c) True: Again, a proof with the same overall logic as the one given in Lemma 4.7 works here. A few tweaks will be needed; and remember that if 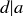 , then
, then 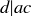 for any integer c.
for any integer c.
(d) False: For example, let  ,
, 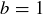 , and
, and 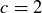 .
.
Exercise 4.7 Yes. The “only if” part of the theorem doesn’t depend on whether a and b are positive, negative, or 0. And by Exercise 4.5, 0 is only relatively prime with 1 and 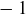 . Since
. Since 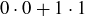 and
and 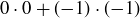 both equal 1, the “if” part of the theorem is true as well.
both equal 1, the “if” part of the theorem is true as well.
Exercise 4.8 Yes. Again, the “only if” part of the theorem doesn’t depend on whether a and b are positive, negative, or 0; and Exercise 4.7 handles the situations when at least one of them equals 0.
We are thus left with two cases not yet handled by Theorem 4.8:
One possible way to handle each of these cases is to use induction on the quantity 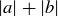 (which of course equals
(which of course equals 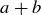 when both a and b are positive). You will need to rearrange and alter some of the inequalities given in the proof, and refer to
when both a and b are positive). You will need to rearrange and alter some of the inequalities given in the proof, and refer to 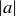 and
and 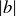 instead of a and b; and for one of the cases, you may need to use
instead of a and b; and for one of the cases, you may need to use 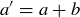 instead of
instead of 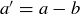 .
.
Another way to handle these cases is just to use Theorem 4.8 directly applied to 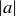 and
and 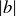 , which are both positive. In any resulting linear combination, you can replace
, which are both positive. In any resulting linear combination, you can replace 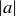 with a and
with a and 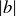 with b, so long as you negate certain coefficients. You would then need only a lemma that says a and b are relatively prime if and only if
with b, so long as you negate certain coefficients. You would then need only a lemma that says a and b are relatively prime if and only if 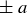 and
and  are relatively prime, regardless of their signs.
are relatively prime, regardless of their signs.
Good luck putting the pieces together!
Exercise 4.9 For certain values of a and b, it may be challenging to find integer combinations that equal 1 by trial and error. There is a method, called the Euclidean Algorithm, that works for any pair of integers; we hope that these exercises motivate you to research it!
(a) Since 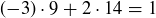 , we have
, we have  .
.
(b) Since 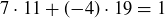 , we have
, we have  .
.
(c) Notice that 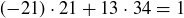 . Do you think it’s a coincidence that 13 is another Fibonacci number?
. Do you think it’s a coincidence that 13 is another Fibonacci number?
Exercise 4.10 Recall the structure of the proof of Proposition 2.13.
Exercise 4.11 There will be a quiz later!
Exercise 4.12 For the first part, you can simply let one of a and b be equal to 15 and the other 225; there are other possibilities as well. For the second part, notice that 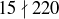 ; explain why this is problematic.
; explain why this is problematic.
Exercise 4.13 For one approach, note that the product ab is a multiple of both a and b, so the smallest common multiple of a and b is in the finite set of natural numbers 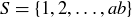 .
.
For a different approach, consider the set M of all common multiples of a and b, and notice that 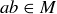 means that it is a non-empty subset of
means that it is a non-empty subset of  .
.
Exercise 4.14 Let 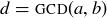 . Since d must divide both a and b, its prime divisors can only be among the primes
. Since d must divide both a and b, its prime divisors can only be among the primes 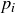 , so
, so 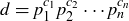 , where each
, where each 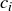 is a non-negative integer. If
is a non-negative integer. If  for each i, then certainly
for each i, then certainly 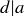 and
and 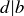 . On the other hand, if some
. On the other hand, if some 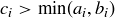 , then at least one of
, then at least one of 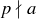 and
and 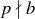 is true because
is true because 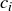 would be greater than one of
would be greater than one of 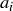 and
and  .
.
The argument for  is similar.
is similar.
Exercise 4.15 Using the notation in the preceding paragraph, the formulas for 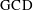 and
and  imply
imply
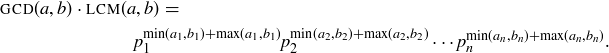
Once you have explained why  , you will know that
, you will know that

Exercise 4.16 Since  , we have
, we have 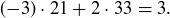
Exercise 4.17 Good luck!
Exercise 4.18 There’s only one such set.
Exercise 4.19 Computations like
![]()
show that 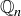 is closed under addition, subtraction, and multiplication. For division, consider
is closed under addition, subtraction, and multiplication. For division, consider 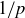 , where p is a prime that doesn’t divide n.
, where p is a prime that doesn’t divide n.
Exercise 4.20 The hardest step involves the computation
![]()
Chapter 5
Exercise 5.1 There are a lot of choices, including the floor and ceiling functions, which are defined later in this section if you have never seen them before. Or you could be boring and just do something like set  for all
for all 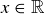 .
.
Exercise 5.2
(a) The number of characters in ω is the sum of the numbers of characters in 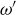 and
and 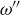 .
.
(b) The alphabet for 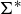 consists of only the characters 0 and 1, so
consists of only the characters 0 and 1, so 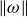 is the number of 0s plus the number of 1s.
is the number of 0s plus the number of 1s.
Exercise 5.3 One possibility for (d) would be
![]()
As examples, 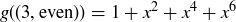 and
and 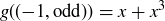 . What is important for your function is that every ordered pair in
. What is important for your function is that every ordered pair in  is sent to a unique and unambiguous polynomial in
is sent to a unique and unambiguous polynomial in 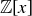 . Thus the following would not define a function for (d), for a couple of reasons:
. Thus the following would not define a function for (d), for a couple of reasons:
![]()
Exercise 5.4 The range of  is
is  , and the range of ϕ is
, and the range of ϕ is  . As for
. As for 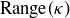 , does any polynomial map to the string
, does any polynomial map to the string 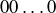 consisting of n zeros for any
consisting of n zeros for any  ?
?
Exercise 5.5 Just two of the seven are not functions. In those cases, there exist elements of the domain whose images are not in the given codomains.
Exercise 5.6
(a) Let 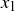 and
and 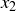 be any elements of (the domain)
be any elements of (the domain) 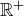 . If
. If 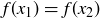 , then
, then 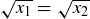 , and squaring both sides gives
, and squaring both sides gives  . Thus, f is injective.
. Thus, f is injective.
(b) The proof of injectivity is essentially the same as the one given in part (a), with reciprocating in place of squaring.
(c) Note that 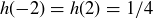 , so h is not injective.
, so h is not injective.
(d) Note that  , so m is not injective.
, so m is not injective.
Exercise 5.7
(a) If a is any element in (the codomain) A, then that same a (which is also in the domain A) satisfies 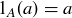 , and thus
, and thus 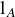 is surjective.
is surjective.
If 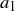 and
and 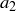 are any elements of (the domain) A such that
are any elements of (the domain) A such that  , then
, then
![]()
so 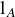 is injective.
is injective.
(b) The floor function is surjective because if n is an integer, then  . It is not an injective function because
. It is not an injective function because  . Similar reasonings imply that the same results hold for the ceiling function.
. Similar reasonings imply that the same results hold for the ceiling function.
(c) If 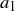 and
and 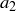 are any elements of A such that the ordered pairs
are any elements of A such that the ordered pairs 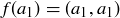 and
and  are equal, then their first coordinates,
are equal, then their first coordinates, 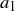 and
and 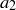 , must be equal, so f is injective.
, must be equal, so f is injective.
If 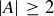 , then there are distinct elements
, then there are distinct elements 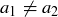 in A, and
in A, and 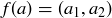 is not satisfied for any
is not satisfied for any 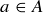 , so f is not surjective. However, if
, so f is not surjective. However, if 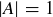 or
or  … you can take it from here!
… you can take it from here!
Exercise 5.8 For (b), perhaps show that  is both injective and surjective. Does this example suggest a formula for a bijection from
is both injective and surjective. Does this example suggest a formula for a bijection from  to
to 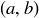 for any real numbers
for any real numbers  ?
?
The same type of formula probably won’t work for (c). Maybe incorporate 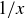 ?
?
Exercise 5.9 Since f is an injection, so is 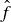 :
:
![]()
And 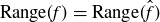 , so
, so  is surjective.
is surjective.
Exercise 5.10
(a) Each of the 3 elements in A can be paired with one of the 5 elements in B, so you can think of this as creating a sequence of length 3 with 5 options for each term. Perhaps Proposition 2.13 would be helpful?
(b) After an element of B has been paired with an element of A, it can not be paired with another element of A. Proposition 2.13 still seems like a good approach, or consult Section 3.8.
(c) None. Why?
(d) The answer to part (a) simply changes in value; the answer to part (b) changes entirely!
Exercise 5.11 It is meaningless, because the codomain of g and the domain of f are different.
Exercise 5.12
(a) g is not injective because, for example, 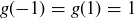 . But
. But 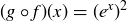 is injective: if
is injective: if 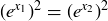 , then
, then 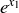 and
and 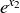 both being positive means that
both being positive means that 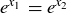 , which implies
, which implies 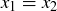 . Plotting a graph of
. Plotting a graph of 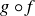 will confirm this result.
will confirm this result.
(b) An example is shown in Figure 4.
Exercise 5.13 Continuing the hints given in the text …
(a) …there is a 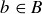 such that
such that 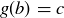 . Since f is surjective, there is an
. Since f is surjective, there is an 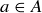 such that
such that 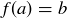 . Thus,
. Thus, 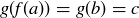 , so
, so 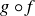 is surjective.
is surjective.
(b) …we know that 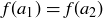 . Since f is injective, we know that
. Since f is injective, we know that 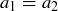 . Thus,
. Thus, 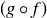 is injective.
is injective.
(c) There’s at most one sentence to write here!
Exercise 5.14 Yes: f must contain an ordered pair of the form 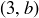 , and nothing else.
, and nothing else.
Exercise 5.15 The function  contains eight such elements: ω can be any element of the set
contains eight such elements: ω can be any element of the set
![]()
Exercise 5.16 A function is injective if 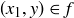 and
and 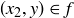 imply that
imply that 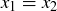 . A function is surjective if for each
. A function is surjective if for each 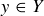 there is an
there is an 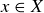 such that
such that 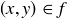 .
.
Exercise 5.17 For the second step, if 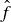 is not injective, there exist distinct elements
is not injective, there exist distinct elements 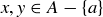 and an element
and an element 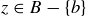 such that both
such that both  and
and 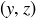 are in
are in 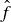 . But
. But 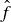 is a subset of f, so
is a subset of f, so 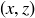 and
and 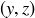 are in f, too.
are in f, too.
Exercise 5.18 To find all points of intersection, solve 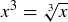 . This leads to
. This leads to
![]()
so the x-values are 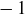 , 0, and 1; and the y-values are the same because these points must lie on the line
, 0, and 1; and the y-values are the same because these points must lie on the line 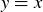 . Be sure that your two graphs are reflections of each other across this line.
. Be sure that your two graphs are reflections of each other across this line.
Exercise 5.19 Using the logical equivalences discussed in Exercises 2.7 and 2.8 and the paragraph that follows them, we just need to show that Q  (
(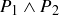 ) is logically equivalent to
) is logically equivalent to  . Try a truth table!
. Try a truth table!
Exercise 5.20 To show that f is injective, suppose that 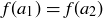 for elements
for elements  . Then
. Then 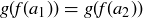 , and so
, and so  , implying that
, implying that 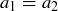 . To show that f is surjective, consider any
. To show that f is surjective, consider any 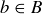 . Since
. Since 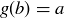 for some
for some 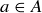 , we have
, we have
![]()
A similar argument implies that g is bijective as well: just swap the symbols f and g, A and B, and a and b!
Finally, since f is bijective and thus the function 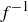 exists, let’s show that
exists, let’s show that 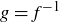 . Let
. Let 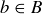 , and suppose that
, and suppose that 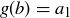 and
and 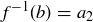 . Then
. Then
![]()
from the given properties of f and g, and
![]()
from the definition of 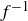 . Since f is injective, we must have
. Since f is injective, we must have 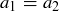 . Thus, g and
. Thus, g and 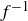 agree for all b in their common domain, B.
agree for all b in their common domain, B.
Exercise 5.21
(a) Since 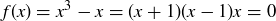 exactly when
exactly when 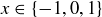 , the pre-image of 0 is
, the pre-image of 0 is 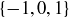 .
.
(b) From the graph (or calculus) it is clear that the pre-image of 6 contains exactly one element. Since 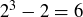 , the pre-image of 6 is
, the pre-image of 6 is 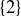 .
.
(c) We have 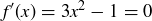 when
when 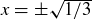 ; these are the x-values of the points where the local minima and maxima occur. Since
; these are the x-values of the points where the local minima and maxima occur. Since 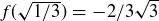 and
and 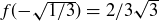 , each of the pre-images of
, each of the pre-images of  and
and 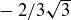 are 2-element sets.
are 2-element sets.
Exercise 5.22
(a) Use the fact that 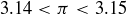 , so
, so 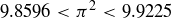 .
.
(b) 
(c) 
(d) 
(e) Since the range of  can only consist of non-negative integers, and since
can only consist of non-negative integers, and since 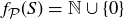 for
for 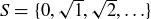 ,
,  as well.
as well.
Exercise 5.23 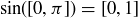 , and
, and 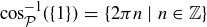 .
.
Exercise 5.24 The graphs are best suggested using dotted lines with very fine spacing. We will see in Chapter 7 that some of the lines should have much finer spacing than others!
(a) 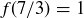 and
and  .
.
(b) 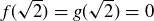 .
.
(c)  , because there are rational and irrational numbers in the interval
, because there are rational and irrational numbers in the interval 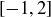 .
.
(d)  .
.
(e) Notice that 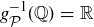 , because
, because  for each
for each 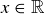 . Thus,
. Thus, 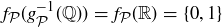 .
.
(f) Since 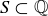 , we know that
, we know that 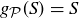 , so
, so  . Since S contains neither 0 nor 1, the answer is
. Since S contains neither 0 nor 1, the answer is 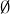 .
.
Exercise 5.25
(a) Try finding a counterexample with  ,
, 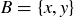 , and
, and  .
.
(b) Let 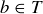 . Since f is surjective, there is an
. Since f is surjective, there is an 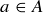 with
with 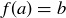 . So we know that
. So we know that 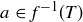 , and this implies that
, and this implies that 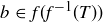 . Thus
. Thus 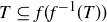 , and with part (b) of Proposition 5.24 we conclude that
, and with part (b) of Proposition 5.24 we conclude that 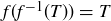 .
.
(c) Which is most helpful: part (a) or part (b) ?
Exercise 5.26 Try letting X and Y be disjoint.
Chapter 6
Exercise 6.1 The graph of A is a line, the graph of B is a closed half-plane, and the graph of C is shown in Figure 5.
Exercise 6.2 C is reflexive since 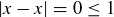 for all
for all 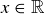 , and it is symmetric because
, and it is symmetric because 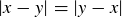 for all
for all 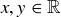 . But it is not transitive: for example,
. But it is not transitive: for example, 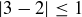 and
and 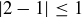 , but
, but 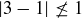 .
.
B is reflexive and transitive; A is all three.
Exercise 6.3 Our coin flips asked us to find a relation that is reflexive and symmetric but not transitive. An example of such a relation is C of Example 6.2 .
Exercise 6.4 By the discussion in Section 5.5, any function f is a subset of 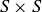 , so it’s a relation! One such g is
, so it’s a relation! One such g is 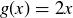 .
.
Exercise 6.5 If 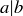 and
and 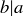 , then we know there are natural numbers m and n such that
, then we know there are natural numbers m and n such that 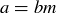 and
and 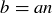 . By substitution this implies
. By substitution this implies 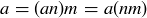 and so
and so 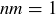 . Thus
. Thus 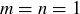 , so
, so 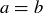 .
.
Exercise 6.6 Yes – for example, move 5 and 10 to the left of the rows they are on.
Exercise 6.7 It is a poset because 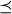 is reflexive, antisymmetric, and transitive. For example, it is antisymmetric since any two rabbit pairs can’t both be descendants of each other, so
is reflexive, antisymmetric, and transitive. For example, it is antisymmetric since any two rabbit pairs can’t both be descendants of each other, so 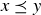 and
and  implies that x and y are the same pair.
implies that x and y are the same pair.
The Hasse diagram for 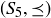 contains five rabbit pairs, with three minimal elements and the original pair at the top as the maximal element.
contains five rabbit pairs, with three minimal elements and the original pair at the top as the maximal element.
Exercise 6.8 This is an interesting infinite poset.
(a) 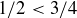 , but
, but 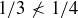 .
.
(b) The most complicated argument should be the one establishing antisymmetry. Try a proof by contradiction, assuming that 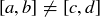 and considering what is implied by
and considering what is implied by  and
and 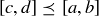 .
.
(c) Assume to the contrary that 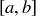 is a maximal element with
is a maximal element with  . Then consider
. Then consider 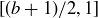 .
.
(d) See the suggestion for part (c) .
(e) 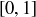 is both maximal and minimal.
is both maximal and minimal.
Exercise 6.9 The only one that isn’t is (c).
Exercise 6.10 The posets (b) and (d) are well ordered.
Exercise 6.11 We need to establish that 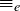 has three properties.
has three properties.
Reflexive: Since 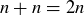 is even for all
is even for all 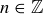 ,
, 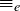 is reflexive.
is reflexive.
Symmetric: If 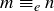 , then
, then 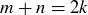 for some
for some 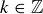 . But then
. But then 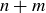 also equals
also equals 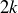 , so
, so 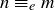 .
.
Transitive: If 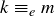 and
and 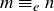 , then
, then
![]()
for some 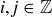 . Thus
. Thus 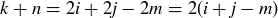 , which is even. Therefore
, which is even. Therefore 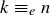 as well.
as well.
Exercise 6.12 The proof of Proposition 6.11 can be adapted to prove this is an equivalence relation, and again we point you to the more general result in Exercise 6.57.
Exercise 6.13 To answer part (c), notice that an equivalence class corresponds to the set of x-values where a horizontal line intersects the graph of sine. If two x-values correspond to the same horizontal line, their equivalence classes are the same; and if they correspond to different horizontal lines, the two equivalence classes have no x-values in common (because sine is a function). The dotted horizontal line in Figure 6 intersects the graph of sine in the equivalence class of 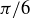 , which may be helpful for part (b).
, which may be helpful for part (b).
Exercise 6.14 It’s equality.
Exercise 6.15 Look at Theorem 6.14 and Exercise 3.28.
Exercise 6.16 The equivalence classes modulo 2 are the evens and odds. The equivalence classes modulo 3 are:

Exercise 6.17 We ask you …
Exercise 6.18 …to complete these three exercises …
Exercise 6.19 …without any additional hints from us.
Exercise 6.20 Each element of 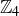 is an equivalence class that must be mapped to a unique element of
is an equivalence class that must be mapped to a unique element of 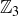 .
.
Exercise 6.21 The formulas follow from the fact that  and
and  in
in  .
.
Exercise 6.22 The multiplication table for 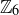 is shown in Figure 7. Notice that we have
is shown in Figure 7. Notice that we have 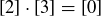 in
in 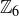 , which is directly related to the factorization
, which is directly related to the factorization 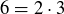 .
.
Exercise 6.23 Recall the proof of Proposition 2.16 and the discussion preceding it.
Exercise 6.24 The last digit is a 9. Here’s a slightly more difficult computation: What’s the last digit of 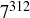 ?
?
Exercise 6.25 The argument given for 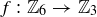 would fail when applied to the proposed squaring function from
would fail when applied to the proposed squaring function from 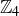 to
to 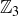 . If
. If 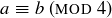 , then
, then 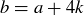 for some
for some 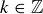 . So
. So
![]()
Since 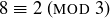 and
and 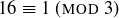 , we can’t reduce
, we can’t reduce 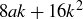 to zero as we could when we were defining the function from
to zero as we could when we were defining the function from 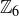 to
to 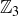 . In particular, we cannot make a statement similar to “Since 3 divides 12 and 36 we know
. In particular, we cannot make a statement similar to “Since 3 divides 12 and 36 we know 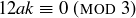 and
and  .”
.”
Exercise 6.26 Here is a proof of part (d).
If 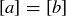 in
in  , then
, then 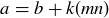 for some
for some 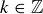 . Therefore
. Therefore
![]()
Thus  , and so
, and so 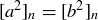 if
if 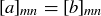 .
.
If you would like an additional challenge, find values of m and n where this squaring function from  to
to 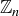 is not surjective.
is not surjective.
Exercise 6.27 You can prove this by mimicking the proof of Theorem 6.19, or you can use an argument inspired by 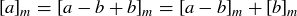 .
.
Exercise 6.28  , so 4 plays the role of “1/4.”
, so 4 plays the role of “1/4.”
Exercise 6.29 Construct the rows corresponding to multiplication by 2 and 10 in order to verify that [2] and [10] do not have inverses. On the other hand, 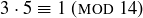 , so
, so 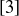 is the multiplicative inverse of
is the multiplicative inverse of 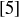 and
and 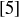 is the multiplicative inverse of
is the multiplicative inverse of 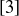 .
.
Exercise 6.30 If 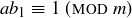 and
and 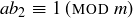 , then
, then 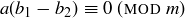 . This means that
. This means that 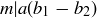 , with
, with 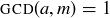 . What can you conclude about m and
. What can you conclude about m and  ?
?
Exercise 6.31 Figure 8 should get you started, if you are truly stuck.
Exercise 6.32 Search for hints among the various facts we have proven about relatively prime integers.
Chapter 7
Exercise 7.1 Suppose that n new guests arrive. Hilbert should announce over the intercom to everyone who already has a room: “I again apologize for the inconvenience, but in order for us to accommodate some new guests, we need you to change rooms. If you are in room #k, please move to room # for the night. Thank you!” He can then send the new arrivals to rooms #1 through #n.
for the night. Thank you!” He can then send the new arrivals to rooms #1 through #n.
Exercise 7.2 Hilbert can first move every current guest into an even-numbered room by announcing: “I once again apologize for the inconvenience, but in order for us to accommodate some new guests, we need you to change rooms. If you are in room #k, please move to room #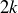 for the night. Thank you!” He then tells the new guests to move into the odd-numbered rooms, with new guest #n sent to room #
for the night. Thank you!” He then tells the new guests to move into the odd-numbered rooms, with new guest #n sent to room #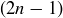 .
.
Exercise 7.3 None! Cookie #n will be eaten in round n, and that accounts for all of them.
Exercise 7.4 The answers are:
(a) Cookies #1 through #9 will be on his plate.
(b) The even-numbered cookies will be on his plate.
If you found this to be an interesting exercise, or if you found it difficult, then you should also work on Exercise 7.22 at the end of the chapter.
Exercise 7.5 If you have worked earnestly on this question for more than two hours and are stuck, then perhaps you should stop and begin reading the remainder of this section and the next, where almost all is revealed.
Exercise 7.6 We recommend using the fact that all of these functions have inverses: the natural logarithm 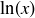 ,
, 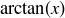 , and
, and 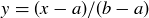 .
.
Exercise 7.7 Constructing an explicit function might help you prove that this is a bijection. Using 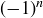 in your formula will allow you to change signs back and forth between positive and negative, and the function
in your formula will allow you to change signs back and forth between positive and negative, and the function  is also handy, as for example
is also handy, as for example  .
.
Exercise 7.8 We already gave you a nice hint!
Exercise 7.9 For part (a), by shifting his current guests from room #n to room #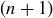 , Hilbert has opened up room #1 for a frog. It’s quite generous of him to go to all of this trouble for a frog.
, Hilbert has opened up room #1 for a frog. It’s quite generous of him to go to all of this trouble for a frog.
For part (b), you might wish to view the partial table presented in this section as one corner of a vast parking lot.
Exercise 7.10 Again, we already gave you a nice hint!
Exercise 7.11 Since 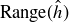 is an infinite subset of
is an infinite subset of  , use Lemma 7.7.
, use Lemma 7.7.
Exercise 7.12 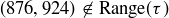 because
because  . There are surely simpler examples than this one.
. There are surely simpler examples than this one.
Exercise 7.13 Randomly selecting the image of each 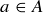 , we created the injective function
, we created the injective function 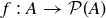 defined by
defined by

The resulting set is 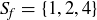 , which is not in the range of f.
, which is not in the range of f.
Exercise 7.14 Just change “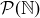 is countable” to “
is countable” to “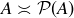 ,” and change all occurrences of
,” and change all occurrences of  to A. And change n to x for style points, if you think n should only represent integers.
to A. And change n to x for style points, if you think n should only represent integers.
Exercise 7.15 We are not uncomfortable with the original argument, so we skipped this exercise.
Exercise 7.16 We know that 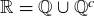 . If we assume to the contrary that
. If we assume to the contrary that 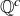 is a countable set, then we have expressed
is a countable set, then we have expressed  as the union of two countable sets. Lemma 7.10 would then imply that
as the union of two countable sets. Lemma 7.10 would then imply that  must be countable, which contradicts Theorem 7.15.
must be countable, which contradicts Theorem 7.15.
Exercise 7.17 The function 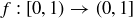 defined by
defined by
![]()
is a bijection, so 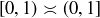 . In the previous paragraph we applied Schröder–Bernstein to prove
. In the previous paragraph we applied Schröder–Bernstein to prove  . Thus, by the transitivity of
. Thus, by the transitivity of 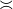 we will be finished if we can show that
we will be finished if we can show that 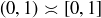 . We can do this by considering containment as the injection
. We can do this by considering containment as the injection 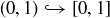 and
and 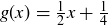 as the injection
as the injection 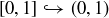 , and then appealing to Schröder–Bernstein.
, and then appealing to Schröder–Bernstein.
Exercise 7.18 First prove that h is a surjection. Then argue that it is sufficient to prove that h is injective when restricted to X and when restricted to 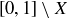 .
.
Exercise 7.19 You could try to do this by mimicking the proof of Lemma 7.20, or you could instead quote results we have already established:  has the same cardinality as the open interval
has the same cardinality as the open interval  , which leads to
, which leads to 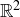 having the same cardinality as
having the same cardinality as  , and then you can apply Lemma 7.20.
, and then you can apply Lemma 7.20.
Exercise 7.20 In fact we only need Lemmas 7.21 and 7.22 to prove
![]()
Chapter 8
Exercise 8.1 One lower bound is 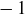 . Any
. Any 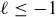 is also a lower bound, because if
is also a lower bound, because if 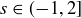 , then
, then  . Similarly, an upper bound is 2, and any
. Similarly, an upper bound is 2, and any  will serve as an upper bound. Figure 9 might help to clarify things.
will serve as an upper bound. Figure 9 might help to clarify things.
Exercise 8.2 Every real number r is an upper bound for the empty set, since 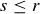 for all
for all 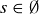 : there are no such s! Similarly, every real number is a lower bound.
: there are no such s! Similarly, every real number is a lower bound.
Since every element of  is an upper bound, there is certainly no least one.
is an upper bound, there is certainly no least one.
Exercise 8.3 A lower bound is 2 and an upper bound is 3. The greatest lower bound is 2.7, and the least upper bound is e. For a proof that e is irrational, see Section 8.6.2.
Exercise 8.4 The set of all lower bounds for A is 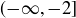 , so the greatest lower bound is
, so the greatest lower bound is  . The set of all upper bounds for A is
. The set of all upper bounds for A is 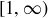 , so the least upper bound is 1.
, so the least upper bound is 1.
Exercise 8.5 Corollary 8.4 guarantees the existence of an  such that
such that 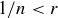 . There is a largest power of 10 within the non-empty finite set
. There is a largest power of 10 within the non-empty finite set  ; suppose it is
; suppose it is 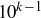 for some
for some 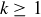 . Then
. Then 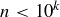 , so
, so 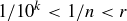 .
.
Exercise 8.6 Assume to the contrary that  is a lower bound for
is a lower bound for 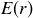 . Since r is negative and
. Since r is negative and 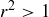 , we know that
, we know that
![]()
for all  . Since r is negative, dividing by r changes the order of the inequalities, giving
. Since r is negative, dividing by r changes the order of the inequalities, giving
![]()
for all 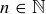 . Thus
. Thus
![]()
for all 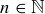 . Since
. Since 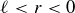 , we know that
, we know that 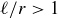 and thus
and thus 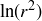 and
and 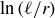 are positive real numbers, so we have a contradiction to Corollary 8.3.
are positive real numbers, so we have a contradiction to Corollary 8.3.
Exercise 8.7 The terms of the first two sequences are heading toward a limit of 0. The terms of the third sequence aren’t heading toward any finite value, so the limit doesn’t exist, or you might say that it’s “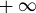 ”; see Exercise 8.27. The fourth sequence does have a limit, but it’s not rational. Write the first few terms of the sequence in decimal notation and see if that helps with your guess.
”; see Exercise 8.27. The fourth sequence does have a limit, but it’s not rational. Write the first few terms of the sequence in decimal notation and see if that helps with your guess.
Exercise 8.8 Parts of the definition are matched with phrases of the sentence: “Regardless of how close [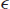 ] you want the sequence terms [
] you want the sequence terms [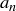 ] to be to the limiting value [L], you will get your wish [
] to be to the limiting value [L], you will get your wish [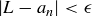 ] so long as you ignore an appropriate number [
] so long as you ignore an appropriate number [ ] of the initial terms of the sequence.” And order is important here: the value of N depends on the tolerance
] of the initial terms of the sequence.” And order is important here: the value of N depends on the tolerance 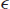 . You might wish to write
. You might wish to write 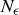 in place of N, if doing so helps you remember this order.
in place of N, if doing so helps you remember this order.
Exercise 8.9 The same argument that worked for 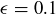 works for
works for 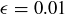 , requiring the solution of
, requiring the solution of
![]()
at the end. Now, sketch a (wide!) extension of Figure 1 on page 190 showing that the terms of the sequence eventually stay inside of a thinner 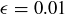 band around
band around 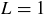 .
.
Exercise 8.10 Since the limit is 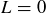 , we need to show that for every
, we need to show that for every 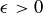 there is an
there is an 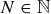 such that
such that 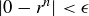 for all natural numbers
for all natural numbers 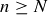 . Since
. Since
![]()
for 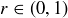 , we can appeal to the first proof given in Theorem 8.5 to conclude that there is an
, we can appeal to the first proof given in Theorem 8.5 to conclude that there is an 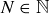 such that
such that 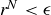 . Since
. Since 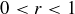 , for any natural number
, for any natural number 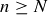 we have
we have
![]()
Exercise 8.11 For the first, it’s
![]()
For the second, it’s
![]()
Exercise 8.12 If 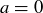 , then the sequence of partial sums is simply
, then the sequence of partial sums is simply 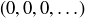 , so the series converges to 0. Otherwise, if
, so the series converges to 0. Otherwise, if 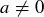 and
and 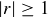 , the series doesn’t converge. For example, if
, the series doesn’t converge. For example, if 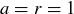 , then the series is
, then the series is 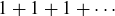 and the sequence of partial sums is
and the sequence of partial sums is 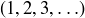 , which has no finite limit.
, which has no finite limit.
Showing that a geometric series doesn’t converge in other cases where 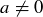 and
and 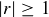 requires other arguments, some of which might be assisted by the Comparison Test of Section 8.5.
requires other arguments, some of which might be assisted by the Comparison Test of Section 8.5.
Exercise 8.13 It is a constant sequence: all of the terms must be equal.
Exercise 8.14
(a) The sequence 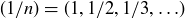 is monotone and bounded.
is monotone and bounded.
(b) The sequence 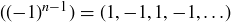 is bounded but not monotone. The sequence presented in Figure 1 (page 190) is another example, and also shows that a sequence need not be monotone to have a limit.
is bounded but not monotone. The sequence presented in Figure 1 (page 190) is another example, and also shows that a sequence need not be monotone to have a limit.
(c) The sequence 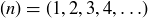 is monotone but not bounded.
is monotone but not bounded.
(d) The sequence 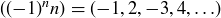 is neither monotone nor bounded.
is neither monotone nor bounded.
Exercise 8.15 Change μ to  , “increasing” to “decreasing,” “least upper bound” to “greatest lower bound,” and so on. Also reverse most of the inequalities and change some – signs to
, “increasing” to “decreasing,” “least upper bound” to “greatest lower bound,” and so on. Also reverse most of the inequalities and change some – signs to 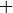 ; but
; but 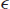 should remain positive!
should remain positive!
Exercise 8.16 You can show that the series converges, and find crude upper and lower bounds for the value of the series, by first comparing it with the geometric series 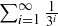 , and then with
, and then with  .
.
Exercise 8.17 First show that 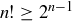 for all
for all  ; induction will work, as will a direct argument. This implies that
; induction will work, as will a direct argument. This implies that
![]()
for all 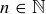 , and the
, and the  terms are both 1, so the Comparison Test applies.
terms are both 1, so the Comparison Test applies.
Exercise 8.18 Integration by parts yields
![]()
where the final term can be replaced via
![]()
whose final term can be replaced via
![]()
and so on, until a final term is 0 because  .
.
When 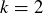 , the resulting expression is
, the resulting expression is
![]()
which evaluates to
![]()
as desired.
Exercise 8.19 Among the results you might need are that
![]()
when 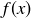 is non-negative and bounded above by M, and that
is non-negative and bounded above by M, and that
![]()
for any real number c.
Chapter 9
Exercise 9.1 There are eight equally likely outcomes:
![]()
Of these eight, three contain exactly two heads: HHT, HTH, and THH. So you might expect this result to occur about three-eighths of the time, if you repeat the activity many, many times.
Exercise 9.2 List the 16 equally likely outcomes and tally the ones you want, as in the previous exercise.
Exercise 9.3 Out of 250 flips, there are 124 heads and 126 tails. Out of all 249 2-flip strings, there are 59 HHs, 64 HTs, 64 THs, and 62 TTs. If you only count 125 2-flip strings starting from flips 1, 3, 5, …, 249, you get 29 HHs, 34 HTs, 32 THs, and 30 TTs.
What does this evidence suggest, if anything?
Exercise 9.4 Only the denominator changes:  and
and 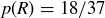 . Since
. Since 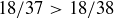 , the ball is slightly more likely to land on red on a European wheel.
, the ball is slightly more likely to land on red on a European wheel.
Exercise 9.5 You can determine the numerators of these fractions…
Exercise 9.6 …by counting carefully in Figure 2 (page 212).
Exercise 9.7 Is it close to 1/8?
Exercise 9.8 Symmetry follows from
![]()
For unimodality, use the fact that
![]()
is true so long as 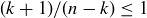 , and so when
, and so when 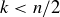 .
.
Exercise 9.9 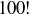 is a 158-digit integer beginning
is a 158-digit integer beginning 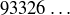 and ending with 24 0s.
and ending with 24 0s.
The real number 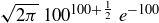 is approximately
is approximately 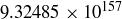 in scientific notation.
in scientific notation.
Exercise 9.10 The general statement is that, for non-negative integers n,
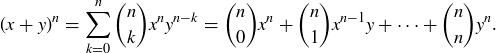
Mathematical induction seems like an appropriate way to prove this, using the identity 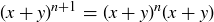 in the inductive step along with Theorem 9.8.
in the inductive step along with Theorem 9.8.
Exercise 9.11 Again, count carefully in Figure 2 (page 212).
Exercise 9.12 The values of the binomial coefficients are
![]()
The sum of these numbers is 100 146 724, which upon dividing by  yields
yields
![]()
Now, what’s your conclusion?
Exercise 9.13 If you’re not close, keep rolling!
Exercise 9.14 If X counts the points you earn on a die roll, then
![]()
Exercise 9.15 If A is the event that at least one 6 is seen, then 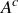 is the event that no 6s are seen. It is easier to compute
is the event that no 6s are seen. It is easier to compute  : by Proposition 2.13,
: by Proposition 2.13, 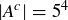 , so
, so
![]()
and thus 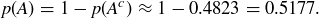 This number is larger than
This number is larger than 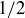 .
.
Exercise 9.16 We know that 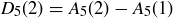 and
and  , so we are left to determine
, so we are left to determine 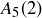 . Since
. Since
![]()
and
![]()
we find that
![]()
Thus, 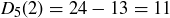 .
.
Exercise 9.17 It was, in fact, faked.
Chapter 10
Exercise 10.1 If 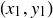 and
and 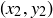 are two points in
are two points in  , then the distance between them is
, then the distance between them is
![]()
which is equal to
![]()
the distance between 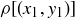 and
and 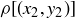 .
.
Now just see where the two corners go.
Exercise 10.2 It is probably easiest to note that 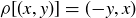 , which can be applied twice for
, which can be applied twice for 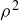 and three times for
and three times for 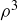 :
:
![]()
Exercise 10.3  and
and 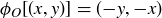 .
.
Exercise 10.4 You are interested in 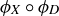 , so you first perform
, so you first perform 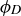 and then
and then 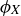 . Since
. Since
![]()
and
![]()
the composition must be 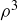 .
.
Exercise 10.5
(a) In order for a subset 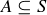 to be an identity element, it must be the case that
to be an identity element, it must be the case that 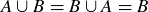 for all
for all 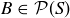 . The empty set can function as an identity element, as
. The empty set can function as an identity element, as
![]()
for all 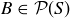 . Let A be a non-empty subset of S. The set A cannot serve as the identity element as we would need it to be true that
. Let A be a non-empty subset of S. The set A cannot serve as the identity element as we would need it to be true that 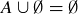 , but
, but  .
.
(b) Since S is non-empty, the set S cannot have an inverse with respect to 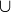 . Such a subset A would have to satisfy
. Such a subset A would have to satisfy 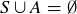 , but
, but 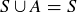 since
since 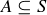 .
.
(c) We’ll let you do these last two parts …
(d) …on your own.
Exercise 10.6 Here are three very strong hints. You can prove that associativity holds by appealing to the fact that it held for G and H; the identity element is the ordered pair of identity elements 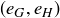 ; and the inverse of
; and the inverse of 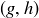 is
is 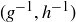 .
.
Exercise 10.7 Table 1 on the next page is a partially completed Cayley table for 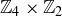 . In order to avoid cumbersome notation we express
. In order to avoid cumbersome notation we express 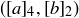 as
as 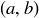 .
.
Table 1 Part of the Cayley table for 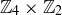 .
.
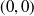 |
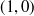 |
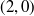 |
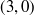 |
 |
 |
 |
 |
|
 |
 |
 |
 |
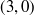 |
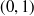 |
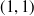 |
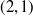 |
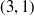 |
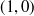 |
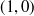 |
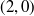 |
? | ? | 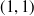 |
? | ? | ? |
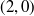 |
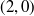 |
? | 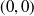 |
? | ? | ? | ? | ? |
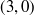 |
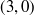 |
? | ? | ? | ? | ? | ? | ? |
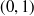 |
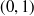 |
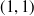 |
? | ? | ? | ? | ? | ? |
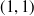 |
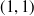 |
? | ? | ? | ? | ? | 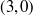 |
 |
 |
 |
? | ? | ? | ? |  |
? | ? |
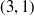 |
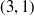 |
? | ? | ? | ? | 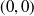 |
? | ? |
Exercise 10.8 You might do this by first proving that a symmetry of  is determined by where it sends any three vertices on a face of
is determined by where it sends any three vertices on a face of 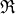 . Then prove that where these three vertices go is determined by where any one of them goes using the fact that the box is irregular.
. Then prove that where these three vertices go is determined by where any one of them goes using the fact that the box is irregular.
Exercise 10.9 In Theorem 10.11 you proved that 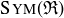 is closed under composition, so you know that
is closed under composition, so you know that 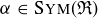 . By tracing out the destinations of the corners you will see that α takes a corner to its opposite corner of the box, which the rotations and reflections cannot do. This map is known as the antipodal map, and it has a simple formula:
. By tracing out the destinations of the corners you will see that α takes a corner to its opposite corner of the box, which the rotations and reflections cannot do. This map is known as the antipodal map, and it has a simple formula: 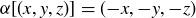 .
.
Exercise 10.10 In doing our work we noticed that 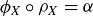 for each
for each  .
.
Exercise 10.11
(a) To show that this is a group, you need to mention that multiplication is associative, 1 is the identity element, and as long as  then
then  . To show it is an Abelian group, you need to highlight that multiplication of rational numbers is a commutative operation.
. To show it is an Abelian group, you need to highlight that multiplication of rational numbers is a commutative operation.
(b) This would be similar to part (a), except that 2 does not have a multiplicative inverse within  , so it’s not even a group!
, so it’s not even a group!
Exercise 10.12 An examination of Table 2 (page 237) shows that 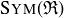 is Abelian. Can you see why a certain form of symmetry in the table implies that the product is commutative? If so, write up your proof by first proving and then using this insight.
is Abelian. Can you see why a certain form of symmetry in the table implies that the product is commutative? If so, write up your proof by first proving and then using this insight.
Exercise 10.13 The proof of Proposition 10.21 shows that  is a cyclic generator in
is a cyclic generator in  . The element
. The element  is as well, since
is as well, since
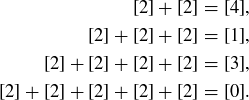
Similar computations will show that every non-zero element of 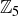 is a cyclic generator.
is a cyclic generator.
Exercise 10.14 Gauss characterized when  is a cyclic group:
is a cyclic group:
For example,  is cyclic while
is cyclic while  is not.
is not.
Exercise 10.15
(a) 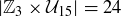 . (You may want to look up your answer to Exercise 3.23 if you think the answer is different.)
. (You may want to look up your answer to Exercise 3.23 if you think the answer is different.)
(b) 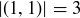 .
.
(c) 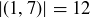 .
.
Exercise 10.16 If you are stuck after a couple of hours …
Exercise 10.17 …then you might want to pause until you get to Section 10.8.
Exercise 10.18 Here’s a proof for part (a). Since we know that 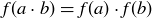 for all
for all  , we know that
, we know that 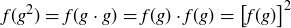 . Assume by induction that
. Assume by induction that 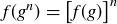 for an arbitrary
for an arbitrary  . Then
. Then
![]()
so this part follows by induction.
Lemma 10.27 establishes (b). An argument like that given above for (a), combined with Lemma 10.28, can be used to prove (c).
Exercise 10.19 There might be some smaller value 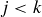 with
with  . For example, in
. For example, in 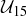 we have
we have 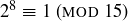 , so
, so  . However it is also the case that
. However it is also the case that 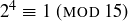 , so
, so  ; and in fact
; and in fact  in
in 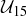 .
.
Exercise 10.20 Let 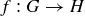 be an isomorphism and assume that G is Abelian. Let
be an isomorphism and assume that G is Abelian. Let 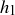 and
and 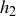 be any two elements of H. Since f is a bijection, there is a unique pair
be any two elements of H. Since f is a bijection, there is a unique pair 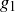 and
and 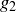 in G such that
in G such that  and
and  . Thus
. Thus  . By applying the definition of isomorphism twice and appealing to our assumption that G is Abelian, we find that
. By applying the definition of isomorphism twice and appealing to our assumption that G is Abelian, we find that
![]()
Thus H is Abelian.
Similarly, if H is Abelian, we may apply the argument above using the isomorphism  to prove that G is Abelian.
to prove that G is Abelian.
Exercise 10.21 Try two adjacent reflections, those whose axes of reflection form an angle of 30 . Their product will be a rotation through 60
. Their product will be a rotation through 60 , but the order in which you multiply them will determine if it is a clockwise or counterclockwise rotation.
, but the order in which you multiply them will determine if it is a clockwise or counterclockwise rotation.