Chapter 21

Neural Decoding I

Discrete Variables

Pascal Wallisch

What is neural decoding? Simply put, it is a mathematical mapping from the brain activity to the outside world. In the sensory domain, the outside world consists of the received visual, auditory, or other sensory information. In the motor domain, the outside world consists of the state of the skeletomuscular system. This is the inverse of neural encoding, which maps the outside world to brain activity. Because signals about motor intention precede movement, decoding can be thought of as “mind reading.” Neuroscientists seek to predict an action as soon as it is intended, before it ever takes place.

Keywords

neural decoding; neural encoding; rate encoding; temporal encoding; population vector; maximum likelihood

21.1 Goals of this Chapter

In the previous chapters, we saw how neural firing can be expressed as a function of some behavioral variable. But what about the inverse of that problem? This chapter will introduce an open-ended approach toward solving the problem of neural decoding, whereby an estimate of behavior is generated from observed neural activity. Specifically, this chapter will address how to predict the upcoming direction of movement from a population of neuronal signals recorded from motor areas of a macaque monkey. Note that this chapter assumes completion of Chapter 17, “Neural Data Analysis I: Encoding,” as it makes use of the preferred directions calculated in the exercises.

21.2 Background

What is neural decoding? Simply put, it is a mathematical mapping from the brain activity to the outside world. In the sensory domain, the outside world consists of the received visual, auditory, or other sensory information. In the motor domain, the outside world consists of the state of the skeletomuscular system. This is the inverse of neural encoding, which maps the outside world to brain activity. For example, in Chapter 17, you looked at how a cosine tuning curve specifies how a neuron modulates its firing rate depending on the upcoming direction of movement. In contrast, estimating this movement direction from one (or many) observed firing rate(s) is an example of neural decoding. Because signals about motor intention precede movement, decoding can be thought of as “mind reading.” Neuroscientists seek to predict an action as soon as it is intended, before it ever takes place.

Neural decoding can also be thought of as pattern recognition. A set of neuronal spike times represents a pattern, and the goal of the decoder is to figure out which stimuli or movements are associated with which patterns. This is a common problem in science. Doctors perform pattern recognition when they produce a diagnosis from a collection of physical and physiological findings. For example, an electrocardiogram (EKG) trace contains a repeated, stereotypical pattern that corresponds to a single heart beat. Each part of the trace corresponds to de- and repolarization of a different part of the heart. Therefore, doctors can use deviations from the normal EKG as clues about underlying abnormalities. An elevation in one part of the trace (ST elevation) is used to help diagnose heart attacks. This is pattern recognition.

Interpreting a raster plot is not quite that straightforward (neither is interpreting EKGs, but that’s another matter). Figure 21.1 shows 10 raster plots and a peri-event time histogram for a motor neuron. Each neuron’s spike times is centered on the start time of repeated movements in the same direction. There is a clear pattern. On every trial, there is a transient increase in the neuron firing rate starting a few hundred milliseconds before the movement starts. However, this is only an approximate relationship. If you look at each raster individually, it is not clear exactly when the movement begins. In addition, each raster plot is different. This means you can’t simply perform pattern recognition by using a “look-up table” because it is unlikely that a neuron’s response will ever exactly repeat itself.

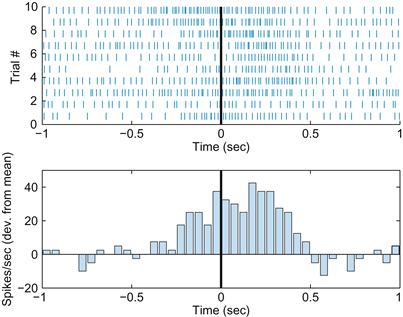
Figure 21.1 Top: A raster plot of 10 trials of a center-out task. Bottom: A peri-event time histogram of the same data. The start of movement occurs at time=0 seconds. The firing rate is expressed as the deviation from the mean firing rate.

In this chapter we will implement different strategies for predicting the direction of an upcoming movement based on the firing rates of a population of neurons. This is relevant to two distinct goals of neuroscience. First, neuroscientists would like to understand the brain on a functional level. Neuroscientists ask, “What is the brain doing and how is it doing that?” Second, neuroscientists are interested in using neuronal signals to do something useful. Neural prosthetics seek to do this. For example, cochlear implants convert sound into digital signals used to stimulate the auditory nerve, thus restoring speech perception in the deaf (Papsin and Gordon, 2007). A decoding strategy introduced in the next chapter (the linear filter) was used in a neuroprosthetic that allowed a human with tetraplegia to control a computer cursor and other devices (Hochberg et al., 2006).

It is important to note, however, that decoding to understand how the brain works is different from decoding for control. You have seen that neuronal activity in the motor cortex is directionally tuned, but that is not the same as saying these neurons encode direction. Properly interpreting what is being encoded requires more experiments than what we have described thus far. In the canonical center-out experiment, the posture is the same for all eight directions. Thus, instead of encoding direction, the neuron might be encoding the specific sequence of muscle activations, the desired end posture, or the spatial location of the target (see Kakei et al., 1999, 2001, for experiments which varied forearm posture during a center-out task). The adage “correlation does not imply causation” applies here.

One area of debate in neuroscience is, “At what time scale should we look for information?” Rate encoding holds that the firing rate calculated over some broad time span (usually hundreds of milliseconds) contains all the necessary information. Temporal coding holds that additional information is available at smaller time scales. At the extreme, you could use a 1 ms time bin where each bin either has a 0 (no spike) or a 1 (spike). This approach likely contains more information about the stimulus than a coarse firing rate. However, it also greatly increases the dimensionality of the potential responses. Instead of one discrete variable (the firing rate over 1 second), which might reasonably take a few dozen values, a 1 ms time bin gives a 1000×1 vector of binary variables with as many as 2¹⁰⁰⁰ possible values, which is a number larger than the estimated number of atoms in the universe. Thus, for computational simplicity, you can start by assuming a coarse rate code. The idea of temporal encoding is explored in more detail in Chapter 20.

21.2.1 Population Vector

In Chapter 17, we introduced the concept of directional tuning of motor cortical neurons. This is an encoding model that translates an upcoming direction of movement into a neuronal firing rate. If you now want to decode direction from a firing rate, you are faced with two problems. First, since a cosine-tuning curve is symmetric, most firing rates are ambiguous because they could be associated with two movement directions. Second, the firing rate signal is very noisy. This is due to both intrinsic neuronal noise as well as measurement noise introduced by the equipment. How, then, can you decode movement direction?

The solution is averaging over a population of neurons, which decreases the effects of noise and allows disambiguation of the movement direction. The “population vector” algorithm introduced by Georgopoulos and colleagues is an intuitive way to use cosine-tuning information from a population of neurons to decode movement direction (1986). In Chapter 17, you determined the preferred direction of each neuron using information from all trials.

Having done this, proceed as follows:

1. Assume that each neuron “votes” for its preferred movement direction. Specifically, each neuron is going to contribute a “response vector” that is aligned with its preferred direction.

2. The magnitude (or length) of each neuron’s response vector is determined by the neural activity of the neuron during each trial. This is the weight given to each neuron’s vote. For now, assume the weight is simply the firing rate during the hold period.

3. Sum all the response vectors from all neurons to arrive at the population vector for this trial. The direction of this population vector corresponds to the predicted direction.

This can be expressed as a formula,

(21.1)

where for n neurons, P is the population vector, w_i is the weight given to each vote, and C_i is a unit vector pointing in the ith neuron’s preferred direction. The arrows above P and C_i indicate that these quantities are vectors. Recall that if you represent vectors with Cartesian coordinates, you can sum the X and Y components separately. Thus, if θ_i is the ith neuron’s preferred direction in radians, then the population vector can be broken down into its X and Y components:

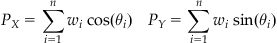(21.2)

Our perspective has changed. Previously, you considered all trials to determine the preferred direction of a given neuron. Now, you consider the neural activity of all cells in a given trial to determine the combined response of the population of neurons: the population vector. The population vector points toward the upcoming movement direction.

The population vector is useful because it is easy to implement and intuitive to understand. It is based on the theory that motor cortex neurons fire to produce muscle forces, which, given a certain posture, act in the neuron’s preferred direction. However, the population vector is limited because a number of conditions must be met for the method to perform well (Georgopoulos, 1986). For example, the neuron’s tuning curves must actually follow a cosine or at least be radially symmetric around the preferred direction. Also, the preferred directions must be uniformly distributed.

21.2.2 Maximum Likelihood

You can develop a more general decoding algorithm by relaxing some of the assumptions made by the population vector. One way to do this is to use statistical methods. You assume that a neuron modulates its firing rate in response to the upcoming movement direction. However, you do not assume exactly how (which a cosine tuning curve does). You assume that the neuron’s target firing rate will be corrupted by noise, so that for a given direction you will observe a distribution of firing rates rather than a single firing rate. If you assume the form of this distribution, you can use standard statistical methods to estimate its parameters. For example, if you thought the distribution of firing rates was Gaussian, you could characterize it fully by computing the mean and standard deviation of all the firing rates for trials moving in one direction.

Once you have estimated the parameters, you can calculate the probability of any firing rate giving a certain direction. This is a conditional probability. We reviewed this in Chapter 20, “Information Theory.” Briefly, the conditional probability of event A given event B is denoted as P(A|B). It is defined as the joint probability A and B divided by the probability of B:

(21.3)

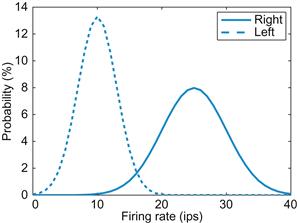
Intuitively, this can be thought of as the probability of A taking into account some piece of information (that B has happened). Here, you are interested in the conditional probability of a firing rate R given the direction d: P(R|d). For one neuron, the maximum likelihood approach is to look at the firing rate and select the direction for which this firing rate is most likely. As an example, consider a simplified center-out experiment in which targets are presented at equal probabilities to the left or right, and you are recording from a neuron that prefers movement to the right. Say this neuron fires 25 spikes/s with a standard deviation of 5 spikes/s before right targets and fires 10 spikes/s with a standard deviation of 3 spikes/s before left targets. If you assume these firing rates follow Gaussian distributions, then the maximum likelihood algorithm would predict a right target for a firing rate ≥17 spike/s and a left target for firing rates ≤16 spike/s (see Figure 21.2).

Figure 21.2 Firing rate distributions of a hypothetical, rightward-preferring neuron.

If there is more than one neuron, the situation is more complicated. You make the simplifying assumption that the neuron’s firing rates are independent. At first, this seems at odds with our understanding of the brain: aren’t connections between neurons the whole point? However, most neurons in the sample are separated by large distances (relative to the size of the neurons), and you may attempt to relax this assumption in the exercises. Independence means you can express the probability of a set of firing rates as the product of the probabilities for each individual firing rate. This calculation is performed when you say the chance of flipping four heads in a row is 1/16=(1/2)⁴. The probability of a set of firing rates R=[r₁, r₂,…,r_n] for a given direction d can be expressed as follows:

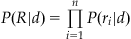(21.4)

The maximum likelihood approach predicts the direction associated with the highest likelihood P(R|d). However, when you’re implementing this in MATLAB, it is more convenient to pick the direction that maximizes the log-likelihood: log[P(R|d)]. Because the natural logarithm is a monotonically increasing function, the choice of direction that maximizes the log-likelihood will also maximize the likelihood. This approach avoids calculating the product of very small numbers in MATLAB, which, due to numerical precision constraints, quickly becomes inaccurate. Instead, you sum negative numbers (since the probabilities are less than 1). The log-likelihood can be expressed as follows:

(21.5)

The algorithm we have described here is more accurately called the “maximum a posteriori” estimation, which will be discussed in more detail in Chapter 22. In this formulation, we are relying on an experimental trick: the prior probability of each direction is equal. This is important, because if you are decoding direction, you want to maximize the conditional probability of the direction given the firing rates, P(d|r). This algorithm is maximizing the reverse: the conditional probability of the firing rates given the direction, P(r|d). This simplification is valid only if all directions are equally probable. If they are not, you will need to calculate P(d|r) using Bayes’ rule, which will be discussed in Chapter 22.

21.2.3 Data

Here, you will use the dataset from Chapter 17, “Neural Data Analysis I: Encoding.” However, there is a second dataset for this chapter, available on the companion web site. The first dataset will be used to train the decoding algorithms, meaning these data are used to estimate the parameters of the model (such as preferred direction). The second dataset will be used to test the algorithm built using the first dataset. It is important not to test a prediction algorithm using the same data you trained with. Otherwise, the optimal prediction would be “the exact same thing is going to happen.” Testing on novel data helps ensure that the model does not overfit the data.

To compare the population vector method to the maximum likelihood method, you will need to bin the population vector to force it to assume one of the eight discrete directions. You can use the function histc in MATLAB to do this, though you should remember that the 0-degree direction will correspond to two bins: 0 to 22.5 degrees and 337.5 to 360 degrees.

You also need to define an accuracy metric for the predictions made. The percentage correct is the easiest to compute. However, the mean squared error may be more appropriate, as it penalizes large errors more than small errors.

21.3 Exercises

Exercise 21.1

Implementation

1. Implement a population vector decoder. Use the preferred directions determined for the training dataset. Predict the movement direction of the test dataset by using the firing rates during the hold period as weights. The hold period start times are stored in the variable instruction. The hold period ends 1 second after the start time. Bin the predicted direction to convert it to one of the eight discrete movement directions.

2. Implement a maximum likelihood decoder. Assume a Poisson firing rate model and independent firing rates. Determine the mean firing rate for each neuron and each direction for the training dataset. Use the function poisspdf to determine the likelihood of each direction. You might want to threshold the observed mean firing rates if they are below 1 spike/s or so to avoid unrealistically small probabilities. Pick the direction that maximizes the log-likelihood of all firing rates for a given trial.

3. Compare the accuracy of these two decoding methods, using a percent accuracy or mean squared error.

Exercise 21.2

Variations

1. The population vector methods make assumptions about the data: that neurons were cosine tuned and that preferred directions are uniformly distributed. Are these assumptions valid? Provide evidence for your answer.

2. Instead of weighting the response vectors using the firing rate, weight using the change in firing rate from baseline. Use the mean firing rate across all directions to determine the baseline firing rate. Does this affect the decoding accuracy? Why might this be?

3. Use a Gaussian firing rate model for the maximum likelihood decoder. The likelihood can be determined with the function normpdf and the mean and standard deviation for each neuron and each direction. Does this affect the decoding accuracy? Why might this be?

21.4 Project

Create a new decoder by either modifying the algorithms introduced here or by developing your own ideas. Report the accuracy of the new decoder as compared to population vector or maximum likelihood methods. Here are some suggested approaches:

Easy: Change the specific implementation of one of the decoders. For the population vector, create a new function to determine the weights from the firing rates. For maximum likelihood, use a different probability distribution as a firing rate model. Alternatively, try to include temporal coding by using principal components analysis or using smaller time bins.

Medium: Transform the data to make it conform to the assumptions made by decoders. For the population vector, change the weighting scheme of the population vector algorithm to compensate for a nonuniform distribution of preferred directions. For maximum likelihood, try to compensate for correlations between neurons, or between a neuron’s current firing rate and its past firing rates.

Hard: Create a new decoding technique. For example, the algorithms introduced treat firing rates as independent. More information might be available if firing rates are treated has a single vector. You could then use a distance metric to classify a novel vector of firing rates that falls into one of eight clusters (for each direction of movement). Using dimensionality reduction techniques (such as principal components analysis, covered in Chapter 19) might allow you plot the clusters in a low dimensional space.

MATLAB Functions, Commands, and Operators Covered in this Chapter

poisspdf

normpdf