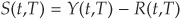. Recall that the price P(t,T) at time t of a risky zero-coupon bond maturing at T can be obtained byWe have so far focused on risk measurement and tried to estimate the key determinants of credit risk such as the probability of default and the recovery rate. We now turn to the important question of how credit risk is reflected in the prices of securities or in their yields.
The yield to maturity (YTM) is the annualized rate of return promised to an investor who buys a bond at the current market prices, holds the security until maturity, and reinvests the interim coupons at a rate equal to the YTM. YTMs are more intuitive than bond prices, as they enable investors to compare the rates of returns on instruments with differing maturities.
Yield spreads are the most widely used indicators of credit quality in the markets. A spread is defined as the difference between two yields. Sovereign spreads, for example, are obtained by taking the yield on a bond issued by a given country, say Germany, and subtracting it from the yield on a bond with the same maturity issued by another sovereign, for example Italy. Convergence trades based on sovereign spreads were particularly popular strategies among hedge funds in the late 1990s. They involved speculating on the narrowing of the spreads between the yields of southern European countries (Italy and Spain) and core members of the European Union such as Germany or France in the run-up to monetary union.
Being able to measure and model spreads accurately is important on several counts. First, a model for spreads and for riskless yields immediately provides a model for corporate bonds. Second, as we will see in Chapter 9, credit derivatives are becoming increasingly important financial instruments. Among this class of products, credit spread options are contingent claims whose payoffs depend on the value and behavior of spreads in the market. A spread model is therefore crucial for pricing these instruments. Third, from a risk management perspective, spreads are a key input of a ratings-based model of credit risk such as CreditMetrics (see Chapter 6). Finally, forward spreads serve to determine the possible future values of the various lines in a credit portfolio and therefore to calculate credit VaR.
Most of our discussion will focus on corporate spreads, which can be calculated as the difference between the yield on a risky corporate bond and the yield of an “equivalent” riskless Treasury bond. By “equivalent,” we mean a bond with the same maturity but also the same embedded options such as calls and puts and, ideally, the same coupon rate.
In this chapter we explain how to construct spreads from corporate and Treasury bond data. We then focus on the dynamics of U.S. credit spreads and discuss possible specifications for a stochastic model of spreads. The appropriateness of spreads as a proxy for credit risk relies on the ability to extract default probability and recovery rate from spreads. The study by Delianedis and Geske (2001), among others, has shown that only a small portion of investment-grade spreads (5 to 22 percent) can be attributed to default risk and has therefore raised doubts on the suitability of spreads to serve that purpose. We review what other factors can impact on yield spreads and how these factors can be proxied in empirical work. Finally we focus on the ability of models based on the value of the firm (structural models) to account for the observed dynamics and levels of spreads.
Corporate spreads are the difference between the yield on a corporate bond Y(t,T) and the yield on an identical but (default) riskless security R(t,T). T denotes the maturity date, and t stands for the current date.
The spread is therefore 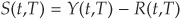. Recall that the price P(t,T) at time t of a risky zero-coupon bond maturing at T can be obtained by
Similarly, for the riskless bond B(t,T):
Therefore
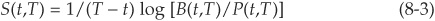
Thus, all else being equal, the spread widens when the risky bond price falls.
For the sake of simplicity, assume for now that investors are risk-neutral. In a risk-neutral world, an investor is indifferent between receiving $1 for sure and receiving $1 in expectation.
Thus, we must have 
, where L is the expected loss in default (1 minus the recovery rate) and p the probability of default. Therefore, using Equation (8-3), we get 
.
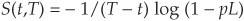The risk-neutral spread reflects both the probability of default and the recovery risk. In reality, of course, investors exhibit risk aversion, which will also be translated into spreads. We will review in some detail below the determinants of corporate spreads, but before we turn to the explanation of the dynamics and levels of spreads, we first focus on the calculation of spreads from the data.
In theory calculating spreads is very straightforward. One just has to compute the risky and riskless yields and take the difference. Unfortunately, in most cases, there will not exist a riskless bond with identical features to the corporate bond.
On many occasions a corporate bond will be associated with an underlying Treasury security with approximately the same maturity.2 Market practitioners would then calculate the spread as the difference between the two yields.
We will now present a way to calculate spreads on an entire cross-section of bonds (say, on a portfolio of U.S. straight corporate securities3) without assuming the knowledge of the specific underlying Treasuries.
Assume that:
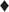We have a portfolio of N corporate bonds with maturity Ti, annual coupon rate Ci, for 
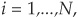and principal $100.
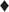We have a sample of n Treasury bills and bonds with maturities θj, annual coupon rate cj, for 
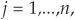and principal $100.
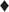minj 
mini Ti and maxj 
maxi Ti.
We start by stripping the Treasury curve,4 i.e., by calculating the yields of riskless zero-coupon bonds from the prices of coupon-bearing bonds. We then obtain n’ zero-coupon bond yields R(t, θk)5 with maturities spanning [minj θj, maxj θj].
As mentioned earlier, there will typically be a mismatch between the maturities of corporate and Treasury bonds in the sample. For the sake of accuracy we need to be able to interpolate the riskless yields in order to have a continuum of maturities and to calculate spreads for all Ti.
Many interpolation methods have been proposed in the literature,6 and an exhaustive review is beyond the scope of this book. One popular choice is the Nelson-Siegel procedure (Nelson and Siegel, 1987) described in Appendix 8A.
Once the entire yield curve is fitted, we can calculate riskless bond prices and yields with exactly the same maturity and coupon rate as the corporate bonds in our portfolio.
Recall that the price Bc(t,θ) of a coupon bond with annual coupon rate c (paid semiannually), maturity θ, and principal $100 can be obtained from the prices of zero-coupon bonds B(.,.) using
where g is the number of periods (half years) between t and θ.
From the entire set of “synthetic” riskless bonds generated above, we can then calculate the yields and finally the desired corporate spreads.
In this section we review the dynamics of credit spread series in the United States. The data consist of 4177 daily observations of Aaa and Baa average spread indices from the beginning of 1986 to the end of 2001. Spread indices are calculated by subtracting the 10-year constant-maturity Treasury yield from Moody’s average yield on U.S. long-term (> 10 years) Aaa and Baa bonds: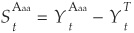 
and 
. All series are available on the Federal Reserve’s web site,7 and bonds in this sample do not contain option features.
Aaa is the best rating in Moody’s classification with a historical default frequency over 10 years of 0.64 percent, while Baa is at the bottom of the investment-grade category and has historically suffered a 4.41 percent default rate over 10 years (see Keenan, Shtogrin, and Sobehart, 1999). Both minima were reached in 1989 after 2 years of very low default experience. At the end of our sample, spreads were at their historical maximum, only matched by 1986 for the Aaa series. 2001 was branded by rating agencies the worst year ever in terms of the amount of defaulted debt. Summary statistics of the series are provided in Table 8-1.
TABLE 8-1
Summary Statistics for Spreads Data
Figure 8-1 depicts the history of spreads in the Aaa and Baa classes, and Figure 8-2 is a scatter plot of daily changes in Baa spreads as a function of their level. The Aaa series oscillates around a mean of about 1.2 percent, while the term mean of the Baa series appears to be around 2 percent.
FIGURE 8-1
U.S. Baa and Aaa Spreads—1986 to 2001
FIGURE 8-2
Daily Changes in U.S. Baa Spread Indices
Several noticeable events have affected spread indices over the past 20 years. The first major incident occurred during the famous stock market crash of October 1987. This event is remembered as an equity market debacle, but corporate bonds were equally affected, with Baa spreads soaring by 90 basis points over 2 days, the biggest rise ever (see Figures 8-1 and 8-2).
The 1991 Gulf War is also clearly visible on Figure 8-1. On the run-up to the war, Baa spreads rose by nearly 100 basis points. They started to tighten immediately after the start of the conflict, and by the end of the war, they had narrowed back to their initial level. Aaa spreads were little affected by the event.
Finally, let us mention the spectacular and sudden rises that occurred after the Russian default of August 1998 and after September 11, 2001.8
As we noted earlier, some events such as the Gulf War did substantially impact on Baa spreads while Aaa spreads were little affected. It is therefore interesting to focus on the relative spread between Baa and Aaa yields. Figure 8-3 is a plot of this differential, showing a clear downward trend between 1986 and 1998, only interrupted by the Gulf War. This contraction in relative spreads was due mainly to the improvement in liquidity of the market for lower-rated bonds.
FIGURE 8-3
Spread between Baa and Aaa Yields
We can observe three spikes in the relative spread (Baa–Aaa): 1991, 1998, and 2001. These are all linked to increases in market volatility, and the peaks can be explained in the light of a structural model of credit risk.
Recall that in a Merton-type model, a risky bond can be seen as a riskless bond minus a put on the value of the firm. The put’s exercise price is linked to the leverage of the issuing firm (in the simple case where the firm’s debt only consists of one issue of a zero-coupon bond, the strike price of the put is the principal of the debt). Obviously the values of Baa firms are closer to their “strike price” (higher risk) than those of Aaa firms. Therefore Baa firms have higher vega than Aaa issuers.9 As a result, as volatility increases, Baa spreads increase more than Aaa spreads.
In the pricing of credit derivatives such as credit spread options, it is important to be able to model the dynamics of spreads accurately. We also believe that dynamic models of credit spreads will be very important in the next generation of credit portfolio models (extensions of the CreditMetrics approach).
The main approach to spread modeling (see Lando, 1998, and Duffie and Singleton, 1999) consists of describing the default event as the unpredictable outcome of a jump process.10 Default occurs when a Poisson process with intensity λt jumps for the first time. λt dt is the instantaneous probability of default. Under some assumptions, Duffie and Singleton (1999) establish that default-risky bonds can be priced in the usual martingale framework11 used for pricing Treasury bonds. Hence the price of a credit-risky zero-coupon bond is
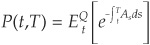
where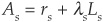 
.
Ls is the loss in default, and the second term therefore takes the interpretation of an expected loss (probability of default times loss given default). It can also be seen as an instantaneous spread, the extra return above the riskless rate. This approach is very versatile, as it allows us to price bonds and also credit-risky securities as discounted expectation under Q but with a modified discount rate. However. the instantaneous spread above does not translate into an explicit process for the spread of a given maturity, say 10 years, which is the variable of interest for some pricing purposes.
Another approach consists of a direct modeling of the spread process. It may be more appropriate if the focus is on the spread itself, for example in the pricing of spread options. Longstaff and Schwartz (1995b) choose a simple specification and implement it on real data. The main stylized fact incorporated in their model is the mean-reverting behavior of spreads: The logarithm of the spread is assumed to follow an Ornstein-Uhlenbeck process under the risk-neutral measure Q:
where the log of the spread is st with long-term mean θ and volatility σ. The speed of mean reversion is κ
Mean reversion is an important feature in credit spreads and has been found in Longstaff and Schwartz (1995b) and Prigent, Renault, and Scaillet (PRS, 2001). Interestingly the speed of mean reversion is not the same for Baa and Aaa spreads, for example. PRS provide a detailed parametric and nonparametric analysis of the credit spread indices described above and find that higher-rated spreads tend to revert much faster to their long-term mean than lower-rated spreads. A similar finding is reported on a different sample by Longstaff and Schwartz (1995b).
Another property of spreads is that their volatility tends to be increasing in their level. This is not captured by the model above. To tackle this, Das and Tufano (1996) suggest an alternative specification, similar to the Cox-Ingersoll-Ross (1985) specification for interest rates:12
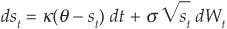
PRS keep a constant volatility but argue that spreads exhibit jumps, which is supported by observation of Figure 8-1. They therefore extend the model of Longstaff and Schwartz (1995b) in a different direction and incorporate binomial jumps13:
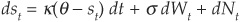
where Nt is a compound Poisson process whose jumps take either the value +a or −a (given that the specification is in logarithm, they are percentage jumps).
Jumps are found to be significant in both series (Aaa and Baa), and a likelihood ratio test of the jump process versus its diffusion counterpart strongly rejects the assumption of no jumps at the 5 percent level. Note that the size of percentage jumps in Baa spreads is about half that of jumps in Aaa spreads. In absolute terms however, average jumps in both series are approximately the same size because the level of Aaa spreads is about half that of Baa spreads.
We have seen earlier in this chapter that spreads should at least reflect the probability of default and the recovery rate. In a careful analysis of the components of corporate spreads in the context of a structural model, Delianedis and Geske (2001) report that only 5 percent of AAA spreads and 22 percent of BBB spreads can be attributed to default risk. We now turn in greater details to the possible components of an explanatory model for spreads.
The expected recovery rate for a bond of given seniority in a given industry is a natural candidate for inclusion in a spread model. Recoveries were discussed at length in Chapter 4; recall that they tend to fluctuate with the economic cycle. So ideally a measure of expected recovery conditional on the state of the economy would be a more appropriate choice.
Spreads should also reflect default probability. The most readily available measure of creditworthiness for large corporates is undoubtedly ratings, and they are easy to include in a spread model. Figure 8-4 is a plot of U.S. industrial and Treasury bond yields. Spreads are clearly increasing as credit rating deteriorates. The model by Fons (1994) provides an explicit link between default rates per rating class and the level of risk-neutral spreads. The main difficulty, as described in Appendix 8D, is to model the risk premium associated with the volatility in the default rate as market spreads incorporate investors risk aversion.
FIGURE 8-4
U.S. Industrial Bond Yield Curves (March 11, 2002)
A similar but dynamic perspective on the relationship between ratings and spreads is provided in Figure 8-5. We again observe what appears to be a structural break in the dynamics of spreads in August 1998. The post-1998 period is characterized by much higher mean spreads and volatilities for all risk classes. While the event triggering the change is well identified (Russian default followed by flight to quality and liquidity), analysts disagree on the reasons for the persistence of high spreads in the markets. Some argue that investors’ risk aversion has durably changed and that each extra “unit” of credit risk is priced more expensively in terms of risk premium. Others put forward the fact that asset volatility is still very high and that default rates have increased steadily over the period. Keeping unchanged the perception of risk by investors, spreads merely reflect higher real credit risk.
FIGURE 8-5
10-Year Spreads per Rating
An alternative explanation lies in the fact that the change coincided with the increasing impact of the equity market on corporate bond prices. The reasons for this are twofold: the recent popularity of equity–corporate bond trades among market participants and the common use of equity-driven credit risk models such as those described in Chapter 3.
In many empirical studies of spreads, equity volatility often turns out to be one of the most powerful explanatory variables. This is consistent with the structural approach to credit risk where default is triggered when the value of the firm falls below its liabilities. The higher the volatility, the more likely the firm will reach the default boundary and the higher the spreads should be. Several choices are possible: historical versus implied volatility, aggregate versus individual, etc. Implied volatility has the advantage of being forward-looking (the trader’s view on future volatility) and is arguably a better choice. It is, however, only available for firms with traded stock options. At the aggregate level, the VIX index, released by the Chicago Board Options Exchange, is often chosen as a measure of implied volatility. It is a weighted average of the implied volatilities of eight options with 30 days to maturity.
The second crucial factor of default probability in a structural approach is the leverage of a firm. This measures the level of indebtedness of the firm scaled by the total value of its assets. Leverage is commonly measured in empirical work as the book value of debt divided by the market value of equity plus the book value of debt. The reason for the choice of book value in the case of debt is purely a matter of data availability. A large share of the debt of a firm will not be traded, and it is therefore impossible in many cases to obtain its market value. This problem does not arise with the equity of public companies. If no information about the level of indebtedness is available or if the model aims at estimating aggregate spreads, then equity returns (individual or at the market level) can be used as a rough proxy for leverage. The underlying assumption is that book values of debt outstanding are likely to be substantially less volatile than the market value of the firms’ equity. Hence, on average, a positive stock return should be associated with a decrease in leverage and in spreads.
At the macroeconomic level, the yield curve is often used as an indicator of the market’s view of future growth. In particular a steep yield curve is frequently associated with an expectation of growth, while an inverted or flat yield curve is often observed in periods of recessions. Naturally default rates are much higher in recessions (see Figure 8-6). Therefore the slope of the yield curve can be used as a predictor of future default rates, and we can expect yield spreads to be inversely related to the slope of the term structure.
FIGURE 8-6
Default Rates and Economic Growth
There has been much debate in the academic literature on the interaction between riskless interest rates and spreads. Most papers (e.g., Duffee, 1998) report a negative correlation, implying that when interest rates increase (or decrease), risky yields do not reflect the full impact of the rise (or fall). Morris, Neal, and Rolph (1998) make a distinction between the negative short-term impact and the positive long-term impact of changes in risk-free rates on corporate spreads. One possible explanation for this finding is that risky yields adjust slowly to changes in the Treasury rate (short-term impact) but that in the long run an increase in interest rates is likely to be associated with a slowdown in growth and therefore an increase in default frequency and spreads.
The credit spread measures the excess return on a bond granted to investors as a compensation for credit risk. Measuring credit risk as the probability of default and the recovery is insufficient. Investors’ risk aversion also needs to be factored in.
If the purpose of the exercise is to determine the level of spreads for a sample of bonds, we can extract some information about the “market price of credit risk” from credit spread indices. Assuming that the risk differential between highly rated bonds and speculative bonds remains constant through time (which is a strong assumption), changes in the difference between two credit spread indices such as those studied earlier in the chapter should be the result of changes in the risk premium.
Many of the variables identified above are instrumental in explaining the levels and changes in corporate yield spreads. A similar analysis could be performed to determine the drivers of sovereign spreads such as that of Italy versus Germany or Mexico versus the United States. The fundamentals in these markets are, however, very different, and we could argue that trading or investment strategies in these various markets should be uncorrelated. This intuition would appear valid in most cases, but spreads tend to exhibit periods of extreme co-movement at times of crises.
To illustrate this, let us consider the Russian and LTCM crises in 1998. We have seen that the Russian default in August did push up corporate spreads dramatically. This was, however, not an isolated phenomenon. Figure 8-7 jointly depicts the spread of the 10-year Italian government bond yield over the 10-year Bund (German benchmark) on the right-hand scale and the spread of the Mexican Brady14 discount bond versus the 30-year U.S. Treasury on the left-hand scale.
FIGURE 8-7
Mexican Brady and ITL/DEM Spreads
Figure 8-7 is instructive on several counts. First it shows that financial instruments in apparently segmented markets can react simultaneously to the same event. In this case it would appear that the Russian default in August 1998 was the critical event.15
Second it explains partly why hedging, diversification, and risk management strategies failed so badly over the period from August 1998 through February 1999. Typical risk management tools, including value at risk, use fixed correlations among assets in order to calculate the required amount of capital to set aside. In our case the correlation between the two spreads from January to July 1998 was −11 percent. Then suddenly, although the markets are not tied by economic fundamentals and although the crisis occurred in a third market apparently unrelated, correlations all turned positive and very significantly so. In this example the correlation over the rest of 1998 increased to 62 percent.
Some may argue that the Russian default may just have increased default risk globally or that market participants expected spillover effects in all bond markets. Another explanation lies in the flight to liquidity and flight to safety observed over that period: Investors massively turned to the most liquid and safest products, which were U.S. Treasuries and German Bunds. Many products bearing credit risk did not seem to find any buyer at any price in the immediate aftermath of the crisis.
From a risk management perspective, it is sensible to consider that a global factor (possibly investors’ risk aversion) impacts across all bond markets and may lead to substantial losses in periods of turmoil.
Finally, and perhaps most importantly, yield spreads reflect the relative liquidity of corporate and Treasury securities. Liquidity is one of the main explanations for the existence of corporate yield spreads. This has been recognized early (see, e.g., Fisher, 1959) and can be justified by the fact that government bonds are typically very actively traded large issues, whereas the corporate bond market is an over-the-counter market whose volumes and trade frequencies are much smaller. Investors require some compensation (in terms of added yield) for holding less liquid securities.
In the case of investment-grade bonds, where credit risk is not as important as in the speculative class, liquidity is arguably the main factor in spreads. Liquidity is, however, a very nebulous concept, and there does not exist any clear-cut definition for it. It can encompass the rapid availability of funds for a corporate to finance unexpected outflows, or it can mean the marketability of the debt on the secondary market. We will focus on the latter definition. More specifically we perceive liquidity as the ability to close out a position quickly on the market without substantially affecting the price. Liquidity can therefore be seen as an option to unwind a position.
Longstaff (1995) follows this approach and provides upper bounds on the liquidity discounts on securities with trading restrictions. If a security cannot be bought or sold for, say, 7 days, it will trade at a discount compared with an identical security for which trading is available continuously. This discount represents the opportunity cost of not being able to trade during the restricted period. It should therefore be bounded by the value of selling16 the position at the best (highest) price during the restricted period. The value of liquidity is thus capped by the price of a lookback put option.
Little research has been performed on the liquidity of non-Treasury bonds. Kempf and Uhrig (1997) propose a direct modeling of liquidity spreads—the share of yield spreads attributable to the liquidity differential between government and corporate bonds. They assume that liquidity spreads follow a mean-reverting process and estimate it on German government bond data. Longstaff (1994) considers the liquidity of municipal and other credit-risky bonds in Japan. Ericsson and Renault (2001) model the behavior of a bondholder who may be forced to sell her position due to an external shock (immediate need for cash). Liquidity spreads arise because a forced sale may coincide with a lack of demand in the market (liquidity crisis). Their theoretical model based on a Merton (1974) default risk framework generates a downward-sloping term structure of liquidity spreads like those reported in Kempf and Uhrig (1997) and also in Longstaff (1994). They also find that liquidity spreads should be increasing in credit risk: If liquidity is the option to liquidate a position, then this option is more valuable in the presence of credit risk, as the inability to unwind a position for a long period may force the bondholder to keep a bond entering default and to face bankruptcy costs. On a sample of more than 500 U.S. corporate bonds, they find support for the negative slope of the term structure of liquidity premiums and for the positive correlation between credit risk and liquidity spreads.
On the empirical side, the liquidity of equity markets (and to a lesser extent also of Treasury bond markets) has been extensively studied, but very little has yet been done to measure liquidity premiums in default-risky securities. Several variables can be used as proxy for liquidity. The natural candidates are the number of trades and the volume of trading on the market. The OTC nature of the corporate bond market makes the data difficult to obtain. As second best, the issue amount outstanding can also serve as a proxy for liquidity. The underlying implicit assumption is that larger issues are traded more actively than smaller ones.
A stylized fact about bonds is that they are more liquid immediately after issuance and rapidly lose their marketability as a larger share of the issues becomes locked into portfolios. (See, for example, Chapter 10 in Fabozzi and Fabozzi, 1995). The age of an issue could therefore stand for liquidity in an explanatory model for yield spreads. In the same spirit, the on-the-run/off-the-run spread (the difference between the yields of seasoned and newly issued bonds with the same residual time to maturity) is frequently used as an indicator of liquidity. During the Russian crisis of 1998, which was associated with a substantial liquidity crunch, the U.S. long bond (30-year benchmark) was trading at a premium of 35 basis points versus the second longest bond with just a few months less to maturity, while the historical differential was only 7 to 8 basis points (Poole, 1998).
In order to conclude this nonexhaustive list of factors influencing spreads, we should mention taxes. In some jurisdictions (such as the United States), corporate and Treasury bonds do not receive the same tax treatment (see Elton, Gruber, Agrawal, and Mann, 2001). For example, in the United States, Treasury securities are exempt from some taxes while corporate bonds are not. Investors will, of course, demand a higher return on instruments on which they are taxed more.
We have reported that many factors impact on yield spreads and that spreads cannot be seen as purely due to credit. We will now focus more specifically on the ability of structural models to explain the dynamics and level of spreads.
In this section we describe how models based on the value of the firm (Merton-type structural models) can account for the level and dynamics of spreads.
There are four major difficulties in the implementation of structural models17 on real data. The first two sources of difficulty are not specific to firm-value-based models. They arise from the nature of the available data and from the very definition of yield spreads. As noted above, yield spreads are not pure credit spreads and will typically include many contractual features of the debt (options, sinking provisions, collateral, etc.), as well as a liquidity premium and, in some countries, a tax differential between private and public debt. As all these components are blended into the yield spread, it is very hard to extract the pure credit component. By construction, most structural models will tend to price only credit risk and to ignore the other factors. This explains the severe mispricing of early models (see below), particularly on investment-grade bonds where only a small portion of spreads is attributable to credit.
The second problem in testing corporate bond pricing models is the lack of corporate bond data. All empirical implementations have been performed on a limited number of databases, suffering either from low frequency or from a small number of bonds.
The two other main difficulties are specific to the structural approach. The first one originates from the estimation of the parameters of the firm value process and, in particular, the volatility (a key parameter in the model). Several approaches have been suggested to estimate this parameter, such as the use of the historical volatility of asset value changes. This is, however, not robust, as balance sheet data are available with low frequency and we have to estimate a variance with as little as 10 data points. As an alternative, we can use the implied volatility, which prices the equity of the firm perfectly.18 This relies on the underlying assumption that the equity pricing model is perfectly specified: In practice, all model misspecifications for the equity component will be reflected in the implied volatility. A third possibility is to calculate the volatility, which minimizes the quadratic error between observed prices and model prices over a given period. This typically leads to unrealistic values for the volatility.
Another source of problems for the structural model derives from the complexity of the capital structures of most firms. Structural models can at most cope with a simple capital structure with senior and junior debt and equity. A realistic capital structure may include five bond issues, some bank debt, trade credit, convertibles, preferred shares, etc. It therefore becomes necessary to aggregate the various instruments into a limited number of claims such as long-term and short-term debt and equity. These approximations no doubt impact on the accuracy of the pricing model. They can also be costly in terms of processing time.
Jones, Mason, and Rosenfeld (JMR, 1984, 1985) led the first studies into the empirical performance of structural models. These articles remained almost the only references for about 15 years and served to the detractors of structural models as proof of the failure of the contingent claim approach to corporate bond pricing.
JMR’s results were indeed very disappointing. The authors report, for example, an average pricing error of 6 percent, which led Fisher Black (1985) to comment: “I am surprised that JMR could create a model with such a large error. Surely an investment banker can price a new bond more accurately than that.” Note, however, that the significance of the empirical analysis of JMR has to be tempered by the small size of their sample (15 issuers and a total of 163 prices), by the complex capital structures implemented in their model (in particular, the number of covenants in the bonds), and by their choice of the simple Merton (1974) assumptions for the underlying default model. JMR’s test is therefore a joint test of the contingent claims approach and of their pricing model for the options embedded in the debt contracts.
A more optimistic contribution for firm-value-based models can be found in Sarig and Warga (1989), who study the U.S. term structures of credit spreads. They find a strong resemblance between observed term structures and those predicted by a Merton-type model for highly leveraged firms.
The following 10 years did not bring any major contributions in the empirical testing of structural models,19 but there has been renewed interest in this area over the past few years. An interesting contribution is that of Anderson and Sundaresan (2000), who estimate several structural models (including a strategic model20) on aggregate U.S. Aaa and Baa yield indices over the period 1970–1996. They obtain mixed results: A structural model seems able to explain large parts of the variation in yield spreads over some periods (1970–1979, for example), but spreads look completely disconnected to the fundamentals over other periods (e.g., 1980–1983).
The GS-spread model of Goldman Sachs is in a similar spirit (see Bevan and Garzarelli, 2000). Bevan and Garzarelli use a model inspired by Merton (1974) and estimate a “fair value” model for long-term Baa spreads using proxies for the corporate leverage and volatility at the macro level.
Both models above are estimated on aggregate, low-frequency data. Ericsson and Reneby (2001) estimate a firm-value-based model on individual bond data. They assume that the total debt of the firm can be modeled as a perpetual debt issue paying a continuous coupon. Their results are quite encouraging. In particular, they report no systematic bias (while most previous studies including JMR reported a systematic underestimation of spreads), much smaller pricing errors, and a satisfactory out-of-sample explanatory power. Among the observations made by Ericsson and Reneby (2001), there is the difficulty of pricing short-term debt accurately using a structural model. Their model indeed generates much larger residuals for short-dated bonds. Similar results have been reported by Bakshi, Madan, and Zhang (2001) in the context of a reduced-form model of credit risk. These results are compatible with a decreasing term structure of liquidity spreads as suggested by Ericsson and Renault (2001), but an alternative explanation lies in the impossibility of a diffusion model reaching a distant boundary in a short time interval.
The CreditGrades model of Riskmetrics is also based on the contingent claims approach and relies on further assumptions about the default boundary/recovery level to generate higher short-term credit spreads and tackle the criticism mentioned above. To do so, the bankruptcy barrier itself is assumed to be stochastic (following a lognormal distribution). A firm may therefore default at any time even if its asset value follows a standard diffusion process (a geometric Brownian motion with zero drift). The model can then be used to calculate default probabilities, credit spreads, or default swap rates.
We have shown that spreads include valuable information about the creditworthiness of corporates. Unfortunately, credit quality is far from being the only driver of spreads, and liquidity is sometimes more important, particularly in the investment-grade bracket. This leads to questioning the approach often adopted by banks to value loan prices on the basis of creditworthiness only. It might fail to track marked-to-market price dynamics. Commercial banks have indeed shown a tendency to price some facilities close to their actuarially fair value, without taking into account a liquidity premium or a level of risk aversion similar to those observed in the markets.
The procedure proposed by Nelson and Siegel (1987) consists of fitting the following nonlinear form through the observed yields R(.,.):
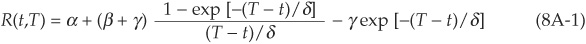
The parameter α takes the interpretation of the infinite maturity yield 
, while the instantaneous maturity yield is
Equation (8A-1) can also be written in terms of forward rates or bond prices. The set of parameters 
is estimated by minimizing the sum of the squared differences between observed yields and model yields. More formally, the estimate 
of Ω is obtained as
The Nelson-Siegel procedure is therefore easy to implement and parsimonious (only four parameters to estimate). It enables us to fit increasing, decreasing, and hump-shaped yield curves. Svensson (1994) has proposed an extension to the specification (8A-1), enabling the capture of term structures with two humps.
In many places in this book we encounter the concept of risk-neutral measure and of pricing by discounted expectation. We will now summarize briefly the key results in this area. A more detailed and rigorous exposition can be found, for example, in Duffie (1996).
Intuitively, the price of a security should be related to its possible payoffs, to the likelihood of such payoffs, and to discount factors reflecting both the time value of money and investors’ risk aversion.
Standard pricing models, such as the dividend discount models, use this approach to determine the value of stocks. For derivatives, or securities with complex payoffs in general, there are two fundamental difficulties with this approach:
1. Determining the actual probability of a given payoff
2. Calculating the appropriate discount factor
The seminal papers of Harrison and Kreps (1979) and Harrison and Pliska (1981) have provided ways to circumvent these difficulties and have led to the so-called fundamental theorems of asset pricing (FTAP).
First FTAP. Markets are arbitrage-free if and only if there exists a measure Q equivalent21 to the historical measure P under which asset prices discounted at the riskless rate are martingales.22
Second FTAP. This measure Q is unique if and only if markets are complete.
A complete market is a market in which all assets are replicable. This means that you can fully hedge a position in any asset by creating a portfolio of other traded assets.
The first fundamental theorem provides a generic option pricing formula that does not rely either on a risk-adjusted discount factor or on the necessity of finding out the actual probability of future payoffs. Assume that we want to price a security at time t whose random payoff g(T) is paid at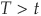 
. By no arbitrage, we know that at maturity the price of the security should be equal to the payoff 
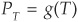. By the first FTAP we immediately get the price:
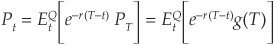
The probability Q can typically be inferred from traded securities. It is called the risk-neutral measure or the martingale measure.
The second theorem says that the measure Q (and therefore also security prices calculated as above) will be unique if and only if markets are complete. This is a very strong assumption, particularly in credit markets, which are often illiquid.
In this chapter we have already discussed structural models of credit risk, i.e., models in which the default event is explicitly related to the value of the issuing firm. One of the difficulties with this approach lies in the estimation of the parameters of the asset value process and the default boundary. For complex capital structures or securities with nonstandard payoffs such as credit derivatives, firm-value-based models are also cumbersome to deal with. Reduced-form models aim at making the pricing of these instruments easier by ignoring what the default mechanism is. In this approach, default is unpredictable and driven by a jump process: When no jump occurs, the firm remains solvent, but as soon as there is a jump, default is triggered.
In this appendix we first review the usual processes used in the pricing literature to describe default, namely Poisson and Cox processes. Once their main properties have been recalled, we give pricing formulas for default-risky bonds and explain some key results derived using the reduced-form approach. Finally we build on the continuous-time transition matrices reviewed in Appendix 2A of Chapter 2 to cover rating-based pricing models for bonds and credit derivatives.
The concepts recalled in this appendix are useful for understanding this chapter and are also useful for understanding credit derivatives in Chapter 9 and loss given default in Chapter 4.
Let Nt be a standard Poisson process. It is initialized at 0 
and increases by 1 unit at random times T1,T2,T3,. . . . Durations betweens jump times 
are exponentially distributed.
The traditional way to approach Poisson processes is to consider discrete time intervals and to take the limit to continuous time. Consider a process whose probability of jumping over a small time period Δt is proportional to time: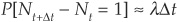 
and24 
. The constant λ is called the intensity or hazard rate of the Poisson process.
Breaking down the time interval [t,s] into n subintervals of length Δt and letting n → ∞ and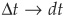 
, we obtain the probability of the process not jumping:
and the probability of observing exactly m jumps is
Finally, the intensity is such that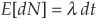 
. These properties characterize a Poisson process with intensity λ.
An inhomogeneous Poisson process is built in a similar way as the standard Poisson process and shares most of its properties. The difference is that the intensity is no longer a constant but a deterministic function of time λ(t). Jump probabilities are slightly modified accordingly:
and
Cox processes, or “doubly stochastic” Poisson processes, go one step further and let the intensity itself be random. Therefore, not only is the time of jump stochastic (as in all Poisson processes), but so is the conditional probability of observing a jump over a given time interval. Equations (8C-1) and (8C-2) remain valid but in expectation; they are replaced with
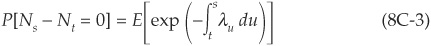
and
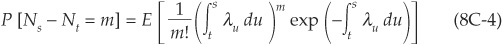
where λu is a positive-valued stochastic process.
We will now study the pricing of defaultable bonds in a hazard rate setting by assuming that the default process is a Poisson process with intensity λ. The case of Cox processes is studied afterward. We further assume that multiple defaults are possible and that each default incurs a fractional loss of a constant percentage L of the principal. This means that in case of default, the bond is exchanged for an identical maturity security with lower face value.
Let P(t,T) be the price at time t of a defaultable zero-coupon bond with maturity T. Using Ito’s lemma, we derive the dynamics of the risky bond price:
The first three terms in the equation above correspond to the dependence of the bond price on calendar time and on the riskless interest rate. The last term translates the fact that when there is a jump 
, the price drops by a fraction L.
Under the risk-neutral measure Q (see Appendix 8B), we must have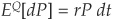 
and thus, assuming that the riskless rate follows
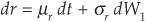
under Q, we obtain
Comparing this partial differential equation with that satisfied by a default-free bond B(t,T):
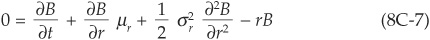
we can easily see that the only difference is in the last term and that if we can solve (8C-7) for B(t,T), the solution for the risky bond is immediately obtained as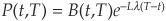 
. The spread is therefore Lλ which is the risk-neutral expected loss.
The example above is simplistic in many ways. The probability of default over an interval of given length is always constant because the intensity of the process is constant. This also implies that default risk and interest rates are not correlated.
A more versatile specification lets the hazard rate be stochastic with intensity λt, such that under the risk-neutral measure26:
and the instantaneous correlation between the two Brownian motions W1 and W2 is ρ.
The derivation closely follows that described above in the case of a Poisson intensity. We start by applying Ito’s lemma to the dynamics of the bond price:
We then impose the no-arbitrage condition: EQ[dP] = rP dt, which leads to the partial differential equation:
The solution of this equation of course depends on the specification of the interest rate and intensity processes, but again we can observe that the spread is likely to be related to Lλ.
Rather than solving Equation (8C-9) directly subject to appropriate boundary conditions, it is possible to derive the solution using martingale methods. It is the approach chosen by Duffie and Singleton (1999).
From the FTAP (see Appendix 8B), we know that the riskless and risky bond prices must, respectively, satisfy
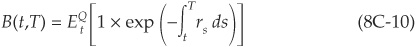
and
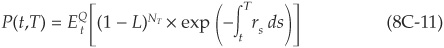
Equation (8C-11) expresses the fact that the payoff at maturity is no longer always $1, as in the case of the riskless security, but is reduced by a percentage L each time the process has jumped over the period [0,T]. NT is the total number of jumps before maturity, and the payoff is therefore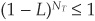 
.
Using the properties of Cox processes, we can simplify Equation (8C-11)27 to obtain
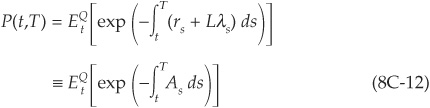
Equation (8C-12) is extremely useful, as it signifies that we can use the familiar Treasury bond pricing tools to price defaultable bonds as well. We just have to substitute the risk-adjusted rate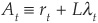 
for the risk-less rate, and all the usual formulas remain valid. Similar formulas can be derived for defaultable securities with more general payoffs.
The seminal article in the rating-based class is Jarrow, Lando, and Turnbull (JLT, 1997). We review their continuous-time pricing approach and then mention two other articles that have removed some of the original assumptions from the JLT model.
The model by Jarrow, Lando, and Turnbull (1997) considers a progressive drift in credit quality toward default and no longer a single jump to bankruptcy, as in many intensity-based models. Recovery rates are assumed to be constant, and default is an absorbing state.
JLT assume the availability of riskless and risky zero-coupon bonds for all maturities and the existence of a martingale measure Q equivalent to the historical measure P. In the remainder of the appendix we work directly under Q.
Appendix 2A in Chapter 2 describes in detail how to calculate a continuous-time transition matrix, which is the main tool in the JLT model. We will not recall that here. JLT assume that the transition process under the historical measure is a time-homogeneous Markov chain with K nondefault states (1 being the best rating and K the worst) and one absorbing default state (K + 1).
The risk-neutral transition matrix over a given horizon h is
where, for example,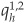 
denotes the risk-neutral probability of migrating from rating 1 to rating 2 over the time period h.
Transition matrices for all horizons h can be obtained from the generator28 matrix Λ:
via the relationship 
. Over an infinitesimal period dt, 
, where I is the 
identity matrix.
Let B(t,T) be the price of a riskless zero-coupon bond paying $1 at maturity T, with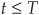 
. It is such that
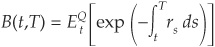
Pi(t,T) is the value at time t of a defaultable zero-coupon bond with rating i due to pay $1 at T. In case of default (assumed to be absorbing in the JLT model), the recovery rate is constant and equal to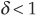 
. The default process is assumed to be independent from interest rates, and the time of default is denoted as τ. Finally, let 
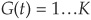be the rating of the obligor at time t.
The price of the risky bond therefore is
Given that the default process is independent from interest rates, we can split the expectations into two components:
where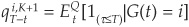 
is the probability of default before maturity T for an i-rated bond.
Looking at the formula for yield spread [Equation (8-3) in the main part of this chapter], we can observe that the term structure of spreads is fully determined by the changes in probability of default as T changes. We return to spreads further below.
The main comparative advantage of a rating-based model does not reside in the pricing of zero-coupon bonds for which the only relevant information is whether or not default will occur before maturity. JLT-type models are particularly convenient for the pricing of securities whose payoffs depend on the rating of the issuer. Some credit derivatives are written on the rating of specific firms, for example derivatives compensating for downgrades.29 More commonly, step-up bonds whose coupon is a function of the rating of the issuer can also be priced using rating-based models.
We will consider a simple example of a European-style credit derivative based on the terminal rating G(T) of a company. We assume that its initial rating is 
and that the derivative pays nothing in default. The payoff of the derivative is Φ[G(T)], and its values are known conditional on the realization of a terminal rating G(T).
From the FTAP, the price of the derivative is
Given that the rating process is independent from the interest rate, we can write
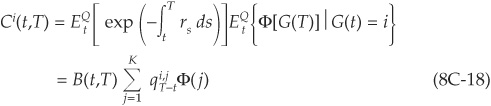
Let
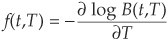
be the riskless forward rate agreed at date t for borrowing and lending over an instantaneous period of time at time T. It is such that 
.
The risky forward rate for rating class i is [from Equation (8C-16)]:
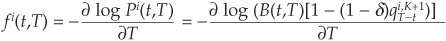
Hence
The credit spread in rating class i for maturity T is defined as 
. From Equation (8C-19) we can indeed observe that spread variations reflect changes in the probability of default and changes in the steepness of the curve relating the probability of default to time T.
In order to obtain the risky short rate, we take the limit as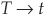 
and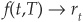 
:
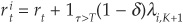
which immediately yields the spot instantaneous spread as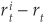 
.
The specificity of the model by Das and Tufano (1996) is to allow for stochastic recovery rates correlated to the riskless interest rate. A wider variety of spreads can be generated due to this flexibility. In particular, the model includes these features:
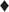Credit spreads can change although ratings are unchanged. In the JLT model, a given rating class is associated with a unique term structure of spreads, and all bonds with the same maturity and rating are identical.
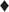Spreads are correlated with interest rates.
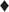Spreads are “firm-specific” and not just “rating class–specific.”
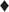The pricing of credit derivatives is facilitated.
While the JLT model assumed that recovery in default was paid at the maturity of the claim,30 Das and Tufano (1996) assume that recovery is a random fraction of par paid at the default time τ. We discussed the various recovery assumptions in Chapter 3.
Arvanitis, Gregory, and Laurent (1999) extend the JLT model by considering nonconstant transition matrices. Their model is “pseudo non-Markovian” in the sense that past rating changes impact on future transition probabilities. This conditioning enables the authors to replicate much more closely the observed term structure of spreads.
In particular, their class of models allows for correlations between default probabilities and interest rate changes, correlation of spreads across credit classes, and spread differences within a given rating class for bonds that have been upgraded or downgraded.
The model by Fons (1994) is an early attempt to model credit spreads using a reduced-form approach. Assuming risk neutrality, the author uses historical default and recovery rates published by Moody’s to derive fair value spreads per class of rating.
In this appendix we review the original specification of the model and suggest ways to incorporate risk aversion. We also update Fons’s empirical results using Standard & Poor’s CreditPro database.
We have seen earlier in the chapter that the two determinants of spreads in a frictionless and risk-neutral world are the probability of default and the recovery rate. As described in Chapter 4, the recovery rate depends on many factors such as the state of the economy and the seniority of the facility. We will now focus on probabilities of default at various horizons per rating class. The first step is to derive marginal default probabilities for all rating classes. For all bonds in the rated universe, we record their rating at the beginning of each year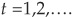 
Then we observe whether the bond defaults in the first year after t or in the second, third, and so on until the end of the period covered by our sample.
Marginal probabilities for a given year are computed in a similar way as in Appendix 2A in Chapter 2. For example, the sample-weighted marginal default rate in rating i at horizon h is31
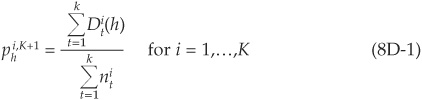
Repeating the calculations for all rating classes and all horizons provides a series of term structures of marginal default probabilities.
The survival rate, i.e., the probability of not defaulting before time h, for bonds in rating i can be calculated as
where D is the cumulative default rate. The probability of defaulting exactly in year h (and not before) is thus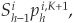 
which is the probability of not defaulting before year h times the probability of defaulting in year h. This probability is instrumental in the bond pricing formula to which we now turn.
Equation (8D-3) below is the price at time 0 of an i-rated risky bond with principal $1 paid at time θ. The security also pays an annual coupon ci if the bond is not in default. In case of default at time h, the recovery rate is δh.
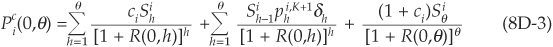
with R(0,h) denoting the yield on a riskless bond with maturity h.
The interpretation of Equation (8D-3) is straightforward. The first term is the sum of the discounted interim cash flows, i.e., coupons weighted by their probabilities of occurrence. The probability of a given coupon being paid at time h is the survival probability until h. The second term is the discounted value of recoveries in default multiplied by the probabilities of default occurring in each specific year. The third and final term is the discounted value of the last cash flow (coupon and principal) times the probability of not defaulting until maturity θ.
The credit spread for maturity θ in rating class i can then be calculated as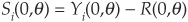 
, where 
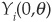is the yield on the risky bond. Assuming that the risky bond is priced at par implies that the coupon rate is equal to the yield and that the spread takes the simpler form:
The required inputs for the model therefore are
Marginal default rates for all maturities and all rating classes
A riskless term structure of interest rate
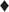Average recovery rates for all rating categories
Figures 8D-1 and 8D-2 are plots of credit spreads calculated with the above methodology using the CreditPro database with data covering the period 1981–2001. The average recovery rate is assumed to be 50 percent.
FIGURE 8D-1
U.S. Actuarial Spreads (BB, B, CCC)
FIGURE 8D-2
U.S. Actuarial Spreads (AA, A, BBB)
Actuarial spreads for high-quality bonds with short maturities are zero because the probability of default is also zero. The shape of the CCC spread curve is particularly striking. It is a convex curve reflecting the fact that marginal probabilities of default at short horizons are very high and quickly decrease. This shape is consistent with the Merton (1974) model for firms with very high leverage.
The main drawback with Fons’s specification is that the investor is assumed to be risk-neutral. Spreads therefore tend to be much lower than those observed in practice. Banks may nonetheless want to use this approach to mark their positions to market by approximating a term structure of spreads for industries with too few issuers per maturity bracket. We thus need a methodology to extract the risk aversion parameter.
If investors are not risk-neutral, Equation (8D-1) must be replaced with
where s is the risk-neutral survival probability and q is the risk-neutral marginal probability of default. We can assume that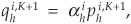 
where 
is constant (and > 1 because of risk aversion), or impose some more restrictions, such as 
(constant risk adjustment for all rating categories) or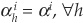 
(constant risk adjustment for all periods in a given rating class).
Then it is possible to extract the α parameters from a cross-industry sample using an average recovery rate (δ) and to extrapolate industry-specific spread curves by selecting an industry-specific recovery rate and assuming that investor’s risk aversion is the same across industries.
The entire process for calculating “fair value” spreads is summarized in Figure 8D-3.
FIGURE 8D-3
Process to Calculate Fair Value Spreads
In this book we have mainly focused on historical probabilities of default, i.e., probabilities estimated on objective data. However, for pricing purposes (for the calculation of spreads), we need to estimate risk-neutral probabilities. In this appendix we show a customary way to obtain spreads from historical probabilities: A similar calculation is used by KMV and many banks (see, e.g., McNulty and Levin, 2000).
Recall that the cumulative default probability (historical probability) for a firm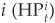 
is defined as the probability of default at the horizon t under the historical measure P. In the KMV model this corresponds to their EDF.
We now introduce the risk-neutral probability 
which is the equivalent probability under the risk-neutral measure (see Appendix 8B). Under Q, all assets drift at the risk-free rate, and thus we should substitute r for µi in the dynamics of the value of the firm.32
The formulas for the two cumulative default probabilities are therefore
and
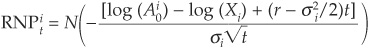
where:
N(.) = the cumulative standard normal distribution
Ai0 = the firm’s asset value at time 0
Xi = the default point (value of liabilities)
σi = the volatility of asset values
µi = the expected return (growth rate) on asset values
r = the riskless rate
The expected return on asset includes a risk premium, and we must therefore have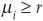 
and thus
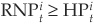
Writing the risk-neutral probability of default as a function of 
we obtain
According to the capital asset pricing model (CAPM—see, e.g., Sharpe, Alexander, and Bailey, 1999), the risk premium on an asset should depend only on its systematic risk measured as the covariance of its returns with the returns on the market index.
More precisely, for a given firm i with expected asset return µi, we have
where E(rm) is the expected return on the market index and πt is the market risk premium.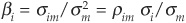 
is the measure of systemic risk of the firm’s assets, where σm, σim, and ρim are, respectively, the volatility of the market and the covariance and correlation of asset returns with the market.
Using these notations, the quasi probability becomes
We now want to calculate spreads in terms of risk-neutral probabilities of default. Let PC(t,T) be the value at time t of a T-maturity risky coupon bond paying a coupon C (there are n coupon dates spaced by Δt years). We assume that the principal of the bond is 1 and that the value recovered in case of default is constant and equal to R.
We have33
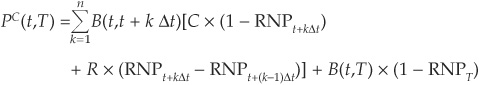
Spreads can then be calculated as shown earlier in the chapter by comparing the price of the risky coupon bond to that of a riskless bond as given by Equation (8-4), for example.
