
How can we push back our opponent in a rugby tackle if the studs on their boots are anchoring them to the ground?

By the end of this chapter you should be able to:
•Define the term ‘friction’ and identify the different forms of it
•Explain the factors affecting friction, be able to manipulate them and measure their effects in order to improve sporting performance
•Design a simple model using a spreadsheet to directly assess the effects of changing the direction of force application on friction and the ability to move an object (or opponent)
If you could select the one force that is the most important for your everyday life, what would it be? Muscle force, without which it would be hard for you to move? Or gravitational force, without which we would fly into space every time we produced a vertical force? I think neither of these. For example, an octopus has no muscles but uses fluid flow through its limbs to produce movements, and spiders and caterpillars make effective use of their silk anchors to counter gravity. Surely we too would have developed strategies to account for a lack of muscles or gravitational forces.
I think the one force we can’t do without is friction. Friction is the force that opposes the movement of two surfaces that are in contact with one another. It occurs when either micro- (very, very small) or macroscopic (big enough to see) bonds form between two surfaces (Figure 12.1).
You can investigate the friction force yourself by slowly applying a horizontal force to a coffee mug sitting on a flat table. A small friction force develops when you apply a small force, preventing the mug from moving. As you increase the force you are applying, the friction force increases until, at a specific force level, the mug starts to move. The exact force that opposed motion just before the mug started to slide is called the force of static friction. Once the mug is moving, you’ll notice that you need less force to keep it moving, even though there is still friction present. This smaller friction force is called the force of sliding friction, or sometimes kinetic friction. If we didn’t have friction, silk anchors wouldn’t work and there would be no point in developing a way to function without muscles because we could never apply our force to anything anyway. Without friction, we couldn’t live.
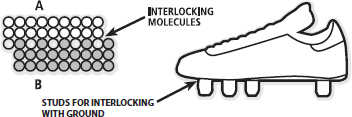
FIG. 12.1 Friction results from an interlocking, or formation, of ‘bonds’ between molecules (A) or uneven surfaces (B). Increases in interlocking results in an increased friction between the two surfaces. The tendency for two surfaces not to slide past each other is quantified by the coefficient of friction.
Football and rugby players use studs on their boots to increase the friction between the playing surface and their feet. Studs make it possible to apply large forces to the ground without the foot sliding. In this case, where there is an interlacing of large surfaces, we often use the term ‘traction’. This is slightly different from friction, where the surfaces themselves create the force. In rugby we have to overcome the traction present between the boot and ground when we want to push another player backwards; of course, it is easier to keep them sliding (sliding friction/traction) than it is to start them sliding in the first place (static friction/traction). To work out the best way to do this, we have to understand the factors that influence friction and traction; in this book, we’ll specifically discuss the factors affecting friction.
The coefficient of friction
The coefficient of friction is represented by the Greek letter µ (mu) and describes the tendency for two contacting surfaces to not slide past each other. For example, the coefficient of static friction between an ice skate and the ice is about 0.03, while the coefficient of friction between two iron plates is 1.0. Unlike the coefficient of restitution, the coefficient of friction can be greater than one, as you can see from Table 12.1. Box 12.1 describes how to measure the coefficient of friction but for now you should just understand that a larger number means there is less of a tendency for two surfaces to slide past each other.
BOX 12.1 MEASUREMENT OF THE COEFFICIENT OF FRICTION
Measurement of the coefficient of friction can be performed in several ways. One way is to slowly apply a horizontal force to an object (such as the shoe in Figure 1) coated with a particular surface that is on a force platform covered in the other surface of interest. As you apply a greater horizontal force to the shoe, the force measured on the platform increases. At a certain point, the object will begin to move and the measured force will drop suddenly. The peak horizontal force measured is the static friction force. If you know the weight (i.e. the normal reaction force – mass in kg × 9.81) of the object, you can calculate the coefficient of friction by re-arranging the equation Ff = µR to µ = Ff /R (see here), where µ is the coefficient of static friction, Ff is the force of friction and R is the normal reaction force.

FIG. 1
If you continue to push the object at a constant rate, the horizontal force will also be constant (but lower than the peak you discovered earlier). This is the force of sliding friction. You can therefore calculate the coefficient of sliding friction in the same way.
If you don’t have access to a force platform, there is a very simple, although mathematically slightly more complex, method to calculate the coefficient of friction. Take an object, such as a square block of wood, and apply your chosen surface to it; apply a second surface to a flat plank of wood or a metal bar. When the plank (with the square block on top of it) is horizontal, the normal reaction force (R) is at a maximum but the horizontal force causing sliding is nil. Tilt the plank: as it tilts, the force of gravity – to be totally accurate, its tangential (parallel to the plank) component – increases, while the normal reaction force decreases. At a certain angle of the plank, the block will start to slide.
You can work out the normal reaction force and friction (that is, tangential to the plank) using the basic cos/sin rules. When you have these, you can use the equation above. You could use this technique to examine the effects of heating and cooling of rubber shoes on their frictional properties, what effect dust has on a court surface or how the waxing of indoor courts affects friction.

FIG. 2
Material 1 |
Material 2 |
µ (static) |
µ (sliding) |
Aluminium |
Aluminium |
1.15 |
1.4 |
Bone joints |
|
- |
0.003 |
Car tyre |
Asphalt (dry) |
- |
0.5–0.8 |
Car tyre |
Asphalt (wet) |
- |
0.25–0.75 |
Car tyre |
Grass |
- |
0.35 |
Ice |
Ice |
0.05–0.50 |
0.02–0.09 |
Ice |
Steel |
- |
0.03 |
Iron |
Iron |
1.0 |
- |
Rubber |
Concrete |
- |
1.02 |
Rubber |
Rubber |
- |
1.16 |
Skin |
Metals |
0.8–1.0 |
- |
Teflon |
Steel |
0.2 |
- |
Teflon |
Teflon |
0.04 |
- |
Tendon sheath |
|
- |
0.0013 |
Wood |
Wood |
0.28 |
0.17 |
TABLE 12.1 Coefficients of static and sliding friction for some common materials. Actual values depend on the precise conditions of the materials, so these values are for reference only.
The second thing you should understand is that there are two different coefficients for a pair of surfaces, because there are two main types of friction: the coefficient of static friction (µ) and the coefficient of sliding friction (µs)*. Remember that it took less force to keep the coffee mug moving than it took to move it in the first place? That’s because the coefficient of static friction is greater than that of sliding friction. For example, µ for two hard steel plates is about 0.78 but µs is 0.42. This is probably because strong bonds are less likely to form between two surfaces moving over each other but are very likely to form when they are stationary.
The coefficient of friction tells us something about the characteristics of the surfaces involved. Rugby and football boots have studs that increase the coefficient of friction (or, in fact, traction). The coefficient would be less on wet, muddy ground, where it is easy to slide and greater on dry, firm ground but it is very hard for us to influence it (at least in the opposing player). If we are going to reduce friction to push our opponent backwards, we need to look elsewhere.
Normal reaction force
Try this experiment:
Lightly place one open hand on top of the other, palm-to-palm, as shown in Figure 12.2. Slowly drag one hand past the other. Notice it is easy? Now, push your hands together as hard as you can and try to slide one past the other. It’s much harder (or impossible if you’re pushing your hands together hard enough). The force pushing one surface onto the other influences the friction between them. Since the force that pushes the surfaces together acts perpendicular to the surfaces, we call it the normal force; remember ‘normal = ninety degrees’. (By the way, a tangential force acts parallel or in line with – or we might say at a tangent to – the surface.)
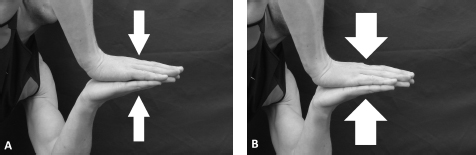
FIG. 12.2 When the hands are pressed only lightly together and the normal reaction force is small (A), friction is less so the hands slide across each other easily. When the hands are pressed firmly and the normal reaction force is large (B), the friction force is large and the hands do not slide.
So, the force of friction is dictated by two factors: (1) the coefficient of friction, which tells us something about how ‘sticky’ two surfaces are, and (2) the normal reaction force, which tells us how hard the two surfaces are being pressed together. We could describe the relationship thus:
Ff = µR
Where Ff is the friction force, µ is the coefficient of friction and R is the normal force, which is a reaction force, just as you saw in Chapters 4 and 5. What this means is that if you were given the coefficient of static friction and the normal reaction force, you could calculate the force required to start the surfaces moving across each other. If you were given the coefficient of sliding friction, you could calculate the force required to keep them moving. The important thing to remember is that the force holding two objects together is always the normal reaction force. If the force is measured at an angle to the surfaces, you have to find out the magnitude of the normal component of it, as shown in Figure 12.3.
FIG. 12.3 In picture (A), the force of friction between the sled at the ground can be calculated using the formula Ff = µR. The normal reaction force, R, is the opposite of the weight force (650 N) and the coefficient of static friction is shown (0.44).
Ff = µR
= 0.44 × 650 N
= 286 N
In picture (B), we have to calculate the force pushing the sled into the ground, the normal reaction force (dotted arrow). To do this, we use the cosine rule outlined in Appendix A (notice that the angle between the solid and dotted arrows is the same as the angle of the sloping ground, so as the angle of the sloping ground increases so too does the angle between the solid and dotted lines).
cos 30° = R/650 N
R = cos 30° × 650 N
= 0.866 × 650 N
= 562.9 N
We can then calculate Ff as above:
Ff = µR
= 0.44 × 562.9 N
= 247.7 N
So on a 30° slope, the friction force is 38.3 N less.
BOX 12.2 A HINT FOR CONSTRUCTING TRIANGLES
It might not be difficult to use the cos/sin/tan rules to calculate the magnitude or direction (i.e. angle) of a force or velocity vector. But it can be very difficult at times to construct the appropriate right-angled triangle in the first place. Take the example in Figure 12.3B. In that example you had to realise that the long side of the triangle (the hypotenuse) was the solid line and that R was the dotted line.
A very important, but simple, rule is that the hypotenuse of the triangle, which is the longest side, always represents the largest possible vector magnitude (i.e. largest force or fastest velocity). So in Figure 12.3B you know that the solid line should be the hypotenuse because gravity always acts straight down and therefore the vertical force must be the largest possible force. The effect of gravity then diminishes as we move away from vertical. You can see this effect in Figure 1 below, where the magnitude of the dotted vector decreases as the angle from vertical increases.
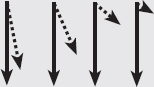
FIG. 1 If an object is falling with gravity, the force of gravity (and acceleration of the object) will always be greatest in the vertical plane. Therefore, the hypotenuse of a right-angled triangle is always drawn vertically (solid arrow). The magnitude of a vector at any angle from vertical will always be less, with the magnitude decreasing with increasing angle (dashed arrows).
This is also the same for other vectors. For example, you might want to know the vertical velocity of a ball thrown at a 45° angle. Since the ball was thrown at 45° then the velocity must have been maximal in this plane. At any other angle, the velocity would be less, so of course the vertical velocity must be drawn with a shorter arrow, as shown in Figure 2. This arrow is drawn so that it makes a triangle with the hypotenuse (I’ve drawn a thin line to complete the triangle). In this case, the magnitude of the dashed arrow (i.e. vertical velocity), which is adjacent to the angle, is found using the cosine rule (cos = adjacent/hypotenuse).
FIG. 2 If a ball is thrown at 45° to the horizontal, the hypotenuse of the triangle is placed along its path (solid arrow). The vertical velocity must be represented by a shorter (dashed) arrow. The vertical velocity can be found, in this case, using the cosine rule.
Knowing the coefficient of friction doesn’t really help solve our problem but it does help to know that the force pressing the two surfaces together is a major factor. The only force pressing the surfaces of the boot and ground together is the weight force of the player (mass × gravity), so friction, or traction, is less if the player’s mass is lower. We might not be able to reduce the actual mass of the opponent but we can apply an upward force to them to reduce the normal reaction force (that is, their effective mass). Providing an upward force (‘driving into your opponent’) during a tackle will increase the likelihood of them being pushed backwards. This isn’t a new idea, indeed Guillaume Amontons (1663–1705) first described the relationship between the force pushing two surfaces together and their resistance to movement more than 300 years ago.
But can we get an idea of the angle at which we might need to push? Is it likely to be a small angle, such as 5°, or do we need to lift at 60°? We can construct a simple model to find the answer.
THE (SECOND, MORE SPECIFIC) ANSWER
First, we need to think about how to tackle the problem (excuse the pun). We know how to calculate the force of friction if we have the coefficient and the weight (normal reaction force) of the player, so we’ll definitely need columns in our spreadsheet for these. We’ll also need to have an idea of how much force the tackler might be able to produce, so I took a rugby player to the gym to measure his best squat lift. It was 200 kg, so I’ll assume that if he is lifting a load (his opponent) with two legs, he could produce about 2000 N of force (200 kg × 9.81m·s-2 = 1960 N, so that’s a pretty good estimate). We then need some columns to calculate the effect of the angle of the push on the horizontal and vertical forces our player generates; as he lifts upwards at a greater angle his horizontal force will decrease while his vertical force will increase. Finally, we will need to calculate the normal reaction force, which will be equal to his body weight minus the vertical force exerted by the tackler. The smallest angle at which the tackler can push his opponent backwards will be found when the horizontal force exerted by the player is greater than the force of friction (remember, if you didn’t quite follow what you just read, re-read it slowly before moving on!).
I constructed the spreadsheet as below:
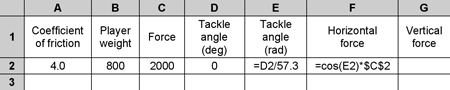

Basic values are placed in columns A to D. The tackle angle is converted to radians in column E, before the horizontal and vertical components of the player’s force are calculated, using basic cos/sin rules, in F and G. (Remember, ‘$’ means ‘fix this reference’, so ‘$C$2’ means ‘fix reference to column C2’.) The corrected weight in column H subtracts the vertical force exerted by the tackler from the opponent’s body weight, to calculate the normal reaction force.
We can thus calculate the force of friction in the usual way in column I. You might have noticed something new in column J; a calculation based on the logical function ‘IF’. This function will return ‘Yes’ if the horizontal force (F2) is greater than Friction (I2). This makes it easier to see whether the tackler would be able to push his opponent backwards. The output looks something like this:
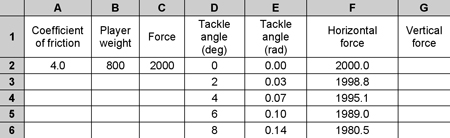
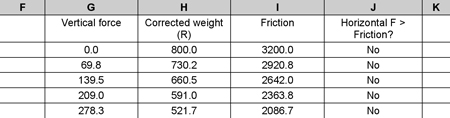
I used a coefficient of friction of 4.0, since this is the highest value I’ve seen for rubber on a solid surface. I made a guess that the boots were ‘rougher’ than rubber but the ground was ‘less rough’ than a normal high-friction solid surface. Ideally, I would have performed an experiment, such as that outlined in Box 12.1. However, I created a graph from my results; see Figure 12.4.
FIG. 12.4 Graph of changes in vertical (normal) reaction force and friction with the change in angle of force provision in the tackle for our experiment.
From this, you can tell that the horizontal force is not reduced much as the tackle angle increases (up to 20°) but there is a dramatic effect on friction. The horizontal force exerted by the player was greater than the friction force of the opponent at about 9° (vertical line on graph). This is a reasonably small angle. While there are a few limits to this type of modelling (we should have accurate measures of the friction coefficient, for example), it at least gives us some idea of the angle to push to limit the effect of friction. There doesn’t seem to be a need to lift our opponent at large angles to reduce the friction of the boots on the ground. So, to push our opponent backwards in the tackle, we should push them backwards and slightly upwards. How do you think the angle of tackle changes for lighter players or when the coefficient of friction is smaller?
HOW ELSE CAN WE USE THIS INFORMATION?
We can use our understanding of friction to improve performance in many sports. We can try to optimise the friction between shoes and court surfaces to improve performance and reduce injury risk, as outlined in Box 12.3. We can use lubricants to minimise friction between clothing and skin, to prevent abrasion injuries. Very importantly, we can use the friction force to impart spin to balls to alter their trajectory (see Chapter 16) and use methods of reducing friction between the skin and air (see Chapter 13) or water (see Chapter 14) to reduce drag and improve speed in other sports. A great example is that dancers, and in particular ballet dancers, rub rosin on their shoes. Rosin increases the coefficient of static friction markedly without significantly affecting sliding friction, so that dancers are stable when stationary but can still perform pirouettes. In the end, your imagination is the limiting factor on how you can use this information to improve sporting performance.
BOX 12.3 IS GREATER FRICTION BETTER FOR PERFORMANCE SPORTS?
We need friction, for example between shoes and a playing surface so that we can stop, change direction or accelerate rapidly. If we slide as we change direction, the time it takes is increased. Also, if the foot slides too far, there is an increased injury risk as the muscles are stretched more. Is it true to say that more friction is better? Probably not, from the point of view of injuries.
Research indicates that injury rates are lower on surfaces of lower friction (for example clay tennis courts as opposed to hard courts) (e.g. Nigg & Segesser, 1988). This probably happens because a sliding foot allows energy to dissipate and consequently the speed of the foot will be lower immediately before the foot stops completely. Lower velocity means lower momentum, so at the point of stopping there is less momentum (that is, a smaller change in momentum from just before stopping to stopping). Since the contact point between the foot and the surface is a pivot point around which the foot can roll, having a smaller momentum before stopping makes it less likely this rolling will occur (see Figure 1). This is because the muscles and connective tissues of the ankle will be more likely to cope with the forces produced during the momentum change. Also, the rate of application of the force will be slower, so the muscles and connective tissues are less likely to be ruptured. Thus, surfaces with lower friction are usually safer than surfaces with high friction.
Playing surfaces should therefore have moderate, safe levels of friction. Since athletes vary in size and therefore their normal reaction forces vary significantly, the best surface (or shoe) type for one player might not be the best for another.

Useful Equations
speed = ∆d/∆t
velocity (v) = ∆s/∆t (rω for a spinning object)
acceleration (a) = ∆v/∆t
momentum (p) = m × v
conservation of momentum: m1v1 = m2v2
impulse (J) = F × t or mv
coefficient of variation (CV) = SD/mean × 100%
sine rule: sin θ = opposite side/hypotenuse
cosine rule: cos θ = adjacent side/hypotenuse
tan rule: tan θ = opposite side/adjacent side
Reference
Nigg, B.M. & Segesser, B. (1988). ‘The influence of playing surfaces on the load on the locomotor system and on football and tennis injuries’. Sports Medicine, 5(6): 375–85.
Hyperphysics (http://hyperphysics.phy-astr.gsu.edu/hbase/frict2.html). Basic and advanced discussions on the topic of friction, including maths simulations and calculations.
The Physics of Sports (http://www.topendsports.com/biomechanics/physics.htm). Website investigating the applications of physics in sports.
* Actually, there are three coefficients because, in addition to static and sliding friction, there is also rolling friction. Rolling friction is commonly very small (1/100th to 1/1000th of static or sliding) but occurs because both the curved and flat surfaces deform slightly at their contact point. Rolling friction is influenced by the normal reaction force, radius of the rolling object (e.g. a wheel), the deformation of the surfaces and their coefficients of friction. So a large, heavy, soft (under-inflated) tyre would have a larger coefficient of rolling friction.