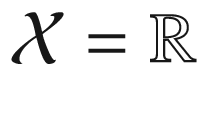SpringerBriefs present concise summaries of cutting-edge research and practical applications across a wide spectrum of fields. Featuring compact volumes of 50 to 125 pages, the series covers a range of content from professional to academic. Briefs are characterized by fast, global electronic dissemination, standard publishing contracts, standardized manuscript preparation and formatting guidelines, and expedited production schedules.
A timely report of state-of-the art techniques
A bridge between new research results, as published in journal articles, and a contextual literature review
A snapshot of a hot or emerging topic
Lecture of seminar notes making a specialist topic accessible for non-specialist readers
SpringerBriefs in Probability and Mathematical Statistics showcase topics of current relevance in the field of probability and mathematical statistics
Manuscripts presenting new results in a classical field, new field, or an emerging topic, or bridges between new results and already published works, are encouraged. This series is intended for mathematicians and other scientists with interest in probability and mathematical statistics. All volumes published in this series undergo a thorough refereeing process.
The SBPMS series is published under the auspices of the Bernoulli Society for Mathematical Statistics and Probability.
More information about this series at http://www.springer.com/series/14353
An Invitation to Statistics in Wasserstein Space
Open Access This book is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
This Springer imprint is published by the registered company Springer Nature Switzerland AG.
The registered company address is: Gewerbestrasse 11, 6330 Cham, Switzerland
To our families
A Wasserstein distance is a metric between probability distributionsμ
andν
on a ground space
, induced by the problem of optimal mass transportation or simplyoptimal transport
. It reflects the minimal effort that is required in order to reconfigure the mass ofμ
to produce the mass distribution ofν
. The ‘effort’ corresponds to the total work needed to achieve this reconfiguration, where work equals the amount of mass at the origin times the distance to the prescribed destination of this mass. The distance between origin and destination can be raised to some power other than 1 when defining the notion of work, giving rise to correspondingly different Wasserstein distances. When viewing the space of probability measures on
as a metric space endowed with a Wasserstein distance, we speak of aWassertein Space
.
Mass transportation and the associated Wasserstein metrics/spaces are ubiquitous in mathematics, with a long history that has seen them catalyse core developments in analysis, optimisation, and probability. Beyond their intrinsic mathematical richness, they possess attractive features that make them a versatile tool for the statistician. They frequently appear in the development of statistical theory and inferential methodology, sometimes as a technical tool in asymptotic theory, due to the useful topology they induce and their easy majorisation; and other times as a methodological tool, for example, in structural modelling and goodness-of-fit testing. A more recent trend in statistics is to consider Wasserstein spaces themselves as a sample and/or parameter space and treat inference problems in such spaces. It is this more recent trend that is the topic of this book and is coming to be known as ‘statistics in Wasserstein spaces’ or ‘statistical optimal transport’.
From the theoretical point of view, statistics in Wasserstein spaces represents an emerging topic in mathematical statistics, situated at the interface between functional data analysis (where the data are functions, seen as random elements of an infinite-dimensional Hilbert space) and non-Euclidean statistics (where the data satisfy non-linear constraints, thus lying on non-Euclidean manifolds). Wasserstein spaces provide the natural mathematical formalism to describe data collections that are best modelled as random measures on
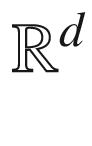(e.g. images and point processes). Such random measures carry the infinite-dimensional traits of functional data, but are intrinsically non-linear due to positivity and integrability restrictions. Indeed, contrarily to functional data, their dominating statistical variation arises through random (non-linear) deformations of an underlying template, rather than the additive (linear) perturbation of an underlying template. This shows optimal transport to be a canonical framework for dealing with problems involving the so-calledphase variation
(also known as registration, multi-reference alignment, or synchronisation problems). This connection is pursued in detail in this book and linked with the so-called problem of optimal multitransport (or optimal multicoupling).
- 1.
To present the key aspects of optimal transportation and Wasserstein spaces (Chaps. 1 and 2 ) relevant to statistical inference, tailored to the interests and background of the (mathematical) statistician. There are, of course, classic texts comprehensively covering this background. 1 But their choice of topics and style of exposition are usually adapted to the analyst and/or probabilist, with aspects most relevant for statisticians scattered among (much) other material.
- 2.
To make use of the ‘Wasserstein background’ to present some of the fundamentals of statistical estimation in Wasserstein spaces, and its connection to the problem of phase variation (registration) and optimal multicoupling. In doing so, we highlight connections with classical topics in statistical shape theory, such as Procrustes analysis. On these topics, no book/monograph appears to yet exist.
The book focusses on thetheory of statistics in Wasserstein spaces. It does not cover the associated computational/numerical aspects. This is partially due to space restrictions, but also due to the fact that a reference entirely dedicated to such issues can be found in the very recent monograph of Peyré and Cuturi [103]. Moreover, since this book is meant to be a rapid introduction for non-specialists, we have made no attempt to give a complete bibliography. We have added some bibliographic remarks at the end of each chapter, but these are in no way meant to be exhaustive. For those seeking reference works, Rachev [106] is an excellent overview of optimal transport up to 1985. Other recent reviews are Bogachev and Kolesnikov [26] and Panaretos and Zemel [101]. The latter review can be thought of as complementary to the present book and surveys some of the applications of optimal transport methods to statistics and probability theory.
Structure of the Book
Chapter 1 presents the necessary background in optimal transportation. Starting with Monge’s original formulation, it presents Kantorovich’s probabilistic relaxation and the associated duality theory. It then focusses on quadratic cost functions (squared normed cost) and gives a more detailed treatment of certain important special cases. Topics of statistical concern such as the regularity of transport maps and their stability under weak convergence of the origin/destination measures are also presented. The chapter concludes with a consideration of more general cost functions and the characterisation of optimal transport plans via cyclical monotonicity.
Chapter 2 presents the salient features of (ℓ 2 -)Wasserstein space starting with topological properties of statistical importance, as well as metric properties such as covering numbers. It continues with geometrical features of the space, reviewing the tangent bundle structure of the space, the characterisation of geodesics, and the log and exponential maps as related to transport maps. Finally, it reviews the relationship between the curvature and the so-called compatibility of transport maps, roughly speaking when can one expect optimal transport maps to form a group.
Chapter 3 starts to shift attention to issues more statistical and treats the problem of existence, uniqueness, characterisation, and regularity of Fréchet means (barycenters) for collections of measures in Wasserstein space. This is done by means of the so-calledmultimarginal transport problem (a.k.a. optimal multitransport or optimal multicoupling problem). The treatment starts with finite collections of measures, and then considers Fréchet means for (potentially uncountably supported) probability distributions on Wasserstein space and associated measurability concerns.
Chapter 4 considers the problem of estimation of the Fréchet mean of a probability distribution in Wasserstein space, on the basis of a finite collection of i.i.d. elements from this law observed with ‘sampling noise’. It is shown that this problem is inextricably linked to the problem of separation of amplitude and phase variation (a.k.a. registration) of random point patters, where the focus is on estimating the maps yielding the optimal multicoupling rather than the Fréchet mean itself. Nonparametric methodology for solving either problem is reviewed, coupled with associated asymptotic theory and several illustrative examples.
Chapter 5 focusses on the problem of actuallyconstructing the Fréchet mean and/or optimal multicoupling of a collection of measures, which is a necessary step when using the methods of Chap. 4 in practice. It presents the steepest descent algorithm based on the geometrical features reviewed in Chap. 2 and a convergence analysis thereof. Interestingly, it is seen that the algorithm is closely related to Procrustes algorithms in shape theory, and this connection is discussed in depth. Several special cases are reviewed in more detail.
Each chapter comes with some bibliographic notes at the end, giving some background and suggesting further reading. The first two chapters can be used independently as a crash course in optimal transport for statisticians at the MSc or PhD level depending on the audience’s background. Proofs that were omitted from the main text due to space limitations have been organised into an online supplement accessible at www.somewhere.com
Acknowledgements
We wish to thank three anonymous reviewers for their thoughtful feedback. We are especially indebted to one of them, whose analytical insights were particularly useful. Any errors or omissions are, of course, our own responsibility. Victor M. Panaretos gratefully acknowledges support from a European Research Council Starting Grant. Yoav Zemel was supported by Swiss National Science Foundation Grant # 178220. Finally, we wish to thank Mark Podolskij and Donna Chernyk for their patience and encouragement.
