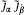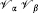Page numbers in italics refer to exercises
(0, 2) compactification 324–6, 376, 472
(2, 0) (tensionless string) theory 204–5
(2, 2) compactification
Calabi–Yau 311–12, 318–19, 323–5
constraints on spacetime action 388–90, 473
A–D–E singularity 425
An−1 see SU(n)
D0-brane 161
Dp-Dp′ system (#ND = 4) 163–4, 172
action (general)
action (spacetime)
anomaly-cancelling terms 99–100, 130
d = 4, N = 1 supergravity 446, 474
d = 4, N = 1 supersymmetry 443, 474
d = 4, N = 4 Yang–Mills theory 443
d = 10, N = 1 Yang–Mills theory 443
eleven-dimensional supergravity 85, 453, 468, 474
and Born–Infeld action 152, 469
from (2,2) compactification 473
from Calabi–Yau compactification 315–20, 404–6, 472
from orbifold compactification 472
in N = 1 heterotic string vacua 359–62, 473
R4 term 117
R–R tadpole term 39
singularities in 411
type I–heterotic relation 93, 192
action (world-sheet)
heterotic string 49
linear dilation 5
N = 2 free SCFT 48
superstring 2
affine Lie algebra 66
annulus, see cylinder
anomaly polynomial 97–101, 374
cancellation for SO(32) and E8 × E8 99–101
gauge 95ff
global gravitational 34
gravitational 95ff
mixed 95ff
see also Green–Schwarz mechanism
anti-de-Sitter space 223
antisymmetric tensor gauge field, see p-form gauge field
Atiyah–Drinfeld–Hitchin–Manin (ADHM) construction 174
bc CFT, bosonization 15
Bk see SO(2k + 1)
BPS bound 449
D0–Dp system 168
F-string–D-string system 164, 176, 182
behavior at strong coupling 180–1
Kaluza–Klein states 456
macroscopic strings 81, 226, 468
zero-force property 146
and picture changing 118–21, 125
in topological string theory 385
BRST quantization 24–5, 43, 45, 50
beta function
and scale transformation 261, 264–6
for gauge coupling 298, 346, 367
vanishes for d = 4, N = 4 460
nonlinear sigma model 247, 321
Bianchi identity
Chern–Simons term in 86, 88, 91
in Calabi–Yau compactification 304, 324, 418
related to field equation by Poincaré duality 141, 451–2
black hole
produced in graviton–graviton scattering 209
black p-brane 183–5, 201, 219–20, 227, 470
blow up (a fixed point) 297, 309–11, 388, 471
bosonization 11–15, 279–80, 467
bc CFT 15
current algebra fermions 54–5, 74–5
higher genus 13
kink operator 12
of U(1) current 68
bound states
and M-theory 198
U-dual to FD-string 189
U-dual to winding string 189
D0–D6 175
F-string–D-string 164–7, 176, 469
SL(2, Z) duality 182
U-dual to D0–D2 state 189
Ck see Sp(k)
c-map 382
and supersymmetry multiplets 441–2, 447
Calabi–Yau compactification 302–24, 472–4
as special case of (2, 2)
compactification 311–12, 386–90
field theory approximation 315
low energy field theory 315–20
Casimir energy 145
Casimir invariant 60
central charge (conformal) 3–5, 15, 43
and BRST nilpotence 24
and density of states 222, 236
and rank of gauge group 421
and renormalization group 262–6, 271
in topological string theory 385
specific
N = 0 minimal models 231
N = 2 minimal models 391
superconformal current algebra 340–2
central charge (supersymmetry) and BPS states 449, 456
from dimensional reduction 454, 456–7, 466
in extended supersymmetry 448–9
in type I/II string 144–5, 475
central extension 67
Chan–Paton degrees of freedom 30
reinterpreted as D-brane label 141–2
Chan–Paton factor 73, 109, 468
charge conjugation matrix C 434
Chern class (first) 309, 366, 402
and modified gauge transformation 92, 107, 469
and anomaly cancellation 99–100
from string perturbation theory 113–14, 127–30
in D-brane action 150
and induced R–R charge 170, 173, 203
chiral gauge couplings 282, 325, 330
constraints from 337, 340–2, 351–2, 447–8
in Calabi–Yau models 313
chiral primary fields 378–9, 384–5
in Landau–Ginzburg models 394–5, 397
chirality
IIA vs IIB 27–9, 415–16, 453–4
of NS5-branes 204
Christoffel connection 106
Clifford (Dirac matrix) algebra 2, 193, 430
cohomology
De Rham 305
Dolbeault 307
ring 385
Coleman–Weinberg formula 31, 156
collective coordinate 139–40, 149
for eleventh dimension 202, 204
commutators and anticommutators
[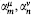 ] 6
] 6
{bm, cn} 16
{βr, γs} 16
[Eα, Eβ] 61
{Gr, Gs} 7
[Hi, Eα] 61
[ ] 66
] 66
[Lm, Gr] 7
[Lm, 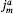 ] 66
] 66
[Lm, Ln] 7
{ψr, 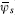 } 14
} 14
{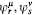 } 6
} 6
N = 2 superconformal 376
{QB, bn} 24
[QB, βr] 24
[Ta, Tb] 59
see also supersymmetry algebras
compactification 274
see also (0, 2), (2, 2), Calabi–Yau, Gepner, orbifold, toroidal compactifications
hyper-Kähler manifold 463
complex structure moduli 291, 314–15, 381
K3 416
moduli space 296, 383–4, 402–9
quintic 310
conformal family 229
conformal field theory (CFT)
nonunitary 232
see also bc, βγ, ψ, coset, Landau–Ginzburg, parafermion CFTs, current algebras, minimal models, superconformal field theory
conformal gauge 20
conformal invariance
constraints on correlators 233–5
vs scale invariance 260, 262–3
conformal perturbation theory 263–6
constraint algebra 3, 20, 24, 45–9
from gauged world-sheet symmetry 251
N = 1 minimal models 255
cosmological constant 226, 372–3, 473
coupling constants
relations among 107–10, 150–2, 335–6, 472
string vs M-theory 199
critical dimension 4, 47–8, 198
critical phenomena 266–71, 393, 400
current algebra 66–73, 243–50, 272, 468, 471
and unification 337–8, 351, 353–4
fermionic representation 68
KZ equation 244
level 67
modular invariants 245–6, 249–50
restriction on representations 72–3, 289, 337–8, 349
collapsing 404, 410–13, 425, 427
D-brane wrapped on 404, 411–13, 425
monodromy 410
world-sheet wrapped on 322–4, 406, 408
cylinder
D-brane interactions from 146–7, 155–60, 176, 196
and black p-branes 219–23, 227
coincident, non-Abelian dynamics 149, 166, 211–23
D0-brane quantum mechanics 161–2
in matrix theory 211–14, 217–18
D0-branes as Kaluza–Klein states 198–9
D1-branes and IIB duality 180–2
D3-branes and Montonen–Olive duality 180–2
Dp–Dp′ system 152–8, 162–4, 175–6
BPS bound 168
effect of T-duality on 143–4, 429
gauge coupling 151
on collapsing cycle 411–15, 425
p even, relation to M-theory 200–8
substring length scale 160–2, 412
see also bound states
D-instanton 142, 145, 334, 372, 469
Dk see SO(2k)
D-terms
four supersymmetries 364–6, 399, 443–4, 473
and orbifold blow-up modes 297
eight supersymmetries 462
in Dp-Dp′ system 163, 172, 221–2
diagonal modular invariant 36
heterotic string 55
type 0 superstring 35
differential forms 305–6, 450–2
dilaton
and string loop expansion 87–9, 360–2, 383–4
in hypermultiplet 380, 383–4, 429
in vector multiplet 428
dilaton-mediated supersymmetry breaking 370
dimensional reduction
of spectrum 78–80, 84–6, 188, 453–5
of supersymmetry 79–80, 311, 454, 458, 463–4
Dirac–Born–Infeld action 149
Dirac equation 1–2, 22, 88, 179
Dirac quantization condition 147–9, 183–5, 196, 247–8, 355, 366
Dirichlet boundary condition 139, 142, 143, 152
discrete light-cone quantization (DLCQ) 217
discrete series, see minimal models
discrete symmetry (spacetime) 328–35, 472
see also S-, T-, U-dualities
disk amplitudes 102, 110–12, 114–16, 134, 175
divergences, cancellation 37–42, 102–3, 135, 142–3, 468
duality, see Montonen–Olive, S-, string–string, T-, and U-dualities
E6 64–5, 82, 285ff, 312, 386–8
see also grand unification
E7 82
energy-momentum tensor 1–5, 50
topological 385
enhanced gauge symmetries
at Gepner point 398
at orbifold points 309–10, 312–13
on coincident branes 149, 185–6
on singular manifolds 425, 427
on small SO(32) instantons 195–6
Euler number (Calabi–Yau) 305, 309, 414–15
extended chiral algebra 253–4, 256
extended supersymmetry 359, 440, 447–9, 473–4
exterior derivative 305, 307, 450
Faddeev–Popov ghosts 15–20, 46–7
Fayet–Iliopoulos term 364–5, 399, 443, 446
Feigin–Fuchs representation 241–2, 272
fermion number
spacetime 32
world-sheet 8–9, 19, 22ff, 32–3
Feynman diagrams 102, 176, 316
fixed point
blowing up 297, 309–10, 388, 471
field theory 266
nontrivial 260–1, 415, 421, 460–1
flipped SU(5) 348
fractional string theory 46, 468
free fermion models 279–80, 471–2
free parameters, absence of 369, 373
fundamental (F-) string 145, 150
fundamental region 31, 40, 284
fusion rule 238–40, 244–5, 256–8, 270–1
gauge coupling, see coupling constants, gauge
gauge-fixing 20
general relativity 183, 408, 429
generation (quark and lepton) 64–5, 288–92, 313–15, 324–6, 387–8, 471–2
gen.-changing transition 414–15, 474
relation to Calabi–Yau 397–402
Gliozzi–Scherk–Olive (GSO) projection 27, 30, 33
and spin–statistics 29
current algebra fermions 51–5, 82, 193, 386
global symmetry 45, 94, 327–8, 334–5
goldstino 140
Goldstone boson 140
grand unification 63–5, 81, 281, 288–90, 351–6
partial 348
symmetry breaking 289, 325–6, 337–8, 349
gravitino 28–31, 79, 286, 315, 441
world-sheet 126
Green–Schwarz mechanism 99–101, 365, 462
Green–Schwarz superstring 29, 49, 133
H-monopole 82
Hagedorn temperature 83
Hamiltonian, D0-brane 161–2, 212
heterotic 5-brane 195
(0,2) and (1,2) 48
amplitudes 112–13, 126–33, 134, 373–4
T-duality between SO(32) and E8 ×E8 78
toroidal compactification 76–82, 422–9
hierarchy (Higgs naturalness) problem 281–2, 350, 369
highest weight (primary) state 229ff
superconformal 105
Hodge numbers 309–10, 315, 402–3, 414, 416
hyper-Kähler manifold 417, 463–4
hypermultiplet 380–4ff, 447, 461–4
from p-p′ strings 163, 172–3, 196
index theorem 330
inheritance principle 290, 293, 314, 351
instanton (Pontrjagin) number 187, 333
world-sheet 323–5, 383, 406, 408, 472
Yang–Mills 172–5, 194–6, 418–20, 470
irrelevant interaction 192, 264
tricritical 269
Jacobi’s abstruse identity 35
and type II string 415–18, 425–8
Kac determinant 230–3, 242, 254, 271, 471
Kac–Moody algebra 66
Kähler class 308
see also hyper-Kähler manifold, special Kähler manifold
effective action 316–19, 323, 381–4, 472
K3 416
moduli space 296, 381–3, 402–9
Kähler potential 294–8, 308, 359–62, 390, 446–7
Kähler transformation 296, 308, 446–7
Kaluza–Klein gauge symmetry 76, 79, 86, 188–9
and supersymmetry algebra 454–6
vertex operators 66
Kaluza–Klein states 198
Klein–Gordon equation 1
Knizhnik–Zamolodchikov (KZ) equation 244, 272
Landau–Ginzburg model 270–1, 392–4, 400, 471, 473
large-N limit 223
large order behavior 145
lattice (momentum) 19, 74–8, 83
Laurent expansion, see mode expansion
level (current algebra) 67
level-matching 25, 57, 276–9, 284–5ff, 395, 468
normalization of generators 67–8, 93, 112, 151, 336
simply-laced 63
light-cone quantization 212, 216
linear dilaton CFT 5, 15, 43, 230
applications 89, 185, 241–2, 272
linear multiplet 294
linear sigma model 398–402, 408
eleven-dimensional 212
local 96
M-theory 198–205, 208–11, 426–7, 470
wrapped 427
macroscopic string 81
magnetic monopoles 81–2, 187, 205, 353, 468, 470
Dirac quantization condition 147–8, 355
Majorana–Weyl spinor 433
manifold
hyper-Kähler 463
quaternionic 464
mass-shell condition 1, 20, 23
matrix theory 211–18, 226, 470
Maurer–Cartan 1-form 248
membrane, see M2-brane
Mermin–Wagner–Coleman theorem 140
Feigin–Fuchs representation 241–2
fusion rule 238
and conifold transition 401, 414
and Kähler moduli space 404–9, 428–9
Möbius invariance 233
b, c, β, γ 16
free scalar (Xµ) 6
ja 66
N = 2 superconformal 376
TB, TF 7
model-independent axion 333
modular invariance 33–7, 235–6, 471
and anomalies 103
Gepner models 395
heterotic string 52–3, 55–8, 82, 388–9
minimal model 251
rational CFT 268
modular transformations 34, 38, 156
modular weights 297
moduli, physical effects 291, 324–6, 331, 370–3, 445
in threshold correction 298–300, 349
moduli space
(2, 2), product form 381, 389–90
branches 172–4, 373, 412–15, 419–21
for toroidal compactification 76–8, 81, 91–2, 427–8, 455–8
with 8 supersymmetries 462–5, 475
with 16 supersymmetries 159, 460, 475
see also complex structure, Kähler moduli
Montonen–Olive duality 186–7, 428, 470
NS boundary condition 5–8, 15–16
NS–NS charge 81
magnetic 81–2, 145, 183–5, 189
NS–NS fields 87
background 106
NS5-brane 470
multiple 186
heterotic 195
Narain compactification 73–9, 83, 468
naturalness problem 282, 350, 369
Neumann boundary condition 141, 143, 152
no-ghost theorem 25, 50, 232–3
no-scale models 371
noncommutative geometry 149, 161
nonlinear sigma model 106–8, 247, 311, 469, 471
nonperturbative definition (of string theory) 180–1, 208–11
nonperturbative effects 49, 134, 145, 178, 343, 366–73, 421–2, 425
see also instantons, strong coupling
nonrenormalization theorems 133–4, 300
α′ corrections 111–17, 185, 321–5, 382–3, 472
perturbative, violation by instantons 323–5, 367–8, 372, 472
4 supersymmetries 361–2, 364–5, 444
8 supersymmetries 381, 383–4, 410–11, 428–9
16 supersymmetries 133–4, 159, 194, 460–1
null state 231–3, 236–9, 243–5, 252–3
decoupling of 98, 101–2, 119, 121
old covariant quantization (OCQ) 3, 20–3, 25
one-loop string amplitudes 31–42, 126–34, 135, 146–7, 155–60, 298–300, 374, 468–9, 472
operator product expansion (OPE) 43, 82–3, 95–6
closure and locality 26, 52–5, 74
H H 11
in Sugawara construction 69–71
jB β 24
jB β 24
λAλB 49
λaλb 73
N = 2 superconformal 37, 47, 375
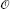 m
m 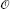 n 234
n 234
ψ 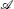 ν 14
ν 14
ψl ψl 252
ψµ Θα 112
superconformal current algebra 339
TB 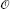 233
233
TF 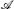 10
10
W W 253
orbifolds 274–301, 331ff, 471–2
asymmetric 279
fixed points 311
blowing up 296–7, 309–10, 312–13
non-Abelian 275
nonsingularity of CFT 275, 410, 425
orientifold plane 138, 142–4, 147, 151, 175, 206–8
p-brane, see black p-, D-, M2-, M5-, and NS5-branes
p-form, see differential forms
field strength 86
see also Chern–Simons term, R–R fields
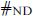 = 8 191
= 8 191
P invariance, see parity
parafermion CFT 251–2, 269, 391–2, 471
parity
and anomalies 95–8, 285, 304, 329–30
and T-duality 137
partition functions 235–6, 266, 272, 471
and bosonization 13
GSO projected 32–7, 51–3, 55–8
Pati–Salam unification 348
Pauli–Villars regulator 95, 285
Peccei–Quinn (PQ) symmetry 333–5, 360–2, 365–6, 371–2, 382–3, 473
physical states 1, 3, 20–3, 28, 45
picture changing operator (PCO) 118–21, 126, 469
Planck scale, eleven-dimensional 199, 212
point group 275
primary field, see highest weight state, tensor field
projective space 310–11, 320, 398, 404, 465
quantum mechanics 210, 225–6, 429
quaternionic manifold 464
rank (algebra) 61, 77, 326, 421, 457–8
Ramond (R) boundary condition 5–9, 15–16
R–R charge
in supersymmetry algebra 144–5
of black p-brane 219
value 147
vanishes for strings 88–9, 92, 381
background 106
Ramond–Neveu–Schwarz (RNS) superstring 29
relevant interaction 166, 264–6, 268–71
renormalization group 259–66, 346, 350, 369
S-duality (weak–strong) 179–82, 186–7, 190–2, 198–9, 205–7, 422–9
SL(2, Z) 182, 186–8, 200, 295–6, 427–8, 474
SL(3, Z) 200
SO(4) = SU(2) × SU(2) 439
[S]O(5, 5, Z) 200
SO(10) 64–5, 82, 289, 338, 346
SU(5) 64–5, 82, 289, 338, 345–8, 352–6
traces 99
[S]O(m, n, R) 61, 76, 187–8, 417, 427–8
S-matrix 124
Scherk–Schwarz mechanism 363–4
simple current 240–1, 272, 354
space group 275
special Kähler geometry 319–20, 381–3, 390, 405, 464–5
relation to disk 116
embedded in gauge connection 284, 291, 304, 324, 418–19
and (2, 2) supersymmetry 311–12, 376
spin–statistics relation 19, 29, 33, 35, 49, 52, 55, 82, 332
spin structure 122–4, 127, 130–2
Standard Model 178, 274, 326, 370–3, 421–2
chirality 98, 282, 288–9, 329–31
gauge couplings 298, 314, 343–52
gauge quantum numbers 337–8, 340–3, 352–5
generations 64–5, 288–92, 313–15, 324–6, 387–8, 471–2
hierarchy problem 281–2, 350, 369
state–operator isomorphism, see vertex operators
statistical mechanics 219, 224–5, 260, 266–71
Stokes’s theorem 450
string coupling, see coupling constants
string metric 205
string–string duality 425, 429
string tension 150, 164–7, 180
strong coupling limit
heterotic string 190–4, 205–8, 421–9
structure constants 59
Sugawara construction 69–72, 82, 243, 247, 250, 339, 468
superconformal algebra 3–4, 7, 272
primary field 105
superconformal current algebra (SCCA) 338–42
superconformal field theory (SCFT) 467–8
(2, 2) 292, 311–12, 380–415, 473
superconformal Killing vector 123
superconformal transformation 2, 10, 43, 103–4
superfield 104
supergravity 468
d = 4, N = 1 293–5, 315, 359–62
eleven-dimensional 84–7, 198–9, 201, 453
long-distance 160, 176, 213–14
toroidally compactified 187–9, 454–7
supermanifold, see superspace
supermembrane, see M2-brane
superpartner scale 343, 350, 369
constraints from holomorphicity 322–3, 359–62, 367–8
Landau–Ginzburg/linear sigma model 392, 398, 400
nonperturbative contributions 323–4, 371–2
superstring, see types 0, I, IIA, IIB
supersymmetry (spacetime) 471
and GSO projection 29–30, 50–1, 359
and vanishing of vacuum amplitude 35, 38, 146
as means of studying strong
conditions for unbroken
d = 2 449
in specific systems
D0–Dp system 168
F-string–D-string system 164
type I/II superstring 144
in statistical mechanics 269
transformations 173, 203, 302, 443
vs world-sheet 29
see also BPS bound, BPS states, nonrenormalization
supersymmetry breaking 473
by D-branes 139–40, 152–5, 168, 175–7
dilaton-mediated 370
scale 369
and mirror symmetry 402–4, 473
as a gauge symmetry 328
combined with S-duality 199, 205–7, 227, 422–7
effect on D-branes 138–45, 163–4ff, 176
on orbifolds 295–6, 298, 300, 472
’t Hooft–Polyakov monopole 82, 187
in nonsupersymmetric D-brane systems 158, 169
removal by GSO projection 27, 31, 52, 54, 58–9
tensionless string theory 205, 260–1, 421, 474
tensor multiplet
tensor superfield 104
Thirring model 36
threshold correction 298–300, 334, 349, 370–1, 472
topological string theory 49, 385
topology change (spacetime)
toric geometry 404
toroidal compactification
heterotic string 76–82, 422–9, 468, 474
torus amplitudes 31–5, 51–9, 126–33, 374
transition functions 122, 125, 306
tree-level amplitudes 110–18, 135
trinification 349
twist (orbifold) construction 55–8, 251, 275–6, 279
twisted boundary conditions 13–4, 32–4, 44, 155–6ff
type II superstrings 26–9, 31–7
on Calabi–Yau manifolds 379–86ff
strong coupling limits 179–87, 198–205
T-duality between 136–8, 143–4
toroidally compactified 187–90, 454–7
U-duality 187–90, 199–201, 226, 328
UV divergence 103
ultrashort multiplet 80, 169–71, 210, 449
unitary CFT 45–6, 228–32, 254–5, 262–3, 391, 471
vacuum amplitudes 31–42, 146–7, 155–8
vacuum selection 373
vector multiplets
d = 4, N = 1 441
d = 4, N = 2 380–4ff, 447, 463–5
vertex operators 10–15, 108–10, 468, 471
gravitino 28
Virasoro master equation 258
current algebra primary 72
unitary CFTs 231, 255, 378, 391
lattice 75
weight (modular) 297
Wess–Zumino term 248
Wilson criterion (computability) 209–11, 214
Wilson line 76–8, 83, 206, 208, 227, 429
gauge symmetry breaking 289–91, 314, 325–6
Yang–Mills theory, d = 4, N = 4 186–7, 428, 460–1
Zamolodchikov metric 362, 374, 389
zero modes 119
sphere 108
torus 121, 123, 127, 130, 132–3
zero-norm states, see null states