The Star tool (the 
key or 
) creates two slightly different kinds of centrally symmetric shapes—polygons and stars. Despite the simplicity of the idea, this is one of the most complex tools in Inkscape, endlessly entertaining and perfect for wowing your friends.
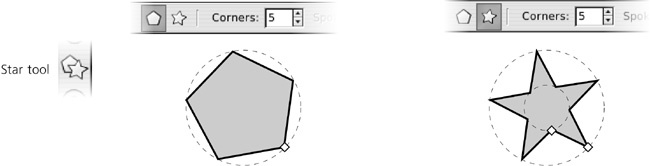
A polygon is just a number of points located equidistant on an imaginary circle and connected by straight line segments. An Inkscape polygon has one diamond-shaped handle used to scale and rotate it.
A star is a much more interesting object: It contains two sets of equidistant points on two imaginary concentric circles, with the outline of the star zig-zagging back and forth between points on the inner and outer circles. Using a star’s two handles, you can vary the diameters of the circles and rotate the circles relative to one another around their common center, which produces a fascinating variety of intricate symmetric shapes.
Before you draw a new shape, decide whether you want it to be a polygon or a star by pressing one of the toggle buttons on the controls bar, and choose the number of corners (convex vertices) in the numeric control. For example, a polygon with three corners is an equilateral triangle, and will have three nodes if converted to path; a star with three corners, however, will have six nodes. You can always change the polygon/star type and the number of corners in an existing shape, too—just select it and edit the values.
Note
The number of corners can range from 3 to 1000, but setting this too high may slow down Inkscape considerably unless you use the Outline mode (3.11 Rendering Modes).
Drawing a shape is, again, as simple as dragging your mouse upon the canvas. A star or polygon is always drawn starting from its center. There’s only one keyboard shortcut: Dragging with 
snaps the angle of one of the shape’s corners relative to its center to 15-degree increments.
A polygon’s single handle can only be used to scale and rotate the polygon—something you can do just as well by transforming it in Selector. The two handles of a star are much more interesting.
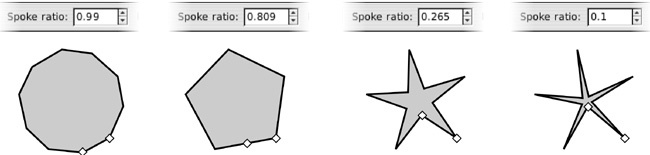
First, by moving one of them to or from the center of the star, you are changing the ratio of the diameters of the two circles on which the corners of the star lie. This ratio is called the spoke ratio and is also adjustable as a numeric parameter (disabled for polygons) in the controls bar:
You can even move what was originally the inner handle farther away from the center than the outer one. The control will still show a ratio less than 1 because it always divides the smaller radius by the larger, regardless of which of them was initially inner and which was outer.
Second, the inner handle (initially on the inner circle) can be moved tangentially (i.e., along an arc around the star center) to skew the star’s vertices. (Rotating the outer handle simply rotates the entire star.)
Drag the inner handle with if you want to keep the vertices strictly radial (no tangential displacement), or -click it to remove any existing tangential skew without dragging.
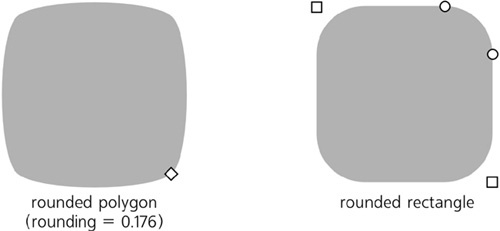
Many fascinating effects with stars and polygons can be achieved by rounding them. A star’s rounding is different from the rounded corners of a rectangle; with a star or polygon, not only the corners lose sharpness but all of the the star’s sides bend into elegant Bézier curves:
As you can see, a rounded square has straight line segments between circular or elliptic rounded corners, whereas a rounded polygon or star has no straight lines at all—all its segments become Bézier curves.
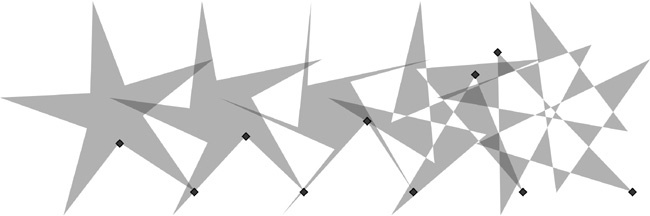
The Rounded numeric control of the Star tool is the ratio of the length of the Bézier handles (12.1.4 Bézier Curves) to the length of the polygon/star side which these handles affect. This parameter can be negative, which reverses the direction of tangents. Typically, values between 0.2 and 0.4 give the most natural-looking results. Negative or too high positive values tend to result in twisting, looping, and self-intersections. By playing with handle positions in variously rounded stars, you can get an infinite variety of beautiful shapes:
Apart from setting the numeric rounding parameter on the controls bar, rounding can be done by 
-dragging any of the handles tangentially. Counterclockwise rotation of a handle around the star’s center results in positive rounding; clockwise rotation makes it negative. -clicking a handle removes any rounding.
If you want the outer corners of a star to be sharp but the inner ones smoothed, or vice versa, try creating an offset path (12.4 Offsetting) from the star.
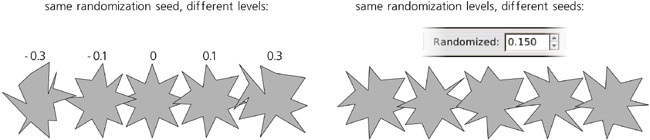
Yet another way to make a star more interesting is by randomizing it. Randomization moves all vertices of a star or polygon in random directions and by random distances. If the star was rounded, randomization preserves the smoothness of all vertices.
The overall force of the effect is controlled by the Randomized parameter in the controls bar, which can take positive and negative values. As you change this value—or simply 
-drag a star’s handle tangentially—the direction of random displacement for each node remains the same, and only the distance changes; negative values simply move the vertices in the opposite directions. In other words, the star remains randomized in the same way but to a different extent.
On the contrary, when you simply drag a randomized star’s handle to scale or reshape it, or when you draw a new star with nonzero randomization, the shape trembles and jitters, abruptly changing the random displacements for all nodes (in mathematical terms, reseeding the randomization) on every slightest move of your mouse. So, if you want your star to get randomized differently by with the same overall amplitude, simply drag any of its handles slightly:
What are randomized stars good for? Randomness is one of the fundamental forces of nature, and randomness in design is a great way to make shapes livelier and less rigid. Your artistic sense and experience will tell you where and how much randomness is appropriate. In Inkscape, there are many sources of artistic randomness; you can easily shuffle the positions of objects (7.5.1 Randomizing, Unclumping, and Removing Overlaps), create patterns with random placement, scaling, and rotation (10.8.2 Editing Patterns), as well as randomly displace nodes in paths to distort them (12.6.6 Roughen Mode). Still, randomized stars are unique in how fast and easy it is to draw a shape where intrinsic symmetry emphasizes its randomness.
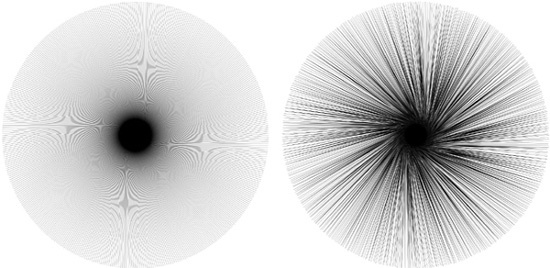
Slight randomization makes a star more humane, sometimes outright funny; strong randomization produces a variety of wild and unpredictable shapes. Messy hairballs, rounded amoeba-like ink blotches, fantastic landscapes at the edge of a large star with many vertices and spoke ratio close to 1—all this and more is possible with star randomization. As an example, Figure 11-30 shows a star with 500 vertices, not randomized (left) and randomized by just 0.005 (right) to look more naturally hairy and to get rid of the moire pattern that mars the star without randomization.
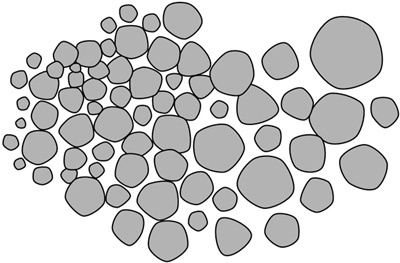
As another example, here are randomly scattered and unclumped pentagons, rounded at 0.28 and randomized at 0.15, looking very much like pebbles on a beach:
