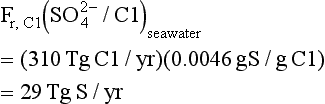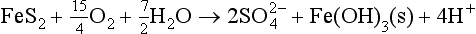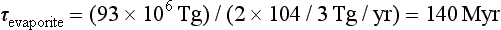The Sulfur Cycle
13.1 Introduction
Sulfur, the fourteenth most abundant element in the Earth’s crust, plays a variety of important roles in the chemical functioning of the Earth. In its reduced oxidation state, sulfur is a key nutrient to life, providing, for example, structural integrity to protein-containing tissues. In its fully oxidized state, sulfur exists as sulfate,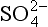 , the second most abundant anion in rivers (after bicarbonate, HCO3−) and in seawater (after chloride, Cl−) and is the major cause of acidity in both natural and polluted rainwater. This link to acidity makes sulfur a key player in natural weathering of rocks and such environmental problems as “acid rain.” Sulfate in the atmosphere has been identified as the dominant component of cloud condensation nuclei in both remote and polluted settings (Bigg et al., 1984). Thus, it has important interactions with clouds (and perhaps the global radiative energy balance which is sensitive to clouds) and with the hydrologic cycle. Finally, of the major elemental cycles (i.e., C, N, O, P, S), the sulfur cycle is one of the most heavily perturbed by human activity. It is estimated that anthropogenic emissions of sulfur into the atmosphere (largely from coal combustion) are currently about double natural sulfur emissions (see Table 13-2).
, the second most abundant anion in rivers (after bicarbonate, HCO3−) and in seawater (after chloride, Cl−) and is the major cause of acidity in both natural and polluted rainwater. This link to acidity makes sulfur a key player in natural weathering of rocks and such environmental problems as “acid rain.” Sulfate in the atmosphere has been identified as the dominant component of cloud condensation nuclei in both remote and polluted settings (Bigg et al., 1984). Thus, it has important interactions with clouds (and perhaps the global radiative energy balance which is sensitive to clouds) and with the hydrologic cycle. Finally, of the major elemental cycles (i.e., C, N, O, P, S), the sulfur cycle is one of the most heavily perturbed by human activity. It is estimated that anthropogenic emissions of sulfur into the atmosphere (largely from coal combustion) are currently about double natural sulfur emissions (see Table 13-2).
Table 13-2
bDeduced to balance budget for “soils and land biota” reservoir.
cBates et al. (1992) global total for volcanic emissions reapportioned as 1/3 continental and 2/3 marine.
dNumber shown represents the sum of fluxes F9 and F10.
eDeduced to balance budget for “ocean” reservoir.
fDeduced to balance budget for “ocean sediments” reservoir.
With the exception of ionic sulfides formed from highly electropositive elements (i.e., Na, K, Ca, Mg), sulfur bonding in natural environments is covalent. When fully oxidized, however, the covalently bonded sulfur atom exists within the sulfate ion which forms either sulfuric acid (a gas or liquid) or ionic compounds such as CaSO4·2H2O (gypsum) and (NH4)2SO4 (ammonium sulfate). Covalent bonding occurs in organosulfur compounds. Hence, the chemistry of sulfur involves chemical complexity not found in elements at the edges of the periodic table.
Sulfur exists naturally in several oxidation states, and its participation in oxidation/reduction reactions has important geochemical consequences. For example, when an extremely insoluble material, FeS2, is precipitated from seawater under conditions of bacterial reduction, Fe and S may be sequestered in sediments for periods of hundreds of millions of years. Sulfur can be liberated biologically or volcanically with the release of H2S or SO2 as gases.
There are nine known isotopes of sulfur of which four are stable:
| Isotope | Average crustal abundance (%) |
| 32S | 95.0 |
| 33S | 0.76 |
| 34S | 4.22 |
| 36S | 0.014 |
The prevalence of sulfur’s second most abundant isotope, 34S, along with the fractionation known to occur in many biogeochemical processes, make isotopic studies of sulfur a potentially fruitful method of unraveling its sources and sinks within a given reservoir.
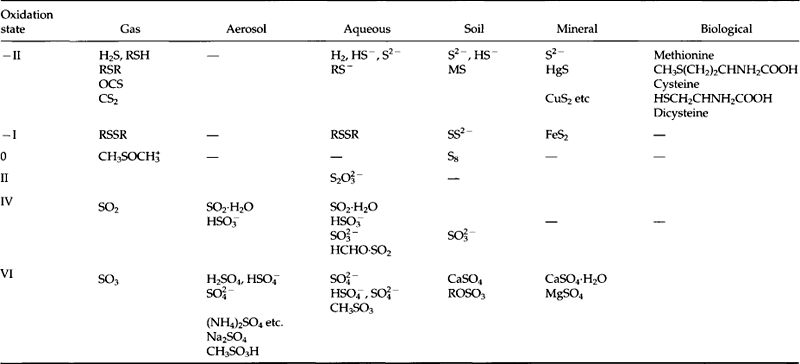
13.2 Oxidation States of Sulfur
Table 13-1 includes many of the key naturally occurring molecular species of sulfur, subdivided by oxidation state and reservoir. The most reduced forms, S(– II), are seen to exist in all except the aerosol form, in spite of presence of free O2 in the atmosphere, ocean and surface waters. With the exception of H2S in oxygenated water, these species are oxidized very slowly by O2. The exception is due to the dissociation in water of H2S into H+ + HS−. Since HS− reacts quickly with O2, aerobic waters may contain, and be a source to the atmosphere of, RSH, RSR etc. but not of H2S itself. Anaerobic waters, as in swamps or intertidal mudflats, can contain H2S and can, therefore, be sources of H2S to the air.
S(–II and –I) also are found in minerals, notably in metal and metaloid sulfides. As many as 95 sulfide minerals appear in standard lists, where sulfur is bound to a wide variety of other elements: Ag, Fe, Cd, Hg, Mn, Ca, Te, Se, As, Sn, Cu, Pb, Pt, Sb, Co, Ni, Mo, Rn, W. Of these, FeS2 (pyrite) is the most abundant.
Highly oxidized forms of organic sulfur exist in folic acid and sulfolipids, but the major form of sulfur in organisms is in amino acids. There are two sulfur-containing amino acids: cysteine and methionine. Although sulfur bonds assume a variety of oxidation states in living organisms, we list the amino acid sulfur as oxidation state –II because the sulfur is generally bonded to carbon or hydrogen. Thus, methionine has a –SCH3 bond like dimethyl sulfide, and cysteine is a mercaptan which can convert to smaller gaseous molecules like CH3SH. A key biological function of sulfur is to provide disulfide (—SS—) linkages between amino acids within protein molecules, thus giving three-dimensional structure to proteins and strength or mechanical structure to tissues composed of proteins. Sulfur in methionine is crucial to the methylation reaction, a biosynthetic process. The amount of sulfur in organisms varies but is typically of the same order of magnitude as phosphorus, e.g. about 0.25% (by dry weight). Even though sulfur is an essential element for biota, its abundance, 29 mmol/kg in seawater, is often so large that other elements (e.g., N and P) provide limits to growth, while S does not.
The most oxidized form of sulfur, S(+VI), is predominantly sulfate,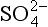 . Sulfate particles ranging in composition from pure sulfuric acid (H2SO4) to fully neutralized ammonium sulfate ((NH4)2SO4) are ubiquitous constituents of the atmosphere (see Chapter 7).
. Sulfate particles ranging in composition from pure sulfuric acid (H2SO4) to fully neutralized ammonium sulfate ((NH4)2SO4) are ubiquitous constituents of the atmosphere (see Chapter 7).
In the ocean, sulfate exists as a free ion,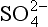 . In sedimentary rock, sulfate is found in evaporite minerals (i.e., minerals produced by the evaporation of seawater), with gypsum, CaSO4·2H2O, being the most common. By contrast, the intermediate oxidation state, S(+IV) has only a transitory existence in the atmosphere and in some volcanic and industrial emissions to the atmosphere. Gaseous SO2 is soluble in water, leading to the presence of HSO3− and
. In sedimentary rock, sulfate is found in evaporite minerals (i.e., minerals produced by the evaporation of seawater), with gypsum, CaSO4·2H2O, being the most common. By contrast, the intermediate oxidation state, S(+IV) has only a transitory existence in the atmosphere and in some volcanic and industrial emissions to the atmosphere. Gaseous SO2 is soluble in water, leading to the presence of HSO3− and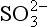 ions which are unstable under aerobic conditions, producing
ions which are unstable under aerobic conditions, producing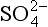 as the stable end-product ( Chapter 5). Oxidation of SO2 to sulfate occurs in the gas phase as well due to the presence of the strong oxidizing agent, OH•.
as the stable end-product ( Chapter 5). Oxidation of SO2 to sulfate occurs in the gas phase as well due to the presence of the strong oxidizing agent, OH•.
Elemental sulfur also occurs naturally, with production either by biological or inorganic processes. In either case, it appears that a higher oxidation state of sulfur may react with the – II (sulfide) state to yield a zero oxidation state product, or that S(0) is an intermediate in the oxidation of S(– II). There are several genera of sulfate-reducing bacteria, two of which are widely recognized: Desulfovibrio and Desulfotomaculum. These organisms utilize sulfur in the sulfate ion as an electron acceptor and produce H2S. This H2S is then available to react with iron and form the insoluble precipitate, FeS2 (pyrite). Other organisms can utilize H2S and produce elemental sulfur, S(0). Elemental sulfur also is produced inorganically, for example by the following reaction in volcanoes:
For completeness, we mention the existence of compounds of mixed oxidation states. Here, two or more atoms of sulfur exist in the molecule or ion, each having a different oxidation state. Numerous examples of these species are known but details of their natural existence are obscure. It is suggested (Grinenko and Ivanov, 1983) that thiosulfate,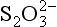 , ion can be produced by bacteria in waterlogged soils, paddy fields and the like. The formal oxidation state for the two sulfur atoms is II, but the two sulfur atoms are chemically different. Such species may play important roles as intermediates between the major species such as S2− and
, ion can be produced by bacteria in waterlogged soils, paddy fields and the like. The formal oxidation state for the two sulfur atoms is II, but the two sulfur atoms are chemically different. Such species may play important roles as intermediates between the major species such as S2− and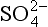 (Jorgensen, 1990).
(Jorgensen, 1990).
Returning to Table 13-1, we see that sulfur is found in gaseous, aerosol, aqueous, soil, mineral, and biological forms. The gaseous forms, which are found in the atmosphere, are generally of the lower oxidation states –II or +IV, while most of the aqueous form is S(+VI) as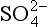 . The vapor pressures of non-ionic S(– II) compounds are large enough that transfer of these species occurs from bodies of water to the atmosphere. Sulfate ion in solution is relatively inert, and much of its processing is due to transport by water or evaporation of the water to form solid evaporites. The sulfate minerals (evaporites like CaSO4) are water soluble, while the sulfide minerals (such as FeS2) tend to be highly insoluble.
. The vapor pressures of non-ionic S(– II) compounds are large enough that transfer of these species occurs from bodies of water to the atmosphere. Sulfate ion in solution is relatively inert, and much of its processing is due to transport by water or evaporation of the water to form solid evaporites. The sulfate minerals (evaporites like CaSO4) are water soluble, while the sulfide minerals (such as FeS2) tend to be highly insoluble.
13.3 Sulfur Reservoirs
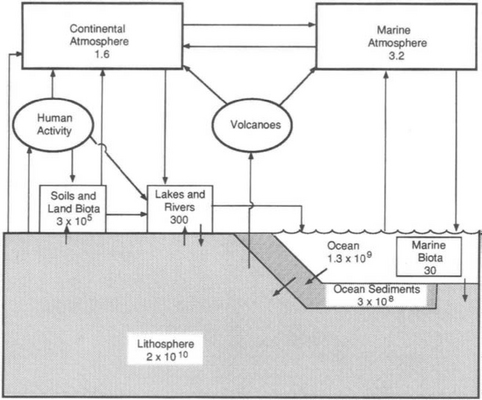
The preceding discussion of oxidation states demonstrates the existence of sulfur in solid, liquid, and gaseous forms and in living organisms. It is thus convenient to organize the remainder of the discussion along these same lines. Figure 13-1 is a box diagram showing the key reservoirs and the approximate burdens of sulfur in each (Freney et al., 1983).
The vast majority of sulfur at any given time is in the lithosphere. The atmosphere, hydrosphere, and biosphere, on the other hand, are where most transfer of sulfur takes place. The role of the biosphere often involves reactions that result in the movement of sulfur from one reservoir to another. The burning of coal by humans (which oxidizes fossilized sulfur to SO2 gas) and the reduction of seawater sulfate by phytoplankton which can lead to the creation of another gas, dimethyl sulfide (CH3SCH3), are examples of such processes.
The remainder of this chapter, which discusses the cycling of sulfur, is divided into an atmospheric part and an oceanic/solid earth part. The amount of sulfur in the atmosphere at any given time is small, and the lifetime of most sulfur compounds in air is relatively short (e.g., days) because the fluxes through the atmosphere are large. Sulfur in the ocean as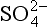 is cycled much more slowly, and the primary interactions in that cycle are with the solid earth.
is cycled much more slowly, and the primary interactions in that cycle are with the solid earth.
13.4 The Atmospheric Cycle of Sulfur
13.4.1 Transformations of Sulfur in the Atmosphere
Figure 13-2 summarizes the chemical and physical transformations of sulfur compounds that occur in the atmosphere. Most of the chemical transformations involve the oxidation of sulfur. The key oxidizing agents are thought to be the OH· radical, for the gas phase, and H2O2, O3, and OH· in the aqueous phase. Many of these transformations, however, can only be identified as “multistep” processes – that is, the detailed chemistry is not currently understood. The rates at which most of the transformations occur are also poorly understood and have been estimated only semiquantitatively. The amounts of sulfur within the various reservoirs (Fig. 13-1) are better known because they can be directly measured, although these data are greatly complicated by the patchy and episodic nature of the distribution of atmospheric sulfur species. Among the fluxes (see Fig. 13-6 and Table 13-2), the best data are available for anthropogenic SO2 emissions and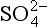 deposition to the surface in rainwater. Recent improvements have also been made in quantifying the natural emissions of reduced sulfur gases, especially from the world oceans. In sum, the qualitative picture of the atmospheric sulfur cycle now appears to be in good focus, although many quantitative details remain to be filled in.
deposition to the surface in rainwater. Recent improvements have also been made in quantifying the natural emissions of reduced sulfur gases, especially from the world oceans. In sum, the qualitative picture of the atmospheric sulfur cycle now appears to be in good focus, although many quantitative details remain to be filled in.
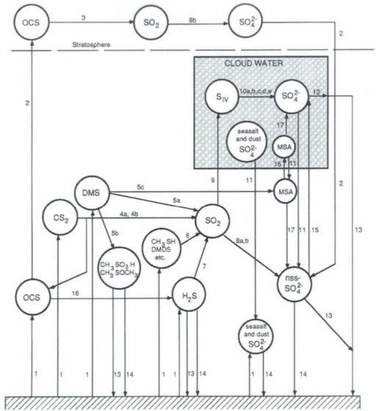
Fig. 13-2 The chemical and physical transformations of sulfur in the atmospheric cycle. Circles are chemical species, the box represents cloud-liquid phase. DMS = CH3SCH3, DMDS = CH3SSCH3, SIV = (SO2)aq + HSO3− +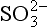 + CH2OHSO3−, and MSA (methane sulfonic acid) = CH3SO3H. The chemical transformations are as follows:
+ CH2OHSO3−, and MSA (methane sulfonic acid) = CH3SO3H. The chemical transformations are as follows:
2. Tropospheric/stratospheric exchange
5a. CH3SCH3 + OH → multistep → SO2
5b. CH3SCH3 + OH → multistep → CH3SOCH3
5c. CH3SCH3 + OH → multistep → CH3SO3H
6. CH3SH + OH → multistep → SO2
8b. SO2 → SO42− (Heterogeneous reaction)
CH2(OH)2 + HSO3−↔H2O + CH2OHSO3−
HSO3− + (H2O2)aq → multistep → H+ + SO42−
HSO3− + (O3)aq → multistep → H+ + SO42−
HSO3− + (H2O2)aq → multistep → 2H+ + SO42−
HSO3− + (OH)aq → multistep → H+ + SO42−
10e. HSO3− + O2 → multistep → H+ + SO42−
12. SO42− in cloudwater → SO42− in rainwater
(Modified with permission from R. J. Charlson, W. L. Chameides, and D. Klay (1985). The transformations of sulfur and nitrogen in the remote atmosphere. In “ The Biogeochemical Cycling of Sulfur and Nitrogen in the Remote Atmosphere” (J. N. Galloway, R. J. Charlson, M. O. Andreae, and H. Rodhe, eds), pp. 67–80, D. Reidel Publishing Company, Dordrecht.)
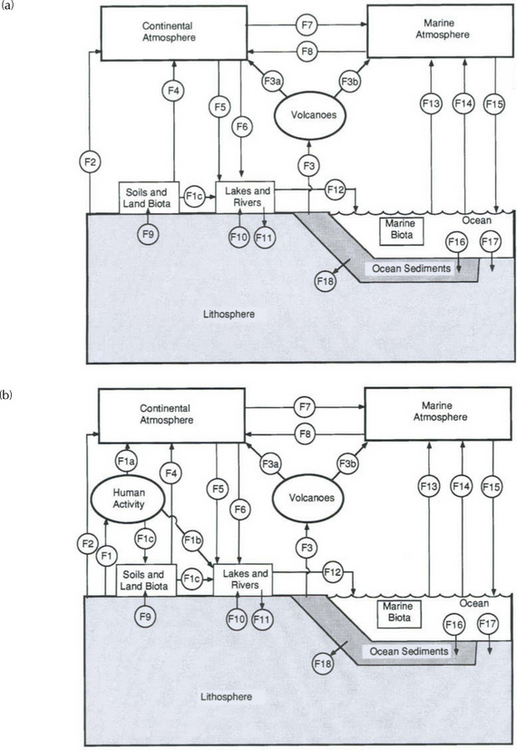
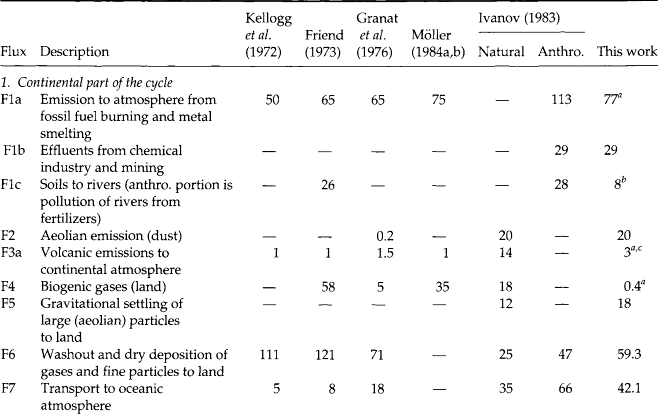
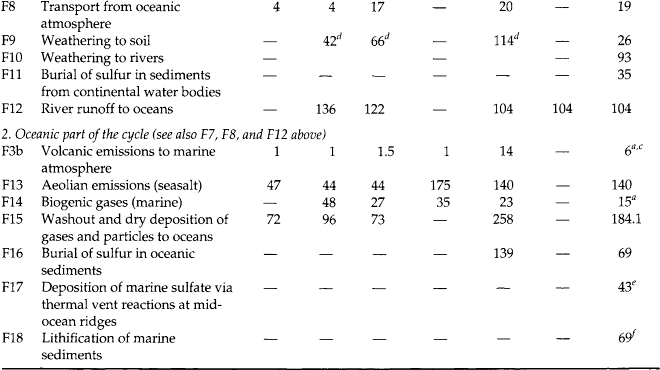
Fig. 13-6 Major fluxes of the global biogeochemical sulfur cycle excluding (a) and including (b) human activity. Numbers in circles designate fluxes described in Table 13-2. (modified from Ivanov, 1983)
The most important pathway of sulfur through the atmosphere involves injection as a low-oxidation-state gas and removal as oxidation-state VI sulfate in rainwater (Fig. 13-2, paths 1, 4, 5, 6, 7, 8, 9, 10, 12, and 13.) Since this pathway involves a change in chemical oxidation state and physical phase, the lifetime of sulfur in the atmosphere is governed by both the kinetics of the oxidation reactions and the frequency of clouds and rain. We will argue below that the overall process is fast – on the order of days – meaning that the atmospheric sulfur cycle is a regional phenomenon and that the distribution of nearly all sulfur species in the atmosphere is necessarily “patchy” over the globe.
13.4.2 Sources and Distribution of Atmospheric Sulfur
Biological processes result in the production of a variety of reduced sulfur-containing gases. The six most important of these are H2S (hydrogen sulfide), CS2 (carbon disulfide), OCS (carbonyl sulfide), CH3SH (methyl mercaptan), CH3SCH3 (dimethyl sulfide or DMS), and CH3SSCH3 (dimethyl disulfide or DMDS). Of these, DMS has been shown to dominate sulfur emissions from the open ocean (Andreae, 1985, 1986; Andreae and Raemdonck, 1983) and may, therefore, modulate the sulfur cycle over a large portion of the globe. A varying mixture of all six of these gases is found over terrestrial ecosystems (Adams et al., 1981). Estimates of biogenic sulfur emissions have been revised substantially downward over the last 15 years, according to a review by Bates et al. (1992). Referring to the final column in Table 13-2, we see that annual terrestrial biogenic emissions (F4) are currently estimated at 0.4 Tg S and marine biogenic emissions (F14) at 15 Tg S, each with large uncertainties due to measurement difficulties and the sporadic nature of the emissions. Other natural sources of low-oxidation state sulfur to the atmosphere are biomass burning and volcanoes (9 Tg S/yr), each of which emit sulfur mostly as SO2 gas. Volcanoes are a sporadic source, of secondary importance to the tropospheric sulfur cycle but capable of causing huge fluctuations locally and in the stratospheric reservoir. Biomass burning has both anthropogenic and natural components (often hard to separate). The sulfur output from this source is highly uncertain; it is not included in the fluxes in Table 13-2.
Emissions of sulfur to the atmosphere by humans are almost entirely in the form of SO2. The main sources are coal burning and sulfide ore smelting. The total anthropogenic flux is estimated to be about 80 Tg S/yr (Ivanov, 1983; Bates et al., 1992) and is thus substantially greater than the natural flux of low-oxidation-state sulfur to the atmosphere. Clearly, the atmospheric sulfur cycle is intensely perturbed by human activity. To estimate the spatial extent of this perturbation, we will need some idea of the residence time of sulfur in the atmosphere.
The definition of turnover time is total burden within a reservoir divided by the flux out of that reservoir – in symbols, τ=M/S (see Chapter 4). A typical value for the flux of non-seasalt sulfate (nss-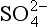 ) to the ocean surface via rain is 0.11 g S/m2 per year (Galloway, 1985). Using this value, we may consider the residence time of nss-
) to the ocean surface via rain is 0.11 g S/m2 per year (Galloway, 1985). Using this value, we may consider the residence time of nss-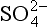 itself and of total non-seasalt sulfur over the world oceans. Appropriate vertical column burdens (derived from the data review of Toon et al., 1987) are 460 µg S/m2 for nss-
itself and of total non-seasalt sulfur over the world oceans. Appropriate vertical column burdens (derived from the data review of Toon et al., 1987) are 460 µg S/m2 for nss-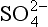 and 1700 µg S/m2 for the sum of DMS, SO2, and nss-
and 1700 µg S/m2 for the sum of DMS, SO2, and nss-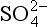 . These numbers yield residence times of about 1.5 days for nss-
. These numbers yield residence times of about 1.5 days for nss-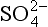 and 5.6 days for total non-seasalt sulfur. We might infer that the oxidation process is frequently slower than the rain removal process of particulate sulfate, although within the accuracy of these estimates it is safer simply to note that the two processes seem to be of similar duration. Direct estimates of the residence time of DMS with respect to oxidation by the OH radical are in the range of 1.5 to 2 days (Andreae, 1985 and references therein).
and 5.6 days for total non-seasalt sulfur. We might infer that the oxidation process is frequently slower than the rain removal process of particulate sulfate, although within the accuracy of these estimates it is safer simply to note that the two processes seem to be of similar duration. Direct estimates of the residence time of DMS with respect to oxidation by the OH radical are in the range of 1.5 to 2 days (Andreae, 1985 and references therein).
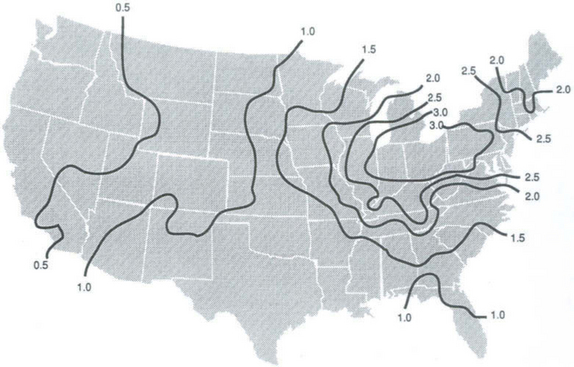
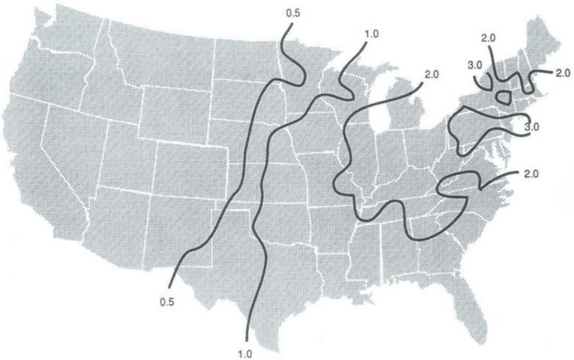
As shown in Figs 13-3 and 13-4, the flux of sulfate in rainwater over polluted industrial regions is of order 1 g S/m2 per year or about 10 times the remote marine flux. Since natural sources of sulfur are probably much weaker over continents, this indicates a massive human perturbation of the sulfur cycle within industrialized areas and a potentially strong perturbation over much larger areas depending on how far atmospheric sulfur is transported on average before being deposited. Figures 13-3 and 13-4 give the impression of a regional phenomenon with a horizontal scale of about 1000 km. This scale is confirmed by sulfur budget studies in polluted regions. For example, Ottar (1978) estimated that 80% of European sulfur emissions are deposited over Europe. For mid-latitude weather, horizontal transport over a spatial scale of order 1000 km corresponds to a time scale of a few days. Studies of the rate of oxidation of SO2 to sulfate in polluted regions indicate that a conversion rate of about 1% per hour is a good average. This corresponds to a residence time for SO2 gas of about 2 days. Once converted to sulfate, washout by rain should occur on a time scale of a few days.
For both polluted and remote conditions, therefore, the cycling of sulfur from low oxidation state gas to sulfate particles and then back to the surface in rain takes place on a time scale of a few days.
Some sulfur gases are directly absorbed at the surface, and particulate sulfur (aerosol) has some flux to the surface due to Brownian motion and gravitational settling. Together, these processes are referred to as “dry deposition” (to distinguish them from the rain removal mechanism). Dry deposition may be an important removal process for SO2 in polluted areas and is probably fairly minor for SO2 and the reduced sulfur gases over the oceans (Galloway, 1985). The dry deposition of sulfate particles (other than seasalt and dust sulfate) is also minor. In any case, these additional sinks for atmospheric sulfur can only have the effect of shortening its residence time.
An interesting exception to the patchiness of atmospheric sulfur compounds is carbonyl sulfide (OCS). This compound, which may be emitted directly or produced by the oxidation of CS2, is highly stable against further oxidation (until it reaches the stratosphere) and so is unavailable for rapid wet removal. As a result, OCS has a long residence time (∼ 1 year) as well as a large and globally uniform concentration (∼ 500 pptv) in the troposphere. Being inert in the troposphere, this compound, like the chlorofluorocarbons, is available for gradual mixing into the stratosphere. Here it can be broken apart by ultraviolet radiation and oxidized to SO2 and sulfate (see top of Fig. 13-2). Through this mechanism, OCS is thought to be the major source of sulfate particles in the stratosphere during volcanically quiescent periods (Crutzen, 1976). In the troposphere, while chemically unimportant, it is actually the largest reservoir of sulfur. This situation is analogous to that of nitrogen, where the dominant species is N2, which, being so inert, is usually ignored in discussions of atmospheric nitrogen chemistry.
Finally, there is a major flux of sulfur through the atmosphere in both seasalt particles (∼ 140 Tg S/yr) and terrestrial dust (∼ 20 Tg S/yr). In each case, the form of sulfur is sulfate, originating mostly as the mineral gypsum in the case of dust and as sulfate ion in seawater in the case of seasalt. Already in its fully oxidized, stable state, this component of atmospheric sulfur does not participate in atmospheric redox reactions, nor does it contribute to the acidity of cloud or rainwater. Instead, it is simply returned to the surface, via dry or wet removal, in the same chemical form in which it was emitted. Sulfate in both dust and seasalt particles is best viewed as an inert, secondary constituent, merely “along for the ride,” with little geochemical consequence. (It is very important to measure this component, however, so that it may be subtracted from total sulfate measurements in order to derive the non-seasalt sulfate quantity of chemical interest.) Since it does not need to be oxidized prior to wet removal and has, in addition, a large sink via dry deposition, the residence time of seasalt and dust sulfate is significantly shorter than that of other sulfur species. Because both seasalt and dust particles are relatively large, they are subject to significant removal by gravitational settling.
We have seen that, except for OCS, sulfur species in the atmosphere have residence times that are short (days) such that their geographical distribution is patchy. This perspective on the atmospheric sulfur cycle has important implications. While human emissions certainly constitute an overwhelming perturbation within heavily industrialized regions, there may be even larger areas of the globe in which the human influence on the sulfur cycle is relatively unimportant, e.g., much of the southern hemisphere (see discussion below on the remote marine sulfur cycle). In addition, we see that the sulfur cycle can only sensibly be studied on a regional basis and that the calculation of global budgets will necessarily be a painstaking process of making myriad measurements over a wide range of regions and seasons to allow accurate averaging.
13.4.3 The Remote Marine Atmosphere
Let us turn now to a detailed, box-model investigation of a regional sulfur cycle. The discussion so far suggests that the sulfur cycle over much of the ocean should be largely uninfluenced by human or other continental input. The absence of complex, polluted-air chemistry, along with a high degree of horizontal spatial homogeneity, should provide the simplest possible system for studying the transformations introduced in Fig. 13-2. We begin by assuming that the atmosphere is in a steady state (fluxes into and out of each box are equal) and that the remote marine environment is a closed system with respect to sulfur (no fluxes from or to the continents). We ignore seasalt sulfate. Finally, we assume that DMS is the only significant reduced sulfur species emitted from the ocean surface.
Figure 13-5 is the box model of the remote marine sulfur cycle that results from these assumptions. Many different data sets are displayed (and compared) as follows. Each box shows a measured concentration and an estimated residence time for a particular species. Fluxes adjoining a box are calculated from these two pieces of information using the simple formula, S=M/τ. The flux of DMS out of the ocean surface and of nss-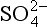 back to the ocean surface are also quantities estimated from measurements. These are converted from surface to volume fluxes (i.e., from µg S/(m2 h) to ng S/(m3 h)) by assuming the effective scale height of the atmosphere is 2.5 km (which corresponds to a reasonable thickness of the marine planetary boundary layer, within which most precipitation and sulfur cycling should take place). Finally, other data are used to estimate the factors for partitioning oxidized DMS between the MSA and SO2 boxes, for SO2 between dry deposition and oxidation to sulfate, and for nss-
back to the ocean surface are also quantities estimated from measurements. These are converted from surface to volume fluxes (i.e., from µg S/(m2 h) to ng S/(m3 h)) by assuming the effective scale height of the atmosphere is 2.5 km (which corresponds to a reasonable thickness of the marine planetary boundary layer, within which most precipitation and sulfur cycling should take place). Finally, other data are used to estimate the factors for partitioning oxidized DMS between the MSA and SO2 boxes, for SO2 between dry deposition and oxidation to sulfate, and for nss-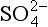 between wet and dry deposition.
between wet and dry deposition.
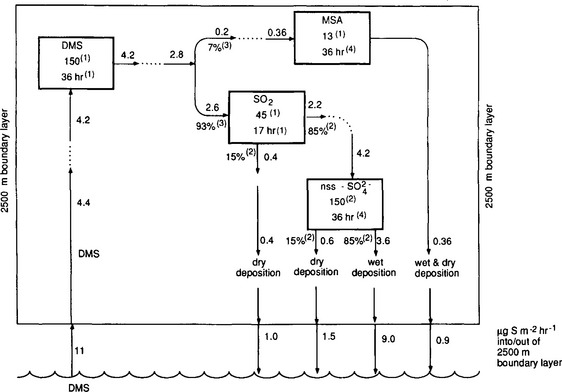
Fig. 13-5 The sulfur cycle in the remote marine boundary layer. Within the 2500 m boundary layer, burden units are ng S/m3 and flux units are ng S/(m3 h). Fluxes within atmospheric layer are calculated from the burden and the residence time. Ellipses indicate that calculations based on independent measurements are being compared. The measured total deposition of 13 ± 7 mg S/(m2 h)(2) agrees well with the calculated sum of 13.4 mg S/(m2 h), suggesting that a consistent model of the remote marine sulfur cycle within the planetary boundary layer can be constructed based on biogenic DMS inputs alone. Data: (1) Andreae (1986); (2) Galloway (1985); (3) Saltzman et al. (1983); (4) sulfate aerosol lifetime calculated earlier in this chapter based on marine rainwater pH; the same lifetime is applied to MSA aerosol. (adapted from Andreae, 1986). (Modified with permission from P. J. Crutzen, D. M. Whelpdale, D. Kley, and L. A. Barrie (1985). The cycling of sulfur and nitrogen in the remote atmosphere. In “ The Biogeochemical Cycling of Sulfur and Nitrogen in the Remote Atmosphere” (J. N. Galloway, R. J. Charlson, M. O. Andreae, and H. Rodhe, eds), pp. 203–212. D. Reidel Publishing Company, Dordrecht.)
We begin our analysis by comparing the surface fluxes. According to the indicated partitioning factors, 74% of the 11 µg DMS-S/m2/h emitted from the ocean surface should be returned as nss-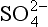 in rain. This leads to a predicted wet deposition flux of nss-
in rain. This leads to a predicted wet deposition flux of nss-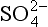 of 8.1 µg S/(m2/h), which is 37% lower than the measured flux of 13 µg S/(m2/h). Since the estimated accuracy of the DMS emission flux is ±50% (Andreae, 1986), this is about as good agreement as can be expected. It indicates that our “closed system” assumption is at least a reasonable first approximation. (A more sophisticated treatment would consider sulfur oxidation on hydrated seasalt particles (Sievering et al., 1992; Chameides and Stelson, 1992) and sulfur emissions from ships (Capaldo et al., 1999.))
of 8.1 µg S/(m2/h), which is 37% lower than the measured flux of 13 µg S/(m2/h). Since the estimated accuracy of the DMS emission flux is ±50% (Andreae, 1986), this is about as good agreement as can be expected. It indicates that our “closed system” assumption is at least a reasonable first approximation. (A more sophisticated treatment would consider sulfur oxidation on hydrated seasalt particles (Sievering et al., 1992; Chameides and Stelson, 1992) and sulfur emissions from ships (Capaldo et al., 1999.))
The two estimates of the flux into the DMS box are in excellent agreement, tending to support our 2.5 km assumed boundary layer height. However, the flux out of the DMS box is about 40% larger than necessary to support the fluxes through the MSA and SO2 boxes. This might suggest a missing sink for DMS. Could DMSO, another known oxidation product of DMS whose concentrations and lifetimes have not been carefully studied, fill this gap? An even larger descrepancy exists between the two estimates of the flux from SO2 to nss-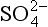 , which differ by almost a factor of two. The fact that the flux out of the DMS box (multiplied by the appropriate partitioning factors) provides better agreement with the flux into the nss-
, which differ by almost a factor of two. The fact that the flux out of the DMS box (multiplied by the appropriate partitioning factors) provides better agreement with the flux into the nss-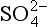 box suggests that the error may lie in the measured SO2 concentration (too low) or the estimated SO2 lifetime (too high). In any case, the various data sets are in reasonable agreement and all of the above comparisons suggest further measurements which would help to refine our understanding of these atmospheric processes.
box suggests that the error may lie in the measured SO2 concentration (too low) or the estimated SO2 lifetime (too high). In any case, the various data sets are in reasonable agreement and all of the above comparisons suggest further measurements which would help to refine our understanding of these atmospheric processes.
13.4.4 The Global Atmospheric Sulfur Budget
Figure 13-5 is an example of direct application of modelling concepts from Chapter 4 to the tropospheric portion of the sulfur cycle. As such, it illustrates two important aspects of the cycle approach:
1. This approach allows independent data sets to be compared.
2. It suggests which measurements would be most helpful to determine more precisely the main features of the system.
Another way in which the cycle approach is often used is in the development of global atmospheric budgets. Here, the only assumption made is that the atmosphere, taken as a whole, is in a steady state. Thus, if the total burden of S compounds in the air is not increasing or decreasing, the global fluxes into the atmosphere must be equal to the total of fluxes out of the atmosphere. A comparison of the flux out (from rainwater analyses) with known fluxes from industrial production led Eriksson (1959, 1960) and many others to suggest that a “missing source” was needed to balance the budget. Indeed, this notion has provided substantial impetus over the past 20 years to study natural sources, including emission of reduced sulfur from swamps (Adams et al., 1981), emission from volcanoes (Warneck, 1988), and biological production in and emission from the oceans (Andreae and Raemdonck, 1983).
Figure 13-6a (Ivanov, 1983) is a depiction of the natural global sulfur budget. Figure 13-6b depicts the budget with natural and anthropogenic sources. Table 13-2 serves to explain Fig. 13-6 and includes the wide range of estimates of various fluxes, and demonstrates the degree of uncertainty inherent in such approaches.
Comparison of Figs 13-6a and 13-6b clearly demonstrates the degree to which human activity has modified the cycle of sulfur, largely via an atmospheric pathway. The influence of this perturbation can be inferred, and in some cases measured, in reservoirs that are very distant from industrial activity. Ivanov (1983) estimates that the flux of sulfur down the Earth’s rivers to the ocean has roughly doubled due to human activity. Included in Table 13-2 and Fig. 13-6 are fluxes to the hydrosphere and lithosphere, which leads us to these other important parts of the sulfur cycle.
13.5 Hydrospheric Part of the Cycle of Sulfur
The ocean plays a central role in the hydrospheric cycling of sulfur since the major reservoirs of sulfur on the Earth’s surface are related to various oceanic depositional processes. In this section we consider the reservoirs and the fluxes focusing on the cycling of sulfur through this oceanic node.
There are three major sulfur reservoirs at the Earth’s surface (Table 13-3): as S(– II) in sedimentary shales, as S(+VI) in evaporite deposits and as S(+VI) in seawater. The rate of cycling through these reservoirs is closely related to the fluxes of sulfur to and from the ocean. However, sulfur is unusual among the major constituents of natural waters in that its fluxes have been significantly modified by human activities. Thus, a useful starting point is the pre-industrial cycle of Fig. 13-6a. The main features are (1) a tightly closed loop through which sulfate is carried by seaspray into the atmosphere, but quickly returned to the ocean, and (2) a larger, slower loop in which sulfate is derived by weathering, carried by rivers to the ocean, and returned to the continents through the cycling of rocks ( Chapter 9). Over geologic periods of time, the ocean composition is thought to be relatively constant, with river inputs to the ocean balanced by depositional processes. What processes maintain this balance?
Table 13-3
Some naturally occurring sulfur compounds

bCalculated from mass of surface freshwater (1.3 × 1020 g H2O) and average sulfate concentration (2.5 × 10−6 g S/g H2O).
cCalculated from carbon in ocean biota (3000 Tg) and approximate mass ratio for sulfur to carbon of 1:100.
13.5.1 Oceanic Outputs
There are both uncertainties and controversies concerning the removal of sulfur from the ocean. FeS2 (pyrite) in sedimentary shales is most often formed in reducing marine sediments, particularly when these sediments underlie waters of high biological productivity. In these areas, the flux of (dead) organic carbon to the sediments greatly exceeds the rates at which oxygen can diffuse into the sediments ( Chapter 8). Iron (III) hydroxides and then sulfate become the terminal electron acceptors for the oxidation of organic matter, thereby providing a source of Fe+2 and HS− for pyrite formation.
Various workers have estimated the rate of pyrite formation. Berner (1972) summed thesulfur accumulation rates of various sediment types in proportion to their areal coverage and found a flux of about 10% of the river flux. Li (1981) carried out a similar calculation and finds 30% of the river flux, probably indicative of the uncertainty of the approach. Toth and Lerman (1977) established that the decrease of sulfate with depth in sediment pore waters is a function of sedimentation rate. This information was used to estimate the diffusive flux of sulfur into sediments driven by pyrite formation, again a value about 10% of the river flux. Apparently, pyrite formation, while measureable, is not the dominant removal process.
Evaporite deposition is a much more episodic process and thus difficult to quantify. Because seawater is significantly undersaturated with respect to common evaporitic minerals, like gypsum and halite, evaporites are only formed when restricted circulation develops in an ocean basin in which evaporation exceeds precipitation. A geologically recent example is the Mediterranean Sea of 5–6 Myr ago. At this time excess evaporation exceeded the supply of ocean water through shallow inlet(s) from the Atlantic Ocean. As salinity increased, first CaSO4, then NaCl precipitated. Over time, salt deposits 2–3 km thick formed. This thickness represents about 40 desiccations of the entire volume of the Mediterranean. How rapidly would the Mediterranean have to evaporate to remove all the sulfate introduced by rivers to the ocean? The time scale τ is given by τ = VMedCoc/Fr, where Fr is the river flux of sulfate, VMed is the volume of the Mediterranean, and Coc is the concentration of sulfate in the ocean. This time is about 25 000 yr, which could be readily achieved (2000 m of water depth in 25 000 yr is only 8 cm/yr of excess evaporation). A second point to consider is that the basin will eventually fill. One meter of seawater evaporates to a layer of solid just over a centimeter thick. Evaporite formation could only be sustained in the Mediterranean for 2–3 Myr, removing only about one-third of the ocean’s sulfate in this time. Evaporite formation can match the river flux, but it must be taking place on a large scale.
A solution, still controversial, has been recently proposed. This is the loss of sulfate from seawater during hydrothermal circulation through mid-ocean ridges (Edmond et al., 1979). The flow of water through these systems is estimated to be about 1.4 × 1014 L/yr, about 0.4% of the flow of rivers. However, sulfate is quantitatively removed, yielding a flux of 125 Tg S/yr, capable of balancing the river flux. The controversy is whether the chemistry involved in removing sulfate is the formation of anhydrite (CaSO4) or reduction and subsequent precipitation as metal sulfides. Anhydrite forms on simple heating of seawater. As the ocean crust ages and cools it would redissolve, creating an equal and opposite flux. In contrast, metal sulfides are much more resistant to subsequent interaction with seawater.
13.5.2 Oceanic Inputs
Referring again to Fig. 13-6a, the materials that constitute the oceanic sinks for sulfur are recycled over time by exposure to weathering on the continents. The rates at which these processes occur help to regulate the flux of sulfur into rivers.
The evaporite source is characterized by covariation of sulfate (from gypsum) and chloride (from halite). That elements can be recycled from the ocean to land by movement of salt-bearing aerosols (so-called “cyclic salts”) has confused the interpretation of river flux data somewhat. While this cycling generally follows the ratio of salts in the sea, the S/Cl ratio is an exception. Taking the S/Cl ratio of the cyclic component to be 2 (based on compositional data for marine rains) and assuming that all chloride in rivers is cyclic, an upper limit for the cyclic influence can be calculated.
where Fr,Cl is the riverine flux of Cl to seawater. However, not all the chloride is cyclic, a fact first appreciated in recent years. An example comes from a detailed study of river geochemistry conducted in the Amazon Basin. In the inland regions, rains typically have a chloride content of 10 µM, while major inland tributaries have chloride contents of 20–100 µM. These data suggest that only 25% of the Cl is cyclic, whereas 75% is derived by weathering of evaporites. Indeed, 90% of this 75% can be shown to have its origin in the Andean headwaters, derived from evaporites that make up only 2% of the area of the Amazon Basin (Stallard and Edmond, 1981). As the ratio of sulfate to chloride in evaporite deposits is generally much higher than seawater (gypsum (CaSO4·2H2O) precipitates first as seawater is evaporated), dissolution of evaporites represents one of the principal sources of riverine sulfate.
The other principal source is weathering of sedimentary or igneous sulfides, mainly pyrite, by the oxidation:
What are the relative contributions of these two sources? Two approaches have been taken. One is to establish the geology and hydrology of a basin in great detail. This has been carried out for the Amazon (Stallard and Edmond, 1981) with the result that evaporites contribute about twice as much sulfate as sulfide oxidation. The other approach is to apply sulfur isotope geochemistry. As mentioned earlier, there are two relatively abundant stable isotopes of S, 32S, and 34S. The mean 34/32 ratio is 0.0442. However, different source rocks have different ratios, which arise from slight differences in the reactivities of the isotopes. These deviations are expressed as a difference from a standard, in the case of sulfur the standard being a meteorite found at Canyon Diablo, Arizona.
Evaporitic sulfur has a range of sulfur isotopic composition from +10‰ to +30‰, while sedimentary sulfur is depleted in the heavy isotope and has a range of isotopic composition of about – 40‰ to +10‰. Most of this variation reflects systematic changes with geological age. The source fractions of a river water can be estimated from an isotopic mass balance:
where Xi is the fraction from that source. This approach has been applied to the Volga River, which has a δ34S of +6‰, suggesting again about 2/3 from evaporites and 1/3 from sulfides (calculated taking δ34Sevap as +15‰ and δ34Spyrite as –15‰).
Accepting these relative proportions from evaporites (2/3) and sulfides (1/3), the characteristic times, τi, of cycling of the evaporite sulfur and sulfide sulfur reservoirs can be estimated from the reservoir sizes (Ri) in Table 13-3, and the river flux of sulfur. For evaporites:
= 140 Myr and for sulfides:τpyrite = (48 × 106 Tg)/(104/3 Tg/yr) = 140 Myr
The characteristic times of sulfur cycling through the two reservoirs are nearly identical. Sulfur cycling through evaporites is on a time scale similar to the cycling of the evaporites themselves, (about 200 Myr, Garrels and Mackenzie, 1971) suggesting that physical factors limit the rate of weathering of this very soluble component. Sulfur cycling through shales is considerably faster than the cycling of the overall shale reservoir (about 600 Myr).
Questions
13-1. What would be the approximate sulfate concentration of rainwater globally for the following cases (assume that rainfall is uniformly 75 cm/yr):
(a) The only source of sulfur were DMS and it was uniform over the globe.
(b) In addition to (a) consider the sulfur from industry uniformly distributed over the globe.
(c) Same as (b), but assume that all industry is in the northern hemisphere and consider the hemispheres separately.
(d) Compare these concentrations to the data for eastern North America (Fig. 13-4).
13-2. Sulfur and oxygen are in the same column of the periodic table. List their chemical similarities and differences and consider the biogeochemical consequences of each.
13-3. Estimate the total amount of oxidation (mol/yr) caused by the reduction of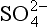 to S(– II). Compare this to the total amount of oxidation by O2.
to S(– II). Compare this to the total amount of oxidation by O2.
13-4. After considering the Redfield-Ketchum-Richards ratio (see Chapter 10) for C:N:P consider the analog for sulfur in land and marine biota. What key biochemical species are the major determinants of the C:S relationship in biota?
13-5. Hypothetical problem for chemists: consider the global cycle of selenium which has many chemical similarities to sulfur. Construct a box diagram for the global selenium cycle based on known similarities and differences of Se and S.
13-6. This problem is a first-order attempt to quantify the possible anthropogenic perturbation of the northern hemisphere (NH) marine sulfur cycle. First, assume that present day anthropogenic sulfur emissions result in 20 Tg S/yr being transported from North America to the atmosphere over the NH Atlantic and 10 Tg S/yr being transported from Asia to the atmosphere over the NH Pacific. Assume a uniform concentration in the N-S direction, average westerly wind speeds of 10 m/s, that both ocean regions are 4000 km in N-S extent, that the NH Atlantic is 5500 km from east to west and that the NH Pacific is 8500 km from east to west. Next, assume that biogenic emissions of DMS from the ocean to the atmosphere are uniformly 0.1 g S/m2 per year (the average value from Andreae and Raemdonck, 1983). Now if we use a 2-day average residence time (or e-folding time – see Chapter 4) for sulfur in the atmosphere, what percentage of total atmospheric sulfur would be anthropogenic sulfur at the middle and western edge of each ocean?
Adams, D. F., Farwell, S. O., Robinson, E., Park, M. R., Bamsberger, W. L. Biogenic sulfur source strengths. Environ. Sci. Technol. 1981; 15:1493–1498.
Andreae, M. O. The emission of sulfur to the remote atmosphere. In: Galloway J. N., Charlson R. J., Andreae M. O., Rodhe H., eds. The Biogeochemical Cycling of Sulfur and Nitrogen in the Remote Atmosphere. Geneva: Reidel, 1985.
Andreae, M. O. The ocean as a source of atmospheric sulfur compounds. In: Buat-Menard P., ed. The Role of Air-Sea Exchange in Geochemical Cycling. Dordrecht: Reidel, 1986.
Andreae, M. O., Raemdonck, H. Dimethyl sulfide in the surface ocean and the marine atmosphere: a global view. Science. 1983; 221:744–747.
Bates, T. S., Lamb, B. K., Guenther, A., Dignon, J., Stoiber, R. E. Sulfur emissions to the atmosphere from natural sources. J. Atmos. Chem. 1992; 14:315–337.
Berner, R. A. Sulfate reduction, pyrite formation and the oceanic sulfur budget. In: Dyrssen D., Jagner D., eds. The changing chemistry of the oceans. Dordrecht: Wiley-Interscience, 1972.
Bigg, E. K., Gras, J. L., Evans, C. Origin of Aitken particles in remote regions of the Southern Hemisphere. J. Atmos. Chem. 1984; 1:203–214.
Capaldo, K., Corbett, J. J., Kasibhatla, P., Fischbeck, P., Pandis, S. N. Effects of ship emissions on sulphur cycling and radiative climate forcing over the ocean. Nature. 1999; 400:743–746.
Chameides, W. L., Stelson, A. W. Aqueous-phase chemical processes in deliquescent sea-salt aerosols: a mechanism that couples the atmospheric cycles of S and sea salt. J. Geophys. Res. 1992; 97:20565–20580.
Crutzen, P. J. The possible importance of CSO for the sulphate layer of the stratosphere. Geophys. Res. Lett. 1976; 3:73–76.
Edmond, J. M., Measures, C., McDuff, R. E., Chan, L. H., Collier, R. W., Grant, B., Gordon, L. I., Corliss, J. B. Ridge crest hydrothermal activity and the balances of the major and minor elements in the ocean: the Galapagos data. Earth Planet. Sci. Lett. 1979; 46:1–18.
Eriksson, E. The yearly circulation of chloride and sulfur in nature: meteorological, geochemical and pedological implications, Part I. Tellus. 1959; 11:375–603.
Eriksson, E. The yearly circulation of chloride and sulfur in nature: meteorological, geochemical and pedological implications, Part II. Tellus. 1960; 12:63–109.
Freney, J. R., Ivanov, M. V., Rodhe, H. The sulphur cycle. In: Bolin B., Cook R. B., eds. The Major Biogeochemical Cycles and Their Interactions, SCOPE 21. Stockholm: Wiley, 1983.
Friend, J. P. The global sulfur cycle. In: Rasool S. I., ed. Chemistry of the Lower Atmosphere. Chichester: Plenum Press, 1973.
Galloway, J. N. The deposition of sulfur and nitrogen from the remote atmosphere. In: Galloway J. N., Charlson R. J., Andreae M. O., Rodhe H., eds. The Biogeochemical Cycling of Sulfur and Nitrogen in the Remote Atmosphere. New York: Reidel, 1985.
Garrels, R. M., Mackenzie, F. T. Evolution of sedimentary rocks. Dordrecht: W. W. Norton; 1971.
Granat, L., Rodhe, H., Hallberg, R. O., The global sulphur cycleSvensson B. H., Söderlund R., eds. Nitrogen, Phosphorus and Sulphur — Global Cycles. SCOPE Report 7. Ecol. Bull., New York, 1976. 89–134.
Grinenko, V. A., Ivanov, M. V. Principal reactions of the global biogeochemical cycle of sulphur. In: Ivanov M. V., Freney J. R., eds. The Global Biogeochemical Sulfur Cycle, SCOPE 19. Stockholm: Wiley, 1983.
Ivanov, M. V. Major fluxes of the global biogeochemical cycle of sulphur. In: Ivanov M. V., Freney J. R., eds. The Global Biogeochemical Sulphur Cycle, SCOPE 19. Chichester: Wiley, 1983.
Jorgensen, B. B. A thiosulfate shunt in the sulfur cycle of marine sediments. Science. 1990; 249:152–154.
Kellogg, W. W., Cadle, R. D., Allen, E. R., Lazrus, A. L., Martell, E. A. The sulfur cycle. Science. 1972; 175:587–596.
Li, Y. H. Geochemical cycle of elements and human perturbation. Geochim. Cosmochim. Acta. 1981; 45:2037–2084.
Migdisov, A. A., Ronov, A. B., Grinenko, V. A. The sulphur cycle in the lithosphere, Part I: Reservoirs. In: Ivanov M. V., Freney J. R., eds. The Global Biogeochemical Sulphur Cycle, SCOPE 19. Chichester: Wiley, 1983.
Möller, D. Estimation of the global man-made sulphur emission. Atmos. Environ. 1984; 18:19–27.
Möller, D. On the global natural sulphur emission. Atmos. Environ. 1984; 18:29–39.
Ottar, B. An assessment of the OECD study on long range transport of air pollutants (LRTAP). Atmos. Environ. 1978; 12:445–454.
Saltzman, E. S., Savoie, D. L., Zika, R. G., Prospero, J. M. Methane sulfonic acid in the marine atmosphere. J. Geophys. Res. 1983; 88:10897–10902.
Sievering, H., Boatman, J., Gorman, E., Kim, Y., Anderson, L., Ennis, G., Luria, M., Pandis, S. Removal of sulphur from the marine boundary layer by ozone oxidation in sea-salt aerosols. Nature. 1992; 360:571–573.
Stallard, R. F., Edmond, J. M. Geochemistry of the Amazon 1. Precipitation chemistry and the marine contribution to the dissolved load at the time of peak discharge. J. Geophys. Res. 1981; 86:9844–9858.
Toon, O. B., Kasting, J. F., Turco, R. P., Liu, M. S. The sulfur cycle in the marine atmosphere. J. Geophys. Res. 1987; 92:943–963.
Toth, D. J., Lerman, A. Organic matter reactivity and sedimentation rates in the ocean. Am. J. Sci. 1977; 277:265–285.
Volkov, I. I., Rozanov, A. G. The sulphur supply in oceans, Part I: Reservoirs and fluxes. In: Ivanov M. V., Freney J. R., eds. The Global Biogeochemical Sulphur Cycle, SCOPE 19. Chichester: Wiley, 1983.
Warneck, P. Chemistry of the Natural Atmosphere. Chichester: Academic Press; 1988.
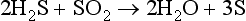
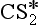
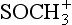 + O2 → CS + SO2
+ O2 → CS + SO2