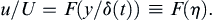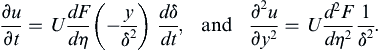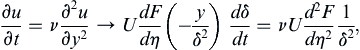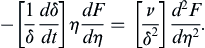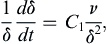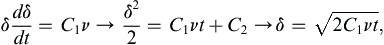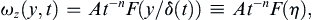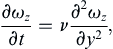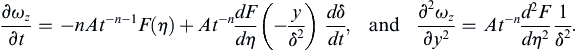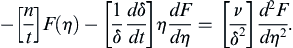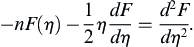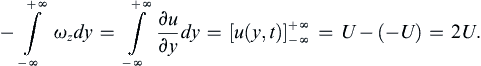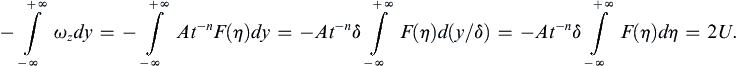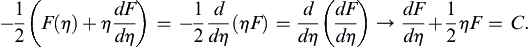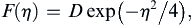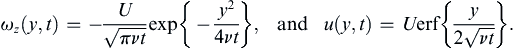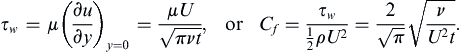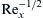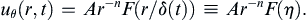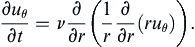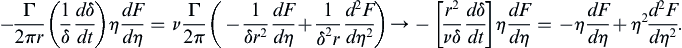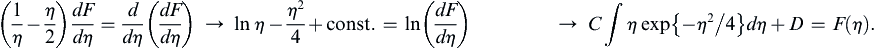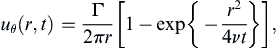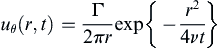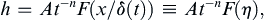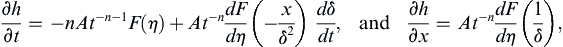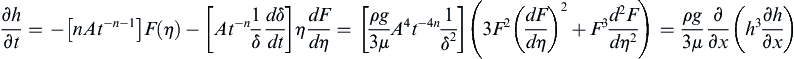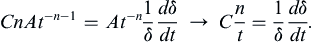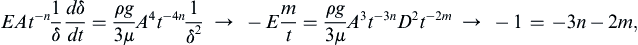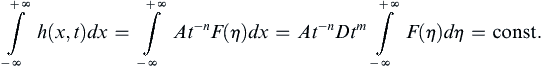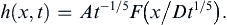9.4. Similarity Solutions for Unsteady Incompressible Viscous Flow

Similarity solutions to partial differential equations are possible when a variable transformation exists that allows the partial differential equation to be rewritten as an ordinary differential equation. Several such solutions for the Navier-Stokes equations are presented in this section.

So far, steady flows with parallel, or nearly parallel, streamlines have been considered. In this situation, the nonlinear advective acceleration is zero, or small, and the stream-wise velocity reduces to a function of one spatial coordinate, and time. When a viscous flow with parallel or nearly parallel streamlines is impulsively started from rest, the flow depends on the spatial coordinate(s) and time. For such unsteady flows, exact solutions still exist because the nonlinear advective acceleration drops out again (see Exercise 9.41). In this section, several simple and physically revealing unsteady flow problems are presented and solved. The first is the flow due to impulsive motion of a flat plate parallel to itself, commonly known as Stokes’ first problem. (The flow is sometimes unfairly associated with the name of Rayleigh, who used Stokes’ solution to predict the thickness of a developing boundary layer on a semi-infinite plate.)

A similarity solution is one of several ways to solve Stokes’ first problem. The geometry of this problem is shown in Figure 9.12. An infinite flat plate lies along y = 0, surrounded by an initially quiescent fluid (with constant ρ and μ) for y > 0. The plate is impulsively given a velocity U at t = 0 and constant pressure is maintained at x = ±∞. At first, only the fluid near the plate will be drawn into motion, but as time progresses the thickness of this moving region will increase. Since the resulting flow at any time is invariant in the x direction (∂/∂x = 0), the continuity equation ∂u/∂x + ∂v/∂y = 0 requires ∂v/∂y = 0. Thus, it follows that v = 0 everywhere since it is zero at y = 0. Therefore, the simplified horizontal and vertical momentum equations are:

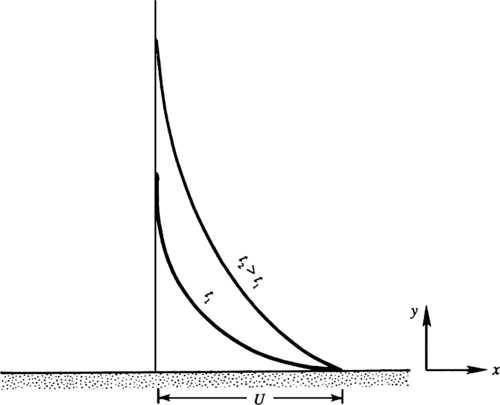
Figure 9.12 Laminar flow due to a flat plate that starts moving parallel to itself at speed U at t = 0. Before t = 0, the entire fluid half-space (y > 0) was quiescent. As time progresses, more and more of the viscous fluid above the plate is drawn into motion. Thus, the flow profile with greater vertical extent corresponds to the later time.

ρ∂u∂t=−∂p∂x+μ∂2u∂y2,and0=−∂p∂y.

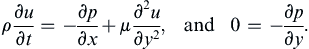
Just before t = 0, all the fluid is at rest so p = constant. For t > 0, the vertical momentum equation only allows the fluid pressure to depend on x and t. However, at any finite time, there will be a vertical distance from the plate where the fluid velocity is still zero, and, at this vertical distance from the plate, ∂p/∂x is zero. However, if ∂p/∂x = 0 far from the plate, then ∂p/∂x = 0 on the plate because ∂p/∂y = 0. Thus, the horizontal momentum equation reduces to:

∂u∂t=ν∂2u∂y2,

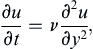(9.20)

subject to the boundary and initial conditions:

u(y,t=0)=0,u(y=0,t)={0fort<0Ufort≥0},andu(y→∞,t)=0.

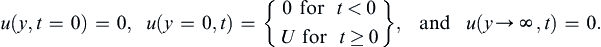(9.21, 9.22, 9.23)

The problem is well posed because (9.22) and (9.23) are conditions at two values of y, and (9.21) is a condition at one value of t; this is consistent with (9.20), which involves a first derivative in t and a second derivative in y.

The partial differential equation (9.20) can be transformed into an ordinary differential equation by switching to a similarity variable. The reason for this is the absence of enough other parameters in this problem to render y and t dimensionless without combining them. Based on dimensional analysis (see Section 1.11), the functional form of the solution to (9.20) can be written:

u/U=f(y/νt,y/Ut).

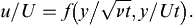(9.24)

where f is an undetermined function. However, (9.20) is a linear equation, so u must be proportional to U. This means that the final dimensionless group in (9.24) must be dropped, leaving:

u/U=F(y/νt)≡F(η),

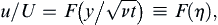(9.25)

where F is an undetermined function, but this time it is a function of only one dimensionless group and this dimensionless group η = y/(νt)^1/2 combines both independent variables. This reduces the dimensionality of the solution space from two to one, an enormous simplification.

Equation (9.25) is the similarity form for the fluid velocity in Stokes’s first problem. The similarity variable η could have been defined differently, such as νt/y², but different choices for η merely change F, not the final answer. The chosen η allows F to be interpreted as a velocity profile function with y appearing to the first power in the numerator of η. At any fixed t > 0, y and η are proportional.

Using (9.25) to form the derivatives in (9.20), leads to:

∂u∂t=UdFdη∂η∂t=−Uy2νt3dFdη=−Uη2tdFdηandU∂2F∂y2=U∂∂y(dFdη∂η∂y)=U∂∂y(1νtdFdη)=Uνtddη(dFdη)∂η∂y=Uνtddη(dFdη)

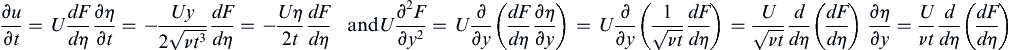
and these can be combined to provide the equivalent of (9.20) in similarity form:

−η2dFdη=ddη(dFdη)

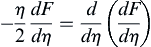(9.26)

The initial and boundary conditions (9.21) through (9.23) for F reduce to:

F(η=0)=1,andF(η→∞)=0,

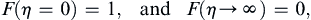(9.27, 9.28)

because (9.21) and (9.23) reduce to the same condition in terms of η. This reduction is expected because (9.20) is a partial differential equation and needs two conditions in y and one condition in t to be solved, while (9.26) is a second-order ordinary differential equation and needs only two boundary conditions to be solved. Equation (9.26) is readily separated:

−η2dη=d(dF/dη)dF/dη,

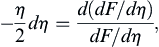
and integrated to reach:

−η24=ln(dF/dη)+const.,ordF/dη=Aexp(−η2/4),

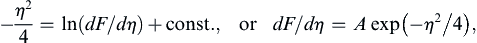
where A is a constant. Integrating again leads to:

F(η)=A∫0ηexp(−ξ2/4)dξ+B,

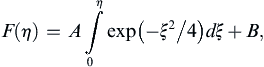
where ξ is just an integration variable and B is another constant. The condition (9.27) sets B = 1, while condition (9.28) gives:

0=A∫0∞exp(−ξ2/4)dξ+1,or0=2A∫0∞exp(−ζ2)dζ+1,so0=2A(π/2)+1,

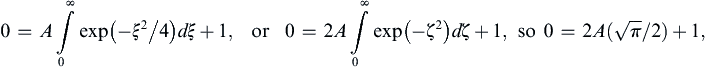
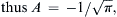thusA=−1/π, where the tabulated integral 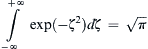∫−∞+∞exp(−ζ2)dζ=π has been used. The final solution for u then becomes:

u(y,t)U=1−erf(y2νt),whereerf(ζ)=2π∫0ζexp(−ξ2)dξ,

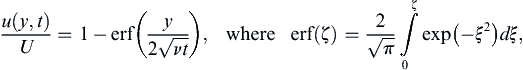(9.30)

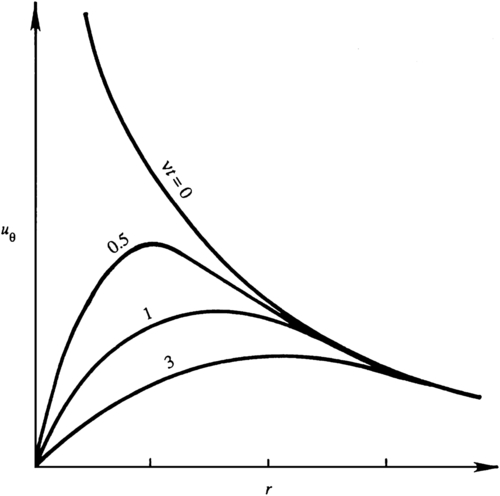
is the error function and again ξ is just an integration variable. The error function is a standard tabulated function (see Abramowitz & Stegun, 1972). Equation (9.30) is the solution to the problem and the form of (9.30) makes it is apparent that the velocity profile at different times will collapse into a single curve of u/U vs. η, as shown in Figure 9.13.

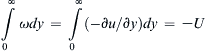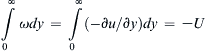The nature of the variation of u/U with y for various values of t is sketched in Figure 9.12, and this solution has a diffusive nature. At t = 0, a vortex sheet (that is, a velocity discontinuity) is created at the plate surface. The initial vorticity is in the form of a delta function, which is infinite at the plate surface and zero elsewhere. The integral ∫0∞ωdy=∫0∞(−∂u/∂y)dy=–U is independent of time, so no new vorticity is generated after the initial time. The flow given by (9.30) occurs as the initial vorticity diffuses away from the wall. The situation is analogous to a heat conduction problem in a semi-infinite solid extending from y = 0 to y = ∞. Initially, the solid has a uniform temperature, and at t = 0 the face at y = 0 is suddenly brought to a different temperature. The temperature distribution for this heat conduction problem is given by an equation similar to (9.30).

We may arbitrarily define the thickness of the diffusive layer as the distance at which u falls to 1% of U. From Figure 9.13, u/U = 0.01 corresponds to y/(νt)^1/2 = 3.64. Therefore, in time t the diffusive effects propagate to a distance of:

δ99∼3.64νt,

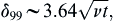(9.31)

which defines the 99% thickness of the layer of moving fluid and this layer's thickness increases as t^1/2. Obviously, the factor of 3.64 is somewhat arbitrary and can be changed by choosing a different ratio of u/U as the definition for the edge of the diffusive layer. However, 99% thicknesses are commonly considered in boundary layer theory (see Chapter 10).

Stokes’ first problem illustrates an important class of fluid mechanical problems that have similarity solutions. Because of the absence of suitable scales to render the independent variables dimensionless, the only possibility was a combination of variables that resulted in a reduction in the number of independent variables required to describe the problem. In this case the reduction was from two (y,t) to one (η) so that the formulation reduced a partial differential equation in y and t to an ordinary differential equation in η.

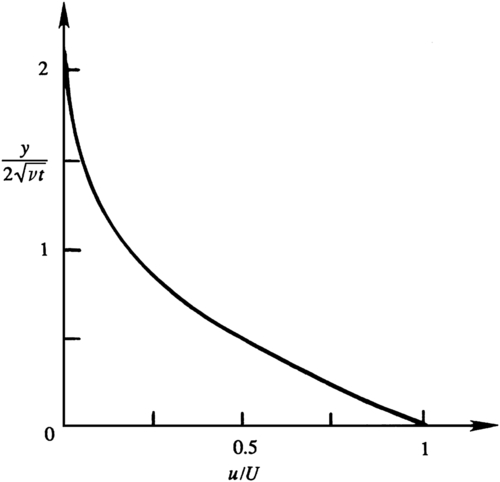
Figure 9.13 Similarity solution of laminar flow due to an impulsively started flat plate. Using these scaled coordinates, all flow profiles like those shown on Figure 9.12 will collapse to the same curve. The factor of two in the scaling of the vertical axis follows from (9.30).

The solution (9.30) for u(y,t) is self-similar in the sense that at different times t₁, t₂, t₃, … the various velocity profiles u(y,t₁), u(y,t₂), u(y,t₃), … fall on a single curve if u is scaled by U and y is scaled by the diffusive thickness (νt)^1/2. Moreover, such a collapse will occur for different values of U and for fluids having different ν.

Similarity solutions arise in situations in which there are no imposed length or time scales provided by the initial or boundary conditions (or the field equation). A similarity solution would not be possible if, for example, the boundary conditions were changed after a certain time t₁ since this introduces a time scale into the problem (see Exercise 9.40). Likewise, if the flow in Stokes’ first problem was bounded above by a second parallel plate, there could be no similarity solution because the distance to the second plate introduces a length scale into the problem.

Similarity solutions are often ideal for developing an understanding of flow phenomena, so they are sought wherever possible. A method for finding similarity solutions starts from a presumed form for the solution:

γ=At−nF(ξ/δ(t))≡At−nF(η)orγ=Aξ−nF(ξ/δ(t))≡Aξ−nF(η),

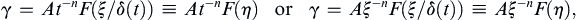(9.32a,b)

where γ is the dependent field variable of interest, (a velocity component, for example), A is a constant (units = [γ] × [time]ⁿ or [γ] × [length]ⁿ), ξ is the independent spatial coordinate, t is time, η = ξ/δ is the similarity variable, and δ(t) is a time-dependent length scale (not the Dirac delta-function). The factor of At^–n or Aξ^–n that multiplies F in (9.32) is sometimes needed for similarity solutions that are infinite (or zero) at t = 0 or ξ = 0. Use of (9.32) is illustrated in the following examples.

Example 9.6

Use (9.32a) to find the similarity solution to Stokes’ first problem.

Solution

The solution plan is to populate (9.32a) with the appropriate variables, substitute it into the field equation (9.20), and then require that the coefficients all have the same time dependence. For Stokes’ first problem γ = u/U, and the independent spatial variable is y. For this flow, the coefficient At^–n is not needed since u/U = 1 at η = 0 for all t > 0 and this can only happen when A = 1 and n = 0. Thus, the dimensional analysis result (9.25) may be replaced by (9.32a) with A = 1, n = 0, and ξ = y:

u/U=F(y/δ(t))≡F(η).

 

Partial derivatives in time and space produce:

∂u∂t=UdFdη(−yδ2)dδdt,and∂2u∂y2=Ud2Fdη21δ2.

 

Reconstructing (9.20) with these replacements yields:

∂u∂t=ν∂2u∂y2→UdFdη(−yδ2)dδdt=νUd2Fdη21δ2,

 

which can be rearranged to find:

−[1δdδdt]ηdFdη=[νδ2]d2Fdη2.

 

For this equation to be in similarity form, the coefficients in [,]-brackets must both have the same time dependence so that division by this common time dependence will leave an ordinary differential equation for F(η) and t will no longer appear. Thus, we require the two coefficients to be proportional:

1δdδdt=C1νδ2,

 

where C₁ is the constant of proportionality. This is a simple differential equation for δ(t) that is readily rearranged and solved:

δdδdt=C1ν→δ22=C1νt+C2→δ=2C1νt,

 

where the condition δ(0) = 0 has been used to determine that C₂ = 0. When C₁ = 1/2, the prior definition of η in (9.25) is recovered, and the solution for u proceeds as before (see (9.26) through (9.30)).

Example 9.7

At t = 0 an infinitely thin vortex sheet in a fluid with density ρ and viscosity μ coincides with the plane defined by y = 0, so that the fluid velocity is U for y > 0 and −U for y < 0. The coordinate axes are aligned so that only the z-component of vorticity is non-zero. Determine the similarity solution for ω_z(y,t) for t > 0.

Solution

The solution plan is the same as for Example 9.6, except here the coefficient At^–n must be included. In this circumstance, there will be only one component of the fluid velocity, u = u(y,t)e_x, so ω_z(y,t) = –∂u/∂y. The independent coordinate y does not appear in the initial condition, so (9.32a) is the preferred choice. Its appropriate form is:

ωz(y,t)=At−nF(y/δ(t))≡At−nF(η),

 

and the field equation:

∂ωz∂t=ν∂2ωz∂y2,

 

is obtained by applying ∂/∂y to (9.20). Here, the derivatives of the similarity solution are:

∂ωz∂t=−nAt−n−1F(η)+At−ndFdη(−yδ2)dδdt,and∂2ωz∂y2=At−nd2Fdη21δ2.

 

Reassembling the field equation and canceling common factors produces:

−[nt]F(η)−[1δdδdt]ηdFdη=[νδ2]d2Fdη2.

 

From Example 9.6, we know that requiring the second and third coefficients in [,]-brackets to be proportional with a proportionality constant of 1/2 produces δ = (νt)^1/2. With this choice for δ, each of the coefficients in [,]-brackets is proportional to 1/t so, the similarity equation becomes:

−nF(η)−12ηdFdη=d2Fdη2.

 

The boundary conditions are: 1) at any finite time the vorticity must go to zero infinitely far from the initial location of the vortex sheet, F(η) → 0 for η → ∞, and 2) the velocity difference across the diffusing vortex sheet is constant and equal to 2U:

−∫−∞+∞ωzdy=∫−∞+∞∂u∂ydy=[u(y,t)]−∞+∞=U−(−U)=2U.

 

Substituting the similarity solution into this second requirement leads to:

−∫−∞+∞ωzdy=−∫−∞+∞At−nF(η)dy=−At−nδ∫−∞+∞F(η)d(y/δ)=−At−nδ∫−∞+∞F(η)dη=2U.

 

The final integral is just a number so t^–nδ(t) must be constant, and this implies n = 1/2 so the similarity equation may be rewritten, and integrated:

−12(F(η)+ηdFdη)=−12ddη(ηF)=ddη(dFdη)→dFdη+12ηF=C.

 

The first boundary condition implies that both F and dF/dη → 0 when η is large enough. Therefore, assume that ηF → 0 when η → ∞ so that the constant of integration C can be set to zero (this assumption can be checked once F is found). When C = 0, the last equation can be separated and integrated to find:

F(η)=Dexp(−η2/4),

 

where D is a constant, and the assumed limit, ηF → 0 when η → ∞, is verified so C is indeed zero. The velocity-difference constraint and the tabulated integral used to reach (9.30) allow the product AD to be evaluated. Thus, the similarity solutions for the vorticity ω_z = –∂u/∂y and velocity u are:

ωz(y,t)=−Uπνtexp{−y24νt},andu(y,t)=Uerf{y2νt}.

 

Schematic plots of the vorticity and velocity distributions are shown in Figure 9.14. If we define the width of the velocity transition layer as the distance between the points where u = ±0.95U, then the corresponding values of η are ±2.77 and consequently the width of the transition layer is 5.54(νt)^1/2.

The results of this example are closely related to Stokes’ first problem, and to the laminar boundary layer flows discussed in the next chapter, for several reasons. First of all, this flow is essentially the same as that in Stokes’ first problem. The velocity field in the upper half of Figure 9.14 is identical to that in Figure 9.13 after a Galilean transformation to a coordinate system moving at speed +U followed by a sign change. In addition, the flow for y > 0 represents a temporally developing boundary layer that begins at t = 0. The velocity far from the surface is irrotational and uniform at speed U while the no-slip condition (u = 0) is satisfied at y = 0. Here, the wall shear stress, τ_w, and skin friction coefficient C_f are time dependent:

Figure 9.14 Viscous thickening of a vortex sheet. The left panel indicates the vorticity distribution at two times, while the right panel shows the velocity field solution in similarity coordinates. The upper half of this flow is equivalent to a temporally developing boundary layer.

τw=μ(∂u∂y)y=0=μUπνt,orCf=τw12ρU2=2πνU2t.

 

When Ut is interpreted as a surrogate for the downstream distance, x, in a spatially developing boundary layer, the last square-root factor above becomes (ν/Ux)^1/2 = Rex−1/2, and this is the correct parametric dependence for C_f in a laminar boundary layer that develops on a smooth, flat surface below a steady uniform flow.

Example 9.8

A thin, rapidly spinning cylinder produces the two-dimensional flow field, u_θ = Γ/2πr, of an ideal vortex of strength Γ located at r = 0. At t = 0, the cylinder stops spinning. Use (9.32) to determine u_θ(r,t) for t > 0.

Solution

Follow the approach specified for the Example 9.6 but this time use (9.32b) because r appears in the initial condition. Here u_θ is the dependent field variable and r is the independent spatial variable, so the appropriate form of (9.32b) is:

uθ(r,t)=Ar−nF(r/δ(t))≡Ar−nF(η).

 

The initial and boundary conditions are: u_θ(r, 0) = Γ/2πr = u_θ(r → ∞,t), u_θ(0,t) = 0 for t > 0, which are simplified to F(η → ∞) = 1 and F(0) = 0 when Ar^–n is set equal to Γ/2πr. In this case, the field equation for u_θ (see Appendix B) is:

∂uθ∂t=ν∂∂r(1r∂∂r(ruθ)).

 

Inserting u_θ = (Γ/2πr)F(η) produces:

−Γ2πr(1δdδdt)ηdFdη=νΓ2π(−1δr2dFdη+1δ2rd2Fdη2)→−[r2νδdδdt]ηdFdη=−ηdFdη+η2d2Fdη2.

 

For a similarity solution, the coefficient in [,]-brackets must depend on η alone, not on r or t. Here, this coefficient reduces to η²/2 when δ = (νt)^1/2 (as in the prior examples). With this replacement, the similarity equation can be integrated twice:

(1η−η2)dFdη=ddη(dFdη)→lnη−η24+const.=ln(dFdη)→C∫ηexp{−η2/4}dη+D=F(η).

 

The remaining integral is elementary, and the boundary conditions given above for F allow the constants C and D to be evaluated. The final result is F(η) = 1 – exp{−η²/4}, so the velocity distribution is:

uθ(r,t)=Γ2πr[1−exp{−r24νt}],

 

which is identical to the Gaussian vortex of (3.29) when σ² = 4νt. A sketch of the velocity distribution for various values of t is given in Figure 9.15. Near the center, r ≪ (νt)^1/2, the flow has the form of a rigid-body rotation, while in the outer region, r ≫ (νt)^1/2, the motion has the form of an ideal vortex.

The foregoing presentation applies to the decay of a line vortex. The case where a line vortex is suddenly introduced into a fluid at rest leads to the velocity distribution:

uθ(r,t)=Γ2πrexp{−r24νt}

 

(see Exercise 9.34). This situation is equivalent to the impulsive rotational start of an infinitely thin and quickly rotating cylinder located at r = 0.

Figure 9.15 Viscous decay of a line vortex showing the tangential velocity u_θ at different times. The velocity field nearest to the axis of rotation changes the most quickly. At large radii, flow alterations occur more slowly.

Example 9.9

Use (9.32a) and an appropriate constraint on the total volume of fluid to determine the form of the similarity solution to the two-dimensional, viscous, drop-spreading equation of Example 9.5.

Solution

The solution plan is to populate (9.32a) with the appropriate variables:

h=At−nF(x/δ(t))≡At−nF(η),

 

substitute it into the equation from Example 9.5, and require that: 1) the coefficients all have the same time dependence, and 2) the total fluid volume per unit depth into the page, ∫−∞+∞h(x,t)dx, is independent of time. The starting point is the evaluation of derivatives:

∂h∂t=−nAt−n−1F(η)+At−ndFdη(−xδ2)dδdt,and∂h∂x=At−ndFdη(1δ),

 

which, when inserted in the final equation of Example 9.5, produces:

∂h∂t=−[nAt−n−1]F(η)−[At−n1δdδdt]ηdFdη=[ρg3μA4t−4n1δ2](3F2(dFdη)2+F3d2Fdη2)=ρg3μ∂∂x(h3∂h∂x)

 

Requiring proportionality between the first two coefficients in [,]-brackets with C as the constant of proportionality yields:

CnAt−n−1=At−n1δdδdt→Cnt=1δdδdt.

 

The second equation is satisfied when δ = Dt^m where D is another constant and m = Cn. Requiring proportionality between the second and third coefficients and using δ = Dt^m produces:

EAt−n1δdδdt=ρg3μA4t−4n1δ2→−Emt=ρg3μA3t−3nD2t−2m→−1=−3n−2m,

 

where E is another constant of proportionality; the final equation for the exponents follows from equating powers of t in the second equation. These results set the form of δ(t) and specify one relationship between n and m. A second relationship between m and n comes from conserving the volume per unit depth into the page:

∫−∞+∞h(x,t)dx=∫−∞+∞At−nF(η)dx=At−nDtm∫−∞+∞F(η)dη=const.

 

The final integral is just a number so the exponents of t outside this integral must sum to zero for the volume to be constant. This implies: –n + m = 0. Taken together, the two equations for m and n imply: n = m = 1/5. Thus, the form of the similarity solution of the final equation of Example 9.5 is:

h(x,t)=At−1/5F(x/Dt1/5).

 

Determining the constants A and D requires solution of the equation for F and knowledge of the bead's volume per unit depth, and is beyond the scope of this example.

After reviewing these examples, it should be clear that diffusive length scales in unsteady viscous flow are proportional to (νt)^1/2. The viscous bead-spreading example produces a length scale with a different power, but this is not a diffusion time scale. Instead it is an advection time scale that specifies how far fluid elements travel in the direction of the flow.