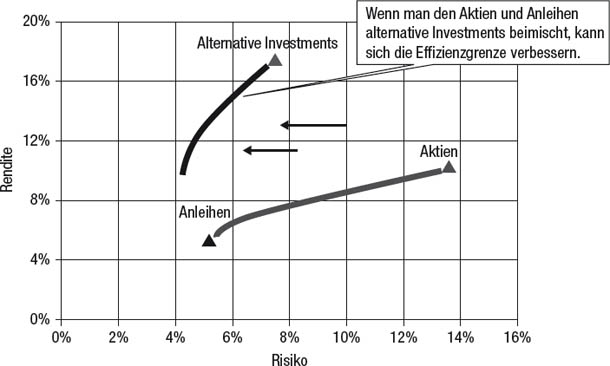
Man könnte meinen, die Zusammenstellung eines Portfolios sei eine leichte Aufgabe. Es gibt schließlich Software für die Optimierung von Portfolios, in die man bloß die Renditen der Portfoliopositionen einzugeben braucht und schon liefern sie die optimalen Allokationen. Die Software erstellt eine Effizienzkurve, die aus denjenigen Portfolios (also Allokationsmischungen) besteht, die bei einer angestrebten Volatilität die höchste Rendite bieten. (Zwei Effizienzkurven – eine nur für Aktien und Anleihen, die andere mit zusätzlichen Alternativen – sind in Abbildung 21.1 dargestellt.) Wenn sich der Anleger als angestrebtes Risikoniveau des Portfolios für acht Prozent Volatilität entscheidet, ist das Portfolio auf der Effizienzkurve diejenige Anlagenmischung, die bei acht Prozent Volatilität die höchste Rendite aufweist. Man könnte also meinen, als Anleger bräuchte man nichts weiter zu tun, als eine Liste von Investments und die gewünschte Portfoliovolatilität auszusuchen, und sofort würde die Software die mathematisch abgeleitete optimale prozentuale Allokation für jede Position liefern. Es wären also weder große Entscheidungen noch ein großer Aufwand nötig.
Abbildung 21.1
Die Portfolio-Optimierung

Quelle: EDHEC-Risk Institute. Abgedruckt mit freundlicher Genehmigung.
Die Portfolio-Optimierung ist zwar eine einfache und scheinbar wissenschaftliche Methode der Portfolio-Allokation, aber sie beruht auf zwei grundsätzlich falschen Annahmen:
Ein sehr gängiges Problem ist, dass die Länge der für die Fonds im Portfolio verfügbaren Track Records nicht ausreicht, damit sie für verschiedene Marktbedingungen repräsentativ sind. Verstärkt wird dieses Problem noch durch den praktischen Aspekt, dass die Analyse für die Portfolio-Optimierung auf den kürzesten enthaltenen Track Record begrenzt ist. Wenn ein Portfolio Fonds mit einem Track Record von nur ein paar Jahren enthält, hat man die Wahl, ob man die Portfolio-Analyse auf einen kurzen vergangenen Zeitraum beschränkt, der alle (oder fast alle) Fonds enthält, oder ob man sie auf einen Teil des Portfolios beschränkt (also auf jene Fonds, deren Track Records eine bestimmte Mindestlänge übersteigen).
Da die verfügbaren Daten diesen Beschränkungen durch die Track Records unterliegen, besteht die Gefahr, dass Portfolio-Optimierungen zu sehr an den jüngsten Marktzyklus angepasst sind. Dann ist die sogenannte optimale Allokation diejenige, die in den letzten paar Jahren die beste Performance gebracht hätte. Wenn sich aber die Marktlage ändert, kann es durchaus sein, dass die Investments, die in den letzten Jahren am besten funktioniert haben, in Zukunft zu den schlechtesten Performern gehören. In solchen Fällen ist die Portfolio-Optimierung nicht nur nutzlos, sondern führt sogar zu schlechteren Ergebnissen, als man bei einer willkürlichen Auswahl erzielen würde. Beispielsweise hätten Anfang 2000 Aktienstrategien mit Long-Schwerpunkt, insbesondere mit Technologiefokus, wegen ihrer astronomischen Performance in den Vorjahren durch die Optimierung eine ungewöhnlich große Allokation bekommen – genau zu der Zeit, zu der sie zu den mit am schlechtesten performenden Anlagen wurden. Auch Anfang 2008 hätte eine Portfolio-Optimierung denjenigen Strategien größeres Gewicht beigelegt, die im späteren Verlauf des Jahres der Finanz-Kernschmelze am stärksten ausgesetzt waren (zum Beispiel Long-Exposure auf Kreditrisiken, illiquide Wertpapiere, Emerging Markets et cetera).
Außerdem werden Berechnungen von Korrelationen dadurch weniger verlässlich, dass Daten nur begrenzt verfügbar sind. Oft schwanken die Korrelationen zwischen verschiedenen Anlagen im Laufe der Zeit stark und wenn die Korrelation über einen zu kurzen Zeitraum berechnet wurde, spiegelt sie vielleicht nur einen Teil des normalen Bereichs wider. Außerdem besteht über kürzere Zeiträume eine signifikante Wahrscheinlichkeit, dass sogar Fonds, zwischen denen kein Zusammenhang besteht, aus Gründen des Zufalls korreliert erscheinen (dass also beide im selben Monat oder in denselben zwei Monaten große Gewinne oder Verluste verzeichnen, aber aus Gründen, die nichts miteinander zu tun haben).
Und selbst wenn eine Fülle an Daten verfügbar ist, ist die Annahme, man könne die Daten aus der Vergangenheit als Näherung für die künftigen Erwartungen heranziehen, sehr heikel. So befanden sich die Schatzanleihen 2012 seit 30 Jahren in einer Hausse und dies hätte ihre optimierte Gewichtung in allen Portfolios erhöht, in denen sie enthalten waren. Ironischerweise verschlechterte jedoch die Tatsache, dass die T-Bonds schon seit so langer Zeit gestiegen waren, ihre künftigen Aussichten und verbesserte sie nicht. Aus den daraus resultierenden niedrigen Zinsen ergab sich nämlich ein viel begrenzterer Spielraum für ein weiteres Absinken der Zinsen (also für einen Anstieg der Anleihepreise). Eine ausführlichere Besprechung dieses Beispiels finden Sie in Kapitel 6.
Man muss immer die Frage stellen: Gelten die Faktoren, die für die vergangenen Renditen verantwortlich waren, wahrscheinlich auch in Zukunft noch? Wenn nicht, bringt die Portfolio-Optimierung bestenfalls bedeutungslose und schlimmstenfalls irreführende Ergebnisse.
Diese in der Portfolio-Optimierung stillschweigend enthaltene Annahme ist oft vollkommen unbegründet, weil sich bedeutende Risiken oft nicht im Track Record äußern. Außerdem kann hohe Volatilität auch auf überdimensionalen Renditen beruhen, die kein symmetrisches Risiko bedeuten. Eine ausführliche Behandlung der Verwechslung von Risiko und Volatilität finden Sie in Kapitel 4. Am besten ist die Volatilität als Anhaltspunkt für das Risiko bei hochgradig liquiden Strategien geeignet, zum Beispiel beim Handel mit Futures oder Devisen (FX), denn dort spielt im Gegensatz zu vielen anderen Hedgefonds-Strategien das Ereignisrisiko keine Rolle.
Die Portfolio-Optimierung liefert eine mathematisch präzise Antwort auf die falsche Frage. Die Frage, die sie beantwortet, lautet: Was ist die optimale Allokationsmischung für ein Portfolio, wenn man davon ausgeht, dass die Renditen, Volatilitäten und Korrelationen in Zukunft genauso aussehen wie in der Vergangenheit? Die Frage, die wir gerne beantworten würden, lautet hingegen: Was ist die optimale Allokationsmischung angesichts unserer bestmöglichen Einschätzung der voraussichtlichen Renditen und Risiken sowie der Anfälligkeit der im Portfolio enthaltenen Investments für gleichzeitige Verluste? Diese beiden Fragen sind definitiv nicht gleich. Häufig sind vergangene Renditen für die potenziellen künftigen Renditen nicht repräsentativ, frühere Track Records geben bedeutende Risiken nicht wieder und Korrelationen stellen die Tendenz zu gleichzeitigen Verlusten nicht zutreffend dar. Die Portfolio-Optimierung liefert eine exakte Lösung für die Aufgabenstellung der Allokation in einer theoretischen Welt. Aber leider legen wir unser Geld in der wirklichen Welt an und die beiden unterscheiden sich oft frappierend voneinander. Deshalb ist eine manuelle Methode, die auch solche Schlüsselfaktoren berücksichtigt, die in Track Records nicht sichtbar sind, der leicht zu erzeugenden scheinbaren Präzision einer Portfolio-Optimierung vorzuziehen. Eine ungefähre Antwort unter geeigneten Annahmen ist besser als eine exakte Antwort unter falschen Annahmen.1
Einige der nun folgenden Prinzipien für die Portfoliokonstruktion wurden bereits in früheren Kapiteln ausführlich besprochen. In solchen Fällen fassen wir das betreffende Konzept an dieser Stelle nur insofern zusammen, als es für die Portfolio-Allokation relevant ist, und verweisen auf das jeweilige Kapitel.
Oft konzentrieren sich die Anleger vor allem auf die Renditen, ohne zu berücksichtigen, dass sich das Risiko-Exposure direkt auf die Renditen auswirkt. Ein Manager, der seine Positionsgrößen verdoppelt, verdoppelt dadurch zwar seine Renditen, aber auch seine Risiken. Es wäre absurd, eine solche Verdopplung der Rendite als viel bessere Performance zu betrachten. Wenn man auf das Rendite-Risiko-Verhältnis achtet, vermeidet man solche unsinnigen, verzerrten Vergleiche. Und was ist, wenn die Rendite eines Managers mit einem höheren Rendite-Risiko-Verhältnis kleiner ist als gewünscht? In diesem Fall kann man die Rendite durch Hebelwirkung erhöhen und dadurch immer noch ein geringeres Risiko haben als bei einem Manager mit geringerem Rendite-Risiko-Verhältnis und akzeptabler Rendite. Wenn zwei Manager qualitativ betrachtet und hinsichtlich der Diversifizierung ihrer Portfolios gleich sind, ist der Manager mit höherem Rendite-Risiko-Verhältnis immer vorzuziehen.
Die Volatilität ist nur ein Risikotyp und aus der Risikoperspektive des Anlegers – basierend auf Wahrscheinlichkeit und Ausmaß von Verlusten – stellt sie oft nicht einmal ein Risiko dar. Viele der bedeutendsten Risiken werden vom Track Record vielleicht gar nicht wiedergegeben. Die einzige Ausnahme, bei der die Verwendung der Volatilität als Näherung für das Risiko grob angemessen ist (wenn auch nicht in allen Fällen), sind hochgradig liquide Strategien (zum Beispiel der Futures- und der Devisenhandel).
Häufig kommen Manager dadurch zu einer beeindruckenden Performance-Bilanz, dass sie in einem günstigen Marktumfeld ein erhebliches Exposure eingehen. Wenn ein Investmentprozess stark schwankende Exposures beinhaltet, kann gute Performance in einer Hausse als Geschick betrachtet werden. Wenn aber der Manager ständig ein beträchtliches Markt-Exposure hat und sein Track Record mit einem steigenden Markt zusammenfällt, spiegeln die früheren Ergebnisse vielleicht mehr den Markt wider als die Fähigkeiten des Managers.
Die Diversifizierung über zehn hinaus bringt zwar im Durchschnitt oft nur mäßige Vorteile, aber diese Sichtweise geht an dem Punkt vorbei, dass der hauptsächliche Nutzen von Diversifizierung darin besteht, die Worst-Case-Ergebnisse zu mildern. Daher bringt auch eine wesentlich höhere Diversifizierung noch einen Nutzen, vorausgesetzt, die zusätzlichen Investments sind von gleicher Qualität und nicht stärker zu anderen Positionen korreliert.
Viele Dachfonds-Manager erzielen ihre Diversifizierung mittels eines Top-down-Ansatzes: Sie entscheiden, wie viel sie jeder Hedgefonds-Kategorie zuteilen (zum Beispiel Long/Short-Aktien, ereignisorientiert, Global Macro et cetera), und suchen dann innerhalb der Kategorien die einzelnen Manager aus. Die Top-down-Methode weist allerdings zahlreiche logische Unstimmigkeiten auf:
•Die Benennungen der Kategorien sind nicht klar definiert. Das geht schon aus der höchst unterschiedlichen Anzahl von Strategie-Kategorien bei verschiedenen Anbietern von Hedgefonds-Datenbanken hervor.
•Manche Hedgefonds passen in mehrere Strategie-Kategorien.
•Manche Hedgefonds passen in keine Strategie-Kategorie wirklich gut hinein.
•Es kann sein, dass Hedgefonds in derselben Kategorie nicht miteinander korreliert sind.
•Hedgefonds verschiedener Kategorien können stark korreliert sein.
Die Bezeichnungen der Kategorien sind inkonsistent und können als Unterscheidungsmerkmale irreführend sein. Wenn man die Auswahl gut diversifizierter Manager anstrebt, ist es viel sinnvoller, auf die individuellen Investment-Kennzahlen (zum Beispiel die Korrelation und das Beta) und qualitative Vergleiche der Strategien zu schauen als auf die Bezeichnungen der Kategorien, denn diese sind unweigerlich willkürlich und inkonsistent.
Die Auswahl von Managern für ein Portfolio unterscheidet sich von der Auswahl von Managern als eigenständige Investments. Die Auswirkungen eines zusätzlichen Managers auf das Portfolio hängen nicht nur von der individuellen Performance des Managers ab, sondern auch von seiner Korrelation zu den anderen Portfoliopositionen. Ein Manager mit geringer oder umgekehrter Korrelation zu den anderen Managern ist als Ergänzung des Portfolios womöglich einem qualitativ gleichwertigen Manager mit einem höheren Rendite-Risiko-Verhältnis vorzuziehen. Und noch ein Beispiel: Ein invers korrelierter Manager mit sehr hoher Volatilität kann die Volatilität des Portfolios senken statt steigern (siehe Kapitel 20).
Als grundsätzliche Richtlinie kann man festhalten, dass man als Manager eines Dachfonds oder als Multimanager-Anleger eine geringe durchschnittliche Paar-Korrelation anstreben sollte. Die Paar-Korrelation ist die Korrelation zwischen zwei beliebigen Investments im Portfolio. Die Anzahl der Paare in einem Portfolio beträgt n × (n-1) / 2, wobei n die Anzahl der Investments ist. Das heißt, wenn ein Dachfonds-Portfolio 20 Manager enthält, gibt es (20 × 19) / 2 = 190 Paar-Korrelationen. Die im nächsten Abschnitt erläuterte Korrelationsmatrix ist eine praktische Möglichkeit, alle Paar-Korrelationen eines Portfolios zu betrachten.
Ein Blick auf das Zusammenfallen der Verluste verschiedener in einem Portfolio enthaltener Fonds ist ebenfalls aufschlussreich. Ein Werkzeug, mit dem man Muster gleichzeitiger Verluste in einem Portfolio erkennen kann, wird im weiteren Verlauf dieses Kapitels in dem Abschnitt „Jenseits der Korrelation“ beschrieben. Als Dachfonds-Manager sollte man die Zahl der Fonds im Portfolio, die stark dazu neigen, gleichzeitig Verlust zu machen, möglichst klein halten.
Nehmen wir an, alle in einem Portfolio enthaltenen Manager gelten als qualitativ ungefähr gleichwertig und alle sind gegenüber den anderen Managern gleich stark diversifiziert. Wie sollte man das Vermögen dann auf sie verteilen? In diesem vereinfachten Beispiel mag es scheinen, als sei eine gleichmäßige Allokation die logische Wahl. Aber in Wirklichkeit kann die gleichmäßige Allokation töricht sein. Die nun folgende fiktive Erzählung von zwei Partnern, die gemeinsam einen Fonds managen, sich aber grundsätzlich uneinig darin sind, wie der Fonds traden sollte, veranschaulicht, wie absurd die gleichmäßige Allokation ist.
Carol und Andrew managen gemeinsam einen Fonds, der eine systematische Futures-Trading-Strategie betreibt. Beide sind mit dem Trading-System, das sie entwickelt haben, glücklich, aber sie haben ein Problem. Im Moment setzen sie bei ihrem System ein Margin-Kapital-Verhältnis von 14 Prozent ein, was für Commodity Trading Advisors (CTAs) ein mittleres Exposure ist. Carol ist sehr konservativ und möchte vor allen Dingen die Kapital-Drawdowns klein halten. Andrew findet hingegen, sei seien zu vorsichtig und sollten ihr Exposure erhöhen.
Eines Tages sagt Carol: „Die Anleger machen sich mehr Sorgen um den Drawdown als um die Rendite und ehrlich gesagt geht es mir genauso. Deshalb finde ich, wir sollten unser Exposure auf ein Margin-Kapital-Verhältnis von sieben Prozent halbieren.“
„Bist du verrückt?“, protestiert Andrew heftig. „Wir traden sowieso schon mit zu wenig Exposure. Unser schlimmster bisheriger Drawdown waren zehn Prozent. Ich finde, wir sollten unser Margin-Kapital-Niveau verdoppeln. Dadurch verdoppeln wir unsere Renditen und die meisten Anleger sind mit einem maximalen Drawdown von 20 Prozent immer noch zufrieden.“
Carol ist dermaßen empört, dass sie gar nicht weiß, wo sie anfangen soll. „Wer sagt denn, dass unser schlimmster Drawdown in Zukunft nur so groß wird wie unser bislang schlimmster? Was ist, wenn er doppelt so groß wird? Dann stehen wir mit deinem Vorschlag bei 40 Prozent Minus und sind pleite.“
Sie beschließen zwar, den Status quo beizubehalten, aber keiner der Partner ist damit glücklich. In den Wochen danach führen sie immer wieder das gleiche Streitgespräch, aber keiner kann den anderen von seinem Standpunkt abbringen. Schließlich beschließen sie, sich zu trennen, wobei jeder die Rechte an dem gemeinsam entwickelten System behält.
Carol und Andrew gründen eigene Fonds. Beide verwenden weiterhin unverändert exakt das gleiche System. Der einzige Unterschied ist, dass Carol mit einem Margin-Kapital-Verhältnis von sieben Prozent tradet, Andrew hingegen mit 28 Prozent.
Und jetzt sehen wir uns einen Dachfonds-Manager an, der bei gleichgewichteter Allokation den Fonds von Carol oder den von Andrew in sein Portfolio aufnimmt. Beide Fonds stehen für die exakt gleiche Strategie und beide haben fast die gleiche Rendite-Risiko-Performance. Die gleichmäßige Gewichtung klingt zwar nach einem neutralen Ansatz, aber sie würde dazu führen, dass das gleiche Investment viermal so groß wäre, wenn sich der Manager für Andrews Fonds anstatt für den von Carol entscheidet. Der Logik zufolge müsste eine Allokation auf Andrew ein Viertel so groß sein wie eine Allokation auf Carol, damit sowohl die Rendite als auch das Risiko gleichwertige Investments ergeben würden.
Das Risikoniveau, auf dem ein Fonds betrieben wird, hängt von den subjektiven Vorlieben seines Managers ab. Es gibt keinen Grund, weshalb ein Anleger die gleichen Risikoniveaus übernehmen müsste. Wenn verschiedene Investments verschiedene Risikoniveaus aufweisen, sollten die Allokationen entsprechend angepasst werden. Wenn zwei Fonds als gleichermaßen attraktiv gewertet werden und wenn einer ein doppelt so hohes Risiko aufweist wie der andere (wobei man das Risiko so bestimmt, wie es einem angemessen erscheint), sollte darauf nur die halbe Allokation entfallen. Der springende Punkt ist, dass die Grund-Allokation auf gleichen Risiken und nicht auf gleichen Investitionsbeträgen beruhen sollte. Natürlich sollten sich auch noch andere Faktoren auf die Größe der Allokation auswirken, zum Beispiel die relative quantitative und qualitative Einschätzung sowie die Diversifizierung mit anderen Positionen. Von allem anderen abgesehen sollten aber riskantere Investments im Verhältnis kleinere Allokationen bekommen.
Ein gleichmäßig gewichteter Fonds ist tendenziell volatiler, weil sich Positionen mit höherem Risiko überproportional stark auswirken. Im Gegensatz dazu dämpft eine auf dem Risiko basierende Allokationsmethode die Volatilität des Portfolios, indem sie riskanteren Investments proportional kleinere Allokationen zuweist.
Wenn ein Dachfonds-Portfolio zur Diversifizierung traditioneller Investments und nicht als eigenständiges Investment eingesetzt wird, sollte es in der Mehrzahl der Baisse-Monate profitabel sein. Damit dieses Ziel mit höherer Wahrscheinlichkeit erreicht wird, sollte man sich Manager aussuchen, die in den Monaten, in denen der Markt während ihres Track Records gefallen ist, netto betrachtet profitabel waren.
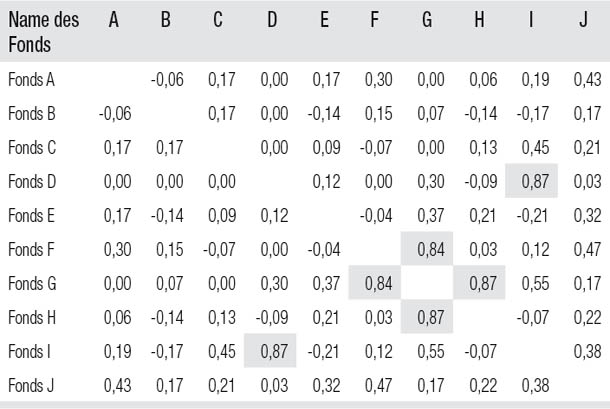
Wenn man aus mehreren Investments bestehende Portfolios miteinander vergleicht, ist es sehr sinnvoll, sich die Korrelationen zwischen den Investments insgesamt anzuschauen, nicht immer nur eine Paarung. Eine Korrelationsmatrix bietet einen Überblick über alle Paar-Korrelationen innerhalb einer Gruppe von Investments (oder anderen Zahlen). Abbildung 21.2 zeigt eine Beispiel-Korrelationsmatrix. Beachten Sie, dass die waagerechten und senkrechten Beschriftungen gleich sind. Die Korrelation zwischen zwei Investments findet man ganz einfach in der Zelle, in der sich die beiden Investments überschneiden. Um beispielsweise die Korrelation zwischen Fonds C und Fonds E zu überprüfen, schaut man, wo sich die Zeile von Fonds C und die Spalte von Fonds E überschneiden – oder die Zeile von Fonds E mit der Spalte von Fonds C. In beiden Zellen steht eine Korrelation von 0,09. Die Zahlen in der diagonal geteilten oberen und unteren Hälfte der Korrelationsmatrix sind gleich. Deshalb wird oft nur die untere Hälfte der Matrix abgedruckt. Die Angaben in der Diagonale würden immer 1,0 betragen, weil jede Zelle in der Diagonale der Schnittpunkt eines Fonds mit sich selbst ist. Da dieser Fall trivial ist, lässt man diese Zellen oft leer. Manchmal ist es nützlich, Korrelationen oberhalb eines bestimmten Schwellwerts hervorzuheben. So sind in Abbildung 21.2 alle Korrelationen über 0,7 dunkler hinterlegt und invers dargestellt. Der Durchschnitt aller Korrelationspaare der Korrelationsmatrix bietet einen guten Überblick über die Diversifizierung des betreffenden Portfolios. Je niedriger die durchschnittliche Paar-Korrelation, umso besser.
Die Korrelation ist zwar ein nützliches Werkzeug, das vor Investments warnt, die für gleichzeitige Verluste anfällig sein könnten, aber aus den in Kapitel 9 erläuterten Gründen bedeutet eine mäßige oder hohe Korrelation zwischen zwei Fonds nicht unbedingt, dass sie gleichzeitig Verluste erleiden werden. Und eine geringe Korrelation garantiert nicht, dass dem nicht so ist. Wenn man nachprüft, wie sich jeder Fonds verhält, wenn die anderen Fonds im Portfolio einen Rückgang erleben, erhält man eine genauere Analyse als durch die Korrelation, weil man damit direkt auf den entscheidenden Punkt abzielt, der einen interessiert: gleichzeitige Verluste.
Abbildung 21.2
Die Korrelationsmatrix
Die CNR-Matrix (CNR = Coincident Negative Return, zusammenfallende negative Rendite) ist ein praktisches Format, mit dem man beurteilen kann, in welchem Maße Investments des Portfolios für Verluste anfällig sind, wenn andere Portfoliopositionen einen Rückgang erleben. Die CNR-Matrix sieht so ähnlich aus wie die Korrelationsmatrix, unterscheidet sich allerdings in den beiden folgenden wesentlichen Punkten von ihr:
1.Sie zeigt nicht die Korrelation zwischen zwei Investments, sondern in jeder Zelle steht der Anteil der Fälle, in denen das in der Zeile angegebene Investment gefallen ist, wenn auch das in der Spalte stehende Investment gefallen ist. Beispielsweise würde die Zahl im Schnittpunkt der Zeile von Fonds E und der Spalte von Fonds C angeben, in welchem Prozentsatz der Fälle, in denen Fonds C gefallen ist, auch Fonds E gefallen ist. Wenn Fonds C in 20 Prozent aller Monate gefallen ist und in 60 Prozent dieser Monate auch Fonds E gefallen ist, steht in Zeile E/Spalte C „60 Prozent“. Man kann für die Berechnung der CNR-Matrix beliebige Zeiträume nehmen, in diesem Beispiel sind wir von Monaten ausgegangen. Wenn sie verfügbar sind, liefern allerdings tägliche (auch bereits wöchentliche) Zahlen statistisch signifikantere Hinweise darauf, welche Investments mit der größten Wahrscheinlichkeit gleichzeitig Verluste erleiden.
2.Im Gegensatz zu der normalen Korrelationsmatrix ist die CNR-Matrix asymmetrisch – das heißt, der Teil über der Diagonale ist kein Duplikat des Teils unter der Diagonale. Das liegt daran, dass der Anteil der Fälle, in denen das in der Zeile angegebene Investment gefallen ist, wenn das in der Spalte angegebene Investment gefallen ist, nicht gleich dem Anteil der Fälle ist, in denen das in der Spalte angegebene Investment gefallen ist, wenn das in der Zeile angegebene Investment gefallen ist.
Für die Berechnung der CNR-Matrix braucht man einen Parameter: den Mindestwert T (für Threshold = Schwellwert), ab dem ein Zeitraum (bei Monatsdaten ein Monat) als Verlustzeitraum definiert wird. Die Standardeinstellung für T ist null – jeder Verlust bedeutet einen Verlustmonat. Es gibt aber auch gute Gründe, einen höheren Schwellwert zu nehmen, denn es kann sinnvoller sein, nur signifikante gleichzeitige Verluste anstatt aller gleichzeitigen Verluste zu betrachten. Vielleicht ist es uns ja egal, ob Fonds E in Monaten gefallen ist, in denen Fonds C nur um einen minimalen Betrag gefallen ist. Wenn man T auf 0,5 Prozent setzt, gibt die CNR-Matrix den Anteil der Zeiträume an, in denen die in den Zeilen angegebenen Manager in Zeiträumen mindestens 0,5 Prozent Verlust gemacht haben, in denen die in den Spalten angegebenen Manager mindestens 0,5 Prozent Verlust gemacht haben.
Die Signifikanz des Anteils der Fälle, in denen ein Manager dann Verlust macht, wenn ein anderer Verlust macht, hängt davon ab, ob dieser Anteil größer oder kleiner als der durchschnittliche Anteil von Verlustmonaten des Managers ist. Deshalb kann es aussagekräftiger sein, wenn man eine normalisierte Version der CNR-Matrix verwendet. Dafür werden alle Prozentsätze durch den durchschnittlichen prozentualen Anteil der Verluste eines Managers geteilt, die über den Schwellwert (T) hinausgehen. Wenn beispielsweise Manager A in 30 Prozent aller Monate Verlust macht, aber nur in 20 Prozent der Monate, in denen Manager B Verlust macht (aus Gründen der Einfachheit setzen wir T auf null), beträgt der normalisierte CNR-Wert 66,7 Prozent (20% / 30% = 0,667) und das deutet darauf hin, dass Manager A in Monaten, in denen Manager B Verlust macht, mit geringerer Wahrscheinlichkeit Verlust macht als in einem zufällig ausgewählten Monat. Wenn Manager A hingegen in 50 Prozent der Monate Verlust macht, in denen Manager B Verlust macht, beläuft sich der normalisierte CNR-Wert auf 166,7 Prozent (50% / 30% = 1,667) und das deutet darauf hin, dass Manager A in einem Monat, in dem Manager B Verlust macht, mit größerer Wahrscheinlichkeit Verlust macht als in einem zufällig ausgewählten Monat.
Anmerkung: Die CNR habe ich selbst erfunden und sie ist in keiner existierenden Software verfügbar. Sie wird allerdings in dem Schwager Analytics Module enthalten sein, das Gate 39 Media für sein System Clarity Portfolio Viewer entwickelt. Das Add-on soll im zweiten Quartal 2013 erscheinen. Interessierte Leser finden unter www.gate39media.com/ schwager-analytics weitere Informationen. Im Interesse der Offenlegung: Ich habe ein finanzielles Interesse an diesem Produkt.
Investment-Missverständnis 51: Die Portfolio-Optimierung ist das beste Mittel, um bei einem angestrebten Volatilitätsniveau die optimale Rendite zu erzielen.
In Wirklichkeit: Die entscheidende stillschweigende Annahme, von der die Portfolio-Optimierung ausgeht, besagt, dass die früheren Renditen, Volatilitäten und Korrelationen brauchbare Schätzungen für ihre erwarteten künftigen Niveaus darstellen. Diese grundsätzliche Annahme ist aber nicht nur oft falsch. Optimierte Portfolios können durchaus schlechtere Ergebnisse liefern als zufällig erzielte, wenn bedeutende Wendepunkte des Marktes vorliegen. Die Genauigkeit der Portfolio-Optimierung ist eine falsche Präzision, denn sie beruht normalerweise auf unzutreffenden Annahmen.
Investment-Missverständnis 52: Die Top-Down-Allokation ist ein nützliches Werkzeug, um eine angemessene Diversifizierung zu gewährleisten.
In Wirklichkeit: Die Bezeichnungen der Kategorien sind unweigerlich willkürlich und können schlechte Anhaltspunkte für die Unterscheidung von Fonds sein. Wenn das Ziel die Zusammenstellung eines gut diversifizierten Portfolios ist, dann ist es viel effektiver, auf die Auswahl von Managern zu achten, die sich voneinander unterscheiden – anstatt bestimmte Anteile auf verschiedene Kategorien-Töpfe zu verteilen. Die Top-Down-Methode kann leicht in einem zu stark korrelierten Portfolio münden, denn die Manager aus verschiedenen Kategorien können am Ende trotzdem für die gleichen Risikofaktoren anfällig sein.
Investment-Missverständnis 53: Wenn mehrere Manager als qualitativ gleichwertig gelten, ist der Manager mit dem besseren Rendite-Risiko-Potenzial immer zu bevorzugen.
In Wirklichkeit: Was bei der Auswahl eines eigenständigen Investments gilt, muss nicht unbedingt auch bei der Auswahl eines Investments für ein Portfolio gelten. Ein Investment mit schlechterer Performance kann durchaus mehr für die Performance eines Portfolios bringen als ein Investment mit besserer Performance, wenn es außerdem zu den anderen Positionen im Portfolio umgekehrt korreliert ist.
Investment-Missverständnis 54: Wenn man die Investments in einem Portfolio für ungefähr gleich gut hält, ist eine gleichmäßige Allokation der richtige Weg.
In Wirklichkeit: Gleiche Risiken sind ein logischeres Kriterium für neutrale Allokationen als gleiche Anlagebeträge und dämpfen wahrscheinlich auch wirksamer das Portfoliorisiko.
Investment-Missverständnis 55: Die Portfolio-Korrelations-matrix ist ein umfassendes Werkzeug, um Fonds zu identifizieren, die wahrscheinlich in den gleichen Zeiträumen Verlust machen.
In Wirklichkeit: Die Korrelationsmatrix ist zwar sehr nützlich, weil sie vor Fonds warnt, die vielleicht mit höherer Wahrscheinlichkeit gleichzeitig Verluste erleiden, aber da die Korrelation hierbei auf allen Monaten und nicht nur auf den Verlustmonaten basiert, kann sie bei der Erkennung von Fonds, die zu den gleichen Zeiten wie andere im Portfolio enthaltene Fonds für Verluste anfällig sind, unzulänglich oder gar irreführend sein. Die CNR-Matrix (CNR = Coincident Negative Returns, zusammenfallende negative Renditen) ist eine nützliche Ergänzung der Korrelationsmatrix, denn sie hilft, Fonds zu erkennen, die für gleichzeitige Verluste anfällig sind.
1 Die obige Diskussion der Portfolio-Optimierung bezieht sich auf ihre Verwendung unter der Annahme, die vergangenen Daten seien für die diversen Investments repräsentativ. Als Instrument für die Bestimmung der optimalen Allokation, die sich aus gegebenen Annahmen ergibt, ist sie zwar durchaus nützlich, aber natürlich sind ihre Ergebnisse nur so gut wie die Annahmen.
Die effiziente Portfolio-Allokation kann Entscheidungen vorschreiben, die für eigenständige Investments irrational wären. Bei der Portfolio-Allokation sollte man manchmal Manager mit einem niedrigeren Rendite-Risiko-Verhältnis gegenüber Managern mit einem höheren Rendite-Risiko-Verhältnis bevorzugen – wenn sie zu dem Portfolio umgekehrt korreliert sind. Die entscheidende Frage ist, welcher Manager zu einem Portfolio mit den besten erwarteten Rendite-Risiko-Eigenschaften führt, nicht welcher Manager an sich die besten erwarteten Rendite-Risiko-Eigenschaften hat.
Die Portfolio-Optimierung verleiht dem Prozess der Portfolio-Allokation mathematische Genauigkeit, beruht aber häufig auf fehlerhaften Annahmen. Typischerweise geht die Portfolio-Optimierung stillschweigend davon aus, die früheren Renditen, Volatilitäten und Korrelationen seien brauchbare Schätzungen für die Niveaus, die in Zukunft zu erwarten sind. Das Problem ist allerdings, dass diese Annahme häufig grundfalsch ist, vor allem im Hinblick auf die Renditen. Anlässlich bedeutender Übergangsphasen eines Marktes kann einem die Portfolio-Optimierung oft schlechtere Ergebnisse bescheren, als man bei einer willkürlichen Auswahl erhalten würde
Die gleichmäßige Allokation gilt häufig als standardmäßige und neutrale Portfolio-Allokation. Da jedoch die Risiken, die verschiedene Manager eingehen, häufig stark voneinander abweichen, teilt ein gleichmäßig gewichtetes Portfolio unwissentlich manchen Managern ein viel größeres Risiko zu als anderen. Eine vernünftigere neutrale Methode ist die Allokation anhand gleich großer Risiken, die ironischerweise zur Folge hat, dass auf manche Manager viel größere Allokationen entfallen als auf andere.