3.1.1 Plan of the chapter. After summarising Cantor’s life and career in the next section, the story is told of his creation of the branch of mathematics which we call ‘set theory’; but when I wish to refer to his version of it I shall conserve even in translations the word ‘Mengenlehre’ which he used especially in his final years of the mid 1890s and which became the most common name among German-writing authors there after (§4.2.1). First, §3.2–3 covers its founding between 1870 and 1885, and §3.4 treats the final papers. Important concurrent work of Dedekind is also included: on irrational numbers in §3.2.4, and on integers in §3.4.1–3. Then §3.5 presents a survey of some of the main unsolved mathematical problems and philosophical questions present in Cantor’s work, followed by considerations of his philosophy of mathematics in §3.6.
The range and status of the Mengenlehre by the late 1890s is reviewed in §3.7. Throughout the emphasis falls rather more on the foundational and general features of the theory than on the mathematical aspects, which we now call ‘point set topology’.
3.1.2 Cantor’s career. Georg Cantor was born in Saint Petersburg in 1845 as the first son of a cultured business man who was to exercise considerable influence on his formation; for example, instilling in him a strong religious spirit. According to a letter which Cantor sent to Paul Tannery in 1896, his father ‘was born of Isrealite parents, who belonged to the Portuguese Jewish community’ in Copenhagen but ‘was christened Lutheran’, while his mother was ‘a born Saint Petersburger’ of a Roman Catholic family (S. P. Tannery 1934a, 306); so he was not a practising Jew, and was unrelated to the Jewish historian of mathematics Moritz Cantor. Three more children were born by 1849, and then in the mid 1850s the family moved to Heidelberg in Prussia, for sake of the father’s health; nevertheless, he died there in 1863, leaving a considerable fortune.
Around that time Cantor went to Berlin University to study mathematics. One of his fellow students was Karl Hermann Amandus Schwarz; his principal professors were Karl Weierstrass, Leopold Kronecker and Ernst Kummer, and he followed the concerns of the latter two, writing both doctoral dissertations (the Dissertation and the Habilitation) on number theory in 1867 and 1869. To begin his academic career he replaced Schwarz as Privatdozent at Halle University, a second-ranking establishment in the German hierarchy, where Eduard Heine (1821–1881) was full ordentlich professor (his significance will be brought out in §3.2.1). To his disappointment, Cantor passed his entire academic career at Halle; but he was not rejected there, being promoted to ausserordentlich professor in 1872 and to a full chair in 1879, an additional post to Heine’s.
PLATE 1. Portrait of Georg Cantor with his sister Sophie, with whom he was always close. He seems to be in his mid twenties, which would date the photograph around 1870, at the start of his career. First publication; made available to me by Cantor’s descendants. Another portrait of the young pair was published, for the first time, in the American mathematical monthly 102 (1995), 408, 426.
Plate 1 is a photograph of Cantor from this period; published here for the first time, it shows him with his sister Sophie, who was very close to him. He married into a Jewish family in 1874, and had six children. His work developed steadily for the next decade; but in the summer of 1884 he seems to have had some sort of mental attack, possibly a mid-term crisis, which leaves the sufferer susceptible to depressive states. Although he seemed to recover and resume teaching duties, his research in Mengenlehre switched emphasis from the mathematical aspects to its philosophical and religious consequences. He also devoted much effort to attempting to prove that Francis Bacon wrote the plays of William Shakespeare; quite a popular topic in Germany at that time, for twenty years Cantor was to be a prominent figure, with support from Sophie (Ilgauds 1892a).
Between 1891 and 1897 Cantor published two more papers on the Mengenlehre. However, his research activity was decreasing, and from the late 1880s he had been giving much time to professional affairs: the launching in 1890 of the Deutsche Mathematiker-Vereinigung (§3.4.5), and of International Congresses of Mathematicians from 1897 onwards.
Then, just when his external life began to flower with the general acceptance of his work, Cantor’s internal life disintegrated. A serious concurrence of difficulties in the Mengenlehre, university politics, a dispute with the Kultusministerium, and the sudden death of his youngest son seems to have triggered a major collapse in the autumn of 1899, much more serious than the crisis in 1884. While he fulfilled his university duties for the majority of the following years until his retirement in 1913, he spent extended periods of the last twenty years of his life after 1899 in the University Nervenklinik and in sanitoria. To a modern view the surviving documentation suggests that he was manic depressive, and that his illness was endogenous, not basically caused by the controversies surrounding his work.1
After his death in 1918 Cantor studies were favoured in the 1930s by an excellent biographical article Fraenkel 1930a for the Deutsche Mathematiker-Vereinigung, and a moderate edition Cantor Papers (1932) of his writings on Mengenlehre prepared by Ernst Zermelo,2 followed five years later by a careful edition of the main bulk of his correspondence with Richard Dedekind (cited as ‘Cantor-Dedekind Letters’) . This was prepared by Emmy Noether and the French philosopher and mathematician Jean Cavaillès,3 who also wrote an excellent historical survey 1938a of set theory (§9.6.5).
Proper research then largely languished for some decades; but in the mid 1960s Herbert Meschkowski traced some of the descendants and located the remaining Nachlass. It turned out that the materials had always been kept by the family, but that they had not been used by any of the scholars just mentioned, and that in the circumstances of the end of the Second World War the family house had been occupied and most of them had been destroyed or disappeared. In the late 1960s the remainder came into my hands, and I set them in some order: at my recommendation to his descendants, they were placed (and later recatalogued) in the University Library at Göttingen during the 1970s (Cantor Papers), to join those of contemporaries such as Dedekind, Felix Klein and David Hilbert.
This co-location carries more significance than is evident at first. Cantor was very lonely in his professional career, and compensated for his situation by carrying on intensive correspondences with a few colleagues, concerning both his Mengenlehre and his other work. The list of mathematical correspondents reflects his career in publishing on the former. From the beginnings in 1870 Schwarz was a major recipient for several years, until he turned against Cantor’s work. Then it was the turn of Klein, who accepted for publication between 1878 and 1884 in Mathematische Annalen the longest sequence of papers. By then a new figure had arisen: the Swedish mathematician Gösta Mittag-Leffler (1846–1927), rich enough on his wife’s money to launch in 1882 a new journal, Acta mathematica. Anxious to gain good copy for his first volumes and already appreciative of the quality of Cantor’s work, he arranged for French translations to be prepared of most of the main papers that Cantor had already published. In the course of its preparation Mittag-Leffler received the usual torrent of letters, and also some original papers; but he was crossed off the list in 1885 when he recommended that a later paper be withdrawn for its lack of major new results (§3.3.2).
Thereafter Cantor corresponded only spasmodically with mathematicians, turning more to theological figures and to Shakespearian experts; his last significant mathematical contact was with Hilbert, by letter, largely during the 1890s. During the 1900s he had an interesting exchange of letters with the English historian and mathematician Philip Jourdain, partly on the development of his work: Jourdain published short extracts from them in some of his own papers, and I have used the whole surviving exchange in my 1971a. I cannot draw here in detail on all of Cantor’s correspondence, but it casts valuable light on both the man and the mathematician; a good selection is available in Cantor Letters.4
3.2.1 Riemann’s thesis: the realm of discontinuous functions. (Dauben 1979a, ch. 1). The publication by Dedekind in 1867 of Riemann’s thesis on trigonometric series (§2.7.3) launches the mathematics. Aware of the technical difficulty of extending Dirichlet’s sufficient conditions for the convergence of Fourier series to handle functions f(x) with an infinity of turning values and/or discontinuities (Riemann 1867a, art. 6), he tried another approach and looked for necessary conditions, probably in the hope of finding some which were both necessary and sufficient. He worked with this series, which he called ‘Ω’:
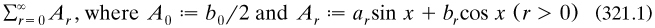
and – π ≤ x ≤ π, with ‘value’ f(x); the coefficients {ar, br} were not specified by the Fourier integral forms. He then defined a function F(x) as the formal second term-by-term integration of Ω:
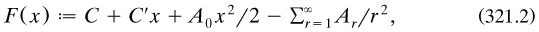
and sought various relationships between these two functions (arts. 8–9). Of main interest are the necessary and sufficient conditions on F for Ω to converge (or, as he put it, for its members to ‘become eventually infinitely small for each value of x’); for he then wondered if the consequences of this property did not obtain ‘for each value of the argument variable’ x (art. 11). His own approach was to examine the series expansion of (F(x + t) + F(x—t)) (art. 12); his followers concentrated on the underlying perception that a trigonometric series might not be a Fourier series.
Of the various papers which followed, notable is the thesis 1870a written at Tübingen University by Hermann Hankel on ‘infinitely often oscillatory and discontinuous functions’. Not only an excellent mathematician but also an historian of mathematics, his early death in 1873 in his mid thirties was a serious loss. In his thesis he developed (321.1) to define functions which did or did not have a Riemann integral, and he went further than Riemann in exploring the topology of the real line. He also introduced the phrase ‘condensation of singularities’ to express the accumulation of points of oscillation and/or discontinuity of functions, and deployed Taylor’s series (again like Riemann) to find expressions for them (art. 4). Among possibilities, he considered points which (in Cantor’s later name of §3.2.6. were everywhere dense in a given interval (art. 7). Impressed by Dirichlet’s mention of the characteristic function of the rationals (§2.7.3., he used Taylor’s series to find in art. 9 (ex. 4) a complicated expression for this function, and in the second appendicial note he offered the definition of a similar function:
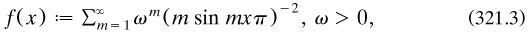
where f(x) = ∞ when x was rational and either tended towards ∞ or took finite values for irrational values of x. We shall see Peano unify these two approaches to find in (521.1) an expression for the Dirichlet function.
The quality of Hankel’s study led to its reprint in 1882 as a paper in Mathematische Annalen, where it gained greater circulation; but before then a rare British contribution was made from Oxford by H. J. S. Smith 1875a. Building upon both Riemann and Hankel to study ‘the integration of discontinuous functions’, he distinguished two kinds of ‘system’ of points along the line, as in ‘loose’ or ‘close order’ (arts. 9–10); the latter notion corresponded to Cantor’s ‘dense in an interval’ (§3.2.9), and looseness was simply its negative. His most interesting exercise occurred in art. 15, where he defined a ‘system’ PS of points with generic member specified by the series 
positive integers., and characterised the distribution of such systems in terms of partitioning a given interval into m equal sections, then all but the first again into m, and so on. The left hand points of these intervals would yield PS after m iterations, and points of discontinuity could be allowed for a continuous function and still leave it Riemann-integrable. In a variant partition method (art. 16), he found a case where non-integrability would hold.
Several features related to Cantor’s work to come are of interest here. Firstly, PS looks like the ternary set (328.2) to be introduced by Cantor nearly a decade later; for example, it is of measure zero (as Smith proved, in the Riemannian language of §2.7.3). However, it is not as interesting an object, for Smith took an end of each of a collection of intervals and not Cantor’s middle thirds, and all his systems were denumerable. Secondly, he introduced both a word and a letter for the collections; in fact, we shall see in §3.2.3 that Cantor had already taken the step three years earlier, but Smith did not cite him and can be regarded as an independent innovator.
Conversely, Cantor seems never to have read Smith, but he did propose a new method of condensing singularities in a paper 1882a using the set-theoretic techniques which he had developed by then. For singularities had become an important part of point set topology and its application to the theory of functions and integration. A notable contributor was Paul du Bois Reymond (1831–1889., a close associate of Weierstrass (Mittag-Lef-fler 1923a); he succeeded Hankel at Tubingen in 1874. He developed his techniques in response to various questions in the theory of functions and integration, including those raised by Riemann’s thesis concerning the distribution of zeros, turning values and/or discontinuities of functions; he also used them to some extent in his ‘calculus of infinitaries’ (‘Infinitarkalkul’), in which he studied the ways and rates at which functions f(x) could go to ±∞ as x did. In the course of this work he constructed parts of point set topology for himself, although not without some errors of conception.5 We shall note one example in §3.2.6.
As was mentioned in §3.1.1, we shall not explore this topic further. The rest of the section will treat another line of thought from Riemann’s thesis, which was taken up by Cantor’s senior colleague in Halle.
3.2.2 Heine on trigonometric series and the real line, 1870–1872. In a paper published in Crelle’s journal Heine 1870a concentrated on trigonometric series. He brought to the topic considerations of uniformity of convergence, using the alternative phrase ‘convergent in the same degree’, due to Weierstrass’s teacher Christoph Gudermann; thereby he joined the concerns of Riemann with the (recently publicised) techniques of Weierstrass (§2.7.4). The bearing of these ideas was based upon the fact that each coefficient in (321.1)1 was calculated by multiplying through the equation by the corresponding trigonometric function and integrating over [ – π,π ] of x; but it was now known both that uniformity of convergence was required for the process to be safe, and that since the trigonometric functions were continuous, then under uniformity so was the sum-function. If uniformity did not obtain, then maybe more than one expansion of a function was possible, and the expandability of a discontinuous function was not clearly understood. These issues were accentuated by the considerations of Riemann’s dissertation, especially the results just mentioned and the “ultra-Dirichletian” functions that he had found, to allow for the possibility that a function may not have any trigonometric expansion at all.
Heine introduced the notion of ‘convergence in general’, by means of which he admitted the possibility of ‘the exception that an infinite number of points might obtain’ (1870a, 354). The intuitive idea was that, since the coefficients were defined as certain definite integrals over [ – π,π ] of x, then their values would be insensitive to changes in the value of f(x) for a finite number of values of x; the main purpose of the paper was to produce a proof of this result of Weierstrassian rigour. Another way of stating the result was in terms of uniqueness: if the series (321.1)1 converged uniformly in general to zero, then each coefficient ar and br must be zero (pp. 356–357). There were consequences also for understanding continuity, and he introduced here the definition of the ‘uniform continuity’ of a function of two variables (p. 361, where he did use Weierstrass’s adjective).
Heine cited Riemann’s thesis twice: on p. 359 for one of the theorems on f and F, and in a footnote on p. 355 for discontinuous functions. For the latter point he thanked Dedekind, who seems to have sent him an off print of the thesis; and in the sentence to which the footnote was attached he also acknowledged his junior colleague Cantor, ‘to whom I made known my investigations’, for remarks in this context and for the reference to an earlier paper introducing uniform convergence.
In a succeeding paper, Heine 1872a discussed ‘The elements of the theory of functions’ within the tradition of Weierstrass, with whom he had discussed these matters (pp. 172 and 182). He began with a theory of irrational numbers, based upon ‘number-series’ of rationals {an} in which ‘for each given quantity η, so small yet different from zero, a value n exists which brings about that an − an + v lies below η for all positive v’ and ‘elementary series’, ‘in which the numbers an, with increasing index n, fall below any given quantity’ (p. 174; he used only rationals, including zero). The ‘more general number or number-sign’ was defined in terms of ordered sequences as
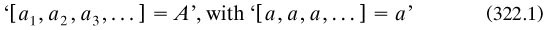
for the special case of rationals {a} (p. 176). The irrational numbers so formed constituted the ‘first order’; those of ‘arbitrary orders’ were definable by iteration of these procedures (p. 180).
Some casualness was evident here. Heine tended to mix sign and its referent in a formalist way of the time seen already in De Morgan and Boole and awaiting us later also. Further, while he laid down the criterion for the equality of two numbers in terms of the sequence of their arithmetical differences forming an elementary one, he did not explicitly mention the case of the reordering of a sequence, and made no association of the numbers with the real line.
The rest of Heine’s paper was taken up with an application of this theory to continuous functions, which he defined in its sequential form; for every ‘number-series {xn} that the signs X possess, also f(x1), f(x2), etc. a number sequence with the number-sign f(X)’ (p. 182, but with no allusion to Cauchy’s similar formulation quoted in §2.7.2). He stressed that continuity at X was so defined; in a footnote he noted ‘uniform’ continuity, referring to his earlier paper, and at the end of the paper he proved (p. 188.)
THEOREM 322.1 ‘A continuous function from x = a to x = b (for all individual values) is also uniformly continuous’.
The proof was effected by dividing up [a, b] into a finite number of sub-intervals, expressing the continuity of the function over each one in the (ε, δ) way (§2.7.2., and taking a δ large enough to apply to all of them. The finitude of N, crucial to the proof, led Schönflies to give the unfortunate name ‘Heine-Borel theorem’ (1900a, 119. to a far more general theorem proved by Emile Borel in the 1890s (§4.2.2., in which a finite covering also occurs.
In the footnote Heine also thanked Cantor for a necessary and sufficient condition for the continuity of f(X), and referred to a paper which his younger colleague had already published in this area of mathematics (p. 182). Cantor’s acquaintance with such topics from Heine was to have a decisive effect on his own later career.
3.2.3 Cantor’s extension of Heine’s findings, 1870–1872. In an early paper ‘On the simple number systems’ Cantor 1869a considered ‘Systems of positive whole numbers’ {br}, and in particular the question of whether expansions of the form
could generate irrational as well as rational numbers. So he was primed to respond to the issues raised by Heine, and between 1870 and 1872 he published five papers on them, switching for venue with the fourth one from Crelle’s journal to the recently founded Mathematische Annalen (Dauben 1971a).
In the first four papers Cantor handled expansions rather like (323.1., Riemann’s theorems (and an extension due to Schwarz., uniform convergence, the uniqueness of expansion for continuous functions, and the possibility of a finite set of points excepted from the in-general convergence. While careful and intricate, they are only respectable footnotes to the work of his predecessors. But with the fifth paper, dated November 1871 and published as 1872a, he opened a new era in these studies, with a proof that an infinite set of exceptional points (to use the modern term. could be allowed.
Drawing on his previous concern with irrational numbers, Cantor showed a fine grasp of the requirements that such a theorem would make upon him; for he gave a definition of them, basically following and developing that of Heine 1872a, which had been completed a month before Cantor’s paper. Taking the rational numbers (but excluding zero) as known, and forming a ‘domain’ (‘Gebiet’) A, he stated that if for any positive rational number ε and arbitrary positive integers n1 and m,
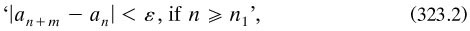
then the sequence {ar} ‘has a specific limit b’ (p. 93). Numbers definable in this way formed a new domain, B, and (in)equality relations and arithmetical operations between them were specified in terms of the analogous properties of the absolute difference between members of the corresponding rationals: for example,
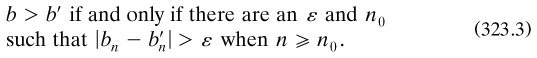
Cantor’s way of expressing the property (323.2) seemed to assume the existence of the limiting value which was being defined into existence. Of course, he was quite aware of the point, and his theory was free of this criticism (which we shall see Russell make in §6.4.7); but his manner of expression was distinctly unfortunate. In addition, he did not properly treat the fact that the same irrational number could be produced by different sequences of rationals; if b = b’, which number was the irrational by definition? In a later paper he named such a sequence (323.2) a ‘fundamental series’, and with great confidence stated that ‘with the greatest simplicity’ uniqueness of definition of an irrational was to be secured ‘through the specialisation of the pertaining sets (av)’ of rationals, such as its decimal or continued-fraction expansion (1883b, 186, 185).
In addition, Cantor was to cause perplexity to commentators such as Dedekind (§3.2.4) when, after stating that ‘The totality of number quantities’ {br} constituted a new domain B, he again followed Heine by allowing that ‘now it generates in a similar way together with the domain A a new domain C’, and rehearsed the procedures around (323.2–3) for ‘number-quantities’ {cr}, and also onwards a finite number of times to obtain the domain L ‘which is given as number-quantity, value or limit of the λth’ (1872a, 93–95). For him, since such procedures as specialisation and the construction of domains could be effected, the objects thereby defined definitely existed (see §3.6.1 on the philosophical background). He affirmed their status when he adjoined as an ‘Axiom’ the assumption that to the ‘distance from a fixed point o of the straight line with the + or − sign’ corresponded the number-quantities of each domain (pp. 96–97). Note the implied omission of zero from the rational numbers; we shall appraise the status of zero in §3.5.3.
The second major feature of Cantor’s paper was his handling of sets of points, which was developed out of this axiom. We have noted that in Cauchy, Dirichlet and Riemann collections of (mathematical) objects were being handled, albeit in a fairly informal way. By contrast, for Cantor ‘I name for brevity a value-set a given finite or infinite number of number magnitudes’ with the letter ‘P’, ‘and correspondingly a given finite or infinite number of points of a straight line a point-set’ (pp. 97–98).
A fundamental concept was that of the ‘limit-point’ (‘Grenzpunkt’) of a set P, defined as a point ‘in such a situation that in each neighbourhood of it infinitely points of P are to be found’ (p. 98). Then, corresponding to the limit-taking generation of higher domains, Cantor defined the ‘derived point-sets’ (‘abgeleitete Punktmengen’) of P, each one comprising the set of limit-points of its predecessor. Like the domains A, B,..., L, the derived sets P, P′,..., P(v) were finite in number, the order of each producing a domain or point-set ‘of the vth kind’ (p. 98), and his extension of Heine’s theorem on exceptional sets stated that they could in fact be of such a kind without infringing convergence in general within the interval [0, 2π] (pp. 99–101). The proof drew on properties of Riemann’s function F(x), and Cantor concluded his paper by restating his result in function-theoretic terms: a discontinuous function which was non-zero or indeterminate over a ‘point-set P’ within [0, 2λ] of every kind ‘cannot be developed by a trigonometric series’.
This theorem hints at Cantor’s insight that there were sets for which P(v) was never empty for finite v. In such a case an infinitieth derived set P(∞) could exist, and so presumably possessed its own derived set P(∞ + 1), and so on. But what were these sets? Cantor did not develop this line of thought at all in his paper, and only referred to it at the end of a later one (1880a, footnote to p. 355; sadly omitted from Papers, 148). Doubtless the theory was a bit too intuitive at that stage, and in any case did not (seem to) bear upon the theorem on trigonometric series. However, such considerations were soon to loom large in his thoughts; and he had the luck to gain a new confidant at exactly this time.
3.2.4 Dedekind on irrational numbers, 1872. We now consider the work of a major figure: Richard Dedekind (1831–1916), student of Gauss, editor of Riemann, and follower of Dirichlet. He passed the main part of his career at the Technische Hochschule at Braunschweig (a very respectable institution) despite receiving various possibilities for chairs at universities (including, we shall note in §3.2.6, at Halle).,6 Principally concerned with abstract algebras and number theory, he also took a strong interest in the foundations of mathematical analysis, partly in connection with teaching (of which he was unusually fond for a professional mathematician). As we saw in §2.7.3, he saw Riemann’s two theses through the press in 1867, and was doubtless oriented by them to think about collections and continuity (Ferreirós 1999a, ch. 3). In 1872 he put out a booklet on ‘Continuity and irrational numbers’ (Dedekind 1872a). Its unusual manner of publication somewhat retarded its reception: for example, it escaped the attention of the reviewing journal Jahrbuch über die Fortschritte der Mathematik, and later Simon 1883a referred to it as ‘much too little known’. But it gradually gained attention, with reprints in 1892, 1905 and 1912, and has become a classic.
In his meticulous way, Dedekind recorded in the preface that he had come to his theory in the autumn of 1858 (when he was teaching at the Technische Hochschule in Zürich., with the key ideas being formulated on 24 November. In his draft he gave more details: discussion a week later with his colleague the analyst Heinrich Durège (who did not use the theory in his own work), and a lecture to a Braunschweig society in 1864.7 However, he does not appear to have used much of the theory in his own lectures, and was motivated to write up his work for publication by receiving Heine 1872a (on 14 March 1872, apparently). When writing his preface six days later he received an offprint of Cantor 1872a, sent presumably at Heine’s suggestion.
After reviewing the properties of the rational numbers and the corresponding relationships in the straight line (1872a, arts. 1–2), Dedekind turned to the ‘continuity of the straight line’ and ‘the creation of the irrational numbers’. The distinction of category between line and number was essential to his assumption of a structure-isomorphism between them. (In a curious coincidence of notation with Cantor, he also wrote ‘o’ for the origin-point of the line). The ‘completeness, gaplessness or continuity’ of the line was assured by the ‘Principle’ that one and only one point on it could divide all its points ‘in two classes’ such that ‘each point of the first class lies to the left of each point of the second class’ (art. 3).
Similarly, numbers were divided into two classes A1 and A2 by a ‘cut’ (‘Schnitt’), written ‘(A1, A2)’. They were of three kinds: I use round and square brackets to symbolise them. In the cases ]( and)[, the cut created a rational number; for the case)(, however, when ‘no rational number be brought forth, we create anew irrational number α, which we regard as fully defined by this cut: we will say that the number α corresponds to this cut, or this cut brings it about’ (art. 4). He also proved here the existence of irrational numbers by a lovely reductio argument that has never gained the attention that it deserves: assume that the equation t2 = Du2 in integers (D not a square) has a solution, and let u be the smallest integer involved; then exhibit a smaller integer also to satisfy the equation, a contradiction which establishes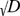 
as irrational. In a painstaking analysis (arts. 4–5), he also showed that the number-system thus defined satisfied the properties of ordering, continuity and combination required of the real numbers, and also that theorems on the passage to limits could be expressed (art. 6).
Dedekind stressed the distinction of category between cut and number in 1888; against the view of his friend Heinrich Weber that ‘the irrational number is nothing other than the cut itself he explained that ‘as I prefer it, to create something New distinct from the cut, to which the cut corresponds [...] We have the right to grant ourselves such power of creation’, and cuts corresponding to both rational and irrational numbers were examples (Dedekind Works 3, 489).
Dedekind also emphasised that ‘one achieves by these means real proofs of theorems (such as e.g.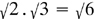 
)’ (art. 6.; and this claim excited the surprise of the analyst Rudolf Lipschitz, who wrote to Dedekind in 1876 that ‘I hold that the definition proposed in Euclid [book 5, prop 5... ] is just as satisfactory as your definition.’ In reply Dedekind explained that the standard proofs were ‘nothing than the crudest vicious circle’, since not ‘the slightest explanation of the product of two irrational numbers flows’ from that for rational numbers. (In fact, Euclid there did not treat numbers at all, but geometrical magnitudes.) Dedekind’s educational streak emerged in the added comment: ‘Now is it really outrageous, the teaching of mathematics in schools rates as an especially excellent means of cultivating the mind, while in no other discipline (such as e.g. grammar) such great violations of logic would be tolerated only for a moment?’ (Works 3, 469–471).
Thus the aim of Dedekind’s study eluded even so distinguished a contemporary as Lipschitz. Another respect in which he was rather isolated from his colleagues concerned his philosophy of mind, and its bearing upon mathematics. His emphasis on the word ‘creating’ the new number exemplifies a philosophy which appeared also in his discussion of discontinuous space, clearly inspired by Riemann (1872a, end of art. 3):
If space undoubtedly has a real existence, then it does not necessarily need to be continuous; numerous of its properties would remain the same, if it were discontinuous. And if we were to know for certain that space were discontinuous, nothing could hinder us, if we wished, from making it into a continuous [space] by filling out its gaps in thought into a continuous one; this filling out however, would consist in the creation of new point-individuals and would be executed in accordance with the above principle.
Even though Dedekind’s philosophy was not fully appreciated, his definition of irrational numbers gradually came to be preferred over all others in textbooks and treatises.8 The simplicity of his approach must have appealed: he structured the real line with his theory of cuts, and then associated real numbers with each cut, whereas other definitions took the real line for granted and obtained the irrational numbers via a process of construction (in Cantor’s case the fundamental sequences (323.2)).
The booklet inaugurated for Dedekind a greater involvement in the foundations of analysis than he probably anticipated at the time, because he became amanuensis to Cantor’s investigations into sets. He received an offprint of Cantor 1872a while completing his booklet; and their friendship was established in April 1872, a few weeks after Dedekind had written the preface, when fate led them both to stay at the same hotel in Gersau in Switzerland. The correspondence was soon launched (Ferreirós 1993a).
3.2.5 Cantor on line and plane, 1874–1877. Cantor’s first paper devoted to set theory proper appeared in Crelle’s journal as 1874a. The title mentioned ‘a property of the concept [‘Inbegriff’] of all real algebraic numbers’, namely, that they were denumerable. He did not use that word, but he stated the property in the standard way: that they could be laid out completely ‘in the form’ of an ordered sequence (art. 1). He also showed that the real numbers did not have this property (art. 2): taking any denumerable sequence S of them, he formed the sequence of nested open intervals {(αr, βr)} by taking the first one arbitrarily and defining the end-points of each one as the first two numbers which lay within the preceding interval. Monotonic sequences of numbers were thereby created: if these sequences were finite, then within the last interval at least one further member of S could be found; if infinite but converging to different values, then again a member of S was available; and if infinite and convergent to the same value η, then the property of nesting prohibited η from belonging to S. He ended by indicating consequences for rational functions. Dedekind had received versions of these and other details in Cantor’s letters; indeed, according to his own note, he had contributed the proof of the case of η ‘almost word for word’ without acknowledgement, or use of his continuity principle either (Cantor-Dede-kind Letters, 19).
Cantor now knew that the infinite came in different sizes. This conclusion was given a firmer form in the next paper, which appeared four years later, as 1878a. Sets were now called ‘manifolds’ (‘Mannigfaltigkeiten’), Riemann’s word (§2.7.4) though with a different reference. When two of them could be paired off by members, ‘these manifolds have the same power, or also, that they are equivalent’. More significantly, he also stressed inequality of power, and the relations ‘smaller’ and ‘larger’. Later in the paper he wrote of the ‘scope’ of a ‘variable quantity’; and if two of these, a and b, could be paired off, then they too were equivalent, a relation expressed by the propositions ‘a ~ b or b ~ a’ (art. 3).
Among the results proved was the equivalence of the irrational and the real numbers (art. 3), of the intervals (0, 1) and [0, 1] (art. 5), and of continuous manifolds of n and of one dimensions. The first proof of the last theorem drew on the uniqueness of the continued-fraction expansion of an irrational number (art. 1); the second was based upon decimal expansions, in the case of n = 2, that the point (0. x1x2...., 0. y1 y2)...) in the unit square could be mapped onto the point 0. x1y1x2y2 …of the unit line (art. 7). At the end of the paper Cantor concluded that the infinite came in only two sizes: namely ‘functio ips. v (where v runs through all positive numbers)’ and ‘functio ips. x (where x can take all real values ≥ 0 and ≤ 1)’. He also characterised the latter case a few lines earlier as ‘Equal to Two’, which was his first statement of the conjecture known later as his ‘continuum hypothesis’; it is discussed in §3.5.2.
In letters Dedekind had been bombarded with versions of every theorem, and indeed in June he had contributed the decimal-expansion proof himself, including the need to distinguish expansions such as 0.30000... from 0.2999... (Cantor-Dedekind Letters, 27–28). Cantor’s reaction to this result was ‘I see it, but I do not believe it’ (p. 34, in French); and he transcribed most of the proof into his paper without acknowledgement ….
Allegedly Kronecker had held up publication of this paper in Crelle’s journal. Cantor himself is the principal source of this story, though at the time he only told Dedekind in October that his paper had been with C. W. Borchardt (a co-editor of the journal) for three months (p. 40). In fact, if there was a delay, it cannot have been a long one (the date of submission of the paper, 11 July 1877, is not obviously out of line with others in the same volume); and, given the way in which Cantor had chosen to express himself, Kronecker deserves our sympathy. His philosophy of mathematics will be contrasted with Cantor’s in §3.6.4.
3.2.6 Infinite numbers and the topology of linear sets, 1878–1883. The results of 1878 on the equivalence of sets of different dimensions led Cantor to consider in detail the question of correctly defining dimension. The success of his endeavours and those of some contemporaries was only partial (D. M. Johnson 1979a, chs. 2–3), and the experience seemed to impel him to concentrate his studies largely on sets of points on the line. In his later work, n-dimensional sets were discussed sometimes, but the dimensional aspects themselves were not discussed. The main product was a suite of six papers with the common title ‘On infinite linear point-manifolds’, published between 1879 and 1884, the fifth part appearing also as a booklet. The venue was Mathematische Annalen, and Klein the relevant member of the editorial board; he became Cantor’s chief correspondent for a while, receiving over 40 letters in 1882 and 1883. One reason followed from Heine’s death in 1881; Cantor had asked Dedekind to put himself forward as successor (my 1974b, 116–123) but Dedekind declined and so Cantor dropped him for many years (§3.5.3).9
Cantor broadly followed the order of interest of his earlier papers, beginning in 1879a with an extended study of the derivation of ‘point-sets’, to quote the alternative name (‘Punktmengen’) to that of his title, which he introduced in the first paragraph. The exceptional sets ‘of the λth kind’, which were allowed in §3.2.2 under the rule of ‘in-general convergence’, were now grouped collectively as ‘of the first species’; those with no empty derived set of finite order constituted ‘the second species’ (p. 140). As an important kind of example of the latter species he defined the ‘everywhere dense set’ within the closed interval [α, β] (itself written ‘(α…β)’), by the property that its members could be found within every closed sub-interval of [α, β], however small; the property that it was contained within its first derived set was a theorem (pp. 140–141).
The rest of this paper was largely concerned with these two ‘classes’ of linear point-sets, each one defined by its common ‘power’ (‘Mächtigkeit’): sets which were ‘countable in the infinite’ including, he now knew, those of the first species; and those to which (interestingly) he gave no name but chose a ‘continuous interval’ as the first ‘representative’, with the cardinality of the continuum (pp. 141–144). The (in)equality of cardinalities of two manifolds M and N was defined, as earlier, extensionally in terms of (no) isomorphism between their members (p. 141); and he began the second paper with the allied statement that ‘the identity of two point-sets P and Q will be expressed by the formula P = Q’ (1880a, 145).
In this paper some basic machinery was presented (pp. 145–147). Disjoint sets were defined as ‘without intersection’ (with no special symbol., and the union of ‘pairwise’ disjoint sets {Pr} was written ‘{P1, P2, P3,...}’. For the inclusion of sets ‘we say: P is included in Q or also that P be a divisor of Q, a multiplum of P’. The ‘union’ and ‘intersection’ of ‘a finite or infinite number’ of sets {Pr} were written respectively as
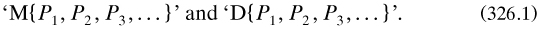
where ‘M’ denoted ‘multiplum’. Finally, for ‘the absence of points […] we choose the letter O; P ≡ O thus indicates that the set P contains not a single point’. We note that Cantor was unclear over whether ‘O’ symbolised the/an empty set, or whether ‘≡ O’ denoted the property that a set were empty (compare Boole in §2.5.4).
Cantor’s first use of these tools was to express certain properties of the sequence P(v) informally conceived in §3.2.2. Now the set ‘P(∞)’ of a set P of the first species was explicitly introduced, as ‘the derivative of P of order ∞’, defined as the intersection of all its predecessors, and stated to be equal to the intersection of any infinite subset of them (p. 147). The idea of P(∞) having its own derived set was now extended into prolonging the sequence to (P(r)), where r was allowed to wander up through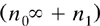 
to
in a ‘dialectical generation of concepts’ (pp. 147–148).
It was at this point that Cantor added the footnote mentioned at the end of §3.2.2, concerning his possession of these ideas ten years earlier. Probably it was a retort to a claim of priority for the notion of the everywhere dense set recently made by du Bois Reymond (1880a, 127–128), whose own point-set topology was noted at the end of §3.2.1; he had named this type of set ‘pantachic’.
The further refinement of the still intuitive formulation (326.2) was to be a major preoccupation for Cantor in later papers in his suite. In the third paper he reintroduced the concept of the ‘limit-point’ of a set, but, in some contrast to §3.2.2, more like the form which we now distinguish as its accumulation point: ‘in each neighbourhood of it, ever so small, points of the set P are to be found’ (1882b, 149). He added that Weierstrass had proved that any bounded infinite set of points possessed at least one such point (the theorem now known as the ‘Bolzano-Weierstrass’).10 He also attributed to Jacob Steiner’s lectures 1867a on projective geometry the name ‘power’ (p. 151), and ruminated on various properties of the cardinality and topology of sets of one and several dimensions. Most interesting was the view, echoing that of Dedekind in §3.2.3, that the axiom of §3.2.2 of the isomorphism between the real line and the real numbers extended to a hypothesis about the continuity of space, and that continuous motion was possible in a space made discontinuous by the removal of a denumerable set (p. 157): as we shall note in §3.3.3 and §3.3.5, early commentators were to pick up on this detail.
Cantor’s fourth paper began with the notation
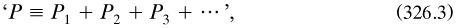
to replace that for the union of pairwise disjoint sets quoted before (326.1. (1883a, 157): in both appearance and content this was now very like Boole’s use of ‘+’ (§2.5.3), but it is unlikely that he knew of Boole’s work, at least in any detail. The principal new idea was of ‘an isolated point-set’ Q in n-dimensional space for which, in the notation of (326.1)1,
The importance of this type of set lay in the fact that one could be created for any set P, namely (P − D(P, P′)); and this insight led him to two ‘important decomposition theorems’:
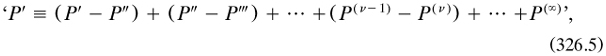
and its companion shorn of the last term P(∞) for first-species sets. An isolated set was countable;11 each component set in (326.5)1 was isolated; if P′ was denumerable, so was P; and first-species sets were denumerable, and so were those of second species when P(λ) was denumerable for any α of the ‘infinity-symbol’ used after (326.1) (pp. 158–160). The use of the nervous word ‘symbol’ shows that the infinite was still somewhat out of his reach.
3.2.7 The Grundlagen, 1883: the construction of number-classes.
That is a wonderful harmony, going into magnitudes, whose exact passage is the theme of the doctrine of transfinite numbers.
Cantor on the number-class, lecture of 1883 (1887–1888a, 396)
In the fifth paper of the series, which comprised 47 pages (including 5 pages of endnotes), Cantor 1883b reached new levels of both length and depth in developing his theory. He republished it at once as a pamphlet 1883c with Teubner, the publisher of Mathematische Annalen, in a slightly revised printing and with a preface. It carried the new title ‘Foundations of a general theory of manifolds’, with the sub-title ‘A mathematical-philosophical study in the doctrine of the infinite’. The account here will be confined to the foundational aspects and the construction of transfinite numbers (as he often now called them): the well-ordering principle and the continuum hypothesis are postponed to §3.5.1–2.
The word ‘manifold’ (‘Mannichfaltigkeit’) attached to this suite of papers was explained in the first endnote as ‘each multiplicity, which may be thought of as a One, i.e. each embodiment [‘Inbegriff’] of particular elements, which can be bound together, by a law into a whole’; he offered ‘set’ (‘Menge’) as a synonym (p. 204). The intensional form of this definition will be noted in §3.4.6, on a later appearance. His choice of name was unfortunate, as it had been used already in a different context by Riemann (§2.7.3), Hermann von Helmholtz and others; we shall note Cantor’s disapproval of their empiricist philosophy in §3.6.2.
The burden of the word ‘general’ was Cantor’s attempt to ground his finite and transfinite arithmetic in a ‘real whole number-concept’, to quote from his first sentence.12 He distinguished two kinds of reality: ‘intra-subjective or immanent’, when numbers ‘on the ground of definitions can take a quite specific place in our mind’; and ‘trans-subjective or also transient’, when they ‘should be regarded as an expression or an imagine of courses of events and relationships in the external world standing opposite the intellect’ (p. 181). He accepted both kinds of reality, and saw the connections between them to be established in ‘the unity of the all, to which we ourselves belong’ (p. 182).
Cantor distinguished two kinds of the infinite: ‘proper’ (‘eigentlich’), which can be translated as ‘real’ or ‘actual’; and ‘improper’ (‘uneigentlich’), which was and is better known as the potential infinite (p. 165). He contrasted his current desire that the infinite numbers ‘possess concrete numbers of real reference’ (p. 166) with his previous use of ‘infinity-symbol’ (a footnote here, which Zermelo failed to include in his edition). So he replaced ‘∞’, with its ambiguities of past use, with ‘ω‘, chosen as the last letter of the Greek alphabet and denoting the smallest transfinite ordinal (a footnote which Zermelo preserved on p. 195).
Cantor grounded ordinal numbers in sets in the following way. A ‘well-ordered set’ was defined by the property that its elements exhibited ‘a specific prescribed succession among them’ with ‘a first element’ and a specific successor for each one (apart from the last element of a finite set). The pre-eminence among types of order of well-ordering, with its alleged applicability to all ‘well-defined’ sets, was precisely the well-ordering principle, which will be discussed in §3.5.1.
Given this assumption, an ordinal was specified as ‘the number of the elements of a well-ordered infinite manifold’; Cantor’s use of ‘Anzahl’ for ordinals rather than cardinals contravened normal practice (p. 168). These ordinals were produced via two ‘principles of generation’: that of ‘the addition of a unit to an existing [and] already constituted number’ (with 1 assumed as the first number., and thereby generated a succession of numbers with no greatest number (p. 195.; and ‘the logical function’ (sic. of creating ‘a new number’ ω ‘as limit of those numbers’. ω served as the new initial ordinal from which the renewed application of the first principle led to a fresh sequence {ω + n}, after which was postulated the new limit-ordinal 2ω,....
The operation of these principles in tandem generated the sequence of ordinals (326.2), with the former ‘dialectical generation of concepts’ now better understood, and more properties of the sequences provided (pp. 196–203). One of them, stated for sets M with cardinality of the second number-class, that if a sub-subset M′′ were isomorphic (‘gegenseitig eindeutig’) with M, then the intervening subset M′ was isomorphic with both M″ and M (p. 201). The proof, only sketched, drew upon the well-ordering principle; the need for a general and sound proof became a major concern for Cantor and others from the mid 1890s, including Whitehead and Russell (§3.4.1, §4.2.5, (786.1)).
The ‘number-classes’ of these ordinals were introduced in a rather enigmatic way. The first class comprised ‘the set of finite whole numbers’ ‘from it follows’ the second class ‘existing from certain infinite whole numbers, following each other in specific succession’ then came to the ‘third, then to the fourth, etc’ (p. 167). Details of only the second number-class were provided in the paper; but it became clear that one purpose of these classes was to serve as a means of defining transfinite cardinal numbers, or ‘powers’. The smallest such cardinal for an infinite set was defined by the property ‘if it can be ordered isomorphically with the first number-class’. Cantor claimed that the cardinality of the class of ordinals possessing this property was not only not equal to that of the first class ‘but that it actually is the next higher power’, since ‘The smallest power of infinite sets [... ]will be ascribed to those sets which can be ordered isomorphically with the first number-class’ (p. 167).
Cardinal numbers, both finite and infinite, were given epistemological priority over ordinals, in that they were defined independently of the orderings of which a set was susceptible. This was Cantor’s position on the relationship between these two types of number, which will be a recurrent theme in this book; we shall note it again in §3.4.6.
3.2.8 The Grundlagen: the definition of continuity. In another important section Cantor studied the continuum of the real line and of continuous sets in general. He rehearsed his theory of irrational numbers of §3.2.3 in terms such as the definition
of a fundamental sequence (p. 186). Two features are worth noting: his failure to specify the moduli of the differences; and the appearance of ‘v = ∞’ under the limit sign rather than the ‘v → ∞’ that would be expected of a Weierstrassian, especially one who had defined ∞ as the limit-ordinal ω a few pages earlier! He also defended his iterative definitions of higher-order numbers against Dedekind’s criticism (§3.2.3), on the interesting grounds that ‘I had only the conceptually various forms of the given in mind’, not ‘to introduce new numbers’ (p. 188). But a retort to Dedekind’s own theory of cuts is harder to cope with: apparently ‘the numbers in analysis can never perform in the form of “cuts,” in which they first must be brought with great pomp and circumstance’ (p. 185), to which editor Zermelo understandably added ‘[?]’.
The real line is itself a set: how was it defined, and how many points did it possess? On the first question Cantor made a definitive contribution in requiring two ‘necessary and sufficient characteristics of a point-continuum’. Firstly, he defined a set P to be ‘perfect’ when it equalled each of its derived sets P(γ) for all ordinals of the first two number-classes (p. 194: by implication for ordinals of higher number-classes?); he distinguished this property from the ‘everywhere dense’ of §3.2.6, and also from ‘reducible’, where ‘P(γ) ≡ 0’ would occur for some γ of either the first or the second number-classes (p. 193). Secondly, P had to be ‘connected’: that is, between any two members t and t′ at least one finite collection of fellow-members {tr} could be found such that ‘the distances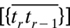 
are collectively smaller than ε’, an arbitrarily chosen (positive. number (p. 194). This second property was bought at the price of spatial, or at least of metric, reflections; these were ensured under some measure-theoretic considerations, which themselves included the questionable assertion that ‘in my opinion, the involvement of the concept of time or of the intuition of space […] is not in order; time is in my view a representation that for its clear explanation has for assumption the concept of continuity, which is independent of it’ (pp. 191–192). Later he was to replace connectivity with a property free from metrical considerations (§3.4.7).
The need for both properties to define continuity was a major advance, and characteristically Cantor crowed over the inadequacy of two of his predecessors: Bolzano 1851a, art. 38 for requiring only connectivity, and Dedekind 1872a for delivering only perfection. Further, given his own (partly) set-theoretic definition of continuity and the construction of the number-classes, Cantor was in a position to restate his continuum hypothesis, in a stronger form than the one noted in §3.2.4: ‘that the sought power is none other than that of our second number-class’ (the somewhat prematurely placed p. 192). ‘I hope to be able very soon to be able to answer with a rigorous proof’, he continued; the fate of these efforts will be recorded in §3.5.2.
In an endnote attached to his definition of continuity Cantor presented the remarkable ‘ternary set’, as it came to be known; its generic member z was defined by the expansion
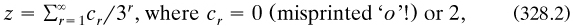
and the totality of combinations of 0s and 2s produced the members (p. 207). He presented it as a countable and perfect set which was not everywhere dense in any interval. He did not himself use the set much, but its properties were to be of great interest to many of his mathematician successors.
3.2.9 The successor to the Grundlagen, 1884. In a short special preface prepared for the pamphlet version of the Grundlagen and dated as of Christmas 1882 Cantor announced that his work ‘goes very far’; but he also doubted that ‘the last word to say was in place’, and in the following April he sent to the Annalen a successor. This appeared as the 36-page paper 1884b, in which the numbering of sections was continued but no endnotes were furnished. A further instalment was promised at the end of the paper, but it did not appear and maybe was not written.
In this instalment Cantor concentrated on topological properties of ‘linear’ sets in n-dimensional space, especially decomposition theorems, although he included many references to older sources. One of his main concerns was with the ‘distributive properties’ of sets, to use the name introduced later in connection with the Heine-Borel and such theorems: he did not himself have this result, but he stated a remarkably original theorem-schemum about points in a set possessing any ‘property Y’ (p. 211). He also modified the definition of union to allow for overlapping sets (p. 226). His greater confidence over the status of transfinite ordinals was shown in the definition of ‘P(ω)’ as the intersection of sets stated before (326.2). He also introduced an important new type of set: ‘dense in itself’ (‘in sich dicht’), for which ‘a set P is a divisor of its derivative P(1)’ (p. 228). This completed a trio of definitions, that
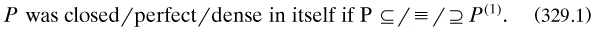
Cantor studied perfect sets in the most detail, partly in the hope of proving the continuum hypothesis (the closing statement on p. 244); his main result of this kind was that a perfect set was of the same cardinality as the closed interval [0, 1] (p. 241), and thus of the continuum. But the result with more lasting consequences (pp. 222–223) stated:
THEOREM 329.1 A closed set of cardinality greater than the denumerable could be (uniquely) decomposed into a perfect set P and one R which was at most denumerable.
This theorem is now known as the ‘Cantor-Bendixson’, and he referred to correspondence with Ivar Bendixson (1861–1935) (p. 224). This exchange occurred partly in connection with his original formulation in 1883c, 193, where R was held to be reducible (defined after (328.1)); Bendixson 1883a corrected this stipulation. The contact was part of an important transfer of Cantor’s circle of supporters, which we now recount.
3.3.1 Mittag-Leffler and the French translations, 1883. Gösta Mittag-Leffler was the leading Swedish member of the coterie of mathematicians who fell under the spell of Weierstrass’s tradition of mathematical analysis. Born in Stockholm in 1846 (the year after Cantor., he duly trekked to Berlin in the 1870s and soon was applying the new methods, with distinction, to elliptic functions and especially to complex-variable analysis. In 1881 he obtained a professorship at the newly founded university in his home town. But more germane to our story is that in the following year he married into a rich Finnish business family with whom he had become acquainted while holding a chair at the university there, and at once applied the financial windfall to the founding of a new mathematical journal.
From the start Acta mathematica was a major serial in its field, and Mittag-Leffler ran it until his death in 1927. He also built a magnificent house in a nice suburb of Stockholm, and assembled a superb library and a valuable archive not only of his own papers and correspondence but also of mathematicians in whom he was passionately interested. The two main heroes were Weierstrass and Cantor; for early on in his career he had read Cantor in Mathematische Annalen and appreciated the importance of Mengenlehre.13
The launch of his journal gave Mittag-Leffler a reason to develop his friendship with Cantor by asking for new papers, and also by suggesting that the bulk of the old ones be translated into French in order to be more accessible to the world mathematical community. Upon receiving Cantor’s consent, Mittag-Leffler secured the assistance of Charles Hermite in Paris, and the translations were prepared there by one Darguet with revisions and corrections made by Cantor himself and Mittag-Leffler, and some of them by Hermite’s younger colleagues such as Paul Appell and Henri Poincaré. Interestingly, ‘Punktmenge’ was rendered as the traditional French word ‘système’, and the pair ‘(un)eigentlich Unendliche’ came out as ‘l’infini (im)proprement dit’.
The ensemble, which I cite collectively as ‘Cantor 1883a’, appeared as 104 pages of the last number of the second volume (1883) of the journal, in an order different from that of their original appearances: 1874a on algebraic numbers; 1878a on dimensions; two papers on trigonometric series, including 1872a; the first four papers in the suite on linear point-sets; and finally the predominantly mathematical articles of the Grundlagen, but in a different (and rather more readable) order and with come cuts and revisions.14 The historical and philosophical remainder, and the preface to the pamphlet version, were omitted, at Mittag-Leffler’s request (and already with Hermite’s prompting). The sixth paper in the suite had not yet been written, but Cantor contributed here his first original piece for Mittag-Leffler, also in French: a miscellany 1883e of theorems on sets in an n-dimensional space, starting out from some in the Grundlagen and the decomposition (326.5).
Finally, Mittag-Leffler’s student Bendixson contributed a melange 1883a of his own decomposition theorems, especially Theorem 329.1. Upon seeing Bendixson’s paper Cantor sent in his own paper 1884a in French, devoted to ‘the power of perfect sets of points’ and to nesting sequences of closed intervals, and also publicising the ternary set (328.2). Mittag-Leffler explained the purpose of the paper in an explanatory note to the title, which Zermelo left out of his edition of Cantor’s papers.
3.3.2 Unpublished and published ‘communications’, 1884–1885) Throughout 1883 and 1884 Cantor and Mittag-Leffler corresponded intensively about the developing Mengenlehre, and also non-friends such as Kronecker. Cantor dropped Klein and Mathematische Annalen in favour of his new contact, and by the autumn of 1884 he was promising four papers of various kinds, some successors to others; it started with a ‘first communication’ in German, on the ‘Principles of a theory of order-types’.
During six weeks of the summer of 1884 Cantor, then in his 40th year, suffered his first mental crisis (Schonflies 1927a). It started and ended suddenly after a few weeks, during which he displaced his research effort into other directions (the numbers of ways of expressing even integers as sums of two primes, and the belief that Bacon wrote the works of Shakespeare). These features strongly suggest that he had experienced a mid-term crisis; the effect will have affected the solidity of his psyche when he was struck by more serious attacks from 1899 onwards (§3.1.2).
Upon resuming work in August, he worked intensively on the continuum hypothesis (§3.5.2). Then in November 1884 he completed and sent off to Mittag-Leffler the first of his promised papers, and over the next four months he added to it two lengthy articles to the six already prepared. Mittag-Leffler designated the full paper for a place in volume 7 of the Acta; but when he reread the text in March 1885 upon receiving the first signature of proofs, he advised that ‘It seems to me, that it would be better for you yourself not to publish these investigations before you can present new very positive results of new means of consideration’ such as the continuum hypothesis; ‘then your new theory would certainly have the greatest success among mathematicians’. As it was,
I am convinced from it that the publication of your new work, before you can present new results, would hurt your repute among mathematicians very much [...] So the theories will be discovered again by somebody 100 years or more afterwards and indeed one finds out subsequently that you already had everything and then one gives you justice at last, but in this way you will have exercised no significant influence on the development of our science.
Mittag-Leffler’s advice was well-meant (and his measure of the time-scale of Cantor’s posterior recognition rather interesting.; but it reflected his strong lack of enthusiasm for matters philosophical, and did not constitute a fair judgement of the paper. Cantor, already low in self-confidence, agreed at once, and in the following January (1885. he sent in a ‘second communication’, very mathematical in content, which appeared in the Acta as 1885b. But this was his last paper to appear there: the frequency of his correspondence with Mittag-Leffler fell away quickly and virtually stopped by 1888, and in later years he was bitter in his recollection of the affair to correspondents.
Apart from such expressions, and a brief and largely unnoticed footnote in a later paper (1887–1888a, 411), the ‘Principles’ remained unknown until my astonished eyes saw it in the surviving Nachlass in 1969. I cite it as Cantor m1885a: I published it as part of my account 1970b of the affair, where are to be found the quotations above, drawn from various other pertinent documents.15
3.3.3 Order-types and partial derivatives in the ‘communications’. One of Cantor’s great achievements was to recognise the variety of orders in which the elements of (especially) an infinite set could be put. Examples of the resulting knowledge had appeared already, especially in 1884b, 213–214; but in the ‘Principles’ he discussed the matter in detail and in some generality.
In the preamble Cantor explained his specific motivation to write the paper. The French mathematician and philosopher Jules Tannery (1848–1910), whose elder brother Paul was mentioned in §3.1.2 as a correspondent of Cantor, had reviewed at length the first two volumes of Acta mathematica in his Bulletin des sciences mathématiques, devoting the last ten pages to the Cantor number (Tannery 1884a, 162–171). He expressed reservations about some of Cantor’s procedures and claims; for example, he preferred Dedekind’s definition of irrational numbers, and cast doubt on the utility of Cantor’s for science in view of the possibility (indicated just before (326.3)) of continuous motion in a discontinuous space. Cantor started his new paper by casting it as a reply to Tannery, to clarify his theory from philosophical and metaphysical points of view (m1885a, 82–83).
‘The real whole numbers 1, 2, 3,... constitute a relatively quite small species of thought-objects, which I call order-types or also simply types (from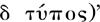 
. Further, those thought-objects ‘which I call transfinite or superfinite numbers, [are] only special kinds of order-type’. Indeed, ‘The general type-theory’, his short name for ‘Theory of order-types’, ‘constitutes an important and large part of pure Mengenlehre (Théorie des ensembles), also therefore, of pure mathematics, of which the latter is in my conception nothing other than pure Mengenlehre’ (p. 84).
Thus an important theme of this book, mathematics as Mengenlehre, made its début, albeit in a text which did not reach the public. Cantor immediately stressed the close relationship ‘to applied Mengenlehre’ (which ‘one takes care to call natural philosophy or cosmology’) such as ‘to point set theory, function theory and to mathematical physics’. He also associated his theory with chemistry (thereby continuing a link noted already in §2.2.1, §2.3.3 and §2.6.1) while distinguishing it from a specific ‘theory of types’ currently being pursued there. The chemical connections continued in his use of the word ‘valency’ as a synonym for ‘power’, a concept which he explained as ‘the representation’ or ‘representatio generalis’ of a set M ‘for all sets of the same class as M’ (pp. 85–86: this term was already in the 1883 lecture).
After rehearsing these fundamental notions Cantor dwelt not on well-ordering but on ‘simply ordered sets’ as a category to embrace all orderings; it was composed of members ‘whether from nature, or through a conventional lawful relationship’ and possessing a complete and transitive ‘determined relation of rank’ (p. 86). Order-isomorphism between two such sets was specified as ‘mutually similar’. Each such set ‘has now a determined order-type [...]; by it I understand that general concept, under which fall collectively the given ord[ered] sets of similar ordered sets’. For example, finite simple order was ‘nothing other than the finite whole numbers’; the sequence of rational numbers (1 – 1/v) was a type given the letter ‘ω’, the rationals within (0, 1) were designated ‘η’, and the real numbers within (0, 1) ‘θ’(p. 87).
Much of the rest of Cantor’s exegesis was taken up with related types; for example, that of the rationals within [0, 1) was ‘1 + η’, within (0, 1] was ‘η + 1’, and within [0, 1] was ‘1 + η + 1’. More generally, for any type α there was the ‘opposite type’ α*, so that the following type-equations ensued:
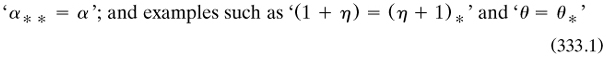
(pp. 87-88). He also took two simply ordered sets 
and 
with respective types α and β and defined their sum α + β and product ‘α β or αβ’ in terms respectively of their union and of a 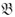-set of 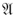s. In one of the articles added later he considered types for n-dimensional space, including 
for the type in which the order of the v th dimension was reversed (p. 97: due to a printer’s error this type was consistently misren-dered as ‘α*v’). His treatment of well-order was rather brief, but he stressed its manifestations in finite and transfinite numbers (pp. 89-90).
The other extra article (pp. 92-95) and the published ‘second communication’ 1885b dealt with this extended topology of respectively order-types and point-sets; but the first text was of course unknown and the second poorly organised. The best account was given in a long letter which Cantor sent to Mittag-Leffler in October 1884. The basic ideas were to write the operation of deriving a set P as ‘∂’ (to produce the set ∂P), and to define five more operations on P:
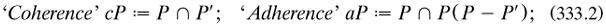
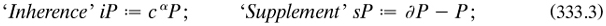
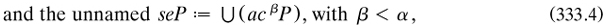
where α was an ordinal of the first or second number-class. ‘The signs introduced in my new work are thus the six: a, c, ∂, i, r, s’, Cantor told Mittag-Leffler in a sequel postcard, where he re-labelled (333.4) ‘rP’ and named it ‘Remainder’;16 properties of these sets were found, and new decomposition theorems presented, involving what I call ‘partially derived’ sets, such as acβP. While all the definitions were nominal and therefore the defined terms eliminable, the aim was to help the topological analysis of sets with an enriched vocabulary. In addition, on the proof-sheets of the paper Cantor changed the name ‘limit-point’ to ‘chief-element’, to reflect the extra conditions required to define this notion correctly for an ordered set (m1885a, 92-93).
It is a great pity that Cantor’s new ideas, both philosophical and mathematical, came through at the time of his mid-term crisis, and the former kind did not meet with Mittag-Leffler’s approval; apart from anything else, they were close to many of Whitehead’s and Russell’s later concerns. From this time on his contributions were made fitfully. We review them in the next section; this one ends with a short survey of the reactions of contemporaries to the work produced to date.
3.3.4 Commentators on Cantor, 1883-1885. Tannery’s review of Cantor’s papers in the Acta exemplified the growing interest in Mengenlehre. The Jahrbuch iiber die Fortschritte der Mathematik had been reviewing them, placing the reviews in the section ‘Principles of geometry’. They were routine pieces, neither polemical nor missionary; several were written by the geometer Viktor Schlegel (1843-1905). Another reviewer was the historian and mathematician Max Simon (1844-1918), who also noticed the Grundlagen for the recently founded book review journal Deutsche Literaturzeitung (Simon 1883a). In §3.2.3 we quoted from this review his lament that Dedekind’s booklet on irrational numbers was ‘much too little-known’; concerning Cantor, he appraised the notion of set, power (with the unhelpful explanation ‘thus more or less, what one commonly calls set’ (‘Menge’), well-ordered sets and the transfinite ordinals and cardinals. As Tannery was also to note (§3.3.2., he remarked on the ‘surprising theorem’, actually in the third paper of the suite and stated just before (326.3), on the possibility of continuous motion in a discontinuous space. Interestingly, just as Cantor himself had recently proposed when the French translation of the Grundlagen was to be prepared, Simon recommended reading its articles in a fresh order.17
In 1885 two treatments of Cantor’s work appeared, of quite different kinds. The Halle school-teacher Friedrich Meyer (1842-1898) published the second edition 1885a of his textbook on algebra and arithmetic. Despite its elementary level, he emphasised the ideas of his distinguished townsfellow: in the second sentence of his introduction he mentioned ‘the concept of set, especially the well-ordered set and the concept of power’, soon followed by reference to ‘a definition of number’ (‘Anzahl‘). Cantor was named several times afterwards, and at the end ‘my friend Dr. Simon’ was thanked for help. Further, the main text began at once with ‘The concept set and quantity’, and the first two chapters contained sprinklings of Mengenlehre; by the next page the novice reader was being confronted with ‘various order-types’ But the account of transfinite arithmetic was mercifully confined to two paragraphs of interjection into a routine account of the finite realm to indicate the transfinite ordinals and their basic properties (pp. 6, 10, 21).
The second treatment was written by Simon’s philosophical colleague at the University of Strasbourg, Benno Kerry (1858-1889); he published in the Vierteljahrsschrift für wissenschaftliche Philosophie an excellent 40-page survey 1885a of ‘G. Cantor’s investigations of manifolds’. Running through all the basic features of Cantor’s current theory, he also picked up several interesting details. Early on he discussed the ‘axiom’ linking the line with the real numbers (pp. 192, also p. 217), and later on he discussed Cantor on continuity, and also Dedekind’s definition of irrational numbers (pp. 202-204, 227). In a good summary of the sequence of derived sets he stressed the question of ‘the reality of the concept’ of the transfinite indices, especially when the ‘kinds of index’ extended to the ‘Babylonian tower’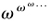 
(p. 199); however, he rather underplayed the role of well-ordering (pp. 205-206). Recording the construction of ordinals in the second number-class, he noted that a third would follow, but was sceptical about the conception of this class and of its associated ‘power’ (pp. 211, 213, 230). By contrast, he saw a possibility of defining infinitesimals as inverses of transfinite ordinals (p. 220); and in connection with Cantor’s definition of the measure of a set, he recalled the integral as ‘alternatively a sum of infinitely-small spaces’ (p. 229). His description of the definition ‘powers’ included a citation of Bolzano (pp. 206-208); this author was very well read indeed, as we shall see again in §4.5.4 when we note his reaction to the work of Frege.
3.4.1 Dedekind’s developing set theory, 1888. Cantor’s former correspondent published a second booklet 1888a; posing the question ‘What are the numbers and what are they good for?’, he gave a sophisticated and novel answer. Despite its rather unusual form of publication, it seems to have gained a quick reception (Hilbert 1931a, 487). He reprinted it in 1893 and 1911, with new prefaces noting some recent developments. Like his other booklet, this one gained various translations and is still in print as a classic text; but it is deceptive in its clarity, for underneath lies a most sophisticated and also formal approach which actually makes it hard to understand. F. W. F. Meyer noted this aspect in an appreciative review 1891a in the Jahrbuch.
As Dedekind mentioned in his preface (dated October 1887), his interest in the concept of number dates back to his Habilitation of 1854, when for his lecture he spoke before Gauss, Wilhelm Weber and his other examiners ‘On the introduction of new functions in mathematics’. He had started out from ‘elementary arithmetic’, where ‘the successive progress from a member of the series of absolute whole numbers to the next one, is the first and simplest operation’ and led on ‘in a similar way’ to multiplication, exponentiation, and the other operations. ‘Thus one obtains the negative, fractional, irrational and finally also the so-called imaginary numbers’ (m1854a, 430-431.. His later examples included the trigonometric functions (they related to the thesis itself, an unremarkable and unpublished essay on the transformation of coordinates), and elliptic functions and integrals.
Dedekind drafted his essay around the time of his previous booklet 1872a on irrational numbers (§3.2.4); but he seems to have abandoned it in 1878 (the drafts are published in Dugac 1976a, app. 56). He returned to it only on the occasion of the recent publication on the concept of number by Helmholtz and Kronecker, since he adhered to neither the empiricism of one nor the contructivism of the other (§3.6.2, 5) and wished to give his own approach some publicity.
In his preface Dedekind also referred to ‘the laws of thought’. He did not intend Boole’s view (§2.5.7), but the supposed power of the mind to create abstract objects which we saw also in §3.2.4. For sets he used the word ‘System’, probably taken from his reading of ‘systeme’ in French mathematics; it refers, in a naive way, to collections of mathematical objects (compare Hankel after (321.3)). It was specified in a way similar to that which Cantor had used (and will be quoted in §3.4.4.; as ‘various things a, b, c... comprehended from any cause under one point of view’, where ‘I understand by a thing any object of our thought’ (arts. 2, 1). It seems that systems were different in category from things, but the matter was not clarified here. For example, he did not define systems of systems but instead the union and intersection of systems (arts. 8, 17), which he named respectively as ‘collected together’ and ‘commonality’ (‘Gemeinheit’.; for a collection of systems A, B, C,... they were notated
Dedekind also defined the relationship of ‘part’ between two systems A and S, and written ‘A ∋ S’ (art. 3); but this relation slid between membership and improper inclusion, a surprising slip to find in a careful reader of Cantor. (Proper inclusion was specified in art. 6 as ‘proper part’). These points were to be treated only in a manuscript conceived soon after publication of the booklet but written after 1899 and published in Sinaceur 1971a. Entitling the piece ‘Dangers of the theory of systems’ he referred to art. 2 and noted that ‘of the identification of a thing s with the system S standing from the single element s’; but even then he proposed to add only the strategy ‘by which we want to indicate this system S again by a, thereby not distinguished from a, which will be permitted with some caution’ (citing arts. 3, 8, 102 and 104 as among pertinent examples). He now drew on his philosophy of mind to claim ‘the capability of the spirit to create a completely determined thing S from determined things a, b, c,...’ and thus to justify the difference between things and systems. To emphasise this point, he formally defined the ‘null system’ as the one ‘for which there is no single thing’; he gave it the letter ‘0’ and proved that it was unique. All of this was absent in 1888.
In tandem with his developing set theory Dedekind gave much attention to the transformation φ of a system S, in which any element s was mapped into s′ (or φ(s)) and any part T of S went into part T′ (1888a, art. 21). If S′ ∋ S, then φ was a transformation of S ‘in itself (art. 36). He laid particular stress on ‘similar’ (‘ähnliche’) transformations, under which different elements mapped into different elements. In this case φ(S) = S, and the (unique) ‘inverse’ transformation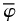 
returned s′ back to s: φ ‘is the identical transformation of S’ (art. 26). Among consequences, ‘One can thus divide up all systems in classes’ in which ‘one takes up all and only the systems Q, R, S,... which are similar to a determined system R, the representative of the class’ (art. 34)—an early example of the partition of a collection of objects by equivalence classes.
Dedekind proved that ‘If A ∋ B, and B ∋ A, then A = B’ (art. 5), as an obvious consequence of his definition of ‘∋’. While preparing the text he had proved the much deeper equivalence theorem that if S′ were transformed isomorphically into S and ‘if further S′ ∋ T ∋ S, so T is similar to S’ (m1887a); but he left it out. This is surprising, for his formulation was more general than Cantor’s (§3.2.8); we shall consider his proof in the context §4.2.5 of those published ten years later by Ernst Schroder and Felix Bernstein, after whom such theorems are often named.
3.4.2 Dedekind’s chains of integers. Another main notion was that of a ‘chain’ (‘Kette’) relative to a transformation φ: a system K (which was part of a system S was a chain if K’ ∋ K (art. 37). After showing that S itself was a chain, as were unions and intersections of them (arts. 38-43), Dedekind took a part A of S and named the intersection of all chains containing A ‘the chain of the system A’ (art. 44). He notated it ‘A0’—curiously in that, like Cantor (§3.5.3), he was chary of zero.
This was Dedekind’s definition of a progression with an initial element in A. To distinguish ‘the finite and infinite’ progressions he offered the reflexive definition (art. 64) of infinitude which he had supplied to Cantor. (He seems not to have noticed C. S. Peirce’s earlier discussion of the distinction between finite and infinite ‘systems’ in 1881b (§4.3.4).) Then he allowed his philosophy of mind much reign with a “proof” that ‘there are infinite systems’ (art. 66); for he gave as evidence ‘the totality S of all things, which may be objects of my thought’, since as well as any of its elements s it contained also ‘the thought s′, that s can be the object of my thought’, and so on infinitely. Some explanation from him would have helped; seemingly he was working within a Kantian framework.18 As it was, this “proof did not gain a good reception (§5.3.8, §7.5.2, §7.7.1).
So armed (as he thought) Dedekind characterised a system N as ‘simply infinite’ if ‘there is such a similar transformation φ of N, that N appears as the chain of an element, which is not contained in φ(N)’ and was called the ‘base-element’ 1; thus one of the defining properties was ‘N = 10’ (art. 71). This insight corresponded to Cantor’s idea of well-ordering; and another similarity occurred when ‘if we entirely ignore the special character of the elements’ of N, then they became ‘the natural numbers or ordinal numbers’ of the ‘number-series’ (art. 73); also like Cantor, he ignored negative ordinals. Later he showed that all simply infinite systems were ‘similar to the number-series’ (art. 132). His theory resembles the Peano axioms for arithmetic, which we shall describe in §5.2.3 in connection with their named patron.
To found arithmetic suitably Dedekind treated mathematical induction with a new level of sophistication. Two main theorems (to us, metarules) were used, which he carefully distinguished in art. 130. Firstly, a ‘theorem of complete induction (inference from n to n′)’ (arts. 59-60, 80) established a result for an initial value m and also from its assumed ‘validity’ for any n to that of its successor n. In the ensuing treatment of arithmetical operations this theorem allowed him to prove results such as m + n > n (art. 142). The second theorem was a deeper ‘theorem of the definition of induction’ (art. 126), which declared that, given any transformation θ of a system Ω into itself and an element ω in ω there existed a unique transformation ψ of the sequence N of numbers into a part of Ω which mapped 1 to ω and the ψ-transform of n′ to the θ-transform of the ψ-transform of n. It legitimated inductive proofs in arithmetic by providing a justification for inductive definitions; for it guaranteed the existence of a means by which θ could successively locate the members of Ω, or any sub-system of them (art. 127). Despite all the concern with the foundations of arithmetic in the succeeding decades, the profundity of this section of Dedekind’s booklet was not appreciated.19
Dedekind finally defined a finite cardinal as the number of members of any finite system ‘∑’ (art. 161); provably unique to each ∑, it obtained also to any system similar to ∑, including finite number-series ‘Zn’ from 1 to any n (arts. 159, 98). Thus, contrary to Cantor (§3.4.5), he gave ordinals priority over cardinals.
Of all resources which the human spirit [possesses] for the facilitation of his life, i.e. the work in which thinking exists, none is so momentous and so inseparable from his most inner nature as the concept of number. Arithmetic, whose only object is this concept, is now already a science of immeasurable extension![;] and it is not thrown into any doubt, that no barriers at all are set against this further development; just as immeasurable is the field of his application, because each thinking person even when he does not follow clearly, is a number-person, an arithmetician.
Dedekind, undated manuscript (Dugac 1976a, app. 58)
Three related aspects of Dedekind’s treatment of arithmetic merit attention. Firstly, like Cantor and possibly following him, Dedekind specified ordinal numbers by abstracting the nature of element from a system and considering only their order; but, contrary to Cantor’s position (§3.2.7), and also use of the word ‘Anzahl’, ‘I look on the ordinal number, not the cardinal number [Anzahl] as the basic concept’. He did not really discuss the matter in the booklet (see art. 161), but it arose in contemporary correspondence with Heinrich Weber. Distancing himself from the usual use of ‘ordinal’, he specified his ‘ordinal numbers’ as ‘the abstract elements of the simply infinite ordered system’, and saw cardinals ‘only for an application of ordinal numbers’.
Secondly, Dedekind did not define numbers from systems in the kind of way which Frege and Russell were to do; on the contrary, whether consciously or not, he followed Boole (end of §2.5.6) in associating numbers with systems, as the cardinal number of elements which a (finite) system contained. For example, in the letter (now lost), Weber seems to have suggested that the (finite) cardinals might be defined as classes of similar classes. Dedekind rejected this apparent anticipation of Frege (§4.5.3) and Russell (§6.5.2) and wished that cardinal to be ‘something new (corresponding to this class) that the spirit creates. We are of divine species, and without any doubt possess creative strength, not merely in material things (railways, telegraph) but quite specially in intellectual things’ (Works 3, 489).
Thirdly, Dedekind was aware of the model-theoretic (as we would now say) limitations of his formulations. His specification of equivalence relations between systems, and theorems about relationships (such as the cardinal number) between systems (arts. 162-165), showed that he saw some relativity in his formulations; and in a letter of 1890 to the school-teacher Hans Keferstein he made quite clear that the basic properties of numbers, such as the status of 1 and successorship to a number
would hold for every system S that, besides the number sequence N, contain a system T, of arbitrary additional elements t, to which the mapping φ could always be extended while remaining similar and satisfying φ(T) = T. But such a system S is obviously something quite different from our number sequence N, and I could so choose it that scarcely a single theorem of arithmetic would be preserved in it. What, then, must we add to the facts above in order to cleanse our system S again of such alien intruders t as disturb every vestige of order and to restrict it to N? This was one of the most difficult points of my analysis and its mastery required lengthy reflection. If one presupposes knowledge of the sequence N of natural numbers and accordingly, allows himself the use of the language of arithmetic, then, of course, he has an easy time of it. He need only say: an element n belongs to the sequence N if and only if, starting with the element 1 and counting on and on steadfastly, that is, going through a finite number of iterations of the mapping φ (see the end of article 131 in my essay [on the theorem of definition by induction]), I actually reach the element n at some time; by this procedure, however, I shall never reach an element t outside of the sequence N. But this way of characterising the distinction between those elements t that are to be ejected from S and those elements n that alone are to remain is surely quite useless for our purpose; it would, after all, contain the most pernicious and obvious kind of vicious circle. [... ] Thus how can I, without presupposing any arithmetic knowledge, give an unambiguous conceptual foundation to the distinction between the elements n and the elements t? Merely through consideration of the chains (articles 37 and 44 of my essay), and yet, by means of these, completely!20
Dedekind realised that without the property of a chain his formulation could only specify a progression and therefore admit of elements additional to those intended; that is, he anticipated the notion of non-cate-goricity of an axiom system, when the various models are not in one-one correspondence with each other (§4.7.3). But he did not relate his insight to this definition in his booklet (arts. 1, 2):
A thing a is the same as b[...] when all that can be thought concerning a can also be thought of b, and when all that can be thought concerning b can also be thought of a. [... ] The system S is hence the same as the system T. In signs S ≡ T, when every element of S is also an element of T, and every element of T is also an element of S.
That is, equality between systems was already defined categorically by the specification of equality of two systems in terms of isomorphism between their members; thus the possibility of extra members was already eliminated—presumably by accident. Even this sophisticated mathematician-philosopher could miss a trick.
Finally, Dedekind’s position may be called ‘creative setism’, covering the central places allotted both to mental powers and to sets and transformations between them. Although he referred in the preface of his booklet to ‘the grounding of the simplest knowledge, namely that part of logic, which the doctrine of numbers handles’, so that ‘I name arithmetic (algebra, analysis) only a part of logic’, he gave no formal presentation of his logic, and little indication of its content; in particular, his transformations are mathematical functions (or functors), not explicitly propositional functions and relations. Thus he was not a logicist in practice, though he may have had some vision of that kind.
3.4.4 Cantor’s philosophy of the infinite, 1886-1888. While Dedekind was delivering the fruits of his thoughts on the foundations of arithmetic, Cantor turned away from the mathematical community after the debacle with Mittag-Leffler (§3.3.2) and towards the philosophical and theological aspects of his new doctrine. The products were two papers, a short one which appeared in two slightly different forms 1886a and 1886b in a variety of places,21 and a long successor 1887-1888a made up of versions of some recent ‘communications’ with colleagues and certain other material. While Cantor succeeded in gaining some attention from philosophers with these publications, they did not make much impact among mathematicians or logicians, and are not clear: the long paper is a repetitive wander around various points well discussed earlier, laced with long footnotes showing his remarkably detailed knowledge of the history of the infinite. However, in places he amplified certain points and published a few for the first time; references are confined to principal passages in the long paper.
On the general doctrine of the infinite, Cantor stressed strongly the difference between the absolute kind, as ‘essentially inextendable’ from the actual kind as ‘yet extendable’ (1887-1888a, 385, 405). In response to enquiries from theologians, he referred to the absolute as ‘God and his attributes’ and contrasted it with the actual infinities evident in nature such as ‘the created individual entities in the universe’ (pp. 399, 400). He also stressed again from the Grundlagen (§3.2.7) the difference between ‘proper’ and ‘improper’ infinities, claiming that their conflation ‘contains in my opinion the reason for numerous errors’, especially why ‘one has not already discovered the transfinite numbers earlier’ (p. 395).
3.4.5 Cantor’s new definitions of numbers. Cantor also published here for the first time definitions of numbers from sets which became much better known from their re-run in the mid 1890s (§3.4.7). The opening sentence is the most pertinent (p. 387):
Under power or cardinal number of a set M [... ] I understand a general concept or species concept (universal) which one grasps by abstracting from the set the nature of its elements, as well as all relations which the elements have with each other or to other things, in particular the order which may govern the elements, and reflecting only on that common to all sets which are equivalent to M.
Dedekind also effected the first abstraction when defining ordinals from simply infinite systems (§3.4.2); we shall consider Cantor’s use in §3.4.7.
Later in the paper Cantor introduced overbar notations: 
for the ordinal of M and 
for its cardinal (p. 411-414), and (for example) 
for the cardinal of the ordinal number 5 (p. 418). This part was described in a surly footnote as ‘a short summary’ of his withdrawn manuscript of 1884-1885 on order-types (§3.3.2); by and large the earlier version was clearer, and an unwelcome novelty here was the proposed synonym ‘ideal numbers’ for ‘order-types’ (p. 420), which did not endure. Each ‘act of abstraction’ (p. 379) was justified by the claim that ‘a set and the cardinal number belonging to it’ were ‘quite different things’, with the ‘former as Object’ but ‘the latter an abstract image of it in our mind’ (p. 416).
3.4.6 Cardinal exponentiation: Cantor’s diagonal argument, 1891. Cantor restored some of his contacts with mathematicians in the early 1890s when he played a major role in the founding of the Deutsche Mathematiker-Vereinigung (hereafter, ‘DMV’) as a professional organisation separate from the hegemonies of Berlin and Gottingen, cities which were not used for its early annual meetings.22 At its opening meeting, in Bremen, he treated the audience to a short but pregnant piece 1892a presenting ‘an elementary question of the theory of manifolds’—namely, a criterion for inequalities between cardinals by means of the ‘diagonal argument’, as it has become known. Two cases were taken, each of importance.
In the first part Cantor took the set M of all elements {E} which could be expressed by the coordinates of a denumerably infinite coordinate space defined over (for examples. a binary pair of ‘characters’ m and w (presumably for ‘Mann’ and ‘Weib’.; a typical element would be, say,
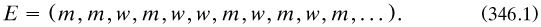
‘I now assert, that such a manifold M does not have the power of the series 1, 2,..., v,...’; for this purpose he took a denumerable sequence S of elements whose collective coordinates formed a matrix-like array {ap, q}. He then defined another element bp of E by diagonalisation:
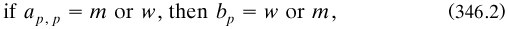
which guaranteed it not to belong to S, as required.
A purpose of the form of expression (346.1. was to accommodate the decimal expansion of the real numbers, of which the non-denumerability was now proved, and by a method which avoided the cumbersome procedure of nesting intervals described in §3.2.5. The argument was direct (Gray 1994a., not the reductio version in which it is sometimes construed today. Further, Cantor did not assume that S comprised the whole of M, although the result obviously held for M. His method went far beyond the selection of the diagonal members of an array of (say. functions Hix, y. made by setting x = y. This procedure had been used before him by, for example, du Bois Reymond 1877a, 156 in the context of his Infinitärkalkül (§3.2.1., and by Dedekind 1888a, art. 125(m. in connection with definitions by induction (§3.4.2. and art. 159 concerning transformations between ‘simply infinite’ systems.
In the second part of the paper Cantor took as M the set of characteristic functions {ƒ(x)} (to use the modern name. of all subsets of the closed interval L = [0, 1]. Obviously M was not of lesser cardinality than L; to show that it was definitely greater he took the function ∅(x, z) of two independent variables, where z was the member of L with which ƒ(x) was associated by the relation
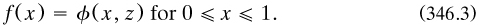
He then considered the function
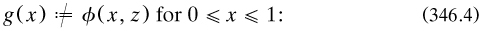
while an element of M, it took no value for z, thus establishing the greater cardinality of M. The argument assumed the well-ordering principle, as he noted at the end, together with the promise ‘The further opening-up [‘Erschliessung’] of this field is exercise for the future’.
3.4.7 Transfinite cardinal arithmetic and simply ordered sets, 1895. (Dauben 1979a, chs. 8-9) During the 1890s Cantor worked at a new formulation of the principles of Mengenlehre (as he now called it, abandoning ‘Mannigfaltigkeit’ presumably for overuse). By mid decade he had work ready for the press, and he granted Klein again the honour of correspondent (Klein Papers, 8: 448-454), which he had broken a decade earlier (§3.3.2). A two-part paper appeared in the Mathematische Annalen as 1895b and 1897a. It became perhaps his best-known writing; Giulio Vivanti 1898a and 1900a described it in the Jahrbuch, and it was translated into French in 1899 and into English (by Jourdain) in 1915. Before that the first part quickly came out in Italian (§5.3.1). We shall note some of its features here; the second part is handled in the next sub-section.
‘By a “set” I understand each gathering-together [Zusammenfassung’] into a whole of determined well-distinguished objects m of our intuition or of our thought (which are called the “elements”). ‘This definition was similar to Dedekind’s in §3.4.1, though we noted Cantor’s priority in §3.4.5. It has often been quoted, usually without enthusiasm, on two counts. Firstly, poor old Cantor did not realise that this definition of a set admitted paradoxes; but in §3.5.3 I shall argue that it was so formulated precisely to avoid paradoxes. Secondly, its idealistic character, considered in §3.6.1, aroused philosophical reservations in various followers.
Cantor proceeded at once to his definitions of cardinals (‘Mächtigkeiten‘) and their arithmetic, and in dealing with them first he showed perhaps more clearly than in the Grundlagen (§3.2.7. their epistemological priority over ordinals. He ran through once again the process of double abstraction of M to form its cardinal number rehearsed in his lecture of 1883, but he gave more details: one consequence was the need to restrict the definition of union to disjoint sets so that addition would avoid the difficulty of elements common to more than one set (art. 1). After stating the basic definitions of (in)equality between cardinals, and asserting an equivalence theorem without proof (art. 2, B), he proceeded to the arithmetical operations and properties such as the trichotomy law (that one of the relations ‘<’,‘=’ or ‘>’ always obtained between any two cardinals..
Cantor handled both the finite realm (art. 5, which suffers from comparison with Dedekind in §3.4.1-2 both for the lack of a definition of finitude and in its treatment of mathematical induction. and the transfinite range. In art. 6 he introduced the symbol ‘
0’ and even also strung out the successors
and their own successor ω without however entering into any details. Like Dedekind, he did not explain the use of the suffix ‘0’—and indeed left unclear the status of all the sufficial numbers (§3.5.3).23
The main novelty was inspired by the diagonal argument (art. 4). Cantor defined the ‘covering for the set N with elements of the set M’, a single-valued function fin. from all elements n of N to the elements m of M; in a rather casual manner he introduced the set function f(N. as ‘the covering of N’. The definition let him proceed to that of the ‘covering set from N to M’, written ‘(N |M.’, comprising all possible coverings; for its cardinality gave a means of defining cardinal exponentiation:
To stress the priority of cardinals over ordinals, Cantor introduced the ‘simple’ ordering of a set, where of any two members one always preceded the other, and then outlined their main arithmetical properties (art. 7: compare his stress in §3.3.3 on simple order and in arithmetic in the unpublished paper). As an example, he studied the rational numbers R over (0, 1) (art. 9). Assigning the letter ‘η’ to their (simple) order-type, he showed that their cardinality 
was 0 and noted various related properties. For example, * = , where the pre-asterisk referred to the inverse of the order-type then indicated: in the manuscript of 1884-1885 he had used a suffixed asterisk, just before (333.1).
These results led to a survey of the continuum X of real numbers between 0 and 1 inclusive, with its order-type designated ‘θ’. After noting that θ was not completely characterised by infinitude and perfection, Cantor replaced the metrical property of connectedness of 1883 (§3.2.8) by the requirement ‘that between any two arbitrary elements x0 and x1 of X elements of R lie in rank’ (art. 11). He then claimed to be able to prove that = θ’, as he put it right at the end of the part; the proof was based on demonstrating that a set M with the three properties just specified took the order-type 
. The issue of definition versus proof is at issue here; his use of irrational numbers as limits of sequences of rational numbers was clever, but one problem in the proof is that he drew upon the notions of the ‘climbing’ and ‘falling fundamental series of first order’ M and their ‘limit-element’. These sequences had been defined in art. 10 as parts of a simply ordered infinite set, of order-types ω and *ω respectively; the ‘limit-element’ of a ‘climbing’ or ‘falling’ simply ordered sequence (av) of members of M was the member which belonged to M and succeeded or preceded each av, and was claimed to be unique. But the succession of notions is not very clear; indeed, the ‘well-ordered sets’ ω and *ω had already been introduced in art. 7, with an appeal to finite cardinals to order the members, although only in the second part of this paper did he formally present well-ordered sets. Question-begging is in the air.
3.4.8 Transfinite ordinal arithmetic and well-ordered sets, 1897. Beginning his second part with a definition of the well-order-type (considered in §3.5.1) and properties of its segments (1897a, arts. 12-13), Cantor defined ordinal numbers as their order-types when the nature of the members was abstracted (art. 14). He then rehearsed their arithmetic, defining limit ordinals in terms of the idea of limit-element. He also presented sums of differences somewhat similar to the set-decomposition theorem (326.5) (art. 14, eq. (22)):
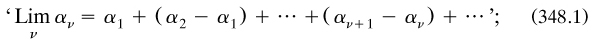
the legitimacy of the procedure (or definition?) was taken for granted. He then treated only the second number-class; but he gave a much more detailed account than before of ordinal inequalities and of polynomials of the form
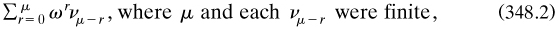
and their convertibility into transfinite products (art. 17). He showed that a number was uniquely expressible as (348.2), which he called its ‘normal form’ (art. 19). He concluded with a survey of ‘The e-numbers of the second number-class’, the numbers which arose after a finite iteration of ordinal exponentiation as the roots of the equation ωξ = ξ (art. 20).
The second part stops rather than ends, for Cantor intended to proceed to at least one more part; but this pair was to be his last major publication on his subject. (Some unpublished results on simply ordered sets were to appear in F. Bernstein 1905a, 134-138.) His plans for the third part are outlined in §3.5.3, among a survey of open and unresolved questions to which the next section is devoted.
3.5.1 Well-ordering and the axioms of choice. Here we take two issues, related but with the difference that Cantor was aware only of the first one. As we saw especially in §3.3.3, one of his major insights was to perceive the variety of orders into which an infinite set could be cast; and since one of his tasks was to provide a foundation for arithmetic, the order-type of finite and transfinite numbers had to be specified. This was the type which he called ‘well-ordered’; and since arithmetic was a general theory, every set had to be orderable that way, even if it arose in some other order (for example, the rational numbers).
As we saw in §3.2.7, Cantor first addressed both definition and generality of well-ordering in detail in the early pages of the Grundlagen (1883c, 168, 169):
By a well-ordered set is to understand any well-defined set, by which the elements are bound together by a determined succession, according to which there is a first element, and both for each individual element (if it not be the last in the succession) a determined successor follows and to each arbitrary finite or infinite set of elements belongs a determined element which is the next following element in the succession to all of them (if it be that there is none following them in the succession) [... ]
The concept of well-ordered set shows itself as fundamental for the entire theory of manifolds. That it is always possible to bring any well-ordered set into this law of thought, foundational and momentous so it seems [and] especially astonishing in its general validity, I shall come back in a later paper.
However, while he returned later to discuss his definition and give it alternative formulations, Cantor was not able to proceed beyond the optimism of the promised proof, which remained as an important task.24 It became known in the 1900s as the ‘well-ordering theorem’; Cantor gave it no name, and the preferable expression ‘well-ordering principle’ is of later origin. When a proof emerged in 1904, from Zermelo, it involved an axiom of choice (as he soon named it), which was concerned with the legitimacy of making an infinitude of independent selections of members from infinite sets, and that it turned out to be logically equivalent to the theorem itself (§7.2.5). Earlier Cantor and others on occasion made infinite selections without qualms—for example, different definitions of well-ordering itself, and in using set-decomposition theorems such as (326.5) that a union of denumerable sets was itself denumerable. He was also not aware of the bearing of these considerations on other results, such as the trichotomy law for transfinite ordinals mentioned before (347.1) (1897a, art. 14, B). Among similar stumbles, Dedekind noted in the preface 1893a of the reprint of his booklet on integers that proving the reflexive and inductive definitions of infinity assumed that ‘the series of natural numbers was already developed’.
3.5.2 What was Cantor’s ‘Cantor’s continuum problem’? One consequence of the well-ordering principle was that every transfinite cardinal number was a ‘power’ (or, in his later notation, an aleph). For the continuum, which aleph did it take? From the early 1900s this question was called ‘the continuum problem’, and Cantor’s answer ‘the continuum hypothesis’.25
This answer went through a variety of formulations as Cantor’s theory developed. The first version occurred at the end of 1878a; as we saw in §3.2.5, it took a rather unclear form, that sets came in only two sizes, denumerable and Two’. (This version is now sometimes called the ‘weak’ form). By the time of the Grundlagen, the definitions of the number-classes (§3.2.7) allowed it to take the second form, ‘that the sought power is none other than that of our second number-class’ (1883c, 192). Finally, cardinal exponentiation (§3.4.7) gave him the theorem in his two-part paper that the cardinality was 20 (1895b, art. 4); it was proved by using the binary expansion of any real number, similar in form to the expansion (328.2) used to define the ternary set. Then the hypothesis took the form
under which it is best known.
Curiously, Cantor did not explicitly state this form in the second part, although 1 was discussed there (1897a, art. 16). He also did not treat any version of the ‘generalised continuum hypothesis’ (as it became known) that
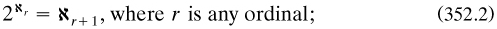
however, he may have perceived it in some intuitive form. For he knew that the covering technique, which produced cardinal exponentiation as in (347.2), was iterable, and it leads to the numbers
If this sequence and (347.1) of alephs did not coincide arithmetically, then transfinite cardinal arithmetic broke down; and since (352.1) claimed the equality of the first member of each sequence, it would surely have been natural to him to suppose that similarly (352.3) linked up the rest. Indeed, in the footnote of the Grundlagen preceding the one which presented the ternary set, he claimed a result amounting to (352.2) for r = 2 in terms of the cardinalities of the sets of continuous and of continuous and discontinuous functions (1883c, 207), and in the second part of the paper introducing covering he had considered the cardinality of characteristic functions (346.3) of subsets of [0, 1].
As for proof of the hypothesis, is seems likely that Cantor hoped to use a decomposition theorem: show that the continuum C was the disjoint union of sets {P}j each one of known topological type, and appeal to lemmas on their respective cardinalities to add them up and obtain 1. The stumbling block, of course, was the continuum itself; the characterisation of C used metrical properties (§3.2.8), about which his lemmas rarely spoke. Evidence for this approach comes in a flurry of letters sent in June 1884 to Mittag-Leffler, shortly before his breakdown (§3.3.2); he was then producing many theorems of this kind (for example, Theorem 329.1 with Bendixson. and referred to some of them. He thought both that he had proved the hypothesis (which then stood in the second form described above. but then that the cardinal of C did not belong to (346.2) at all (Schönflies 1927a, 9-11). In the end he was to get no further; the techniques associated with the third form doubtless seemed promising, but he was not able to profit, possibly because of the onset of deeper mental illness at the end of the century.
3.5.3 “Paradoxes” and the absolute infinite. (Jané 1995) Cantor realised that his prolongation of the sequences of transfinite cardinal and ordinal numbers was unending, and that proposing a completion would lead to trouble. The key to his understanding of the point was mentioned in §3.4.4, where he distinguished between the actual and the absolute infinities. The former were the home of his doctrine of transfinite numbers; by contrast, as we saw, ‘God as such is the infinite good and the absolute splendour’ (1887-1888a, 386) with no place for humankind. Thus if man were to posit the existence of the largest ordinal β, then the process of its construction would entail that β > β as well as β = β, thus infringing trichotomy. But for Cantor no paradox as such was involved: ‘keep off the absolute infinite’ was the conclusion, both β and for any analogous cardinal.
Although Cantor did not publish this analysis, he communicated it to various colleagues in correspondence. One of these was Jourdain, who received the above story in 1903 and was informed that Hilbert had been told around 1896 and Dedekind in 1899.26 Hilbert had been the main contact, receiving several letters between 1897 and 1900: Cantor reported that he had developed his theory years earlier and even had ready the third paper of his new suite for the Annalen. He defined a set as ‘ready’ (‘fertig’) when it ‘can be thought without contradiction as collected together and thus as a thing for itself’. Theorems included that a set of ready sets was ready, as was its power set; a particular case was the continuum. Excluded were sets containing β or its corresponding cardinal. He also hoped to winkle out a proof of the well-ordering principle.27
By late 1899 Cantor changed ‘ready sets’ to ‘consistent multiplicities’, with the other sets as ‘inconsistent’. He had put Dedekind back on his visiting list in 1897, giving a lecture on this topic in Braunschweig;28 in a suite of letters of July and August 1899 he sketched out a theory of consistent and inconsistent multiplicities, of which β was associated with the latter.29
However, a mathematical difficulty had to be faced; namely, the need to set up criteria for going up the sequence of ordinals as far as possible while avoiding β. (As we shall see in §7.4.4, this approach was to be called ‘limitation of size’ by Russell.) To this end Cantor returned to his definition of a set and assigned as ‘inconsistent’ (or, synonymously, ‘absolutely infinite’. those multiplicities for which ‘the assumption of a “being-together” [‘Zusammenseins’] of all its elements leads to a contradiction’. He regarded the sequence (347.2) of alephs as inconsistent if “all” members were taken, and wondered if trichotomy could always obtain. But he did not avoid vicious circles of assumption and deduction, and never published his solution, which became known mainly through Jourdain quoting in papers short statements made to him by Cantor in letters.
A related curiosity is that while Cantor had zero in his theory of real numbers, its status as an integer was unclear. We noted that his sequence of ordinals began with 1 (§3.4.5), and that ‘0’ was used without explanation in ‘0’ after (347.1); in his second 1899 letter to Dedekind he even consciously launched the series of ordinals with zero (Letters, 408). The hesitancy may have been caused by his abstractionist definitions of numbers from sets in §3.4.5, where again 1 was the first one so obtained; for if a set were empty, how could one abstract from it to find its order-type or cardinal? Was it also well-ordered? His nervousness about the empty set ‘O’, recorded after (326.1), could have a similar source. The issue is philosophically difficult, whiffing of paradox; and, as was shown in §3.4.1, even Dedekind was not lucid on the matter. The tri-distinction between zero, the empty set and literally no thing was to remain muddled until Frege and Russell, as we shall see in §4.5.3 and §6.5.3 respectively.
The transfinite numbers are in a certain sense themselves new irrationalities [... they] stand or fall with the finite rational numbers [... ]
Cantor 1887-1888, 395
Although Cantor wrote extensively about the philosophical features of his Mengenlehre and was very well read in its history, he did not exhibit a very clear position. Some features will be exhibited in this section, partly to round off the story but also to prepare the later ground for negative as well as positive aspects of his influence. For a more detailed survey, see my 1980a and Purkert 1989a. The metaphysical and religious aspects have attracted attention recently; the background is surveyed in Bandmann 1992a, pt. 1.
Cantor was a formalist in the sense that he felt that a consistent construction of a mathematical object guaranteed its existence. This seems to have been the motive behind the surprising construction after (323.3) of number-domains beyond those of the rationals and irrationals. It also underlay the quotation at the head of this sub-section; the construction of transfinite ordinals via the generating principles (§3.2.7) was also consistent, and so the constructed objects were on a par with the (mathematically respectable) irrational numbers.
This brand of formalism was Cantor’s own. It is to be distinguished from the numbers-as-marks-on-paper type of formalism which we will find Frege attacking in §4.5.8-9. It differs also from the position which Hilbert was to promote from the late 1890s onwards (§4.7.3), in which questions such as consistency were examined in metamathematics; Cantor had no such category, so that with him consistency had only the status of a naive belief. There may well be a line of influence here, for Cantor’s work had a strong effect on Hilbert.
In addition to this brand of formalism, Cantor exhibited traits of Platonism. The first part 1895b of his final paper stated them explicitly in two of its three opening mottoes: a tag from Bacon (or, for him (§3.1.2), Bacon/Shakespeare., ‘For we do not arbitrarily give laws to the intellect or to other things, but as faithful scribes we receive and copy them from the revealed voice of Nature’; and Newton’s ‘I feign no hypotheses’.
Finally, and with least enthusiasm among his contemporaries and followers, Cantor drew on idealist elements in granting a place to mental acts. The processes of forming a set by means of ‘our intuition’ and of abstracting from a set to form its order-type and cardinal (§3.4.7) are important and prominent examples, but not the only ones; others include associating an irrational number with a fundamental sequence of rationals and the ‘specialisation’ of one of them to guarantee uniqueness of definition (§3.2.3). This double use of idealism and Platonism relates to his acceptance of the ‘immanent’ and ‘transient’ realities of numbers noted in §3.2.7. In a way he linked them together in the first footnote of the Grundlagen, where he associated the formation of a set by abstraction ‘with the Platonic 
from Plato’s Philebus (1883b, 204). Maybe he saw abstraction as a generalisation of Socrates’s teaching strategy of, say, associating five with the fingers and thumb of a hand. Some more explicit discussion from him on his philosophy would not have come amiss; in particular, he still seems to need order (Hallett 1984a, ch. 3).
3.6.2 (No) logic and metamathematics. Cantor encapsulated his philosophy in a phrase in the Grundlagen: ‘The essence of mathematics lies precisely in its freedom’ (1883b, 182).30 We are free to construct objects, to draw upon mental processes, and to gain access to God—and later to have a professional association of mathematicians free from the dominating influences of Berlin and Gottingen (§3.4.5).
Since this freedom was presumably confined by the logical requirement of consistency, it is a curious irony that Cantor was cold to the developments of logic in his time. His only explicit point was to insist (often) that sets be ‘well-defined’, (for example, in the quotation in §3.5.1), and once he explained that this requirement entailed that ‘on the ground of its definition and as a result of the law of the excluded third, it must be seen as internally determined as whether any object belonging to any same sphere of concept belongs to the considered manifold or not’ (1882b, 150). Elsewhere he hoped to publish a version of his theory of ordinals ‘developed forth with logical necessity’ (1887-1888a, 380), but this language was only flourish. In §4.5.5 we shall consider his non-discussion in 1885 with Frege.
Frege was rather outside both the mathematical and logical communities. Much more prominent in Germany was the psychologist Wilhem Wundt, who published a treatise on logic in the 1880s. Like Boole (§2.5.3), he saw mathematics as applied logic, but he also involved the perception of time and space, counter to Cantor’s assertion of the independence of arithmetic from such considerations; Cantor corresponded with him at some length on these and related issues (Kreiser 1979a). Soon afterwards he repeated some of the same points in letters to the mathematician and historian Kurd Lasswitz, who was close to Wundt (Eccarius 1985a).
Although Cantor was concerned with basic principles in his Mengenlehre, he showed no interest in finding axioms for it; the word ‘axiom’ occurs very rarely (one case occurs after (323.3)). He also gave little welcome to a contemporary development in axiomatisation, which was called ‘metamathematics’. This word did not carry the modern meaning noted in §3.6.1, in connection with Hilbert; it was then associated with the views of Riemann and von Helmholtz on the foundations of geometry, especially ‘metageometry’, as non-Euclidean geometries were then called, with the prefix ‘meta’ alluding to the readiness to admit hypotheses concerning the geometry of space (§6.2.1). As Helmholtz noted at the start of a paper 1878a, ‘the name has been given by opponents in irony, as suggesting “metaphysic”; but, as the founders of “non-Euclidean geometry” have never maintained its objective truth, they can very well accept the name’. But for Cantor this reliance upon experience ran counter to his desire to abstract from it (as with Wundt), its acceptance of hypotheses infringed his (alleged) avoidance of them. As for its ‘speculations with my works, they have not the slightest similarity and no proper contact’ with his own theory of the infinite (1887-1888a, 391).
3.6.3 The supposed impossibility of infinitesimals. The formalist aspect of his philosophy seemed to have informed also his views on infinitesimals. As we saw in §2.7.4, Weierstrass inaugurated at Berlin a tradition of rigour in mathematical analysis in which infinitesimals were not used. For Cantor they were only a way of speaking about ‘a mode of variability of quantities’ (1882b, 156), associated with the ‘improper-infinite’ (1883b, 172); however, more loyal than the king, he also claimed to be able to prove that their existence was impossible.
For heresy had been practised in the Holy Weierstrassian Empire: mathematicians such as du Bois Reymond, Otto Stolz, and the Italian Giuseppe Veronese attempted to develop theories of ‘non-Archimedean quantities’. Cantor responded by presenting his proof of non-existence; but it was an unimpressive display. Defining ‘linear number-quantities’ as ‘presentable as the image of bounded rectilinear continuous segments’ and satisfying Archimedes’s law, he claimed that for any such quantity ζ for which nζ, 1 for any finite ordinal n, ‘certain theorems of transfinite number theory’ showed that vζ, ‘is smaller than any finite quantity ever so small’, contradicting the definition of a linear number (1887-1888a, 407-408). However, he never gave the details of these theorems; presumably they beg the question at hand, and maybe he realised this. In a letter 1895a to Vivanti, published at the time, he thought that the work of his opponents ‘drifts in the air or much more is a nonsense’, and contains a ‘vicious circle’; unfortunately his own position was not dissimilar.
One does not have to be a formalist to think that demonstration of contradiction entailed non-existence; but this imperative seems to have underlined his opinion here. Thus Cantor was not to instigate the view that mathematical inverses of his consistently constructed transfinite numbers could lead to a consistent theory of infinitesimals.31 He may also have thought there was no “room” in the continuum of real numbers as given by his 1872 definition (323.2) of real numbers (compare 1887-1888a, 405-407); however, ironically it does not lead to Archimedes’s principle
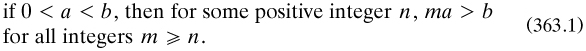
as a theorem, so that infinitesimals can be defined; only his 1895 definition (§3.4.7), or Dedekind’s (§3.2.4), lead to Archimedean continua.32
3.6.4 A contrast with Kronecker. We saw in §3.2.5 that Cantor thought that Kronecker had delayed publication of his paper (and also found reasons for sympathy with Kronecker, if in fact he did so act). No doubt there was conflict—indeed, for Kronecker himself it applied to the whole Weierstrassian approach—but his position is not easy to determine, since he never made an explicit statement of it. This point was made at the time; for example, by Dedekind in a frustrated footnote in his booklet on integers (1888a, art. 2; see also the manuscript published in H. Edwards and others 1982a). However, one can gain some impression, especially from H. Edwards 1989a and Jourdain 1913a, 2-8.
It is well known that Kronecker was a constructivist for mathematics; but his famous motto ‘The dear God has made the whole numbers, all else is man’s work’, made to a general audience at the Berlin meeting of the Gesellschaft Deutscher Naturforscher und Ärtze in 1886 (Weber 1893a, 19), was only a hint. He seems to have objected to talk of ‘any’ or ‘every’ function, series or whatever in mathematics; he wished to know how it was to be put together. This comes out, for example in his work on algebraic number fields, where the emphasis on constructivity and computational procedures using formulae makes a marked contrast with the competing approach of Dedekind and Weber.
In a paper ‘On the number-concept’ (to which Dedekind addressed his puzzled footnote) Kronecker 1887a wrote of a ‘bundle of objects’ being counted in various ways, and of its cardinal (Anzahl ‘) as a property of the collection as a whole independent of any ordering (to which the ordinal was related: see esp. art. 2). He also replaced negative and rational numbers by talk of algebraic congruences (art. 5), so that, for example,
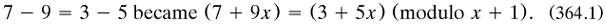
Focusing upon algebraic properties of numbers, his studies included finite sequences of integers, and the properties preserved when their order was changed by permutation.33 But he saw no need to go beyond the rationals; for example, an elegant paper 1885a on properties of the fractional remainder function of a rational quantity was called ‘the absolute smallest remainder of real quantities’.
In his lectures on the integral calculus Kronecker 1894a proceeded in much the same way with continuous functions as did the Weierstrassians; but all quantities (ε, and the like) were rational. He used limits, but only in contexts where the passage to the limiting case was determined, with known functions. He objected to Heine’s Theorem 322.1 on uniform convergence on the grounds that the maximum of a collection of increments on the dependent variable was not defined, although its value could be approximated arbitrarily closely (pp. 342-345). Complex variables and integrals were handled as combinations of their real-variable analogues with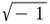 
in the right places (pp. 50-65).
Clearly there was plenty in Cantor for Kronecker to dislike; many features of the work on trigonometric series and irrational numbers even before wondering how one arrived at after 1, 2, 3,... (this difficulty, not the infinite numbers as such). The extent of their personal differences will never be known, as Cantor seems to be our only source; apparently he effected a reconciliation in the summer of 1884 (Schönflies 1927a, 9-12., when he was trying hard to prove the continuum hypothesis (§3.5.2), but there may not have been a great dispute on Kronecker’s part anyway.
On the other hand, there were other differences between them. Kronecker did not attend the opening meeting of the DMV in 1891 for reasons of health (he was to die later that year), but he sent organiser Cantor a pointed letter (1891a, 497):
Therefore I do not even like the expression ‘pupils’ with us; we do not want or need any school [... ] the mathematician must make himself at home intellectually in his research sphere free from any prejudice, and freely look around and pursue discoveries [... ]
As to infinites, I hold 1/0 to be the infinite of infinites.
For 0 marks the change from + to—, which ∞ does not. [... ]
I am out of all fear about ∞2. I believe in ∞2, ∞3, &c. &c.: and I intend to write a paper against the skim-milky, fast- and loosish mealy-mouthedness of the English mathematical world upon this point. My assertion is that the infinitely great and small have subjective reality. They have objective impossibility if you please; or not, just as you please [... ]
I therefore accept the concept infinite as a subjective reality of my consciousness of space and time, as real as my consciousness of either, because inseparable from my consciousness of either.
De Morgan to Sir John Herschel, 29 April 1862
(S. De Morgan 1882a, 313)
De Morgan’s statement, made before Cantor began to develop his doctrine, exemplifies the point that Cantor was not the first mathematician who thought that the infinite was not an indivisible entity but that orders of the infinitely large could be distinguished: indeed, a variety of mathematicians and also eminent philosophers had put forward such views from time to time, sometimes in connection with orders of the infinitesimally small. De Morgan alluded to his ideas in a paper ‘On infinity’ written shortly after his letter to Herschel, stating that ‘The number of orders of infinity is to be conceived as infinitely—as 
, indeed—exceeding the unlimited multitude of values which a letter may take’.34 However, not even he developed his insight into a pukka theory, with (reasonably) clear definitions and general criteria for cardinal and ordinal in equality and arithmetic.
Such advances are due almost entirely to Cantor. Starting out from a standard problem of the early 1870s in mathematical analysis concerning trigonometric series, he gradually elaborated and also generalised his Mengenlehre. Surpassing all predecessors in studying the topology of sets, he clearly separated five distinct but related properties of sets:
1) topology: how is a set distributed along a line/plane/... ?;
2) dimension: how is a linear set distinguished from a planar one, a planar set from…?;
3) measure: how is its length/area/... to be measured?;
4) size: how many members does it possess?
5) ordering: in which different ways may its members be strung?
He also massively refined the notion of the infinite into theories of transfinite cardinal and ordinal arithmetic, and also introduced a range of order-types. The many links between the various sides were furnished basically by the infinitieth derived set P(∞), and Cantor himself never abandoned his view that his Mengenlehre was an integrated theory. But most of his followers reacted otherwise.
1 See my 1971c for much new information on Cantor’s career, including evidence on his mental illness. I learnt from Bernard Burgoyne that some of the notes had been used by the Hungarian psychiatrist I. Hermann in a paper 1949a on psychological aspects of set theory; he may have been drawn to Cantor by a collaboration with the logician Rosza Petér (see her letters to P. Bernays during 1940 in Bernays Papers, 975: 3472–3474). Charraud 1994a has also used the notes, in an interesting psychoanalytical study of Cantor which however suffers from shaky understanding of the mathematics.
An influential source of misinformation on Cantor’s illness is Russell’s autobiography, where he chose to publish two undeniably eccentric letters of 1905 from Cantor, and to preface them with the claim that Cantor ‘spent a large part of his life in a lunatic asylum’ (1967a, 217–220; the first also in Cantor Letters, 457). Russell heard this phrase uttered at an Encyclopaedia Britannica dinner in November 1902 (see his journal entry in Papers 12, 11).
2 My lack of enthusiasm is stimulated by Zermelo’s omission of some important footnotes from his papers (some will be mentioned in due course), frequent changing of notations (mostly from roman into italic format), and addition of his own technical terms (albeit in square brackets, but omitted here). For materials used in preparing the edition see Zermelo Papers, Box 6.
3 Cantor-Dedekind Letters contains their correspondence up to 1882; according to a letter of 1932 from Zermelo to Cavaillès, the publisher of Cantor’s Papers, J. Springer, rejected the edition (Dugac 1976a, 276), so it appeared from Hermann in Paris. Some of these letters are now also in Cantor Letters, 30–60, and many are translated into English in Ewald 1996a, 843–877. Noether took the manuscripts with her to the U.S.A. on her emigration in 1933, and after her death two years later they lay unknown with her lawyer, before being found and reported in Kimberling 1972a; they are now held in the library of Dedekind’s institution, the Technische Hochschule in Braunschweig. For the texts of the non-mathematical parts of the correspondence, see my 1974b; for some reason Dugac’s transcription (1976a, 223–262) lacks some folios. On the publication of the letters of 1899, see footnote 29.
4 Among the biographies of Cantor, the most valuable are Dauben 1979a and Purkert and Ilgauds 1987a; Kertesz 1983a is not of this calibre, but it is well illustrated and contains more information on his Halle career, including on pp. 89–94 a full list of his lecture courses.
5 On du Bois Reymond’s successes and failure in set topology and integration, see T. Hawkins 1970a, ch. 2. On his Infinitärkalkül, see especially Hausdorff 1909a and Hardy 1924a, and an historical survey in Fisher 1981a.
6 Some manuscripts from the Dedekind Papers pertinent to our theme were published in his Works 3 (1932), and a substantial selection of manuscripts and correspondence from this and other sources is presented in Dugac 1976a, pt. 2.
7 The draft of Dedekind 1872a is printed in Dugac 1976a, app. 32; compare the recent edition in 1862a of an earlier lecture course on the calculus. The source of all these exact dates was a diary (or collection of them), which has unfortunately been lost. On his work in analysis, see Sinaceur 1979a, Zariski 1926a passim, and (with caution) Dugac 1976a, pt. 1.
8 The history of Dedekind’s “victory” has in fact not been traced, though much information on the English and American side is contained in Burn 1992a. For an exhaustive account of foundational processes in analysis, including irrational numbers, see Pringsheim 1898a. A significant figure in Germany early in this century was Oscar Perron: see, for example, his 1907a and, much later, the preface to his book on irrational numbers 1939a for his extraordinary sarcasm against Nazism in preferring Dedekind’s theory over others’ on the grounds of being good German mathematics.
9 Cantor s letters are in Klein Papers, 8:395–436; seven are transcribed in Cantor Letters. They are well used in Dauben 1979a, chs. 4–5. In a letter of 15 November 1899 to Hilbert, Cantor claimed that Dedekind had stopped their correspondence around 1873 ‘aus mir unbekannten Gründen’! (Hilbert Papers, 54/14; quoted in Purkert and Ilgauds 1987a, 154, and transcribed in Cantor Letters, 414).
10 Cantor had himself already stated this theorem in his major paper on trigonometric series (1872a, 98), without citing any mathematician. The name seems to be due principally to Cantor’s friend Schwarz, in a paper on Laplace’s equation published at the same time in Crelle’s journal (1872a, 178). As a name it is unfortunate, as it associates Weierstrass’s result with the very special case that a bounded set of values has an upper bound, proved much earlier in Bolzano 1817a, art. 12. Paying tributes with inappropriate names both muddles together different levels of rigour (a matter of especial importance in this sort of mathematics. and also takes away from the quality of the earlier work: compare the ‘Heine-Borel’ Theorem 322.1.
11 Cantor proved this result by a measure-theoretic argument which was defective in as much as his definition of measure, formally introduced in 1884b, art. 18, did not distinguish the measure of a set from that of its closure and so admitted of inadmissible additive properties (T. Hawkins 1970a, 61–70).
12 Cantor’s word was ‘real’; sometimes in this paper he also mentioned ‘reellen Zahlen’ in the mathematical sense, as contrasted to (hyper)complex numbers (see, for example, 1883b, 165, 169).
13 Unfortunately there is no worthwhile obituary or biography of Mittag-Leffler, but some information and references are contained in Dauben 1980a and G
arding 1998a, chs. 7–8. In my 1971b I announced the riches contained in his house, which has existed since 1919 as the Institut Mittag-Leffler. The archives include the manuscripts and some proof-sheets of various papers of Cantor to be discussed in this section, including the translations about to be described and the manuscript dealt with in §3.3.2–3; but apparently the Insititut has not employed an archivist to organise the holdings in the manner which their importance warrants, so that I cannot cite an item by callmark. A substantial selection of Mittag-Leffler’s correspondence with Cantor is published in Cantor Letters.
14 The articles (some revised. of Cantor’s Grundlagen were published, carrying their original numbers, in the order 1, 11, 12, 13, 2, 3, 14, 10; compare footnote 17. Of the endnotes, the mathematical trio 10–12, including the ternary set (328.2) were placed together as unreferenced ‘Notes’.
15 In my 1970b, see pp. 101–103 for Mittag-Leffler s fateful letter, and pp. 104–105 for Cantor’s reminiscences of the mid 1890s to F. Gerbaldi (where my editorial remark about Klein as another recipient is, I now think, mistaken) and Poincaré (of which the original has now been located in his Nachlass, still held by the family but denied to exist at the time of preparation of my paper). I have also since learnt that Mittag-Leffler’s letters, which I had been told were copies, are in fact the originals, sent back to him after Cantor’s death by his daughter Else. These and other letters of that period are published in Cantor Letters, 208–242.
16 Quoted from my 1970b, 79; Cantor s long letter is on pp. 74-79 (also in his Letters, 208-214), with my explanation on pp. 70-72. I have used modern notation here; he deployed his symbols of (326.1, 3).
17 As was mentioned in footnote 14, Simon s order of sections was 1, 11-13, 2, 3, 14, 9, 10. His review of the Grundlagen appeared in May 1883, two months after Cantor had proposed 1-3, 11-14, 9, 10, and then exactly Simon’s order, in letters of 15 and 18 (postmark) March to Mittag-Leffler (footnote 14). The final order is the second one but with 9 omitted. The similarity is strange; sadly, no correspondence between Simon and Cantor seems to survive.
18 On a Kantian influence on Dedekind, see McCarty 1995a; and on the acceptability of such proofs within phenomenology, see B. Smith 1994a, 91-94. Bolzano had already offered this proof in his 1851a, art. 20. Dedekind referred to it for the first time in the preface to the second (1893) edition of his booklet, and of Bolzano confessed that ‘even the name was completely unknown’ when he had completed this part of it. The draft version material mentioned in §3.4.1 (Dugac 1973a, app. 58) does not contain this proof, and Cantor had sent him Bolzano’s book in October 1882 (my 1974b, 125).
19 The classic location for an appreciation of Dedekind’s treatment of inductive definitions is the textbook on foundations of analysis by Edmund Landau (1930a, preface and ch. 1), where he acknowledged an idea by Laszlo Kalmar. However, he made the point already in his obituary of Dedekind, in a version for which he thanked Zermelo (Landau 1917a, 56-57).
20 Dedekind s letter is published in Sinaceur 1974a, 270-278. An English translation of part of it was published in Wang 1957a accompanied by an unreliable commentary, and in revised and complete form in van Heijenoort 1967a, 98-103 (quoted here). For good discussions of Dedekind’s theory of chains, see Cavailles 1938a, ch. 3; and Zariski 1926a passim.
21 This paper is unique in Cantor s corpus for its bibliographical complication. It began as a letter to the historian of mathematics and Mittag-Leffler’s assistant Gustaf Enestrom (draft of most of it in Cantor Papers, letter-book for 1884-1888, fols. 31-34), who placed it and some later additions with the Stockholm Academy as the paper Cantor 1886a. Meanwhile, another version, containing also three letters for the long succeeding paper 1887-1888a, was prepared (presumably by Cantor himself) and was published both as the paper Cantor 1886b in the journal Natur und Offenbarung and as a short pamphlet. It also came out as a paper in the philosophical journal which also took the long paper, and the pair were reissued as the pamphlet 1890a. This version was used in Cantor Papers, where a few words were printed twice on pp. 416-417. The titles and contents of these versions vary, but not substantially.
22 On the early history of the DMV, see Gutzmer 1904a. Its archives have recently been placed and sorted in the Archives of Freiburg University, too late for use here.
23 Cantor changed his numbering of alephs so as to start with 0 rather than 1 in July 1895, while the paper was in proof: see his letter (which contains no explanation. to Klein as editor of the journal in Letters, 356. He knew that ‘aleph’ also meant ‘cattle’ in Arabic, so that his cardinals were a cattle-herd (‘Rinderherde’: letter of 28 August 1899 in Hilbert Papers, 54/13).
24 See, in particular, Cantor 1887-1888a, 387-388; 1892a; 1895b, art. 6 or the sequence of transfinite cardinals.; and 1897a, art. 12 (different definition). For commentary pertinent to this sub-section, see G. H. Moore 1982a, ch. 1.
25 The title of this sub-section is an allusion to a famous and nice survey Gädel 1947a of this problem. For an excellent survey of its formulations by Cantor and reception by contemporaries, see G. H. Moore 1989a. The term ‘continuum problem’ was introduced in the preface of the Dissertation F. Bernstein 1901a, and in the revised version 1905a (§4.2.5); ‘continuum hypothesis’ is due to Hausdorff 1908a, 494.
26 Cantor s letter to Jourdain is published in my 1971a, 115-116; Jourdain quoted it in 1904a, 70. Hessenberg soon cited Felix Bernstein as a source for Cantor’s priority (1906a, art. 98; on this work see §4.2.5).
27 See Cantors letters in Hilbert Papers, especially 54/3-9, 15-18; excerpts are transcribed in Purkert and Ilgauds 1987a, 224-231 (with discussion on pp. 150-159, and in Purkert 1986a. and in Cantor Letters, 390-400. Hilbert liked Cantor’s approach but found ‘ready’ an unclear concept: see his report of a talk of 25 October 1898 to the Gottinge Mathematische Gesellschaft in the record book (Gottingen Mathematical Archive 49:1, fol. 43) and a note in his mathematical diary (Hilbert Papers 600/1, fol. 91). Note also Schonflies’s letter of 12 July 1899 to some friends, kept in Klein Papers 11:735.
28 Paul Stackel took notes of the lecture (according to Fraenkel 1930a, 265-266), but I have not found them. Schonflies (1910a, 251) stated that Cantor had defended the use of the law of the excluded middle against French criticisms (presumably by Borel and/or Poincare; compare §4.2.2).
29 These letters of 1899 were published in Cantor Papers, 443-451; but Zermelo fouled up Cavailles’s transcriptions, changing many spellings and even Cantor’s mathematics in some places, and meshing the first two letters into one of the former date (28 July 1899, pp. 443-447: the break should be inserted on p. 443, at ‘zukommt. Gehen’.. On this vandalism, and the non-technical parts of these letters, see my 1974b, 126-136; they are now reliably available in Cantor Letters, 405-411, and are translated into English, with some others and also letters to Hilbert, in Ewald 1996a, 923-940.
30 This phrase is often quoted, but incorrectly, with the important emphasis precisely (‘gerade’) omitted. The source is Schonflies 1900a, 1 and repetitions later. Cantor was perhaps alluding to Hegel’s System der Philosophie (1845): ‘The essence of the spirit is hence formally freedom’.
31 This remark alludes to the inauguration in our time of non-standard analysis (Dauben 1995a). The study of infinitesimals in Weierstrass’s time would form an interesting history of heresy; for some information, see Dauben 1979a, 128-132, 233-236.
32 This point seems to have been made first in Stolz 1888a; he mentioned his own definition of ‘moment of systems of functions’ and also du Bois Reymond’s ‘Nulls’, both defined from considering ways in which ƒ(x) 
0 as x → ∞, as defining infinitesimals by means not refuted by Cantor’s claim. On Veronese’s version of infinites and infinitesimals, see the extensive but unknown review 1895a in the Jahrbuch by Ernst Kotter, interesting also as showing a mathematician from another area (in his case, principally geometry) studying Mengenlehre.
33 In June 1898 Russell acquired, presumably by purchase, the offprint of 1887a that Kronecker had sent ‘Herrn Prof. Weierstrass mit freundschaftlichem Gruss’ on 11 July 1887 (Russell Archives). The context is striking, for the two men had split severely in 1883 when Kronecker in effect accused Weierstrass of plagiarism in the theory of theta functions (Schubring 1998a).
34 De Morgan 1866a, 168; this study may have been stimulated by his work on iterated convergence tests (on which see my 1970a, appendix), which also partly inspired du Bois Reymond’s Infinitärkalkül (§3.2.1). On the history of orders of the infinitely large, see especially Schrecker 1946a and Bunn 1977a; the literature on infinitesimals touches on it occasionally.