 1 (§3.2.7); the general result became a popular topic in the mid 1890s, with various proofs produced over the next decade. It was usually presented in two versions: I give both, with inclusions to be taken as proper. Firstly,
1 (§3.2.7); the general result became a popular topic in the mid 1890s, with various proofs produced over the next decade. It was usually presented in two versions: I give both, with inclusions to be taken as proper. Firstly,In this chapter are collected six concurrent developments of great importance which, with one exception, ran alongside mathematical logic rather than within it. It is largely a German story, with some important American ingredients; among the main general sources is the reviewing Jahrbuch uber die Fortschritte der Mathematik. Set theory is the main common thread, and §4.2 deals with the growth of interest in it, both as Cantorian Mengenlehre, and more generally.
Next, §4.3 describes the contributions to algebraic logic made by C.S. Peirce and some followers at Johns Hopkins University. The union of Boole’s algebra with De Morgan’s logic of relations led not only to the propositional calculus but also to the predicate calculus with quantifiers. In §4.4 some notice of the Grassmann brothers is followed by the contributions of Ernst Schröder, the main follower of Peirce. Working more systematically than his mentor, he articulated an elaborate algebra of logic, including relations, and developed a kind of logicism. The reactions of the Peirceans during the 1890s are also noted. By contrast, mathematical logic is introduced in §4.5, as practised by Gottlob Frege, now highly esteemed but then rather neglected; his work is taken from its start in 1879 to a major book in 1903.
Then §4.6 traces the early career of Edmund Husserl, trained under Weierstrass, developing with Cantor, and espousing phenomenological logic in important books of 1891 and 1900-1901. He then came into contact with the main subject of §4.7, David Hilbert, whose first phase of proof theory is described. It was stimulated by axiomatising geometry and arithmetic, but was also profoundly influenced by Cantor, and drew Ernst Zermelo into set theory, with spectacular consequences. Also included here is the allied emergence around 1900 of model theory (as it is now known), mostly in the U.S.A.
4.2.1 National and international support. During the final years of the 19th century the importance of Cantor’s Mengenlehre became generally recognised, but his own conception of it as an integrated topic was not often followed. Most mathematicians were primarily interested in the technical aspects; but the logicians and philosophers normally concentrated on the general and philosophical sides, including his vision of the Mengenlehre as a foundation for arithmetic and thereafter for “all” mathematics (§3.3.3). On the many developments of the 1900s, see especially Schönflies 1913a (§8.7.6), T. Hawkins 1970a, G. H. Moore 1982a and Hallett 1984a.
One type of occasion for publicity was the sequence of International Congresses of Mathematicians, which was launched at Zürich in 1897. Cantor had been a major figure in their founding, so it was meet that Mengenlehre should be featured. For example at Zürich, in the plenary address on analytic functions in the tradition of Weierstrass and his followers Adolf Hurwitz 1898a included early on several pages of explanation of basic Cantorian concepts, including perfect and closed sets, the continuum, and the transfinite ordinals derived from the principles of generation (§3.2.7). However, as we shall see later (§4.2.7, §7.2.2), the treatment at these congresses was not always competent!
4.2.2 French initiatives, especially from Borel. (Medvedev 1991a) Courses in set theory began to be taught in a few centres, a practise which Cantor himself was never able to pursue at Halle. An important example of increased interest is provided by the three-volume Cours d’analyse by the Frenchman Camille Jordan (1838-1922). The first edition had concluded its last volume 1887a with a collection of notes on set theory and related topics such as limits, continuity, irrational numbers and the integrability of functions; but six years later this material was moved and expanded to commence the second edition, on the grounds that such knowledge could not be presupposed among the students and was needed early (1893a, 1–54).
Jordan delivered his courses at the Ecole Polytechnique, traditionally the first choice of the mathematically talented in France. But over recent decades the Ecole Normale Supérieure had been rising in importance for mathematics. One of the key figures was Jules Tannery (1848-1910): placed first in 1866 to enter both schools as a student, he had chosen the latter and six years later was on the staff. We saw him in §3.3.3 as an early commentator on Cantor in a long review article 1884a. Two years later he published a textbook Introduction a l’étude des fonctions d’une variable (Tannery 1886a), which covered the Mengenlehre and related topics.
Among Tannery’s students, one of the most notable was Emile Borel (1871-1956), who emulated him in 1889 as top student for both schools and also chose the Normale. Rapidly drawn into mathematical analysis by Tannery’s lectures, he wrote a thesis 1894a ‘On some points in the theory of functions’ while based at the University of Lille; it was quickly reprinted in the school’s Annales, and was soon recognised as a significant contribution to point set topology. One of its results, rather casually presented, became known as the ‘Heine-Borel Theorem’ (the origin of this unfortunate name was explained in §3.2.2.) that if a bounded set of points on a line can be covered by an infinitude of intervals, then a finite number will do also. It was typical of his constructivist philosophy, which was similar to Kronecker’s (§3.6.4.) in that he worked only with at most a denumerable number of unions and complementations of given sets.
Appointed in 1897 to the staff of the school, Borel began with a lecture course on functions which led to his first textbook, dedicated to Tannery and presenting Le¸cons sur la théorie des fonctions (1898a.). Its success led his (and also Tannery’s). publisher, Gauthier-Villars, to invite him to edit a collection of volumes on this and related topics. A distinguished run was launched, written mainly by members of Borel’s circle (not only French.); a score of titles had appeared by 1920. Some aspects of set theory featured in virtually all of them, often significantly. One of the most important books was a volume 1904a by normalien Henri Lebesgue (1875-1941.), building on his thesis 1902a presented to the Faculté des Sciences of the Universite de Paris. He generalised the Riemann integral (§2.7.3.) to a theory of ‘measure’, with two major consequences (T. Hawkins 1970a). Firstly and more importantly, his theory greatly weakened the sufficient conditions on theorems involving the processes of mathematical analysis such as integrating or differentiating infinite series of functions, where traditionally uniform continuity and/or convergence were required. Secondly, the exotic discontinuous or oscillatory functions which Riemann himself had presented and Hermann Hankel and others had examined (§3.2.1) were now integrable; for example, the characteristic function of the rational numbers had no Riemann integral but Lebesgue measure zero.
The following year another normalien, Réné Baire (1874-1932) (Dugac 1976b.) built upon his Faculté thesis 1899a to publish a volume 1905a on discontinuous functions. Extending Hankel’s work on the classification of functions, he took continuous functions ƒn(x)as the ‘zeroth’ class F0 and defined members of the first class F1 as the (discontinuous) limiting functions limn→∞ƒn(x) of some sequence of functions from F0. The second class F2 was defined similarly from F0 and F1, and so on. He hoped that all functions could be expressed this way, but Lebesgue 1905a refuted him. Cantorian ideas of various kinds permeated all this work; for example, Baire defined classes of functions up to Fα for any member α of Cantor’s second number-class, while Lebesgue drew upon both Cantor’s ternary set (328.2) and the diagonal argument (347.1) in constructing his counter-example function.
Tannery’s and Borel’s remarkable entry performances were matched by Jacques Hadamard (1865-1963), who also chose to be a normalien, in 1884. After graduation he too was based in the provinces for some years. In 1897, when Borel began to teach at the school, Hadamard returned to the capital with assistantships in both the Faculté and the Collége de France. His main researches lay in mathematical analysis and its applications to other branches of pure mathematics such as number theory but also applications such as hydrodynamics (Maz’ya and Shaposhnikova 1998a.) While set theory did not feature in his work to a Borelian extent, it appeared enough to make him another focus, and a commentator on foundations.
4.2.3 Couturat outlining the infinite, 1896. (Couturat 1983a′) These mathematicians formed much of the nucleus of the new generation in France for the new century; but the most important Frenchman for our story was an outsider. Once again a normalien, Louis Couturat (1868-1914) entered in 1887, specialising in philosophy. Much of his subsequent career was devoted to the interactions between mathematics, philosophy and logic. He also worked on their various histories, where his main figure was Leibniz, on whom he did important archival work in the early 1900s. Perhaps inspired by Leibniz’s notion of a characteristica universalis, from then on he became passionately concerned with international languages. Much of his career was passed in the provinces, with occasional periods in Paris. His liking for logic seems to have condemned him to isolation from his mathematical compatriots: proud of their long Cartesian tradition of raisonnement, they despised the explicit analysis of reasoning. Poincareé’s contempt for logic (and also ignorance of it) is unusual only in its explicitness (§6.2.3, §7.4.2, 5).
For one of his two doctoral theses, Couturat published as 1896a his first and philosophically most important book: 660 pages on De l’infini mathématique. Impressed by Immanuel Kant, he began with a preface defending the place of metaphysics in philosophy, followed by in introduction seeking to distinguish the a priori and the a posteriori and considering the relationships between mathematics and physics. The compass of concern reduced still further in the text, which treated only number and quantity, although in great mathematical and philosophical generality. He was much influenced by Tannery’s textbook, and also by an interesting study 1847a of the relationships between algebra and geometry by the mathematician and economist Augustin Cournot (1801-1877), perhaps not by coincidence the second normalien (after the notorious Evariste Galois) of note in mathematics.
Part One of Couturat’s book treated in 300 pages the ‘generalisation of number’. Taking the integers for granted, he passed from the rationals through the irrationals (where on p. 60 he followed Tannery in adopting Dedekind’s definition), transcendentals, negatives and imaginaries. The ‘mathematical infinite’ was handled in detail in the fourth and last livre of the Part; apparently influenced by Cournot, he presented various natural or intuitive encounters with the infinite in arithmetical or geometric contexts and resolved them, often by arguments in one of these branches but drawn from the other.
Part Two handled ‘number and magnitude’ (‘grandeur’) again in four livres, this time in 280 pages. More philosophical in treatment, Couturat began by comparing ‘empiricist’ and ‘rationalist’ definitions of integers, largely Helmholtz versus Dedekind. Then he drew upon Kant’s treatment of number, but including a brief début of Cantor’s transfinite ordinals (p. 363). His sources on magnitudes included ‘a magisterial lecture’ by Tannery, apparently unpublished (p. 375); this time Helmholtz was contrasted with a largely Weierstrassian approach given in Stolz 1885a. A very long discussion of the axioms of (in)equality (pp. 367-403) was followed by continuity; again Dedekind was the leading light but Cantor’s definition was also noted (pp. 416-417).
The status and theory of the infinite was presented in the form of extensive dialogues between a ‘finitist’ and an ‘infinitist’ (pp. 443-503). Each speaker appealed to Great Men to support his position; Cantor was now more prominent, not only concerning ordinals but also his understanding of the isomorphism between the members of an infinite set and an infinite subset to counter the finitary tradition. Surprisingly, the alephs were not discussed.
The book was rather too long; in particular, the dialogues would need severe editing before being put on stage. In addition, in the final chapter on Kant’s antinomies Couturat did not fully resolve the tension between his support for Kant and awareness of the limitations and even errors in the philosophy of mathematics (pp. 566-588). But overall he gave an excellent impression of both the range of mathematical situations in which the infinite was at issue and the philosophical questions which had to be tackled. In addition, much useful technical information was provided by a substantial appendix of notes (pp. 581-655) on hypercomplex numbers, Kronecker’s theory of algebraic numbers (§3.6.4), the processes of limits in the theory of functions, and 40 pages on the Mengenlehre (but little on the alephs). A bibliography, well up to date, completed the book. Far beyond a typical doctoral thesis, it introduced or at least updated many readers to the new theories—including, as we shall see in §6.2.7, reviewer Russell.
4.2.4 German initiatives from Klein. We saw in §3.2.6 and §3.4.7 that Cantor had published many of his main papers in Mathematische Annalen, thanks to the support of Felix Klein. This journal continued to take papers from Cantor’s students and followers. Among the latter, the most noisy, though not the most competent, was Artur Schönflies (1853-1928). He came to the Mengenlehre relatively late after distinguished work in projective geometry and crystallography, but he took to it with a passion sustained for the rest of his life.1 One of his first acts was initiated by Klein.
In 1894 the Deutsche Mathematiker-Vereinigung (hereafter, (DMV)) launched the Encyklopadie der mathematischen Wissenschaften as a vast detailed survey of all areas of mathematics at the time. Klein was the main instigator, and Teubner the publisher. French mathematicians soon began to prepare their own translation and elaboration of the project, as the Encyclopédie des sciences mathématiques, put out by Gauthier-Villars with Teubner. For the first of its six Parts, on arithmetic and algebra, Schönflies was invited to write a piece on Mengenlehre, which duly appeared as his 1898a. It was divided about equally between the transfinite arithmetic and the point-set topology. While well referenced, and not only to Cantor’s writings, it was pretty short, at 24 pages; he and Baire substantially reshaped and more than doubled its length in the French version Schönflies and Baire 1909a, adding more than just the results found in the intervening decade.
Much more significant was the report on the Mengenlehre which Schönflies prepared for the DMV, in their annual series published in their Jahresbericht (Schönflies 1900a.): of book length, Teubner put it out also in this form. The order of material was hardly well, as Cantor might have said: generous to a fault were Vivanti’s review 1902a in the Jahrbuch, and Tannery’s lengthy piece 1900a in the Bulletin des sciences mathématiques. Starting by mis-quoting Cantor’s statement that the essence of mathematics lay in its freedom (§3.6.2)—a mistake (in lacking ‘precisely) which has been repeated infinitely ever since—the first section covered ‘the general theory of infinite sets’, taking cardinals first and proceeding to order-types, well-order and ordinals, and ‘the higher number-classes’. Then followed a section on point set topology, including the sequence of derived sets (but not the motivation from trigonometric series). Perfect and closed sets dominated the account, followed by the content of sets (after the Riemann integral but before Lebesgue measure). Among ‘point sets of a particular kind’ Cantor’s ternary set was included. The third section, on ‘Applications to functions of real variables’, took up nearly half of the report: Schönflies covered continuity, discontinuous and oscillatory functions of exotic kinds, the integral (nearly 30 pages, and intersecting with the earlier material on the content of sets), and the convergence of infinite series (ending with trigonometric series). Here he also named Borel’s theorem on finite coverings ‘the Heine-Borel theorem’ because of its superficial similarity with Heine’s Theorem 322.1 on the uniform continuity of functions (pp. 119, 51). A second part of the report appeared in 1908 (§4.2.7, §7.5.2).
Despite its drawbacks, the report also attracted new figures to the subject. Among the most significant were the English mathematicians Grace Chisholm Young (1868-1944) and her husband William Henry Young (1863-1942). She had taken a Dissertation under Klein in 1895 in a pioneering programme of higher education for women, and after her marriage the next year to this Cambridge University coach they went to the Continent to learn some genuine mathematics. The definitive choice of topic came when they visited Klein, who recommended them to try the Mengenlehre as written up in Schönflies’s report. The conversion decided their entire research career, the first of a married couple in mathematics, which lasted for 25 years (my 1972a). With some financial independence provided by his earnings as coach, they lived in Gottingen until 1908, and came to know Cantor personally. Attracted to the topological aspects, William’s first major achievement was ‘a general theory of integration’ constructed differently from Lebesgue’s but more or less equivalent to it (Young 1905a). His version was produced after Lebesgue; priority was readily acknowledged, and indeed the phrase ‘Lebesgue integral’ is Young’s. They also published with Cambridge University Press a treatise on The theory of sets of points (Young and Young 1906a), the first in English. (As Table 643.1 shows, Russell’s The principles (1903) had concentrated more on the general aspects). They also translated into English some of the Encyklopädie articles on mathematical analysis, to start an English edition; but they found only apathy from their compatriots on the island (‘write textbooks’, they were told). So they abandoned the project, and an edition was never prepared.
4.2.5 German proofs of the Schräder-Bernstein theorem. (Medvedev 1966a) Unproven in the Mengenlehre was the equivalence of sets, as part of trichotomy; that is, that any cardinal was either equal, less than or greater than any other one. Cantor had proved equivalence, but only for sets of cardinality  1 (§3.2.7); the general result became a popular topic in the mid 1890s, with various proofs produced over the next decade. It was usually presented in two versions: I give both, with inclusions to be taken as proper. Firstly,
1 (§3.2.7); the general result became a popular topic in the mid 1890s, with various proofs produced over the next decade. It was usually presented in two versions: I give both, with inclusions to be taken as proper. Firstly,
THEOREM 425.1 If set S is equivalent to its sub-subset R, then any subset U ‘between’ S and R is equivalent to each.
As was noted in §3.4.1, Dedekind was the first prover, in his booklet on integers, but in a sketched manner (1888a, art. 63). For some reason he omitted a much clearer proof laid out the previous year in a manuscript m1887a which was to be published only in 1932, in his Works. By the assumption in the second version, a ‘similar’ (that is, one-one) mapping 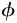 took S onto R. Defining the set U := (S—T), he considered its chain U0 under
took S onto R. Defining the set U := (S—T), he considered its chain U0 under 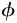 a new mapping ψ over S by the properties
a new mapping ψ over S by the properties
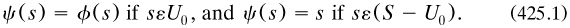
After proving that ψ was similar, he applied it to the two decompositions
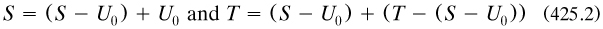
related to the two clauses of the definition, where ‘+’ indicated disjoint union of sets. Then he used the various relationships of inclusion between the sets to show that
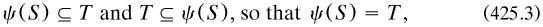
from which the similarity of T and S was proved; that between R and T followed by imitation.
Dedekind seems to have communicated this jewel first only to Cantor, in 1899 (Cantor Papers, 449). Proofs of this type, found independently, were published only by Peano 1906a, and Poincaré 1906b, 314-315, the latter credited to a letter from Zermelo.2 By then a quite different proof of this logically equivalent theorem had been in the literature for eight years:
THEOREM 425.2 If each of the sets M and N is equivalent to a proper subset N1 and M1 of the other one, then they are equivalent to each other (and so have the same cardinality).
For brevity I use ‘~’ to denote equivalence between sets. There must be a subset M2 of M1 for whichN1 ~ M2; and so M ~ M2. Hence the theorem reduces to the first version, that M ~ M1. To prove it, define the disjoint sets
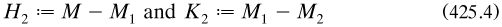
and apply repeatedly to the trio of mutually disjoint sets M2, H2 and K2 a similar mapping from M to M1; this yields Mr, Hr and Kr respectively, each trio still disjoint. Let L be the intersection, maybe empty, of all the Mr after denumerably many applications. Then
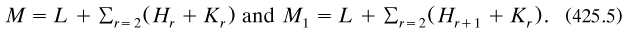
Now map L and each Kr identically onto itself, and each Hr isomorphically onto its subset Hr+1; the equivalence between M and M1 follows.
The theorem was all but named by Schönflies in his report, after the two independent creators of this proof (1900a, 16). The first was offered by Schröder, who (thought that he) had proved it in a long paper on finitude to be noted in §4.4.8 (1898c, 336-344); unfortunately, he had falsely assumed that the cardinality of each limiting set in the two sequences was equal to that of its predecessors. The slip was pointed out to him in a letter of May 1902 written by a school-teacher active in the foundations of mathematics, Alwin Korselt (1864-1947); Schröder replied that he had already noted it himself. This information was given in a short paper Korselt 1911a in Mathematische Annalen: it contains also his own version of the first proof, which he stated he had submitted in 1902 to the journal that year but which for some reason had not then been published.
No such slip in derivation tainted the version by the second figure, a young newcomer to the Mengenlehre: Felix Bernstein (1878-1956) (Frewer 1981a). He spent the years 1896-1901 at various universities before writing his Dissertation 1901a under Hilbert’s direction; a somewhat revised edition appeared in Mathematische Annalen as 1905a. In both versions he mentioned this proof; but, like Poincare with Zermelo later, it had already appeared with acknowledgement in Paris, in Borel’s Fonctions (1898a, 104-107). He had presented it in the previous year to Cantor’s own seminar at Halle University, where his father was professor of physiology.3
Further versions appeared in the fertile year of 1906, from Julius König 1906a, and in Hessenberg 1906a, arts. 34-37. Gerhard Hessenberg (1874-1925) belonged to a group of philosophers called ‘the Fries school’, after the neo-Kantian philosopher Jakob Fries (1773-1843). His proof was given within a long article on the ‘Fundamental concepts of Mengenlehre’, which was reprinted in book form. He paid much attention to equivalence, being especially impressed by the difficulty, evident since Cantor 1883b, of proving such basic properties about sets. Like others of the time, he included his proof within a general discussion of trichotomy. Narrower in range but of greater philosophical weight than Couturat’s book, he discussed in detail the more general aspects of the subject, such as order-types, transfinite ordinals, cardinal exponentiation, and definitions of integers. Some parts were unusual; for example, in ch. 22 on decidability he decomposed a set into the subset of members known to have a given property and the complementary subset. His views on the paradoxes, including one due to his colleague Kurt Grelling, are noted in §7.2.3.
By 1906 the role of the axioms of choice and the well-ordering principle were becoming evident, so that all proofs required not only examination but autopsy. In particular, Whitehead and Russell were to handle the Schroder-Bernstein theorem very carefully (§7.8.6).
4.2.6 Publicity from Hilbert, 1900. The leading German mathematician around 1900 was Klein’s younger colleague at Göttingen, David Hilbert (1862-1943). His own work on foundational areas of mathematics (§4.7.1) had advanced sufficiently for him to be convinced of the basic correctness and importance of Cantor’s Mengenlehre and of his own ideas on proof theory; and an occasion arose which allowed him to give both enterprises good publicity among mathematicians. A Universal Exhibition was held in Paris in 1900 to launch the new century (or, as the more mathematically minded might have noticed, to presage its commencement on 1 January 1901), and in this connection various disciplines held International Congresses in the city. The mathematicians met from 6 to 12 August for their ‘Second’ congress, succeeding the one held in 1897 in ZÜrich; it followed a corresponding jamboree for the philosophers (§5.5.1).4
Hilbert’s general familiarity with mathematics gave him a fairly strong perception of its major open questions and research areas; so he chose to describe his view of the principal ‘mathematical problems’ awaiting attention in the century to come. The historian of mathematics Moritz Cantor was in the chair for the morning session of 8 August, when Hilbert spoke on 10 problems: the full version Hilbert 1900c, which contained 23 problems, made history on its own, with two printings and translations into French (for the Congress Proceedings. and English.5 Strikingly, and doubtless bearing order in mind, he placed Cantor’s continuum problem (352.1). as the first problem (with the well-ordering principle as an associated question), and ‘the consistency of the arithmetical axioms’ as the second.
4.2.7 Integral equations and functional analysis. A significant application of set and measure theory to mathematical analysis was in integral equations. The task was to find which functions g, if any, satisfied an equation such as
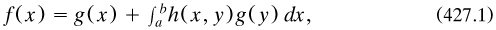
with ƒ and h known. The topic had arisen occasionally in the 19th century, usually in connection with differential equations or a physical application; but interest increased considerably from the 1890s. Hilbert became engaged from around 1905; for him (427.1. was a principal concern when ƒ and h were continuous functions. A principal method of solution was to convert them into a denumerable number of linear equations with the corresponding number of unknowns.6
Finding sets of functions satisfying certain properties was a main method of solution, for such study of functions had also gained new interest in the 1890s; the name ‘functional analysis’ became attached to it later. They were conceived as objects belonging, in a set-like manner, to a ‘space’ by virtue of properties such as continuity, say, or differentiability (Siegmund-Schulze 1983a). Publicity at the ZÜrich Congress came from Hadamard 1898a, who outlined some of the basic ideas, including the use of set theory; however he displayed own limited knowledge of the Mengenlehre by misdefining the concept of well-ordering! Progress was leisurely, and explanation to outsiders essential; Maurice Fréchet (1878-1973. began his doctoral thesis 1906a with several pages of very elementary explanation of the basic idea of functions being members of a space.7
Under this view, trigonometric series, which had drawn Cantor into sets in the first place (§3.2.3), were now construed as defining a space S of functions ƒ(x) expressible over some interval [a, b\ of values in a series (321.1) of sine and cosine functions which served as its basis. One of the most important theorems, proved in 1907 by Ernst Fischer (1875-1956) and Frigyes Riesz (1886-1969) and known after them, stated that if the sum of the squares of the coefficients were convergent, then there was indeed a function ƒ(x) belonging to S which was the sum of that series and for which
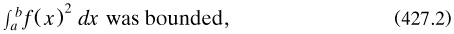
a property satisfied also by the component sine and cosine functions.
The integrals, and indeed the whole theory, were handled with a generality provided by Lebesgue theory of measure. But still greater generality was envisaged by a leading American mathematician, E. H. Moore (1862-1932). Impressed by the range of algebras and linear forms such as Fourier series in analysis and especially infinite matrices and integral equations, he sought a ‘General analysis’. The governing principle of his theory was that ‘The existence of analogies between central features of various theories implies the existence of a general theory which underlies the particular theories and unifies them with respect to those central features’, and drawing upon ‘These theories of Cantor[, which] are permeating Modern Mathematics’ i1910a, 2, 1). He told Fré chet in 1926 that he had chosen this name in imitation of the phrase ‘general set theory’;8 in §6.6.3 we shall reveal his little-known role in the paradoxes.
Among his references, Moore cited the second part 1908a of the report on the Mengenlehre, which Schönflies had recently published with the DMV. We saw in §4.2.4 that in the first part, 1900a, he had treated the basic features in his own way. Here he handled ‘the geometrical applications’, with a more detailed treatment of the topological aspects followed by the invariance of dimensions, continuous functions and curves, and elements of functional analysis. He was more in his special areas in this part, and its 331 pages (80 more than its predecessor) give a more confident and clearer impression. The first two and the final chapters updated and corrected the first part; in particular, the integral now included Lebesgue measure (pp. 318-325).
The most significant new theory for Schönflies was ordered sets, which he presented in his second chapter largely following an important pair of 60-page articles 1906a and 1907a by Felix Hausdorff (1868-1942). He greatly extended Cantor’s treatment of non-well-ordered types, especially of non-denumerable sets, by using ‘transfinite induction’, as he christened it (1906, 127-128). He had come to the Mengenlehre around 1900 after a debut in applied mathematics, and became one of its most distinguished practitioners (§8.7.6);9 these articles were to influence Whitehead and Russell substantially (§7.9.5).
Thus the peculiar Mengenlehre of the late 19th century became the established set theory of the new century; further books appeared, as we see in §8.7.6. Yet the Mengenlehre had already been eclipsed by a still more general theory of collections which, however, gained little attention then or ever after.
4.2.8 Kempe on ‘mathematical form’. (Vercelloni 1989a, prologue) If Couturat was an outsider, Alfred Bray Kempe (1849-1922) lay almost out of sight. He was that characteristically British object, a highly talented mathematician who did not hold a professional appointment. He made his career as a lawyer, but his mathematical work earned him a Fellowship of the Royal Society in 1881—indeed, he was to be its treasurer from 1898 to 1919, and he was knighted in 1912 for those services (Giekie 1923a).
Among his various mathematical interests, a remarkable achievement was contained in a long paper Kempe 1886a on ‘the theory of mathematical form’, published in the Society’s Philosophical transactions. I cite it by the number of the many short sections into which it is divided. Seeking ‘the necessary matter of exact or mathematical thought from the accidental clothing—geometrical, algebraical, logical, &c’ (sect. 1), he found it in ‘collections of units’, which ‘come under consideration in a variety of garbs—as material objects, intervals or periods of time, processes of thought, points, lines, statements, relationships, arrangements, algebraical expressions, operators, operations, &c, &c, occupy various positions, and are otherwise variously circumstanced’ (sect. 4). Individual units were written,say, ‘a, b, …’ separated by commas; but a pair ‘ab’ could be taken, and even ‘may sometimes be distinguished from the pair ba though the units a and b are undistinguished’, as in the sensed line ab from point a to point b (sect. 5). The same situation obtained for triads,…up to ‘m-ads’ for any positive finite integer m (sect. 7). Thus form, his key concept, was predicated of a collection ‘due (1) to the number of its component units, and (2)to the way in which the distinguished and undistinguished units, pairs, triads, &c., are distributed through the collection’ (sect. 9).
Kempe may have been inspired by the mathematical study of graphs launched by Arthur Cayley and J. J. Sylvester in the 1870s, for he had applied it in 1885a to their theory of algebraic invariants. Indeed, they were the Society’s referees for 1886a;10 while generally favourable, understandably they did not realise the extent of its novelty. His main advance over all predecessors was that he allowed units to belong more than once to a collection, unlike the single membership of set theory. We noted in §2.5.8 the example of the roots 3, 3 and 8 of a cubic equation; Kempe used cases such as the shape ‘Y’, construed as a collection containing one ‘distinguished’ central node together with three ‘undistinguished’ extremal ones (sect. 9). Sub-collections were ‘components’, and a disjoint pair was ‘detached’ (sects. 18-19); a collection of units in which every component was distinguished from each of its detached units was called a ‘system’ (sect. 25). This is curiously like Dedekind’s phrasing in his booklet on integers published two years later (§3.4.1): ‘various things a, b, c,... are comprehended from whatever motive under one point of view [... ]and one then says, that they form a system’ (Dedekind 1888a, art. 2).
A very important kind of finite system of n units for Kempe was a ‘heap’. It was ‘discrete’ when every component s-ad was distinguished from all others of the same number for all s n; ‘single’ when every s-ad was undistinguished; and ‘independent’ in between, such as in the ‘Y’ (1886a, sects. 37-38, 44). A ‘set’ was defined as a collection of units such that any pair of undistinguished components could be extended by further units already in it. ‘A system is obviously a set. A set is not necessarily a system’ (the unclear sects. 130-131).
Special symbols were introduced in Kempe’s theory of ‘aspects’ of a unit in a collection, which highlighted its location when mapped isomorphically across to a mate unit in another undistinguished collection (sect. 73); the notion corresponded in role to Dedekind again, and also to Cantor’s abstraction from (his kind of) set §3.4.7.. Among their ‘elementary properties’ (sects. 89-99), two m-ads being undistinguished was written
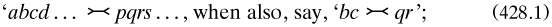
but if distinguished, then
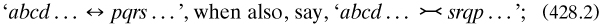
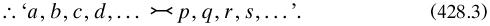
In another strange anticipation of Dedekind’s terms, he also considered ‘chains’ starting out with ‘A succession of undistinguished pairs, ab, bc, cd,...’, which ‘may be termed a simple chain’ (sects. 211-221).
As in the case of ‘Y’, Kempe also used ‘graphical representations of units’ (sect. 39), usually graphs or grids of little lettered circles to represent particular cases. One of them was a mechanical linkage (sect. 82); maybe earlier work 1872a on this topic had also helped to inspire him, for a linkage is a graph in wood or metal. His most extensive use of graphs provided a large classification of groups and quaternions (sects. 240-327).
Among other branches of mathematics, Kempe treated the geometry of the plane, especially concurrent and coplanar lines, and collinear and triads of points (sects. 350-359). But the last part, on ‘logic’ (sects. 360-391), was rather disappointing: an essentially unmodified review of the basic features of Boole’s algebra of logic with Jevons’s modifications (§2.6.2) interpreted in terms of ‘classes’, a term which Kempe did not explain.
4.2.9 Kempe—who? With one exception to be noted soon, the reception of the paper was silence; for some reason it was not even reviewed in the Jahrbuch. Perhaps this non-reception provoked him to seek more publicity at the end of the decade. A general paper 1890b in Nature on ‘The subject matter of exact thought’ largely concentrated on the uses of the theory in geometry, with some emphasis on symmetric and asymmetric relationships (for example, as between the extremities of the unsensed and the sensed line). It came out soon after a more ample statement 1890a placed with the London Mathematical Society, to which he later offered in his Presidential Address 1894a a survey of his theory, ending with this definition of mathematics: ‘the science by which we investigate those characteristics of any subject-matter of thought which are due to the conception that it consists of a number of differing and non-differing individuals and pluralities’.
Mathematicians’ ignorance of Kempe has always been great: his theory has been re-invented in recent years, under the name ‘multisets’, without knowledge of his priority (see, for example, Rado 1975a). But he soon gained some surprising followers in two American philosophers: Josiah Royce in the early 1900s (§7.5.4), but quickly from C.S. Peirce. When the large paper appeared, Peirce wrote to Kempe about the theory of aspects,11 with the result that Kempe sent to the Royal Society a short note 1887a modifying some sections. But later the reaction was opposite; in retort to Peirce attributing to him the view that relationship was ‘nothing but a complex of a bare connexion of pairs of objects’ (Peirce 1897a, 295: the context is described in §4.4.7), Kempe 1897a replied that on the contrary, while often subsidiary, in general they lay among the basic units which he sought as ‘the essential residue of the subject-matter of thought’, and that lines in his diagrams served only to distinguish one arrangement of units from another one.
A more radical effect of Kempe occurred on 15 January 1889 (Peirce’s own dating on the folios involved): presumably from looking at the various graphs in the original paper, Peirce suddenly conceived of a similar manner of representing the syntax of well-formed English sentences, in a theory which he came to call ‘entative’ and ‘existential graphs’. For example (one of his), the ‘Y’, which was treated as a graph by Cayley and Sylvester and as a heap containing one distinguished and three undistinguished elements by Kempe, represented a ‘triple relative’ for Peirce. The development of this insight, quite foreign to Kempe’s own purposes, became a major concern of Peirce for many years, and the recent recognition of its importance has made him a darling of the artificially intelligent.12 Its consciously topological character signified a basic change from his severely algebraic approach hitherto to logic, a matter which dominates our next section.
Much of my work never will be published. If I can, before I die, get so much accessible as others may have a difficulty in discovering, I shall feel that I can be excused from more. My aversion to publishing anything has not been due to want of interest in others but to the thought that after all a philosophy can only be passed from mouth to mouth where there is opportunity to object and cross-question; and that printing is not publishing unless the matter be pretty first class.
C. S. Peirce to Lady Welby, as transcribed by her in a letter to Russell of 16 December 1904 (Russell Archives; Hardwick 1977a, 44)
4.3.1 Peirce, published and unpublished. Of all figures in this book Charles Sanders Santiago13 Peirce (1839-1914) is the most extraordinary, many-gifted, frustrating and unfortunate. A son of Professor Benjamin Peirce (1809-1880) of Harvard University, his career was much oriented around that institution in positive and negative ways. After graduation from there, he worked for the Coast Survey as a mathematician and astronomer, achieving much scientifically and offending many personally.
However, by a variety of bad behaviours and social gaffes—among the latter, taking a Miss Juliette Pourtelai (or maybe ‘Froissy’) as mistress while married and, even worse, divorcing his wife Melusina in 1883 in order to marry her—he was left from the mid 1880s on to live on his own savings and earnings. Both were quite considerable, the respective proceeds of a good Survey salary and writings for American journals and dictionaries; but an excessive purchase of land in Pennsylvania combined with financial incompetence and bad luck in business left him heavily in debt. He lectured at Harvard occasionally, and corresponded widely, but he was on the academic fringe. He died Hollywood style without the music, on a cold April day without a stick of firewood in the box or scrap of food in the larder.
After that Harvard punished him further (Houser 1992a) Juliette sold his manuscripts to the Department of Philosophy on condition that they be kept and an edition be made of them. A young graduate student, Victor Lenzen (1890-1975), was sent one winter’s day with a horse and buggy to collect them (Lenzen 1965a); but Juliette failed to tell him of the correspondence and financial papers stored in the attic, and they were destroyed by the farmer who bought the premises after her death in 1935.
At that time a rather sloppy six-volume edition of some manuscripts and publications had just been produced by the Department (Peirce Papers). Later, staff and students were allowed to take the original manuscripts as souvenirs until the Harvard librarians collected the rest and at least had them safely conserved even if unread. Juliette had also sold the library on the understanding that it would be kept together; but the books were widely scattered to the extent that some are thought to be now in other libraries.
While a thread of interest in Peirce’s philosophy endured after his death, serious study dates only from the late 1950s, and came from outside Harvard. It included two more volumes of the edition (1958), properly done by Arthur Burks. A splendid biography was prepared as a doctoral dissertation for the University of California at Los Angeles in 1960 by Joseph Brent; but the Department refused him permission to publish any of the quoted manuscripts until the early 1990s, so that his achievement remained virtually unknown until a somewhat revised version was published as Brent 1993a. Many of Peirce’s manuscripts on mathematics and logic were edited by Carolyn Eisele and published in four volumes by the house of Mouton in 1976 (Peirce Elements). Then two years later a massive selected chronological edition of his writings in 30 volumes was launched at Indiana University under the leadership of Max Fisch, and is published by its Press (Peirce Writings). The main editorial task is to select material from the enormous mass of manuscript essays, draft letters (often pages long) and notes that Peirce left. There was much disorder, partly due to poverty: in his later years Peirce had to use the blank versos of essays written long before because writing paper was too expensive. Dating is thereby rendered difficult; handling of the texts by others has made the problem harder.14
Peirce’s only academic phase was the years 1879-1884 at Johns Hopkins University in Baltimore, where he interacted with Sylvester, a highly volatile immigrant (Parshall 1998a, 201-208). He built up a small but fine circle of students (§4.3.7) with a common interest in logic, which had been his infatuation since reading a copy of Whately’s Logic around his 12th birthday.
4.3.2 Influences on Peirce’s logic: father’s algebras. (My 1997d) Peirce is the next great contributor to algebraic logic after Boole and De Morgan; indeed, much of his work unified the two in developing a Boolean logic of relations. The influence of Boole himself was quite conscious: Peirce studied The laws of thought and adopted most of its aims and principles. He seems to have begun developing a theory of relations before reading De Morgan 1860a on them (§2.4.7), but it confirmed the rightness of his approach. They met in 1870, early in his career and at the end of De Morgan’s, when Peirce was in London en route with a Survey group to observe an eclipse in Sicily. Benjamin, the leader, gave him a charming letter of introduction for De Morgan (transcribed in my 1997a), together with a copy of a new work of his own (B. Peirce 1870a), which itself constituted the third formative influence on Charles.
Benjamin’s own research interests lay largely in applied mathematics, including a strong enthusiasm for the quaternion algebra proposed by W. R. Hamilton in the 1840s. Here four independent basic units 1, i, j, and k, were taken, and the ‘quaternion’ q defined as a linear combination of them over a field of values a, b,...:

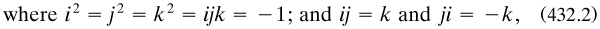
together with permutations among i, j, and k. Commutativity was lost, but associativity (Hamilton’s word) preserved. Benjamin hit on the idea (Charles claimed credit for it …) of generalising this case to take any finite number of units and enumerating the algebras with two means of combination which satisfied associativity and also other important properties. He noted commutativity and distributivity; and also these two, which he christened for ever:
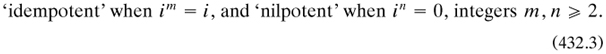
Working with algebras with 1 up to 6 units, he found 163 algebras in all, with 6 subcases. He wrote the multiplication table for each case, where the product of each pair of units was displayed (a technique introduced in Cayley 1854a in connection with substitution groups.. One of the ‘quadruple algebras’ is shown in Table 432.1. The main task was taxonomy, not applications. Rather surprisingly, the catalogue excluded complex numbers, because he allowed them to appear in the coefficients of the units.
Peirce began with a philosophical declaration about mathematics that has surpassed the succeeding text in fame: ‘Mathematics is the science that draws necessary conclusions’. Charles would quote it later with great approval, and even claim to have moved his father towards the position. But the slogan is enigmatic, since the sense of necessity is not explained. Maybe he was following a stress laid by George Peacock on necessary truths in symbolic algebra (§2.3.2), though enigma is there also. In drafts of the lithograph Peirce wrote ‘draws inferences’ and ‘draws consequences’, which seem preferable. Clear, however, is the active verb ‘draws’: mathematics is concerned with the act of so doing, not the theory of doing it, which belongs elsewhere such as in logic. Thus it was an anti-logicist stance, which Charles would always maintain.
TABLE 432.1. A Quadruple Algebra in Peirce

As a sign of the financial poverty of American science in the 1860s, the Academy of Arts and Sciences (hereafter, ‘AAAS’), recently founded as the prime such body in the country, could not afford to print the lengthy researches of one of its founding members. So in 1870 Benjamin’s Survey staff came to the rescue, finding a lady in Washington with no mathematical training at all but a fine calligraphic hand who wrote out his scrawl with lithographic ink so that 12 pages could be printed together on a stone. The final product ran to 153 pages; he distributed the 100 copies produced to friends and colleagues, including (via Charles) to De Morgan, whose own work on double and triple algebras had been a valuable influence.
Charles was the first reader to stress the importance of the lithograph; in particular, while at Johns Hopkins in 1881, the year after Benjamin died, he had it printed in the usual way as a long paper in the American journal of mathematics, which Sylvester had founded in 1878. In a new headnote he hoped that his father’s contribution would be recognised as ‘a work which may almost be entitled to take rank as the Principia of the philosophical study of the laws of algebraical operation’. He also adjoined some ‘notes and addenda’ of his own. This version appeared in 1882 as a book from von Nostrand, with a short new preface by Charles. In its volume for 1881 the Jahrbuch promised a review; but, unusually and regrettably, none appeared. Nevertheless, it became sufficiently influential for the American mathematician J. B. Shaw to prepare a book-length survey 1907a of the known results.
4.3.3 Peirce’s first phase: Boolean logic and the categories, 1867-1868. (Merrill 1978a) By 1882 Charles’s own logical researches were well under way. His first public presentation had been given in 1865, his 26th year, in a series of 11 lectures ‘On the logic of science’ at Harvard (Peirce m1865a). Following the normal understanding at that time, he covered both inductive and deductive logic; in the latter part of the sixth lecture he treated Boole’s contribution, while others outlined syllogistic principles. The following year he delivered the Lowell Lectures there, another eleven-some in the same area (Peirce m1866a), but with the balance more in favour of induction; it brought him to Boole the probabilist as much as to Boole the logician (pp. 404-405).
Peirce first published on deductive logic in two short papers accepted in 1867 by the AAAS. A short ‘improvement’ 1868a was based upon dropping Boole’s restriction of union to disjoint classes; later he recognised Jevons’s priority (§2.6.2) for this move (1870a, 368-369). Then in 1868c he reflected ‘Upon the logic of mathematics’, a recurring theme; in this debut he stuck to syllogisms, with some symbols used for the basic connectives. In a footnote he mentioned De Morgan, and did not advance beyond him.
So far, so unremarkable: of far greater significance for Peirce’s logic and especially philosophy was ‘A new list of categories’, presented to the AAAS in May 1867 between the other two papers and published as 1868b. The Kantian in him put forward five categories based upon ‘Being’ and ‘Substance’, with the former divided into three ‘accidents’: the monadic ‘Quality’, referring to a ‘ground’, or general attribute; the dyadic ‘Relation’ referring to a correlate and a ground; and the triadic ‘Representation’, referring to ground, correlate and ‘interpretant’ or sign. The latter manifests an early concern with the theory of signs, or ‘semiotics’, to use the Lockean word (§2.3.3) which he was later to revive.
4.3.4 Peirce’s virtuoso theory of relatives, 1870. The importance of this triad emerged in January 1870, when Peirce presented to the AAAS a 60-page paper on logic. They printed it in time for him to take it on his European trip in the summer and (for example) to give a copy to De Morgan, along with his father’s lithograph; it appeared officially as a paper in the 1873 volume of the Memoirs, but I shall cite it as Peirce 1870a. His main intention was made evident: he conjoined the modified Boole with De Morgan 1860a (mentioned in the opening lines) in ‘a notation for the logic of relatives’, and the outcome was not merely a new collection of symbols but a substantial extension of the logics which Boole/Jevons and De Morgan had introduced.
The paper, 62 pages long in that printing, is notoriously difficult to follow, not least for frequent conflations of notions and symbols. The new theory of categories supplied his triad of ‘logical terms’, which were associated with classes; unfortunately he spoilt this care by characterising his trio as ‘three grand classes’ (1870a, 364), the noun being a technical term elsewhere. The first “class” was of ‘absolute terms involving ‘only the conception of quality’ and so representing ‘a thing simply as “a—”’. Then ‘simple relative terms’ involved ‘the conception of relation’ such as ‘lover of. Finally, ‘conjugative terms [...] involves the conception of bringing things into relation’, such as ‘giver of—to—’ (p. 365). In this way he introduced a predicate calculus in symbolic logic, and with relations and not just classes; moreover, he went beyond De Morgan by bringing in three-place relations.
Peirce gave each kind of term its own kind of letter—roman t, italic l, cursive  —although sometimes he confused individuals with classes, and absolute and infinite terms (for example, around formulae 102.-(108.)). Taking ‘∞’ rather than the over-worked ‘1’ to denote the universe, ‘when the correlate is indeterminate’ then ‘l∞, ‘will denote a lover of something’ (pp. 371-372): many of his examples involved lovers, including of servants, maybe revealing features of his private life. He used pairs of ‘marks of reference’ in compound relations to indicate the connections between components: for example, the wallpaper design ‘
—although sometimes he confused individuals with classes, and absolute and infinite terms (for example, around formulae 102.-(108.)). Taking ‘∞’ rather than the over-worked ‘1’ to denote the universe, ‘when the correlate is indeterminate’ then ‘l∞, ‘will denote a lover of something’ (pp. 371-372): many of his examples involved lovers, including of servants, maybe revealing features of his private life. He used pairs of ‘marks of reference’ in compound relations to indicate the connections between components: for example, the wallpaper design ‘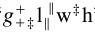 ’ denoted ‘giver of a horse to a lover of a woman’ (p. 372).
’ denoted ‘giver of a horse to a lover of a woman’ (p. 372).
Often these expressions and their verbal versions denoted classes, usually a ‘relative’; that is, the domain satisfying a relation. This feature has often been misunderstood because Peirce’s verbal account used relational words (Brink 1978a) In symbolising the means of combining classes (including relatives., he maintained some analogies with arithmetical symbols. In particular, he continued to use Boole’s ‘+’ for the ‘invertible’ union of disjoint classes, but symbolised his preferred ‘non-invertible’ version with ‘+,’; the corresponding subtractions were notated ‘—’ and ‘—’ (pp. 360-362). Similarly, intersection, or multiplication, was written ‘x, y’ if commutative between the components, and ‘xy’ if not; the corresponding divisions were notated ‘x; y’ and ‘x: :y’ respectively (p. 363).
Above all, instead of equality of classes as the primary relation Peirce took improper ‘Inclusion in or being as small as’ (sic!), giving it the symbol ‘ ‘; proper inclusion was ‘<’. Thus implication took over from equivalence as a basic connective: ‘To say that x = y is to say that x
‘; proper inclusion was ‘<’. Thus implication took over from equivalence as a basic connective: ‘To say that x = y is to say that x 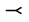 y and y
y and y 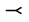 x’ (p. 360).
x’ (p. 360).
Unlike Boole, Peirce worked with expressions like ‘x + x’; indeed, ‘it is natural to write’
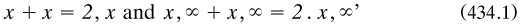
(p. 375), and he treated the denoted objects as multisets in the way which Kempe was to develop later (§4.2.8). One can understand his enthusiasm over Kempe’s work, which must have come as an unexpected surprise.
Much of Peirce’s exegesis was based on stating relationships between relatives and their ‘elementary’ components in linear expansions like quaternions (432.1), or more specifically after Boole’s manner (255.5); sometimes the product form was used. The means of combination of classes were commutative multiplication and both types of addition. He also showed that the relationships between the ‘elementary relatives’ in a compound one could be expressed not only by an expansion but also as a multiplication table; one of his examples used nine units, and another was the quaternion case (432.4) in his father’s lithograph (pp. 410-414). Later, in many short notes 1882a which he added to his reprint of the lithograph, he restated an algebra in terms of its ‘relative form’, and he explained the general procedure in one of his addenda. In a short note 1875a published by the AAAS he had shown the converse: that any of those tables could be given a ‘relative form’ as an expansion. These features show him contributing to matrix algebra (Lenzen 1973a), then still a new topic.
Peirce’s enthusiasm for algebraic symbols in 1870a led him to use binomial and Taylor’s series to produce his expansions. He used the symbols ‘Σ’ and Π to abbreviate additions and multiplications, with superscript commas adjoined if the means of combination with subscript commas were used (first on p. 392); at this early stage the possible need for a horizontally infinitary logical language was not broached.
Peirce also used powers to symbolise ‘involution’ (p. 362), eventually explaining ‘that xy will denote everything for every individual which is an x for every individual of y. Thus lw will be a lover of every woman’ (p. 377). But in a surely unhappy move he also deployed powers to express negation: if x were a term, then its negative was ‘nx’ (p. 380., and at once he stated the principles of contradiction and excluded middle respectively as
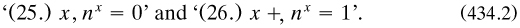
Further, only a few lines later did he give ‘the symbolic definition of zero’, and none explicitly for 1; in a later summary they were given as
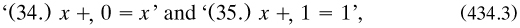
both credited to Jevons. The inverse operation, ‘Evolution’, was associated with taking logarithms (p. 363). One recalls Boole’s use (255.4) of MacLaurin’s theorem, and the consequences were no less wild, or at least difficult to follow.
Perhaps the hardest part of the paper is Peirce’s theory of ‘infinitesimal relatives’. They were “defined” as those relatives [x] whose correlatives are individual’ and number only one, so that x2 can never relate two individuals; that is, like infinitesimals, x2 = 0 (p. 391). The exegesis, successfully decoded in Walsh 1997a, shows difference algebra in place ‘by the usual formula,
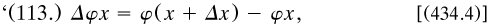
where Δx is an indefinite relative which never has a correlate in common with x’ (p. 398). This curious clause is the clue to the theory, for he found an interpretation of higher-order differences under ‘+’ and sought relationships between the pertaining relatives. However, it was not helpful to call such relatives ‘infinitesimal’ in this discrete theory, or to name as ‘differentials’ (p. 398) the operation of differences corresponding formally to differentiation in the calculus. He applied his theory by, for example, forbidding anyone from both loving a person and being his servant, taking the class of lovers of servants of certain people, and forming the class of lovers of servants of some of them who love the others (pp. 400-408, my illustration).
4.3.5 Peirce’s second phase, 1880: the propositional calculus. After this performance, innovative but confusing and probably confused, Peirce published very little on his algebraic logic for some years, although he worked hard on a book on it and published extensively in science and its ‘logic’ (to us, its philosophy: Writings 4 passim). But his five years at Johns Hopkins University, especially the interaction for the first time in his life with talented students, inspired him to major fresh developments.
One nice detail was that all the five basic logical connectives could be defined from ‘not A and not B’ of two propositions A and B. It is now abbreviated to ‘nand’; Peirce gave it no name, but symbolised it ‘AB’. Unfortunately, for some reason he never published his note m1880b; and it came to light only in 1928 when the Harvard edition of his Papers was being prepared.15 By then the companion ‘Sheffer stroke’ for ‘nor’ (another Harvard product: §8.3.3) was well known.
Peirce’s first Baltimore publication, possibly drawing upon a lecture course, was a complicated 43-page paper 1880a ‘On the algebra of logic’ published in Sylvester’s American journal of mathematics when he was 42 years old. As its title suggests, he presented his system in a more systematic manner; but it was less innovative than its chaotic predecessor in paying much more attention to syllogistic logic. He also went back to De Morgan’s early papers on logic (§2.4.5) rather than the last one on relations.
The opening ‘chapter’, on ‘Syllogistic’, included an account of ‘The algebra of the copula’, which began by reviving the traditional word ‘illation’, the act ‘∴’ of drawing a conclusion from a premise (p. 165). After stating the identity law as ‘x x’ for proposition x, Peirce stated one of his most important rules: conditional illation, with the inter-derivability of
x’ for proposition x, Peirce stated one of his most important rules: conditional illation, with the inter-derivability of
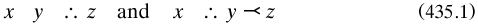
(p. 173: he displayed the inferences vertically). Negation was indicated by an overbar over the proposition letter or over ‘ ‘, so that the ‘principle of contradiction’ and of ‘excluded middle’ were written on p. 177 respectively as
‘, so that the ‘principle of contradiction’ and of ‘excluded middle’ were written on p. 177 respectively as
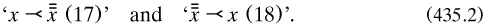
He presented many inferences, with syllogisms often used as examples, and also ran through his logic of relatives.
In the next chapter, on ‘The logic of non-relative terms’ (that is, purely classial ones., Peirce laid out many basic principles and properties of the propositional calculus, although their statusses as such were was not always clear. They included on p. 187 two ‘formulae (probably given by De Morgan)’ (§2.4.9) and ‘of great importance:
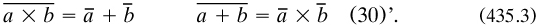
Unfortunately he did not properly handle the ‘cases of the distributivity principle’
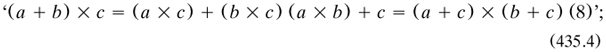
for he claimed them to be provable ‘but the proof is tedious to give’ (p. 184). There are four cases here, since the ‘=’ in each proposition unites the ‘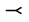 ‘case and its converse; and it turned out that neither (435.4)1 with ‘
‘case and its converse; and it turned out that neither (435.4)1 with ‘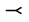 ‘, nor its dual, could be proved from the assumptions presented. This matter was one of Schröder’s first contributions, in 1890 (§4.4.4); sorting it all out is quite complicated (Houser 1991b) In addition, Peirce should have more clearly explained switches between terms and propositions and between lower- and upper-case letters.
‘, nor its dual, could be proved from the assumptions presented. This matter was one of Schröder’s first contributions, in 1890 (§4.4.4); sorting it all out is quite complicated (Houser 1991b) In addition, Peirce should have more clearly explained switches between terms and propositions and between lower- and upper-case letters.
In a final chapter on ‘The logic of relatives’ Peirce concentrated largely on the ‘dual’ kind ‘(A:B)’ between individuals A and B, and its converse and their negatives. He showed that this quartet could be compounded with the corresponding quartet relating B and individual C in 64 different ways to deliver the quartet of relatives between A and C (pp. 201-204). The whole array could be read as the 64 truth-values for the 16 connectives between two propositions; but he did not offer this interpretation, putting forward instead other quartets of combination. He promised a continuation of the paper at the end, but only a short introduction on ‘plural relatives’ was drafted(Writings 4, 210-211).
4.3.6 Peirce’s second phase, 1881: finite and infinite. (Dauben 1977a) Peirce’s next paper for Sylvester’s journal, 1881a ‘On the logic of number’, revealed his growing concern with the relationship between his logic and the foundations of arithmetic. He assumed 1 as ‘the minimum number’, and defined addition and multiplication of positive integers from 1 upwards, and then proved the basic properties (no trouble with distributivity this time). He also extended his definitions to cover zero and negative integers (pp. 304-306) by reversing mathematical induction via the lemma that
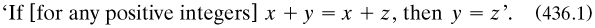
The contrast with the Peano/Dedekind axioms (§5.3.3) is striking; so is Peirce’s concern with the distinction between finite and infinite, which came not from Cantorian considerations but De Morgan’s syllogism of ‘transposed quantity’ (§2.4.6). Peirce gave as an example
Every Texan kills a Texan,
Nobody is killed but by one person,
Hence, every Texan is killed by a Texan,
and realised that the form was valid only over predicates satisfied by finite classes (p. 309). Thus it was essential to define an infinite class, which he did inductively ‘as one in which from the fact that a certain proposition, if true of any [whole] number, is true of the next greater, it may be inferred that that proposition if true of any number is true of every greater’ (p. 301). He repeated this example of the syllogism several times in later writings (with ‘Texan’ replaced by ‘Hottentot’: perhaps some or all Texans had objected to this Unionist slur), and even contrasted the ‘De Morgan inference’ involved in it with the ‘Fermatian inference’ of mathematical induction.16
The reaction of mathematicians seems to have been indifferent or sceptical. For example, these papers were reviewed in the Jahrbuch (it missed Peirce 1870a because it did not cover the Academy’s journal). The author was C. T. Michaelis, a mathematician-philosopher of Kantian tendencies. Of Peirce’s algebra 1880a of logic, ‘as in similar work of his predecessors and colleagues, much astuteness and careful diligence is shown; but whether logic gains overmuch through such refinement and intensification may be very doubtful’ especially as ‘the ties of syllogistic will be broken’ (Michaelis 1882a, 43), while Peirce’s study 1881a of number caused ‘difficulties of comprehension, without raising the certainty of theorems’ (Michaelis 1883a). Such would be the common reaction of philosophers and mathematicians to all symbolic logics and logicisms!
4.3.7 Peirce’s students, 1883: duality, and ‘Quantifying’ a proposition. The main fruits of Peirce’s collaboration with graduate students at Johns Hopkins was a 200-page book of Studies in logic prepared under his editorship (Peirce 1883a). The book seems to have been some time a-coming, due to financial difficulties which he helped to resolve.17 In a ten-page review in Mind, Venn 1883a generally welcomed the novelties of the book while regretting departures from Boole’s principles. Indeed, the scope of the eight essays, by Peirce and four followers, was wide; for example, Peirce’s own main piece 1883b dealt with ‘probable inference’, and moreover in the direction of statistical distributions rather than the probability logic that had been studied by De Morgan, Boole and a few others. Three other contributions need notice here.
One algebraic benefit of Peirce’s adoption of inclusive union had been that duality obtained between laws of union and of intersection; he had used it, though naively, in the distributivity laws (435.4) His student Christine Ladd (1847–1930) had already stressed duality in a paper 1880a for Sylvester’s journal extending De Morgan’s work 1849b with an operational algebra going from the arithmetical operations to logarithms and powers. She made great use of it in a long essay 1883a here on ‘the algebra of logic’, in which she developed a term calculus and then used it to express the propositional calculus and solve particular exercises (Castrillo 1997a) She used two copulas, a ‘wedge’ as a ‘sign of exclusion’ and an ‘incomplete wedge’ for ‘incomplete exclusion’: respectively, for propositions A and B,
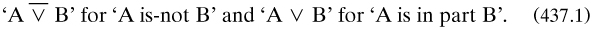
Following Peirce’s use of ‘∞’ for the universe of discourse, she expressed on p. 23 (non-)existence for a predicate x thus:
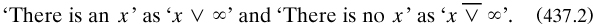
She emphasised duality to the extent of presenting some of her definitions and theorems in such pairs; this feature was to stimulate Peirce himself later (§4.3.9).
Ladd’s most striking innovation was based on the insight that the negation of the conclusion of a syllogism was incompatible with its major and minor premises. This situation could be expressed in the form ‘ABC is false’, where A, B and C were appropriate propositions; and the commutativity of conjunction led at once to the forms ‘BCA’ and ‘CAB’, so that two more syllogisms were handled (pp. 41–45). The trio came to be called ‘the inconsistent triad’ by Royce; the method was called ‘antilogism’ by Keynes (see Shen 1927a in Mind, the most available presentation).
Peirce added a footnote to Ladd’s (437.2) on the need for two copulas for existence and for non-existence, notions which he and his followers were now gradually transforming into quantification theory. The key figure was Oscar Mitchell (1851–1889), who handled adventurously ‘A new algebra of logic’ in his contribution 1883a to Peirce’s book. He stated that the extension of a term F comprised the universe not in Boole’s manner ‘F = 1’ but with a subscript as ‘F1’; if the extension was the class u, then ‘Fu’; for vacuous terms, ‘F0’. Then, for example,
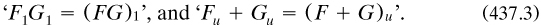
(Like Ladd, he presented results in pairs.) More significantly, he allowed for more than one universe, such as ‘1’ of time and ‘∞’ for ‘relation’, or indeed any appropriate but prosaic universe; thus a term became a function of two of them. For example (both his), take the universe U of a village where the Brown family lives and V as some summer; then ‘Some of the Browns were at the sea-shore some of the time’ was written ‘Fuv’ for the classes u and v from these respective universes, while ‘All of the Browns …’ was written ‘F1v’.
Mitchell saw such propositions as being of two ‘dimensions’, and realised that one could go further. ‘The logic of such propositions is a “hyper” logic, somewhat analogous to the geometry of “hyper” space. In the same way the logic of a universe of relations of four or more dimensions could be considered’ (pp. 95–96). These changes were not just notational: still more emphatically than Ladd, he stressed the existence of objects satisfying the term, which can easily be transferred to thinking existential quantifiers for u and the universal one for 1. The traditional opposition between affirmation and negation was being switched to that between existence and comprehension and from there towards quantification. While Peirce had more or less anticipated these ideas, Mitchell crystallised them clearly and with a compact symbolism which his master was to acknowledge and use with profit.
Mitchell also proposed a more efficient way of combining propositions, whether ‘categorical hypothetical or disjunctive’: draw inferences by forming their ‘product’ and erase the terms to be eliminated; no inference was possible if the middle term m was left (p. 99.) To increase algebraic perspicuity, he used ‘–1’ instead of the overbar to denote negations, and so wrote, for example, the valid mood Barbara as
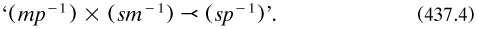
He also used display in converse pairs.
Regrettably, this paper was Mitchell’s sole major contribution, although he published some papers on number theory in Sylvester’s journal. After his time with Peirce he went back to college lecturing in his home town in Ohio and produced nothing more until before his early death (Dipert 1994a.)
To his book Peirce added a couple of ‘Notes’, of which the second, 1883c, summarised ‘the logic of relatives’. Distributivity was rather better handled (p. 455) Some advance in symbolism was evident, especially thanks to Mitchell, in the layout of collections of terms in matrix form, and in summation and product signs and subscripts. Thus pairs of the objects A, B,… in the universe of discourse under a relative l (‘lover’ again) were aggregated in the linear expansion

where the coefficient was 1 or 0 Boole-style according as I loved J or not (p. 454). After symbolising syllogistic forms he brought in Mitchell’s approach and presented propositions with multiple quantifiers.
4.3.8 Peirce on ‘icons’ and the order of ‘quantifiers’, 1885. The importance of symbols was emphasised in Peirce’s next paper, the last in this sequence and one of his finest: 23 concentrated pages of Peirce 1885a ‘On the algebra of logic’, offered as ‘a contribution to the philosophy of notation’. The opening section presented one of his most durable innovations, developing 1868a (§4.3.3) into ‘three kinds of signs’. This new triad was motivated by the relationship between a sign, ‘the thing denoted’ and the mind. Normally the signs themselves, ‘for the most part, conventional or arbitrary’, were ‘tokens’. But should the triad ‘degenerate’ to ‘the sign and its object’, such as with ‘all natural signs and physical symptoms’, then the former is ‘an index, a pointing finger being the type of the class’. Finally, when even this ‘dual relation’ degenerated to a ‘mere resemblance’ between the components, then the sign was an ‘icon’ because ‘it merely resembles’ the corresponding object (pp. 162–164). He went on discuss their own relationships; in particular, the Euler diagrams for syllogistic reasoning were icons (of limited scope) supplemented by Venn’s token-like use of shading (§2.6.4). Peirce was to become well remembered for this tri-distinction, mostly in later versions; the notion of an icon, treated here rather as the runt of the litter, has become especially notable.
In this paper Peirce markedly changed his treatment of the propositional calculus; for truth-values f and v now entered the algebra, in a manner implicit in Boole’s law of contradiction (256.2). From
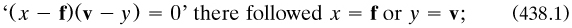
that is, ‘either x is false or y is true. This may be said to be the same as “if x is true, y is true”’ (p. 166). Further, (v – f) was available to the algebra, including as a divisor since it ‘cannot be 0’ (p. 215). The status of this zero was not discussed apart from not being associated with falsehood itself: ‘I prefer for the present not to assign determinate values to f or v, nor to identify the logical operations with any special arithmetical ones’ (p. 168). He stated, as ‘icons’, five laws for the calculus, starting with identity but covering ‘the principle of excluded middle and other propositions connected with it’ with

a ‘hardly axiomatical’ proposition which is sometimes associated with him (p. 173).
In the third section, on ‘first-intentional logic of relatives’, Peirce acknowledged Mitchell in splitting a proposition into ‘two parts, a pure Boolian expression referring to an individual and a Quantifying part saying what individual this is’ (p. 177); a few pages later he called the latter the ‘Quantifier’ (p. 183). Then he gave a much more elaborate exhibition of multiple quantifiers in expressions, bringing out the importance of the order in which the quantifiers lay; but he did not individuate any formulae as icons.
In ‘second-intentional logic’, the name taken from the late medieval ages, Peirce defined the identity relation ‘1ij’ to state that indices i and j were identical, that is, that ‘they denote one and the same thing’ (p. 185). Four more icons were put forward to found its logic (pp. 186–187), starting with the principle that ‘any individual may be considered as a class. This is written
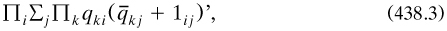
another example of mixedly quantified propositions in the paper. Finally, he rehearsed his views on the syllogism of transposed quantity of De Morgan, ‘one of the best logicians that ever lived and unquestionably the father of the logic of relatives’ (p. 188).
4.3.9 The Peirceans in the 1890s. Venn noted their contributions, with a score of references in the second edition 1894a of his Symbolic logic (§2.6.4). He praised Mitchell the most, for the ‘very ingenious symbolic method’ (p. 193); but he did not highlight the logic of relatives, or even Ladd’s antilogism. Let us turn to her later work.
Ladd’s writings in the early 1880s launched a long and noteworthy career as a logician, the first of several female logicians from this time onwards. She combined it with other careers: colour physicist (another inspiration from Peirce); from September 1882 wife to and mother for the mathematician Fabian Franklin (1853–1939), then another member of the Johns Hopkins group and later a newspaper editor; teacher at Columbia University, New York; and proponent of feminist causes.18 In a noteworthy stance which her husband supported, she always signed herself ‘Christine Ladd(-)Franklin’, not the normal submissive style ‘Mrs. Fabian Franklin’ of the time.
In a paper in Mind Ladd Franklin 1890a presented her version of the algebraic propositional calculus, building upon her piece in Peirce’s Studies. She showed first how many propositions as used in ordinary discourse are equivalent; for example, for terms x and y in the case ‘All x is non-y’, ‘The combination xy does not exist’ and ‘There is no x which is y’ (to quote three from her list of ten on p. 76). The ‘entire lot of propositions to be named’ was presented Benjamin-style in a 22 × 22-table, with the symbolism based upon Charles’s ‘x–<y’ for ‘All x is y’. Each row gave four equivalent propositions, including the second example above as
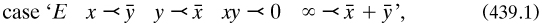
with ‘∞’ read as at (437.2) Each column presented four different propositions in the same form, for example (laid out in a row here):
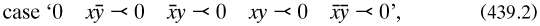
of which the first stated ‘No x is non-y’ (pp. 79–80). Algebraic duality was very prominent, and later in the paper ‘the eight copulas’ were treated somewhat semiotically, with her wedge and its incomplete partner (437.1)2 as one of the four pairs (pp. 84–86). The signs were chosen such that, as with her pair in (437.2), each universal or particular proposition used only logical connectives with an odd or even number of strokes.
Two years later Ladd published a review of Schröder in Mind, to be noted in §4.4.4. The same volume also contained another Baltimorean piece: Benjamin Ives Gilman19 (1852–1933) presented some aspects of Cantor’s theory of order-types in terms of relations. He used the symbol ‘A r B’ to state ‘The relation of anything A to anything B’, with ‘cr’ for the converse relation (Gilman 1892a, 518). While the paper is not remarkable—he had contributed to Peirce’s Studies a modest item 1883a on relations applied to probability theory—it was to attract the attention of Russell (§6.3.1).
Peirce himself was attempting to write mathematical textbooks, prepare a 12-volume outline of philosophy, develop his theory of existential graphs and so on and on; but none of these projects was ever finished (several logical ones are in Papers 4), and often not even his immense letters to colleagues and correspondents. In a long manuscript of around 1890 he argued that three-place relations could represent those of more places. He gave as example where a specific relation between A, B, C and D could be so reduced by bringing in an E related to A and B and also to C and D (m 1890b, 187–188); but the generality was not established (for example, for all mathematical contexts.. In a later piece m1897b on ‘Multitude and number’ he reviewed the principles of part-whole theory and then analysed inequalities arising in ‘the superpostnumeral and larger collections’ from cardinal exponentiation; but he failed to handle them correctly (Murphey 1961a, 253–274) and found no conclusive results such as Cantor’s paradox.
During this period Peirce was also desperately trying to make money by publishing articles that were paid (Brent 1993a, ch. 4). In an essay 1898a ‘On the logic of mathematics in relation to education’ he affirmed his anti-logicist stance by stressing that (his kind of) logic was mathematical, and he cited De Morgan as a fellow traveller; he also quoted with enthusiasm his father’s definition of mathematics as drawing necessary conclusions (§4.3.2).20 Partly inspired by Ladd’s paper 1883a in his own Studies (§4.3.7), he worked across the turn of the century on symbolising the 16 logical connectives in four quartets of signs which imaged the relationships denoted; but he never published this fine extension of semiotics into shape-valued notations, and it has only recently been developed (Clark 1997a) In a short note 1900a to Science, edited by his former student J. M. Cattell, he asserted priority over Dedekind concerning the distinction between finite and infinite. We shall note this detail in the next section, for it had already interested Schroder, the main subject.
4.4.1 The Grassmanns on duality. Boole’s logic was publicised in Germany especially by the philosopher and logician Hermann Ulrici (1806–1884) a colleague of Cantor at Halle University (Peckhaus 1995a). A frequent reviewer in the Zeitschrift für Philosophie und philosophische Kritik, he produced there a long and prompt review 1855a of The laws of thought. Treating in some detail Boole’s index law and its consequences the laws of contradiction and excluded middle, he discussed 0 and 1 in connection with the latter. The former was to be understood as ‘“Not-class or no class’” whereas ‘Nothing as class-sign thus contradicts the algebraic meaning of 0’ similarly, 1 was ‘Alles’ for a given context, not a ‘Universum, totality, allness’ (‘Allheit’: 1855a, 98–100).
Boole might not have fully agreed, though we recall from §2.5.4 that all and nothing were tricky objects with him; but he would have been astonished by Ulrici’s conclusion from a brief discussion of the expansion theorems (255.5–6) ‘that mathematics is only an applied logic’ (p. 102) Nevertheless, the review will have attracted Continental readers to this English author; at the beginning Ulrici stressed the contrast with the typical English empiricism of J. S. Mill’s Logic (which he had reviewed earlier), and at the end he cited a passage from Boole’s final chapter on the intellect to show that Boole ‘stands much nearer to the spirit of German philosophy and its contemporary tendencies than most of his compatriots’. Much later Ulrici 1878a guardedly reviewed Halsted 1878a on Boole’s system (§2.6.4) in a shorter piece.
The other main import into German algebraic logic was home-grown, although from another field (Schubring 1996a) The Stettin school-teacher Herman Grassmann (1809–1877) had published in 1844 a book on Die lineale Ausdehnungslehre, a ‘linear doctrine of extension’ in which he worked out an algebra to handle all kinds of geometric objects and their manners of combination (H. Grassmann 1844a) Two ‘extensive magnitudes’ a and b could be combined in a ‘synthetic connection’ to form ‘(a ∩ b)’, where the brackets indicated that a new object had been formed; he formulated novel rules on their removal. Conversely, an ‘analytic connection’ decomposed ‘(a ∪ b)’ such that
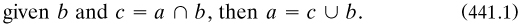
He examined the basic laws of ‘∩’ and ‘∪’, especially ‘exchangeability’ (commutativity) and distributivity; and properties such as linear combination and the expansion of a magnitude relative to a basis (to us, by implicit use of a vector space). Also a philologist, he may have chosen the unusual word ‘lineale’ for his title to connote ‘Linie-alle’—all linear.
Grassmann was influenced philosophically by the Dialektik (1839) of the neo-Kantian Friedrich Schleiermacher (1768–1834), whose lectures he had heard while a student in Berlin (A. C. Lewis 1977a.) In particular, he drew upon pairs of opposites, of which (441.1) is one of the principal cases. Known in German philosophy as ‘Polarität’, it covered many other features of his theory: pure mathematics (or mathematics of forms) and its applications, discrete and continuous, space and time, and analysis and synthesis.
As he well knew, Grassmann’s theory enjoyed a remarkable range of applications, which indeed are still sought and developed; the recent English and French translations of the Ausdehnungslehre were not prepared just for historical homage. Indeed, the uses went beyond geometry and physics which he had had in mind, including to arithmetic (as we see in the next sub-section) and to new algebras and thereby into logic. This last inquiry was effected by his brother Robert (1815–1901), a philosopher and logician by training, and a teacher and publisher by profession: they also ran a local newspaper together.
Robert’s best-known publication was to be a group of five little books under the collective title Die Formenlehre oder Mathematik (R. Grassmann 1872a) In this visionary compendium he went beyond even Hermann in generality. To start, Formenlehre laid out the laws of ‘strong scientific thought’ of ‘Grösen’ (the word for ‘shine’) which denoted any ‘object of thought’; each of them could be composed as a sum of basic ‘pegs’ (‘Stifte’) ‘e’ (set roman, not italic). Like Hermann, he stipulated two means of ‘connection’ between pegs: ‘inner’ and ‘outer’, symbolised respectively by ‘+’ and ‘×’; then he defined 22 special kinds of Formenlehre, with the Ausdehnungslehre only an example of the last one. The members of the quartet were distinguished by the basic laws which their pegs obeyed, under suitable interpretations of them and their means of connection:

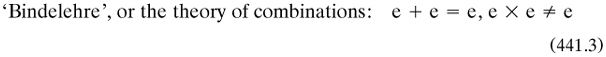

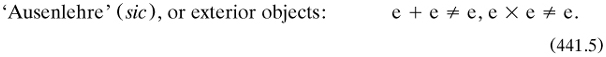
These objects satisfied the relations of identity, non-identity (for which latter he used the symbol ‘ ’), and subordination (‘Unterordnung’), written ‘a < b’ or ‘b > a’
’), and subordination (‘Unterordnung’), written ‘a < b’ or ‘b > a’
The logic was presented in the first book of the other four, as ‘the simplest and also most central’ kind of Formenlehre: 43 pages of Die Begriffslehre oder Logik. The three parts covered, in turn, the development of concepts, judgements and deductions. Robert’s signs ‘.’ and ‘+’ stood respectively for ‘and’ and ‘with’ (‘mal‘) between concepts (‘Begriffe’) rather than their associated classes; like Jevons, he allowed that a + a = a (pp. 8–9). Rather unhappily, he also used ‘=’ for equivalence between propositions as well as in (441.2).
Apart from the reading of ‘+’, the ensemble of Robert’s results strongly resembles Boole’s, even to the same orthogonality relation between pegs (in his own symbols, ‘e1. e2 = 0’. and the same symbol ‘ ’ for the negation of a concept with respect to the ‘totality’ T. But he cited nothing published after 1825, and seems to have been ignorant of both Boole and Jevons. Indeed, his approach was much less radical than Boole’s in The laws of thought (1854). His theory of judgements centred around solving for x the identity a = xu (‘x is a u’), and finding equivalents for given judgements; his treatment of deduction did little more than algebrise Aristotelian syllogisms rather than solve sorites for a selected unknown, so that he had no analogues of Boole’s expansion theorems.
’ for the negation of a concept with respect to the ‘totality’ T. But he cited nothing published after 1825, and seems to have been ignorant of both Boole and Jevons. Indeed, his approach was much less radical than Boole’s in The laws of thought (1854). His theory of judgements centred around solving for x the identity a = xu (‘x is a u’), and finding equivalents for given judgements; his treatment of deduction did little more than algebrise Aristotelian syllogisms rather than solve sorites for a selected unknown, so that he had no analogues of Boole’s expansion theorems.
Later Robert devoted ten volumes to Das Gebäaude des Wissens (1892–1899), ranging across epistemology, biology, chemistry, technology, ethics, law, politics, education and religion in its five thousand self-published Stettin pages. Nobody seems to have read it. Here and (yet) elsewhere he cited some works by most of the algebraic logicians, and to some extent solved logical equations. But he did not pick up the logic of relations, or quantification theory, despite Peirce’s publicity: he seems always to have followed the tradition of conceiving of logic as independent of language, a view then becoming rather passé.
However, the Grassmanns’ basic conceptions were far ahead of their time, and publication in the mathematical steppes of Pomerania further assured a very slow reception; Robert never received general recognition, and Hermann’s simplified version 1862a of his doctrine made little change. Not until the late 1870s did the importance and merit of his work begin to be recognised; but they were the last years for Hermann. After his death a long obituary appeared in Mathematische Annalen, where he had published several papers (Grassmann 1878a′) one of its three authors was Schroder.
4.4.2 Schröder’s Grassmannian phase. (Peckhaus 1996a.) After graduation in mathematics from Heidelberg, Königsberg and Zürich, Ernst Schröder (1841–1902) taught for a few years at a school in Baden-Baden and then passed his career in Technische Hochschulen: after two years in Darmstadt he moved in 1876 to the Polytechnische Schule (as it was then called) at Karlsruhe and stayed for the rest of his life (Dipert 1991a). But these professional requirements hardly corresponded to his research interests, which matched Boole and De Morgan in a joint focus upon algebra and logic (Ibragimoff 1966a.) As Direktor of the School for 1890–1891 he treated his colleagues to a discourse Schröder 1890a on signs, of which an English translation soon appeared as 1892a.
Schröder seems to have started not from the Ausdehnungslehre but from a textbook on arithmetic written by Hermann with Robert’s help (A. C. Lewis 1995a.) The subject was algebrised by taking a basic unit ‘e’ and defining numbers in terms of iterated additive successions with subtraction the polaredly opposite means of combination. Thus if b were the successor of a,
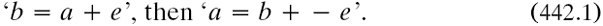
Zero and negative numbers were introduced thus:
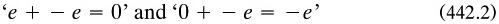
(H. Grassmann 1861a, arts. 8–10) Both here and elsewhere his rigour was rather compromised by mixing properties with definitions in the ubiquitous ‘=’; on the other hand, the generality was stressed by identifying the integers only later, both positive and negative thus (art. 55):
Multiplication was defined in arts. 56–58 for integers a and b from
Multiplication was defined in arts.56–58 for integers a and b from
Many of the proofs were based upon mathematical induction, used to a degree perhaps new in a textbook. In this and the definitions of integers Grassmann’s later influence upon Peano is evident (§5.2.2); the effect upon Schröder came first, in his own textbook 1873a ‘on arithmetic and algebra’, which started a long association with the house of Teubner. In the subtitle he mentioned ‘the seven algebraic operations’: addition and subtraction at the ‘first level’, multiplication and division at the second, and exponentiation, roots and logarithms at the third (a trio which spoilt the polarity!). In a variant upon the Grassmanns, he put forward mathematics as ‘the doctrine of numbers’, rather than of magnitudes; and he stressed the algebraic bent by seeking an ‘absolute algebra’ of which common algebra was an example. Another one was algebraic logic, as he noted when reporting his late discovery of Robert Grassmann (pp. 145–147).
Schröder developed his system somewhat in an essay 1874a written for the school in Baden-Baden where he taught; probably nobody read it, but he had now read Boole. He presented his theory quite systematically in a 40-page pamphlet 1877a from Teubner on Der Operationskreis des Logikkalküls. The second noun made its début in symbolic logic here, I believe; the first one showed the main influence from the Grassmanns, especially Robert’s Formenlehre. After the usual nod towards Leibniz’s ‘ideal of a logic calculus’ (p. iii), he presented two pairs of ‘grand operations’ on classes: ‘determination’ (conjunction) and ‘collection’ (disjunction), and ‘division’ (abstraction) and ‘exception’ (complementation, in Boole’s way (255.2)) (pp. 2–3) He emphasised duality by laying out definitions and theorems in double columns, with quirky numberings, all features to endurein his logical writings. He reworked Boole’s theory of solving logical equations, presenting as his ‘main theorem’ that for classes a, x and y
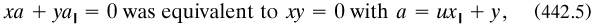
with class u arbitrary, where a1 was the class complementing a relative to a universe 1 (p. 20, thm. ‘20°’). He solved a particular problem from Boole’s The laws of thought (pp. 25–28); like Boole (§2.5.5), he did not seek singular solutions. He also did not cite Jevons.
The booklet enjoyed some success. Robert Adamson 1878a gave it a warm welcome in Mind, and Venn was complimentary in his textbook (1881a, 383–390). Peirce used it in his teaching at Johns Hopkins University, and Ladd was influenced by it to highlight duality in her paper 1883a in his Studies (§4.3.7). Above all, it led Schroder to a huge exegesis which was to dominate his career—untaught ‘lectures on the algebra of logic’.
4.4.3 Schröder’s Peircean ‘lectures’ on logic. (Dipert 1978a) The main product of Schröder’s career was a vast series of Vorlesungen über die Algebra der Logik (exacte Logik) which he published with Teubner in three volumes. They appeared at his own expense; as a bachelor, he may not have found this too onerous, but apparently only 400 copies were printed. At his death in 1902 the second volume was incomplete; three years later the rest of it appeared (making a total of nearly 2,000 pages), including a reprint of an obituary 1903a written by Schröder’s friend Jacob Lüroth(1844–1910) for the DMV. The editor was Lüroth’s former student the school-teacher Eugen Müller (1865–1932), who also put out as Schröder 1909a and 1910a a two-volume Abriss of Schröder’s logic, edited out of the Nachlass. This posthumous material will be described in more detail in §4.4.9, but the contents of the entire run is summarised in Table 443.1.21The first two volumes contained excellent bibliographies and name indexes, but sadly none for subjects; the third volume had no apparatus at all. Each (part) volume is given its own dating code, and cited by Lecture or article number if possible. Of the many topics indicated in the Table, the account below concentrates upon algebraic aspects, duality and the part-whole theory of collections. Some main features are described in my 1975b and passim in Mehrtens 1979a; on the general background influence of Leibniz, see Peckhaus 1997a, ch. 6.
4.4.4 Schröder’s first volume, 1890. Schröder used largely unchanged the main technical terms and symbols from his earlier writings. In this first volume of over 700 pages, published in his 50th year, he introduced the basic properties of ‘domains’ (‘Gebiete’) across a given ‘manifold’ (‘Mannigfaltigkeit’) with subsumption (‘Subsumtion’ or ‘Einordnung’) as the basic relation, symbolised ‘ ’. Both duality and polarity were stressed in the frequent use of pairs of definitions, theorems or even discussions printed as double columns on the page. Schröder probably took over this nice TABLE 443.1. Summary of the contents of Schröder’s Vorlesungen über die Algebra der Logik (1890–1905) and Abriss der Algebra der Logik (1909–1910).
’. Both duality and polarity were stressed in the frequent use of pairs of definitions, theorems or even discussions printed as double columns on the page. Schröder probably took over this nice TABLE 443.1. Summary of the contents of Schröder’s Vorlesungen über die Algebra der Logik (1890–1905) and Abriss der Algebra der Logik (1909–1910).
The book is divided thus: vol. 1 (1890) Lectures 1–14 and Appendices 1–6; vol. 2, pt. 1 (1981) Lectures 15–23; vol. 2, pt. 2 (1905), Lectures 24–27 and Appendices 6–8. vol. 3, pt. 1 and only (1895) had its own numbering of Lectures, each one titled. In the Data column, ‘a/b–c; n’ indicates Lecture a, articles b–c, n pages. The order of topics largely follows that of text. An asterisk by a word or symbol marks a (purported) definition. My comments are in square brackets. The two-part Abriss was divided into unnumbered sections, which guide the division below; and also into short articles, which are indicated by number, followed by the number of pages.
Data |
Description |
Section A; 37 |
Volume 1, Introduction Philosophy; induction, deduction; contradiction. ‘Presentations’ and ‘things’. |
Section B; 42 |
Nouns and adjectives. Names; general, individual, species. Classes and individuals. |
Section C; 46 |
Concepts. Pasigraphy. Intension and extension. Judgement, deduction and inference. Purpose of the algebra of logic. |
1/1–3; 42 |
Volume 1, Lectures *Subsumption and *judgement. Euler diagrams. *‘Identical calculus’ of *‘domains’ of a *‘manifold’. |
2/4; 23 |
First two principles of subsumption; properties. *Equality, *0 and *1. |
3/5–7; 26 |
Identical *‘addition’ and *‘multiplication’; Peirce. *‘Consistent manifolds’. |
4/8–9; 37 |
Calculus of classes, including the *null class; their *‘addition’ and *‘multiplication’. *‘Pure manifolds’. |
5/10–11; 28 |
Propositions lacking negation; multiplication and addition. Propositions ‘0’ and ‘1’. |
6/12; 17 |
Non-provability of the law of distributivity (§4.4.2). |
7/13–15; 43 |
*Negation; its laws. Duality principle. Negative judgements. |
8/16–17; 23 |
Complementary classes. Laws of contradictions and of excluded middle. Double negation. Dual theorems of subsumption. |
9/18; 31 |
Applications to logical deductions, impreciseness; examples from Peirce, Jevons. |
10/19; 38 |
Expansions of logical functions [mainly following Boole]. |
11/20–22; 44 |
Synthetic and analytic propositions. ‘Pure theory of manifolds’. Simultaneous solutions and elimination, for one and for several unknowns. |
12/23–24; 43 |
Subtraction and division as inverse operations. Negation as a special case. General symmetric solutions. |
13/25; 38 |
Examples taken from Boole, Venn, Jevons, MacColl, Ladd Franklin and others. |
14/26–27; 33 |
Other methods of solution: Lotze, Venn, MacColl, Peirce. |
Apps. 1–3; 22 |
To arts. 6 and 10. Duality; other properties of multiplication and addition. Brackets. |
Apps. 4–5;30 |
To art. 12. Group theory and functional equations; ‘algorithms and calculations’. |
App. 6; 53 |
To arts. 11, 19 and 24. ‘Group theory of identical calculus’; combinatorics |
15/28–30; 48 |
Volume 2, Part 1 Propositional calculus, sums and products of domains. Duality. |
16/31–32; 36 |
Basic theorems of propositional calculus. Consistency; truth-and duration-values. |
17/33–35; 33 |
Categorical judgements; Gergonne relations. Basic relationships of domains. |
18/36–39; 61 |
Logical equations and inequalities. Sums and products of basic relationships. Negative domains. Propositions for n classes, including De Morgan’s. |
19/40–41; 38 |
Solved and unsolved problems. Mitchell; dimensions. Uses of elimination. |
20/42–44; 39 |
Traditional views of syllogistic logic. Ladd Franklin’s treatment. Correction of old errors. ‘Subalternation and conversion’. |
21/45–46; 52 |
Propositional and domain calculi. Modus ponens/tollens. Applications to examples of De Morgan, Mitchell, Peirce. |
22/47; 32 |
*Individual and *point; basic theorems. |
23/48–49; 51 |
‘Extended syllogistic’ [quantification of the predicate: §2.4.6]. *‘Clauses’ (products of propositions); basic properties. |
24/50–51; 36 |
Volume 2, Part 2 Additions to Vol. 1, esp. art 24 on general symmetric solutions. |
25/52; 27 |
Review of recent literature: MacFarlane, Mitchell, Poretsky, Ladd Franklin, Peano. |
26/53–54; 29 |
Controversy over Ladd Franklin 1890a. Particular judgements. ‘Negative’ characteristics of concepts. |
27/55–56; 18 |
‘Formal properties in the identical calculus’. Modality of judgements. |
App. 7; 49 |
McColl’s propositional calculus, with the use of integrals (§2.6.4). |
App. 8; 29 |
Kempe in the context of the ‘geometry of place’ (§4.2.8). |
1/1–2; 16 |
Volume 3, Part 1 [and only] Plan. *Binary relatives. ‘Thought regions of orders and their individuals’. |
2/3–5; 59 |
Basic assumptions. Expansion of a relative; matrix and geometrical representation. |
3/6–7; 39 |
General properties of binary relatives. Duality, conjunction. Propositional calculus. |
4/8–10; 33 |
Algebra of binary relatives; product expansion. Basic ‘correlation of modules’ with identity. *Null relatives. |
5/11–14; 51 |
Basic laws of compounding of propositions. Types of solution. including by iteration of functions. Simple examples. |
Development of a general relative in 28 rows or columns. |
|
7/17–20; 52 |
Elementary ‘inversion problems’. |
8/21–22; 53 |
Types of solution for problems in two or three letters. |
9/23–24; 59 |
Dedekind’s theory of chains (§3.4.2); complete induction. |
10/25–27; 63 |
‘Individuals in the first and second thought-regions’; ordered pair. ‘Systems’ as unitary relatives; connections with ‘absolute modules’. |
11/28–29; 85 |
Elimination, mostly following Peirce 1883c (§4.3.7); methods of solution. |
12/30–31; 96 |
15 kinds of mapping; uniqueness. Dedekind similarity and equipollence (§3.4.2.) |
1–32; 26 |
Abriss, Part 1 Main assumptions, including propositional calculus and domains. |
33–75; 23 |
Deduction. 0 and 1. Multiplication and addition of domains; negation. |
76–107; 24 |
Abriss, Part 2 Domains for propositions and ‘relations’. ‘The propositional calculus as a theory of judgements’. |
108–121; 18 |
Theory of logical functions; normal forms. |
122–150; 34 |
Elimination and methods of solution. |
151–165; 22 |
‘Inequalities’; normal forms, elimination, Boole’s approach. |
practice from the projective geometers: J. V. Poncelet and J. D. Gergonne had introduced it in the 1820s (with a French-style priority row, of course) when stating dual theorems about point/lines/planes and planes/lines/points (Nagel 1939a). The Grassmanns were present in the use of analogies between algebra and logic, including the same names and symbols in the calculi of domains and classes (and in the later volumes, in propositions and relatives), and also in the organisation and removal of brackets in symbolic expressions. But Peirce was the main source, as Schröder made clear in his foreword. However, the enthusiasm was not uniform; in his bibliography he recommended especially those items marked with an asterisk, and of Peirce’s strictly logical papers only the opening trio of 1868 (§4.3.3) and the final piece 1885a (§4.3.8) were so honoured.
The calculus was grounded in these ‘principles’ of subsumption (Schröder 1890a, 168, 170):
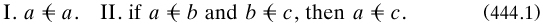
He called the first ‘Theorem of identity’, but did not really furnish proofs of either one. However, he was aware of the chaos about laws (435.4) of distributivity as left by Peirce, devoting art. 12 to the clean-up by assuming (p. 243) a new
Although the book carried the subtitle ‘exact logic’, some imprecisions are evident. One concerns definitions; although Schröder used ‘Def.’ sometimes and admitted only nominal definitions (p. 86), it is not always clear whether the overworked ‘=’ symbolised identity, equality, or equality by definition. For example, he explained in his first Lecture that, as its symbol ‘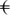 ’ suggested, subsumption between domains covered both the cases of inclusion and equality; yet he merged the latter with ‘the complete agreement, sameness or identity between the meanings of the same connected names, signs or expressions’ (pp. 127–128), and he called his theory the ‘identical calculus’ (pp. 157–167). He even named on p. 184 the following definition ‘identical equality (identity)’ for domains a and b:
’ suggested, subsumption between domains covered both the cases of inclusion and equality; yet he merged the latter with ‘the complete agreement, sameness or identity between the meanings of the same connected names, signs or expressions’ (pp. 127–128), and he called his theory the ‘identical calculus’ (pp. 157–167). He even named on p. 184 the following definition ‘identical equality (identity)’ for domains a and b:
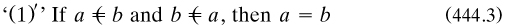
‘(read a equals b)’ (p. 184): Husserl will spot the slip in §4.6.2.
A list of Schröder’s basic notions included not only domains but also ‘classes or species of individuals, especially also concepts considered in terms of their range’ (p. 160), which reinforces the extensionalist character of the theory and thereby makes the difference between identity and equality more moot. Both manifolds and classes contained ‘individuals’ as ‘elements’, named by ‘proper names’ (‘Eigennamen’: pp. 62–63). The intensionalist aspect was associated in this list with ‘concepts considered in terms of their content, especially also ideas’; he even distinguished a horse, the idea of a horse, the idea of the idea of a horse, … (p. 35: compare §4.5.4) and dwelt a little on the concept of a concept (p. 96). However, he only skated around philosophical issues—a little disappointing after a thorough survey of the zoo of terms used in naming collections (pp. 68–75). He also found a paradox.
Schröder defined a ‘pure’ manifold as composed ‘of unifiable elements’, presumably by some governing property or intension. Classes of such individuals were elements of a ‘derived’ (‘abgeleitete’) manifold, ‘and so on’ finitely up (p. 248). This is a kind of type theory; but it would be foolhardy to follow Church 1939a and see this construction as a theory of types anything like that which Russell was to create, for Schröder worked only with one type of manifold at a time. But this led him into trouble further on, when he solved for domains) x the following dual pair of equations:
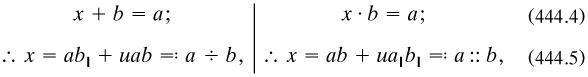
where u was an arbitrary domain. Now elementhood to these solution domains ‘should be interpreted as relating to the derived manifold, and not to the original one’ for x ‘be contained as an individual in a class of domains’ in the solution (p. 482). But if the class (a ÷ b)
itself comprises only one domain, the sign for subsumption would be open to misunderstanding, in that it seems to allow subsumption (as part) where, as mentioned, only equality can hold. To avoid such drawbacks, one must strictly speaking make use of two kinds of sign of subsumption, one for the original and one for the derived manifold.
But Schröder did not pursue his strict speech, which would have led him to some kind of set theory instead of the part-whole theory to which he was always to adhere. To his description of subsumption he added a footnote, that in Cantor’s ‘famous’ Mengenlehre and Dedekind’s ‘epoch-making’ work on number theory and algebraic functions ‘subsumption plays an essential role’ (p. 138)—not incorrect, but off the point in either case. Russell was to seize on its use of part-whole theory as one of his criticisms of algebraic logic (§8.2.7).
One major playground for analogy was the domains 0 and 1 for a given manifold. Schröder “defined” them on p. 188 in a dual manner down even to the numberings:
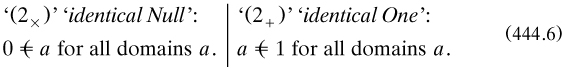
He then argued that each of these domains was unique, and by implication that ‘1’ was the manifold itself (p. 190: see also p. 251). On considering ‘the class [M] of those manifolds, which are equal to 1’, he reasoned that necessarily 0 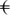 M, so that 0 = 1, which could hold only for ‘a completely empty manifold 1’ (pp. 245–246). 0 ≠ 1 was still more assumed than proved. Classes also had a 0 and a 1, understood respectively as ‘Nothing’ and ‘All’ (esp. p. 243). The empty domain of a derived manifold was written ‘O’, a ‘large Null’ (p. 250).
M, so that 0 = 1, which could hold only for ‘a completely empty manifold 1’ (pp. 245–246). 0 ≠ 1 was still more assumed than proved. Classes also had a 0 and a 1, understood respectively as ‘Nothing’ and ‘All’ (esp. p. 243). The empty domain of a derived manifold was written ‘O’, a ‘large Null’ (p. 250).
In this connection Schröder also defined on p. 212, in dual manner, ‘consistent’ manifolds, rather akin to pure ones:

Cantor may come to our mind, over both the positive property (§3.4.7) and the adjective in the context of paradoxes (§3.5.3); but Schröder has priority, and the two theories seem to be independent (my 1971a, 116–117).
This volume received several reviews; those by Husserl and Peano will be considered in §4.6.2 and §5.3.2 respectively, when the work of the reviewers is discussed. Among the others, the most unexpected piece came from Spain. In 1891 Zoel Garcio de Galdeano (1842–1924) at the University of Zaragoza started a mathematical journal, El progreso matemático, and its opening trio of volumes contained several pieces on algebraic logic. His reviews 1891a and 1892a of the first two volumes totalled 22 pages; he made no particular criticisms but reasonably covered features, including the use of double columns. His colleague Ventura Reyes y Prósper (1863–1922) chipped in with seven short articles on logic (del Val 1973a): a short article 1892a on Schröder was followed by 1892b on ‘Charles Santiago Peirce y Oscar Honward [sic] Mitchell’ and 1892c on the classification of logical symbolisms.
Reyes y Prósper’s first article, 1891a, dealt with Ladd-Franklin, on the occasion of a visit by her to Europe (when she met Schröder22). She reviewed Schröder’s first volume in Mind, stressing the influence of Peirce, concentrating on properties of subsumption, and finding unclear the treatment of negation (Ladd-Franklin 1892a). By contrast, in the Jahrbuch Viktor Schlegel 1893a found Boole and Robert Grassmann to be the main sources, and never mentioned Peirce! At six pages, his review was very long for that journal; a similar exception was made for Korselt by the editors of a journal in mathematics education, for they took from him a two-part review of 36 pages, in view of the ‘high significance of the work’. Korselt 1896–1897a provided a rather good summary of the basic mathematical features and methods, and noted difficulties such as the laws of distributivity; but he did not analyse foundations or principles very deeply.
4.4.5 Part of the second volume, 1891. In 400 pages Schröder 1891a dealt mainly with propositions and quantification (again not his word), rather mixed together; for example, the outlines of both calculi were given in the opening Lecture 15. In the analogies the arithmetical signs were given (too?) much rein, to mark the logical connectives; disjunction (‘+’) was inclusive (p. 20), to match the union of domains. But the symbols most affected by multi-use were ‘0’ and ‘1’ (as he now wrote it, to indicate that a different kind of manifold was involved: unconvincingly, he rejected on p. 5 the need for ‘0’). These symbols now not only denoted respectively contradiction and tautology but also, when prefaced by ‘=’ and read as one compound symbol, symbolised truth-values; thus, for example, the arithmetical example ‘(2 × 2 = 5) = 0’ (p. 10) is rather disconcerting to read! Indeed, the two categories were intimately linked in this ‘specific principle of the propositional calculus’ for a proposition A:

that is, a proposition was equated/identified with its truth (p. 52). All kinds of multiply interpretable corollaries followed; for example from many, on p. 65
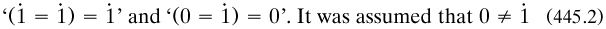
to avoid triviality; he claimed it to be provable (p. 64) Among other cases, the ‘theorems’ of contradiction and of excluded middle were respectively
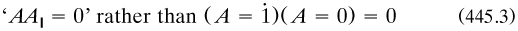
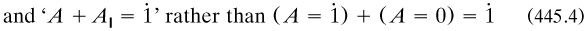
as one might expect (p. 60): compare Russell at (783.5).
To us Schröder has meshed logic with its metalogic; at that time logic would have been linked with the assertion of a proposition (compare §4.5.2 with Frege) or with a judgement of its truth-value, and indeed he called ‘0’ and ‘1’ ‘values’ (p. 256). But he also followed Boole’s temporal interpretation of these symbols (§2.5.7) in terms of the ‘duration of validity’ of the truth of a proposition between never and always true (p. 5). One motive was to claim that categorical and hypothetical propositions were basically different; for example, for him only the former could take the values 0 and 1.
Subsumption now denoted this sort of implication between propositions A and B: ‘If A is valid, then B is valid’ (p. 13). The basic notions and principles were broadly modelled upon (445.1–4). The layout was very messy, between a rehearsal of the calculus of domains a, b, c, … on pp. 28–32 and its re-reading for propositions A, B, C, … both there and, with re-numberings, on pp. 49–57:
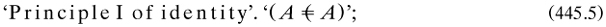
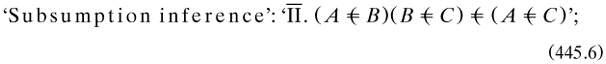
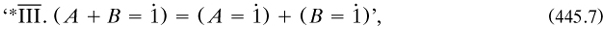
this latter read in terms of propositional validity; but not
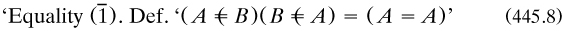
because of the ‘vicious circle’ allegedly involved in the two ‘=’s. The ‘identical Null and One’ propositions were defined for domains on p. 29 and numbered on p. 52:
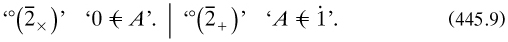
Propositional equivalence did not use analogy (p. 71); for reasons concerning period of validity, instead of
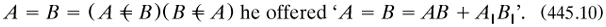
Quantification theory was based upon Peirce 1885a (§4.3.8), with a strong emphasis on the ‘duality’ between the union ‘Σ’ and disjunction ‘π’ of domains (art. 30); the algebra made the text look like an essay on series and products. Multiple additions or multiplications were used, but not mixtures (‘πΣ’ or ‘Σπ’) involving quantifier order; in the account of ‘clauses’ (art. 49) each term in the products was written out. Presumably the truth-values of propositions should have been defined in a manner analogous to (444.6) for empty and universal domains (p. 29):
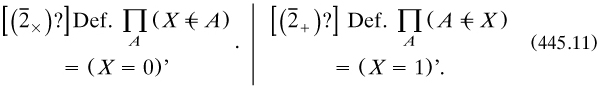
Much of this second volume was concerned with syllogistic logic. The ‘incorrect syllogism of the old times’ was replaced by a modern version (art. 44), including the ‘extended’ quantification of the predicate (art. 48), extensions of De Morgan’s propositional laws (435.3) (art. 39), and Ladd-Franklin’s inconsistent triad (§4.3.7: pp. 61, 228) and copulas (§4.3.9: art. 43).
One of the most interesting Lectures, 21, dealt with ‘individuals’ and ‘points’, the ultimate parts of any manifold (or class). Schröder recorded on p. 326 Peirce’s definition of an individual (1880a, 194), that any part of an individual must be empty. But his own definition (p. 321) used the (impredicative) property as a non-empty domain i which could never be a part of both any domain and its complement:
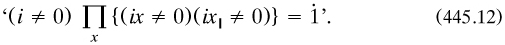
He gave various other versions of this property, including on p. 325 that it be non-empty and a part either of any domain or of its complement. Oddly, this version appeared again twenty pages later (p. 344) as a seemingly independent definition of the property ‘Ja’ that a was a point:
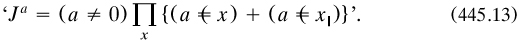
He then defined the cardinality of a class a (sic!), ‘num. a’, thus:
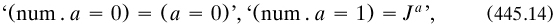
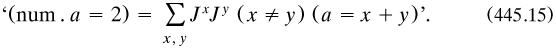
and so on finitely; note ‘=’ hard at work again. This sequence does not anticipate Russell’s logicist definitions of cardinals (§6.5.2), or try to; it belongs to a tradition of associating numbers with collections.
After the extensive reaction to the first volume, this one was poorly noted; for example, neither the Jahrbuch nor Mind reviewed it. But Galdeano 1892a devoted several pages of El progreso matemático to a reasonable survey of the principal definitions and some of the applications, especially those of algebraic interest. He also reported on p. 355 that his colleague Reyes y Prósper was translating the book into Spanish; but nothing was published.
In England, Venn praised Schröder’s work to date in the second edition of his Symbolic logic, giving a score of references, mostly to the lectures. But they always concerned particular details, such as symbols of individual problems; no connected statement was made about his ‘admirably full and accurate discussion of the whole range of our subject’ (Venn 1894a, viii).
4.4.6 Schröder’s third volume, 1895: the ‘logic of relatives’. In his mid fifties Schröder published as 1895a his third volume, the first part of it and in the end the only one. The topic, ‘the algebra and logic of relatives’, is arguably his most important contribution, greatly developing Peirce’s theory. The Lectures were numbered afresh, 1–12, over 650 pages. No bibliography was given, presumably because nothing new was to be cited; in his opening paragraphs he recalled De Morgan’s and especially Peirce’s contributions.
If a ‘thought-domain’ was comprised of individuals A, B, C, D,…, then it was ‘first-order’, and
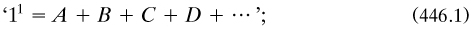
its ‘second-order’ companion was similarly composed of a collection of ‘binary relatives’ (to us, ordered pairs)
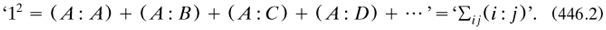
This was Schröder’s introduction to his theory (pp. 5–10): the first expansion of ‘12’ used a Peircean (§4.3.2) matrix-style expansion in rows, which was discussed in painstaking detail in art. 4; the second version gave a generic form which he used more often. The theory of individuals itself was worked out in detail in Lecture 10, where classes were also recast as ‘unitary relatives’.
In this part Schröder concentrated on binary relatives; presumably the ternary, quaternary,... ones would have been treated in its second part had he lived to write it (compare p. 15). He did not follow Peirce in handling the domains (using the word in our sense) of relatives, but construed a ‘binary relative a’ (regrettably, the same letter again) extensionally as a class of ordered pairs, expressible in terms of its ‘element-pairs’ as

(pp. 22–24). The relative coefficient’ of each pair was ‘ai, j = (i is an a of j)’, a proposition which gave the values 1 or 0 to the coefficient when it was true or false (p. 27). Logical combinations or functions (‘*’, say) of relations could be defined as an expansion in the manner of (446.3) as
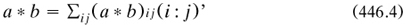
(p. 29), where ‘*’ took values such as ‘ ’ for negation, ‘
’ for negation, ‘ ’ for the converse relative, ‘+’ for disjunction, ‘·’ for conjunction, and the cases about to be described.
’ for the converse relative, ‘+’ for disjunction, ‘·’ for conjunction, and the cases about to be described.
As usual ‘0’ and ‘1’ were busy, used not only for the ‘null’ and universal relations respectively but also identity (‘1”) and diversity (‘0”): following (446.3),
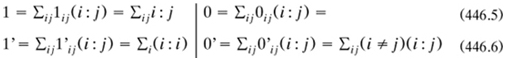
(pp. 24–26). The empty space in (446.5)2 follows Schröder on p. 26, with a reading of the relative as (another) ‘nothing’; but he did not resolve the issues raised of empty names. ‘1’ij’ is in effect the Kronecker delta, recently introduced in Kronecker’s lectures in Berlin (§3.6.4); Schröder seemed not to know of this, but he presented his coefficient in the same way on p. 405.
Duality was again prominent, the topic of much of art. 6 and elsewhere with the use of dual columns. For example, Schröder defined this pair:
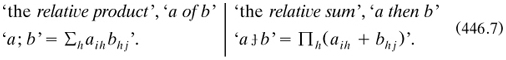
(pp. 29–30: their own duals, ‘Transmultiplication’ with ‘∏’ ‘Transaddition’ with ‘Σ’, were introduced on p. 278). Quantification was also well to the fore, with explicit use of mixed types, especially on p. 41 this important case on reversion of order:
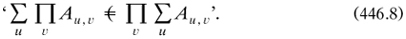
Among other examples, he devised a classification of many kinds of relatives by five-string characters, each one with its dual or serving as self-dual (arts. 15–16).
In his opening paragraphs Schröder also promised to take note of Dedekind’s booklet on integers. He devoted a very appreciative Lecture 9 to the theory of chains reworked in terms of relations and their subsumption. This may seem a misunderstanding, but we recall from §3.4.2 that Dedekind himself had worked mostly with parts and wholes and in fact had not individuated membership. The treatment of mathematical induction omitted Dedekind’s deep theorem on definability but included a reworking of parts of the theory in terms of iterated (mathematical) functions and functional equations (one of Schröder’s other interests). Later, Lecture 12 on transformations began with a general classification and presentation (art. 30) before focusing upon Dedekind’s kind of ‘similar’ isomorphisms between ‘systems’, called on p. 587 ‘one-one’ (‘eineindeutig’). In the preface to the second (1893) edition of the booklet, Dedekind had praised the first two volumes of Schröder’s book, and made notes on them (Papers, File III, 30); he then acknowledged priority in 1897a, 112 in the context of the law of distributivity (compare 1900a, art. 4). The overlaps lay mainly in collections and in lattice theory, especially in Schröder’s fourth and sixth appendices; Dedekind does not seem to have responded to Schröder’s theory of relatives.
As with the second volume, the reaction was slight, although once again Schlegel 1898a took six pages in the Jahrbuch to give a warm and rather nice survey of the main notions and methods, and the reworking of Dedekind. More penetrating, but also much more rambling, were a pair of papers by Peirce.
4.4.7 Peirce on and against Schröder in The monist, 1896-1897. Peirce’s venue was a journal launched by the zinc millionaire Edward Hegeler, a German immigrant who had founded the Open Court Publishing Company initially to publish translations of books in and on German philosophy and scholarship. He also started the journal The open court in 1887 partly to sustain this aim; the translation 1892a (§4.4.2) appeared there. The monist was launched three years later, with a rather broader remit, and it became recognised internationally; for example, in the 1910s it was to be an important venue for Russell (§8.2.6). The editor was a fellow immigrant, the philosopher and historian Paul Carus (1852–1919), a former student of Grassmann and later a son-in-law of Hegeler.23 At this time he published both an article by Schröder (§5.4.5) and, after some difficult correspondence, two pieces on Schröder by Peirce.
Although footnoted as reviews of the third volume, Peirce’s papers, his first on logic since 1885a, were commentaries on Schröder and Peirce, together with various other things of current interest. The first one, 1896a, carried the optimistic title ‘The regenerated logic’; while Schröder’s volumes were a main source, he criticised them on various points. Concerning the propositional calculus, the main one was to reject Schröder’s distinction between categorical and hypothetical propositions, since all propositions could be cast in the latter form (p. 279). He also discarded Schröder’s assignment of a time-period of validity to hypothetical propositions, since ‘Every proposition is either true or false’ and ‘“this proposition is false” is meaningless’ (p. 281). But his main preoccupation was with the ‘quantifier’ (p. 283); he disliked Schröder’s use of quantification of the predicate, because it stressed equations rather than ‘illation’ (or inference: p. 284).
Similarly, in his second commentary Peirce 1897a queried Schröder’s keenness to find equational solutions of logical premisses, and the merit of finding algebraically general solutions rather than considering their bearing upon logic itself, because solution and premiss could equally be reversed (pp. 321–322). He appraised as Schröder’s ‘greatest success in the logic of relatives’ (p. 327) the classification by five-string characters; the patronising tone is easy to detect. Among other topics, he touched upon his existential graphs, commented upon Kempe (whose reaction was quoted in §4.2.9), and ended with some unoriginal remarks on Cantor’s diagonal argument.
Despite nearly two more decades of intensive work to come, these commentaries were Peirce’s last papers on logic, a subject which he defined rather surprisingly as ‘the stable establishment of beliefs’ 1896a, 271.; apart from illustrating his existential graphs, they are far from his best. They also show differences between the two algebraic logicians, Schröder driving the algebra hard while Peirce preferred the logic. In 1893 Schröder had told Carus how difficult it was proving to prepare this third volume, with the first two ‘pure children’s games’ by comparison24; he must have been disappointed by his mentor’s reaction.
4.4.8 Schröder on Cantorian themes, 1898. Following traditional logic and Peirce in particular, Schröder always used the part-whole theory of classes in his logic; but outside it he studied aspects of Mengenlehre closely. In particular, he considered Cantor’s and Peirce’s definitions of infinitude in a long paper 1898c expressed in his logical symbols. One section treated simply ordered sets, largely following Burali-Forti 1894a (§5.3.8); another treated equivalent sets, with his proof of the theorem named after him and Bernstein which we saw in §4.2.5 was faulty. He ended with a hope for a general recognition that ‘algebraic logic is an important instrument of mathematical research itself.’
In a shorter successor Schröder 1898d restated from his book the concept of the cardinality of a finite manifold; for example, for (445.14),
Further thoughts on relations at this time led him to rethink his views on the relationship between mathematics and logic; we shall record the outcome in §5.4.5, along with Peano’s reaction, in connection with Peano’s review of his book.
Although these papers were published by the Leopoldina Academy in Halle, Cantor’s town, their relationship was not warm. Both men had also placed papers recently in the same volume of Mathematische Annalen—Schröder 1895b on relations applied to Dedekind’s theory of transformations, then Cantor 1895b as the first part of his last paper on Mengenlehre (§3.4.7)—and both corresponded soon afterwards with editors. Schröder told Klein in March 1896 of ‘Mr. G. Cantor, from whose geniality I am far distant; to want to place my modest talent in comparison, he has occupied himself with his own researches, although a deepening of them always hovers for me as a desideratum’.25 Exactly a year later Cantor told Lazarus Fuchs, the editor of the Journal fur die reine und angewandte Mathematik, that ‘in my opinion the sign language of the logic calculus is superfluous to mathematics. I will not regret it, if you do not publish the relevant papers in your [Crelle’s] journal’.26
4.4.9 The reception and publication of Schröder in the 1900s. One of Cantor’s firm admirers was Couturat, who enthused over the definition of continuity, and of well and simple order in a piece 1900b in the French philosophical journal the Revue de métaphysique et de morale (his favourite watering-hole, as we shall see in §6 and §7). But earlier in the same volume he was sceptical about Schröder’s handling of integers both in the book and in the recent papers. Schröder’s definition (445.11) of an individual as incapable of being part of two disjoint classes surely ‘is prior to the definition that one gives’ of 1 in (446.5), so that a vicious circle arose (1900a, 33). He also doubted that a nominal definition of integers were possible, and wondered if the use of notions such as isomorphism in Dedekind’s theory of chains, which had inspired Schröder, really was logical.
At the same time but in different mood, Couturat presented a warm and extensive two-part review 1900c of Schröder’s volumes in 40 pages of the Bulletin des sciences mathématiques. Mostly he just described the main features, since they would not have been familiar to most readers. He concluded the first part by praising the definition of the individual, and stressing that an ‘algorithmic calculus’ of deduction was now available. Presumably his doubts noted above arose between preparing the two parts, for he cited them at the end of the second part. By 1905 he found great fault in Schröder’s conflation of membership and inclusion, describing it in a letter to Ladd-Franklin as a ‘colossal error’.27
As was mentioned in §4.4.1, after Schröder’s death Eugen Müller edited the second part of the second volume in 1905, and prepared the Abriss in two parts (Schröder 1909a, 1910a). This travail was effected on behalf of a commission set up by the DMV to handle Schröder’s Nachlass. According to his forewords, Müller seems only to have had to edit the first part but to write much of the second. He ran through most of the main ideas of the first two original volumes in welcomely crisp style, with the newer ones rather more evident in the second part. One was ‘normal form’ (‘Normal-formen’), products of sums for functions of domains and of logical expansions (arts. 110–111, 153–154); this term may have come from its use in the theory of determinants, and/or maybe from Hilbert (§4.7.5). He also twice cited Löwenheim 1908a on somewhat similar forms of solution (arts. 117, 127), an early piece written by one of Schröder’s few admirers outside his circle (§8.7.5). Presumably the announced third part would have covered relatives; but it never appeared, maybe because Müller’s teacher Lüroth, another member of the commission, nicely summarised the theory in a long essay 1904a in the Jahresbericht, soon after his obituary 1903a there of Schröder.
The posthumous part of Schröder’s second volume began with a reprint of this obituary, and then contained three Lectures appraising events ‘since the appearance of the first  volumes’ (1905a, 401). The main topic was a disagreement with Ladd Franklin’s criticism of him on negative judgements in her review of the first volume; his reply constituted a rather ponderous wallow through negated propositions of various kinds (art. 53).
volumes’ (1905a, 401). The main topic was a disagreement with Ladd Franklin’s criticism of him on negative judgements in her review of the first volume; his reply constituted a rather ponderous wallow through negated propositions of various kinds (art. 53).
Despite all this effort, Schröder’s logic made little impact outside the commission members, and the Abriss was much of a tombstone. Further, all of his Nachlass seems to have been destroyed during the Second World War: the part that Müller had held was lost in a bombing campaign of Frankfurt am Main in 1943 that also eliminated Schonflies’s, and the rest was destroyed with Frege’s (§4.5.1) two years later at Münster.
Apart from this loss, it is not easy to assess the longer-term influence of Schröder’s book. It was the only compendium on algebraic logic, Peirce’s contributions being scattered among several papers and some difficult to follow anyway; and the theory interested algebraists as well as logicians. But direction and strategy is often hard to determine; and the length and expense cannot have encouraged sales anyway. Maybe it was a pity that he paid for publication himself; had Teubner picked up the bill, they might have asked for a much tighter text. In 1912 J. N. Keynes opined to Ladd-Franklin with typical Cambridge snobbery that it ‘is rather full of German stupidities, but the core is sound’ (her Papers, Box 73). At all events, the algebraic tradition of logic of which Schröder and Peirce were the chief representatives was largely to be eclipsed in the new century by the mathematical logic of Peano, Whitehead and Russell—and of Frege, whose contributions are reviewed in the next section.