8.6 PERIPHERALS: ITALY AND FRANCE

8.6.1 The occasional Italian survey. Italian interest faded during the 1910s as Peano switched interest steadily more to international languages, though we saw his work of 1913 in §8.2.4. But one lingering worry concerned the clash between Peano’s method of definition of cardinals by abstraction and Russell’s nominal definition by classes of classes (§6.5.2). Burali-Forti 1909a had proposed, as a third option, definitions of function(al)s of ordered pairs ‘(a;b)’ of ‘simple entities’ a and b, such as arithmetical operations on numbers, or (Russellian) classes of ordered pairs of integers. One of Peano’s minor followers, Eugenio Maccaferri (1870–1953), took up this idea to suggest that if members x and y of a class u satisfied an equivalence relation α, then each member of the corresponding equivalence class v was a function ϕ of some member of u, so that

(Maccaferri 1913a, 165; on p. 167 he specified the second ‘=’ as logical equivalence). Then this kind of definition could be based on appropriate α and ϕ; for example, for integers 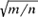under equality of rational numbers m/n or n/m as ordered pairs, or of numbers of the form Further, the classes defined this way were clases of classes, so that Russellian definitions could be expressed; in particular, Russell’s definition of irrational numbers (p. 169).

The most substantial Italian item of the 1910s was the second edition 1919a of Burali-Forti’s textbook on ‘mathematical logic’, published in his late fifties. We saw in §5.3.7 that in 1894 the first edition had been a slim but pioneering work; now at over 480 (small) pages it had more than trebled in length. The five chapters covered, in turn, ‘Ideographical symbols’ for mathematical logic and set theory, still basically Peanist; ‘Operators and connectives’, including some attention to the axioms of choice; ‘Ideographical algorithms in general’, with syllogistic logic and the calculus of classes; ‘Definitions’, nominal (maybe under hypothesis), or by abstraction or induction; and finally and briefly ‘Some applications’, to real and complex numbers, and point-set topology. Theories not Peanist were not well received; already in the introduction, ‘the method of relation, that, like foreign goods, is received at once in Italy’ such as ‘the chaotic and imprecise geometrical system of HILBERT’ (p. xxxii) despite the existence of the ‘superior’ version of Mario Pieri (§5.5.5). He disparaged ‘such empty discussions’ of non-self-membership of classes (p. 84), incorrectly gave Russell’s definition of cardinal 0 (pp. 355–357) and dismissed as ‘impossible’ that of 1 (p. 167), and found it ‘more simple and more common’ to take relations as operators rather than a Russell-style primitive (pp. 226–227).

The book did not circulate well, perhaps due to the poor economic state of Italy after the Great War, which may have also inspired the bitter tone. However one reader was Enriques, who published a suite of comments 1921a in Periodico di matematico; Burali-Forti 1921a responded, exciting a reply Enriques 1922a. Among the issues, Enriques preferred to distinguish a class from an abstract concept, rather than membership from inclusion in order to cope with ‘apostle ⊃ twelve’ (in Peanese): Burali-Forti rejected the latter on the ground of simple entities not being classes, and, attending to second-order predicates, he related apostlehood to dozen-ness. He also retained the non-identity of an object with its unit class, which did not assuage Enriques’s puzzlement over the role of identity in Burali-Forti’s book. Enriques also questioned the form of definition by abstraction, citing Maccaferri while regretting the use of disjunction to specify class abstraction; Burali-Forti cited his paper 1912a on abstracting a class without characterising the members. On the status of mathematical induction and the legitimacy of the axioms of choice, Enriques’s nominalism split him from his colleague’s contented realism.

At this time Enriques was completing a history of logic, deductive and inductive, from antiquity to modern times. Much broader a book but shallower than Burali-Forti’s, it became far better known, with translations into French, German and (American) English within the 1920s. He rather mixed algebraic and mathematical logics together, with Peirce and Schroder under-represented. Russell’s contribution was found to be ‘refined and profound (perhaps in places too subtle)’, a judgement which Enriques verified by mistaking a proposition for a propositional function (1922a, art. 18).

8.6.2 New French attitudes in the Revue. While interest in logicism remained sporadic, the situation among French authors changed: the polarity between sneers from Poincare (died 1912) and applause from Couturat (died 1914) was replaced by more neutral positions, even in the Revue de metaphysique et de morale. Its co-founder, the idealist philosopher Leon Brunschvicg (1869–1944), preferred in 1911a intuition among current philosophies of mathematics, especially as handled by Poincare (pp. 165–169); he distrusted dogmas such as Ockham’s razor, and did not welcome logicism (p. 146). But a softer line came through the following year in his large book surveying various stages in the development of philosophies of mathematics. Of its seven Books the sixth was devoted to ‘the logistic movement’. Its 58 pages began with a short treatment of Boole’s methods before passing to Frege’s programme and especially Russell’s, where he clearly indicated the prime influences of Cantor and Peano (Brunschvicg 1912a, 381–383). But at the end he was sceptical of Russell’s empiricist ‘realism’ in both epistemology and logic: ‘it is on the terrain of positive science that the positive mathematical philosophy must be placed in future’ (p. 426). To stress his own position he devoted his long last Book to the need for intuition and psychology in mathematics when, for example, understanding complex numbers (pp. 542–550). As in many such writings, there is an unresolved tension between the philosophies of grounding mathematical theories and of creating them.²⁶

In his survey Brunschvicg drew upon the first volume of PM, which was reviewed in a mathematical journal by Henri Dufumier 1911a. Far from the Poincaresque sneer, he praised the enterprise, even pointing out the need for the axioms of choice, unusual among the reviews. He continued more amply in this manner in a ‘critical essay’ for the Revue of both the volume and Russell’s Philosophical essays; applauding both the ‘courageous precision and solid originality’ of the logic and ‘the originality and profundity’ of the epistemological enterprise (1912a, 539, 564), he underlined the respect which he had already shown in that journal in 1909 (§7.5.1).

Padoa renewed his crusading efforts for Peano’s programme with a septet of lectures at the University of Geneva, which the Revue published at over 100 pages and also in a separate book version (Padoa 1911-1912a). To the latter Peano 1912a contributed a preface reporting Padoa’s lecture courses since 1898, not only Brussels (§5.4.6) and Rome (§5.5.4) but also in Pavia, Padua and Cagliari. Padoa’s title promised ‘Deductive logic in the latest phase of development’, thereby updating the (scrappy) survey Vailati 1899a there (§5.4.6); but in fact he largely told the story as known in Turin for a long time. He explained most of the symbolism (though rather little on quantification), and made applications to syllogistic logic rather than to logicism or even Peano’s programme. But he gave an able and clear account; and its length and manner of publication shows the maintained French interest.

Some years later another rehearsal appeared there: a posthumous piece Couturat 1917a, taken from his uncompleted ‘manual of logistic’ (§7.4.1). Written seemingly around 1906, it covered so much of the same ground as in Padoa’s lectures that the publication seems unnecessary. In the same volume another Swiss connection appeared, when Arnold Reymond (1874–1958) (§7.5.1) considered ‘the transfinite ordinals of Cantor and their logical definition’. He did not cite Padoa’s article, which would have helped his chatter; his logic depended only upon the notions of individuality and plurality, so that PM was absent. He mentioned the 1914 Paris Congress, upon which he had reported (§8.2.2), and he also cited Richardson and Landis (Reymond 1917a, 695, 700).

Reymond also mentioned a recent essay on ‘geometric proof and deductive reasoning’ by Louis Rougier (b. 1889). Rather unclearly, Rougier relied upon syllogistic logic if possible; but he also presented many features of mathematical logic, including relations, and stressed the role of definitions and ‘formative principles’ such as axioms to furnish existence theorems (1916a, 613–619). He thus opposed the position of Poincare on geometry, a topic to which he later devoted a book; but there he was in line with his master, with the dispute with Russell of the late 1890s (§6.2.3) receiving only a few lines at the end (Rougier 1920a, 197–198).

8.6.3 Commentaries in French, 1918–1930. In his Revue essay Rougier also differed from the Lyon philosopher Edmond Goblot (1858–1935), who published a large Traité de logique in 1918, after delay caused by the War. In his preface Goblot explained that ‘logistic’ would not be addressed, since he wished to treat ‘reasoning in general and not just mathematical proof (1918a, xix), which for some logisticians begged questions. The chapters on ‘deductive reasoning’ were driven by syllogistic logic and Kantian concerns, together with doubts over Poincare´’s claims for the generality of mathematical induction (pp. 257–272).

Goblot’s silence on logicism reflected the decrease in Francophone interest, over several years. However, the volume for 1922 of the Revue contained both Nicod highly praising both Russell’s logic and philosophy as ‘This glory of logical and mathematical reasoning’ (1922a, 84) and, in an issue devoted to ‘American thought’, Lewis 1922a surveying both traditions of symbolic logic up to and (briefly) including his own modal version.

Belgium came into the story in the mid 1920s, when Robert Feys (1889–1961. published two 85-page three-part articles in the Catholic Revue néo-scholastique de philosophie. In the first one, 1924-1925a, he treated ‘the logistic transcription of reasoning’, but rather under-stated the differences between the algebraic and mathematical traditions; he touched upon modalities (art. 9). Not surprisingly, he concluded that logistic ‘does not seem to have revolutionised logic’ because it was ‘founded upon essentially different PRINCIPLES’ (art. 14). The second article, 1926-1927a, dealt specifically with the bearing of ‘Russellian logistic’ upon reasoning; here he was more detailed and positive, and also more up to date in noting Sheffer, Wittgenstein, Nicod (arts. 9–12), Lewis, and the first volume of the second edition of PM (especially in arts. 17–20 the new theory of predicative functions). But he said little on the paradoxes, logicism or Frege; and nothing on Russell’s epistemological writings, though they bore closely upon his interests. Thus the impression was inconclusive.

The Polish mathematician Stanisłav Zaremba (1863–1942) contributed a short book 1926a on ‘the logic of mathematics’ to a Gauthier-Villars series of short monographs similar to the Cambridge tracts for which Whitehead had written (§7.6.2). He largely followed the Peanist/PM lines, except for muddling in algebraic logic in places; and in a section on the theory of proof he outlined the algebra of classes but judged the logic of relations to be irrelevant (pp. 45–47). The most original contribution, inspired by Poincaré’s warning over impredicativity (§7.4.5), was to interpret Russell’s paradox as proving the theorem that to any class E of classes there corresponded another class which did not belong to E; thus there was a notion broader than class, which he called ‘category’ and to which this theorem itself applied (pp. 11–15). Further, type theory was ‘unsustainable’ for stratifying only classes (p. 44). We shall find in §8.8.4 something more substantial from a former student of Zaremba, and in §9.6.6 that he gained at least one brilliant reader.

Intuitionism rather than logicism inspired various authors to short exchanges, especially in the 1926 volume of the Revue; Borel reproduced them two years later in the new edition of his textbook on the theory of functions (§4.2.2), as an appendix ‘for and against empirical logic’ (1928a, 254–278). In Switzerland Ferdinand Gonseth (1890–1974) produced a book on ‘the foundations of mathematics’, concentrating on geometries, general relativity and intuitionism. Logicism was rejected because numbers needed experience for their ground whereas logic did not (Gonseth 1926a, 186); so it was almost entirely ignored in the final chapter on ‘mathematics and logic’.

Among new authors Albert Spaier (1883–1934), a phenomenologist by inclination, produced two long books on ‘thought’ in 1927. One, his doctoral thesis 1927a, was a survey of psychological notions, such as consciousness and intuition. A short section near the end dealt with ‘construction of mathematical concepts’, but none too valuably, since his claim that numbers formed ‘the basis for all mathematics’ was followed by examples from plane geometry (pp. 383–400). The second book was a lengthy discussion of number and quantity as handled not only by Russell (more The principles than PM) but also by Frege and Hilbert among others. Anxious to give experience an important role in a study of ‘existential questions’, he regarded Russell’s logical definition of cardinals as ‘some illusion’ since no concept was provided for the intuition to grasp (1927a, 12); however, he misunderstood it in stating that all numbers were ‘equally infinite’ in using classes of classes, and also for assuming order when successively deploying operations (p. 184).

Finally, Jules Tricot produced a ‘treatise’ handling ‘formal logic’ quite nicely, based largely on traditional logics (including quantification of the predicate), with Goblot a main cited author. But ‘Logistic and the algebra of logic’ appeared in only the last 10 of his 317 pages, and was judged as ‘a very special discipline’ of which ‘their very foundation is vicious’ (1930a, 306, 312). He did little more than list its principal authors (Whitehead not at all), and none of their works appeared in his bibliography—not even the recent French translation 1928a of Russell’s popular Introduction.

Both French and Italian authors took some note of recent German writings on logic and the foundations of mathematics. We shall now do the same.

8.7 GERMAN-SPEAKING REACTIONS TO LOGICISM, 1910—1928

Different countries, different scale of reaction, and quite a different philosophical climate. This section briefly notes some of the reactions to (or ignoring of) mathematical logic and logicism, in an environment where Kantian and/or Hegelian traditions still reigned strongly, so that logic was usually regarded as analytic and mathematics synthetic, and intuition played a significant epistemological role. For some philosophers symbolic logics were irrelevant; for example, Wilhelm Koppelmann in the 700 pages of his two-part Untersuchungen zur Logik der Gegenwart (1913–1918). In a book on ‘Symbols’ Richard Gatschenberger (b. 1865) regarded the ‘giant work’ PM as a ‘formula-cemetery’ involving an ‘elimination of the calculus of classes’ (1920a, 121). The young Martin Heidegger (1889–1976) noted the first volume of PM at the end of a review 1912a of recent literature in logic: after mis-stating logicism as an identity thesis, he reasonably judged that ‘the deeper sense of its principles remain in the dark’ for the lack of a theory of judgement, and he did not bother with it later, including not in his various courses on logic.

In the account to come the words ‘(neo-)Kantian’ and ‘phenomenology’ are broad characterisations of the positions of the authors described, although often they are pretty exact. Logicism features explicitly only in §8.7.3 with Frege, and then primarily with his rejection of it; however, the logic of PM appears quite regularly, and some mathematical features such as the definitions of integers. Several of the papers cited, especially by Hilbert and Brouwer, are translated into English in Ewald 1996a and/or Mancosu 1998a.

8.7.1 (Neo-)Kantians in the 1910s. Paul Natorp (1854–1924. produced a book-length survey 1910 of ‘the logical foundations of exact knowledge’. He followed a brand of neo-Kantianism in which ‘pure thought’ and logic were distinguished from mathematics; but he was not hostile to Russell or predecessors such as Cantor and Dedekind, who were treated in some detail (chs. 3–4). Patriotically he found Frege’s work ‘essentially reproduced in Russell and Couturat’ (p. 114). The range of mathematics treated was wide, including foundational, pure and applied branches; but the insights into logic and set theory were shallow, as Jourdain 1911b showed in a review for Mind.

Much more impressive a neo-Kantian was Ernst Cassirer (1874–1945) (Ferrari 1996a). Also in 1910, he published an extensive study of Substance and function, to quote the title of the English translation which Open Court published in 1923 (and cited here). He saw science as structured by concepts drawn actively from reality rather than imposed by it. His title took up the balance between substance, ‘to which the purely logical theories of Aristotle have reference’, and ‘logical relations’, to be expressed by functions and avoiding defective ‘psychology of abstraction’ (1910a, 7–21); in the Marburg school, to which he belonged, thought was preferable to sensibility wherever possible. Mathematics was an essential component of the processes required, especially for creating general laws and concepts (ch. 1); his first example was ‘the concept of number’ (ch. 2), where he stressed the logic of relations as embodied in Dedekind’s definitions and brought out by Frege and Russell. He then proceeded through geometry and space to physics and chemistry, and in a supplement of 1921 he added ‘Einstein’s theory of relativity’. The rest of the book was philosophical, treating (scientific) induction and ‘the concept of reality’, and relations in more detail.

We noted Cassirer in §7.5.2 as a commentator on Russell’s logic; here Russell appeared mainly though rather incidentally in the chapter on numbers, as treated in The principles (PM had not yet appeared), alongside Frege’s Grundlagen and Dedekind’s booklets. Russell was cited mainly for the logic of relations (on which, curiously, Cassirer did not draw) and the definitions of cardinals (especially on pp. 50–54 over the relationship between cardinals and concepts, with particular reference to 0 and 1). On real numbers Dedekind gained prime place (pp. 58–62). More attention was paid, however, to Cantor, and to Frege for attacks on Mill and on (symbol-writing) formalists. Surprisingly, he did not cite any Peanist or algebraic logician.

Less inspiring is Hugo Dingler (1881–1954). After studying mathematics at Göttingen with Hilbert and Klein, he wrote at length on Mengenlehre. In a pamphlet 1911a on ‘Burali-Forti’s antinomy’ he made a rather fine distinction between ‘contradictory’ concepts to which no objects corresponded, and non-contradictory ones for which however allied assumptions led to trouble. Regarding reductio ad absurdum proof methods as typical of the second kind, he argued, for example, that that antinomy was such a proof against the assumption of the existence of the series of all ordinals (pp. 5–9); he also analysed Zermelo’s recent two proofs of Cantor’s well-ordering principle (§4.7.6) from this point of view (pp. 10–17).

Dingler rehearsed some of this material in his Habilitation 1912a written at Munich University (where he was to make his career for twenty years), in which he discussed well-ordered and ‘scattered’ sets in general. His analyses were largely based upon Gerhard Hessenberg and Hausdorff respectively; ‘scattered’ (‘zerstreut’) came from Hausdorff 1908a, defining a point set which contained no dense subsets (see §7.9.5 for context). Dingler made papers out of both parts of the thesis; for the Deutsche Mathematiker-Vereinigung (hereafter, ‘DMV’) he took many of the paradoxes, including Russell’s and Richard’s, to be reductio proofs of impossible situations within a ‘logical building’ of axioms, theorems and rules of inference (1913a, 308).

So far so fairly good, though not always competent; Dingler inserted a sticker into his pamphlet disclaiming its last section, on consequences of his position for Cantorian limit ordinals. A short book 1915a on ‘logical independence in mathematics’ looked no better; he explored the foundations of arithmetic and ‘infinite processes’ and a few aspects of mathematical analysis, as ‘an introduction to axiomatics’. However, while he dedicated it to Hilbert, he followed the paper-formalism attributed to Johannes Thomae (§4.5.9), as Löwenheim 1922a noted in a very cool review for the Jahrbuch. Some Mengenlehre featured in the account, and consistency was deployed; but no mathematical logic appeared, even though he outlined ‘relation-arithmetic’ (pp. 73–75). A later book on the foundations of physics included a 70-page chapter on logic (1923a, 43–113); but the main notion was that of concept, with much space given to simplicity (such a complicated idea). Algebraic and mathematical logics were taken together; set theory, as used by Frege and Russell, formed an ‘astonishing complication’, with classes difficult to characterise as logical—including his own error over the definition of 1 (p. 83).

Dingler 1915a also warmly reviewed a recent volume proposing ‘New foundations for logic, arithmetic and set theory’. He liked many of the details involved, especially (without stressing the point) its Kantian leanings. The author was not German, but the Hungarian Julius Konig, with an incomplete posthumous book 1914a published soon after his death by his mathematician son Dénes with help from Hausdorff. We saw Konig last in §7.2.2, failing to prove Cantor’s continuum hypothesis but instead finding paradoxes of naming; they were treated here also, but in a much wider canvas. The book contains an interesting fusion of elements of logicism, metamathematics and axiomatic set theory.

König showed his philosophical inclination by starting with ‘experiences of my consciousness’ as his principal notion (pp. 1–3); but the ensuing narrative was not purely idealist or solipsist. Of major importance was ‘the experience’ of naming object B as A, written ‘A nom. B’, within a ‘thought domain’; collections of such namings led to the class-concepts’ (pp. 24–26), each one associated with ‘property-’, ‘relation-’ and ‘order-concepts’ (pp. 50–57). They were all the products of synthetic judgements, another main notion; his first title for the book had been ‘synthetic logic’ (p. iii).

Upon this framework König rebuilt set theory upon ‘logical basic concepts’ based upon the relation between experiences A and B of ‘not different from’; called ‘Isology’, it and its name were symbolised respectively ‘A id. B’ and xy’ (pp. 70–74). He built up a calculus like the propositional, using ‘’ over the corresponding algebraic symbols for connectives, such as ‘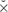’ for conjunction (pp. 70–81). Truth values ‘b’ and its contrary ‘b’ were associated with experiences by the notations such as ‘A v’; tables of them were given for simple compound propositions (pp. 81–89), but not as an equivalent for truth-tables, which had just been born (§8.3.2) The law of excluded middle came out as

where x was the name for the ‘logical form’ X (pp. 122–125), of which several were exhibited. He explicitly gave rules for substitution, using the column notation from permutation theory (pp. 92–98).

In ch. 6 König attempted an axiomatisation of set theory, after Zermelo’s but less formal. He was especially concerned to show the axiom of choice to be’proved evident, like any other fundamental intuition of logical-mathematical knowledge’ (p. 163); the reason was that the choice function created a new domain of thought and so was a synthetic judgement (pp. 166–172). Earlier in an unconvincing footnote he stated that Dedekind’s construction of an infinite set (§3.4.2) by iterated thought processes was meant only to show the legitimacy of such generation, not the existence of the set as such (pp. 62–63). The book ended with an incomplete survey of key results of set theory such as the Schroder-Bernstein Theorem 425.1 (chs. 8–9).

On arithmetic, finite and transfinite, Cantor and Dedekind were the stars; König’s theory of real numbers used dyadic expansions not unlike Frege’s (458.1), though seemingly independently (p. 206). Formalism arose in the assumption, following Hilbert, that consistency implied existence (p. iv); in the text he sought to show that it was possessed by his calculus, and by set theory in order to avoid the ‘antinomies’. They were oddly treated, in various places: Russell’s first (pp. 28–32), then the naming ones (pp. 211–214), and finally ‘the antinomy of the set of all things’ pp. 223–229, after a warm-up on pp. 149–151). His solutions broadly followed Poincare on avoiding impredicative definitions (§7.4.5) rather than limiting size.

In addition to Dingler’s review, König was also noticed by a newcomer. In a Dissertation 1918a defended at Kiel University, Georg Behrens (b. 1892) compared König, Schroder and Russell, the latter apparently a ‘Professor in London, and Professor of Logic in Trinity College Cambridge’ (p. 5); Peirce and Frege were omitted. Grouping the trio under ‘mathematical logic’, he did not fully bring out the differences between Schroder and the other two in a largely descriptive and oddly ordered comparison; thus no meticulous analyses à la Wiener (§8.2.7) appeared, although he made some nice contrasts. König featured the least (pp. 44–46, 53–54) with the logical calculus and the paradoxes, this latter topic occupying the third and last chapter. Behrens never published again in this area, not even making a paper out of the thesis; so his work was virtually without influence.

Finally, Aurel Voss (1845–1931) contributed in 1914 a long essay to a volume of mathematics edited by Felix Klein for a series on ‘Contemporary culture’. Long interested in such questions in addition to his specialism in differential geometry and mechanics (Reich 1985a), Voss considered both psychological and epistemological aspects of mathematics from a broadly Kantian perspective, with a strong historical component and fine bibliography. But his treatment of ‘the newer logistic’ was brief and disappointing, muddling the algebraic and mathematical traditions together. He quoted and rejected both Russell’s implicational definition of mathematics from The principles and the short version about not knowing what is being talked about; but he construed logicism as an ‘abstract formalism’, which smudged a distinction which Russell wished to address (1914a, 29–31). Concerning the paradoxes, he favoured limiting the size of classes, but with no discussion (pp. 88–89).

8.7.2 Phenomenologists in the 1910s. The Austrian Alexius Meinong (1853–1920), a former student of Franz Brentano, had developed a theory of reifying non-existents such as ‘round square’, to the cautious interest of Russell 1904e (§7.3.3). A main source for Russell was a book of 1902 ‘On assumptions’, and in later articles and the second edition Meinong extended it to objects of thought of ‘higher order’ (1910, 253–266). This work inspired his own former student Ernst Mally (1879–1944), who was interested in symbolic logics, especially the algebraic tradition; a short book Mally 1912a on ‘logic and logistic’ was quite close to Schröder. In a paper ‘on the independence of objects from thought’, Mally considered ‘a thought, which does not happen to itself and came to a paradox akin to Russell’s (1914a, 39–43). Soon afterwards, in a long article on ‘emotional presentations’, Meinong avoided the ‘Russell-Mally paradox’ by the principle that no higher-order object such as a class could contain ‘its own inferior’ (‘Inferius’), so that the paradox-forming clause referred to a ‘defective object’ (Meinong 1916a, 12, 10, 27). Langer was to draw a similar conclusion, from a different background (§8.5.4).

Meinong’s solution was hailed as new by a fellow Brentanian, the Viennese Alois Höfler (1853–1922), in the second edition 1922a of a treatise on logic, which was dedicated to the recently deceased Meinong. He showed much more sympathy for mathematics and even physics, with several long footnotes on their ‘logic’ and teaching. His logic was still based upon judgements and their contents within this tradition; taking the laws of contradiction and of excluded middle as basic (pp. 542–549: not exactly early on!), he relied on syllogistic procedures, including Euler diagrams and Gergonne relations (pp. 202–207, 454–460, 626–638). In a discussion of Russell’s paradox and the vicious circle principle, he noted with regret the British departure from Kant’s sense of analyticity (pp. 564–577). Mally added four passages, including detailed summaries of the axioms and principles in Schröder and in PM, and a contrast of their treatments of implication between propositions (pp. 577–592, 886–892). The range and limits of interests of this over-long but fine book are striking: Bolzano’s Wissenschaftslehre (§2.8.2) among Hofler’s influences, but nothing on Frege; concern with relations but not with their logic; attention to mathematical logic, but not to logicism.

In contrast to most contemporaries, the Halle philosopher and psychologist Theodore Ziehen (1862–1950) took Frege as a central figure in a short book 1917a published by the Kantgesellschaft on ‘the relationship of logic to set theory’. The title suggested that logic came first, but he gave much more space to set theory, through various forms from Cantor through Artur Schonflies to a recent treatment by Hausdorff to be noted in §8.7.6; his coverage included cardinality, infinitude and transfinite induction, well-ordering and the need for axioms of choice, order-types, and continuity. No logicism was offered: Russell featured only in details such as defining cardinals from similar classes (p. 23) and solving his own paradox (p. 38, paradox mis-attributed to Burali-Forti). Instead, ‘Set theory then starts, as it were, where logic stops’ (p. 24), and, as his final remark, ‘Set theory is no part of logic but its preferred daughter science, from whose inspiration many more results are to be awaited’ (p. 78). He took this view because set theory contradicted basic logical laws such as the whole being greater than the part (p. 61–63); but in a review for the Jahrbuch Paul Bernays 1922b rightly retorted that this law was not logical, at least not in the sense of being tautological, but only one obeyed by ‘extensive magnitudes’.

Ziehen returned to this topic in much greater length but rather less merit in a huge textbook 1920a on logic and its history. The 240 pages of the latter included only a short review of both traditions, though with a good bibliography (pp. 227–236). His own approach used a little formal logic in connection with Mengenlehre (pp. 410–416), but basically it was psychological and cognitive, using some strange notions which A. E. Taylor 1920a assessed as ‘almost unreadable’ in a review for Mind.

8.7.3 Frege’s positive and then negative thoughts. Ziehen 1917a exemplifies the higher level of attention which Frege was gaining in the 1910s, especially because of Russell’s publicity. In particular, for his series of articles on the history of logic (§8.2.3) Jourdain sent his account of Frege to its subject in April 1910 and received detailed comments which he incorporated into the published version (Jourdain 1912a, 237–269).²⁷ No basic change of view was presented, but Frege stressed the central place in his system of the notion of thought, independent of thinkers and their mental acts or beliefs in its truth-value (§4.5.2).

However, Frege published nothing. He drafted a reply to Schonflies’s proposed solution 1906a of the paradoxes (§7.5.2) but did not complete it (Manuscripts, 191–199); and the failure may have led him to despair of finding one. When the young Wittgenstein visited Frege in 1911 for advice about studying logic, he was recommended to go to Russell. At that time and also two years later Rudolf Carnap took Frege’s course on logic (Carnap m1910–1913a), and in later reminiscence he described more a wake than a lecture course, with the paradoxes never mentioned (1963a, 4–5). The material of the lectures included irrational numbers, and seemed to come from the third volume of the Grundgesetze; Jourdain asked after it when corresponding about his article (Frege Letters, 124–125), but it never appeared.

In 1918 Frege retired from Jena University in his late sixties, and moved the next year to the spa town of Bad Kleinen. Then he published three articles on ‘Logical investigations’ in a philosophical journal. In the first one he dealt with ‘The thought’, stressing its objective existence of a ‘third realm’ (‘drittes Reich’) separate from those of ‘things’ and of ‘ideas’ (1918a, 353) and relating it to the judgement of its truth-value (only two of those available, of course). The second article dwelt upon ‘Negation’, where he stressed that philosophical concern sometimes failed to recognise its place as an artefact of language: of the propositions ‘Christ is mortal’ and ‘Christ is immortal’, for example, ‘Where do we now have here an affirming, where a denying thought?’ (1919b, 369). He played down the action of negation in various contexts, especially in his final statement that ‘a thought clothed in double negation does not alter the truth-value of the thought’ (p. 378)—a position which Brouwer was challenging (§8.7.7). The third article appeared some years later, as Frege 1923a: failing powers are suggested by the rather pedantic run through ‘Compound thoughts’, showing how the various logical connectives produce different compound propositions to which thoughts related but not making clear the relationship of the whole to its component parts. He did not mention the Sheffer stroke, or tackle the predicate calculus.

As with his notes for Jourdain, apart from the new prominence of the concept of thought, Frege exhibited no major changes of position. However, the draft m1924b? of a fourth article on ‘Logical generality’ was much more promising, and it is sad that he was not able to complete it before his death. Wondering how language translated compound thoughts into laws of physics, he focused upon the appearance of sentences and the letters of which words were composed. This led him to distinguish the ‘auxiliary language’ (‘Hilfssprache’) in which the physical discourse is conducted and the ‘explanation language’ (‘Darlegungssprache’) in which the propositions of the auxiliary language were studied. This is the distinction between object and metalanguage, like Russell’s hierarchy (§8.4.3) but individuated mainly by Godel and Tarski later (§9.2.3, §9.6.7).

The journal where these articles were published or intended was of a right-wing persuasion; Frege’s contact was with his younger Jena colleague (and anti-Semite) Bruno Bauch (1877–1942), a neo-Kantian philosopher. In the mid 1920s, with Germany in economic collapse, Frege enthused in his diary m1924a over the rise of young Adolf Hitler. He also then wrote a sequence of short essays and diary entries which death also prevented him from developing into a book for a series co-edited by Bauch (Frege Letters, 9, 83–87). Maybe in a mood of negativism and professional disappointment, he rejected his life’s aim: ‘My strivings to bring light to the question as to what has been attached to the word “Number” by its particular number-words and number-signs, seem to have ended in a complete lack of success’ (m1924–1925a, 285). Surprisingly, the main reason lay not in paradoxes but in continuity and infinitude. Proposing three distinct ‘sources of knowledge’ (‘Erkenntnisquellen’)—sense perceptions, logic and geometry with time—he claimed that only in the last source ‘the infinite flows’ (sic) where ‘infinite’ was used ‘in the proper and strongest sense of the word’, not the common sense which may mean merely ‘very many’. Apparently ‘The both-ways [‘beiderseits’] infinite time is equal to a both-ways infinite line’ (pp. 293, 294). Thus ‘Counting, coming psychologically from a requirement of trading life, has misled scholars’ (p. 297).

Frege’s appeal to geometry, space and time recalls Russell’s empiricism, such as his interpretation of the axiom of infinity (§7.9.3); but such analogies cannot be pressed hard between that committed reductionist and this enthusiastic Platonist. In any case, the consequences of Frege’s new stance for his general position are not clear; for example, the difficulty over the paradoxes remain unassuaged. The reasons for it are also murky, and surely he exaggerated a fruitful philosophy to say that ‘all mathematics is properly geometry’ (p. 297, my italics). If he had read the third volume of PM, he should have found a treatment there of continuity (§7.9.8) which could have been adapted to his system without drastic new assumptions. Was an old man, bitter over the lack of reception of his fine work, trying to throw it away now that his life would surely soon end?

Apart from Bauch and his colleague, nobody seems to have heard about the change of mind. Gottlob Frege died in July 1925, still largely a footnote to logic and philosophy.

8.7.4 Hilbert’s definitive ‘metamathematics’, 1917–1930

 

The procedure of the axiomatic method, as it is expressed here, thus comes equally to a deepening of the foundations of the individual sciences […]

Hilbert 1918b, 148

 

From obscurity to fame; for we take now Hilbert’s revival of interest in the foundations of mathematics. I avoid the common name ‘formalism’ for his position, because he never used it; we note its origins in §8.7.7. The sources for his work are of two kinds: unpublished lecture courses delivered at Gottingen University and usually edited and typed up by a follower; and papers, normally based upon public lectures. The story is very rich: only general features and aspects related to logic and logicism are treated here, though also some contributions by followers. More details may be found especially in Sieg 1990a and 1999a, Hallett 1995a and G. H. Moore 1997a.

After a dozen years largely elsewhere in mathematics (§4.7.5–6) Hilbert came back to foundations in the summer of 1917 with a course on set theory (§8.7.6); the last chapter dealt with the ‘application of set theory to mathematical logic’, of which ‘the Russell-Zermelo paradox’ was an example (m1917a, fol. 132). In September he spoke in (politically neutral) Zurich to the Swiss Mathematical Society on ‘axiomatic thought’, a lecture 1917b which became better known (including the motto above) as a paper 1918b in Mathematische Annalen. Emphasising syntax thoughout, he covered the four main features of axiomatisation: independence, completeness and consistency of systems, and to ‘the decidability of a mathematical question through a finite number of operations’ (p. 153). He mentioned a wide range of applications to both pure and applied mathematics.²⁸ One was to logic, where Frege’s ‘profound investigations’ were followed by Russell’s ‘magnificent enterprise of the axiomatisation of logic as the crowning achievement of the work of axiomatisation as a whole’ (p. 153), Bernays 1922b reviewed the paper enthusiastically and at length in the Jahrbuch, without reference to logicism.

The scale of the enterprise emerged in Hilbert’s course on the ‘Principles of mathematics’ delivered in the winter of 1917–1918; it was to be the most original of the sequence. After exemplifying the axiomatic method in detail with Euclidean geometry, Hilbert m1918a turned to ‘mathematical logic’. In a novel division, he handled the four calculi separately: propositional, ‘predicate and class’ (a short and incomplete survey of syllogistic modes, but not quantification of the predicate), ‘narrower functional’ (first-order) and ‘extended functional’ (higher-order). However, for some reason he omitted the logic of relations. Perhaps inspired by Schroder, he put forward that kind of axiomatisation of the propositional calculus, including symmetries and duality. He also drew upon ‘normal forms’, conjunctive or disjunctive, to which any formula could be reduced (especially fols. 176–182); this move simplified analysis of the main features. Consistency of the axioms was proved by assigning 0 or 1 to each proposition and its negation and showing that each axiom evaluated at 0 (fols. 150–151). ‘Completeness’, no longer carrying his model-theoretic connotation of the early 1900s (§4.7.3), conveyed two other senses: that every well-formed formula or its negation was provable, and that the addition of any non-derivable formula to the calculus rendered it inconsistent (fols. 151–153).

The paradoxes gained due attention, with a theory of ‘levels’ (‘Stufen’) of predicates proposed as the solution; but instead of the stratification of types of PM, each level contained all of its lower predecessors (fols. 213–226). In an original passage Hilbert used Cantor’s diagonal argument to show that the number of one-place predicates ‘F_n(x)’ in each nth level was not denumerable by considering the set S of those that were satisfied by only one value a of x, and treating that property itself as a predicate of the next level up; by definition, it could not belong to S (fols. 227–230). The procedure resembles that which Godel was to use in his incompletability theorem (§9.2.3); Hilbert interpreted it as a difficulty in grounding set theory and mathematical analysis in logic (fol. 229). He also proved that the definition of identity at any given level could be proved only from the corresponding one at any lower level (fols. 230–235).

This lecture course was typed up by Paul Bernays (1888–1976), who was to became Hilbert’s most important follower on foundational studies. He used it in his Habilitation m 1918a on ‘the axiomatic treatment of the logical calculus’. In fact he treated only the propositional calculus, but in a manner quite different from that of the course; in particular, he replaced Hilbert’s symmetries with the axiom system from PM, an orientation of logic towards PM which was to become standard in the Hilbert school. However, after its manner he showed that the fourth of its five axioms for propositions was provable from the others; he also distinguished axioms from rules of inference(modus ponens and substitution), and tried some other systems by replacing certain axioms by additional rules. Unusually and perhaps due to wartime conditions, this important thesis was not printed; but several years later he published a paper containing some of its main features and results, including the new definition of completeness and the non-independence result (Bernays 1926a, cited in §7.8.3).

Hilbert gave various courses on logic, foundations and/or set theory in the early 1920s, not all noted here. Bernays edited most of them, including one on the ‘logical calculus’. Based much on the course m1917a on set theory, the main novelty was a ‘start of a new founding of the theory of numbers’ (Hilbert m1921a, ch. 3), where he considered the signs used to present arithmetic. More details were given in various public lectures in 1922, from which two papers resulted.

In the first paper, Hilbert 1922a stressed the importance of axiomatics and secure foundations for mathematics, and of distinguishing signs from their referents. Using arithmetic as his case study, ‘number-signs [.. ]are themselves object[s] of our consideration, but otherwise they have no meaning [Bedeutung’ ] at all’. The theory of them was developed by rules of formation, such as setting up the compound sign ‘1+1+1’ and (maybe) abbreviating it by ‘the sign 3’ (pp. 163–164). This was the beer-mugs stance of the 1890s (§4.7.2), now formulated in terms of mug-signs and clearly meaning by ‘sign’ its ideographic sense, not any inscriptive instance of it; ‘3’, say, without concern for its font, size or printed colour (compare §4.5.9). In contrast to signs lay the properties of arithmetic proper, such as the ‘principle of complete induction’, a ‘higher level of pertaining principle’ (pp. 164–165); and to make the distinction still more important, he introduced into print the word ‘a metamathematics’ (‘Metamathematik’), which ‘serves for the securing of that’ mathematics (p. 174).²⁹ The rest of the paper was taken up with rules for the signs, and axioms and rules of inference for arithmetic (including the propositional calculus); Gothic and italic letters were used respectively, although the same sign ‘=’ acted in each theory. While not referring to PM, Hilbert must have known that many of its unclarities were removed by invoking metamathematics. But his own treatment was not always clear; he sometimes let the signs stand for their referents, such as ‘1’ for 1 (Hallett 1994a)

The second lecture-paper, Hilbert 1923a in Mathematische Annalen on ‘the logical grounding of arithmetic’, was related to a recent lecture course m1922–1923a with the same title. Here he went further, in recognising that both the sign theory and its metatheory could have axioms, and he stressed more explicitly that the latter was finitary. In addition, he grounded both quantifiers and the axioms of choice in a new ‘transfinite axiom’, which announced that if a one-place predicate ‘A(a)’ was satisfied by some object ‘τa’ then it was also satisfied by all the other applicable ones: Zermelo’s form of the axiom of choice was proved (Hilbert 1923a, 183, 191). He concluded by claiming that mathematical analysis could now be grounded ‘and that of set theory opened up’.

Hilbert’s later writings were largely individual lectures and papers, although he also gave two more lecture courses. As a spectacular case study, he sketched (but failed to complete) in Mathematische Annalen a proof of Cantor’s continuum hypothesis from the axioms of arithmetic. Among these he included the transfinite axiom in a converse form and with a new Greek letter (1926a, ax. 3): for a propositional function A(a),

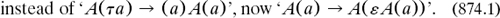
He also outlined a means of constructing an infinitude of ‘levels’ (lemma 2).

Hilbert’s crusade was popularised in 1928 by a 120-page textbook written with his former doctoral student Wilhelm Ackermann (1896–1962). The title, ‘Founding of theoretical logic’, was new, but the text was based upon three of Hilbert’s earlier lecture courses, especially m1918a; so the book carried both men’s names (Hilbert and Ackermann 1928a). A few features will be noted: their parentages are not always recorded, though m 1918a was especially influential.

The separate treatment of the four calculi was maintained: the propositional calculus was based upon the PM version as modified by Bernays, with the Sheffer stroke merely a ‘curiosity’ (p. 9). Two rules of inference were given: modus ponens, and the substitution of propositional variables (p. 23). The four main tasks of metamathematics dominated the later account, including both senses of completeness. The status of metalogic was stressed, but sometimes oddly; in particular, two propositions were ‘equal-valued’ (‘gleichwertig’, symbol ‘~’) if both were ‘correct’ or both ‘false’, while they were ‘equal-referring’ (‘gleichbedeutend’, symbol ‘aq’) if logically equivalent (pp. 4–5), so that the first notion rather than the second seems to be metalogical. Duality and normal forms were prominent, and the bibliography of principal writings included Schroder’s Vorlesungen as well as (the first edition of) PM (p. 116). Curiously, for the narrower calculus separate axioms for existential and universal quantification were given (p. 53), although negation was freely used thereafter; the names ‘free’ and ‘bound’ variables were introduced (p. 46).

The main appearance of logicism came in the chapter on the extended calculus. Some of the paradoxes were stated; surprisingly in view of Zermelo’s role, and moreover at Gottingen (§4.7.6), Russell was said to have ‘first discovered’ the one named after him (p. 93). As a means of solving them, the authors rehearsed their cumulative version of type theory, though only for functions of one variable and with the propositional hierarchy omitted (pp. 98–106). The axiom of reducibility now distanced them from logicism: a good survey of its unwelcome consequences included the theory of identity, and the manner of constructing non-denumerable classes and of defining real numbers (pp. 106–115). However, they did not seem to notice its effective dismemberment of orders.

In the same year, 1928, the latest International Congress of Mathematicians was held at Bologna. Hilbert led the German delegation at their first such attendance since the Great War, and spoke on foundational issues in mathematics in general; a revised version appeared in Mathematische Annalen as 1929a. Once again he exalted axiomatics and proposed various analyses for metamathematics, including the consistency of axiom (874.1)₂, the axioms of choice, impredicative definitions with the ‘very problematic axiom of reducibility’ of Russell and Whitehead (p. 3), and the completeness ‘of the logical system of rules’ including identity (p. 8). Mis-quoting Cantor’s motto about freedom in mathematics (§3.6.2), he repeated from the 1900s (§4.7.5) that ‘in mathematics there is no Ignoribamus’ (p. 9), a hope for completeness which Godel was soon to rebuff (§9.2.3).

Hilbert’s metamathematics was then taking prime place among the competing philosophies of mathematics, both inviting conceptual questions and stimulating mathematical techniques. His followers prosecuted the doctrine; for example, Bernays gave an elementary course on mathematical logic at Gottingen in the winter of 1929–1930 (Bernays Papers, 973:212). But he retired in 1930, and his own health went into steep decline during the 1930s; from the mid 1920s he had been suffering from pernicious anaemia. Thus, although he was still to appear in print as author (§9.6.2), his career as a researcher was largely over.

8.7.5 Orders of logic and models of set theory: Löwenheim and Skolem, 1915–1923. (G. H. Moore 1980a) Hilbert may have been influenced to stress normal forms by the use made of them in a remarkable paper in Mathematische Annalen written by Lopold Löwenheim (1878–1957). Like Eugen Muller (§4.4.9), Lowenheim passed most of his career as a school-teacher (in Berlin), and was inspired to research by Schröder’s algebra of logic (Thiel 1975a, 1977a). After some papers on the solvability of class equations in that calculus, Löwenheim 1915a continued Schroder’s way (446.8) of treating quantification as infinite con- or disjunctions; dual normal forms were even used with an infinitude of quantifiers of various orders.³⁰ Aware that this calculus was infinitary, he used infinite matrices (art. 3); he might have been drawn to them by their recent development, especially by Hilbert in connection with integral equations (Bernkopf 1968a).

Löwenheim’s main result stated that if a well-formed formula was not valid in any domain, it was also not valid in a denumerably large one (thm. 2). His proof amounted to a model-theoretic demonstration of the compactness theorem; but he did not seem to envision it as such (he cited only Schroder 1895a on the logic of relatives), although he mentioned E. V. Huntington. The proof was simplified and the consequences considered in the early 1920s by the Norwegian Thoralf Skolem (1887–1962). None of this work drew specifically on logicism, although the formulae involved lay within the calculus of PM; the closest contact came in Skolem 1923a, where, after a weak criticism of Russell’s theory of definite descriptions (art. 1), he founded arithmetic upon recursive procedures.

TABLE 875.1. Views on the character of the predicate calculi

These researches heightened the role of model theory, because of the seeming paradox of the satisfiability of axiom systems due to Löwenheim’s theorem. They also emphasised the differences between kinds of logic (first-order, higher-order, finitary and infinitary), and also quantification (Goldfarb 1979a); no agreement was found, though the desire of Skolem to confine logic to first-order and finitariness gradually became common. The various positions on the use of a logic in set theory are shown in Table 875.1. Zermelo is there for an initiative of around 1930 (§9.2.5); and PM is included, although neither Whitehead nor Russell took part in the discussion.

8.7.6 Set theory and Mengenlehre in various forms. We saw in §4.2 how Cantor’s Mengenlehre became widely adopted in the 1900s, although not normally accompanied by his philosophy. It gradually spread beyond mathematical analysis to other branches of pure mathematics and into physical applications.³¹ We pick up a few major texts from 1913 concerned with the foundational sides, with the main focus on logicism as usual. Most of the writing was in German.

In §4.2.4 and §5.7.2 we noted the two parts of Schönflies’s report on Mengenlehre for the DMV, and their influence. In 1913, his 61st year, he published a heavily revised edition of the first part 1900a; the second, on the theory of functions and related topics, was reworked later by Hans Hahn.

As before, Schonflies 1913a covered both general and set-topological aspects, but he took 400 pages for the purpose. The new edition was better organised than before and the references were pretty complete; but, like last time, he deliberately left out the paradoxes and the relationship to logic (p. v). No reason was given; and in any case it does not excuse his virtual silence over Russell in the description of well-ordering and the axioms of choice (pp. 170–184). In a similar prejudice, the Peanists were dismissed in a footnote (p. 257).

Much more significant was a treatise on ‘the basic characteristics’ (‘Grundzüge’) of Mengenlehre by Hausdorff, published the following year, his 47th (Hausdorff 1914a). We saw him praised and used in PM for his treatment of order-types (§7.9.5); here, like Schonflies, he covered both general and topological aspects of the subjects but left out paradoxes almost entirely—curious in a mathematician whose work often involved paradoxes in the colloquial sense of surprises (with some caution, Czyz 1994a). Even Zermelo’s axiom system received only a passing mention (Hausdorff 1914a, 2–3, 450, this latter one of two citations of Russell’s The principles in a rather spare appendix on literature). Dedicating the book to Cantor, Hausdorff followed him in working with an intuitive conception of sets, including the empty set (p. 3). He felt no apprehensions over the axioms of choice, mainly because he grounded Cantor’s well-ordering principle in transfinite induction (pp. 133–139); so the painstaking analysis in PM was ignored. In his preface he described his book as a textbook—a fine but daunting one, where ‘no difficulties remain and none but mild climaxes are reached’, as Henry Blumberg 1920a concluded in a long and admiring review for the AMS. Later Hausdorff produced a second edition 1927a, with title reduced just to ‘Set theory’ and text also cut down by a third, and the authority lessened (as noted in H. M. Gehman 1927a, also for the AMS); paradoxes and Russell were now absent.

However, in 1917 a new paradox had been introduced in the Swiss journal L’enseignement mathèmatique by Dmitry Mirimanoff (1861–1945), a Russian-born mathematician long on the staff of the University of Geneva. Taking any well-ordered class E containing an ‘indecomposable element e, he formed the class E of all its segments ; then E was similar to E, and had e as a member. Iteration of this procedure led him to consider descent of membership of classes in nesting segments, and especially to notice that the class α of all classes descending to e in a finite number of steps was paradoxical; for it admitted an infinite descent of self-membership, in inverse well-order: … ε α ε α (Mirimanoff, 1917a, 45–48).³² He saw his paradox as in ‘a form a little different’ from Burali-Forti’s. In a following paper, Mirimanoff 1917a reworked his approach partly under the influence of Konig 1914a, which he had reviewed admiringly in 1914a. Perhaps due to its appearance in wartime, neither Russell nor Ramsey seems to have noticed this new entry to their list of paradoxes.

A major new entrant into set theory at this time, after a first career in ring theory, was Adolf Fraenkel (1891–1965), as he signed himself at that pre-Nazi time. As well as papers, he wrote an introductory textbook while serving in the German Army during the Great War. Rejected by Teubner as part of their declining commitment to publishing mathematics (Fraenkel 1968a, 135–136), it came out in 1918 from the house of Julius Springer, as part of their rising commitment; eventually there appeared three greatly expanded editions (the inverse order of revision from Hausdorff s practise!).

As indicated in the sub-title of the first edition, ‘a comprehensible introduction in the realm of the infinitely large’, Fraenkel 1919a concentrated on the general aspects. Its 156 pages started out rather unhappily with an extensional conception of classes, so that the empty one was only ‘so-called’ (pp. 9, 13). The bulk of the 23 pages on paradoxes was devoted to Zermelo’s axiom system, but among the paradoxes, he left out (or did not know) Mirimanoff’s. However, he included Russell’s in both its class and impredicativity forms, the latter as one ‘with which mathematics has nothing to do’, apparently (pp. 132–133). Logicism was not discussed.

In an important paper Fraenkel 1922a clarified the notion of ‘definite-ness’ in Zermelo’s separation axiom by restricting the function involved to a finite number of logical operations; untypically of this ardent bibliographer, he had not (yet) noticed the anticipation by Weyl 1910a (§4.7.6). This was one of his modifications to Zermelo’s system which has led his name to be attached to it, and the acronym ‘ZF’.

Fraenkel’s second edition 1923a was now called an ‘elementary introduction’. At 251 pages, and larger ones, it followed the same structure as its predecessor, but with amplifications throughout, a much better subject index and now a name index, and more references (including Mirimanoff 1917a on p. 152). Among the solutions of the paradoxes, the axiom system was preferred, and influence from Hilbert was also evident in a new passage on the completeness of Zermelo’s system and more material on its consistency (pp. 226–241). But other solutions were noted, including eight pages on logicism and related attempts. Type theory was (too) briefly described and not welcomed, partly for its ‘arbitrariness’ and especially the ‘weak point’ of the axiom of reducibility; Konig’s book was more warmly received (pp. 182–184).

Next year Kurt Grelling published an introduction to set theory in a Teubner series of short books on mathematics and physics. Confining himself to basic properties of classes, order and transfinite arithmetic, he finished with some of the paradoxes (including Russell’s and his own); Zermelo’s axiom system was the preferred solution, with just a few lines on type theory (Grelling 1924a, 48).

Three years later Fraenkel published, also with Teubner, a short book 1927b containing ‘ten lectures on the founding of set theory’ which, at the invitation of the logician Heinrich Scholz (1884–1956) (§9.6.3), he had delivered at Kiel University over five presumably hectic days in June 1925. Logicism appeared in various places: in connection with impredicativity (pp. 26–43); and with the relationships between mathematics and logic, where all main standpoints were noted (pp. 50–56). In a careless footnote he asserted that numbers were presupposed in type theory (p. 144). Axiomatisation naturally took the main place; Russell was excluded from the lengthy discussion of the axioms of choice (pp. 88–97). Presumably the lectures were well received; in 1928 he was to move to Kiel from Marburg when Scholz took a chair at Munster (Fraenkel 1968a, 180–181).

In that book Fraenkel collected his references together in an excellent bibliography. Soon he followed this format in the third edition of his introduction, Fraenkel 1928a, authoritative if rather long at 424 pages. On the axioms of choice Russell was now noted, for his example of infinite pairs of boots (p. 345).

Fraenkel divided the paradoxes into ‘logical’ and ‘epistemological’ ones, but with Grelling’s placed in the first group; the latter was confined to those concerned with naming (pp. 210–218). Without comment he used the name ‘logicism’ to characterise the Whitehead/Russell position (in the title of the section on p. 244, explanation on p. 263): Carnap also introduced it around this time (§8.9.3), apparently independently and with a greater influence on others later. Fraenkel’s account of logicism was much fuller than before (pp. 244–268), especially the place of both types and orders in type theory; presented as an exercise in non-predicativity, he mentioned commentators on the role of the vicious circle principle, especially Poincare. Fraenkel’s attitude remained cool, including to the role now given to tautologies, which to him seemed satisfactory for logic but not for mathematics (pp. 263); but when reviewing the three main schools, he inclined towards logicism (p. 384). However, he ended the book ‘on the significance of set theory’ (pp. 388–393).

Some years earlier Fraenkel had encountered an amazing newcomer to mathematics, the Hungarian schoolboy Janos Neumann von Margitta (1903–1957). Beginning in 1923a with a new definition of ordinals using iterated nestings from the empty set, von Neumann next gave a new axiomatisation 1925a of set theory; Fraenkel refereed the first paper and proposed the second one after receiving an astounding 14-page letter dated 26 October 1923 from the lad.³³ Logicism did not feature in von Neumann’s concerns, which focused on axiomatisation and models, and so were oriented towards Hilbert’s proof theory, on which he also soon wrote a long paper 1927a attempting to prove that ‘mathematics’ was consistent. PM was mentioned right at the end, where he claimed that consistency had been proved for that system ‘without’ the axiom of reducibility.

Another and older newcomer was Paul Finsler (1894–1970), supplementing a noted career in differential geometry. In his inaugural professorial lecture of 1923 at Cologne University, published by the DMV as Finsler 1925a, he wondered ‘are there contradictions in mathematics?’; after a review of all foundational traditions of that time, he concluded that circular definition was the true cause of malady, not only Russell’s paradox but even Cantor’s 1895 general definition of a set. However, he followed Cantor in the consistency-implies-existence kind of formalism, and Platonism over sets (§3.6.1). He wished to confine them to ‘pure’ ones containing only their own kind as members with the empty set as basis (hence a combinatorial aspect came in), and began his construction in a paper 1926a.

Like von Neumann, Finsler took no special notice of mathematical logic or of logicism. Unlike von Neumann, his approach was not well received, and it has been neglected until recently, with editions and discussions of these writings (Finsler Sets, Essays). No set theorist, not even Fraenkel, bothered about Kempe’s multisets.

8.7.7 Intuitionistic set theory and logic: Brouwer and Weyl, 1910–1928. (van Dalen 1999a, ch. 8) However, Fraenkel took notice of another kind of set theory, introduced by the Dutch mathematician L. E. J. Brouwer (1881–1967) as a central part of his rethinking of the foundations of mathematics. His mathematical career shows two main and largely distinct parts: a)topology and dimension theory, to which he contributed brilliantly, partly by largely ignoring b)his philosophy of mathematics. Great mathematician but ghastly philosopher (and difficult person); we note here the latter two aspects.

The origins of Brouwer’s philosophy lie partly in poor understanding of certain mystical texts, and partly on a naive reading of Kant’s views on the place of intuition. He outlined his position in his doctoral thesis 1907a ‘on the foundations of mathematics’ defended at the University of Amsterdam; being printed but not really published (and moreover in Dutch), it made little impact, although it received an unusually long review in the Jahrbuch from his friend and doctoral opponent Johan Barrau (1910a). His position developed in various stages. A basic stand was to reject the law of excluded middle (hereafter, ‘LEM’), once he had disentangled it from the propositional implication A ⊃ A (van Dalen 1978a, 300).

Much concerned with point-set topology, partly in connection with topology in general, Brouwer saw the Cantor-Bendixson Theorem 329.1 as ‘fundamental’ for perfect sets (van Dalen 1999a, ch. 8; Hesseling 1999a). However, he wished to reprove it: Cantor’s proof had used the Ωth derived set of a set, where Ω was the initial ordinal of the third number-class, which young Brouwer had decided did not exist because the transfinite ordinals from ω onwards could not form a set. So with him the theorem became: ‘If we destroy in a closed set an isolated point, in the rest set again an isolated point, and so on transfinitely, this process leads after a denumerable number of steps to an end’ (1910a, art. 2, his English, non-italics inserted). In 1918-1919a he reworked Mengenlehre as a set theory with the LEM banned from the comprehension of sets but the transfinite ordinals still allowed. Then, in a three-part paper 1925–1927a, published in Mathematische Annalen, he offered a general re-founding of mathematics, based upon set theory, order and ordinals.

Brouwer sometimes allied his position to the ‘old intuitionism’ of Poincaré and Borel, though not to Kronecker (for example, 1930a, art. 1). His basic principles, some going back to 1907, were 1. mathematics was languageless, to be distinguished from any literal or symbolic presentation of it, of which there was no preferred version; 2. it needed for source only the ‘primordial intuition’ (hence the name) of time;³⁴ and 3. logic was part of mathematics, allied especially to arithmetic.

More valuably, in a footnote of his thesis Brouwer 4. distinguished between mathematics and ‘mathematics of the second order, which consists of the mathematical consideration of mathematics or of the language of mathematics’ (1907a, 61; see also p. 101). Sadly, he rarely mentioned this distinction later; but he publicised his position(s) regularly, even in book reviews. For example, despite having helped Schonflies much with the new edition of his report, he wrote a long nominal review 1914a of it for the DMV in which he concentrated on his own position. (Later, in 1930b he treated there Fraenkel’s book of ten lectures in similar manner). He polemicised against Hilbert’s position, which he came to call ‘formalism’; presumably it was intended as a criticism, for he caricatured it as the marks-on-paper-only brand of which Frege’s opponents may have been guilty but which cannot be maintained against Hilbert. In response Hilbert was vigorous (see especially his 1922a), seeing intuitionism as a dangerous successor to Kronecker’s pessimistic constructivism which he had attacked in the 1900s (§4.7.5). He tried to turn the tables by also using only finitary methods, though at the metamathematical level rather than in the mathematics itself.

One factor which greatly helped Brouwer’s cause, and probably also increased the intensity of friction with Hilbert, was that Hermann Weyl (1885–1955) became an ally after he met Brouwer in Switzerland in 1919.

Weyl had been a doctoral student with Hilbert, working on integral equations; but he had shown early interest in foundational questions. An important influence was a lecture on ‘Transfinite numbers’ delivered in Göttingen by Poincaré on 27 April 1909 and published as 1910a. Richard’s paradox suggested that classes were denumerable, whereas Cantor had shown that the continuum was not so; following his usual line (§7.4.5), Poincare had (dis)solved the apparent contradiction by pointing out that Richard’s argument used an impredicative definition while Cantor’s did not.

This lecture seems to have encouraged Weyl’s interest in foundational issues. (As we shall see in §8.8.4, he was not the only such listener to be influenced). Soon he published the paper 1910a, cited in §4.7.6, in which he clarified Zermelo’s separation axiom; it was based upon the lecture delivered at the defence of his Habilitation. He continued this line with a short book 1918b on Das Kontinuum. Motivated by the importance of the paradoxes, early on he stated the paradox of heterologicality (p. 2); however, he did not mention Grelling although he must have known of its Gottingen genesis (§7.2.3) when he was a student there, and it was and is often mis-attributed to him. For solution/avoidance he followed Poincare in adopting the vicious circle principle as fundamental and using mathematical induction to define the cardinals, and he attempted to rework in predicative form all the basic components of mathematical analysis, including Zermelo’s axiom system and the continuum, up to (but not including in detail) measure theory (Feferman 1988a). Hilbert’s system was the main guide for his logical calculus, including some notations; as far as logicism was concerned, he accepted the principle and the simple theory of types but not the axiom of reducibility, so that predication was restricted to the first order (pp. 35–37). Rademacher 1923a described the book at unusual length in the Jahrbuch.

Weyl’s opinion that ‘To formalise is indeed the mathematician-illness’, expressed in a paper on vicious circles published by the DMV (1918a, 44), and his silence over PM, show that he sought salvation in neither formalism nor logicism. Seemingly impressed by Brouwer’s construction of the continuum, more sophisticated than his own, he switched to Brouwer’s position while avoiding most of the philosophy; for example, like Poincaré he took mathematical induction as primitive (and in its normal form), and considered some consequences for applications (Beisswanger 1966a).

In a succeeding paper Weyl 1921a coined the phrase ‘foundational crisis’ (‘Grundlagenkrise’), with principal reference to the conflict between Brouwer and Hilbert; however, he did not describe a crisis as such but presented his own and Brouwer’s versions of the continuum. (Perhaps sensing weakness in the camp, Fraenkel 1925a noted differences between the two versions in a long piece for the Jahrbuch). Nevertheless, the paper was read widely, and his phrase became popular to the extent that Hasse and Scholz 1928a even planted a ‘foundational crisis’ upon ancient Greek mathematicians, for their alleged treatments of irrational numbers; this claim has long been a source of historical misunderstanding.

Among Weyl’s own occasional later contributions, a 40-page essay on ‘the current state of knowledge in mathematics’ did include logicism; while he praised the effort put into PM, he found intuitionism to be ‘an achievement of the greatest epistemological weight’ (1927a, arts. 3–4). In a contemporary book on ‘the philosophy of mathematics and natural science’ Weyl 1927a began with two chapters on logic and foundations, favouring ‘intuitive’ over ‘symbolic mathematics’ (arts. 9–10); but he ignored logicism, although type theory had been mentioned in the preceding passage on set theory. This book also received an unusually long description in the Jahrbuch, from Helmut Grunsky 1935a (by the time of its tardy publication, the editor of the journal); he did not mention the silence over logicism.

Thus the impact of intuitionism upon logicism was much less than that upon metamathematics. Brouwer mentioned PM very occasionally, and only as a system sadly using the LEM; Weyl usually referred only to Russell’s paradox, and to type theory and the regrettable axiom of reducibility. Conversely, Russell 1925a merely listed Brouwer and Weyl in the bibliography of his new introduction to PM. Ramsey referred to them occasionally and dismissively in his writings (for example, 1926a, 65–67), and made notes on Brouwer’s notion of ‘absurdity of absurdity’ in Brouwer 1925a and elsewhere, used to found intuitionistic logic (Ramsey Papers, 6–06-07). In his paper on mathematical proof (§8.5.2) Hardy 1929a dismissed intuitionism, and also mis-represented ‘formalism’ as mere marks-on-paper philosophy (he twice lectured on ‘Hilbert’s logic’ while on tour in the U.S.A. early in 1929).

The conflict between metamathematics and intuitionism was sharper than would now be recognised because then intuitionism was often identified with finitism in general. There were also personal factors: in particular, Brouwer had been a member of the editorial board of Mathematische Annalen since 1914, but Hilbert removed him in 1929 by the device of sacking everybody and inviting back everybody else. (Not everybody accepted: see van Dalen 1990a). The “betrayal” of Hilbert’s former graduate student Weyl must have raised the temperature; nevertheless, when Hilbert retired in 1930, Weyl succeeded him.

These personal aspects, ideal for coffee-time chats, increased the notoriety of the conflict, helping the eclipse of logicism. However, the number of professing intuitionists remained small. On a trip in Europe, Huntington told E. H. Moore on 28 October 1928 that Brouwer ‘has no large following in Europe, even in Holland’. Again, during the spring of 1929 Bentley spent six weeks ‘in the neighbourhood of Brouwer’ but, probably in a double entendre, reported that intuitionism ‘can easily be reduced to a patchwork of absurdities’;³⁵ in the chapter on intuitionism in his book on mathematical philosophy (§8.5.5) he was to be untypically sarcastic (1932a, esp. ch. 9). However, when outlining his philosophy in Vienna in 1928, Brouwer made some impact (§8.9.5).

8.7.8 (Neo-)Kantians in the 1920s. By far the most substantial contribution by a mathematician came from Otto Holder (1859–1937), who had been trained in Weierstrassian mathematical analysis but had since worked notably also in abstract algebra and in geometry. In addition, he treated philosophical questions, including an extended essay 1914a on the real number system concentrating upon compatriots’ theories but with Frege’s as well as Russell’s ignored: Weyl had sub-titled the paper 1918a on vicious circles as an extract from a letter to him.

Hölder presented his standpoint in 1924 in a large book on Die mathematische Methode. The title was unfortunate; as his impressive coverage shows, mathematics has methods, several of them. He included mathematical analysis, and some aspects of mechanics and physics. Set theory was quite prominent in the treatment of analysis, and in the second of the three Parts he considered the ‘Logical analysis of methods’. Largely guided by Kantian and some phenomenological concerns, he saw method as concerned with treating given concepts and proof methods as objects for study by higher-stage ‘synthetic concepts’. Not to be confused with synthetic judgements in Kant’s sense (1924a, 361), these concepts were built up from given ones by some mathematical construction; for example, the centre of mass of a given collection of mass-points, or the creation of a square upon a given line (pp. 292–297). This structuring sounds like metamathematics, and he noted similarities with Hilbert on some contexts (pp. 319–326), although his distinctions were not so clearly drawn or technically developed.

On logic itself, Holder dealt with some older questions, such as Lewis Carroll’s worry (§6.7.4) over the paradox of implication (pp. 269–272). He followed mathematical logic without deploying much of the machinery; the predicate calculus was construed in terms of ‘species-concepts’ (‘Gattungs-begriffe’), relations and judgements (pp. 247–253, 272–292). He discussed ‘Russel’ a certain amount, mainly citing The principles and Couturat 1908a, but only on specific issues such as abstraction and the continuum (pp. 260, 138). Agreeing with Natorp 1910a (§8.7.1) that ‘logistic’ was ‘a comparably subordinate province’ of mathematics (p. 5), he saw it mainly as a ‘calculus’, mixed with the algebraic tradition (pp. 272–274, including one of only two citations of Schröder).

Hölder closed with a nice appendix distinguishing ‘Paradoxes and antinomies’ (pp. 533–556). The former were just mysteries, such as dividing by zero or the odd integers being isomorphic with all integers, and Kant’s antinomies were also only ‘so-called’. The real ones were those of Burali-Forti, Richard and Russell; for this non-logicist the last was ‘at its base not mathematical’ but concerned difficulties over handling species (the rather disappointing pp. 551–552).

Hölder’s book is now undeservedly neglected; then it was well recognised, with several reviews. Wrinch 1925a in Mind found it to be too daunting to say anything useful, A. R. Schweitzer 1926a in the Monthly liked it in general but was surprised that PM was ignored, and Fraenkel 1927a in the Jahrbuch admired it at some length while querying the treatment of set theory.

Other readers included two fellow senior German mathematicians with philosophical interests. We saw in §6.4.7 that Max Pasch (1843–1930) had anticipated Russell’s theory of irrational numbers: in later life he wrote also on philosophical questions in mathematics, but his concerns lay with formation of concepts, axiomatic set theory and proofs as practised by mathematicians (hence overlapping with Holder). However, he did not consider logic explicitly, not even in a short book 1924a on ‘Mathematics and logic’, reprinting four earlier articles. He was answered by Eduard Study (1862–1930), a student of Klein who had made his mathematical mark in line geometry and invariant theory but was also concerned with cultural (including historical) aspects of mathematics. In a short book musing upon ‘thought and presentation in mathematics and science’ he took issue with Pasch on ignoring the creative sides of mathematics (Study 1928a, 5, 27). Surprised that Pasch had not mentioned ‘logisticians’, he referred to Russell in a footnote when acknowledging the great extensions made to syllogistic logic (p. 7); however, he regarded the paradox of implication (§6.7.4) as a ‘thought-error’ (pp. 32–33). He praised Holder’s book (p. 36), and also Whitehead’s little introduction 1911c (§8.2.1) on mathematics (pp. 45–46).

Hilbert’s former doctoral student Heinrich Behmann (1891–1970) published a short introduction 1927a to ‘Mathematics and logic’, in the same Teubner series as Grelling 1924a (§8.7.6). He placed a sketch of the recently deceased Frege on the cover; but he ran closer to PM in his presentation of logic and set theory, including some paradoxes and cardinal arithmetic. His innovation was notations: nice combinatorial designs to display kinds of relation, but a rather clumsy system of overmarks, sub-and superscripts for the predicate calculus (which he construed in terms of ‘concepts’). Some exercises were given at the end. In a review for the AMS A. A. Bennett 1930a preferred E. H. Moore’s notations in general analysis (§4.2.7), which led Behmann in 1931 to seek and receive enlightenment from their creator.³⁶

Behmann’s friend Walter Dubislav (1895–1937), a Berlin philosopher with mathematical training including with Hilbert, first expressed views in an unusual setting; his entries for a ‘systematic dictionary of philosophy’ prepared with a medical colleague (Clauberg and Dubislav 1922a). Under ‘Logic, mathematics’, mainly quotations from Kant, he did not distinguish ‘logistic’ from the ‘algebra of logic’ (pp. 275–279); and the latter suffered, for he followed Cantor in some detail over both ‘Menge’ in mathematics and ‘Klasse’ in logic (pp. 292–299, 249–251), giving Cantor’s definition of integers in ‘Number’ (pp. 545–557) and summarising Zermelo’s axiom system in ‘Sets, measurable’ (299–302). Even ‘Part’ was handled Cantor’s way (p. 462), with part-whole theory treated briefly elsewhere (pp. 177–178, 191–192). However, he contrasted Kantian ‘Antinomy’ pp. 26(28) with ‘Paradox’ (pp. 325–326) such as Russell’s and Cantor’s. Propositional functions appeared under both that name and ‘Function’ (pp. 175–176), contrasted in the latter entry from mathematical functions.

Logicism fared quite well, with an accurate summary of ‘Hierarchy of types’ including a warning that ‘Russel’ did not always distinguish a sign from its referent (pp. 218–220). But in a paper ‘on the relationship of logic to mathematics’ Dubislav 1926a rejected logicism on the grounds that logic and mathematics needed different axioms. However, he considered PM in a short book ‘On definition’, building upon a careful entry in the dictionary; I take the second edition, 1927a. After a list on p. 6 of much of the relevant literature (where he acknowledged advice from Scholz), he ran through four prevailing theories of definition: specification of an essence, of a concept, ‘establishment (not stipulation)’ (‘Feststellung (nicht Festsetzung.)’) of the referent of a sign, and vice versa of the latter. Then he drew upon Gergonne 1818a (§2.4.6) to discuss implicit definitions, cited Burali-Forti 1919a (§8.6.1) on definition by abstraction, and accepted Frege’s strictures (§4.7.4) against creative definitions (pp. 51–57). However, he left out both contextual definitions and definite descriptions even though, as a case study in predicativity, he listed the primitives and axioms of the propositional calculus of the first edition of PM (pp. 37, 42–46). The much revised third edition (1931) of his book is described in §9.3.5.

Lastly, in one of his finest books, Cassirer provided a massive study of ‘The philosophy of symbolic forms’ as a historico-philosophical study of signs.³⁷ In the introduction of the first volume, published in 1923 when he was in his early fifties, he explained that he wished to extend his earlier philosophy of mathematics and science (§8.7.1) to cultural studies in general. One principal device was to merge Kant’s distinction of regulative forms for knowing the world into the constitutive ones used in achieving that knowledge, calling them all ‘symbolic’ in order to emphasise the central place of signs. To meet this end he took a wide-ranging look at languages, including a survey of ‘the linguistic development of the concept of number’ which contrasted the absence of intuition in the definitions of Dedekind, Frege and Russell (but hardly linguistic definitions in the first place. with number systems in African tribes 1923a, ch. 3, sect. 3). His principal treatment of mathematics came in the third volume, devoted to ‘The phenomenology of knowledge’. In its third part, on ‘the building up of scientific knowledge’, he gave an intelligent survey of all the main foundational positions for mathematics (1929a, pt. 3). His Kantian inclinations (§7.5.2) led him to find fault with all of them; for Russell, the issue of intension versus extension, and the lack of grounding of the theory of types. He also considered phenomenology, a tradition to which we now turn.

8.7.9 Phenomenologists in the 1920s. Husserl retired from Freiburg University in 1928, to be succeeded by Heidegger; but his phenomenological school continued vigorously, although with diminished connections to arithmetic and set theory. This is well shown by two book-length articles of that time in the Jahrbuch für Philosophie undphänomenologische Forschung, which he had founded in 1913. His own account of ‘formal and transcendental logic’ included ‘apophantic analytic’, his hardly limpid name for that part of formal logic which sought conditions under which judgements could be made ‘clearly’ (that is, consistently). In this programme set theory and ‘ordinal numbers of various levels’ were regarded as ‘not apophantic mathematics’ (1929a, art. 24); so Cantor, Frege and PM were out (though Boole appeared in art. 25), and the treatment was almost entirely prosodic.

Husserl’s article finished with a short note on tautologies by his assistant and former doctoral student at Freiburg, Oskar Becker (1889–1964), who had written on ‘Mathematical existence’ two years earlier. However, Becker’s chief concern was the conflict between formalism and intuitionism viewed in phenomenological terms.³⁸ Thus both Cantorian Mengenlehre and later set theory featured quite well; but logicism was rarely mentioned, and then mainly on the shattered hopes for a logical foundation for mathematics because of the paradoxes, and on Konig’s reading of type theory as the objectification of thought processes (Becker 1927a, 446, 556–559). He gave time a high status, which Cassirer queried in a note appended to the end of his own consideration of scientific knowledge (1929a, pt. 3).

The Rostock Privat-Dozent Wilhelm Burkamp (1879–1939) published in the same year as Becker a study of ‘concept and relation’ for the ‘founding of logic’. His innovation was to take individuality as a basic notion with concept as its opposite. Thus he construed logic in terms of form rather than existence or meaning; for example, he lamented Lewis’s failure to argue for strict implication (§8.3.3) rather than its material counterpart on grounds of the ‘conceptually logical sense of the calculus’ (1927a, 173–175). Nevertheless, when explaining quantification and relating the universal to the existential he used necessity (pp. 169–172).

Burkamp considered in some detail the constructions of arithmetic by Frege (to whom he dedicated his book) and in PM. But he took Russell’s new extensionality too far in mistakenly attributing to him instead of Schroder the view that ‘Brown and Jones together are a class, and Brown alone is a class’ (p. 185). Yet when discussing the definitions of cardinals he clearly distinguished an object from its unit class, and preferred the empty class to Schroder’s empty manifold (pp. 224–229). His study of part-whole relationships included cases where parts existed only because of a pertaining whole (husband in a married pair, for example), and he also deployed Euler diagrams and Gergonne relations (§2.4.6) when discussing Schroder (pp. 190–196). A thoughtful book which gained positive reviews for its philosophical acuity (A. C. Benjamin 1927a in the Journal of philosophy, J. N. Wright 1928a in Mind), nevertheless its treatment of collections is difficult to grasp, and it did not make a large impact.

In a sequel analysis of ‘the structure of wholes’, conceived very generally with flames and ocean-flows among the many examples mentioned, Burkamp examined parts and moments. While he touched upon counting and well-ordering, he hardly used either Cantor or Russell, and took counting to be the epistemological basis for both cardinal and ordinal arithmetic (Burkamp 1929a, 37–41). Again, he was not widely read.

One welcoming reader of Burkamp’s first book was Cassirer 1929a, with several statements of praise. Another was Gerhard Stammler (b. 1898) at Halle, who soon published his own book on ‘Concept judgement inference’. Distinguishing in his foreword ‘logistic’ from ‘the algebraising tendency of the logical calculus’ (Stammler 1928a, ix–xi), he recalled as his original aim ‘to introduce the logic calculus into philosophy’, but then saw it as only ‘an exact technique of logic’. So, partly under Burkamp’s influence, he switched to a study of logicism, partly Frege’s but mainly the new edition of PM; regrettably, the Peanists were almost entirely ignored. In the second part he contrasted the two traditions as between ‘the calculation of ranges’ (‘Umfangsrechnung’) in the part-whole sense and ‘the calculating with truth-values’; and to the axioms of the latter’s propositional calculus he added one stating ‘Each axiom is true’ (p. 209). To us this newcomer is a meta-axiom, and indeed Stammler moved in the same direction, such as noting that Russell had not explicitly stated rules of substitution (p. 210). The most startling manifestation came at the end, where he noted that determining the limits of logic was an ‘extralogical problem’ (p. 294) and so raised the possibility of ‘Metalogic’. However, he rejected it, on the grounds that logic could be appraised by the trio of ‘thoughts’ of his title, which were handled in broadly Kantian styles: thus ‘There is no metalogic as extralogical grounding of logic. Logic stands for itself (p. 317). Stammler reached a major issue in logic at his time, but offered a conservative response to it. Perhaps for this reason, like Burkamp he has never gained the attention that he deserved; the excerpts above do not do justice to his book.

Among other groups, the Fries school (§4.2.5) maintained some interest. Gerhard Hessenberg came back to philosophical questions in his late forties when he took a chair at Tubingen University. He devoted his opening lecture 1922a to the ‘sense of number’, including foundational questions; but he ignored logicism and metamathematics completely, appealing to Cantor and Dedekind (p. 28) (and to group theory rather than relations for handling transformations pp. 38–45). He even spurned the notions of function and variable in handling numbers, citing Thomae’s sequence (459.1) of ‘3’s of different sizes as a counter-example (p. 37), though that had hardly been Thomae’s own point.

Some years later Grelling surveyed German ‘philosophy of the exact sciences’ for The monist; in the section on mathematics, he treated intuitionism, set theory, axiomatics such as with Pasch, and above all metamathematics (Grelling 1928a, 99–106). Typically of German authors on the foundations of mathematics at this time, the logic of PM was noted but logicism gained least attention, here none at all.

8.8 THE RISE OF POLAND IN THE 1920S: THE LVÓV-WARSAW SCHOOL

8.8.1 From Lvóv to Warsaw: students of Twardowski. New country, new initiatives: one consequence of the defeat of Germany in 1918 was the re-creation of Poland to its east, and very soon major schools of mathematicians and logicians emerged. Moreover, many of the mathematicians worked in set theory, so that links with logic could be close. This impression was confirmed in 1920 when the Poles launched in Warsaw a journal, Fundamenta mathematicae, to cover both disciplines (Lebesgue 1922a). But in fact the union was not successful; little logic appeared there, and the two co-editors for logic resigned in 1928, with little regret from the mathematicians (Kuratowski 1980a, 33–34).

Those two had become the leaders of the new school; and their background goes back to a common teacher, the Austrian-born philosopher Kazimierz Twardowski (1866–1938). Trained at Vienna largely in phenomenology under Brentano’s influence (Twardowski m1927a), he moved in 1895 to a chair at the university at Lvov, which was then the town named ‘Lemburg’ in the Austro-Hungarian Empire. While not a major philosopher (B. Smith 1994a, ch. 6), he did much to raise the professional status of philosophy in Poland to a level comparable with his home country and Germany. The university came to have a fine seminar room for philosophy, incorporating his own personal library.

Although not a specialist in logic, Twardowski taught it from 1898, including the algebraic tradition; thus it came to the attention of his many students. Two especial beneficiaries were the future leaders, Jan Łukasiewicz (1878–1956) and Stanisłav Leniewski (1886–1939). After taking doctorates at Lvov, they were given chairs at Warsaw University in 1915 and 1919 respectively. They had begun to publish before the re-creation of Poland, especially in philosophical journals which Twardowski had helped to create; but the main flowering dates from 1920.

During the 1920s, Twardowski’s students and grand-students formed the largest community in the world working on logic and related topics. Partly under his influence, they tended to start out from specific problems rather than build up large systems Russell-style, although Leniewski became such an architect later. Many of them published in their own language (which, I am told, contains many properties relevant to logic and set theory, which may have helped stimulate the interest in the first place). But, knowing that the consumption would be almost entirely local, they also published in standard languages, and abroad. Thus their achievements gradually became known, especially during the early 1930s.

However, their country came to an end with Hitler in 1939; Leniewski had died in May, and of the others several lived or died at home, or went away (Tarski to the U.S.A. just before the War, Łukasiewicz to Ireland just before its end). Many manuscripts were lost, including Leniewski’s during the Warsaw insurrection and Łukasiewicz’s later by bombing; some publications also stopped, especially the journal Studia philosophica which had started in 1935 to replace the Fundamenta for logic, and Łukasiewicz’s new Collectanea logica.

But historical interest has been considerable. The survey Z. Jordan 1945a, in English, quickly brought information, and much of it was reprinted in the English edition McCall 1967a of main papers by various authors. Since then, a new generation of students has examined the history of modern Polish philosophy in general; among products not in Polish, Wolenski 1989a is especially important (ch. 2 here), and Szaniwaksi 1989a more generally but also on the Vienna Circle. Editions of many of the works of the leading Warsaw trio (and others) have also been published, and further material is being prepared under the general direction of Jan Srzednicki. The trio occupies the next two sub-sections; in §8.8.4 we consider Leon Chwistek, not a member of the school, but upon whom Russell’s influence was the closest.

8.8.2 Logics with Łukasiewicz and Tarski. Łukasiewicz’s first book, published in his 33rd year, was an analysis 1910a of the status of the law of contradiction in Aristotle’s logic; efforts to prove it brought him to consider paradoxes, including Russell’s. As a result he tried to construct a non-classical propositional logic; success came in 1918, which he advertised twice, in a Polish journal. Łukasiewicz 1920a was a note stating a ‘three-valued logic’ in which propositions could take the values 0, 1, and 2, the latter named ‘possible’ (and later symbolised ‘1/2’). His innovation was contemporary with that of Post (a fellow Pole, incidentally: §8.3.4), but independent. In a longer successor Łukasiewicz 1921a presented ‘two-valued logic’ (a main origin for this name, by the way), so that the three-valued case could be seen as a natural extension. His use of propositional quantification followed the algebraic way as infinite con- and disjunctions. He drew upon both Peirce and Schroder, as presented in the survey of algebraic logic in Couturat 1905a (§7.4.1), which had recently been translated into Polish as Couturat 1918a; but he also adopted truth-values and assertion from Frege.

At that time Łukasiewicz met Alfred Tarski (1902–1983), Leniewski’s doctoral student (in the end his only one). Taking his doctorate in 1923 (his 22nd year), Tarski quickly published a version of it as two papers in French in Fundamenta mathematicae. Like Bernays (§8.7.4), he examined the propositional calculus, and started out from PM; like Łukasiewicz, he worked with the equivalential form (which is now known as the ‘equivalen-tial calculus’). In the first paper, Tarski 1923a defined all the other connectives from the bi-conditional, and rebuilt the calculus including universal propositional quantification. Interestingly, he cited Peirce 1885a for the origin of the word ‘quantifier’ (§4.3.8), and also interpreted the resulting formula as ‘involving logical multiplication’ (pp. 15–16). He could also replace equality by definition, a primitive notion in PM, by stating the equivalence of propositions appropriate for the defined term and the defining clause: for example, for negation, he offered

in the style of PM, where I quote his use of square brackets to mark quantification (p. 16).

In the second paper Tarski 1924a was concerned with truth-functions f of propositions, which he defined by a new ‘law of substitution’

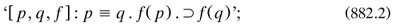
in the usual formulation f was not quantified. He found various necessary and sufficient conditions for/to be truth, noting the similarity of some to Boolean expansion theorems (255.5) (p. 29). He extended the conditions to functions of several propositions (pp. 35–37).

Tarski became Łukasiewicz’s assistant, but for the rest of the decade he published little on logic, concentrating on transfinite arithmetic and point-set topology. Łukasiewicz himself published very little, though in the note 1925a, cited in §7.8.3 with Bernays 1926a, he showed that the propositional calculus in PM contained a redundant axiom. But in 1930 professor and student came together with three papers placed with the Polish Scientific Society. Firstly, Tarski 1930a treated ‘some fundamental concepts of metamathematics’, formalising logical consequence in a Hilbertian framework; one outcome was the deduction theorem, as it was to become known. The calculus itself was deductive, not necessarily a logic, an enlargement which he was soon to stress (§9.6.7). Then Łukasiewicz and Tarski 1930a presented the propositional calculus both without and with quantification, and admitting any number of truth-values even up to ₀. They also used Łukasiewicz’s bracket-free notation for connectives based upon ‘Np’ for ‘~ p’ and ‘Cpq’ for ‘p ⊃ q’, with compound propositions expressed by concatenation and rules of binding; Łukasiewicz had developed it in 1924, following a suggestion by Chwistek, and this paper was an early appearance. Finally, Łukasiewicz 1930a defended these new calculi philosophically, using quotations from Aristotle to help. He also displayed their truth-values in ‘matrix’ form, an extension of bivalent truth-tables after the style of Benjamin Peirce’s tables (432.4).

Other students of Łukasiewicz, such as Jerzy Słupecki (1904–1987) and Mordechai Wajsberg (1902–1939), took up these new logics (Wolenski 1989a, ch. 6.; but the advance beyond two-valuedness was achieved at some pain for Łukasiewicz. News of the innovation had been circulating, but usually both he and Tarski were credited as its originators. Upon being told the truth by Łukasiewicz, Lewis 1933a corrected his own impression in a note in the Journal of philosophy; but the error generally remained in place, and clouded the rest of Łukasiewicz’s life.³⁹

8.8.3 Russell’s paradox and Leniewski’s three systems. (Wolenski 1989a, ch. 7. Leniewski’s main stimulus to mathematical logic came when he learnt of Russell’s paradox in Łukasiewicz’s book on Aristotle. He published a few papers in Polish journals up to 1916: in particular, in Leniewski 1914a he tackled Russell’s paradox by considering the relationship of the name of a class to its members (Sinisi 1976a). If K were the class of bs, then it was also both the class of classes of bs, and (the class of bs or the class of bs), and so on; he deduced that every class was subordinated to itself, Russell’s paradoxical one included. ‘Russell’s “paradox” is “slain”’, he ended, ‘Let it rest in glory!’. However, he must have realised, as Russell had long before, that this association of K with its defining property b was too simple; for example, the class of cardinal integers may be taken as the union of even numbers and odd ones, but the sub-class of, say, multiples of 7 cannot be so specified.

Another durable early reaction to PM was negative. Leniewski found the notion of assertion unsatisfactory, because as a truth-functor it muddled up a proposition p with its name; further, ‘p’ was not a proposition, so where did it belong? The consequences of avoiding assertion were profound: 1)abandon assertion and instead distinguish a language from its metalanguage; 2)shun psychological predicates such as asserting and believing, and also the abstract objects that pertained to them, and instead adopt nominalism (this in tune with a predilection for J. S. Mill’s philosophy of logic (§2.5.7) from his youth); and 3) for the same reason, treat logic extensionally as much as possible.

Leniewski deepened his analyses with a subtlety hitherto unsurpassed, and gradually evolved three doctrines. His disenchantment over assertion did not prevent him from planning a Polish translation of PM; he wrote to Russell about his intention on 12 October 1923 (RA), though nothing seems to have been done in the end. He regularly taught logic and foundations of mathematics after receiving his chair at Warsaw in 1919; but he did not go to print again until 1927, when in a long paper in several chapters, written in Polish and dedicated to Twardowksi, he repudiated several early papers (though not 1914a) in the course of rejecting assertion, appreciating the superiority of Frege over PM in the handling of quotation marks, and reminiscing about his researches generally (Le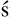niewski 1927–1931a, 182, 189–193, 198). The reception of his mature trio of doctrines was more gradual than that for Łukasiewicz or Tarski, but interest has increased in recent decades, partly inspired by the general study Luschei 1962a; Polish non-readers have been much helped by recent English translations of his writings, especially Leniewski Works.

‘Protothetic’ was described in a long essay Leniewski 1929a on the ‘Fundamentals of a new system of the foundations of mathematics’, written in German and published in Fundamenta mathematicae. Słupecki later published an extensive account 1953a based upon notes made by a colleague student of a course given in the semester of 1932–1933. Wishing to replace the propositional calculus of PM, Leniewski adopted the equivalential calculus, and extended it to quantification over (his version of) predicates; quantifiers seem again to be interpreted as con- and disjunctions. Inspired by a suggestion made by Chwistek in 1920, he developed a semiotic notational system for connectives based upon little wheels with four spokes. He could have symbolised each of the 16 possibilities, but he concentrated upon the two most important: ‘’ for the conditional, and ‘’ for the bi-conditional (pp. 456, 441). He gave various axiom systems for the calculus; it became an obsession in Warsaw to find the shortest one(s) for all calculi and to compare different versions, and in a review of this paper for the Jahrbuch Skolem 1935a noted the ‘huge set of terminological explanations’ required.

Leniewski also recorded the importance of his theory of ‘semantic categories’, created in 1922 (pp. 421–422). An extension of the theory of types in PM (but without orders) to classify parts of speech and partly developed by Husserl, it is notable at a time when logic was still usually dominated by syntax.

On ‘Ontology’, the ‘calculus of names’ based upon Protothetic, Leniewski published, again in German, only a paper 1930a of 22 often obscure pages; in compensation, Słupecki later published an extensive account 1955a, in English, based upon various student notes of Leniewski’s lectures of 1929–1930. Reacting to a question of Łukasiewicz, Leniewski developed a calculus based upon singular predication, where A ‘is’ the sole b; akin to the ‘is’ (‘jest’) in Polish, he saw it also as a refinement of part of syllogistic logic. It also resembled a special form of set theory, which he over-emphasised by using Peanese to write ‘A e b’. Finding it possible to assume only one axiom, in the Polish way he sought the shortest form, and found it in 1929. Placed at the end of his paper, it stated the transitivity of ‘is’: for all names A and b, A ‘is’ b if and only if there exists at least one C such that A ‘is’ C and C ‘is’ b.

‘Mereology’, originally called ‘general set theory’, was an extensional treatment of non-empty collections of objects, and so more in tune with Leniewski’s philosophical inclinations; he published on it in most detail, especially much of his long paper (1927–1931a, chs. 4–10). This paper was called ‘On the foundations of mathematics’, so that he imitated logicism though offering a very different underlying theory of collections. His ‘collective’ treatment of collections of objects P, Q,…followed the part-whole tradition, but handled with a new level of sophistication. The one relation, ‘part’, was given axioms such as transitivity and the assumption that if P were a part of Q, then Q were not a part of P. Collections were not objects; a class of objects was the same as the class of classes of those objects, and the empty class was no thing (pp. 215, 211–214).

Leniewski seems to have first thought of linking mereology to ontology, but then he split them; one advantage was that he could now Solve Russell’s paradox (Soboci´nski 1949–1950a, arts. 6–7). It arose because the collective formation of classes was mixed with the Ontological; when separated, at least one axiom of each theory was not satisfied, so that its construction was blocked.

In the course of developing his systems Leniewski advanced beyond Dubislav in understanding the roles of definitions in formal calculi (Rickey 1975a). In a paper written in German, Leniewski 1931a formalised the procedures used in developing the propositional calculus; for example, rules for making legitimate substitutions within well-formed formulae. He also conceived of a kind of definition which became known as ‘creative’; it aided in the proof in a calculus of at least one otherwise unprovable theorem which contained neither the defined term nor any term dependent upon it. But he published nothing on his theory (not even in this paper), Łukasiewicz mentioned only occasionally, and their students rarely discussed it (for example, in Słupecki 1955a, 61–66); so it remains an important but shadowy part of both logic and axiomatics.

8.8.4 Pole apart: Chwistek’s ‘semantic’ logicism at Cracov. While his Warsaw colleagues used PM for its logic and/or set theory, Leon Chwistek (1884–1944) attempted to reconstruct its logicism. Trained in philosophy at Cracov, mainly under Zaremba (§8.6.3) and the philosopher Jan Sleszy´nski (1854–1931), he was appointed a lecturer there. He was also a talented painter, with many canvasses displayed in Polish galleries.

Chwistek spent several months in 1909 and 1910 at Göttingen. Hilbert’s work presumably made an impact, although foundations were not then his main concern; more significant was the lecture of April 1909 by Poincaré on (im)predicativity and Richard’s paradox, described in §8.7.7 in connection with Weyl. As Chwistek recalled later (1948a, 78–79) both he and Weyl were in the audience, and in November he sent Russell a manuscript on specifying mathematical induction impredicatively and asking for Russell’s opinion (Jadacki 1986a, 245–251). There was then a pause in contact of a decade, during which time Chwistek rethought logicism. In a Polish paper on paradoxes he joined the chorus against the axiom of reducibility, but for a new reason: it admitted a version of Richard’s paradox within simple type theory (1921a, art. 1). However, he was mistaken; when he repeated the claim in a paper in German (1922a, 239–241), Ramsey was to point out that even if a propositional function were finitely definable in terms of some given symbols, the equivalent elementary function allowed by the axiom may not be (1926a, 28–29). Neither man noticed the paradox at the end of Russell’s The principles, which does seem to be constructible in the simple theory (§6.7.8).

There are various similarities between the theories of Chwistek and of Ramsey, with priority resting with the former. They became clearer in Chwistek’s main production, which he sent in manuscript to Russell: a long essay in English on ‘the theory of constructive types’, published in two parts by the recently formed Polish Mathematical Society after rejection by Fundamenta mathematicae (1924a, 1925a).

One similarity has been foreshadowed: in his earlier papers Chwistek spoke of the ‘simple’ theory, meaning the types only, distinguishing it from the full version. We saw in §8.4.6 that Ramsey was to make the same distinction; maybe he was inspired by Chwistek’s allusion. We also noted that he did not name the kinds; by contrast Chwistek was bountiful, for the simple theory was also ‘simplified’ or ‘primitive’, while the full version was variously ‘pure’, ‘branched’ or ‘constructive’ (1924a, 12–13, 20; 1925a, 92, 95–98, 110). The last name occurred in his title, indicating his intention to confine propositional functions Richard-style to finitely constructible ones and so avoid the axiom of reducibility. In addition, his simple theory differed from that in PM in that types were defined from a given class by its sub-classes, sub-classes of sub-classes, and so on (1924a, 26–28, 36–40); further, classes were not incomplete symbols relying upon contextual definitions in terms of propositional functions but treated on an epistemological par with them, so that ‘there is no difference at all between a function with I variable and a class, or between a function with II variables and a relation’ (p. 40). The most interesting and influential change was to alleviate the problem of identity by defining it only for classes and relations, since they sufficed for all mathematical purposes (p. 19). Thus for classes α and β (p. 42, here in PM symbols):

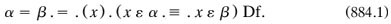
Chwistek also discarded the theory of definite descriptions in favour of a surely inadequate collection of nominal definitions (pp. 45–47). He laid out his ‘Directions concerning the meaning and use of symbols’ in a very formal way, claiming that it ‘may be called the real “Metamathematic”’, because it was ‘more precise’ than Hilbert’s (p. 22). However, his general rule of definition (p. 28) was to be shown by Leniewski to lead to a contradiction (1929a, 488–491).

The second part of Chwistek’s paper was largely devoted to a reconstruction of ‘cardinal arithmetic’. He used his simple type theory to imitate the theory of homogeneous cardinal arithmetic (§7.9.4) in PM (Chwistek 1925a, 110–137). But the theory was limited, both mathematically and philosophically. For example, the new definition of identity gave his calculus an extensional flavour, although he was guarded about its measure (pp. 93–95). Again, the restriction to constructive types and their functions prevented him from defining any transfinite cardinals, even though he adopted an axiom of infinity (pp. 133, 137). In the introduction to the second edition of PM Russell noted that ‘a great deal of ordinary mathematics’ was lost (1925a, xiv).

Chwistek promised to publish a ‘complete system of Logic and Mathematics’ (1925a, 99); the closest approximation during that decade was a paper 1929a, written in German. The ‘and’ in his phrase is significant: logic no longer grounded mathematics, but both had some common basis. This lay in ‘semantics’, which for him referred to the study of signs and their means of manipulation. It was a development of his ‘Metamathematic’, which differed from Hilbert’s in that its language incorporated both symbols and their referents. In this paper he presented his calculus in which all formulae were symbolised by a string comprising five letters and ‘special signs’ when necessary, and concatenations thereof; thus it was not unlike Łukasiewicz’s notation. For example, the Sheffer stroke ‘p | q’ was expressed as ‘*cpccq’ (where ‘c’ was a place-marker), and ‘H is the result of the substitution of G for F in E’ became ‘*EFGHc’ (pp. 705, 707). He laid out a long table of logical and mathematical notions, including a number-coding system strikingly similar to a list of characters in a modern computer manual (pp. 714–717).

At the time Chwistek’s enterprise must have seemed mysterious; but it was sufficiently well regarded for him to be preferred over the young Tarski for the chair in logic at Lvov in 1930. Russell had supported the candidature in a letter of 23 December 1929 to the University, while adding that he did not know Tarski’s work.⁴⁰ In the 1930s Chwistek’s ‘semantics’ was to gain some currency (§9.3.2), and he was to extend it (§9.6.7). But the main centre of activity for Polish logic remained in Warsaw, with Tarski and his colleagues and seniors.

8.9 THE RISE OF AUSTRIA IN THE 1920S: THE SCHLICK CIRCLE

8.9.1 Formation and influence. In this final section we move south of Poland to consider another group circle of philosophers and mathematicians, which formed in the mid 1920s and came to have great influence world-wide. I avoid their name ‘Vienna Circle’ here, since it was introduced in 1929, in a phase of work heralded in §9.2.1; here the earlier period is described.

The origins goes back to 1900 when Hans Hahn (1879–1934), Otto Neurath (1882–1945) and Philipp Frank (1884–1966), students together at Vienna University, began to discuss philosophical questions about mathematics and science. Hahn was to make his career as a mathematician, especially in the calculus of variations and also in the theory of functions; his achievements bought him back to a chair in Vienna in 1921, after five years at Bonn. By then his interest in philosophy had begun to develop, and he started off a discussion group with his old chums and some others. He also sought for the chair of ‘inductive philosophy’, which had been established in 1889 for Ernst Mach, to be given to the German philosopher Moritz Schlick (1882–1936).

Schlick had started as a physicist, writing a Dissertation in 1904 under Max Planck at Berlin (his home town); but then he transferred to philosophy, specialising in epistemology and ethics. He devoted his Habilitationsschrift 1910a at Rostock University to a search for ‘the essence of truth according to modern logic’, and plumped for one in which judgement ‘univocally designates a specific state of affairs’ (pp. 94–95)—strikingly similar to Russell’s theory then in embryo (§8.2.6), though without the apparatus of relations. Professor at Rostock from 1917, he developed this approach in a book 1918a on epistemology, where he followed Hilbert in relying upon implicit definitions (§4.7.2). Widely admired, but with reservations from Weyl 1923a in the Jahrbuch, its appearance helped Hahn’s hope to be fulfilled in 1922.

Thereafter the Vienna discussions fell under Schlick’s leadership; a philosophical circle was created, with invitation from him as the criterion of membership. New figures joined from time to time, including our two major figures: Rudolf Carnap (1891–1970) and Kurt Gödel (1903–1978). The circle met quite regularly, usually in certain Vienna coffee-houses; a member gave a talk, and discussion followed. Often notes were taken by a stenographer, and sometimes also by those members who had learnt a shorthand. A collaborator from the Mathematics Department was Karl Menger (1902–1985), who also organised a mathematical colloquium of his own, which ran a yearly Ergebnisse of its results from 1928 to 1937 (Menger 1998a); co-editors included Gödel.

The circle wished to bring to philosophy the standards of rigour and exactness that were (presumed to be) found in mathematics, logic and science. Positivism and reductionism were held to govern both epistemology and ontology, and metaphysics was disliked; father figures included Mach and especially Russell, and Wittgenstein’s Tractatus exercised both positive and negative influence. The members used phrases such as ‘scientific philosophy’, surely inspired by the full title of Russell’s Our knowledge (§8.3.2), which had recently appeared in a German translation as 1926d. However, on many specific issues and special interests they differed quite widely.

The influence of the circle gradually grew, especially from late in the decade. A book series on ‘the scientific world-view’, co-edited by Schlick and Frank, started in 1928, when also Schlick and Hahn led a Verein Ernst Mach to hold meetings and conferences; and a journal was taken over two years later (§9.2.1). But after 1933 many members left the influence of the ever-widening Hitler Circle, going mainly to the U.S.A.; and thereby the influence increased further, leaving a heavy mark on philosophy for decades, especially in Anglo-Saxon countries. The scale of this influence has led in the last thirty years to great historical interest, including editions and translations of the writings of several members.

In addition, and in contrast to the poor Poles, several large Nachlässe and other collections of manuscripts have been conserved; they include not only protocols but also notice-books of lecture courses, versions of lectures, and vast collections of correspondence (often typed, with carbon copies). I cannot do justice to this range of published or manuscript material, not even to my own partial knowledge of it; the survey here and in §9.2–3 is strictly confined to the concerns with logic and the philosophy of mathematics, though it takes note of some peripheral members.⁴¹

8.9.2 The impact of Russell, especially upon Carnap. (My 1997c) During 1924–1925 Hahn conducted a year-long seminar on PM; it must have been detailed, but no records seem to survive. It may have suggested emulation to Schlick, who, although publishing little on logic, took a deep interest in the subject. At all events, for the winter semester of 1925–1926 he gave a general course on the philosophy of mathematics (Schlick Papers, 23-B1), and for the summer he chose Russell’s Introduction, presumably in the German translation 1923a, as the text for a seminar on ‘philosophy of number’. Following normal practise, a student was assigned to prepare a chapter or two and lead its presentation, while another student took notes for the record book (Papers, 52-B32-2). No new insights emerged, but the students will have gained a good impression of the scope and limitations of logicism. Curiously, while Gödel was one of the students, he neither made presentations nor took notes; maybe at this stage he was not too interested.⁴² But the effect on Schlick must have been great; for when the German translation of Russell’s The problems of philosophy appeared (Russell 1926c), he wrote an ecstatic review 1927a:

 

The method of his philosophising can hardly be estimated highly enough. In my strong conviction it is the method of the future, the only method through which LEIBNIZ’s ideal can be realised, and will introduce the rigour of mathematics (Russell is a recognised mathematician) into the treatment of philosophical questions.

 

Maybe Schlick had been counselled by Carnap, who had been appointed Privatdozent to Vienna University in 1926. After attending Frege’s lectures at Jena in the early 1910s (§8.7.3) and Army service throughout the Great War, he returned to Jena for a few years; then, from 1921 until his call to Vienna he lived under his own means near Freiburg. His initial philosophical forays were neo-Kantian studies of space and time, following especially Natorp and also Dingler to some extent; but then, as he recalled later, he moved towards Russellian positions and remained there for many years (Carnap 1963a, 16–17). After reading PM in 1919–1920 (Carnap Papers, 81–39) and then Our knowledge, he wrote to Russell on 17 November 1921, explaining that his own conception of space was closer to that in Russell’s neo-Hegelian Essay on the foundations of geometry (§6.2.1) than in the positivistic The problems of philosophy. He also listed in seven pages ‘the most important signs, definitions, axioms and theorems’ in PM, perhaps to check his catalogue with the master. The next June he enquired about buying the first volume, and Russell responded in July by writing out all the main definitions and results of the work in a manuscript of 35 folios.⁴³ This extraordinarily generous effort by a famous and mightily busy figure for a promising but little-known philosopher in Germany at the time of its massive inflation of currency must have impressed young Carnap, over and above the philosophical kinship.

Carnap also sent to Russell news of a proposed meeting for 1923 on the ‘Construction of reality (structure theory of knowledge)’ and on the ‘Doctrine of relations’ (‘Beziehungslehre’) He invited the participants: they included fellow philosophers such as Hans Reichenbach (1891–1953), Schlick, Dubislav, Paul Hertz (1888–1961), Behmann (1891–1970, an exact contemporary), and Fraenkel (Thiel 1993a). Two meetings took place in March at Erlangen, under the auspices of the Kantgesellschaft (Reichenbach Papers, 15–50-03). No publications were produced, but the stage was set for the kind of philosophy which Carnap wished to pursue: one of his talks at the second meeting dealt with Russell’s logic of relations.

Around then, when in his mid thirties, Carnap began to write books on logicism largely following PM, and on epistemology much based upon Our knowledge. (The influence of Russell thus extended from subject matters to concurrent writing!) They appeared in different countries in reverse chronological order, which we follow here.

8.9.3 ‘Logicism’ in Carnap’s Abriss, 1929. Carnap’s account, published in Vienna in the Schlick-Frank book series as Abriss der Logistik, was much more substantial than Behmann’s recent little book (§8.7.8). It begins with a durable innovation, not reflected in its title. As we saw in §7.5.1, the French word ‘Logistique’ was introduced by Couturat and others at the 1904 International Congress of Philosophy, and was used by Russell and others from then on, in versions appropriate for various languages. However, it covered both the views of the Peanists and the different position adopted by Russell and Whitehead. It seems that in the manuscript he had used ‘Logistik’; for, upon receiving a copy, Behmann told Carnap on 29 December 1927 that he found it to be an ‘unlucky bastard word’, like ‘logical product’ and ‘propositional function’.⁴⁴ Carnap retained the word in the published Abriss; but, perhaps for this reason, he also proposed there ‘Logizismus’ (1929a, 2–3) to name positions like that proposed in PM. As we saw in §8.7.6, at this time and seemingly independently Fraenkel had adopted the word for the same purpose; but the spread was mainly due to Carnap, from 1930 onwards (§9.2.2). ‘Logizismus’ had been used before (sometimes as ‘Logismus’), mostly in connection with phenomenological logic; in line with the German practise of’).. ismus’ indicating a negative stress, it connoted a rejection of a reduction of the non-logical to the purely logical, granting the latter an independent existence.⁴⁵ There was also a positive sense, such as grounding metaphysics in logic alone; maybe Carnap had seen that use in Dubislav’s recent book on definition (§8.7.8: 1927a, 67).

Carnap packed a lot of material into his 114 pages. The first part, ‘System of logistic’, ran through the calculi, with the Sheffer stroke and other connectives defined from truth-tables. For the latter he missed Post and cited only Wittgenstein; however, he redefined tautology as ‘contentless (but not meaningless.)’ (pp. 8–9). Then he treated paradoxes, with only Russell’s discussed; Russell’s theory of definite descriptions; and type theory, including its ‘verzweigte’ part involving orders and the pertaining paradoxes of naming (pp. 15–23, 30–33). ‘Verzweigte’ reads like a translation of Chwistek’s ‘branched’ (§8.8.4); but he did not cite Chwistek and may not have known his work. The word may have come back later into English as ‘ramified’ (§9.4.5), now the standard name.

Carnap also presented Euler diagrams, together with the ‘controversial’ issue of classes conceived extensionally (pp. 23–25). However, he missed Wiener’s definition (827.1) of the ordered pair. The logicist construction of arithmetic went through the finite cardinals and ‘relation-numbers’, and touched upon the infinite, limit points and continuity (pp. 45–50). The second part, on ‘applied logistic’, included the Peano axioms, bits of topology and projective geometry, and the analysis of language. The tight links forged between notions gave an overall structure to the parts of mathematics handled; indeed, his version of Russell’s ordinal similarity (795.1) between two relations was called a ‘structural property’ of a relation (p. 54). Curiously, he did not discuss model theory, although it had featured in a recent logicist article 1927a in which he preferred ‘proper’ (‘eigentlich’) concepts over ‘improper’ ones, which were specified only by implicit definitions and so lay open to non-categoricity (Howard 1996a). The end matter of the Abriss included some of the most popular current symbols and terms then in use. In the index Russell and Whitehead were the longest entries; Frege was cited in the text three times, and only for references.

Although it sold respectably into the 1930s,⁴⁶ Carnap’s Abriss is now largely forgotten, even by historians of the period. Its sub-title, ‘with especial consideration for relations theory and its applications’, indicated that the logic of relations linked it together. This feature was prominent also in Carnap’s companion volume.

8.9.4 Epistemology in Carnap’s Aufbau, 1928. The publisher of the Abriss, Julius Springer, had rejected the other book, which, by contrast has become a classic.⁴⁷ Apparently based upon part of his Habilitationsschrift at Vienna in 1926,⁴⁸ Der logische Aufbau der Welt was published as Carnap 1928a in Berlin by the Welt-Kreis Verlag, with a print-run seemingly of 600 copies. The house was closely linked to the circle; it had recently published the translation 1926c of Russell’s Problems mentioned in §8.9.2, which had been prepared by Hertz.

Again Carnap’s sub-title, ‘Attempt at a constitution-theory of concepts’, is instructive, for it reflects the fact that while preparing the book he often used ‘Konstitutionstheorie’ as the intended title. The change is instructive: from a neo-Kantian noun to the catch-word ‘construction’, in Germany and Austria, in the 1920s, where post-war aspirations were to be fulfilled in fields social, architectural (such as the Bauhaus) and philosophical (Galison 1996a). Maybe also the publisher had asked for a catchier title.

Carnap provided a quite formalised construction, drawing upon logicist techniques and methods; prominent was the logic of relations, which he stressed briefly in the opening sects. 7 and 11 and in detail in the formal outline in Part 3, where various different kinds were used (sects. 69–79). Algebraic logic was entirely absent.

Carnap imitated type theory by assuming a ‘basis’, so that ‘objects of each level were “constructed” from the objects of the lower levels’ by creating ‘basis, ascension form, object form, and system form’ (sect. 26, launching Part 3). His processes of construction, worked out in Part 4, drew heavily upon ‘structure descriptions’, which comprised ‘all formal properties’ of a relation (sect. 12). He associated his concept of structure with ‘relation-number’, Russell’s generalisation of ordinal arithmetic in PM; Russell had made this link himself in the Introduction, and Carnap cited both passages here.

Russell’s theory of definite descriptions was also used to handle uniquely specifiable objects (sects. 13, 50). It led Carnap to ‘the general possibility of structural definite descriptions’ (title of sect. 15), an epistemological notion since ‘all scientific statements are structure statements’ (title of sect. 16). In addition, it helped him avoid considering the metaphysical essence of objects with his requirement that ‘the indication of the nominatum of the sign of an object, consists in an indication of the truth criteria of those sentences in which the sign of this object can occur’ (sect. 161). He noted that Russell had used the contextual definition of definite descriptions (and also of classes and relations) in the same spirit of avoiding assuming existence (sects. 38–39).

The technical details of Carnap’s ‘constructional system’ were based upon such notions from PM, together with many of the symbols (sects. 106–122). A notable technique was ‘quasi-analysis’, where primitive elements were examined by the pertaining relations between them (sects. 71–83). As with Russell and like the restricted compass of mathematics in their logicisms, Carnap treated almost entirely only the physical sciences; a few nods were made towards biology (sect. 137), but none to, say, medicine or geology. Also following Russell in the second edition of PM, Carnap treated classes and relations extensionally (especially sects. 40–45 in constructing ascension forms); but as a result universals could not be handled, and generality was compromised (Popper 1935a, art. 14). Like his Abriss, the tight links between notions made his epistemology highly structured.

While Carnap’s overall system resembled Russell’s type theory, his broader aims made the choice of the basis more tricky than Russell’s assumption of structureless (and physical. individuals. The neo-Kantian in Carnap came through in his discussion of ‘possible psychological bases’, where he decided upon the ‘autopsychological basis’ of the single person; objectivity was secured through the ‘forms of experience’ started by members of a community, and thus was markedly structural (sects. 61–68).

Wittgenstein’s Tractatus was only cited three times, though warmly (sects. 43, 180 and 183). It had become a major talking point in Schlick’s circle, read ‘page by page’, Schlick wrote to Carnap on 29 November 1925 (Carnap Papers, 29-32-34); but Carnap chose from it warily. We noted his different definition of tautology, and he also defined analytic theorems as ‘deduced from the definitions alone’ (sects. 106–107). A major difference concerned the hierarchy of languages, which Russell had proposed in his introduction to the Tractatus without recognising its significance (§8.4.3). The circle split over its merits. Orthodox Wittgensteinians such as Felix Kaufmann and Felix Waismann followed Their Master in rejecting it; but Carnap, and also Hahn and Gödel, recognised its major importance—with momentous consequences for Gödel’s contributions.

8.9.5 Intuitionism and proof theory: Brouwer and Gödel, 1928–1930. During the 1920s Menger had been working on the topological definition of dimension, and stayed for some time in Amsterdam with Brouwer (Menger 1979a, ch. 21). Their relationship was to flounder in 1929, due to Brouwer’s conduct; but before that Brouwer gave two lectures on intuitionism in Vienna in March 1928.

The first lecture was published in the Viennese Monatshefte für Mathematik und Physik, then edited by Hahn, as Brouwer 1929a. He discussed ‘mathematics, knowledge and language’, with his mixture of weird psychology and sociology. But he argued his case for languagelessness clearly, and near the end he distinguished ‘correct theories’, in which the law of excluded middle was forbidden, from the broader collection of ‘non-contradictory’ ones, in which it was allowed but his other restrictions still applied. In the second lecture, which for some reason appeared only as a pamphlet, Brouwer 1930a contrasted the classical and the intuitionistic continua with more clarity than usual. Logicism was mentioned only once, when Russell was classified as a formalist, along with Peano and Dedekind….

The impacts on the audiences of these lectures, especially the first one, were unexpectedly great. Wittgenstein was drawn back to philosophy after several years’ absence, perhaps by Brouwer’s stress, congenial to a monist, upon personal will and the state of reverie (1929a, art. 1); and both Carnap and Gödel were impressed by the pessimistic idea that there might be unsolvable problems in mathematics (Köhler 1991a, drawing upon Carnap’s diary). The fruits of this seed, if sown then, were to blossom surprisingly at the end of 1930; but meanwhile Gödel continued with the optimism inherent in the circle’s position, and also in Hilbert, by establishing another important case of completeness.

In February 1930, during his 25th year, Gödel defended his Dissertation, written under Hahn’s supervision; a re-written version appeared in the Monatshefte as Gödel 1930b. Noticing in Hilbert/Ackermann that the syntactic completeness of the ‘narrower calculus of functions’ was not proved or disproved (1928a, 68), he established the former; that is, assuming it to be consistent, each of its well-formed formulae was either ‘refutable or satisfiable’. He used metamathematical and model-theoretic notions and notations to work out the details, with Hilbert/Ackermann as his main source, and also some kinship to Skolem (§8.7.5). PM, as modified by Bernays 1926a (§8.7.4), provided the axioms and rules of inference, and the theorem partially vindicated its authors’ assumptions about completeness; but their broader aims were soon to suffer from Gödel a fundamental rebuff, as we shall see in the next chapter.

 

 

¹ Shortly before this tragedy Whitehead contributed his War effort: a short paper 1918a sent to the Royal Society the previous November, in which he gave graphical estimates for calculating the paths of shells projected at high angles.

² I am grateful to Kenneth Blackwell for identifying the reviewer as James Strachey, from the publisher’s file copy of The spectator. Also a younger brother of the famous writer Lytton, James became well-known later as an editor of the writings of Sigmund Freud.

³ For the production schedule and costs of the book, see Reading University Archives, Longmans, Green Papers, Impression Book R34B.

⁴ The details for Russell’s courses may be retrieved from the lists of courses in mathematics published in the Cambridge University reporter. It stated the intended courses; insufficient support would cause their cancellation.

⁵ For this correspondence see Wittgenstein Letters, 23–27; and Russell’s letters 760–820 passim to Morrell (copies in RA). Historical interpretation has become an endless exercise, in which Nicholas Griffin’s pioneering efforts are impressive (1980a, 152–169, and 1985a); among other studies, see Iglesias 1984a.

⁶ For details of Hardy’s course, see the lists of courses in mathematics in the Cambridge University reporter from 1913–1914 to 1918–1919. G. E. Moore’s notes are in his Papers, 10/6/1–4.

⁷ Eliot’s notes on both courses are held in his Papers at Houghton Library, Harvard University, File Am. 1691.14.(3); the truth-tables are written on fol. 43, for inclusive disjunction, implication, and the Sheffer stroke. For some reason the notes of Russell and Wittgenstein were left out of Russell Papers 8; but their substance is summarised in McGuinness 1988a, 160–162, and they appear, with good discussion, in Shosky 1997a.

⁸ Cambridge University reporter (1913–1914), 483; for an auditor’s notes, see G. E. Moore Papers, 10/4/4. Russell gave, or at least offered, the course a year later ((1914–1915), 91).

⁹ There are 50 boxes in confetti-ish state in the Sheffer Papers; I confess to have rummaged in only a few of them. In compensation, less mangled parts include some good correspondence with various figures, mainly after 1921 but also including a letter to Peano of 1911 while on his European trip. On his Harvard doctorate, see the documents in the University Archives, file UA V 687.235, no. 39. Michael Scanlan is studying Sheffer, confetti included.

¹⁰ Royce Papers, Incoming Correspondence, Box 1.

¹¹ Ladd-Franklin Papers, Box 1; there seems to be no reply in the meagre Lewis Papers at Stanford University Archives (letters to me from Polly Armstrong).

¹² For the production schedule and costs of the book, see Reading University Archives, Longmans, Green Papers, Impression Book R34B. The publisher issued a short review in its house journal Notes on books (1918), 38.

¹³ A fresh translation appeared much later as Nicod 1969a; Russell gave money to help publish it, supporting an anonymous donor (the poet W. H. Auden, according to letters of the time in RA from R. F. Harrod).

¹⁴ For an excellent survey of Wrinch’s careers, see Abir-Am 1987a. Wrinch spent her later career at Smith’s College in Massachusetts; her papers there contain nothing of note on logic or mathematics, although there are good letters in RA and also in the Ogden Papers (about to be used in §8.4.2).

¹⁵ Wittgenstein’s correspondence with Ogden, and a discussion of the origins of the Tractatus, are contained in Wittgenstein Ogden (1973). An important source was the papers of Ogden’s solicitor Mark Haymon, whose Nachlass has just become available in University College London Archives: Box 4 contains Wittgensteiniana, including the rebuffs by Russell and Wrinch in the early 1960s of claims by the disciples that The Master played no role in the translation. Wittgenstein’s correspondence with Russell is included in Wittgenstein Letters (1974), with some already in Russell 1968a, 116–121; later finds are published in McGuinness and von Wright 1991a. The Ogden Papers is a vast collection, including correspondence with almost everybody described in this section in alphabetically ordered Boxes.

¹⁶ According to possibly faulty notes taken by G. E. Moore (1955a, 297), Wittgenstein had read quantifiers this infinitary way in the Tractatus but later rejected it because ‘grammar’ was needed to grasp their ranges of values.

¹⁷ The original of this letter is lost; Sheffer included this passage in a letter of 27 October 1923 to Hoernle (Sheffer Papers, Correspondence Box; copy in RA). In a letter of 16 May 1960 to A. Shalom, Russell defended his reading of the Tractatus, stressing its syntactical side and playing down the metaphysics (RA).

¹⁸ In July 1923, on completing four years of study at Göttingen University, the Hungarian logician Alfred Boskowitz (1897–1945) sent to Russell a detailed list of errors and possible changes for the first edition (RA; see also Behmann Papers, File I 08); it seems that only the former category was acted upon. Boskowitz turned to a career in banking in Hungary (information from C. Thiel and P. Boscowitz).

¹⁹ Ramsey 1926b, 20, 42–46; compare Ramsey Papers, 2–20 to 2–22, 5–12. He attributed Grelling’s paradox to Weyl 1918b (§8.7.7).

²⁰ In the Ramsey Papers there are some manuscripts relevant to this axiom and related issues, seemingly concurrent: they are published in Notes, especially pp. 131–148, 178–194. Wittgenstein rejected Ramsey’s definition (847.1) of identity, largely on the grounds that the negation of nonsense was also nonsense, rendering unacceptable the switch between tautology and contradiction (see, for example, Carnap’s notes of a discussion in 1927 between Wittgenstein and Ramsey in Carnap Papers, 102-77-01). A late paper Ramsey 1930a on the partition of infinite and finite classes was to stimulate much mathematical research in combinatorics and some aspects of proof theory.

Another mathematician with Trinity connections was H. T. J. Norton (1886–1937), who knew Russell (and Hardy. around the time of his doctorate in 1910. Perhaps in the late 1920s, he wrote several manuscripts on aspects of PM₂ such as Nicod’s axiom, quantification and the axiom of reducibility; unpublished at the time, they do not seem worthy of revival now (University College London Archives, London Mathematical Society Papers, Norton Manuscripts).

²¹ In 1927 Russell also published a popular Outline of philosophy (entitled ‘Philosophy’ in the U.S.A). in which logicism was not mentioned, and no mathematics seriously addressed.

²² RA possesses the copy of an undated letter to Greg where Russell announced that the third volume of PM₁ was about to appear (in 1913): ‘it will be thin, & there will be a final thin Vol. IV.’ The letter was found by a bookseller in Greg’s copy of this volume, which was later owned by Karl Popper.

²³ On the early career of Church, see E. H. Moore Papers, Box 4, Folder 5, where Veblen described him in 1927 as ‘one of our very strongest doctors’; and his own letters to Veblen in Veblen Papers, Box 3, including mention of Curry in Gottingen (a file on Curry is held in Box 4). Curry had thought of combinators in 1922 from trying to simplify substitition procedures in the propositional calculus of PM₁. In the mid 1930s he annotated in detail his copy of PM₂ without however publishing anything. Thanks for this information are due to Jonathan Seldin (University of Lethbridge, Canada).

²⁴ An electronic edition of Dewey s correspondence is currently in preparation from the originals in the Dewey Papers, University of Southern Illinois at Carbondale. Klyce’s side of the correspondence with Dewey is held in his Papers, Box 4. His main book is Universe (1921: drafts in Box 16), again self-published after Open Court rejected a version of it in 1915–1916 (Open Court Papers, Boxes 32/17, 19).

²⁵ The Bentley Papers, at Indiana University at Bloomington, deserve to be far better known; the letters are filed in alphabetical order of writer. On his paper and book, see also his correspondence with Ogden in Ogden Papers, Box 3. Like Klyce (another correspondent, incidentally), his book was rejected by Open Court (Bentley Papers, Box 3). His Philosophical correspondence with Dewey was published in 1964; during their lifetimes they had jointly issued a book on Knowing and the known (1949).

²⁶ Brunschvicg’s consideration of logistic soon received some unintended further publicity when it was “heavily used” by the Argentinean philosopher Camilo Meyer in a paper 1918a on this topic. Meyer had already helped himself to chunks of the third and fourth Books in a survey 1916a of 19th-century views on continuity and arithmetic.

²⁷ The history of the manuscript of Frege s comments to Jourdain is curious. At Russells request Jourdain had forwarded those folios that he could find in August 1911 (now RA); but he did not find the rest in his own notebook! (Russell 1967a, 217). I was able to reconstruct the whole from these two sources (my 1977b, 141), and they are published in full, with Jourdain’s letters, in Frege Letters, 114–124; Jourdain’s article is reprinted on pp. 275–301. The history of Frege’s Nachlass was recorded in §4.5.1.

²⁸ Some of Hilbert s examples from applied mathematics were in fact not fully axiomatised theories; his choice was led by his current concern with the foundations of physics (Corry 1997a). He showed his lack of patriotism by inviting Russell to lecture at Gottingen in 1917; Russell, without a passport because of subversive pacifism, had not been able to accept (Hilbert Papers, 339).

²⁹ In an astonishing coincidence of timing, at this time the British applied mathematician Sir George Greenhill (1847–1927) introduced the word in his Presidential address 1923a to the Mathematical Association on ‘Mathematics of reality and metamathematics’. He referred to ‘the Tyranny of Mathematical Rigour, converting our subject into one which Aristotle might have called Metamathematics’.

³⁰ In 1909 Lowenheim had been stimulated to study the foundations of arithmetic as a result of the non-discussion between Frege and Thomae (§4.5.9). His correspondence with Frege was destroyed before Scholz had transcribed it (§4.5.1), but he mentioned his motivation to Bernays in a letter of 25 May 1937 (Bernays Papers, 975:2938–2939; noted in Frege Letters, 161).

³¹ Fraenkel s massive bibliography of set theory in 1953a deliberately does not cover physical applications. Among a rather spotty literature, see F. Bernstein 1912a on perturbation theory; Zermelo 1913a on chess; van Vleck 1915a on dynamics; and Bouligand 1928a on potential theory, 1931a on hydrodynamics, and 1932a on differential geometry. Later literature includes Brush 1967a on statistical mechanics.

³² The adjective grounded has become attached to this kind of class (Hallett 1984a, 185–194); Mirimanoff used no special name. In the course of expounding his idea of nested segments, he used the forms for his ‘types 1, 2 and 3’ which von Neumann 1923a was to give in defining the ordinals 1, 2 and 3 in his own foundations of arithmetic (Mirimanoff 1917a, 46). In a letter of perhaps 1908 to Russell G. G. Berry had named as ‘epsilonic classes’ those showing infinite ascent of membership (Garciadiego 1992a, 177).

³³ For recollections, see Fraenkel 1968a, 166–169. I saw this letter in the presence of his widow in 1982, at her flat in Jerusalem; it is now in his Papers. It includes also letters from Carnap, Godel and Quine. No copy of this letter exists in the von Neumann Papers, held at the Library of Congress, Washington.

³⁴ From this naive conception of time Brouwer infused his intuitionism with two-ities of various kinds, such as before and after. Whitehead was then developing his ‘process philosophy’, especially in his 1929a, using a far more sophisticated conception of time as a spread-like interval where experience was ‘anticipation tinged with reminiscence’ (Lowe 1990a, chs. 10–11 passim).

³⁵ Huntington letter in E. H. Moore Papers, Box 2, Folder 1. Letters from Bentley of 29 April 1931 to the Open Court Publishing Company, and of 21 March 1930 to E. D. Grant, in Bentley Papers, Box 1.

³⁶ E. H. Moore Papers, Box 16; Behmann Papers, File I 49. Behmann’s correspondence with Russell is in File I 60, and in RA.

³⁷ An edition is in preparation of Cassirer’s manuscripts, which are held mainly at Yale University (Krois 1997a); many of them relate to this book.

³⁸ In an interesting exchange of letters in the autumn of 1930 following the receipt of Becker’s article in book form, Hilbert recalled to him the impact of Dedekind’s booklet on integers and saw Becker’s reservations over metamathematics as a source of strength. In reply Becker wondered about the obviousness of the e-axiom (874.1)₂ (Hilbert Papers, 457).

³⁹ Lewis 1933a corrected the assumption made in Lewis and Langford 1932a, a textbook to be described in §9.4.1. When G. E. Moore mentioned ‘Tarski’s “3-valued” Logic’ in an article on Wittgenstein’s lectures of the early 1930s (1954a, 300), Łukasiewicz wrote to him on 21 January 1955, bitter that ‘Tarski does nothing to rectify’ the situation (Moore Papers, 8L/26). Moore published a correction when reprinting his article, while making clear that his records seemed to record Wittgenstein’s understanding accurately (1959a, 324). In 1955 a selected English edition of Tarski’s papers was being completed, and Łukasiewicz’s letter to Moore suggests that he himself wrote the correcting note at the head of the translation of their joint paper (Tarski Semantics, (1956), 38). In 1977 his widow wrote an equally bitter letter to the editor of an Italian journal in logic, which was published there as Łukasiewicz 1990a. On the other hand, the Łukasiewiczes had been regarded during the War as Nazi sympathisers.

⁴⁰ Russell’s letter, kept in the Archives of Lvov University with a copy at RA, is printed in Jadacki 1986a, 243; his correspondence with Chwistek is on pp. 251–259.

⁴¹ The most valuable single source on the c(C)ircle is Stadler 1997a, a Baedecker guide to the whole story, together with transcriptions of the surviving meeting protocols, bio-bibliographies and teaching records of all members and peripheral figures, and a bibliography of historical literature. Among the latter, Dahms 1985a and Haller and Stadler 1993a comprise relevant collection of essays; Menger’s posthumous reminiscences 1992a are also well worth noting. The most extensive source in English is the ‘Vienna Circle’ collection of translations and editions published by Reidel (now Kluwer); among the commentaries, Coffa 1991a takes some nice sideways looks, and Giere and Richardson 1996a stands out among the collections of essays.

The various Nachlässe are held in several centres, with microfilm copies available from the Sozialwissenschaftliches Archiv at the University of Konstanz. Since correspondents quite often made carbon copies of texts or letter, there is duplication across collections; I may well not have registered all cases in my citations. In addition, the Behmann Papers is a rich but little-known source, catalogued in Haas 1981a.

⁴² A fellow student was Olga Taussky, who later recalled Godel leading one seminar and being generally active (Taussky-Todd 1987a, 35–36). But in general her recollections are inaccurate.

⁴³ Carnap’s November letter is in RA, Dora Russell Papers; copy in his Papers, 102–68-32. Russell’s manuscript is at 111–01-01, his thanks of 29 July 1922 at 102–68-31. The later letters in the latter file include news of obtaining a copy of the first edition of PM, seemingly from Ogden, in 1926 (68–28), soon after the first two volumes of PM₂ were available. He lent Russell’s notes to Behmann, asking for their return on 19 February 1924 (Behmann Papers, File I 10). On October 1923 Russell had given the proofs of the first volume of PM₂ to Reichenbach (Papers, 16–40-05; and RA).

⁴⁴ Carnap Papers, 28–07-05; Behmann Papers, File I 10.

⁴⁵ See Wundt 1910a for this use of ‘Logizismus’. Ziehen deployed it similarly in his textbook on logic (§8.7.2) to characterise logics opposed to psychologistic, sensualistic or inductive trends, such as those of Bolzano, Brentano, Husserl and Meinong (Ziehen 1920a, 172–173, with some historical notes on the word).

⁴⁶ Springer told Carnap that 951 copies were sold by 1937 (Carnap Papers, 27-40-109). He had told them in the summer of 1927 that Bruno Cassirer had rejected the Abriss as financially too risky (29-37-02). Russell received a copy from Carnap, but he did not slit many pages (RA).

⁴⁷Springer told Schlick on 25 May 1926 that they rejected Carnap’s Aufbau, because of sales prospects (Schlick Papers, File 119); the following March he gave the manuscript a very warm testimonial (for Welt-Kreis Verlag?), and discussed the title with Carnap later in the year (21-A89, A85).

⁴⁸ On this somewhat obscure point, see Vienna University Archives, Philosophy Faculty Board Minutes, 13 March and 9 June 1926; and Schlick Papers, 85-C29-4 and -9.