7.5 REACTIONS TO MATHEMATICAL LOGIC AND LOGICISM, 1904–1907
By 1905 Whitehead and Russell each had several papers in print on logicism, and Russell also The principles. This work began to take its place among the corpus of foundational studies of the time, especially among mathematicians. We note the reactions in this section, starting internationally, and then taking in turn Germany, Italy, the U.S.A. and Britain. They form only a part of a considerable concern with foundations at that time: in particular, the intense discussion of the axioms of choice is not described here.
7.5.1 The International Congress of Philosophy, 1904. This assembly succeeded the Paris Congress of 1900 and launched a four-year series, like the mathematicians (and some other disciplinary communities). However, unlike last time there was no closer link; for the mathematicians met at Heidelberg (§7.2.2) while philosophy was prosecuted at Geneva, in September 1904.
Another difference was that neither Whitehead nor Russell attended; however, their concerns were well represented, as Couturat showed in his report in the Revue of the Section on ‘Logic and philosophy of science’. For example, he reported Peano’s reservations over Russell’s logic of relations thus: ‘One can (as Mr. Russell has done) define mathematical functions by means of the Logic of relations; one can also, inversedly (as Mr. Peano has done in the Formulaire), define relations by means of functions, on the condition of taking for variables, no more numbers, but classes of numbers’ (Couturat 1904c, 1046). Again, to Boutroux’s contribution (§7.4.2) Peano commented that ‘the relation xRy of Russell is not identical to the function of Mathematics [...] the relation of Russell is always invertible: the function of Mathematics does not have this property’ (Boutroux 1905b, 719). Thus he did not understand Russell’s papers on the logic of relations that he had recently accepted for the Rivista! (§6.5.2, 4).
Among other talks, the President of the Section, the Genevan mathematician Henri Fehr (1870–1954) envisaged ‘the progressive fusion of logic and of mathematics’. Unlike many mathematicians, he enthused over ‘the magisterial studies of Mr. RUSSELL’ and the ‘remarkable papers of Mr. COUTURAT’ in the short extract 1905a published in the proceedings. Further, Couturat recorded him as seeing ‘the union, if not the unity, of these two disciplines,’ of which ‘Logic is a mathematical science by its form’ while ‘Mathematics is a purely logical science by its methods and by its principles’ (1904c, 1037).
Couturat’s own talk 1905c reviewed some basic principles of logic. He started by discussing its title, ‘On the utility of algorithmic logic’: ‘I prefer this name to that of symbolic logic’ for stressing symbols too much, or to ‘Algebra of Logic, which presents it as an Algebra, and not as a Logic; [or] to that of Mathematical logic, which is equivocal’. He then recalled that the word ‘Logistique’ had been used to characterise arithmetical calculations by Augustin Cournot, in the volume 1847a on algebra and geometry which had influenced his own book on the infinite (§4.2.3); indeed, he had mentioned Cournot’s use of the word there (1896a, xxi).16 Now he suggested ‘logistique’ as a name for mathematical logic with mathematical intent.
Couturat also noted with pleasure that two Congress colleagues had thought of this word independently: the French philosopher André Lalande, and a participant, Gregorius Itelson (1852–1926). He is a fascinating outsider in our story; he seems to have published only one paper, on psychophysics (Schröder 1890b, 704), but he could make good one-line comments at conferences (§10.1.1). Russell was to meet him at the International Congress of Mathematicians at Rome in 1908, and tell his wife of a Russian living in Berlin who was ‘very poor, and lives in an apartment without any servant’, possessing ‘“eine noble Passion” for old books, of which he has a fine library’; apparently by then Itelson saw Couturat as a plagiariser of the word ‘logistique’ (Russell Letters 1, 318).
Couturat reported Itelson’s two talks at Geneva at generous length (1904c, 1037–1042). One on ‘The reform of logic’ covered Renaissance and 17th-century history, doubtless gleaned from his old books. In the other talk, perhaps under the influence of reading Bolzano, Itelson made the prophetic suggestion that logic be construed as the ‘study of objects in general’, whether constant or not, rather than the tradition of analysing modes of reasoning. He also examined the relationship between ‘Logic and mathematics’ in a spirit distant from Couturat’s. Logic was ‘the Logic of extension’ while ‘pure mathematics’ was defined as ‘the science of ordered objects’; both disciplines deployed ‘the same method’ in handling ‘ensembles of objects’, but the differences were significant. He also claimed that, in its ‘pure’ rather than transcendental form, ‘Logic is distinguished from ontology in that it does not inquire of the existence of objects’ (p. 1041):
Moreover, no science, no theory can be prior to or higher than Logic, which is the foundation of any science and of any theory; one can say, in parodying the word of Pascal: that which surpasses Logic surpasses us; thus there cannot be metalogic.
What a pity that Russell was not there, to hear this early use of ‘metalogic’; he would have concurred with the opinion expressed about it.
Itelson’s remarks were quoted by authors in the Revue: in Boutroux 1905 (§7.4.2), and in a piece on ‘Metaphysics and mathematical logic’ by the mathematician Maximilien Winter. Obviously well familiar with the Peanist literature—he cited their lectures at the 1900 Congress—Winter took an idealist stance, and felt himself unable to tell in the writings of Couturat and Russell whether he was in philosophy or in ‘the most abstract branch of mathematics’ (1905a, 602–603); they could have replied that they were in both at the same time. Later he reworked his paper and two others in the Revue as a book 1911a on ‘method in the philosophy of mathematics’, which contained a fairly wide survey of proofs and derivations in arithmetic and algebra.
By then the Revue had published two more notices. Henri Dufumier 1909a gave a warm and well-referenced survey of Russell’s and Moore’s new philosophy. The Swiss philosopher Arnold Reymond (1874–1958) wondered in 1909a whether the definition of cardinals as the class of all similar classes could embrace indeterminate classes such as that of living men, and proposed that zero could be defined as the class of such classes (an unhappy idea, similar to MacColl’s empty class in §7.3.6). This paper followed Reymond’s doctoral thesis 1908a at the University of Geneva on the supposed history of the infinite; although he had corresponded with Russell and Frege among others, he still made some rather basic mistakes, as reviewers Russell 1909a and Sheffer 1910a pointed out.
7.5.2 German philosophers and mathematicians, especially Schönflies. Now we catch up on German reactions. The general question of ‘Kant and modern mathematics’ was treated by Ernst Cassirer (1874–1945) in a long paper in Kantstudien inspired by The principles and Couturat’s Principes. His neo-Kantian background led him to emphasise the distinction between analytic and synthetic judgements (Smart 1949a). After summarising Russell’s programme, he regarded as a ‘basic lack of Couturat’s critique’ that from the ‘purely logical nature’ of his system ‘its analytical character is in no way proven’ (Cassirer 1907a, 35). He also noted that Couturat stressed that Kant recognised ‘the simply analytic significance of mathematical propositions’, while Russell appraised as a weakness the denial of the same status to logical judgements (p. 37). He also shared the dislike of Winter 1905a for sharply separating mathematical and empirical judgements (p. 46), and he criticised Russell’s definition of mathematics as the subject where we do not know what we are talking about (§6.5.1), on the grounds that a mathematician would have some idea of (say) a point or a surface when analysing it (pp. 47–48). Surprisingly, he did not discuss the paradoxes, or Part 7 of The principles on mechanics.
The German translation of Couturat’s Principes led Joseph Geyser 1909a to consider, with a similar Kantian reserve, ‘Logistic and Relation-logic’ in the Philosophisches Jahrbuch. He gave more attention to the status of judgements than to the logicist thesis, which he did not specifically mention; and he objected to inclusion differing from identity, which he seemed to regard as the dominant relation. This paper was cited in an essay on ‘the significance of Couturat’s researches in logic’ by Joseph Schnippenkotter 1910a in the next volume of the journal. Among the topics which Couturat had treated, he covered especially set theory (not, however, the paradoxes. and Leibniz’s view of logic. While unoriginal, the tone was noticeably warm.
Among mathematicians, Cantor’s fervent follower Artur Schönflies, in his early fifties, addressed the Deutsche Mathematiker-Vereinigung (hereafter, ‘DMV’) on ‘the logical paradoxes of set theory’. Labouring the point that they were caused by ‘inconsistent concepts’ which did not satisfy the law of excluded middle (hereafter, ‘LEM’), Schönflies 1906a invalidly concluded that Russell’s class ‘is thereby nothing other than the “class of all classes”’. The same level of logical acuity was evident in a reply by Alwin Korselt; rather than appraising senses of existence, he held that non-existent objects did not satisfy the LEM, and could be valuable in developing mathematics (undoubtedly the case, of course). Thus ‘all’ and ‘nothing’ were valuable concepts ‘in the works of exact logic by Peano and Schröder’ (1906a3, 217; a remarkable pairing!). He could not ‘find in the Russell paradox any reason for doubt in the basic truths of Mengenlehre’ “because” ‘logicians and mathematicians operate only with a finite number of inferences’ (p. 218); and he mistakenly thought that since Russell’s definition of ‘number of the class a names the totality of classes, then ‘“to have the equal number with a”, gave ‘an interpretation of the word “number”’ (p. 219). In a succeeding piece 1906b ‘On logic and set theory’ he rather confused the name ‘A’ of a set with a pertaining ‘Attribute α’ and so allowed the latter only to name numerals in the context of arithmetic.
The Austrian philosopher Benno Urbach criticised Schönflies in a paper seeking ‘the essence of logical paradoxes’; for him self-reference was admissible, and one should deny the LEM to predicates which generate paradoxes. Of Russell’s solutions, he liked the ‘zick-zack theory’ (Urbach 1910a, 102). In a long paper on ‘the place of definitions on mathematics’ with the DMV Schönflies disagreed with Urbach that the paradoxes were difficult to solve (1910a, 254), and stressed that the naming paradoxes cast doubt only on certain concepts and not on finite sets (p. 236). Throughout he affirmed his enthusiasm for Mengenlehre, where definitions could be used as elsewhere in mathematics. Noting the logical character of mathematical deduction, he even suggested that mathematics might be defined as the only branch of knowledge admitting indirect proofs, which involved concepts with no corresponding mathematical objects (p. 254). However, he regarded Russell’s logic as mistaken, for self-(non-)membership infringed the distinction between subject and predicate (p. 253). So he ended with a polemical declaration: ‘For Cantorism, but against Russellism!’. Korselt 1911b replied, reviewing forms of definition and noting definitional equivalence, disliking Dedekind’s definition of an infinite set (§3.4.3), and praising Frege and above all his hero Bolzano (§4.5.9). This profile placed him closer to Russell than to Cantor.
In the second part of his report on Mengenlehre (§4.2.7), which concentrated upon point-set topology and some applications, Schönflies gave the paradoxes just five pages. Starting with the footnote ‘It must suffice, to go into this in all shortness’, quickly but competently he went through the cardinal, ordinal, Russell’s and Richard’s (Schönflies 1908a, 26–31). His solution was to avoid ‘contradictory concepts’, a view which all would share; for him ‘Comparability and well-ordering constitute the basic problems of Mengenlehre’ (p. 31). Fearing that the paradoxes would help ‘a nearly increasing scepticism’ against the subject, he hoped that it ‘will not let itself go astray into scholastic dead-ends’ (p. 39).
However, Schönflies also considered the paradoxes of naming in a paper 1909a in Acta mathematica. Objecting to Richard’s claim that the class of objects definable in a finite number of words was denumerable, he offered among his counter-examples a constant-valued function, which had a non-denumerable range of values available; he took Richard’s argument as proof by reductio ad absurdum of the contrary theorem. In a reply Poincaré 1909a defended his countryman on the grounds that in this and indeed all of his examples Schönflies ‘defines an object A as having a relation B with another object C. This relation B does not suffice to define A; one must equally define the object C’, such as the constant values themselves.17
7.5.3 Activities among the Peanists. The Italian campaign was still in progress, with the fourth edition of the Formulaire mathématique (current title) coming out in 1902–1903 at 420 pages; but the next one, Formulario mathematico (1905–1908, around 500 pages18), was to be the last. The aim and style of this compilation (§5.4) was not much affected by English logicism, although its works were duly cited. No logic of relations was shown; functions were given all the work. This increased to encompass the calculus and differential geometry, some elementary theory of functions, and more point-set topology.
Elsewhere the Peanists continued to popularise their movement. Alessandro Padoa, in his late thirties, addressed a Venetian cultural society on ‘logical ideography’. Giving simple examples of arithmetical and set-theoretic propositions in partly symbolic form, Russell was mentioned only for having adopted his own notation ‘Elm’ (§5.4.7) of the class of unit classes (Padoa 1906a, 337).
In the same year Pieri 1906b performed a similar task with a lecture on the ‘new logico-mathematical direction of deductive sciences’ at the University of Catania, where he currently taught. The relationship between the new symbolic logics and mathematics was a main theme, and he claimed to quote The principles, 9 that ‘Logic constitutes the most general part of Mathematics, and Mathematics consists in the application of logical principles to certain special relations’ (p. 403); but this is far too free, and waters down logicism. However, he emphasised one aspect of logicism, for he had affirmed it himself earlier (§5.5.5): the hypothetical character of mathematics (pp. 425–431). Mentioning Fehr’s lecture at Geneva (§7.5.1), he saw a ‘progressive fusion [...] in the works of Boole, Schröder and C. Peirce on one side, and of Weierstrass, Cantor and Peano on the other’ (p. 435). On the paradoxes, he referred to a ‘a most ingenious and happy solution of the paradox of Richard’ (p. 424), but for some reason he did not give the details: it was Peano’s remark quoted in §7.2.4 that that paradox belonged to language rather than to mathematics, recently put forward in the Rivista as a ‘NEW SOLUTION’, in reaction to ‘“THE TRUE SOLUTION” of M. POINCARÉ’, namely the VCP (1906b, arts. 5, 4). Unfortunately, as was mentioned, nobody took it further at the time, including its creator and followers.
Outside the Peano school Federigo Enriques (1871–1946) caused quite a stir with his book Problemi della scienze (1906a); for a German translation (by Grelling) appeared in 1910, and an English one four years later. His long ch. 3 treated ‘problems of logic’, followed by one on ‘Geometry’ (his own mathematical speciality). The contrast with the Peanists continues, for he treated symbolic logic only briefly, and saw it ‘as a part of psychology’ (pp. 106–109), which must have appalled his Turin compatriots and their Cambridge allies. Earlier in the book he presented Russell’s paradox; but he concluded merely that the process which produced the generating class was ‘transcendental’, and so should be banished from mathematics, like all metaphysics (pp. 16–17). His compatriot Beppo Levi (1875–1961) was more definite: in a long paper 1908a on ‘Logical antinomies?’ he favoured limitation of size and imposed restrictions on permissible forms of definition and on correspondence between elements and sub-classes of a class.
Italian interest in mathematical logic was continuing, but on a much smaller scale. We pick up the next fragments in §8.6.1.
7.5.4 American philosophers: Royce and Dewey. The English translation of Enriques’s book would have appeared soon after Grelling’s in German, had the husband of the translator not been slow in checking the technical parts; when it came out in 1914, he apologised in his preface. He was the philosopher Josiah Royce (1855–1916), and the edition was put out by the Open Court Publishing Company. By then Americans had been writing for over a decade on foundational issues in mathematics, such as model theory (§4.7.3); here we note views in and around, or avoiding, logicism.
Royce’s first book had been a short primer 1881a on applying (post-) Boolean algebra to the teaching of English. In the late 1890s he deepened his concern with logic, and wrote papers of various levels of technicality during the rest of his life. The most significant item here is a long and difficult paper 1905a sent to the American Mathematical Society (hereafter, ‘AMS’), in which he related ‘the principles of logic to the foundations of geometry’. He produced the first major treatment of Kempe’s theory of multisets (§4.2.8), which he reworked by replacing Kempe’s ‘between’ relation by analysis of the relationships between the ‘elements’ of an ‘O-collection’ of mutually disjoint multisets which filled a universe, and between collections which were O- and those which were not. Laying down six principles for the existence and basic properties of an O-collection (p. 367), he produced a very general theory of collections, emphasising the various kinds of ‘series’ into which the elements could be ordered; he regarded as ‘probably quite superficial’ Russell’s emphasis on the difference between the logics of relations and of classes and propositions (p. 355). The word ‘logic’ of his title should have been ‘algebra’, perhaps; he treated Boolean algebra as a special case, with single membership of elements to a collection (pp. 401–404). One of his main concerns, inspired by Kempe 1890a, was to reduce all relations to combinations of symmetrical ones, and over the next decade he devoted enormous energy to the study of such expansions, and representation by Venn diagrams.19 He cited Veblen and Huntington, and used the same postulate techniques to show that his six principles were independent (pp. 412–415).
In an extensive review of Royce’s paper for the Journal of philosophy Theodore de Laguna 1906a claimed that the title promised more than the text delivered; he attacked Kempe’s enterprise rather than Royce’s version of it, which he liked (Kuklick 1972a, esp. ch. 10). The issue rests more on whether the theory is properly logical. Later Lewis 1914a reworked it in terms of ordered elements.
We recall from §4.7.3 that Veblen accepted the term ‘categorical’ around 1904 from John Dewey while he was studying under E. H. Moore at the University of Chicago. Dewey edited a volume of Studies in formal logic in 1903 (his 45th year), written by himself and colleagues and associates of his Department of Philosophy. Despite the adjective of its title, no symbolic logic was used; only Venn and Jevons of that ilk received mentions, and then in passing. After his four-part examination of ‘thought and its subject-matter’ (Dewey 1903a, 1–85), his colleagues treated logic as an empirical search for norms somewhat like J. S. Mill (§2.5.8) but more concerned with the social and ethical aspects (Sleeper 1986a, ch. 3).
In 1904 Dewey moved to Columbia University in New York, where he became a colleague of Keyser. In a popular lecture on mathematics delivered there in October 1907 Keyser praised the ‘creators of modern logic’; in particular, logicism showed that ‘mathematics is included in, and, in a profound sense, may be said to be identical with, Symbolic Logic’ (1907a, 13). So in his good wishes Keyser captured one of the confusions which pestered Russell’s logicism.
Keyser was both philosopher and mathematician (and also historian of sorts). Let us turn to his mathematical colleagues, who became interested in Russell’s work without adopting logicism.
7.5.5 American mathematicians on classes. In his Presidential address to the AMS, delivered in his 45th year, E. H. Moore 1903a prefaced a review of mathematics education with a survey of ‘abstract mathematics’ of all kinds, including Hilbert’s and Veblen’s. The Peanists were duly noted, but he judged that ‘this symbolism is not an essential part of their work’, and he wondered in general ‘whether the abstract mathematicians [...] are not losing sight of the evolutionary character of all life processes, whether in the individual or in the race’ (p. 405). His own research on ‘general analysis’ (§4.2.7) used many of the Peanist ‘logical signs’, listed as taken from the recent edition of the Formulario (Moore 1910a, 150); but they were there for utility rather than philosophy. However, letters during 1908 to his former student Veblen show him developing the symbolism extensively (Veblen Papers, Box 8).
Then in his late twenties and just appointed to Princeton University, Veblen had become more engaged in logicism. Flattered by Whitehead’s and Russell’s interest in his own work, he carefully read Russell’s reply 1906a to Hobson (§7.4.4) and wrote at length on 13 May 1906 (text in §11.2). As usual among mathematicians, set theory itself was his main concern, and he made a proposal like Padoa’s of 1899 (§5.4.7) but doubtless conceived independently; that membership of objects to a class should be distinguished from that of classes to the class of all classes, so that ‘The paradoxes are all gone, and all real mathematics remains’. Russell might have pointed out that neither claim could be affirmed so categorically (as it were).20
Royce’s colleague at Harvard, the mathematician Maxime Bôcher (1847–1918), also corresponded with Russell. The contact came from an address on ‘The fundamental concepts and methods of mathematics’ which Bôcher gave to an International Congress of Arts and Sciences at St. Louis in September 1904 and published as 1904a in December with the AMS. At the end he stressed the presence of ‘fundamental’ in his title; he did not try to tackle the use of intuition or the creative aspects of mathematics. He contrasted three positions within his chosen remit, with a representative figure for each. First was the standpoint enigmatically expressed in 1870 by Benjamin Peirce (§4.3.2) about mathematics as ‘the science which draws necessary conclusions’ (p. 117). Bôcher extrapolated from it the position that mathematics ‘does not deal directly with reality’, to him a nicely unifying view (p. 124, where he also cited C. S. Peirce 1896a); but he regretted the unclarity of Peirce’s phrase and the ignoring of the creative side of the subject. He contrasted this emphasis on methods with the position of Kempe, based on a very general conception of mathematical objects and relationships between them. Bôcher liked the way that here ‘mathematics is not necessarily a deductive science’, but he wondered, vaguely, if these two positions were ‘co-extensive’ for axiomatised theories (pp. 129–131).
The third position considered by Bôcher was Russell’s logicism as expressed in The principles, which he saw as a mixture of the other two in treating both objects and methods. On the former, he noted the unclarity with which Russell handled existence theorems. However, his own understanding of Russell’s position was defective, for he thought that Russell did not proffer a Peircean stress on hypotheses for pure mathematics (pp. 131–132). Russell understandably objected in a letter (now lost), and in reply on 21 April 1905 (RA) Bôcher apologised, and hoped feebly that clarity had flowed from his next sentence in his paper, about establishing the existence of a mathematical system from logical principles.
In his paper Bôcher also deplored Russell’s ‘unequivocal repudiation of nominalism in mathematics’ (p. 132), and in this letter he made his grounds more precise:
The central point at issue is your ‘class as one’. Your attitude towards this term is that of the realist, if I understand you correctly; mine is that of the nominalist. I cannot admit that a class is in itself an entity; it is for me always many entities (your ‘Class as many’) [...] If you were to accept my position here, which of course you will not do, your remarkable paradox would crumble to pieces.
Presumably Russell defended his realism over classes, for in a letter of 16 June (RA) Bôcher took the somewhat oddly named institution ‘The Rugby Cricket Eleven’ as merely ‘a name (sign, mark, what you will.’ when he wished to say of them (rather than of any members. that they had won a game. ‘[I]t may happen that at some school exactly the same boys formed the foot-ball eleven as the cricket eleven. In this case we should need two marks each associated with these same boys’. Presumably Russell replied that this was realism under some other guise; at all events, Bôcher did not understand his reply.21
Another difference between the two men concerns Kempe’s work. Whereas Bôcher found it valuable (like Royce), Russell told Couturat on 4 July 1905 that he knew of it only through those two commentators, whereas he had received offprints from Kempe the previous October (Kempe Papers, Packet 37).
7.5.6 Huntington on logic and orders. Bôcher’s Harvard colleague Huntington addressed such questions for logic in general when he teamed up with Ladd-Franklin to write an article on ‘Logic, Symbolic’ for The Americana encyclopaedia, published by the Scientific American Compiling Department (Huntington and Ladd-Franklin 1905a). He seems to have been largely responsible for it, incorporating her ‘suggestions, but I fear with rather tame results in places’ he confessed to her on 30 July 1905.22 They gave a reasonable survey of the topic; the algebraic tradition gained rather more space than the mathematical one, fairly reflecting the balance of published material at that time. But their opening definition of the subject shows how unclear even to experts was the ensemble of logics which used symbols:
Symbolic Logic, or Mathematical Logic, or the Calculus of Logic,—called also the Algebra of Logic (Peirce), Exact Logic (Schröder), and Algorithmic Logic or Logistic (Couturat),—covers exactly the same field as Formal Logic in general, but differs from Formal Logic (in the ordinary acceptation of that term) in the fact that greater use is made of a compact symbolism—the device to which mathematics owes so largely its immense development.
At this time Huntington also published in two parts a study 1905a–b of ‘the continuum as a type of order’, taking up around 60 pages of the Annals of mathematics. Harvard University quickly put out the offprints as a separate publication; and in 1917 its Press issued a slightly revised version as a book, reset and with the conventional pagination. It became a standard source in English for Cantorian order-types developed from postulates.
In the first part Huntington began with the basic notions of set theory, and then he treated simple order (ch. 2), ‘Discrete series: especially the type of the natural numbers’ (ch. 3) and ‘Dense series: especially the type of the rational numbers’, the latter including a ‘Theorem of mathematical induction’ proved from the postulates of simple order and the Dedekind cut (art. 23). The second part, which he read to the AMS in September 1905, treated ‘Continuous series: especially the type of the real numbers’ in one and several dimensions (chs. 5–6), and in an appendix he summarised transfinite arithmetic. Russell’s The principles had covered this material in prosodic form with far fewer explicit theorems and an elaborate philosophical framework; Huntington largely avoided the latter (he did not mention the paradoxes), but he cited Russell’s book regularly on various details and renderings in prose of Cantor’s technical terms. In art. 63 he presented Russell’s definition of irrational numbers but also noted the priority in Pasch 1882a (§6.4.7).
Huntington may have sent an offprint to Russell; at all events he received a letter from Russell (now lost) to which he replied on 6 January 1906 (RA). He mentioned some intended cuts (which in the end were not carried out): one was the example, due to Royce, of a ‘self-representative system’ by a map of London laid out on a pavement in London (art. 28). ‘I am also quite disconsolate’ over Russell’s scepticism about various proofs in set theory: the use of an axiom of choice seems to have excited Russell’s doubts over, for example, the equivalence of the reflexive and inductive definitions of finitude (art. 27), and the theorem that a dense series was dense-in-itself (art. 62); Cantor’s diagonal argument and the basic covering inequality (663.1) were also causing qualms which Huntington did not share. This postulate theorist made a good general point with which Russell should have concurred:
In fact the central problem in all the recent discussion about the transfinite ordinals seems to be this: How shall we prove the consistency of a set of hypotheses in the cases where no finite or denumerable example can be exhibited?
7.5.7 Judgements from Shearman. Finally we consider reactions to logicism from an Englishman. In a lecture on 3 April 1905 to the Aristotelian Society, A. T. Shearman 1905a reviewed ‘Some controverted points in symbolic logic’. These included the primacy of classes (Venn, say. or of propositions (MacColl), the place of ‘Modals’ in view of ‘MacColl’s very ingenious system’, inclusive or exclusive disjunction, and the worthwhile role of inversion procedures and of the logic of relatives. The published version does not contain the discussion: this is a pity, for on the last topic he mentioned only Peirce, and Russell was present in the audience.
Shearman used this lecture in a ‘critico-historical study’ of The development of symbolic logic, which was published the following year, his 41st. Related to his teaching at University College London, where he was a lecturer, his coverage was quite wide: all the algebraic logicians, MacColl, Frege and Peano (but unfortunately not his disciples, or Couturat. as well as Whitehead and Russell. They came mainly in a passage on ‘The new treatment of mathematical conceptions’ (Shearman 1906a, 196–220). After quoting Russell’s definition of logicism from the head of The principles, he stressed its quantitative as well as qualitative character (p. 200). As well as discussing Russell’s and Peano’s choices of indefinables, he gave Russell’s definition of cardinals and even mentioned the multiplicative class (though not its current disputes), and also emphasised the place of relations in logicism. He included some guarded remarks on Whitehead’s Universal algebra, and five appreciative pages on Frege, the latter seemingly drawn from Russell’s appendix in The principles (pp. 213–218, with ‘Kerry’ (§4.5.4) misspelt as ‘Kelly’).
By and large Shearman gave a good impression to the general reader of the range of theories within symbolic logic without, however, bringing out sufficiently the great differences between them. On the contrary, he began his preface by indicating that he followed Johnson, who had written to him in 1903 of the ‘error’ of thinking of the various symbolic systems as being radically distinct (p. v.—which indeed they are! In addition, he did not present much set theory (Cantor was never mentioned), and so he could not contrast it with part-whole theory. Thus his study was still less critical than historical.
Shearman followed with a sequel volume 1911a in which he described Frege, Peano and Russell in roughly equal measure, including their notations (Frege’s praised but its consumption of paper disliked). But he did not analyse logicism or even the paradoxes, or explain sufficiently the mechanics of set theory, and gave a fair-minded but not penetrating ‘survey of symbolic logic’.
At least Shearman had an attitude: at Cambridge itself logic was still dominated by the syllogistic tradition with a few splashes of the algebraic tradition. Such at least is the impression conveyed by the fourth edition of J. N. Keynes’s Studies and exercises in formal logic (1906), where no mathematical logician was mentioned. Whitehead was extremely isolated in the city.
7.6 WHITEHEAD’S ROLE AND ACTIVITIES, 1905—1907
[Principia mathematica], which was of great importance in its day, doubtless owed much of its superiority to Dr. (after Professor. Whitehead, a man who, as his subsequent writings showed, was possessed of that insight and spiritual depth so notably absent in Russell; for Russell’s argumentation, ingenious and clever as it is, ignores always those higher considerations that transcend mere logic.
Russell 1936b
7.6.1 Whitehead’s construal of the ‘material world’. (Lowe 1985a, ch. 14. On 18 August 1904 he spoke on ‘Peano’s symbolic method’ to the British Association for the Advancement of Science (notice in their Report 1904), 440); no text survives. In September 1905 he sent a long paper to the Royal Society, to which he had been elected two years earlier (§6.8.2). In 1899 he had had to withdraw his last paper, for lack of originality (§6.2.4); but this one was accepted, although he had some tussles with his referees, largely on presentation and use of logical symbols.23 It was published in their Philosophical transactions as 1906b. Russell, who had not been much involved in it, made several pages of notes after its appearance (RA).
In 61 pages Whitehead examined ‘mathematical concepts of the material world’ by laying out in axiomatic form elaborate constructions from basic ‘entities’ which ‘constitute the “stuff” of space’ (p. 465). For general background he cited Kempe 1890a, Veblen 1904a and Royce 1905a (p. 469). It reads like logicism, and not just logical notations (especially relations), but applied to physical science; it lay within his planned treatment of geometry in PM (§11.5), and also presaged some later philosophical concerns (§9.4.3).
Five ‘Concepts’ were presented (pp. 478–484). The first was ‘the classical concept of the material world’, composed of points of space, instants of time and particles of matter. The next Concept treated physical particles statically in space; Whitehead defined particles in terms of two-place relations between points, acknowledging The principles, 468 for the idea. ‘Concept III’ handled them in motion, so that three-place relations were need in order to include time. The last two Concepts dealt correspondingly with the aether in static and dynamic states; we recall from §6.2.4 that his first mathematical interest had lain in electromagnetism.
‘In what sense can a point at one instant be said to have the same position as a point at another instant?’ (p. 481). To provide a framework Whitehead used the four-place relation ‘S;(uvwt)’, where u, v and w were rectangular ‘kinetic axes’ at instant t, from which velocity and acceleration were definable. One of his reductionist aims was to avoid the predicament of treating a physical point both as a basic notion and as a complex (Russell in The principles, ch. 51, for example) by defining it from lines, a primitive notion which he called ‘objective reals’. He offered two strategies, one using a theory of dimensions and the other working via ‘interpoints’. This latter notion, an abbreviation of ‘intersection points’, was an extension to space-time of relationships of order in projective geometry with the notion of intersection taken as primitive. He assumed that any given entity a determined the order of three more entities b, c and d at time t in a relation ‘R;(abcdt)’, defined two entities x and y to be ‘in a similar position’ if they could be exchanged at any of the three central places in R (and so have the same position in the order), and specified the ‘class of interpoints’ of a at t to be composed of a and all points which were similar to any x substitutable in R (pp. 484–488). This gave him a general means of treating points in space-time.
Although deploying quite different methods, Whitehead’s foray is not unlike Royce 1905a in its generality and concern with geometry. But some of his notations were not friendly: the segment of between points a and b was symbolised ‘R;(a;b)’, its prolongations beyond a and beyond b were respectively ‘R;(ab;)’ and ‘R;(;ab)’, and the class of entities on a with positions similar to x was 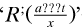 —a horrible notation. This forbidding appearance must have deterred even symbolically literate readers; and naming the Concepts merely by Roman numerals hardly excites the intuition, either. Like Royce’s, Whitehead’s paper made little impact—apart from upon his own philosophy when it flowered in the 1920s after he had finished with logicism (Lowe 1962a, chs. 7–8).
—a horrible notation. This forbidding appearance must have deterred even symbolically literate readers; and naming the Concepts merely by Roman numerals hardly excites the intuition, either. Like Royce’s, Whitehead’s paper made little impact—apart from upon his own philosophy when it flowered in the 1920s after he had finished with logicism (Lowe 1962a, chs. 7–8).
7.6.2 The axioms of geometries. Whitehead soon presented some of this material on geometry at a more elementary level when in 1905 Cambridge University Press launched an important series of short ‘tracts in mathematics and mathematical physics’. He was one of the first authors, producing the fourth and fifth volumes as his 1906a and 1907b (the prefaces are dated October and March of their respective years). Conceived as a pair, he presented the axioms of projective and of descriptive geometries, distinguishing them by the property that in projective geometry ‘two coplanar lines necessarily intersect. Thus Euclidean Geometry is not projective, but becomes so’ when the points of infinity were adjoined; ‘A non-projective Geometry will be called a Descriptive Geometry’ (1906a, 5–6), for which he concentrated upon transformations (including Sophus Lie’s theory), congruence and distance.24
Whitehead’s treatments were quite converse to Russell’s; he gave elementary but technical presentations, and not much philosophy (for which he referred the reader to The principles). Unlike the 1905 paper, he used no logical symbols, although he came close to talking propositional functions when formulating the ‘general theory of correspondence’ (1907b, 34–36). However, the philosopher appeared in a few places; in particular, the first tract began with an extensive discussion of the nature of axioms and of definitions (a part of it was translated in the Revue as Whitehead 1907a). For projective geometry he cited Pieri 1898a (§5.5.5) as his main source; for descriptive geometry he relied similarly on Peano 1888a (§5.2.4). However, although he had been in contact with Veblen and cited his 1905a (1907b, 7) he did not allude to categoricity.
7.6.3 Whitehead’s lecture course, 1906–1907. While Whitehead worked on the second tract he also gave a substantial course on ‘The principles of mathematics’ at Trinity College in Lent (Spring) term 1907. No manuscripts survive, as usual, but luckily we have the notes taken by H. W. Turnbull (1885–1961), who later made his career as a mathematician and historian of mathematics. Below I have silently expanded some abbreviations; and most of the folios are not numbered.
Whitehead began by sketching various views on numbers, including that of ‘Frege (following Herbart)’, which was ‘practically that of B. Russell’ (Turnbull m1907a, fol. iv). This latter naturally dominated the subsequent discourse; for example, ‘the present king of France is 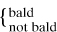 are both not bald false and one contradicts the other’ (fol. 3). But he treated mainly the mathematical side, from the integers produced by MI (the ‘nerve of the whole thing’) through rational and real numbers to transfinite arithmetic, including cardinal exponentiation and uses of the multiplicative axiom. His current understanding of model theory was that the basic notions (number, zero, successor) in the Peano axioms ‘might be fitted on to anything. B. Russell doesn’t seem to object to this’. In the last part of the course he summarised the material of his new tracts, and then also parts of his recent Royal Society paper in his symbols (all those quoted in §7.6.1, for example).
are both not bald false and one contradicts the other’ (fol. 3). But he treated mainly the mathematical side, from the integers produced by MI (the ‘nerve of the whole thing’) through rational and real numbers to transfinite arithmetic, including cardinal exponentiation and uses of the multiplicative axiom. His current understanding of model theory was that the basic notions (number, zero, successor) in the Peano axioms ‘might be fitted on to anything. B. Russell doesn’t seem to object to this’. In the last part of the course he summarised the material of his new tracts, and then also parts of his recent Royal Society paper in his symbols (all those quoted in §7.6.1, for example).
In the middle part Whitehead explained some features of the logical system that he and Russell were developing. No mention was made of substitution; instead, he presented propositional functions, their ‘ranges of significance’ divided into types, functions of functions, truth-functions and functional quantification; curiously, he seemed not to mentioned the paradoxes. Referring to Russell 1906h, he reported that ‘Russell says a proposition is an entity, in contrast to the view that p ⊃ q had meaning when p and q are any entities whatever. This must be dropped and propositions must be looked on as entities distinctly by themselves’. What was going on at Bagley Wood?
7.7 THE SAD COMPROMISE: LOGIC IN TIERS
7.7.1 Rehabilitating propositional functions, 1906–1907. Meanwhile Whitehead’s collaboration with Russell continued, now in a definitive form. They had referred to ‘volume II’ up to at least November 1905;25 but Russell told Couturat on 21 August 1906 that ‘We are thinking of doing an independent book, which we call “Principia mathematica”’. The new title was chosen perhaps not in imitation of Isaac Newton but in line with G. E. Moore’s book Principia ethica (1903), which treated ethics within the new philosophical framework within which they wished to site logic and logicism.
After abandoning the substitutional theory, Russell reverted to propositional and denoting functions with free and apparent variables. From the late summer of 1906 through 1907 he wrote many manuscripts, focusing especially on functions but also considering their relationships to classes. The main common factor was the VCP and some stratification into types, although more than one version was put forward. Much could be said on the changes which Russell rang on the various possibilities; a small selection of points is made here, with the texts awaited in Papers 5.
One of the most striking transitional manuscripts is a diary-type text m1906i of 108 folios called ‘the paradox of the liar’, which Russell started in September of that year. He started out with that conundrum, stressing the place in it of negation. Granting existence to propositions led to great difficulties with MI, and he wondered about taking ‘and so on’ as a primitive idea (fols. 15–17). But this was abandoned, and a propositional hierarchy was proposed; ‘propositions’ had no quantifiers, and the location of a ‘statement’ was determined by its apparent variables (fols. 30–34). Later he used substitutional theory before rejecting it for its complications (fols. 66–87); although he added a note in June 1907 doubting this reservation, this was its last appearance in full regalia. Otherwise he deployed propositional functions; a type theory involving the VCP was imposed, with (lack of. quantification again determining the bound and free variables. The base was occupied by individuals, defined as ‘any single existent’, so that Dedekind’s proof of an infinitude of objects by a sequence of thoughts (§3.4.2) had to be abandoned (fol. 65). Near the end he wondered whether the axiom of infinity was an empirical question about the universe, and saw the need of both it and the multiplicative axiom for proving existence-theorems in mathematics (fols. 101–104).
In another long journey through ‘Fundamentals’ Russell m1907b started with the distinction between a propositional function and the class that could be formed from it. A rumination on functions included worry that the difference between predicative and non-predicative functions was not clear, whether truth-functions could be values of apparent variables, and the place of belief predicates in the overall structure (fols. 8–12). As regards his paradox, he noted that non-self-membership could sometimes lead to true or to false propositions and that self-membership was ‘not always nonsense’; so he mooted the idea of restricting the use of the law of excluded middle (fols. 24–25). For classes (fol. 38), ‘we are to have
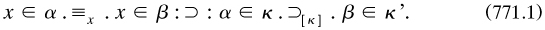
However, despite (or because of?) such flights, no substantial theory resulted.
A group of manuscripts on functions, which seem to belong to this period and are cited as m1907c, included in the second text a different approach drawing on the notion of the form of an expression X containing a variable x, called ‘function’ and written 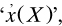 specified as that ‘which may be preserved constant [in X] while x varies’. Conversely, when x was introduced into the form F, then the expression ‘F | x’ was produced. These converse indefinable notions were based on the following assumptions
specified as that ‘which may be preserved constant [in X] while x varies’. Conversely, when x was introduced into the form F, then the expression ‘F | x’ was produced. These converse indefinable notions were based on the following assumptions
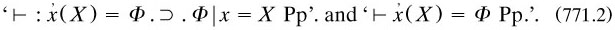
The approach was ambitious, even encompassing implication:
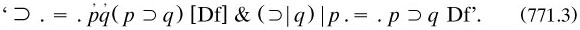
While these ideas were not durable, the notion of logical form was to appear later in his philosophy of logic (§8.2.4).
7.7.2 Two reflective pieces in 1907. On 9 March Russell addressed the Cambridge Mathematical Club on ‘The regressive method of discovering the premises of mathematics’. Although he discussed an important aspect of logicism which otherwise was rather ignored, he never published his manuscript (it appeared in the collection Russell Analysis). He was concerned with the philosophical consequences of analysis (in his narrower sense of §6.6.1); that ‘in the logical theory of arithmetic’ a theorem such as ‘2 + 2 = 4 [...] is more certain than the premises, and the supposed proof therefore seems futile’ (m1907a, 272). His justification was surprising, and hard to articulate: the ‘logical simplicity’ of a proposition, ‘measured, roughly speaking, by the number of its constituents’, the fewer the better (p. 273). He argued that aiming at simpler premises ‘gives a greater chance of isolating possible pervading elements of falsehood’, and that they ‘have many more consequences than the empirical premises’. Then he contrasted Peano’s axioms for arithmetic with the regresses to Frege’s and his own definitions of integers as classes of similar classes (pp. 276–278, where he noted also the paradoxes). Admitting that some of Frege’s logical premises were ‘more intrinsically obvious’ than others, he assessed similarly his own axioms for the propositional and predicate calculi. He also mentioned the need for an (empirical. axiom of infinity (p. 282), but passed over the issue of its obviousness!
In October Russell published an introductory essay 1907d of similar intent on ‘the study of mathematics’. He had written it five years earlier, as part of a general consideration of educational questions (the little piece 1902b on teaching Euclid (§6.2.2) may belong to the same concern); but it had been rejected by the original journal, so he offered it to his friend Desmond McCarthy to help launch The new quarterly. Demanding that textbooks be written in a more systematic manner than was customary, he proffered ‘Symbolic Logic’ as ‘the fundamental science which unifies and systematizes the whole of deductive reasoning’, and argued against the psychological interpretation of logic (1907d, 90, 91).
7.7.3 Russell’s outline of ‘mathematical logic’, 1908. Between the views on logic presented in these two essays lay a difficult area of heuristics which Russell addressed in July 1907, when he wrote an important paper outlining the form which PM was to take. Published ten months later in the American journal of mathematics as his 1908c, it is one of his most famous; for in 41 pages he sketched out the apparatus of ‘Mathematical logic as based on the theory of types’—an early use by him of Peano’s phrase ‘mathematical logic’ (§5.3.2). He started in art. 1 with seven ‘contradictions’ (the liar, his own, the relations version, Berry’s, the least indefinable ordinal, Richard’s and Burali-Forti’s, in that peculiar order), diagnosed ‘self-reference or reflexiveness’ as the illness, and prescribed as medicine the VCP, which he cast in the form ‘Whatever involves all of a collection must not be one of the collection’. In each of the seven cases some totality no longer belonged or referred to itself; but various harmless features of logic and mathematics, such as the law of excluded middle and MI, also required modification (art. 3). In the rest of the paper he sketched out some details.
The exposition started in art. 2 with ‘all and any’ in quantification; the VCP showed the importance of ‘The distinction between asserting ϕx and asserting (x). ϕx [, which] was, I believe, first emphasized by Frege’. The predicate calculus split into a ‘hierarchy of types’ and also orders; the presentation (art. 4) is too brief, and often misunderstood, but the theory is different from that to be used in PM (compare §7.9.1–2). ‘A type is defined as the range of significance of a propositional function’; that is, a class (of humans for ‘x is a man’, say); at the bottom are individuals, “defined” as ‘something destitute of complexity’. Quantification over x, to make it an ‘apparent variable’ in a hitherto unquantified ‘elementary proposition’, produced ‘first-order propositions. These form the second logical type’, that is, the class of such propositions. Quantification over these propositions produced new ones belonging to the third type, and so on. Some examples would have been helpful; for example, that the second type contained both
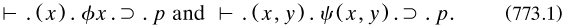
Since each quantification was effected independently of others, a function might have only some of its lower-order functions quantified; for example, (∃ϕ). ϕa. Substitution remained in that Russell briefly related his theory of functions to matrices within propositions (for an elaboration, see Landini 1998b, ch. 9).
Functions which were ‘of the order next above’ that of at least one of their variables were called ‘predicative’, and marked with an exclamation mark as in §7.3.1: for example (Russell’s own), in ‘f!(ψ!ž)’ f contained only ψ!ž as apparent, within which only z was apparent. The importance of this kind of function resided in the repair needed to render to mathematics; the VCP forbad, say, subtractions such as 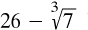 because the latter number was irrational, defined in terms of a class of classes of rationals and so determined by a function of an order different from that for 26. To save arithmetic and mathematics in general, he assumed ‘the axiom of classes, or the axiom of reducibility’ (art. 5), also ‘the axiom of relations’ for functions of more than one variable. It claimed that every propositional function had a logically equivalent mate among the predicative sub-class: for example for ‘double functions’,
because the latter number was irrational, defined in terms of a class of classes of rationals and so determined by a function of an order different from that for 26. To save arithmetic and mathematics in general, he assumed ‘the axiom of classes, or the axiom of reducibility’ (art. 5), also ‘the axiom of relations’ for functions of more than one variable. It claimed that every propositional function had a logically equivalent mate among the predicative sub-class: for example for ‘double functions’,
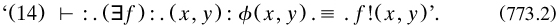
It seems strange that he (and Whitehead. did not realise that this assumption minimised, maybe even nullified, the hierarchy of orders; evidence in the same article is given by the Leibnizian definition (732.3. of the identity relation, now quantified over predicative functions. However, he stressed that asserting a function was not equivalent to asserting its predicative mate.
Formula (773.2. occurred in art. 6, where Russell launched a systematic and symbolic account of the logical system: the indefinables (propositional function, the truth of any and of all its values, negation and disjunction, predicative function in any type, and assertion); axioms for the propositional and predicate calculi; the determination of classes and relations from predicative functions by means of contextual definition (art. 7); his form (734.1) of definite description, and intensional and extensional functions (art. 8); and the definitions of cardinal and ordinal numbers up to ωn and  n for any finite ordinal n, and the need in the arithmetics for the multiplicative axiom (arts. 9–10). The axiom of an infinitude of individuals was adopted reluctantly in art. 9, again made as an empirical assumption. Curiously, he did not explicitly state logicism, although the nature of the enterprise should have been clear to his mathematical audience.
n for any finite ordinal n, and the need in the arithmetics for the multiplicative axiom (arts. 9–10). The axiom of an infinitude of individuals was adopted reluctantly in art. 9, again made as an empirical assumption. Curiously, he did not explicitly state logicism, although the nature of the enterprise should have been clear to his mathematical audience.
7.8 THE FORMING OF PRINCIPIA MATHEMATICA
7.8.1 Completing and funding Principia mathematica. (My 1975b) By the time that that article appeared in May 1908, Russell and Whitehead were well into writing the book which it presaged; they more or less completed it during the winter of 1909–1910. Not much record survives of the details of the labour; Whitehead discussed his current progress and reported various matters in letters passing between Grantchester and Bagley Wood during 1908 and 1909. An outside reader was Ralph George Hawtrey (1879–1975), then early into his distinguished career in Treasury; an undergraduate in mathematics at Trinity of the same year as Jourdain, he had retained sufficient Tripos mathematics to make valuable comments in long letters (RA and copies).
While Whitehead and Russell revised each other’s work (Russell 1948a), Russell seems to have written out the final version for publication. He reported progress to Ivy Pretious (1881–1958), whom he had come to know in connection with his work on Free Trade (§6.1.2). On 25 May 1908 he told her that ‘On average days I do 9 or 10 hours’ work at my book [...] I have written about 2000 pages of the manuscript of my book since last September; there will be about 6000 or 8000 altogether’ (RA). On 18 October 1909 he reported to Lucy Donnelly (RA) that
tomorrow I go to Cambridge taking with me the manuscript of the book for the printers. There is a certain amount at the end that is not yet finished, but over 4000 pages are ready, and the rest can be finished easily. [...] the manuscript is packed into two large crates [...] It is amusing to think how much time and trouble has been spent on small points in obscure corners of the book, which possibly no human being will ever discover.
The reaction of the Press to the crates was financial shock. Whitehead received from them a letter of 29 October announcing that ‘the manuscript sent would make 1648 pages, and the cost of 750 copies, without binding or advertising, would be £920’. An application for financial support from the Royal Society was suggested and acted upon. Russell had been elected Fellow in May 1908, after nomination in October 1906 by Whitehead (my 1975a): so they were able to apply jointly for £300, in a fascinating document written together (text in §11.5). On 22 January 1910 £200 was agreed by Council of the Society, so that, as Russell put it in his autobiography, ‘we thus earned minus £50 each by ten years’ work’ (1967a, 152).
Russell’s memory of the financial loss was once again selective, though this last time probably intentionally. Composition was ‘slow work, as there is only one compositor who can read our queer symbols’, he told R. B. Perry in April 1910 (Sheffer Papers, Correspondence Box). But the first Volume appeared without apparent hitch in December 1910, in 750 copies at £1.5s. each for around 670 pages; they sent copies to the Society, Trinity College, Berry, Couturat, Forsyth, Frege, Hardy, Hawtrey, Hobson, Johnson (the Press’s reader), Jourdain, Peano and Royce. However, during 1911 Whitehead found that he had made a serious mistake in the second Volume by using the axiom of infinity without restriction (§7.9.3). Several passages had to be rewritten, and a special preface prepared for the Volume, which did not appear until the spring of 1912. The extra cost was considerable: Russell seems to have borne it alone. The third Volume came out a year later, like its predecessor in 500 copies; they sold respectively at £1.10s and £1.1s each for around 800 and 490 pages.
The period of publication straddled Whitehead’s 50th birthday and Russell’s 40th; and the two were together for a time, since in October 1910 Russell started a five-year lectureship in ‘logic and the principles of mathematics’ at Trinity College. By 1920 all three Volumes were nearly out of print, and a second edition was being mooted between the Press and Russell (§8.4.4).26
In fact, the first edition was still not complete. In January 1913 the Press had agreed that the third Volume be split into two; Whitehead was to write the fourth Volume, on geometry. However, while he prepared quite a lot of it, he was to abandon it during (and partly because of. the Great War, and the material was destroyed with all his effects after his death in 1947. It joined its predecessors, for they had burnt the contents of the crates soon after publication; only one folio survives, for *208·4, in a letter of 3 November 1911 to Ottoline Morrell in which Russell said that he wrote out the book on a little oak table which had belonged to his mother (copy in RA). However, Russell kept over 680 folios of discarded or replaced folios and also a 250-folio concordance of cross-references in the work. They show that various passages had been omitted from the final printed version, whose design will now be summarised.27
7.8.2 The organisation of Principia mathematica. After a short preface, the book opened with a general introduction of 88 pages comprising three chapters on basic ‘ideas and notations’, type theory and ‘incomplete symbols’. The rest was divided into six Parts numbered by Roman numerals, each one going into ‘Sections’ ordered by letters; I shall cite a Section as, say, ‘IVB’. Each Section contained ‘numbers’ (of all names to choose!. with definitions or propositions numbered in Peano’s way as cited already (say, ‘*35·812’ of number 35); as mentioned in §1.3.1, citation by page number is to the second edition. Table 782.1 summarises the contents of each Section, indicating also the asterisked numbers and the numbers of pages in the first edition; ‘+’ indicates that a quantity of the replaced or discarded ones belongs to the Section, not necessarily with the same numbers. I shall refer to ‘the authors’ when ‘they’ is ambiguous.
TABLE 782.1. First edition of Principia mathematica (1910–1913).
The numbers of pages are for the first edition. Volume 2 started at Section IIIA, Volume 3 at Section VD. The titles of the Parts, and numbers of pages (omitting ithe introductions) were I. ‘Mathematical logic’ (251); II. ‘Prolegomena to cardinal arithmetic’ (322); III. ‘Cardinal arithmetic’ (296); IV. ‘Relation-arithmetic’ (210); V. ‘Series’ (490); VI. ‘Quantity’ (257).
Section; pages |
(Short) ‘Title’ or Description: other included topics |
IA: *1–*5; 41 |
‘Theory of deduction’: Propositional calculus, axioms |
IB: *9–*14; 65 |
‘Theory of apparent variables’: Predicate calculus, types, identity, definite descriptions |
IC: *20–*25, +; 48 |
‘Classes and relations’: Basic calculi: empty, non-empty and universal |
ID: *30–*38, +; 73 |
‘Logic of relations’: Referents and relata, Converse(s) |
IE: *40–*43; 26 |
‘Products and sums of classes’: Relative product |
IIA: *50–*56; 57 |
‘Unit classes and couples’: Diversity; cardinal 1 and ordinal 2 |
IIB: *60–*65; 33 |
‘Sub-classes’ and ‘sub-relations’: Membership, marking types |
IIC: *70–*73; 63 |
‘One-many, many-one, many-many relations’: Similarity of classes |
IID: *80–*88, +; 69 |
‘Selections’: Multiplicative axiom, existence of its class |
IIE: *90–*97; 98 |
‘Inductive relations’: Ancestral, fields, ‘posterity of a term’ |
IIIA: *100–*106; 63 |
‘Definitions of cardinal numbers’: Finite arithmetic, assignment to types |
IIIB: *110–*117; 121 |
‘Addition, multiplication and exponentiation’ of finite cardinals: inequalities |
IIIC: *118–*126; 112 |
‘Finite and infinite’: Inductive and reflexive cardinals, X0, axiom of infinity |
IVA: *150–*155, +; 46 |
‘Ordinal similarity’: Small ‘relation-numbers’ assigned to types |
IVB: *160–*166; 56 |
‘Addition’ and ‘product’of relations: Adding a term to a relation, likeness |
IVC: *170–*177; 71 |
‘Multiplication and exponentiation of relations’: Relations between sub-classes, laws of relation-arithmetic |
IVD: *180–*186; 38 |
‘Arithmetic of relation-numbers’: Addition, products and powers |
VA: *200–*208, +; 97 |
‘General theory of series’: Generating relations, ‘correlation of series’ |
VB: *210–*217; 103 |
‘Sections, segments, stretches’: Derived series, Dedekind continuity |
VC: *230–*234; 58 |
‘Convergence’ and ‘limits of functions’: Continuity, oscillation |
VD: *250–*259, +; 107 |
‘Well-ordered series’: Ordinals’, their inequalities, well-ordering theorem |
VE: *260–*265, +; 71 |
‘Finite and infinite series and ordinals’: ‘Progressions’, ‘series of alephs’ |
VF: *270–*276; 52 |
Compact, rational and continuous series: Properties of sub-series |
VIA: *300–*314; 105 |
‘Generalisation of number’: Negative integers, ratios and real numbers |
VIB: *330–*337; 58 |
‘Vector families’: ‘Open families’, vectors as directed magnitudes |
VIC: *350–*359; 50 |
‘Measurement’: Coordinates, real numbers as measures |
VID: *370–*375; 35 |
‘Cyclic families’: Non-open families, such as angles |
The book reveals itself as a Principia Peaniana atque Cantoriana rather than a veritable Principia mathematica: meticulous detail on these mathematical topics, but complete silence on the rest. The coverage was far less than in The principles: the absence of mechanics clarified logicism (§6.7.6), but the silence over the calculus and all its consequences, mathematical topics then in very vigorous development, is hard to understand, especially as PM advanced as far as continuous functions (§7.9.8). The rather scrappy design of the third Volume was much guided by the scope of the fourth one; but that does not explain the silence over, say, statistics. The four-page preface made no reference to any omissions; but then the logicist thesis was not stated there either! Maybe Whitehead and Russell had become too engrossed with the endless details; or perhaps the three dubious axioms (reducibility, infinity, choice) held them back.
As a technical exercise PM is a brilliant virtuoso performance, maybe unequalled in the histories of both mathematics and logic; the chain-links of theorems are intricate, the details recorded Peano-style down to the last cross-reference, seemingly always correctly. However, one has to pass beyond the unclear introductory material—an eccentricity these days—before these virtues emerge, especially in the second Volume, which is easily the best of the trio. The rest of this section deals with the general principles of the system; the next one treats the type theory and the handling of mathematics.
In addition to the book, some French articles are available. Firstly, in the Revue Poincaré 1909b expressed doubts about logicism as presented in Russell 1908c; so the author brought him up to date in a reply 1910b based upon a translation of much of the last two chapters of the general introduction. Secondly, there are the products of a hectic time in Paris when Russell gave three lectures: 1911d on 22 March 1911 on the axioms of infinity and of choice, 1911b the same evening on the philosophical aspects of mathematical logic (published later in the Revue), and 1911a the next day on ‘analytic realism’. The occasion of his visit had an unexpected but profound consequence for his life: on the way to Paris he stayed overnight in London at the home of Morrell, and fell in love with her to a depth which he had never previously experienced.
7.8.3 The propositional calculus, and logicism. The first chapter of the introduction of PM, and the opening Sections IA and IB of the main text, are unfortunately the most unclear in the entire work. In them the authors laid out the propositional and predicate calculi (not their names), but in a bizarre manner. For example, as in Russell’s paper on implication (§7.4.8) they used the phrase ‘propositional function’ and notation ‘ϕx’ at first to refer to a logical combination of propositions before turning to the usual sense; the explanation was buried on p. 15, to back up the explanation of ‘elementary proposition’ as a proposition free of quantifiers and variables and containing only a finite number of connectives (p. 91). The ‘primitive proposition’
‘*1·11. When ϕx can be asserted, where x is a real variable, and ϕx ⊃ ψx can be asserted, where x is a real variable, then ψx can be asserted, where x is a real variable. Pp.’
has to be understood in the first sense; the example following, which concerns the proof of a theorem (*2·04. in the propositional calculus, makes this tardily clear.
Another ambiguity is also present here; *1 · 11 concerns inference, following
‘*1·1. Anything [sic] is implied by a true elementary proposition is true. Pp’.
on implication. (Their definition of truth is quoted in §7.9.2). The difference of the latter from inference was given as between
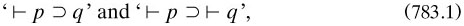
with the former omitted for convenience as the intermediate proposition of the latter. The explanation ‘An inference is the dropping of a true premiss; it is the dissolution of an implication’ (p. 9. makes nice English but muddy logic. In *1 the difference was expressed more simply as between ‘it is true that p implies q’ and ‘p is true; therefore q is true’ (p. 92). However, in the predicate calculus,
‘*9·12. What is implied by a true premiss is true. Pp.’
was held to deal ‘with inference to or from propositions containing apparent variables, as opposed to implication’, which muddied the logic again.
All this talk of implication belies the fact that it was not a logical primitive. The authors assigned this status to negation and disjunction, specifying them informally via truth-values of propositions p and q as ‘p is false’ and ‘p is true or q is true’ respectively (pp. 93–94). Since the latter clause uses ‘or’ (presumably inclusively), then more muddiness is evident; the earlier account on p. 6 is better. They then defined implication, conjunction and equivalence for propositions (*1·01, *3·01, *4·01); these definitions locate their connectives contextually within the propositions involved, although they may also be construed as rules of substitution.
Apart from these general axioms, they offered straightforward symbolic ones, giving them short names for convenient referencing: for example,
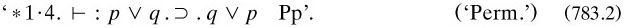
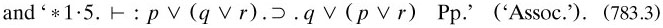
Since they chose to have no means of testing the independence of the axioms of the calculi (p. 91), it is not surprising that *1·5 turned out to be redundant (Łukasiewicz 1925a and Bernays 1926a (§8.7.4)). On 22 June 1908 Russell told Hawtrey that ‘I consider the proof of the [Pps] to be inductive’ (copy in RA), obviously in the scientific sense of induction rather than that of MI; and, as in science, the research was found not to be foolproof. They required their system to ‘embrace among its deductions all those propositions which we believe to be true and capable of deduction from logical premises alone’, and also to ‘lead to no contradiction’ (pp. 12–13); but they had no means of establishing completeness or consistency.
In these Sections the authors ran through many of the basic theorems. The treatment of equivalence was rather slight, and lacked theorems such as
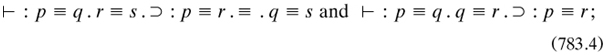
the first is needed at least once (in *20·51), while the lack of the second was pointed out to Russell by G. H. Crisp on 7 October 1919 (RA). Some other proofs in Part 1 have slips of this kind.
Since the substitutional theory had been abandoned, substitution was handled rather casually, unlike the explicit principle in Russell’s paper 1906b on implication (§7.4.8). The fractional notation of (746.4)1 was used; for example, the proof of
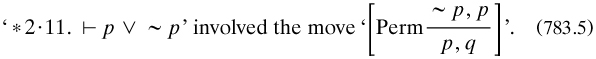
This theorem was ‘the law of excluded middle’, a metalaw to us; others of this status include the laws of contradiction and of double negation (*3·24 and *4·13 respectively).
Related to these unclarities is the logicist thesis itself. The short introduction to Section IA announced that the ensuing ‘theory of deduction’ would ‘set forth the first stage of the deduction of pure mathematics from its logical foundations, where deduction was ‘the principles by which conclusions are inferred from premisses’ and ‘depends upon the relation of implication’ (PM1, 90). This sounds like the implicational logicism of The principles; however, pure mathematics was mentioned for the first time in the book here: elsewhere ‘mathematics’ was mentioned, and an inferential standpoint about its relationship to logic seems to have been intended. Only admittedly doubtful principles such as the axiom of infinity or the multiplicative axiom were stressed as antecedents ‘so that our propositions, as enunciated, are true even if the axiom of infinity is false’ (to quote a typical example from 3, 234). But this view is surely too easy an option: hope that the premisses are true, but if not, the truth of the theorems will not be affected. The ambiguities of implication and inference strike at the heart of their logicism.
7.8.4 The predicate calculus, and descriptions. After stating a propositional function ϕx as being of a variable, the authors rather unfortunately asserted that ‘the essential characteristic of a function is ambiguity’ (p. 39), whereas of course the function itself is quite determined, or should be. Both here and elsewhere the status of variables was, well, ambiguous: early on ‘variables will be denoted by single letters’ (p. 5), but pretty often and surely correctly they were letters. Moreover, they ranged over not only ‘entities’ but also non-entities such as ‘propositions, functions, classes or relations’ (p. 4). Here and elsewhere x usually ranged over individuals—an important mystery of their own, explored in §7.9.3.
Quantification was defined veridically in terms of truth values. For ϕx ‘there is a range, or collection, of values of x yielding true or false propositions’: then ‘the symbol “(x). ϕx” may be read [...] ϕx is always true’, while ‘“(∃x). ϕx” may be read “there exists an x for which ϕx is true”’ (p. 15.: better, surely, there exists a value a of x for which ϕa is true.
The other axioms of the calculus were
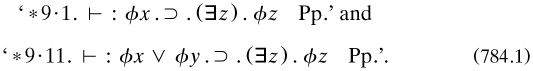
(McKinsey 1935a showed that the first one was redundant). Rather oddly, they then defined ‘∃x’, thus;
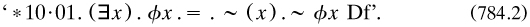
‘Descriptions’ were based in *14 upon definition (734.1. and its brother for two independent variables, with the companion sense ‘E!’ of existence (*14·02). They emphasised the need to watch the ‘scope’ (their word. of descriptive terms within formulae, so as to avoid ambiguities; for example, the basic contextual definition was now written
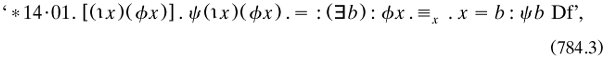
where the square-bracket expression launched the scope.
As we have seen, a main purpose of this theory was to specify single-valued mathematical (that is, denoting) functions f(x) in terms of propositional functions ϕx; they might have stressed the relationships more. For example, in the equation f(x) = 0 ‘x’ is an unknown constant taking the zeroes of the mathematical (denoting. function as its values; but in the corresponding propositional function

‘x’ is still a free variable, determining a true proposition when x takes a zero of f for its value and a false one otherwise.
Most of the basic notions for one variable were repeated for two; for example, for (784.3. at *14·111. The role within logicism of functions of several variables emerged in the companion theories of classes and relations, which we now consider, postponing type theory until §7.9.1.
7.8.5 Classes and relations, relative to propositional functions. In the rest of Part I the authors laid out these calculi as pure façon de parler in that they avoided ‘the assumption that there are such things as classes’ but subsumed them under predicative propositional functions, again written ‘ψ!x’ (p. 187). This was the sense of the title ‘incomplete symbols’ of the last chapter of the general introduction, a name perhaps chosen in imitation of Frege’s ‘unsaturated’ signs (§4.5.5).
The status of functions themselves had to be made clear. While keeping to an intensional view of functions as properties, they stressed the extensional relationship that two were ‘formally equivalent’ if they always took the same truth-value, and defined a function of a function as ‘extensional when its truth-value is the same as with any formally equivalent [functional] argument’ (p. 72): symbolically (p. 187),
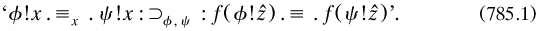
Thus the ‘extension’ of a function, the class of arguments satisfying it, did not need to be taken as an object; the only requirement was the equivalence between same ones. In this way, and in line with ‘the mere principle of economy of primitive ideas’, ‘an extension (which is the same as a class. is an incomplete symbol, whose use always acquires its meaning through a reference to intension’ (p. 72); that is, contextually again:
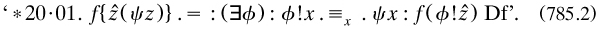
Further, ‘intensional functions of functions only occur where some non-mathematical ideas are introduced, such as what somebody believes or affirms’ (p. 74). But are the needs of mathematics suitably met? For example, if belief functions are admitted under the quantifier, is the equivalence of classes guaranteed? Is it not sly to ‘have our classes and delete them too’ (Hill 1997b, 101)?
This definition of a class drew upon universal quantification over its (potential. members x which satisfied the corresponding propositional function, which in turn bears upon the relationship between identity and equality. Identity of two terms was introduced in *13, based upon the Leibnizian definition (732.3); and equality, especially as used in mathematics for classes, numbers and so on, was to be construed as various special cases of it. Identical objects belonged to the same classes while equal classes had the same objects as members, as stated in two strikingly adjacent propositions
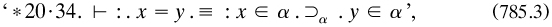
which also compare interestingly with (732.2-3).
The identity relation was repeated for relations in *21·43 as part of ‘The general theory of relations’ (*21), which closely followed the same philosophy using functions of two variables (rarely were functions of more variables discussed). The universal class V was defined by self-identity as x(x = x), with the empty class defined as its complement (*24·01·02). But far more machinery had to be developed concerning their domains, converse domains and fields. Whitehead devised the notations, with rather excessive enthusiasm; several combinations are only rewrites of each other. Thus we have, unnecessarily,
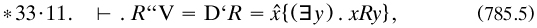
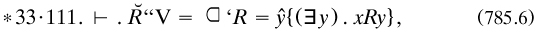
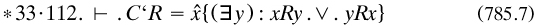
(‘C’ for ‘campus’). Further, for the classes of referents and of relata of a given term under R,
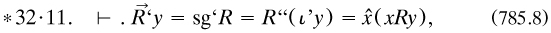
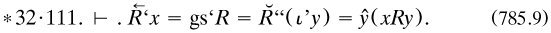
In Section IIC, which dealt in great detail with ‘ONE-MANY, MANY-ONE, AND ONE-ONE RELATIONS’, they used respectively ‘1ε → Cls’, ‘Cls → 1’ and ‘Cls → Cls’ (p. 419)—unhappy extra roles for ‘1’. In general, if the domain and converse domain were sub-classes respectively of α and β, then R was classified as ‘α → β (*70).
But many notations were unique, and symbolised notions used frequently in the book. A typical example is this one for a relation P:
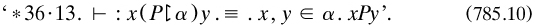
Classes of classes κ were treated carefully, in view of the forthcoming definitions of numbers: for example, the intersection and union of classes became respectively
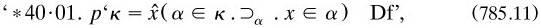
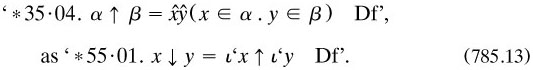
A companion pair of definitions dealt in the same way with classes of two-place relations (*41·01·02).
One major definition for the theory of relations was that of the ‘ordinal couple’ of x and y, based upon the relation between members of two classes
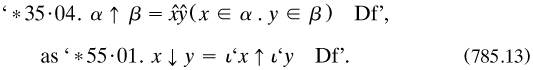
But the defining expression is a conjunction, and so commutative; thus the order itself is determined by that of the class abstraction operator, which is no real advance. Couturat had raised this matter with Russell in letters of May and June 1904 (RA. without clear resolution; perhaps the best solution is to take propositional functions in more than one variable as primitives. Soon after its publication, PM was to inspire Norbert Wiener to define the ordered pair in (827.1).
To link relations to mathematical needs, the ‘descriptive function’ for a relation R was defined as the denoting function
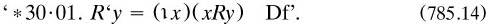
In the theory of ‘double’ functions structural similarity obtained between several ‘double descriptive functions’ such as the union and intersection of two relations (or of two classes), the relative product of two relations, various relations between relations and the (restricted. classes of its relatives and referents, and the addition and subtraction of cardinals. They proved the required results in *38 simultaneously by using a two-place connectival schematic letter ‘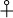 ’, which took “values” such as ‘∪’, ‘|’ (the compounding of two relations. and ‘+’ from these definition schemae:
’, which took “values” such as ‘∪’, ‘|’ (the compounding of two relations. and ‘+’ from these definition schemae:
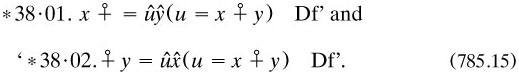
This strategy was Whitehead’s idea, and the ensuing simplifications pleased him (Quine 1985a, 84).
It is surprising that these definitions were nominal, for important in logicism is the central role of contextual definitions of classes and relations, and of definite descriptions. In Moore’s reductionist spirit, over and above the reductions to propositional functions or the criteria of referentiability, the class, relation or description may not exist anyway. As we saw at (734.1), Russell was well aware of the central role of these definitions, and he was to stress it again to Wiener in 1913 (§8.2.7).
7.8.6 The multiplicative axiom: some uses and avoidance. As we saw in §7.2.6, Russell had realised in the summer of 1904 that the theory of infinite products required a new ‘multiplicative axiom’, which was named here ‘Mult ax’. They presented it in the account of set theory in Section IID, in the form
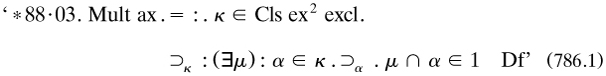
for each type; they stated various equivalent axioms. Sharing the doubts of many contemporaries of their legitimacy, in the rest of the book they gave an excellent and careful display of their need and use as then understood. However, they did not mention the special difficulty raised by Jourdain concerning the definability of such a class by a (finite. propositional function; the specifying expression,
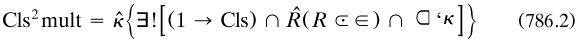
(*88·02 with *80·01 and *61·12), is finite—the members are selected by the many-one membership relation applied to each class in a class κ of mutually exclusive classes—but it was not shown how the defining clause would be reducible to a propositional function.
Among major properties of classes, the Schröder-Bernstein Theorem 425.1 was proved, twice. Firstly, they obtained it as the last result (*73·88. in the number on similar classes, following Zermelo precisely because Mult ax was not needed; Russell had praised his proof in a letter to him of 23 May 1908 (Zermelo Papers, Box 1). Then they imitated Felix Bernstein’s use of transfinite induction in the context of the relative product of relations (*94·53, *95·71), giving an excellent diagrammatic representation on pp. 589–590. They presented the theorem as a result concerning similar classes as such rather than about cardinal numbers; to the latter, and the type theory within which they were located, we now turn.
7.9 TYPES AND THE TREATMENT OF MATHEMATICS IN PRINCIPIA MATHEMATICA
7.9.1 Types in orders. The theory was again based upon the VCP, phrased in various ways such as ‘Whatever involves all of a collection must not be one of the collection’ (PM1, 37); as before, the authors also spoke of (in)definability. Somewhat precariously, they seemed to regard the formulations as equivalent; but common to all was the requirement that ϕ(ϕx) be forbidden for all variables, and for any finite number of them (p. 40). It amounted to a distinction of grammatical categories (a class cannot be named by a noun and a verbal clause at the same time. although unfortunately Russell did not exploit or develop such a reading.
The hierarchy was presented both in the introduction (ch. 2. and in *12, with some differences; the latter version will be followed here. Propositional functions were stratified by the systematic consideration of quantifiers. ‘A ‘matrix’ (the old word from the substitutional theory, with a similar meaning. had no quantifiers, and its arguments were individual variables; it was given the special notation ‘ϕx’ and also the additional name ‘predicative’. If some or all of the arguments were quantified, then a ‘first-order’ function was produced (pp. 161–162). Then the VCP required that one move up to ‘a second-order matrix[, which] is one which has at least one first-order matrix among its arguments, but has no arguments other than first-order matrices and individuals’; quantification led to functions and propositions again in this order (p. 163). So one could continue, finitely many times; the order of a function was one above that where all variables were quantified. Quantification was restricted to predicative cases; in class terms, the VCP permitted its members to belong only to the order one above. At any order, ‘A function is said to be predicative when it is a matrix. [...] “Matrix” or “predicative function” is a primitive idea’ (p. 164, tardily on an important point!).
In addition to orders, there were types, where ‘a “type” is defined as the range of significance of some [propositional] function’ (p. 161). After quantification of some or all the variables of a matrix, the remaining free ones determined the type of the function, and it has become customary to regard a type as divided into orders, each one specified by its quantifiers. However, the prior place given by the VCP to quantification shows that the relationship is reversed: an order is divided up into types, each one specified by the free variables left after quantification, and a propositional function is specified by both its order and type indices.
But the underlying strategy remained unclear, in that * 9 developed the theory constructively from ‘elementary propositions’ and successive quantification of its variables, a ‘purely philosophical’ exercise which was complemented in * 10 by an ‘alternative method’ based upon taking negation and implication as primitive and proceeding more formally. Russell clearly had different ‘reasons for ramification’ (Goldfarb 1989a), but he did not fully explain the variety, either here or in use in the later numbers.
The stratification of functions led to a companion hierarchy of propositions when the free variables were given values. On 26 May 1909 Whitehead had queried with Russell this feature of the type theory in Russell’s 1908 paper, puzzled by the relationship between the (propositional. values of functions of different types and the hierarchy of propositions itself (RA). Presumably Russell explained that the VCP stratified propositions by propositional quantification, in order to Solve the liar paradox: ‘p. (p is false)’ is a proposition whose ‘second falsehood’ does not belong to the ‘first falsehood’ of the original propositions, and so on up finitely (pp. 41–43). After this explanation in the introduction one reads in disbelief in * 9 that ‘we never have occasion, in practice, to consider propositions as apparent variables’ (p. 129).
Further on they gave the axioms (784.1. of the predicate calculus, and interpreted the first as ‘if ϕx is true, then there is a value of ϕ which is true’ (p. 131.—which is surely not a correct reading of a propositional function. In both hierarchies ‘typical ambiguity’ was deployed, where theorems applied to any appropriate collection of orders and/or types (for example, not only individuals and classes but also classes and classes of classes).
which is true’ (p. 131.—which is surely not a correct reading of a propositional function. In both hierarchies ‘typical ambiguity’ was deployed, where theorems applied to any appropriate collection of orders and/or types (for example, not only individuals and classes but also classes and classes of classes).
In the context of type theory the authors introduced their definition of truth: ‘When we judge “a has the relation R to b,” our judgement is said to be true when there is a complex “a-in-the-relation-R-to-b,” and is said to be false when this is not the case’ (p. 43). While it was framed again in terms of correspondence, the old uncertainties of Russell 1906g over objective falsehoods (§7.4.7) were over; indeed, when he reprinted that article in a book anthology of Philosophical essays (§8.2.4), he wrote a new piece 1910b in this vein to replace its uneasy final pages.
The motivation for the theory of types was, of course, the need to construct mathematics logicistically while Solving all the paradoxes. However, the latter were not presented until after the summary of type theory in the introduction. This time the paradoxes reported were, in order, the liar, Russell’s, the relations version of it, Burali-Forti’s, Berry’s, the least indefinable ordinal, and Richard’s; the list was followed by a summary of each Solution as furnished by the VCP (pp. 60–65). Notable omissions include the cardinal paradox(es), and especially the one stated at the end of The principles arising from associating a class m of propositions with the proposition ‘every member of m is true’, which once again (§7.4.8) is constructible within the simple theory (de Rouilhan 1996a, 223–230). Grelling’s recent paradox on heterology (§7.2.3) was also ignored.
7.9.2 Reducing the edifice. (Hill 1997a, ch. 9. As in Russell’s 1908 preview, this Byzantine partition of propositional functions into orders and types sabotaged the reconstruction of mathematical theories and operations; hence was introduced ‘the axiom of reducibility’ (sometimes named ‘Reduc ax’), also ‘axiom of classes’ and ‘axiom of relations’ as at 773.2). It claimed that any propositional function had a logically equivalent quantifier-free predicative function with the same free variables (PM, *12); thus it restored Leibnizian identity (732.3) in full form. However, it seems to destroy the structure of orders, in that any propositional function up there had a mate on the ground floor. (They stated on p. 58 that the axiom could equally well assert the existence of the function at any same order). Somehow, however, the semantic paradoxes to not seem to be restored; Myhill 1979a presents a modern type theory in which avoidance is assured even with such an axiom in place.
One of the more useful queries about logicism made in the Revue by Poincaré 1909b (in reaction to Russell 1908c, we recall from §7.8.2) concerned the place of this queer axiom; in particular, whether it was more or less general than MI, and whether it could be justified psychologically. Russell’s reply 1910b, based on the introduction to PM, argued for greater generality, in that MI was derivative; as for the second point, he included a somewhat isolated passage on judgement which we shall consider in §8.2.6 when it took a more developed form after PM appeared.
When reading the manuscript of the book Hawtrey had expressed his puzzlement over the axiom on 3 September 1908 (RA):
You have adopted a hierarchy which is not the most general possible and which is not consistent with the Science of Pure Mathematics. You have then made your hierarchy consistent with the Science of Pure Mathematics, by adopting as an axiom a statement about the functions existing within your hierarchy, which there is no ground for believing to be true.
While not quite the criticism that the axiom amputated the hierarchy of orders, his point was well put; Russell’s reply of 5 September (RA) only recalled the raising of types in the definition of identity, and the text in PM does not really answer it. He also gave the definition of inductive cardinals as another example, whereupon two days later Hawtrey worked through the theorem that the sum of two of them was also inductive (compare *110·02). Russell accepted the proof on 23 September, and in a discussion of identity he mooted, not for the first time (§6.3.1), that ‘Speaking as a philosopher rather than a mathematician, I should say that “diversity” is an ultimate notion, & that identity may perhaps be correctly regarded as the negation of diversity’ (copy in RA).
A final question is the status of the theory in another sense; whether objects of some sort are being stratified, or their symbols. In later writings Russell preferred the latter view, regretting that he had not adopted it when developing the theory (1918&38211;1919a, 267; 1944a, 691); we see his tendency to conflate symbols and their referents. Possibly the type theory was a central feature of his calculus of logic rather than of the logic itself, which remained universally general although its formulae had to be split up into orders and types. Variables and constants surely have to be taken as symbols, and the former distinguished from schematic letters—another conflation in their calculus, especially grave when typical ambiguity was deployed.
Hawtrey raised but attacked this position in an undated letter probably written, like most of his others, in the autumn of 1908. He saw Russell as having ‘felt bound to make all variables unrestricted’ especially because ‘A restriction on the variable can only take the form of a hypothesis about the variable’; however, ‘the use of the unrestricted variable led to the contradiction, and you now use the [VCP] to show that, in order that a proposition containing an apparent variable may have any meaning at all, there must be a certain restriction on the variable implicit in it’. He opined that asserting propositionhood as such ‘was in reality fundamentally different’ a proposition from the proposition concerned, so that non-restriction did not apply anyway. Russell’s reply, if written, seems not to have survived; once again Hawtrey’s query was penetrating.
7.9.3 Individuals, their nature and number. One consequence of abandoning the substitutional theory was that the generation (746.1. of an infinite class was also lost: so Russell was forced, reluctantly, to adopt an axiom of infinity (named ‘Infin ax’). Due to the return to propositional functions and orthodox variables, it took a quite different form, which we now summarise. The issues arising, very significant for logicism, are rarely recognised.
Firstly comes the question of the nature of individuals. PM was not a happy text; the “definition” as ‘neither a proposition nor a function’ (p. 132; see also p. 51. does not exclude, for example, logical connectives or assertion. A further explanation as ‘something which exists on its own account’ (p. 162. is perhaps worse given Russell’s many senses of existence. The phrase ‘destitute of complexity’ in the 1908 paper (1908c, art. 4. is more specific; but the status of structureless entities in logicism is still unclear (Prior 1965a).
Type theory bears upon this issue. In PM it was held to be relative in that ‘In practice, we never need to know the absolute types of our variables, but only their relative types’ (p. 165); *65 was devoted to typical ambiguity, where examples were given of propositions and definitions (in cardinal arithmetic, in that case. which applied across any collection of neighbouring types. However, in one of his lectures in Paris in March 1911 (§7.8.2) he explicitly took the absolutist position: ‘Here the word individual contrasts with class, function, proposition, etc. In other words, an individual is a being in the actual world, as opposed to the beings in the logical world’ (1911d, 23). But this empirical status for individuals entailed that logic was a posteriori—surely a mistake, requesting the physicists to decide about a basic feature of logicism! Was Russell influenced by current speculations about molecules? It is worth noting his talk soon afterwards of ‘atomic’ and ‘molecular’ propositions in his epistemological writings (§8.3–4).
Secondly is the question of the number of individuals assumed. Infin ax took the form of asserting that there existed a non-empty class of any finite number of members (*120·03). The structure of type theory required such a class, ‘Indiv’ (2, vii, 18), to exist at the lowest level of types in order to allow logicism to ascend to(wards) the Cantorian transfinite clouds. However, the reductionist spirit decreed that it be used only when absolutely essential, especially when, ‘as monists aver, there is only one individual’ (2, 325: compare *22·351, *24·52, *50·33 and *254·431); they had even named its unit class as ‘1 (Indiv)’ (1, 345). However, the identity relation is thereby trivialised, for x = y becomes x = x.
Perhaps for this reason, Whitehead’s mistake (§7.8.1) was to have forgotten this restriction when preparing Part III of Volume 2 on cardinal arithmetic. During 1911, while publication was suspended, he altered proofs and text in various places. A letter to Russell of 19 January (text in §11.6) shows him rethinking *100·35 on the equal cardinality of non-empty classes being equivalent to their similarity, and worrying about *126 on ‘typically indefinite inductive cardinals’ (§7.9.4) and other passages; Russell noted theorems in *117 and *120 on the letter. On 20 May Whitehead reported that *118 and *119, respectively on substitution and the subtraction of cardinals, were redone.
To explain his new procedures Whitehead prefaced Volume 2 with a long and very difficult ‘Prefatory statement of symbolic conventions’. Following Russell’s definitions as classes of all similar classes and starting from 0 defined as the unit class of the empty class, he tried to lay down ways of using only ‘adequate’ types T for a cardinal c; that is, those Ts within which c was definable. For 0 and 1 occurred in all types, but not 2,... in Indiv, or 3,4,... in ‘Indiv, Cl‘Indiv, Rl‘Indiv; and so on’ (2, x). He asserted that there were three kinds of hierarchy: a ‘functional’ one of the various types of propositional function; a ‘propositional’ one built up from elementary propositions (without quantifiers) by means of substitution of non-elementary functions; and an ‘extensional’ one, which started from any point in the functional hierarchy and relative to it generated classes, classes of classes, and so on. There were also two kinds of ‘formal number’: ‘constant’ ones identical with a cardinal number in the given type; and ‘functional’ ones, defined ‘by enumeration’ and using the standard arithmetical operations (p. xiv). The type of such a number was its ‘actual type’, whose adequacy was established by an existence theorem for that type (pp. xv–xvi). Compound formal numbers could contain components from other types, which had to be ‘normally adjusted’ to ensure non-empty classes, and ‘arithmetically adjusted’ for adequacy. ‘Symbolic forms’ could be ‘equations’ or ‘inequations’, and formal numbers might make ‘argumental’, ‘arithmetical’, ‘equational’, ‘attributive’ or ‘logical’ occurrences in them (pp. xvii–xix).
Further, two conventions limited the choice of types for formal numbers: one concerned the relationships between different kinds of occurrence, while the other insisted that a type be adequate, leading to restrictions on the substitutivity of numbers in arithmetical equations (pp. xxi–xxiv). Ambiguous types in a symbolic form were identifiable with types, ambiguous or specified, in any other one. Failures of adequacy were removed by conventions that all equations involving arithmetical formal numbers were arithmetical, and that inductive cardinals should be taken in a type adequate to ensure the existence of all cardinals and an avoidance of non-empty classes (pp. xxviii–xxxi). Whitehead concluded, somehow, that ‘all discrimination of the types of indefinite inductive numbers may be dropped; and the types are entirely indefinite and irrelevant’ (p. xxxi).
Their failure to spot this elementary slip must have been traumatic for both men. Russell referred later to the assumption of any individual at all as a ‘defect in logical purity’ (1919b, 203), and in 1912 he had become agitated about it. In a recollection made to me in 1972 by a mathematics undergraduate of that time who wished to remain anonymous,
McTaggart and Bertrand Russell held periodic coffee parties on Sunday evenings in the latter’s rooms attended by a dozen students or so from various colleges; the ‘audience’ sat in silence in a half ellipse with McTaggart to the left and B.R. to the right [... ]
At the last conference [... ] Bertrand Russell called me aside as a mathematician I suppose and likely to appreciate the gravity of his statement—‘I have just realised that I have failed—it is easy to establish the unit one but I have omitted to establish a second like unit’—(I won’t guarantee the precise wording but it’s not far off). He went on to say ‘I have finished’.
With this ringing in my mind and the dreadful distress of a great scholar I was glad I was alone.
7.9.4 Cardinals and their finite arithmetic. This was developed, within each type, in two somewhat distinct forms. Throughout the treatments the authors indicated carefully the roles of both Mult ax and Infin ax, and Whitehead added on proof some remarks on his new procedures to minimise the role of the latter.
Firstly, the definite description ‘the cardinal number of a class α’, written ‘Nc‘α’, was defined as the class of all classes β similar to α; its type lay one above that of α itself (*100·1), but the β were taken from all types. When β was restricted to the type ‘t‘α’ (*63·01) of α, then the ‘homogeneous cardinal N0c‘α’ (*103·01) was defined. As an exercise, they showed in * 105 how to define the cardinals relative to any class of lower type.
So far so Peanist, in that the cardinals were tied to one-one correspondences although defined within logicism; their “direct” definitions of numbers started from the initial definition of 0 as the unit class of the empty class Λ (*54·01), 1 and 2 as the classes of unit classes and of unordered couples respectively (*52·01, *54·02), and successively on upwards (*100–102). None of these integers was an object, since as classes each of them relied on the contextual definition (785.2) of classes—a major difference from Frege’s nominal definitions of cardinals (§4.5.3).
Cardinal arithmetic was defined within each type, and moreover needed classes of disjoint classes to work, which in general does not obtain. We recall Whitehead’s emphasis (653.2) on such classes; now he devised in * 110 a way of defining the ‘arithmetical sum’ α + β of any two classes α and β by forming two disjoint classes α′ and β′ each of the type (β, α) and respectively similar to α and β: essentially,
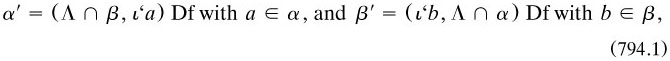
where each empty class Λ came from the type of its partner class.28 Such restrictions did not obtain in defining the ‘arithmetical product’ β × α of α and β (*113), but they showed why and how ‘The arithmetical product of a class of classes’ (*114) required Mult ax. They also gave a treatment of ‘double similarity’ between two classes of classes κ and λ, which obtained not only between the member classes but also between their own members:
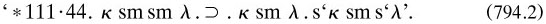
It was needed in arithmetical properties such as equality of sums or products of cardinals.
The connective variable ‘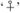 ’ (785.15) was used to define, via arithmetical addition, the relation ‘(+c ν)’ between two homogeneous finite cardinals μ and ν:
’ (785.15) was used to define, via arithmetical addition, the relation ‘(+c ν)’ between two homogeneous finite cardinals μ and ν:
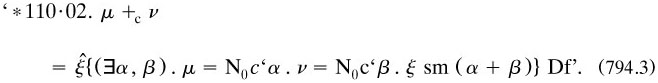
where ‘+c 1 is the relation of a cardinal to its immediate predecessor’ (2, 203). Similarly, subtraction of a cardinal from a greater one was defined thus:
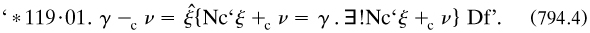
The extension to negative cardinals is described at (799.1).
7.9.5 The generalised ordinals. There now followed, as Part IV, Russell’s most substantial contribution to the mathematics of logicism: his ‘RELATION-ARITHMETIC’, built upon his insight of 1901 (§6.5.4) of generalising from well-order to order-types. Russell told the Press on 27 May 1961 (RA) that when Johnson had read the manuscript of PM for them, he had stressed the importance of this Section.
Two relations P and Q were ordinally similar (‘smor’) under a ‘correlator’ relation S (*151) when
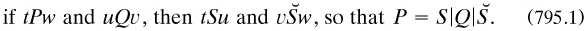
Then the relation-number of P was given by
with the corresponding class NR of such numbers as its domain (*152·02). In *164 they described the ‘Double likeness’ of two classes of relations by a ‘double correlator’; the needs corresponded to those in (794.2) for the double similarity for cardinals.
Much of the Section was taken up with the “arithmetic” of these numbers, imitating that of cardinals already presented and ordinals still to come: homogeneous numbers, addition (but not subtraction), multiplication, exponentiation, laws such as associativity, and inequalities. The greater generality made the exegeses much more extensive, and Mult ax still more ubiquitous (for example, to choose correlators in certain circumstances). From the mathematical point of view the generality was especially evident in *170– *171, where they presented in detail Felix Hausdorff’s exposition of various kinds of order-types 1906a and 1907a (§4.2.7) in what they described as ‘brilliant articles’ (2, 391; see also 3, 171). The procedure worked in terms of ordering the sub-classes of a relation by taking away members from classes until they became different from each other; adapting his name of it to ‘the principle of first differences’, they handled sub-types similarly.
Notations were again rather over-prolific; and, since much structure similarity was evident, the schematic connective letter ‘ ’ of (785.15) might have been deployed earlier than *182. The symbols for operations with cardinals were adopted, with some graced by overdots. Links to cardinal arithmetic were exhibited; for example,
’ of (785.15) might have been deployed earlier than *182. The symbols for operations with cardinals were adopted, with some graced by overdots. Links to cardinal arithmetic were exhibited; for example,
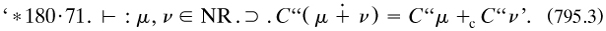
7.9.6 The ordinals and the alephs. The ordinal numbers were rather unclearly presented in PM: some small ones in Part II, and the rest in Part IV on Relation-Arithmetic and Part V on Series, where they appeared as special cases of two theories that were more general in different ways. Here the portions are gathered together.
The theory started out in *250 from the notion of a well-ordered relation, ‘when every existent sub-class of its field has one or more minima’ (3, 4); from the class Ω of these relations the class NO of ordinals formed in * 251·01 the domain of the relation-number relation when Ω was placed in its converse domain (‘NO = Nr“ω Df’). They showed how to produce Cantor’s series (326.2) of ordinals, and how Burali-Forti’s paradox was avoided by the raising of types (p. 74); Zermelo’s proof of the well-ordering theorem was treated in *258.
In order to generate the required domains they drew on Frege’s ancestral relation (452.1) in *90 to launch Section IIE on ‘INDUCTIVE RELATIONS’. They worked with Frege’s own ‘proper’ non-reflexive version, written ‘Rpo’, but started with the reflexive relation ‘R*’:
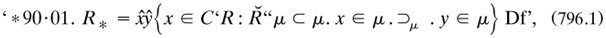
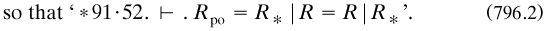
This theory was also used to distinguish finitude from infinitude, where they drew upon both the reflexive and inductive definitions of infinity. The former was provided via the ancestral relation; for inductive cardinals, ‘those that obey mathematical induction starting from 0’ (2, 200), were defined by successive additions of 1 to 0, so that their class, ‘NC induct’, was the posterity of 0 relative to the relation ‘(+c 1)’ (*120·01·02: these cardinals were used in (794.3–4)). But the ‘Cls infin’ of infinite classes was defined not as non-inductive but reflexively, ‘when there is a one-one relation which correlates the class with a proper part of itself (2, 270). Then an infinite series was defined as one with a reflexive field, so that its class was given by
The treatment of reflexive and inductive definitions of infinitude was handled with a care that is still rare (Boolos 1994a). Mult ax haunted the account; at * 124·01·02·03 they defined together Cls refl, the class ‘NC refl’ of such cardinals, and the class ‘NC mult’ of classes satisfying the axiom.
The transfinite ordinals and the alephs were defined by their versions of Cantor’s definitions. His well-order-type ω was changed into the class ‘Prog’ of ‘progressions’ generated by ancestral relations:
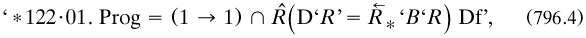
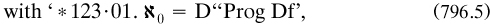
where  ‘R was the complement of the domain of R with respect to its converse domain (*93·101), so that its member(s) could launch the progression (‘B’ for ‘begin’.) Similarly,
‘R was the complement of the domain of R with respect to its converse domain (*93·101), so that its member(s) could launch the progression (‘B’ for ‘begin’.) Similarly,
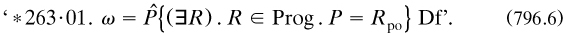
Higher alephs were defined from the corresponding initial ordinals of the number-classes, starting with
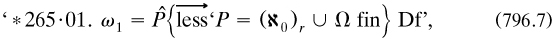
where ‘less’ was the relation of ordinal dissimilarity between two well-ordered series (*254·01), and ‘( 0)r the class of well-ordered series whose fields have
0)r the class of well-ordered series whose fields have  0 terms’ (3, 169, using *262·03). Then
0 terms’ (3, 169, using *262·03). Then
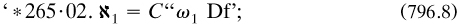
the field of ω1 was taken rather than its domain because of Cantor’s way of defining the number-classes into terms of rearrangements of order of the members (§3.2.7).
The further pairs of definition followed this pattern, with the additional requirements for cardinality added into the defining clauses of the ωS. However, as in the 1908 preview (§7.7.3), since only a finite number of types was permitted,  ω and its successors could not be defined; ωω and beyond were also inaccessible (as it were) (PM 2, 183–184; 3, 170, 173). Perhaps for this reason, they did not include Cantor’s alephs paradox (663.2) in the construction of ‘the series of alephs’ (*265); for the Solution of both it and of Burali-Forti’s paradox were rendered rather pointless since they could advance so far up the series of ordinals anyway—significant lacunae in this highly Cantorian logicism.
ω and its successors could not be defined; ωω and beyond were also inaccessible (as it were) (PM 2, 183–184; 3, 170, 173). Perhaps for this reason, they did not include Cantor’s alephs paradox (663.2) in the construction of ‘the series of alephs’ (*265); for the Solution of both it and of Burali-Forti’s paradox were rendered rather pointless since they could advance so far up the series of ordinals anyway—significant lacunae in this highly Cantorian logicism.
The authors handled beautifully Cantor’s theory of cardinal exponentiation, forming the class ‘α exp β’ of (Nc’α)Nc‘β ordered couples x ↓ y chosen from α and β respectively such that each y took only one x (*116). They also connected the operation with multiplication in * 116·361 (thanks to MI), again with a fine diagrammatic representation to clarify the proof.
7.9.7 The odd small ordinals. The ordinal numbers started out surprisingly (*153, with parts of an overture curiously placed as *56 in the Section on cardinal arithmetic). ‘0r’ (‘r’ for ‘relation’) was defined as the unit class of the diversity relation ‘ ’ and so was the correlator of relations ordinally similar to it:
’ and so was the correlator of relations ordinally similar to it:
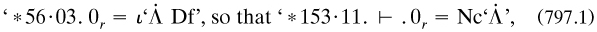
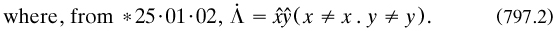
Similarly, 2r was the class of ordered pairs:
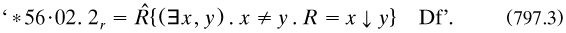
But, since ‘series must have more than one member if they have any members’ (1, 375), the identity relation, being symmetrical, was not serial. Hence the relation-number 1 was not an ordinal; so they offered
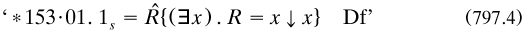
as ‘the nearest possible approach’ (‘s’ for ‘series’?). They also defined another cousin number:
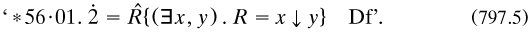
Another relation-number ‘ ’ arose, for the purpose of adding one term to a relation-number μ to produce ‘μ
’ arose, for the purpose of adding one term to a relation-number μ to produce ‘μ 
 ’ or ‘
’ or ‘
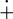 μ’ (*181·02·021). It was granted the property
μ’ (*181·02·021). It was granted the property
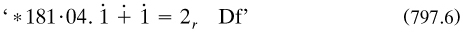
in order ‘to minimize exceptions to the associative law of addition’ (2, 467).
7.9.8 Series and continuity. Part V dealt with ‘SERIES’ in general, based upon a non-identical relation P which was transitive and connected:
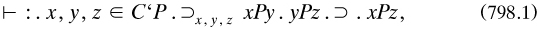
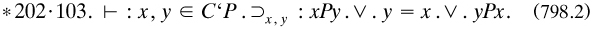
The former property was not stated; instead ‘P2 ⊂ .P’ was used (*201·1). The class of series was notated ‘Ser’ (*204 ·01).
Among the basic notions of series given in Section VA, the most significant were the ‘minimum points of a class α with respect to a relation P’, namely ‘those members of α which belong to C‘P but have no predecessors in α’; and similarly the ‘maximum’ points of α with no successors in α (2, 541). *205 gave a variety of properties of these points for various kinds of relations (for example, connected ones). Then the authors treated the ‘sequent points’ of α relative to P in *206; both the class ‘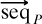 ‘α’ of ‘its immediate successors’ whether or not α had a maximum, and “
‘α’ of ‘its immediate successors’ whether or not α had a maximum, and “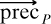 ‘α’ of its immediate predecessors (p. 559). The key notion in much of the entire Section was the ‘limit or maximum’: ‘A term x is said to be the “upper limit” of α in P if α has no maximum and x is the sequent of α’, symbolised ‘ltP’α’ (p. 575). Similarly, ‘the lower limit of α will be the immediate predecessor of α when α has no minimum; this we denote by tlP ‘α’. Thus the key umbrella notions, ‘limit or maximum’ and ‘minimum’, were given thus:
‘α’ of its immediate predecessors (p. 559). The key notion in much of the entire Section was the ‘limit or maximum’: ‘A term x is said to be the “upper limit” of α in P if α has no maximum and x is the sequent of α’, symbolised ‘ltP’α’ (p. 575). Similarly, ‘the lower limit of α will be the immediate predecessor of α when α has no minimum; this we denote by tlP ‘α’. Thus the key umbrella notions, ‘limit or maximum’ and ‘minimum’, were given thus:
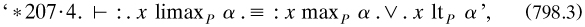
with ‘liminP’ handled via 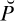 (*207·401).
(*207·401).
With these and earlier notions, especially ancestral relations, the authors were able to treat in Sections VB–C several features of real line theory. It was guided by the notion of dividing a series into two parts after the manner of a Dedekind cut of the continuum (*210–*215), and Cantorian derived sets (323.3) as ‘Derivatives’ of series with limit points (*216). From there they proceeded into mathematical analysis as far as defining the oscillation and the continuity of a mathematical function (itself expressed as a relation), its upper and lower limiting values, and other delicate tools from the Weierstrassians’ surgery (§2.7.5). As in The principles (§6.4.7), Ulisse Dini’s textbook in its German edition 1892a was the principal source (mistitled in 2, 724), and in connection with his definition of continuity in both the (ε, δ) and sequential forms they noted ‘that practically nothing in the theory of continuous functions requires the use of numbers’ (p. 725)—a feature of many of the later Sections of PM.
The theory of ordinal numbers described in §7.9.5 was contained mostly in Sections VD–E. It included transfinite induction, then by no means routine, in contexts such as ‘The transfinite ancestral relation’ (*257), where the ‘transfinite posterity’ of a relation was generated by a method imitating Cantor’s principles (§3.2.6). Some other material was described in §7.9.6.
The final Section VF dealt with three of Cantor’s other principal order-types. His dense sets became ‘compact series’ in their hands, ‘in which there is a term between any two, i.e. in which ‘P ⊂ ·P2, where P is the generating relation’ (3, 179), a formulation of compactness (*270·01) delightfully converse to their definition of connectivity stated after (798.2) ‘Rational series’ was ‘ordinally similar to the series of all rational proper fractions (0 excluded)’ (p. 199) following Cantor of 1895b (§3.4.7): compact and containing a progression within its field (*273·01).
The Part ended with continuous series, where the authors again followed Cantor, using his second definition, also of 1895. It was preferred over Dedekind’s cut procedure because two Cantor-continuous series were ordinally similar (*275·3·31); but in *214 they had worked out in detail ‘Dedekindian relations’, where ‘every class has either a maximum or a sequent with respect to it’. They used Hausdorff’s theory to determine the sub-classes of such a series, and used it to show that its cardinality was 2 0(*276·43). They did not mention Cantor’s continuum hypothesis—unanswered mathematical questions were not their concern—but the German heritage was well in evidence in this Part.
0(*276·43). They did not mention Cantor’s continuum hypothesis—unanswered mathematical questions were not their concern—but the German heritage was well in evidence in this Part.
7.9.9 Quantity with ratios. Part VI, on ‘QUANTITY’, was largely Whitehead’s work; his surviving letters to Russell suggest that much of it was done during 1909, especially in the autumn when they were also applying to the Royal Society for a grant and he was scheduled to give a two-term course on ‘The principle of mathematics’.29 The importance of the theory ‘grows upon further consideration’, he opined to Russell on 14 September, ‘the modern “arithmeticisation of mathematics” is an entire mistake’—of course a useful mistake as turning attention upon the right points’. However, it ‘leaves the whole theory of applied mathematics (measurement etc) unproved’. He then advised that
You will have to devote some attention to my ms, since their results will come as a shock to the current orthodoxy. In fact mathematicians will feel much like Scotch Presbyterians who might find that a theological professor in one of their colleges had dedicated his work to the Pope.
In fact, as he might have expected, the mathematical community has always treated this Part as if it was, say, ‘The Assumption of Moses’—not among anyone’s normal reading.
By 12 October Whitehead found that ‘The whole part on quantity is naturally rather long—for it embraces the whole theory of ordinary [real-variable] mathematical analysis—The comforting thing is that our previous ideas and notations are exactly adapted for the exposition’, although much attention had to be paid to typing of notions and to proving existence theorems (in the Peanist sense of classes being non-empty). He reported that the Part had two ‘subdivisions’: ratios, and then ‘the Quantitative Relations (or, quantity proper)’. But in print it began with a theory of ‘positive’ and ‘negative integers’, extending the treatment (794.3–4) of the addition and subtraction of cardinals. In *121 on ‘intervals’ the authors had treated various relations of ‘the class of terms between x and y with respect to some relation P’, specifically the case ‘Pμ’ where (μ + 1) terms were counted from x to y inclusive (*121·013·02, with ‘μ for ‘ν’). Then they introduced in * 300·232 these integers in terms of addition and subtraction of two positive inductive cardinals by μ:
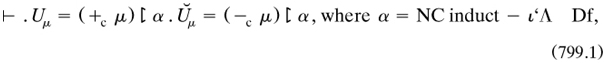
and from (785.15)2 for the connectival schematic letter ‘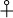 ’ ‘(±c μ)’ were the relations of (μ ±c ν. to μ (compare PM 2, 181). In order to include 0, they appealed to the identity relation (785.3. (*300·03). The change over the previous theory was that these integers were relations (effectively counting forwards and counting forwards. rather than classes of classes, and so more suitable for the theories of ratios and quantity to come. As before, subtraction was still of the lesser from the greater; but ‘negative ratios’ were handled in *307 by using the converses of the relations furnishing the positive ones.
’ ‘(±c μ)’ were the relations of (μ ±c ν. to μ (compare PM 2, 181). In order to include 0, they appealed to the identity relation (785.3. (*300·03). The change over the previous theory was that these integers were relations (effectively counting forwards and counting forwards. rather than classes of classes, and so more suitable for the theories of ratios and quantity to come. As before, subtraction was still of the lesser from the greater; but ‘negative ratios’ were handled in *307 by using the converses of the relations furnishing the positive ones.
They needed a definition of ratios ‘(1) narrow enough to preserve all the algebraic properties (2) wide enough to include all the applications’, as Whitehead nicely put it to Russell on 12 October. In an undated letter of this time he found Russell’s proposed definition of the power Rσ of a relation R to any inductive cardinal σ to be ‘excellent, and must have a chapter for its own sake’; this was duly prepared as *301. Then ratios were defined as follows: distances lay in the ratio μ/ν of co-prime cardinals if their corresponding relations R and S possessed at least one pair of terms x and y such that xRνy. xSμy (*303·01). ‘The series of real numbers, positive and negative’ was defined Dedekind’s way by specifying an ‘irrational number’ by the condition that a class of ratios had neither a maximum nor a minimum point with respect to the ‘less than’ relation between ratios (*310). Again, negative numbers came via relations converse to those for positive ones (*312·01·02·1); maybe they were influenced by Frege’s similar strategy in his theory (458.1) of real numbers. The treatment was rather disappointing, however, for their reductionist philosophy led them to be ‘mainly concerned with just those few simple properties which are independent of the axiom of infinity’ (3, 316); but they did present the arithmetic operations (*311-*314).
Quantitative relations drove the other three Sections, which concentrated the notion of ‘vector’. This was the somewhat restricting choice of name for ‘conceiv[ing] a magnitude as a vector, i.e. as an operation, i.e. as a descriptive function in the sense of *30’. It was specified as a one-one relation that ‘shall be capable of indefinite repetition’ (p. 339: Russell’s definition once again), and a ‘vector family’ as a class of those relations which commuted (‘Abel’, * 330·02). Much of the rest of Section VIB dealt with various special kinds (for example, connected relations); but throughout they assumed that the family took no upper bound over the class of permitted magnitude. Norbert Wiener was to find here a fruitful source for modifications (§8.2.7).
Section VIC, ‘MEASUREMENT’, wedded the theories of ratios and real numbers with those of vector families. Ground was prepared for Volume 4 by a means called ‘rational nets’ for the ‘introduction of coordinates in geometry’, in which a class of rational multiples of a given vector family was set up in a way that it also formed a group (*354·14–17). Thus Whitehead’s hopes to use algebra in logic (§6.4.4, 9) were revived, albeit in a different context.
The final Section VID treated ‘CYCLIC FAMILIES’, where a vector could have more than one multiple: for example, angles between two straight lines, for which the ratio α/β could also be (α + 2Nπ)/β for any cardinal N. The definition included the condition that ‘it might contain a non-zero member which is identical with its converse’ relation, such as π in this example (p. 458); the other conditions ensured that this member was unique (*370·23). Thus in Benjamin Peirce’s terms (§4.3.2) cyclic families formed an algebra with one idempotent element, and the theory was similar to defining complex numbers as ordered pairs; they mentioned neither feature.
The modifications to the theory were not great, so that ‘we have given proofs rather shortly in this Section’, since many were ‘perfectly straightforward, but tedious if written out at length’ (p. 461). It is surprising to read such a statement in the Bible of logicism; doubtless it was motivated by the role of the theory as a tool for use in the Volume 4 to come. In the end Whitehead was to abandon it; we note this disappointment in the next chapter, which begins with their work immediately following PM.
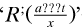 —a horrible notation. This forbidding appearance must have deterred even symbolically literate readers; and naming the Concepts merely by Roman numerals hardly excites the intuition, either. Like Royce’s, Whitehead’s paper made little impact—apart from upon his own philosophy when it flowered in the 1920s after he had finished with logicism (Lowe 1962a, chs. 7–8).
—a horrible notation. This forbidding appearance must have deterred even symbolically literate readers; and naming the Concepts merely by Roman numerals hardly excites the intuition, either. Like Royce’s, Whitehead’s paper made little impact—apart from upon his own philosophy when it flowered in the 1920s after he had finished with logicism (Lowe 1962a, chs. 7–8). are both not bald false and one contradicts the other’ (fol. 3). But he treated mainly the mathematical side, from the integers produced by MI (the ‘nerve of the whole thing’) through rational and real numbers to transfinite arithmetic, including cardinal exponentiation and uses of the multiplicative axiom. His current understanding of model theory was that the basic notions (number, zero, successor) in the Peano axioms ‘might be fitted on to anything. B. Russell doesn’t seem to object to this’. In the last part of the course he summarised the material of his new tracts, and then also parts of his recent Royal Society paper in his symbols (all those quoted in
are both not bald false and one contradicts the other’ (fol. 3). But he treated mainly the mathematical side, from the integers produced by MI (the ‘nerve of the whole thing’) through rational and real numbers to transfinite arithmetic, including cardinal exponentiation and uses of the multiplicative axiom. His current understanding of model theory was that the basic notions (number, zero, successor) in the Peano axioms ‘might be fitted on to anything. B. Russell doesn’t seem to object to this’. In the last part of the course he summarised the material of his new tracts, and then also parts of his recent Royal Society paper in his symbols (all those quoted in 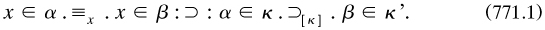
 specified as that ‘which may be preserved constant [in X] while x varies’. Conversely, when x was introduced into the form F, then the expression ‘F | x’ was produced. These converse indefinable notions were based on the following assumptions
specified as that ‘which may be preserved constant [in X] while x varies’. Conversely, when x was introduced into the form F, then the expression ‘F | x’ was produced. These converse indefinable notions were based on the following assumptions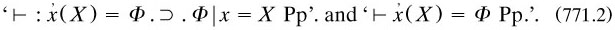
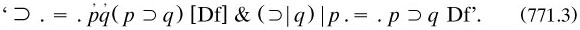
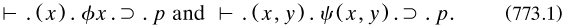
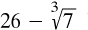 because the latter number was irrational, defined in terms of a class of classes of rationals and so determined by a function of an order different from that for 26. To save arithmetic and mathematics in general, he assumed ‘the axiom of classes, or the axiom of reducibility’ (art. 5), also ‘the axiom of relations’ for functions of more than one variable. It claimed that every propositional function had a logically equivalent mate among the predicative sub-class: for example for ‘double functions’,
because the latter number was irrational, defined in terms of a class of classes of rationals and so determined by a function of an order different from that for 26. To save arithmetic and mathematics in general, he assumed ‘the axiom of classes, or the axiom of reducibility’ (art. 5), also ‘the axiom of relations’ for functions of more than one variable. It claimed that every propositional function had a logically equivalent mate among the predicative sub-class: for example for ‘double functions’,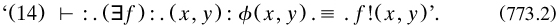
 n for any finite ordinal n, and the need in the arithmetics for the multiplicative axiom (arts. 9–10). The axiom of an infinitude of individuals was adopted reluctantly in art. 9, again made as an empirical assumption. Curiously, he did not explicitly state logicism, although the nature of the enterprise should have been clear to his mathematical audience.
n for any finite ordinal n, and the need in the arithmetics for the multiplicative axiom (arts. 9–10). The axiom of an infinitude of individuals was adopted reluctantly in art. 9, again made as an empirical assumption. Curiously, he did not explicitly state logicism, although the nature of the enterprise should have been clear to his mathematical audience.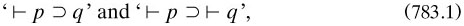
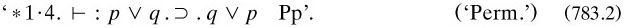
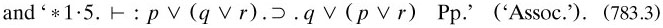
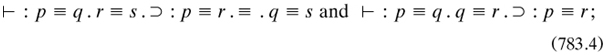
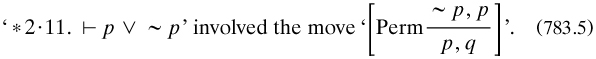
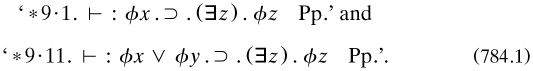
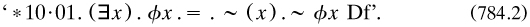
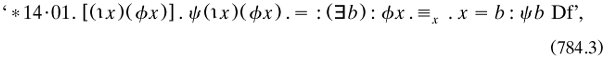

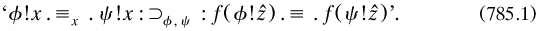
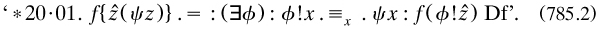
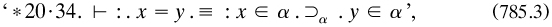
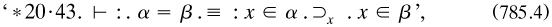
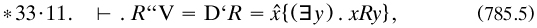
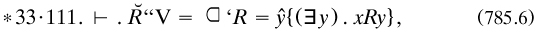
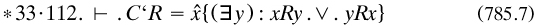
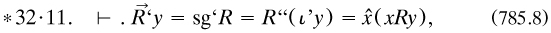
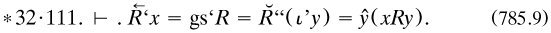
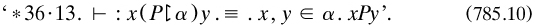
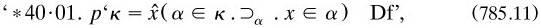
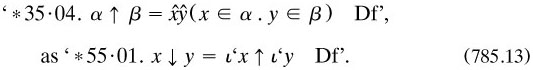
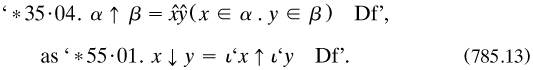
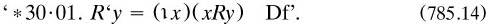
 ’, which took “values” such as ‘∪’, ‘|’ (the compounding of two relations. and ‘+’ from these definition schemae:
’, which took “values” such as ‘∪’, ‘|’ (the compounding of two relations. and ‘+’ from these definition schemae: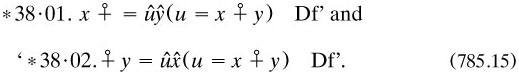
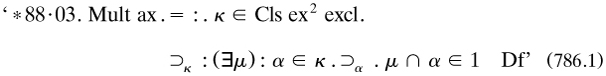
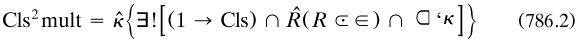
 which is true’ (p. 131.—which is surely not a correct reading of a propositional function. In both hierarchies ‘typical ambiguity’ was deployed, where theorems applied to any appropriate collection of orders and/or types (for example, not only individuals and classes but also classes and classes of classes).
which is true’ (p. 131.—which is surely not a correct reading of a propositional function. In both hierarchies ‘typical ambiguity’ was deployed, where theorems applied to any appropriate collection of orders and/or types (for example, not only individuals and classes but also classes and classes of classes).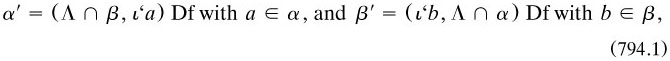
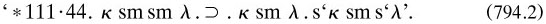
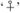 ’ (785.15) was used to define, via arithmetical addition, the relation ‘(+c ν)’ between two homogeneous finite cardinals μ and ν:
’ (785.15) was used to define, via arithmetical addition, the relation ‘(+c ν)’ between two homogeneous finite cardinals μ and ν: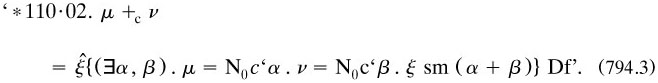
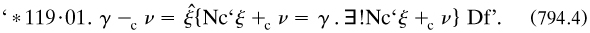
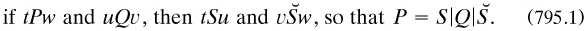
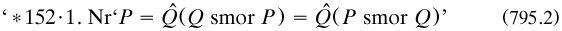
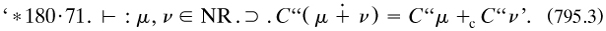
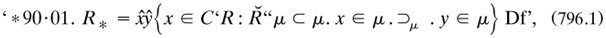
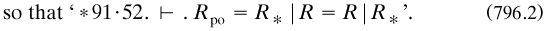
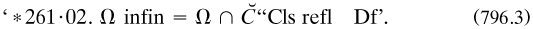
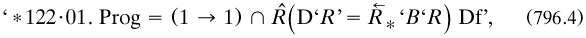
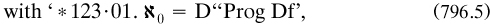
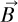 ‘R was the complement of the domain of R with respect to its converse domain (*93·101), so that its member(s) could launch the progression (‘B’ for ‘begin’.) Similarly,
‘R was the complement of the domain of R with respect to its converse domain (*93·101), so that its member(s) could launch the progression (‘B’ for ‘begin’.) Similarly,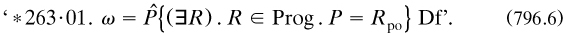
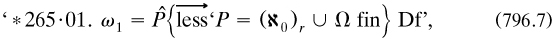
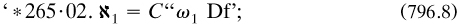
 ’ and so was the correlator of relations ordinally similar to it:
’ and so was the correlator of relations ordinally similar to it: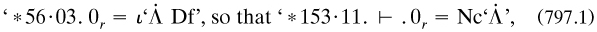
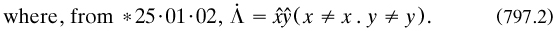
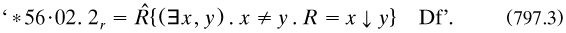
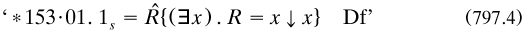
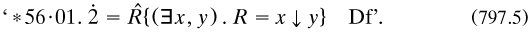
 ’ arose, for the purpose of adding one term to a relation-number μ to produce ‘μ
’ arose, for the purpose of adding one term to a relation-number μ to produce ‘μ 
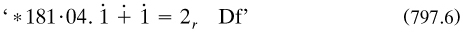
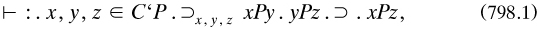
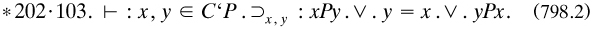
 ‘α’ of ‘its immediate successors’ whether or not α had a maximum, and “
‘α’ of ‘its immediate successors’ whether or not α had a maximum, and “ ‘α’ of its immediate predecessors (p. 559). The key notion in much of the entire Section was the ‘limit or maximum’: ‘A term x is said to be the “upper limit” of α in P if α has no maximum and x is the sequent of α’, symbolised ‘ltP’α’ (p. 575). Similarly, ‘the lower limit of α will be the immediate predecessor of α when α has no minimum; this we denote by tlP ‘α’. Thus the key umbrella notions, ‘limit or maximum’ and ‘minimum’, were given thus:
‘α’ of its immediate predecessors (p. 559). The key notion in much of the entire Section was the ‘limit or maximum’: ‘A term x is said to be the “upper limit” of α in P if α has no maximum and x is the sequent of α’, symbolised ‘ltP’α’ (p. 575). Similarly, ‘the lower limit of α will be the immediate predecessor of α when α has no minimum; this we denote by tlP ‘α’. Thus the key umbrella notions, ‘limit or maximum’ and ‘minimum’, were given thus: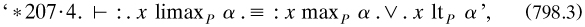
 (*207·401).
(*207·401).
 ka 1996a on identity theories, and de Rouilhan 1996a on concepts and objects. I do not attempt to appraise the total literature.
ka 1996a on identity theories, and de Rouilhan 1996a on concepts and objects. I do not attempt to appraise the total literature.