CHAPTER 8
The Influence and Place of Logicism, 1910–1930
8.1 PLANS FOR TWO CHAPTERS
The reception of PM from its publication to around 1940 is covered in this and the next chapters, with the break coming around 1930. There was a wide range of reactions both to the logical calculus of PM and to logicism; some striking similarities arose from different backgrounds. I associate each main philosophy with a ‘school’, in contrast to the ‘traditions’ of algebraic and mathematical logics.
This chapter falls into two roughly equal parts, with Anglo-Saxon attitudes followed by reactions elsewhere. §8.2 surveys Whitehead’s and Russell’s very different transitions from logic to philosophy till around 1916. Whitehead did not adopt empiricism, but Russell’s empiricist philosophy built closely upon logicism. §8.3 describes an influential visit made by Russell to the U.S.A. in 1914, and his further work in epistemology during the decade. §8.4 is dominated by Cambridge, with the reactions to logicism of Wittgenstein and Ramsey, and Russell’s own revision of PM in the mid 1920s. §8.5 notes the new responses until around 1930 of Britons and Americans to logicism, especially the second edition of PM.
Then the focus falls upon Continental Europe. After the limited interest in Italy and France (§8.6), German-speaking countries take over. §8.7 continues the story of parallel processes from §4 by noting Frege’s late rejection of logicism; Hilbert’s second phase of proof theory; developments in set theory, and the rise of intuitionism with Brouwer; and the reactions of various mathematicians and philosophers.
Next, §8.8 records the remarkable rise of interest during the 1920s in the new country of Poland; a superb group of logicians emerged under the leadership of Łukasiewicz and Le niewski. Finally, §8.9 describes the emergence in Vienna of a circle of mathematicians and philosophers, among whom logic was a major concern. The two dominant figures are Carnap and Gödel; the chapter stops with the latter’s completeness theorem of 1930. The next chapter starts with its successor on incompleteness published in the following year, and then concentrates upon the place of logicism in the 1930s, with only summary note taken of parallel developments.
niewski. Finally, §8.9 describes the emergence in Vienna of a circle of mathematicians and philosophers, among whom logic was a major concern. The two dominant figures are Carnap and Gödel; the chapter stops with the latter’s completeness theorem of 1930. The next chapter starts with its successor on incompleteness published in the following year, and then concentrates upon the place of logicism in the 1930s, with only summary note taken of parallel developments.
Among the bibliographical sources, the reviewing Jahrbuch is still the best single source, with the literature under headings such as ‘Philosophie’, ‘Grundlagen’, and ‘Mengenlehre’ and ‘Logic’—itself a sign of emergence of the field. Herbertz 1912a is a useful ‘study guide’ to philosophy which not only informs on logic and foundations of mathematics but also shows all the main tendencies in philosophy of its time; understandably it is skewed towards German work.
For the U.S.A. the Open Court Publishing Company comes into its own, with many articles and reviews published in its philosophical journal The monist and also new editions, translations and original books by Russell and others (McCoy 1987a). Furthermore, from 1905 the Philosophical review published almost every year until the Second World War a review of developments of philosophy in France; the author was usually Couturat’s friend André Lalande (1867–1963). A companion series from Germany started in 1907 with Oscar Ewald; halted in 1914 by the Great War, it was resumed in 1927 by Arthur Liebert. While valuable for general context, it never treated work in symbolic logics or the philosophy of mathematics in much detail; so it is not cited here. But use is made of the articles and book reviews there, and also in the older Journal of philosophy.
8.2 WHITEHEAD’S AND RUSSELL’S TRANSITIONS FROM LOGIC TO PHILOSOPHY, 1910–1916
8.2.1 The educational concerns of Whitehead, 1910–1916. For Russell PM completed his philosophical programme for mathematics (geometry to come and the three dubious axioms excepted, of course); but for Whitehead it was an (important) stepping-stone for a broader vision of mathematics, which included its creative aspects. Their application for a grant to the Royal Society (§7.8.1) shows the difference in a small but striking way: in three places Whitehead had described their intention of deriving ‘mathematics’ from logic, and each time Russell added the adjective ‘pure’ (§11.5).
At that time Whitehead resigned from his Trinity College Fellowship, in protest over the treatment of A. R. Forsyth concerning a scandale d’amour. He moved to London, and a readership in applied mathematics at University College London became available in 1912 when Karl Pearson moved over to the new Galton Chair in Eugenics. In his application Whitehead presented a ‘large scheme of work, involving the logical scrutiny of mathematical symbolism and mathematical ideas’, and having ‘its origin in the study of the mathematical theory of electromagnetism’ (Lowe 1975a). He secured the post, in his 52nd year; but two years later he moved to a chair at Imperial College, which he held until 1924.
The scope of Whitehead’s ambitions is suggested in a little Introduction to mathematics (1911c) which he wrote for the Home University Library. After opening chapters on ‘The abstract nature of mathematics’ and ‘Variables’ (an interesting choice of starters) he treated some mechanics, real and complex numbers, trigonometry, and aspects of the calculus, series and functions. His 180 pages show a mixture of nice heuristics and pop history; but he never mentioned logicism, logic or even set theory. However in a substantial article 1911b on ‘Mathematics’ for the new 11th edition of Encyclopaedia Britannica he gave logicism disproportionate space, in order to stress that mathematics was more than the study of number and magnitude. He compensated for the long article ‘Logic’ and its history, written by two Oxford philosophers, which ignored all symbolic logics, even Boole’s!
In his article, and with acknowledgement to Benjamin Peirce (§4.3.2), Whitehead defined mathematics as ‘the science concerned with the logical deduction of consequences from the general premisses of all reasoning’ (1911b, 880). It is surely too broad in scope: he may have been influenced by questions of mathematical education, which loomed large in his new career in London. His lecture 1913b to the Fifth International Congress of Mathematicians at Cambridge in 1912 (§8.2.4) dealt with the education of boys. He focused upon the formation of ‘abstract ideas’ and on the ‘logical precision’, but he did not advocate teaching logic itself to promote the latter; interestingly, he supported instruction in the history of mathematics. That year, as President of the London branch of The Mathematical Association, he followed the same line in a more discursive piece 1913a; logic was now linked mainly with mathematical functions. In his later Address 1916a as President of the full Association he pleaded for ‘reform’ in mathematics education, though in the direction of teaching fewer topics thoroughly rather than emphasising logic or reasoning. But in his Presidential Address 1917a to Section A of the British Association for the Advancement of Science, on ‘the organisation of thought’, he gave much space to logicism, outlining its four ‘departments’: ‘arithmetic’, dealing with connectives between propositions; ‘algebraic’, using propositional functions and relations (A. B. Kempe praised); ‘general-function theory’, where mathematical functions were introduced via definite descriptions; and finally ‘analytic’, where he summarised the mathematical contents of PM.
Although his later career was dominated by philosophy and relativity theory, Whitehead maintained an interest in education. He included these four essays in an anthology 1917b entitled The organisation of thought, and the last three again in a later collection 1929b on The aims of education.
8.2.2 Whitehead on the principles of geometry in the 1910s. Whitehead also contributed to the Encyclopaedia Britannica a substantial survey 1911a of the ‘axioms of geometry’. Concentrating on the projective and descriptive parts, he broadly followed his two Cambridge tracts of the mid 1900s (§7.6.2). He also wrote with Russell the article 1911a on non-Euclidean geometry to replace Russell 1902c in the previous edition (§6.2.3); he was largely responsible for the changes, which consisted in leaving the historical part almost intact, eliminating much of the philosophy, and adding in technical matters such as metrics (Russell Papers 3, 472).
In 1914 Whitehead participated in an event stimulated by the Encyklopädie der mathematischen Wissenschaften and its French counterpart (§4.2.4). Both projects were to be completed with a final seventh Part on the history and philosophy of mathematics, and for the French version Federigo Enriques (1871–1946) had been appointed editor. To help fulfil his aims he initiated ‘The First Congress on Mathematical Philosophy’, held in Paris early in April 1914 immediately after one on mathematics education (Reymond 1914a). He planned to create an ‘International Society’ to further these efforts, but they foundered with the start of the Great War in August, and the Part was never produced for either version of the Encyklopädie. The Congress proceedings were to appear in the September issue of the Revue de métaphysique et de morale; but only the opening address appeared there (a scribble 1914a by Pierre Boutroux on mathematicians and philosophers working together), though a few other talks were published in later issues, including Whitehead 1916b on the relational theory of space.
This study was related to the fourth volume of PM, which Whitehead continued to prepare after the earlier ones had appeared. However, he stopped work on it in 1918, seemingly after the death in War action of his younger son Eric.1 After his own death in 1947 his widow followed his instruction to burn all his manuscripts; so we can never know the extent to which it was written. But the application document to the Royal Society (§11.5) shows that he had four Sections in mind. Those on the projective and descriptive branches presumably drew upon his two tracts of the mid 1900s (§7.6.2); then came the metrical branch, where much of the material in the third volume, especially concerning quantity and measurement, was already waiting to be used; finally was promised the ‘Constructions of space’, probably following the scheme of his paper 1906b (§7.6.1) and maybe the Paris paper cited above. Surviving letters to Russell up to 1914 suggest that he was making considerable progress, so that one can form a good impression of the intended product (Harrell 1988a). Clearly several branches would be missing; for example, the absence of the calculus excluded differential geometry. So our sceptical query about the amount of mathematics in logicism (§7.8.2) remains.
For Whitehead PM ended in sad circumstances. Further, in a letter of January 1917 he objected to Russell’s use of his ideas on the construction of space in Our knowledge of the external world (Russell 1968a, 78), despite Russell’s full acknowledgement in the preface; so their collaboration ceased. Let us turn now to the initial reception of their great effort.
8.2.3 British reviews of Principia mathematica. Philip Jourdain was the most assiduous reviewer, with seven pieces. Three appeared in the Jahrbuch: 1913c on the first volume, mostly citing other literature with little discussion of its contents; then 1915a summarising the treatment of arithmetic (more detail was given in a review 1913b elsewhere); and by far the longest, an extended summary 1918a of the last volume. Throughout the decade he both wrote much on Russell’s logic and philosophy and also secured him publication in The monist, of which he became the English Editor in 1912 (my 1977b, ch. 23). The most significant work was a pair of articles on ‘The philosophy of Mr. B*rtr*nd R*ss*ll’ (1911a, 1916a), to which Russell himself contributed a few chapters; with great wit they satirised many of Russell’s main concerns, such as paradoxes and definite descriptions. The asterisks followed a practise of the Cambridge University humorous magazine The granta, where two chapters had first appeared in 1907. Further, in imitation of Russell’s appendix of original texts to his book on Leibniz (§6.3.1), Jourdain showed in appendices that Lewis Carroll had anticipated many of the topics, principally in his Alice books (though not in the ones on logic). A book version Jourdain 1918b was put out with Russell’s blessing by Allen and Unwin, his publisher from 1916.
Jourdain also published in a mathematical journal a long and valuable series of studies on logicians from both traditions: 1910a on Leibniz and Boole; 1912b on MacColl, Frege (§8.7.3) and Peano; and 1913d on Jevons. Apart from the first one his accounts were good, with many references and perceptive comments; and those on Frege and Peano were graced by important remarks on the drafts made by their subjects and added as footnotes. Russell read all the drafts, though he had few remarks to add; one wonders about the reaction had Jourdain fulfilled his intention of writing on C. S. Peirce. Among related activities, Jourdain also published with the Company an English translation of Cantor’s last two-part paper with his own long introduction (Cantor 1915a).
Apart from Jourdain, PM did not receive many other British reviews of substance (some American ones are recorded in §8.3.2); and unlike his, the majority dwelt upon the first volume. An interesting one appeared in The spectator in July 1911. The anonymous reviewer was James Strachey (1886–1967), a younger brother of editor John, and of Oliver of the liar paradox in §7.2.2.2 He gave a good survey 1911a, ending with an analogy worthy of Russell himself: the book ‘seeks to establish the immensely complex structure of mathematics upon a basis more solid that the universe itself, because it is independent of the universe, namely, upon a set of axioms that would remain true if the universe were swept away, and that are true now, even if the universe is merely a delusion’.
Another anonymous review of the first volume appeared, in the Times literary supplement. After lamenting mathematicians’ lack of interest in such studies, G. H. Hardy 1911a urged it to their attention, and of its components he stressed that ‘mathematics, one may say, is the science of propositional functions’, and ‘The theory of “incomplete symbols” is one of the authors’ triumphs’. On type theory he was more reserved, although in wondering if there could be an infinitude of types he had not read the book carefully enough.
8.2.4 Russell and Peano on logic, 1911–1913. In 1910 Russell prepared a collection of his general essays, including 1907d on the study of mathematics (§7.7.2), as a volume 1910a for Longmans, Green entitled Philosophical essays.3 In October he joined Hardy again when he was appointed to a lectureship at Trinity College, in effect taking over the teaching of foundations of mathematics from Whitehead (§7.9.9). He normally gave a two-term course on ‘The fundamental concepts of mathematics’ for a ‘Fee 10s. 6d.’, together with free three-term courses on ‘The principles of mathematics’ and some years one term on ‘mathematical logic’.4 Rather little is known about Russell’s teaching (§7.9.3 contains a hint), but G. E. Moore took the paying course in the winter of 1911–1912; his notes (Papers, 10/4/3) show that Russell dealt with all the main notions and intentions of The principles, including geometry and mechanics, without the technical contents of PM. Mathematics, ‘more certain than philosophy’, was analytic in the sense of being derivable from logic alone, not in the traditional sense that the predicate be part of the subject. ‘Logic in some sense = pure form’, that which remained constant when all constituents had been changed. Russell became quite keen on this approach, and wrote a short manuscript m1912b answering ‘What is logic?’ with ‘Logic is the study of the forms of complexes’, with ‘form’ specified as above. ‘A complex is logical if it remains a complex whatever substitutions may be effected in it. Df.’, so that ‘Logic = the class of logical complexes’. In line with his current avoidance of objective falsehoods (§7.4.7), he associated complexes only with true propositions. The text peters out inconclusively.
At the request in January 1912 of organiser E. W. Hobson, Russell invited speakers to a section on ‘philosophy and history’ of the Fifth International Congress of Mathematicians; it took place at Cambridge in September, with the proceedings coming out the following year. Couturat and Frege declined, but of the Peanists Peano 1913b contrasted the existence of definite description with that of the non-emptiness of classes, Cesaro Burali-Forti 1913a treated functional and operational symbols, and Alessandro Padoa 1913a discussed the status of mathematical induction (and also argued at length with Russell: Papers 6, 444–448). Other contributors to this or other sessions included Ernst Zermelo, Emile Borel and Jourdain. Among visitors from the U.S.A. were Maxime Bôcher and E. H. Moore—and also Paul Carus (1852–1919), editor of The monist, who met Jourdain and recruited him as the English Editor for Open Court. Russell himself did not give a paper, but in his Chairman’s Address 1913b for his section he regretted the absences of Cantor and Frege, and the recent death of Henri Poincaré.
In his paper Peano had noted logicism without comment; but soon afterwards he reviewed the first volume of PM at length in an Italian journal (not his Rivista, which had stopped in 1908). Peano 1913a contrasted his own use of ‘logic-mathematics’ as an ‘instrument’ with its role in PM ‘for science in itself’. Using classial rather than logical formulations, he quoted many of the symbolic definitions and properties of classes and relations (of which the logic was ‘all new’), and the construction of cardinal arithmetic as far as the need for the multiplicative axiom. In three lines at the end he noted the contents of the second volume, promising to write at greater length later; but he never did so, for his passion had switched to his international language of Latin without inflection, in which he had written the review.
8.2.5 Russell’s initial problems with epistemology, 1911–1912
I found Matter a large and fruitful theme, and I think very likely I shall work at it for some years to come. I have done the philosophy of pure mathematics, and this would be the philosophy of applied mathematics.
Russell to Lucy Donnelly, 19 December 1912 (Letters 1, 444.
Like his master Peano, Russell was leaving logic behind at this time. He devoted most of 1911 to philosophical writing, of which the best-known product was a short book on The problems of philosophy, written for the Home University Library series at the request of editor Gilbert Murray. It appeared early the next year as Russell 1912a, soon after Whitehead’s Introduction to mathematics. As he made clear in his opening note, he presented his own preferred selection of problems, so that epistemology was prime, with Moorean reductions and techniques from logic prominent. Indeed, his title was misleading, since he was always a systems philosopher rather than a problems philosopher. While he did not describe logicism, he asserted that ‘All pure mathematics is a priori, like logic’ (p. 43, surely recalling The principles!), and alluded to the definability of arithmetic from logic (p. 65). He also announced that the laws of identity, contradiction and excluded middle were ‘self-evident’ (p. 40), without reference to the inductive processes of finding basic principles which he had mentioned to Ralph Hawtrey (§7.8.3).
Russell’s epistemological principles were guided by the search for certainty, which he mentioned three times in the opening two paragraphs. In ch. 5 he distinguished ‘knowledge by acquaintance’, drawn from sense-data presented directly before the mind, from ‘knowledge by description’, given by physical objects and presented indirectly for expression via definite descriptions; the account was partly based upon, and even copied from, a lecture of this title delivered to the Aristotelian Society in March 1911 and published by them as his 1911c. Again, in chs. 9 and 10, built upon his first Presidential Address 1911e to the Society, he stressed the importance of universals, and assumed that relations played a major role. But soon after the book appeared Oliver Strachey suggested on 4 January 1912 that he rethink the distinction between universals and particulars and demote relations in some ways (RA); Russell noted on the letter that it ‘influenced me considerably’, so it is transcribed in §11.7. (Strachey was to make similar points in Mind, not so sharply, in 1915a, 20–23.) In ch. 12 on ‘Truth and falsehood’, Russell appealed again to the correspondence theory, and discussed the status of judgements, which were to come to the fore in his next epistemological phase.
8.2.6 Russell’s first interactions with Wittgenstein, 1911–1913. 1911 saw two important changes in Russell’s life: the start in March of his affair with Ottoline Morrell; and the beginning in October of his relationship with Ludwig Wittgenstein (1889–1951), then a young Austrian graduate engineer from Manchester University. Wittgenstein had been aware of Russell’s work already in 1909, when he corresponded with Jourdain about Russell’s paradox and a solution proposed in terms of regarding paradoxes as meaningless limiting cases of meaningful propositions (see Jourdain’s text in §11.4). Now in personal contact, they experienced an intense exchange until the Great War started in 1914 (McGuinness 1988a, ch. 5).
One major consequence concerned the fate of Russell’s first effort at a book on epistemology, which he wrote at speed during May 1913. He intended to work out in detail his theory of knowledge by acquaintance, firstly with a Part ‘On the nature of acquaintance’ (with predicates, sensation, time and so on), and then Parts on ‘atomic’ and ‘molecular propositional thought’, the latter formed by linking up examples of the former with logical connectives such as ‘or’ and ‘unless’ (Russell m1913a). His rejection of objective falsehoods led him to replace a two-place theory relating a judgement to a proposition P to assess its truth-value by a ‘multiple relation’ theory (his name), where the judgement was made of the various constituents of P; typically, ‘person S understands that a is in the relation R to b’.
However, Wittgenstein criticised this theory on some fundamental grounds. The exact details are hard to make precise, for the main surviving evidence comes only in June letters from Wittgenstein to Russell (fragments drawing on doubtless long chats) and from him to Morrell.5 But clearly Russell’s old and new philosophical concerns were involved, since the epistemology of logic was a major issue. One criticism was that Russell’s theory could not handle asymmetrical relations and discriminate between ‘S believes that a precedes b’ and ‘S believes that b precedes a’. This ‘direction problem’, as it has become known, struck at the heart of Russell’s epistemological aims; for example, he gave prominence to logical forms and complexes, and his third part would have contained a taxonomy of complexes.
Another dart was aimed at Russell’s logic, where already in June 1912 Wittgenstein was convinced that ‘The prop[osition]s of Logic contain ONLY APPARENT variables’, so that ‘there are NO logical constants’ (presumably meaning that they were not objects: Letters, 10). He must have realised that Russell’s logic was muddled up with logicism and so needed its own characterisation; he may have been led to his view of variables by noting that a logical order was specified by its quantified variables. He seems to have accepted type theory; but he did not subscribe to logicism, since he concluded this letter that ‘Logic must turn out to be of a TOTALLY different kind than any other science’, presumably including mathematics.
For logicist Russell, however, such issues were still more serious, and confidence in his new book gradually disintegrated; as with his substitutional theory (§7.4.6), several different factors may have been involved. At all events, he abandoned it in June after writing only the first Part and much of the second one. He did publish the first six chapters of the first Part during the first half of 1914, sending them to Jourdain as a quartet of articles for The monist; but their appearance may reflect his financial difficulties more than any intellectual conviction. (The text appeared in full only in Russell Papers 7 (1984).) However, the general thrust of his philosophy—empiricist and reductionist epistemology drawing upon techniques from logic—was unimpaired, and a more successful successor was soon written (§8.3.1).
8.2.7 Russell’s confrontation with Wiener, 1913. (My 1975b) Three months later, in October 1913, Russell had another acquaintance with a foreigner, less consequential than that with the Austrian but tricky enough. This time it was an American, still younger than Wittgenstein but already the possessor of a doctorate from Harvard University: Norbert Wiener (1894–1964). He came over to Cambridge with his father, who ‘looks like a Hindoo, but I think it would come off in water’, Russell told Morrell on 26 September 1913 (letter 877, copy in RA). ‘The son is fat, bland and smug’, and
after a period of dead silence—suddenly woke up and began an equal torrent, on the subject of his doctor’s thesis—pulling out books from my shelves and pointing out crucial passages, pointing out, kindly but firmly, where my work is one-sided and needs his broad view and deep erudition to correct it [... ] I believe the young man is quite nice and simple really, but his father and teachers have made him conceited.
Partly through the influence of Josiah Royce’s lectures at Harvard (§7.5.4), Wiener had found a nice topic for his teenage investigations: ‘A comparison between the treatment of the algebra of relatives by Schröder and that by Whitehead and Russell’ (Wiener m1913a). It was the first, and still the only substantial, contrast between the two traditions of algebraic and mathematical logic, drawing upon an especially interesting context. For Wiener showed that from a structural point of view there were very many similarities between the two theories, even down to specific kinds of relation defined in each. However, on their respective foundations, he was much less sure. In particular, while he noted that Schröder treated collections as part-whole theory whereas Whitehead and Russell deployed Cantorian set theory, he did not grasp the consequences; he even praised Schröder’s conflation of membership and inclusion as subsumption. Curiously, he used Schröder as his only algebraic representative; fellow Harvard graduate Peirce, still alive though in isolation, was not mentioned.
The ‘infant phenomenon is staying here until I go to America’, Russell opined to Morrell on 28 September (letter 879, copy in RA). ‘I have read his Dr. thesis, and think him more infant than phenomenon. Americans have no standards’. Some of his written comments to Wiener are of great historical value; in particular, he recorded the cause of his initial attachment to Peano in 1900 (quoted in §6.4.1), and stressed the central importance of contextual definitions in logicism (§7.8.4–5). Throughout he was hard-hitting, especially on the inferior power of part-whole theory. Presumably as a reaction, Wiener kept these comments but never published a line of his thesis, not even a summarising paper (my 1975b serves as a partial substitute). This is a great pity, as the vast differences between the two traditions have never been properly recognised historically or even philosophically, and he had plenty of good material and examples to present.
However, Wiener made other useful contributions to logic then. One was a note 1914a on ‘A simplification of the logic of relations’, where he showed how the calculus of relations could be reduced to that of classes by a proper definition of the ordered pair to replace (785.13)2:
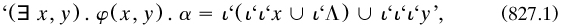
for the class α contained only the ordered pair (x, y), as provided by the respective clauses in the union. His motive was to reduce the axiom of reducibility (§7.9.2) for relations to that for classes. The definition is somewhat clumsier than needed; the job can be done by 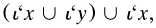 as Kuratowski 1921a was to show later.
as Kuratowski 1921a was to show later.
Wiener’s note was published by the Cambridge Philosophical Society after its presentation in February 1914 by Hardy, with whom Wiener had also become acquainted. (827.1) was only a technical device, albeit interesting, without consequences for the philosophy of relations, such as possible relationships between x or y; naturally he had made no such claim for it, although he showed how several definitions in PM could be simplified. Perhaps for that reason, or for residual annoyance, Russell did not react at all; but he had noticed the infant’s prodigious gifts. He suggested that Wiener apply the logic of transitive and unconnected relations to non-overlapping intervals and the theory of instants of time; it soon led to a succeeding paper Wiener 1914b which was to influence Russell himself much later (§9.5.4), and to an extension 1914c on relations of many variables with application to the theory of intensities of sensation. At the end of the decade he returned to this topic, modifying the theory of magnitudes by vector-families given in Part VIB of PM (§7.9.9) to allow for those which have a finite upper bound. He submitted this paper to Hardy for the London Mathematical Society, and Russell wrote a very warm report (Papers 9, 469–470); so it duly appeared as Wiener 1919a.
Maybe inspired by this extra exposure to foundational questions, from 1914 to 1919 Hardy himself offered a free course in the Easter term (summer to everyone else. on ‘Elements of mathematics (for non-mathematical students.’. G. E. Moore took it, seemingly in 1915; his notes reveal a course of set theory influenced by PM, and including variables, finite and transfinite cardinal and ordinal arithmetic, mathematical induction, the multiplicative class, continuity, and some elementary geometry.6 But he published none of it, and returned in print to foundational questions only a decade later (§8.5.2).
8.3 LOGICISM AND EPISTEMOLOGY IN AMERICA AND WITH RUSSELL, 1914–1921
8.3.1 Russell on logic and epistemology at Harvard, 1914. Another foreign product came into Russell’s hands late in 1913: the English edition of a recent German compendium of logic, intended to launch an ‘Encyclopaedia of the philosophical sciences’ but prevented by the Great War from proceeding further (Windelband and Ruge 1913a). Royce, Couturat and Enriques were among the sextet of authors, surveying various kinds of logic or its applications to other disciplines, especially philosophy. The whole is a mish-mash: even Couturat’s long survey 1913a of symbolic methods, mainly Peano’s and PM’s, lacks life. Arguably the most interesting piece is Royce 1913a on the notion of order as he was developing it from Kempe’s theory (§7.5.4). In a short review Russell 1914a was wittily sarcastic: ‘The book, in fact, resembles a compendium on the British Constitution composed during the Civil War, with an introduction by King Charles and an epilogue by Oliver Cromwell’.
During that autumn and winter Russell had the regular company of Wittgenstein, Wiener and Jourdain, and occasionally he used Jourdain’s secretary to take down dictation of various papers and also Wittgenstein’s notes on logic. But his main concern was the visit to America mentioned to Morrell above: he had negotiated to visit Harvard between mid March and mid May 1914 to give two lecture courses in the Philosophy Department. Early in April Peirce died; a student of the courses, Victor Lenzen (1971a), went to collect Peirce’s Nachlass at the end of the year (§4.3.1).
One of Russell’s courses comprised a highly technical account of PM, whose three volumes were now all published. The audience included T. S. Eliot (1888–1965), a post-graduate student specialising in the philosophy of F. H. Bradley, who was much taken with Russell’s very different philosophical world: further, his notes on the course on logicism are much the more extensive. They record one innovation since PM appeared: the presentation of logical connectives as tables of the truth-values, which Russell and Wittgenstein seem to have thought up between them in 1912 or 1913.7
Russell’s other course, on epistemology, had been partially delivered at Cambridge as a course on ‘The fundamental concepts of physics’ in the Lent term of 1914.8 Russell had largely written a book version during the previous autumn, and much later he claimed that he dictated it to a secretary at the beginning of 1914 in one session (1956a, 195–196; 1967a, 210); but the faulty memory was on form again, for the torrent of letters to Morrell tell a far more prolonged story. If any work of that time was produced this way, it may have been a related paper on ‘sense-data and physics’ prepared with the help of Jourdain’s secretary and published as Russell 1914b (Blackwell 1973a).
The book appeared from Open Court in August 1914, just before the Great War (Russell 1914c). A somewhat revised edition was published by Allen and Unwin in 1926 in Britain, and a different one with rather fewer changes three years later in the U.S.A.; both versions were reprinted, with the British one of 1993 being mis-described as of the original edition!
The long title strikingly encapsulates Russell’s philosophical hope: ‘Our knowledge of the external world as a field for scientific method in philosophy’. Unfortunately, some of the reprints only give the first six words of its title, under which it is generally known. In an opening chapter he summarised the prevailing philosophies, idealism and evolutionism, which he wished to replace: Bradley and Henri Bergson were the respective prime targets. The positive doctrine was displayed across six chapters, prefaced by his creed of ‘Logic as the essence of philosophy’ (ch. 2); he made a quick historical survey of modern versions, especially his own, though without the symbols. Then in ch. 3 using those first six words, he summarised a version of knowledge by acquaintance, although he neither used that name nor analysed judgement or truth-values of propositions: the failed book of the previous year seems to have reduced his ambitions. The main novelty was a passage on ‘perspective space’, effectively the class of all individual perspectives of a physical object, which served like an invariant for them. This passage closely resembled part of his paper 1914b on sense-data; maybe it was added later, causing him to mis-remember the manner of composition of the book. In a succeeding ch. 4 on ‘the world of physics and the world of sense’ he displayed his reductionism in ‘the maxim that inspires all scientific philosophising, namely “Occam’s razor”’.
Much of the next three chapters was concerned with continuity and infinity, where Russell discussed Zeno’s paradoxes at length and the views of Cantor. At their end he considered the relationship between classes and mathematical logic, and mentioned Wittgenstein’s recent unpublished idea that logical constants were not objects. The final ch. 8 dealt with cause and free-will, giving him chances to extol certainty and describe induction. Overall the book has a patchy scenario, more mathematics than necessary and not really enough science. But the important role of logic was clear; and while he avoided a symbolic treatment, the fusion of logic with epistemology was to give the book a warm reception, with long complimentary reviews such as Jourdain 1914a in the Mathematical gazette and C. D. Broad 1915a in Mind.
Back home from Harvard, Russell rehearsed his position in a lecture on ‘the scientific method in philosophy’, delivered on 18 November 1914 at Oxford University. He also drew upon his recent thoughts on the logical forms of complexes (§8.2.4) to distinguish between two ‘portions’ of logic: one handling ‘general statements’ and the other ‘concerned with the analysis and enumeration of logical forms’ (Russell 1914d, 65).
By contrast, reactions in America, both to the book and to PM, were also substantial but more mixed, as we now see.
8.3.2 Two long American reviews. The Journal of philosophy carried a fine critical piece on ‘the logical-analytic method in philosophy’ by Theodore de Laguna, who taught at Bryn Mawr College. While praising the merits of the method in its mathematical contexts (1915a, 451), he greatly doubted its utility in Russell’s new book, stressing the epistemic dangers of using Ockham’s razor (p. 453) and sensing a vicious circle in constructing space via perspective spaces: ‘Mr. Russell has deduced his conclusion from his knowledge of physical space; nobody ever induced it’ (p. 460). He concluded that ‘Mr. Russell’s philosophy is as complete and radical a failure’ as a theory of ethics which Russell had recently aban doned (p. 462).
Logicism was discussed also in mathematical journals, especially those published by the American Mathematical Society (hereafter, ‘AMS’). One of the best reviews of the first volume of PM was 25 pages written by J. B. Shaw in its Bulletin. We last met him in §4.3.2, summarising knowledge about Benjamin Peirce’s linear associative algebra five years earlier; here, after reviewing some of the main techniques used, such as types, relations and descriptions, he stressed how little mathematics seemed to fall with the logicist purview, and among notable absentees he noted ‘structure and form’ (Peirce in mind?), ‘invariance’, ‘functions as functions’ and ‘inversions’ (Shaw 1912a, 410). ‘A Principia Mathematica should cover the field, or it ceases to justify its title’: regretting the limited amount of mathematics covered, he noted that PM ‘examines the rules of the great mathematical game. But it does not play the game or undertake to teach its strategy’ (pp. 389, 411). Among other authors, he mentioned Kempe for the ‘whole consideration of mathematical form’ (p. 406).
In a sequel paper in The monist Shaw 1916a continued in the same vein, concluding that ‘Logistic has a right therefore to exist as an independent branch of mathematics, but it is not the Overlord of the mathematical world’ (p. 414). He reprinted this review in a book of Lectures on the philosophy of mathematics given at the University of Illinois, published by Open Court as Shaw 1918a after some delay (Open Court Papers, Boxes 32/16–18 passim). While not penetrating philosophically, he gave a nice survey of the variety of such concerns: he also considered possible reductions of mathematics to algorithms, algebra, and ‘transmutations’ such as Royce on order (§7.5.4). Other topics included form in the spirit of Kempe, and the theories of number, functions and equations.
8.3.3 Reactions from Royce students: Sheffer and Lewis. When Royce died in September 1916 in his early sixties, four years after William James, the Department of Philosophy at Harvard University was at a low ebb (Kuklick 1977a, ch. 21). In June and July the Chairman J. H. Woods had corresponded with Russell about lecturing there again, but his pacifist activities prevented him from obtaining a visa (Russell 1968a, 65–66). On 23 September, a few days after Royce’s death, Woods invited Russell to edit some of Peirce’s logical manuscripts which they had acquired (§8.3.1); Russell declined this obviously inappropriate proposal (RA).
Despite the languor, the best remembered American contribution to logic from this time came from a junior member of the Department, Henry Maurice Sheffer (1882–1964). His philosophical training under Royce had drawn him strongly to logic (they may have been writing a textbook together, though it was not finished. and especially to logicism. Sheffer made a tour in Europe during the winter of 1910–1911, when he met Peano and Russell, among others; and back home he published with the AMS a short paper Sheffer 1913a on ‘Boolean algebras’ (the origin of this phrase), in which he showed that they could be defined solely from an operation written ‘|’ and four laws, assuming two elements in the algebra. Then he showed that the propositional calculus could be produced with this operation applied to two propositions as their joint denial (‘neither-nor’, or ‘nand’); he called it ‘rejection’. In a footnote he appealed to duality to show that alternative denial, ‘either not-p or not-q’, could play the same role; this reading has became known as the ‘Sheffer stroke’.
This paper eclipsed a recent one by the Polish mathematician Edward Stamm (d. 1940), who had accomplished in 1911a a similar reduction using ‘nand’ and ‘or’. Sheffer seems not to have known of Stamm; and neither author could have been aware of the anticipation of ‘nand’ in a manuscript m1880a by his Harvard predecessor Peirce (§4.3.5).
This paper has left Sheffer’s name on the philosophical scene; thereafter he became notorious for publishing virtually nothing. He seems to have become paranoid about the printed page, or even the hand-written one; most of his Nachlass consists of collections of lectures and research notes cut into small rectangles, so that the texts are very hard to reconstruct.9 In 1919 he sent to Russell a manuscript which he claimed would ‘make a great portion of Principia mathematica superfluous, meaning, I think, that his was much a much simpler method of getting your results’, as his colleague R. F. A. Hoernlé reported to Russell on 28 November (RA).
Maybe this work was a version of a substantial manuscript Sheffer m1921a describing ‘The general theory of notational relativity’, in which he combined the American penchant for postulational studies (§4.7.3) with tableau-like ‘grafs’ showing which individuals did (not. satisfy a given two-place relation (more like the displays of Benjamin Peirce than truth-tables, which presumably he had come to know during Russell’s visit). He sent copies of his manuscript to Russell and Hardy among others, but published only a few details in a congress paper 1927a. On July 1928 he told Heinrich Behmann (§8.7.8) that he had written ‘about one-third of a book’ on notational relativity before being held up by a nervous breakdown (Behmann Papers, File I 68).
An exact contemporary at Harvard and fellow student under Royce was Clarence Irving Lewis (1882–1964); during the 1910s he taught at the University of California at Berkeley. His review 1914b of the second volume of PM in the Journal of philosophy was comprehensive; he noted details which were often missed, such as the assumption of only one individual and homogenous cardinals, and he found relation-arithmetic to be ‘a miracle of patience and ingenuity’ (p. 501). He admired the enterprise: ‘The “Principia” is to intellect what the pyramids are to manual labor. And the “Principia” has the added wonder that the whole structure is balanced on the apex of logical constants’ (p. 502).
But the main influence of PM on Lewis was negative: he was repelled by Russell’s all-purpose use of implication, especially that ‘a false proposition implies any proposition’ (PM, *2·21), which for him betrayed the construal of implication. In a sequence of papers from 1912 he developed an alternative logic of ‘strict implication’, based on impossibility as a primitive notion. ‘I am quite convinced now’, he told Royce on 15 October 1911, ‘of the possibility of modifying the calculus of propositions so as to bring its meaning of implication into accord with that of ordinary inference and proof’.10 He also mentioned a ‘preliminary paper’ 1912a sent to Mind, where he introduced his version; in a succeeding paper there he described impossibility as ‘intensional disjunction’ (symbolised ‘V’) such as no Tuesday being a Wednesday, in contrast to the traditional extensional case (written ‘+’: 1914a, 241–242). He presented calculi for both strict and material implication, laying out each one American style as a system of postulates, and comparing the status of the new calculi with that of non-Euclidean geometries relative to their Euclidean parent. In a companion presentation in the Journal of philosophy he introduced substitution as one of his ‘primitive ideas’ (1913a, 434), thus making explicit a common assumption of symbolic logicians.
Lewis 1914c developed his symbolism of ‘The matrix algebra for implications’ in The philosophical review by writing ‘~p’ for ‘[proposition] p is impossible’, in contrast to ‘–p’ for ‘p is false’. He stressed the role of semantics, indicating that five truth values were now available: these two, truth itself, and also those due to ‘– ~ p’ and ‘~ –p’; further ones were imaginable. He worked through his systems in more detail, including rules of substitution, and closed by claiming that ‘the consequences are important not only for logic, but also for epistemology and metaphysics’.
The reaction to Lewis’s innovation was mixed. In Mind Oliver Strachey felt that strict implication belonged to ‘applied’ logic while Russell had properly concerned himself with the more general ‘pure’ logic (Strachey 1915a, 26–28). In the Journal of philosophy Wiener 1916a took Lewis’s criticism of Russell as guilty of the fallacy of denying the antecedent (that if the postulates delivered an incorrect logic, then they must be incorrect themselves); but he saw strict implication as a theory worth developing in its own right.
Lewis produced a book 1918a of over 400 pages, published by his University as part of its semicentennial celebrations. Entitled A survey of symbolic logic, it included a chapter on strict implication containing his latest version. Some of the previous versions had been faulty; and this one was also to be found wanting, so that the systems with which his name is now associated came only in the 1930s (§9.4.1). When the book was reprinted in 1960 he had this chapter omitted.
Lewis then also left out the final chapter, which had reviewed the relationships between ‘Symbolic logic, logistic, and mathematical method’. He contrasted in detail three ‘types of logistic procedure’: the ‘simple’ one of the Peanists, of translating mathematics into logical language; ‘the hierarchic method, or the method of complete analysis, exemplified by Principia mathematica’; and ‘the method of Kempe and Royce’, dominated by order (these titles on pp. 367, 368). Assessing their strengths, he imposed his own formalist definition of a ‘mathematical system’ as ‘any set of strings of recognizable marks in which some of the strings are taken initially and the remainder derived from these by operations performed according to rules which are independent of any meaning assigned to the marks’ (p. 355). Perhaps he realised later the unsatisfactory nature of this characterisation, leading him to omit the chapter from the reprint.
The rest of Lewis’s book may surprise: very little on mathematical logic, but a good review, partly historical, of algebraic logic from his hero initiator Leibniz through Boole, De Morgan and Peirce to Schröder, followed by a detailed account of the methods such as expansion theorems and elimination, and of ancillary techniques such as Euler and Venn diagrams and the Gergonne relations. All this material was reprinted, although by 1960 much of it was out of fashion; indeed, the account had been an unintentional tombstone in 1918.
Within this surprise was another one: the small space assigned to Hugh MacColl, seemingly Lewis’s predecessor in modal logic (§7.3.6). However, to Lewis MacColl’s procedures only ‘suggest somewhat’ (p. 108) his own strict implication; the differences are considerable, especially because between the two logicians lay the recognition of Peano, Frege and PM (Parry 1968a).
A curious feature of the book is Lewis’s use of ‘class’. When he finally reached mathematical logic, he clearly explained Cantorian properties such as membership differing from inclusion (pp. 260–265); but he did not stress the differences from part-whole ‘class’ theory used in the earlier account of algebraic logic (especially pp. 184–189). Similarly, when he introduced quantification there, he used the Peirceian symbols ‘Σ’ and ‘II’ and defined the quantifiers as infinite disjunctions and conjunctions respectively (p. 236); thus he admitted horizontally infinitary language without qualms, maybe without noticing. Again, his account of Kempe and Royce did not include a definition of multisets. In these respects Lewis’s survey was rather undiscriminating; but his bibliography is still superb.
8.3.4 Reactions to logicism in New York. In January 1913 Lewis had written to Christine Ladd-Franklin, fearing that ‘similar difficulties’ over implication to those in Russell’s logic obtained in her system, which was based on her inconsistent triads of propositions (§4.3.7).11 He was thanking her for an offprint of her recent paper 1912a in The philosophical review on ‘Implication and existence in logic’. Although rarely publishing, she had continued her interest in logic, largely in the algebraic style of her master Peirce. In this paper she used her method to interpret (rather inconclusively) the case of consistency as involving possibilities and thereby existence: Russell’s notions of material and formal implications were held to be over-rated in importance (pp. 642–643, 656–657).
Late in 1917, her 71st year, Ladd-Franklin delivered a series of lectures on ‘symbol logic for the logician’ at Columbia University in New York, where she held a lectureship. Presumably in this context, she drafted papers on Russell’s logic; among a mass of notes in files sometimes called ‘Bertie’ (Ladd-Franklin Papers, Boxes 10 and 38) the most developed account is m1918a?, of 18 folios. Like Lewis, Ladd objected to Russell’s all-purpose use of implication; to her the lack of paradox lay in the negation of the antecedent, not in distinguishing implication from inference. But she also disliked Lewis’s alternative, on the grounds that it could not properly handle qualities.
Ladd’s main disagreement with Russell concerned the arrangement between propositional functions and classes chosen for PM; she preferred the no-classes theory of Russell 1906a, which she had recently read (fol. 5). As we saw in §7.4.6, Russell had developed it as the substitutional theory but had published virtually none of it; Ladd understandably misread the (small) use made of it in PM as the foundation of that calculus. She liked it for its avoidance of propositional functions and (as she saw it) the reinstatement of classes, despite the presence of paradoxes. She also did not grasp the significance of membership to Cantorian classes, regarding its non-transitivity as merely a fallacious use of the copula (fols. 11–12). While furnishing a nice sideways look at logicism, her paper might not have been well received if published, although perhaps the lecture course was successful.
New Yorkers also reviewed the first volume of PM. The first was Morris Cohen (1880–1947), a Russian-born immigrant and Harvard student of Royce (like Sheffer on both counts) and newly promoted to professor at his alma mater, College of the City of New York. In The philosophical review Cohen 1912a admired the logicist thesis while being critical of repetitions in the presentation and sceptical of type theory. In an article 1918a in the Journal of philosophy he advocated, rather lamely, the new approaches to logic, though he took logicism as an identity thesis (pp. 679–680). An interesting detail was his recalling Russell saying that ‘all inference is deductive’ (p. 686).
Next came Cassius Keyser, Ladd’s colleague at Columbia and the victor over Russell a decade ago on the need for the axiom of infinity (§7.2.7). Then in his fifties, he wrote a praising though waffly review 1912a in Science of the first volume of PM, showing general sympathy with logicism. More importantly, in 1917 he organised a seminar on PM, and excited the interest of Emil Post (1897–1954), who then wrote a most remarkable doctoral thesis which appeared in the American journal of mathematics as Post 1921a. In art. 2 he presented ‘truth-tables’ (his name), with ‘+’ and ‘–’ symbolising the two values. We saw in §8.3.1 that Russell had publicised them at Harvard six years earlier; Post seems to have been independent, for he unconvincingly cited as precursors PM itself, and texts before that in Jevons and Venn. He also made far greater use of the tables, to prove that the propositional calculus was consistent and complete (art. 3). Further novelties came when he generalised the tables to n values, and thereby introduced many-valued logics, at least from a postulational point of view (arts. 5–7). Finally, in a ‘generalisation by postulation’ he presented his logics as systems of inference (arts. 8–16).
8.3.5 Other American estimations. In The philosophical review de Laguna 1916a attacked the theory of types. After querying the status of the variable as a symbol or with some kind of referent, he considered three paradoxes. The liar held ‘very little significance’, since apparently it could be solved by not asserting propositions to be true (p. 23). Much more important was Russell’s, and his own variant in terms of a property of a property not holding of itself: types failed because inclusion of sets was not ‘a constant property’ across types, and self-membership was quite acceptable, especially if construed in terms of properties (p. 27).
The Pennsylvanian scholars Robert P. Richardson and Edward H. Landis published an article 1915a in The monist on ‘Numbers, variables and Mr. Russell’s philosophy’ as handled in The principles; they seem not to have seen PM. Some points were silly, such as preferring the word ‘group’ to ‘class’ (p. 324). But others were perceptive; for example, Russell’s confusion over ‘term’ and ‘object’ as the most general philosophical notion (p. 331), and over symbols and their (possible) referents (pp. 349–351). Taking variables to be ‘things represented by symbols’ (p. 350), they found Russell’s use of ‘variable’ to be ‘in a sense peculiar to himself’ in denoting ‘either a general class name [...] or else the object represented by the distributed class name’; thus his definitions of numbers and of variables were a ‘failure [... ] complete and utter’ (pp. 362–363). While detecting several cases of conflation in Russell, they did not appreciate that he gave variables a much wider remit than that of the ordinarily mathematical; they also failed to discuss propositional functions or quantification.
Their article was reprinted as a booklet by Open Court, who soon put out also their book Richardson and Landis 1916a on Fundamental conceptions of modern mathematics. Again variables were to the fore; and this time mathematical logic gained some attention, though not happily. Frege’s definition in the Grundlagen of 0 as ‘the number which belongs to “unequal to itself”’ was sloppy enough a translation (compare §4.5.3) to lead them to conclude that his ‘zero is simply nothing’ (p. 59); thus ‘As a logician he cannot be ranked above the level of Schröder and Peano’, whose ‘treatises’, however, were ‘a hindrance rather than a help to precision of thought and speech’ (p. 152). Russell was more summarily treated this time, but his definition of cardinals as classes of similar classes was ‘such as though one were to define whiteness as the class of all white objects’, an absurdity due to his failure, shared with Peano, ‘to recognize the important distinction between equality and identity’ (pp. 152–153). While again ignoring propositional functions and quantification, they gave a wide selection of examples of conflation of symbols with their referents from writings in algebras and mathematical. So their choice of hero is very surprising: ‘It is a crying shame that the University of Cambridge, which has recently stood sponser [sic] for so many treatises of dubious value, has not yet set her press to the work of issuing an edition of the collected works of Augustus De Morgan, one of the greatest of her sons’ (p. 121).
This volume was the first of 13 planned parts ‘dealing with ‘Algebraic Mathematics’, summarised at its end; to come were most parts of mathematical analysis, Cantorian infinitude and the theory of functions—but not algebraic or mathematical logics. A vaster collaboration even than that for PM was envisaged, but no more parts appeared.
While no author in this sub-section made a durable contribution, they all touched nicely on issues relating to the distinction between logic and metalogic. We shall hear more and better on it from the Americans in §8.5.5.
8.3.6 Russell’s ‘logical atomism’ and psychology, 1917–1921. The start of the Great War in August 1914 changed Russell’s priorities completely, and he devoted most of his energies to a personal ‘make love not war’ campaign, with pacifist lectures and writings mixed in with a not-well-ordered series of sexual relationships. The former activity led to his dismissal from his lectureship at Trinity College Cambridge in July 1916 (Hardy 1942a) and imprisonment two years later (§8.3.7). But during 1917 he prepared a collection of his general essays on mathematics and science, partly overlapping with that in Philosophical essays (§8.2.4); including 1901d and 1907d, it appeared as 1918a from Longmans, Green, under the title Mysticism and logic.12
In the autumn Russell’s interest in philosophy began to revive, leading to two public courses delivered between October 1917 and March 1918 at Dr. Williams’ Library in London. As at Harvard three years earlier (§8.3.1), one course treated logic and the other epistemology. The latter course was recorded by a stenographer and typed up for publication, including some of the questions from the audience and Russell’s answers. Thanks to Jourdain, the eight lectures appeared in four consecutive issues of The monist between October 1918 and the following July, around 130 pages in all (Russell 1918–1919a).
The title of the course, ‘The philosophy of logical atomism’, reflected Russell’s use of ‘analysis’ in both senses (§6.1.1), breaking a complex into its basic components and then synthetically reconstructing. As in his pre-War writing, he mulled over the (non-.existence of objective falsehoods, propositions and facts as complexes, and the relationship to all of beliefs; but he acknowledged at the head a greater influence of Wittgenstein. In particular, ‘propositions are not names for facts’, since, for example, ‘Socrates is dead’ and ‘Socrates is not dead’ correspond to the same fact, one truly and the other falsely (p. 187). This finding by ‘a former pupil of mine’ led him to rethink his own reductionist enterprise, in which analysis (in the narrow sense. led him at one point to revive the approach of his abandoned book of 1913 (§8.2.6) by associating ‘atomic propositions’ with simple facts and ‘molecular’ ones to combinations formed from these atoms by means of logical connectives (pp. 203–208).
This procedure brought logic most explicitly to the fore in Russell’s course. He included the truth-table (§8.3.1) for ‘or’, in a horizontal layout, probably for convenience of printing:

he then explained the Sheffer stroke, calling it ‘incompatibility’ but not mentioning its creator (pp. 209–210). He presented his own definition of (impossibility in terms of the (non-)existence of a values satisfying a propositional function (§7.3.6); he may have had Lewis as a target, since a few pages earlier he had used a similar Tuesday/Wednesday example (pp. 231, 223). The old substitutional theory (§7.4.6) made a brief appearance, with the Socrates/Plato example again (pp. 237–239); and he exhibited the limitations of logicism by stating the axioms of infinity and choice as cases of non-logical propositions (pp. 239–241). Definite descriptions had the sixth lecture to themselves, followed by one on type theory and classes. The last lecture dealt with ‘what there is’ as he saw it: as usual, he brandished Ockham’s razor, and he stressed his methodology of preferring ‘logical’ constructions to inferred entities, much like his use of definitions in logicism to reduce assumptions.
Just as the last part appeared in The monist, in July 1919, Russell followed up with a lecture 1919c to the Aristotelian Society on propositions, which were defined at the head as ‘What we believe when we believe truly or falsely’. Truth and falsehood were prominent: he adhered to the correspondence theory but dithered (as in the earlier lectures) over the status of ‘negative facts’, in face of a recent essay in Mind on ‘negative propositions’ by Raphael Demos (1892–1968), who had studied with Russell at Harvard in 1914. Demos 1917a argued (rather naively) that ‘not’ introduced an opposition to positive propositions similar to that between truth-values. Russell, who helped in the publication of this essay, supported William James’s view (which he had previously rejected) that the distinction of mind from matter lay only in the causal laws involved. Admitting that ‘Logicians, so far as I know, have done very little towards explaining the nature of the relation called “meaning”’ (1919c, 290), he transferred the problem to psychology, where he broadly followed the American psychologist J. B. Watson on behaviourism, the reductionist philosophy of psychology.
Between May 1919 and the following March Russell gave three public courses on ‘the analysis of mind’ at Dr. Williams’ Library (Russell Papers 9, 477–484), and completed a book under this title which appeared from Allen and Unwin as Russell 1921a. Thanking Watson for reading the draft, his approach largely adopted behaviourism; not wishing to reify ‘consciousness’ or ‘introspection’ (lectures 1 and 6), sense-data became non-entities, and sensations the chief human epistemic source. Truth and falsehood occupied lecture 13; as usual they were predicated of a belief, and negative falsehoods were eschewed. Notably absent from the book was logic, although most of his July lecture 1919c ended up in it; in particular, its traditional links with psychology were abandoned.
G. E. Moore, who had chaired Russell’s lecture, addressed the Aristotelian Society himself in December 1919 on ‘External and internal relations’, with Whitehead chairing. Arguing as previously (§6.2.4) for the former interpretation, Moore 1920a gave the issue a welcome fresh airing; he tried to isolate entailment out of Russell’s all-purpose notion of implication, and also to link up with Lewis’s strict version.
8.3.7 Russell’s ‘introduction’ to logicism, 1918–1919. Russell’s first London course in 1917 had been called ‘Introduction to modern logic’, and he planned to make a book of it also. His publisher for a year, Allen and Unwin, had seen an announcement of the course, and on 17 October 1917 asked about a published version (RA). The writing was achieved thanks to Russell’s unpatriotic pacifist behaviour, for which he was convicted to six months in prison in 1918. In the end he spent 4 months in Brixton, with six weeks’ remission for good conduct; the privileged status of Category A allowed him time for much reading and writing (Papers 8, 312–328). Some of the book on mind was prepared there, but the most substantial outcome was the book on logic. Upon release Russell’s manuscript was typed up by one Mrs. Kyle; on the verso of one of her bills he later recalled her as ‘an admirable typist but very fat. We all agreed that she was worth her weight in gold, though that was saying a great deal’ (RA).
months in Brixton, with six weeks’ remission for good conduct; the privileged status of Category A allowed him time for much reading and writing (Papers 8, 312–328). Some of the book on mind was prepared there, but the most substantial outcome was the book on logic. Upon release Russell’s manuscript was typed up by one Mrs. Kyle; on the verso of one of her bills he later recalled her as ‘an admirable typist but very fat. We all agreed that she was worth her weight in gold, though that was saying a great deal’ (RA).
Allen and Unwin proposed to publish it in their series ‘Library of philosophy’ edited by J. H. Muirhead. The book did so appear, in March 1919, as Introduction to mathematical philosophy (Russell 1919b); but Muirhead inserted a note at the front, apologising for the book to those sophisticated enough to observe ‘the distinction between Mathematical Philosophy and the Philosophy of Mathematics’. Despite this aggressive sales talk and relatively few reviews, it sold well enough for a new printing (misnamed ‘second edition’. to appear in the next year, and several more later. It was also translated into German as 1923a (one of the translators, Emil Gumbel, praised the original version in a review 1924a in the Jahrbuch), and later into French (Russell 1928a).
In 18 short chapters and just over 200 pages Russell reviewed, in prosodic manner, all the main features of the three volumes of PM (geometry was avoided): definitions of integers, mathematical induction, order relations and ordinals, Cantorian transfinite arithmetic, limits and continuity, and the axioms of choice and of infinity. This latter chapter covered also type theory and the paradoxes; near the end of the book he confessed that his assumption of the existence of at least one individual (§7.9.3) was ‘a defect in logical purity’ (p. 203).
By contrast, logic was curiously fugitive. The propositional calculus appeared only in chapter 14; in a review of connectives Russell gave prime place to the ‘incompatibility’ newcomer, with Sheffer credited (p. 148). In a footnote he introduced a ‘non-formal principle of inference’ to sanction substitution, and lamented its omission from PM (p. 151). The next three chapters treated propositional functions (including his treatment of modality), definite descriptions, and classes (oddly including a more extended account of type theory, with the axiom of reducibility).
In the final chapter, on ‘mathematics and logic’, Russell started unhappily by stating logicism as an identity thesis instead of inclusion (p. 194). But he explained clearly the inferential character of both subjects, and reviewed the connectives. He also sketched out the notion of forms of propositions in terms of logical constants; but he spared his reader the anguish of negative falsehoods and the conundrums of belief.
Russell referred several time to Frege, introducing him as one ‘who first succeeded in “logicising” mathematics’ (p. 7). Apart from the mis-representation (which Russell partly rectified by explaining his own view of the role of arithmetic in mathematics), the passage is notable for the word which he put in quotation marks; but their presence suggests nervousness, and he never used the word again, so that ‘logicism’ did not emerge until the later 1920s (§8.7.6, §8.9.2).
8.4 REVISING LOGIC AND LOGICISM AT CAMBRIDGE, 1917–1925
8.4.1 New Cambridge authors, 1917–1921. In his Introduction Russell cited a paper by another new pupil, the Frenchman Jean Nicod (1893—1924). In October 1916 Nicod had submitted to the Cambridge Philosophical Society, through Hardy, a paper applying Sheffer’s Boolean algebra (§8.3.3) to PM; it appeared as Nicod 1917a. Noting that Sheffer had interpreted his operator both as alternative and as joint denial, he adopted the former for its simpler definition of implication. He also noted that it corresponded to the ‘disjunctive relation’ of W. E. Johnson (1892a, 19), although not given the same role there.
With this connective Nicod reconstructed the propositional calculus of PM with two ‘Non-formal’ axioms: that the stroke operator created a new elementary proposition ‘p|q’ for propositions p and q; and PM, *1·1 about anything implied by a true proposition being true. He added
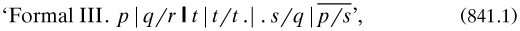
where the stroke took the forms ‘/’, ‘|’ and ‘I’ in rising order of bracketing, and the overbar indicated negation (itself defined in terms of the stroke). He worked out some of the main features of the calculus; the derivation of the axioms of PM was to be executed later in Quine 1932a.
In an appendix to his paper Nicod commented on a strikingly similar one. By curious coincidence, two months before his paper arrived Hardy had communicated to the Society by one C. E. Van Horn (b. 1884) of the Baptist College in Rangoon, India, and the two were printed together. Van Horn 1920a also used the stroke (symbolised ‘Δ’), proposed the same two axioms as Nicod’s non-formal duo, and added a third which however merely gave the truth-value of ‘p Δ q’ in terms of those of p and q. He derived the axioms of PM; however, as Nicod commented, he had not clarified the status of the law of excluded middle, and his contribution has been eclipsed.
After the War Nicod returned to France. Perhaps at Russell’s suggestion, he wrote a new article 1922b for the latest edition of the Encyclopaedia Britannica on ‘Mathematical logic and the foundation of mathematics’, a rather parochial review of Peano, Frege and PM without mention of, for example, Hilbert. His main concern had switched to the philosophy of science, and he prepared doctoral thèses at the University of Paris on geometry and the perception of space and on induction in science; they appeared in 1924, after his premature death in February. Rare cases of serious French interest in Russellian epistemology, a joint English translation soon appeared (Nicod 1930a), to which Russell wrote a very warm prefatory tribute 1930a.13
Quite different were Russell’s relations with Jourdain in the late 1910s. The creeping paralysis from which Jourdain suffered seems to have crept to his brain, for his desire to prove the axioms of choice became an obsession. Russell’s failure to recognise his achievement led to sad letters and bitter remarks in The monist and elsewhere which Russell had formally to repudiate. The tension continued after Jourdain’s death in 1919 over financial issues—a very unfortunate end to a fine relationship (my 1977b, chs. 24–25).
Involved in this sorry affair was another new follower of Russell, Dorothy Wrinch (1894–1976). In 1917 this student at Girton College travelled down to London weekly to join Nicod and also Victor Lenzen in a study group on PM run by Russell (Lenzen 1971a). Later she helped Russell as secretary, setting up some of his lecture courses at Dr. Williams’ Library, going regularly to Brixton prison with material that he wished to read, and negotiating about his books with Allen and Unwin. Her mathematical interest centred on transfinite arithmetic and order-types, usually deploying PM versions in terms of relations. For example, in 1923a she picked up the question posed in *124·61 about what properties ‘mediate’ cardinals, those which are defined neither inductively nor reflexively, might possess if they existed at all. She also continued Russell’s application of logic (especially relations. to epistemology, with papers 1919a on judgement and 1920a on memory in Mind. Then she switched to relativity theory in the 1920s and to mathematical biology in the 1930s, although she wrote on logic and mathematics from time to time later.14
Finally, we note A treatise on probability (1921) by John Maynard Keynes (1883–1946). Much influenced by Russell (Dejno ka 1999a, ch. 10), he took probability to measure the logical relevance between a premise and a conclusion: a notable consequence was a ‘definition of inference distinct from implication, as defined by Mr. Russell’, with the latter placed within probability theory (Keynes 1921a, 117–119).
ka 1999a, ch. 10), he took probability to measure the logical relevance between a premise and a conclusion: a notable consequence was a ‘definition of inference distinct from implication, as defined by Mr. Russell’, with the latter placed within probability theory (Keynes 1921a, 117–119).
8.4.2 Wittgenstein’s ‘Abhandlung’ and Tractatus, 1921–1922. When acknowledging Wittgenstein’s influence at the head of his lectures on logical atomism in 1919, Russell confessed that ‘I do not know if he is alive or dead’. In fact, this combatant in the Austrian army had prepared a manuscript called ‘Der Satz’ in moments of tranquillity, and he showed it to Russell when they met again at The Hague in December 1919. He tried to publish it with various German houses but without success; in addition, Frege was mystified by it (1989a, 19–26). He sought Russell’s help, and Wrinch became a key figure; after it was rejected by the Cambridge University Press (was Johnson a reader?) and by a publisher and some journals in Germany, she placed it with the Annalen der Naturphilosophie, edited by the chemist and zoologist Wilhelm Ostwald—an improbable venue, secured by Ostwald’s high opinion of Russell and the promise of an introduction from him. The essay appeared as Wittgenstein 1921a, entitled ‘Logisch-philosophisch Abhandlung’, including a German version 1921b of Russell’s introduction.
For the next stage a main role was played by C. K. Ogden (1889–1957). Of considerable wealth, by profession he was a (minor) philosopher (Gordon 1990a); his main importance lay as editor from 1912 of the Cambridge review, and from 1919 the founding editor and subsidiser of the journal Psyche. He published it with Kegan Paul, for whom he also launched a book series in philosophy and psychology in 1921; Nicod 1930a was to appear in it. To organise an English translation of the ‘Abhandlung’, he recruited another new Russell student, Frank Ramsey (to be introduced in §8.4.5), to dictate one; it took 10 hours. After typing out, it was revised by Ogden and Russell before despatch to Wittgenstein, who went over it line by line and suggested many revisions to Ogden, especially over the rendering of technical terms. It appeared as Wittgenstein 1922a in Ogden’s series under the title ‘Tractatus logico-philosophicus’ (which may have been suggested by G. E. Moore), set page by page opposite the original; Russell’s introduction 1922a had been somewhat revised (Iglesias 1977a).15
hours. After typing out, it was revised by Ogden and Russell before despatch to Wittgenstein, who went over it line by line and suggested many revisions to Ogden, especially over the rendering of technical terms. It appeared as Wittgenstein 1922a in Ogden’s series under the title ‘Tractatus logico-philosophicus’ (which may have been suggested by G. E. Moore), set page by page opposite the original; Russell’s introduction 1922a had been somewhat revised (Iglesias 1977a).15
Following the Peanist numbering system of PM, and maybe also a similar one used in the structured numbering of laws in the Austro-Hungarian Empire, the main text was organised in a sequence of short numbered clauses, where the fewer digits in the number indicated the greater importance of the text (thus 5 was important, 4.04 less so, and 6.1233 still less). Sometimes the disclosed order of importance is interestingly unexpected. We shall consider first Wittgenstein’s conception of logic, and then the bearing of his views on mathematics; the translations are mine, as usual. Russell’s introduction (in its English original) is also noted where appropriate.
8.4.3 The limitations of Wittgenstein’s logic. From their earlier discussions Wittgenstein must have realised that Russell had mixed logic and logicism together (§8.2.6), and so he sought to characterise logic separately. In his preface he stated as an aim ‘to set a limit to [...] the expression of thought: for in order to be able to set a limit to thought, we should to be able to think on both sides of this limit (thus we should be able to think, what cannot be thought.’. This passage may have stimulated Russell to counter ‘that every language has, as Mr. Wittgenstein says, a structure concerning which, in the language, nothing can be said, but that there may be another language dealing with the structure of the first language, and having itself a new structure, and that to this hierarchy of languages there may be no limit’ (1922a, xxii).
To Russell this proposal extended his propositional hierarchy of types (1940a, 62). But to us a feature of capital importance to philosophy was proposed here: a general and fundamental distinction of language from metalanguage, and by implication (as it were) of logic from metalogic, and of theory from metatheory. But Wittgenstein rejected it totally. ‘The limits of my language marks the limits of my world’ (1922a, clause 5.6); ‘The world and life are one’ (5.621), so that ‘Whereof one cannot speak, thereof must one be silent’ (the famous closing clause 7, which followed a Viennese philosophical tradition). Thus, as a main consequence, ‘What can be shown, cannot be said’ (the astonishingly minor 4.1212). Similarly, ‘Logic fills out the world; the limits of the world are also its limits’ (5.61), so that ‘It is clear: the logical laws may not themselves fall again under logical laws’ (6.123). Likewise, ‘Philosophy should set limits to the thinkable and thereby to the unthinkable’ (4.113–114).
Wittgenstein was a metaphysical monist, believing all physical and mental entities to be unified; so that ‘There is no thinking, representing subject’ (5.631) with his own private mental products (Cornish 1998a, ch. 5). (Such passages may have pleased Ostwald, who was a monist for science). Thus, as a special case, he affirmed Russell’s logical monism, affirming the all-embracing generality of logic, in its bivalent form. Now Russell had just refuted this stance with his hierarchy, but did not recognise the gold in his hands: although he mentioned it in some later writings, he never gave it a major place (§10.2.3). In particular, it played no role in his revision of PM, prepared only two years later (§8.4.4). Those equipped with metalanguage and -logic know better, that speaking then comes into its own. For example, Wittgenstein’s distinction between showing and saying is itself said; so where is it?
Wittgenstein’s monistic way ahead was to base his epistemology on ‘facts’ (‘Tatsachen’, 1.1) which showed ‘the existence of states of affairs’ (‘Sachverhalten’, 2). He then proposed a rather naive metaphysics founded upon the notion of a picture (‘Bild’. theory of the meaning of a proposition relative to a state of affairs, true or false when corresponding to a correct or an incorrect one (2.21–2.225), and involving ‘positive’ or ‘negative facts’ respectively (2.06). Thus he adopted Russell’s position before 1906 of admitting objective falsehoods (§7.4.7), in the form of admitting possible as well as actual states of affairs Kreisel 1968a).
The link between a picture and reality was the ‘logical form’ (2.18), which can depict the world’ (2.19), allowing logic to be ‘a mirror-image of the world’ (6.13). ‘Each statement about complexes can be resolved into a statement about its components and into the propositions that the complexes completely describe’ (2.0201, ‘complex’ unexplained). Thus the link was like an isomorphism, down to ‘An elementary proposition[, which] consists of names’ (the unbelievable 4.22) but which nevertheless ‘asserts the existence of a state of affairs’ (4.21).
The corresponding atomicity of propositions was handled in terms of ‘proposition-signs’, the truth-tables thought out by Wittgenstein with Russell around 1912 (§8.3.1), which treated a compound proposition as a truth-functions of its components (4.31, 5.54). His example connective was implication (4.442), in both a tabular form and a horizontal one like Russell’s (836.1):

In addition, assertion was abandoned (4.124, 6.2322).
From such tables Wittgenstein took the ‘two extreme cases’: where it is ‘true for the entire possibilities of truth value of the [component] elementary propositions’, when it was ‘tautological’ and the converse cases of non-stop falsehood, when it was ‘contradictory’ (4.46). Moreover, ‘There is one and only one complete analysis of the proposition’ (3.25). His view resembles Russell’s logical atomism (§8.3.6), but he must have thought it out independently in the trenches, following the bipolarity of propositions which he had suggested to Jourdain back in 1909 (§8.2.6): ‘Tautologies and contradictions lack sense. (Like a point from which two arrows go out in opposite directions to one another).’ (4.461); they are limiting cases’ of the logical ‘combination of signs’ denoting the constituents (4.466). Now he could characterise logic thus: ‘the propositions of logic are tautologies’ and ‘say nothing. (They are the analytic propositions.)’ 6.1(6.11). Both cases ‘are not pictures of reality. They do not represent any possible situations’ (4.462), so that logic was detached from reference, and tautology and contradiction lost their more fruitful connotations of being respectively true or false by virtue of the meanings of their constituents. Moreover, his doctrine was applied only to the propositional calculus.
Under this regime Wittgenstein devoted a whole section to the consequences of the principle that ‘The proposition is a truth-function of elementary propositions’ (5), whether tautological, contradictory, or in between. He used the horizontal layout in (836.1) to present all 16 possible connectives between two propositions (5.101), and went through the usual ones. He stressed that the proposition was prior to any logical combination that it may contain: ‘The occurrence of an operation [or connective] does not characterise the sense of the proposition’ (5.25), so that any two logically equivalent propositions were identical. In particular, ‘The operation can vanish’, as in the case ‘~ ~ p = p’ (5.254)—unhappily written, given his abandonment of identity.
Wittgenstein treated the predicate calculus in terms of ‘formal concepts’ (4.126), but rather briefly. ‘The existence of an internal relation between possible situations expresses itself linguistically by means of an internal relation between the propositions representing them’ (4.15): a claimed answer to the internalist/externalist question (4.1251) which however only transfers it. On quantification, ‘I disassociate the concept all from truth-functions’, but he falsely asserted that ‘Frege and Russell have introduced generality in association with the logical product or the logical sum’ (5.521).16
So logic was trivialised to a mere algorithm, though now specified without reference to logicism; but what about mathematics? While allegedly ‘Mathematics is a logical method’ (6.2) or ‘a method of logic’ (6.234), ‘A proposition of mathematics does not express a thought’ (6.21), the latter being ‘A logical picture of facts’ (3). In such ways did Wittgenstein reject logicism. But he also seems to have abandoned mathematics (or forgotten what he knew when an engineer. when characterising its propositions as ‘equations, and therefore pseudo-propositions’ (6.2) and decreeing that ‘The theory of classes is quite superfluous in mathematics’ (6.031).
On PM, Wittgenstein rejected the theory of types, since Russell ‘had to mention the referent of signs when [making] the line-up of the sign-rules’ (3.331); similarly, though in a weak analogy, Russell’s paradox was solved by preventing a propositional function from being an argument of itself (3.333). The axiom of reducibility was also banished because ‘It is possible to imagine a world in which [it] is not valid’; however, the underlying reason was that ‘logic has nothing to do with the question of whether our world really is so or not’ (6.1233).
Another casualty was Russell’s definition (732.3) of identity: ‘not satisfactory; because according to it one cannot say, that two objects have all properties in common. (Even if this proposition were never correct, it still has sense).’ (5.5302). Presumably universal classes, defined by Russell via self-identity (§7.8.5), also had to go. However, the concept of ‘numerical equality’ survived, as ‘the general form of all special cases’ (6.022). This “definition” is hardly lucid, but presumably as a non-logicist Wittgenstein did not have treat equality as a derivative of identity; after all, ‘there are no numbers in logic’ (5.453).
A further victim of Wittgenstein’s abandonment of identity was the axiom of infinity, which ‘is intended to express in language, that there be infinitely many names with different referents’ (5.535). But he did not explore this possibility as a philosophical issue; thus, while it is too much to say that his ‘whole theory overlooks the distinction between finite ranges and infinite ranges and is, therefore, quite irrelevant to the foundations of mathematics’ (Wang 1968a, 21), its utility is very limited. While accepting the attack on identity, Russell had queried this feature in August 1919 when reading the manuscript, in connection with Wittgenstein’s definition of only finite ordinals (6.03. (McGuinness and von Wright 1991a, 108), and he raised it again in his introduction (Russell 1922a, xx).
After the publication of the Tractatus, Wittgenstein rejected the possibility of an academic career and became a school-teacher in Lower Austria. Russell soon become very disappointed with his star. ‘He was very good’, he told Sheffer perhaps in 1923,
but the War turned him into a mystic, and he is now quite stupid. I suspect that good food would revive his brain, but he gave away all his money, and won’t accept charity. So he is an elementary schoolmaster and starves. I do not believe his main thesis; I escape from it by a hierarchy of languages. He wrote his book during the War, while he was at the front; hence perhaps his dogmatism, which had to compete with the dogmatism of bullets.17
Nevertheless, Wittgenstein’s thought was much on his mind when he came to revise PM.
8.4.4 Towards extensional logicism: Russell’s revision of Principia mathematica, 1923–1924. After the popular Introduction of 1919 Russell worked little on logic. In October 1920 he recommenced his lectureship in logic and the principles of mathematics at Trinity College Cambridge. In 1921 he visited China and lectured on logic and set theory among other topics; his Introduction was translated into Chinese the following year. He was accompanied by Dora Black, to whom he had been introduced by Wrinch. Later in the year they married, and he resigned his lectureship. This marriage yielded children; in January 1925 he asked Ogden to be the guardian of his children and executor of his will should he and Dora die (RA). His main interest switched to education, although he maintained a stream of philosophical writing and reviewing.
One occasion to consider logic arose when Muirhead asked Russell to wax autobiographical in a survey of Contemporary British philosophy under his editorship. Russell responded with a summary 1924a of ‘Logical atomism’. After characterising logicism in terms of ‘pure mathematics’ in the manner of The principles rather than PM (p. 325), he turned to Ockham’s razor, a ‘very important heuristic maxim’, expressed as ‘Wherever possible, substitute constructions out of known entities for inferences to unknown entities’ (p. 326), and gave examples of its use in logicism as well as in epistemology (for example, defining integers as classes of classes, definite descriptions, and Whitehead’s construction of points). Unusually for him and showing the impact of Wittgenstein (as in other writings of the time), he stressed the importance of language in philosophy, reviewing in some detail syntax, relations and paradoxes (pp. 330–336). He was much more positive than usual about type theory: it had led him to ‘a more compete and radical atomism than any that I conceived to be possible twenty years ago’ (p. 333), and he characterised ‘an ideal logical language’ as not only avoiding paradoxes but preventing Ockham-like illegitimate inferences ‘from the nature of language to the nature of the world’ (p. 338). The essay is a beautiful cameo of Russell’s life’s ambitions in logic and philosophy to date. An early sentence set his scene perfectly: ‘I hold that logic is what is fundamental to philosophy, and that schools should be characterized rather by their logic than by their metaphysic’ (p. 323).
With PM now out of print, Russell agreed with Cambridge University Press to prepare a new edition. Most of the work was done during the summers of 1923 and 1924 at his summer home near Land’s End in Cornwall. The outcome was a new introduction 1925a of 34 pages in the first volume, and three new numbers reworking certain theories at its end. (Two short manuscript notes are printed in Papers 9, 155–160.) Another addition was an index of symbolic definitions; maybe Wrinch prepared it, for she had so offered in an undated note to Russell (RA). Whitehead was initially interested in the venture; on 29 June 1923 he promised to send some notes, including on the ‘various meaning of “function”’ in the second volume, ‘entirely due to the niggly criticisms of Johnson’ (§7.8.1) as the Press reader (RA, Dora Russell Papers). However, in the end he played no role; when he found no mention of this fact in the new first volume, he sent a testy note 1926a to Mind. Nevertheless, Russell still referred to ‘we’ in later reminiscence! (1959a, 122).
The first two volumes appeared in 1925 and 1927; for some reason their texts were reset by Cambridge University Press, at about 4% more pages. Some typographical errors were corrected, but who knows if changes in text are not buried in odd places?18 Sadly, not I, though some random checking did not reveal any changes. Mercifully the third volume was photo-reprinted for publication in 1927.
A major alteration, stimulated by Wittgenstein but which Russell had himself been following, was to adopt an extensional view of logical notions. The old idea of elementary propositions was now replaced by ‘atomic’ ones, which might contain individuals and propositional functions and relations but not quantifiers; ‘molecular’ ones were constructed as usual by linking up atoms with logical connectives (PM2 1, xv–xix). However, he did not refer to tautologies, doubtless feeling that mathematics could not be grounded in them; nor did he present truth-tables.
The new Appendix C, on ‘Truth-functions and others’, was based upon such functions f of propositions p and q preserving equivalence:
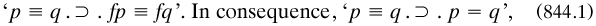
so that identity was still present, although some of Russell’s uses of ‘=’ seem to be equality by definition (see especially pp. xxxiii–xxxviii). Thus he had dropped Wittgenstein’s abandonment of identity, accepted in his introduction to the Tractatus (Russell 1922a, xvii); doubtless he realised meantime that Wittgenstein had not handled numerical equality well.
Russell also doubted that belief predicates could be satisfactorily handled. Concerning the status of judgement, he also noted ‘the difference between propositions considered factually and propositions as vehicles of truth and falsehood’, according to which apparently ‘The paradoxes rest on the confusion between factual and assertive propositions’ (pp. 664, 666). This was his closest approach to his new idea of a hierarchy of languages each talking about the one(s. below. However, he explicitly stressed again ‘implication (as opposed to inference)’ (p. xxiv; note also p. xxviii).
Among the connectives, the Sheffer stroke was given prime place, along with Nicod’s single axiom (841.1); the modus ponens role of inference was suitably restated, and substitution also allowed for (pp. xv–xix). Russell hailed these two innovations as ‘the most definite improvement [... ] in mathematical logic’ since the first edition (p. xiii), which shows how out of general touch he had become; even Wiener’s definition (827.1) of the ordered pair was omitted. However, in a bibliography at the end of the introduction he did include some weightier literature, for example by Brouwer and Hilbert (§8.7.4, 7).
The predicate calculus was reconstructed similarly; a propositional function without quantifiers taking elementary propositions as values was still called a ‘matrix’ (p. xxii). Concerning quantification (which, presumably following Wittgenstein, Russell unusually named ‘generalisation’), the quantifiers were even defined as infinite conjunctions and disjunctions (p. xxxiii), with no concern over the horizontally infinitary logic invoked. Again after Wittgenstein, ‘there is no need of the distinction between real and apparent variables’ or of assertion (p. xiii); yet one page later, when subsuming propositional quantification under functional and individual quantification, ‘in place of “ .(p). fp” we have “
.(p). fp” we have “ .(ϕ, x). f(ϕx)”’!
.(ϕ, x). f(ϕx)”’!
Propositional functions of functions were also presented extensionally:
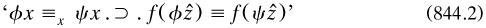
(p. xxxix). Russell wrote a new * 8, as Appendix A, to replace the old *9 on the basic features of the predicate calculus. In addition, from this premise ‘φ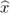 = ψ
= ψ ’ (identity again), so that ‘there is no longer any reason to distinguish between functions and classes’ (p. xxxix). Further, the deployment of truth-functions dispensed with the troublesome axiom of reducibility. However, it was still necessary to distinguish the orders of classes which might have members from the same order, a point illustrated by a nice discussion of examples such as Zermelo’s proof of the Schröder-Bernstein Theorem (§7.8.7) and mathematical induction (pp. xxxix–xliii). He reworked the latter, together with the ancestral relation, in Appendix B as the new * 89; however, the theory faltered in the proof of a theorem about ancestral relations (*89–29), seemingly irreparably (Myhill 1974a). Further, several parts of mathematics, such as the theory of real numbers, were not captured anyway, so that a replacement axiom of some kind was needed (p. xlv).
’ (identity again), so that ‘there is no longer any reason to distinguish between functions and classes’ (p. xxxix). Further, the deployment of truth-functions dispensed with the troublesome axiom of reducibility. However, it was still necessary to distinguish the orders of classes which might have members from the same order, a point illustrated by a nice discussion of examples such as Zermelo’s proof of the Schröder-Bernstein Theorem (§7.8.7) and mathematical induction (pp. xxxix–xliii). He reworked the latter, together with the ancestral relation, in Appendix B as the new * 89; however, the theory faltered in the proof of a theorem about ancestral relations (*89–29), seemingly irreparably (Myhill 1974a). Further, several parts of mathematics, such as the theory of real numbers, were not captured anyway, so that a replacement axiom of some kind was needed (p. xlv).
As this summary suggests, the second edition is hardly a philosophical advance upon the first, at least for clarity; for example, as before, it is still uncertain whether or not the calculus is consistent (Fitch 1974a). The influence of Wittgenstein was in some ways unfortunate: he was not a logicist, but in adopting some of his positions Russell had now to assume that mathematical propositions said nothing about the world—pure mathematics, indeed, but in the traditional sense rather than the implicational form of The principles. Again, the emphasis on extensionality hardly fits well with a logicism in which, for example, non-denumerability is central. But a trend was now in place, and would soon be taken still further.
8.4.5 Ramsey’s entry into logic and philosophy, 1920–1923. Russell was helped in the proof-reading of the first two volumes of PM by a new star in his circle, Frank Ramsey (1903–1930). Son of the applied mathematician A. S. Ramsey, then President of Magdalene College Cambridge, Frank centred his short life on the University, entering Trinity as an undergraduate, moving to King’s as a Fellow in 1924, and holding a university lectureship two years later until a perforated ulcer in his fat frame took him away. A selected edition of his writings soon appeared in 1931 (Ramsey Essays), in Ogden’s series; for some reason two more and different selections appeared in 1978 and 1980. He left an interesting Nachlass (Ramsey Papers), from which a nice selection, largely centred on probability theory, was published in 1991 (Ramsey Notes).
Ramsey’s other interests lay in logic(ism), Russell-style philosophy and mathematical economics. He seem to have come to this unusual quartet early on: letters of 1920 sent from school to Ogden (a Fellow of his father’s college) deal with them all. Concerning Russell’s work, he reported on 17 June reading the Introduction, and a month later the German translation 1908a of Couturat’s book on Russellian mathematical logic (§7.4.1), which ‘is always referring to Russell’s Principles of Mathematics vol 1 which I hadn’t heard of before’ (Ogden Papers, Box 111, File 1).
Ramsey published first on logic and philosophy in book reviews, mostly in Mind. In a long piece 1923a on the Tractatus he was largely descriptive, emphasising the picture theory of meaning; he also tried to understand the mystical passages. But he doubted that Wittgenstein’s rejection of identity was adequate for mathematics, and also the decree that mathematics consisted of equations (pp. 279–280). In addition, he disagreed with Russell’s construal of the book as concerned primarily with a logically perfect language (p. 270); curiously, he passed over Russell’s proposal of a hierarchy of languages. On the first volume of the new PM he wrote two similar short reviews, 1925a in Nature and 1925b in Mind, picking out the Sheffer stroke and Nicod’s axiom, and the attempt to eliminate the axiom of reducibility; he judged Appendix C on truth-functions to be the most interesting innovation.
Privately Ramsey was much more critical of Russell. ‘[I] am reading the manuscript of the new stuff he is putting into the Principia’, he wrote to Wittgenstein on 20 February 1924 (Wittgenstein Ogden, 84),
You are quite right that it is of no importance; all it really amounts to is a clever proof of mathematical induction without using the axiom of reducibility. There are no fundamental changes, identity is just as it used to be. I felt he was too old: he seemed to understand and say ‘yes’ to each separate thing, but it made no impression so that 3 minutes afterwards he talked to me on his old lines.
8.4.6 Ramsey’s recasting of the theory of types, 1926. The major revision of theory was published in two papers: a lengthy account 1926b of ‘The foundations of mathematics’ with the London Mathematical Society, and a shorter version 1926a for the Mathematical gazette. In the latter piece he stated very clearly the need to unwrap Russell’s logic from its logicism (p. 75):
When Mr Russell first said that mathematics could be reduced to logic, his view of logic was that it consisted of all absolutely true general propositions, propositions, that is, which contained no material (as opposed to logical) constants. Later he abandoned this view, because it was clear that some further characteristic besides generality was required. [...]
If, then, we are to understand what logic, and so on Mr Russell’s view mathematics is, we must try to define this further characteristic which may be vaguely called necessity, or from another point of view tautology.
The details were presented in Ramsey’s main paper. His commitment to extensionality carried through to the extent that he used Wittgenstein’s theory of truth-tables for an infinity of argument places, adding as weak explanation that ‘an infinite algebraic sum is not really a sum at all, but a limit, and so cannot be treated as a sum except subject to certain restrictions’ (1926b, 7). Similarly, he followed Russell’s new interpretation (844.2) of quantification of propositional functions in terms of infinite conjunction and disjunction (p. 8).
Sceptical of always subsuming classes under propositional functions, Ramsey mooted the option of restricting the action to specific kinds: ‘although an infinite indefinable class cannot be mentioned by itself, it is nevertheless involved in any statement beginning “All classes” or “There is a class such that”, and if indefinable classes are excluded the meaning of all such statements will be fundamentally altered’ (p. 22). He emphasised here the difference between restricting classes or functions to particular kinds or allowing all possible kinds to be quantifiable; it has become known as the distinction between ‘non-standard’ and ‘standard’ interpretations (Hintikka 1995b). Distinguished predecessors include Kronecker disliking talk of “any” function (§3.6.5), and discussants of the legitimacy of axioms of choice (§7.2.5–6).
Next Ramsey reconstructed the theory of types. Adopting Russell’s definitions of ‘elementary proposition’ and ‘elementary function’, he gave Russell’s old term ‘predicative function’ a new reference. Starting out from atomic functions, a ‘predicative function of individuals’ was a truth function of a (finite of infinite. number of atomic functions of individuals or of propositions. Similarly, a ‘predicative function of predicative functions of individuals and of individuals’ was such a function of propositions or of ‘atomic functions of functions of individuals and of individuals’ (which had only one functional but many individual arguments), and so on. The value of a function was a proposition of the corresponding type. Any function occurred in a predicative function through its values, and quantification was interpreted in terms of truth-functions of an infinity of arguments; thus every function was predicative in Ramsey’s sense, so that the axiom of reducibility was not needed (1926b, 38–42, 46–47; compare Quine 1936b).
Ramsey also criticised the vicious circle principle for its denial of harmless descriptions presupposing a totality, such as ‘a man as the tallest in a group’ (p. 41). In the old PM this principle had prohibited any value taken by an intensionally specified class from presupposing that intension; but with functions now defined extensionally, their values could be defined separately and thus involve objects from higher types. Thus he also abandoned this principle. Since he preserved the theory of types, he might have concluded that the principle was independent of it (compare §9.3.5, §10.2.5).
Ramsey’s new theory of types yielded a calculus which hopefully was equivalent to that of the new PM and therefore avoided the paradoxes. Yet his best remembered suggestion entailed that part of his reconstruction was unnecessary anyway. For he pointed out that the paradoxes divided by subject matter into two groups which we now call ‘mathematical’ and ‘semantic’, to be solved respectively by the ‘simple’ and the ‘ramified’ theories of types. (Ramsey used no names: on their origins, see §8.8.4 and §9.4.5.) In the first group of paradoxes he listed Russell’s, its relation version, and Burali-Forti’s, formulated in terms of classes; they were solved by the simple theory of types. But within each type the paradoxes of the second group were constructible—he listed the liar, Berry, the least indefinable ordinal (König), Richard and Grelling—and they needed the ramified theory.19 While not distinguishing paradoxes such as the liar involving truth-values of propositions from those of definability based upon properties of sentences in a language, he noted that their mathematical character was contaminated by linguistic or semantic elements; but he regarded the mathematical element as sufficiently significant to proceed with his complete restructuring of the theory of types. But later opinion has sided with the remark in Peano 1906b that they had no place in logic (§7.2.4); and it is surprising that Ramsey did not draw the same conclusion, for he cited Peano here, and also recognised the distinction for the two roles for logic involved: the paradoxes ‘would not be relevant to mathematics or to logic, if by “logic” we mean a symbolic system, though of course they would be relevant to logic in the sense of the analysis of thought’ (1926b, 21). We return to this matter in §10.2.2, among the general conclusions.
8.4.7 Ramsey on identity and comprehensive extensionality. Perhaps Ramsey pursued his full restructuring because he saw for it a role greater than merely avoiding (or Solving) some paradoxes; for another of his proposals concerned the definition of identity. While not adopting Wittgenstein’s rejection of it, he did accept the view that two objects being identical is nonsense and one object being identical is vacuous (p. 50). So he defined the identity of terms x and y as a non-predicative combination of a predicative contradiction and a predicative tautology (pp. 51–52):
This need for non-predicative functions also led Ramsey ‘to drop altogether the notion that ϕa says about a what ϕb says about b; to treat propositional functions like mathematical functions, that is extensionalize them completely’ (p. 52). He called his new primitive notion a ‘function in extension’, symbolised ‘ϕe’; under it and the interpretation of quantification the Leibnizian form of identity
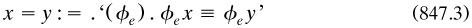
was acceptable, for it covered all possible associations of proposition and individual and so would be a tautology if x were identical with y and a contradiction otherwise (pp. 52–53).
Classes were subordinated to functions in extension. Among their roles, their identity sufficed for a condition of identity in higher types, so that only predicative functions of classes (and therefore predicative functions of functions) were required there (p. 54) In addition, the multiplicative axiom was legitimised, since no difficulty arose in positing a function in extension to deliver the choice class (pp. 57–59).
Ramsey ended by revising the axiom of infinity.20 Following Russell’s empirical interpretation of it in PM (§7.9.3), and also Wittgenstein’s retort that it must be a tautology or a contradiction, he proposed that any proposition of the form ‘there are at least n individuals’ be taken as one about diversity, starting out from ‘(∃x, y) · x ≠ y’ for n = 2. As n increased, either such propositions would become contradictory when some finite value N of n was reached, in which case there were only N individuals; or tautologies would continue to arise up to  0 or even
0 or even  1 individuals. While it may never be known which of the two cases obtained, the axiom had a logical character (pp. 59–61).
1 individuals. While it may never be known which of the two cases obtained, the axiom had a logical character (pp. 59–61).
What Ramsey meant by ‘necessity’ in the opening quotation above was a total commitment to extensionality, especially as represented by predicative functions in extension, enlarging Wittgenstein’s characterisation of logic in terms of tautologies. This extensionality resembled Frege’s system in some respects (Chihara 1980a). Ramsey did specify logic independently of the logicist thesis (which he upheld); and moreover, as he noted, it used functions in a way commonly attributed to mathematics anyway. However, conceptual misgivings arise, especially concerning infinitary language, and the handling of non-denumerable classes and their defining functions. At the end of his shorter paper Ramsey confessed to some disquiets, although they concerned the status of certain axioms rather than his general strategy (1926a, 79–81). But it launched an enterprise of great and original promise, whose completion was prevented by his death a few years later.
After the mid 1920s Ramsey concentrated upon probability theory and philosophical questions, the latter largely within Russell’s approach. For example, in 1927 he and G. E. Moore conducted a symposium at the Aristotelian Society on ‘Facts and propositions’. Preferring Russell’s view of judgement as a multiple relation, he suggested that believing proposition p and disbelieving not-p were equivalent judgements (Ramsey 1927a, 147–148). But his paper was not very original or even well thought out, as Moore 1927a gently indicated in an intricate analysis of the distinction between judging a fact and the fact that one is making (or not) such a judgement at some given place and time.
When the posthumous edition of Ramsey Essays appeared in 1931, Russell 1931a reviewed it at length in Mind. Lamenting the early death of his student, he accepted two of Ramsey’s criticisms of logicism: always subsuming classes under propositional functions, and not distinguishing between two kinds of paradox. But he did not discuss Ramsey’s hint of removing the semantic ones from logic; his own conception of logic as completely general would have prohibited such a move. Further, he was doubtful about the revisions of identity, pointing out that ‘take two things, a and b’ already takes diversity as primitive; he preferred to read it as saying that a and b ‘have different properties’, which does not solve this difficulty. Much later and against Wittgenstein, he went further, treating it as a primitive notion (Russell 1959a, 115).
8.5 LOGICISM AND EPISTEMOLOGY IN BRITAIN AND AMERICA, 1921–1930
8.5.1 Johnson on logic, 1921–1924. In §2.6.4 we noted Johnson 1892a in Mind as a significant paper for diffusing algebraic logic. Over the years he lectured on logic regularly at Cambridge, and often read manuscripts of other logicians (for example from §7.8.1, of PM for the University Press), but he published rarely. His Logic finally appeared from the Press at about 700 pages in three Parts in 1921, 1922 and 1924, when he was in his mid sixties. While he still linked logic with laws of reasoning and stressed the importance of syllogistic logic, he also noted the symbolic traditions; a few features are noted here.
In the first Part Johnson 1921a saw the difference between mathematics and logic as lying in that ‘between form and matter’ (pp. xxii–xxiv)—another traditional distinction (§2.4.4). But pure mathematics was an application of ‘pure logic’, with applied mathematics marked out from both by its reference to reality (p. xxv). Finite classes were handled in the part-whole way in ch. 8, with a ponderous explanation of parts of parts of.... The only mention of PM in this Part was a disagreement over existence: for him the definition there of non-emptiness in terms of existential quantification should be reversed (p. 172), although he did not really handle quantifiers anywhere. He noted, with approval, Russell’s theory of definite descriptions, but in the context of identity and substitution rather than referentiability (p. 198).
Johnson had lectured on mathematical logic in the winter of 1916–1917, with G. E. Moore present (Moore Papers, 10/5/1), and he engaged with it most closely in the second Part. The start was unhappy, for he connected ‘the mental act of inference and the relation of implication’ as ‘analogous to that between assertion and the proposition’ (Johnson 1922a, 1), which is no better than Russell himself. He proposed another reversal from Russell’s procedure, that propositional functions be derived from descriptive ones (pp. 66–68)—or rather from mathematical functions in general. However, he thereby masked one consideration underlying Russell’s logicism, which he did not discuss. But later on he quite nicely distinguished Boole’s algebraic logic from the work of Peano, Cantor and PM (pp. 135–138); not a logicist of any kind, he felt that ‘The current phrase mathematical logic is ambiguous inasmuch as it may be understood to mean either the logic of mathematics or the mathematics of logic’ (p. 137). He even described some aspects of transfinite arithmetic (pp. 173–180), although he misunderstood the continuum hypothesis as ‘the number [of points in a line] may be assumed to be 2exp ’ (p. 174). He also reworked Russell’s principle of abstraction for symmetrical and transitive relations (§6.4.4), but by an odd method stressing adjectives (pp. 145–150). In a survey of methods in syllogistic logic he described the antilogism (pp. 78–79) without mentioning Ladd-Franklin (§4.3.7), to which she objected bitterly in a note 1928a in Mind.
’ (p. 174). He also reworked Russell’s principle of abstraction for symmetrical and transitive relations (§6.4.4), but by an odd method stressing adjectives (pp. 145–150). In a survey of methods in syllogistic logic he described the antilogism (pp. 78–79) without mentioning Ladd-Franklin (§4.3.7), to which she objected bitterly in a note 1928a in Mind.
Johnson’s third Part was largely taken up with inductive logic and the philosophy of science, especially causality. However, in the introduction he pointed to identity as a mark of ‘transition from pre-mathematical logic to mathematical logic’ (1924a, xv).
Johnson’s book has many nice touches; but its view of logic is a heterogeneous mixture of old and new, with no clear direction emerging either technically or philosophically. Ramsey 1922a reviewed the second Part very warmly, but was sad that Johnson had not really engaged in some of his points of disagreement with Russell (for example, the existence of classes in terms of that of individuals). Although the book was used for years in the basic logic course at Cambridge, most logicians and mathematicians, such as Russell and Ramsey, largely ignored it in their own work.
8.5.2 Other Cambridge authors, 1923–1929. One newcomer was the mathematician Max Newman (1897–1984). For his fellowship thesis m1923a at Saint John’s College he chose ‘The foundations of mathematics from the standpoint of physics’, and presented an axiom system broadly similar to that of PM but with a more subjective cast in treating logic as an investigation of means whereby ‘acts of belief may be rendered possible’ (fol. 15). Treating such as acts as ‘performances’, he denoted the corresponding beliefs by ‘performance functions’, and regarded as a sequence of them as a ‘process’, starting out from ‘primitive performances’ which ‘are believed possible without any proofs’ (fol. 27). Many of his notations were based upon those of PM, and among notions he used ordinal similarity (795.1) between two processes (fol. 49). Aware of other current work on foundations, he adopted Hilbert’s version (874.1.1 of the axioms of choice as a ‘selection function’ (fol. 40). Among ‘mathematical processes’ he defined the integers in a manner akin to Peano’s axioms, referring the reader to the Formulaire for full details about the real-number system; and he presented long division as an example of a process which he could express (fols. 85, 68). As for the physics promised in his title, he treated the measurement of quantities on scales (fols. 102–120), but little else.
It is a pity that Newman published none of this essay, which bears some similarity to Carnap’s later formalised epistemology (§8.9.4); but some years later he assisted in Russell’s latest epistemological enterprise, a study of The analysis of matter which appeared in Ogden’s series as Russell 1927a.21 As usual, Russell replaced inferred entities by logical constructions, but he also paid attention to recent developments such as relativity theory and quantum mechanics. Logic and set theory were rather more prominent than in the book on mind for Muirhead (§8.3.6); in particular and thanks to Newman’s advice, in ch. 28 he presented recent developments in topology, including some due to Felix Hausdorff (§8.7.6), and new definitions of dimension (on which see D. Johnson 1981a). In ch. 24 he even drew on his idea of relation-number (§7.9.5) to characterise similar spatio-temporal ‘structures’ for which ‘all their logical properties are identical’. Newman himself sent to Mind an adumbration 1928a of Russell’s ch. 20 on the ‘causal theory of perception’. Russell thanked him for the essay on 24 April, accepting the criticism on aspects of his theory of perception (1968a, 176–177). Thereafter, like Russell, his interest in foundations decreased; it also changed to metamathematics and set theory (§9.5.3).
In the front material of Russell’s book the publishers had listed a forthcoming volume from Hardy on ‘mathematics for philosophers’ for the series; but it never appeared, and none of it seems to survive. Then in his early fifties and professor at Oxford University, in December 1928 he delivered at Cambridge a lecture on ‘mathematical proof’ which appeared in Mind as 1929a. Complaining about the dubious three axioms in logicism, he welcomed Wittgenstein’s revision of Russell’s theory of judgement (§8.2.6), which for him had lacked the feel for correspondence which a decent theory of truth should possess.
Ogden himself and his younger Magdalene colleague I. A. Richards (1893–1979) had published as 1923a in his series a volume on The meaning of meaning. The title suggests a descent into essentialism, but in fact they were primarily concerned with linguistics and semiotics. In an agreeable if rather superficial way they considered words as signs and their relationships to thoughts and things (ch. 1). Concerning ‘The meaning of philosophers’ (ch. 8), itself a double meaning, they quoted Russell’s admission about the small contribution of logicians quoted in (§8.3.6) ‘The meaning of meaning’ itself was treated in a wry ch. 9 where, for example, Russell’s theory of definite descriptions was held to ‘have only led to further intricacies which logicians are once more endeavouring to unravel’ (p. 190). Again, ‘all definitions are essentially ad hoc’ (p.111), which revealed their limited familiarity with mathematics—contextual definition, for example, which cannot be so dismissed. The only general contentual remark on mathematics concerned clause 6.2 of a recent book in the same series: ‘Some, like Wittgenstein, have been able to persuade themselves that “The propositions of mathematics are equations, and therefore pseudo-propositions”’, a view which ‘can be presented without the background and curtain of mysticism which this author introduces’ (p. 89).
The comments most pertinent to logic came at the end of the book. In Appendix E ‘On negative facts’, the authors attacked the notion of opposition stressed in Demos 1917a (§8.3.6). Appendix D treated ‘Some moderns’: Frege and Russell received routine summary, but Husserl and Peirce had several pages each, the latter covering both aspects of his algebraic logic and his existential graphs (§4.4.7) and including some letters, then unpublished, to his main British follower Lady Welby (1837–1912).
In a warm and quite long review Russell 1926b recalled that he had once ‘become acquainted with Lady Welby’s work’ on meaning and symbolism ‘but failed to take it seriously’. However, a few lines later he expressed the astonishing opinion ‘that a logic independent of the accidental nature of space-time becomes an idle dream’. In Mind Ramsey 1924a dismissed the book, rating as ‘valueless’ their conception of sensory perception, although he was glad that they presented ‘a lot of amusing writings on the use of words by plain men, savages and philosophers’. However, the book became well known, mainly in a reduced second edition which appeared three years later; the several later editions show only minor revisions.
An unusual application of mathematical logic was made by W. W. Greg (1875–1959) in a book on The calculus of variants (Greg 1927a). This was not a new kind of mathematics, but ‘An essay on textual criticism’ by a scholar and also the former head librarian at Trinity College when Russell and Whitehead had been there.22 Greg used the logic of relations, especially the ancestral relation, to confect a symbolic representation of the relationships between an original text and its various later versions. While the display of graph-like notations is at first startling, the calculus is rather impressive, especially in its clear generality. By such means he became known as a founder of the notion of the copy-text, though presumably he did not know of the habits of the younger Russell of transferring folios from one version of a manuscript to the next one! But in a later discussion of symbolic systems, he gave PM as an example of one where the symbols ‘form a silent language of their own’ (Greg 1932a, 248).
8.5.3 American reactions to logicism in mid decade. The second edition of PM received a good deal of notice in the U.S.A. A surprising place is the history of science journal Isis, run by the History of Science Society, which Russell joined for some years in 1927. On the first volume Sheffer 1926a modestly noted the role of his own connective (which he called ‘non-conjunction’). Writing admiringly of the project which produced the first edition, he contrasted it with postulate theory; but he puzzled that ‘In order to give an account of logic, we must presuppose and employ logic’, and saw no way out of this ‘«logocentric predicament»‘(p. 228).
The logician C. H. Langford (1895–1965) was assigned the last two volumes; but he found them unchanged and so devoted his review to the new material. Sceptical of the extensionality that he found, such as infinite conjunctions, he worried if a ‘notational pantomime’ had taken place (1928b, 516). His review framed two papers in Mind: 1927 a against Wittgenstein’s emphasis on tautologies and in favour of existential import and individuals, and 1929 a attempting a theory of ‘general propositions’ based upon functions which took ‘non-general facts’ as values. In Langford 1926–1927a he studied the semantic completeness of some axiomatised theories.
Langford was later a collaborator with Lewis, who himself produced a review 1928a of the second edition of PM for the American mathematical monthly. Also concentrating on the changes, he too noted the ‘Sheffer-Nicod “stroke-function”’ but disliked Russell’s name ‘incompatibility’ for it, on grounds similar to his reading of ‘impossibility’ (§8.3.3). He gave a truth-table for material implication, using Post’s ‘±’ notation §8.3.4). But he did not read the later volumes carefully, for he claimed that the preface on symbolic conventions to the second one (§7.9.3.) ‘was considerably expanded’, whereas it had been reprinted without change.
For the AMS the first volume was reviewed by B. A. Bernstein (1881–1964) of the University of California. While lamenting the small impact of the first edition upon mathematicians, Bernstein 1926 a pointed to the prominence of notions such as assertion and intensionality which they would find ‘not sufficiently convincing’. Summarising the postulatary approach, he applied it later to the propositional calculus of PM (§.9.4.1).
The other two volumes of the second edition were reviewed by Alonzo Church (1903–1995). He proposed that the definition of cardinal numbers as classes of similar classes could be replaced, via Russell’s principle of abstraction, by defining ‘the class determined by a propositional function ø as the class of propositional functions equivalent to ϕ’, and also assuming the existence of the abstraction: an approach like Peano’s (§5.3.3), as he noted (Church 1928 b, 238–239). Russell would not have been keen; and he would also have been surprised by Church’s acceptance of the Bolzano-Dedekind “proof” of the axiom of infinity (p. 240), with his old The principles (§7.2.7) cited as the source.
Church wrote the review soon after graduating at Princeton University under Oswald Veblen with a thesis 1927a on alternatives to the axiom of choice (Aspray 1991a). Then he spent part of 1929 at Göttingen, where Haskell Curry (1900–1982) was writing his Dissertation under Hilbert on combinatory logic; it duly appeared in German in the American journal of mathematics (Curry 1930a), thus continuing the German influence.23 Later Church 1932a reviewed the edition of Ramsey’s writings for the Monthly, in general warmly but with objections: 1.) to abandoning identity, on the usual grounds that if x and y had all properties in common, then one of them was being identical with x, so that y =x; 2. to reading universal quantification in terms of infinite conjunction, since every component proposition had to be understood to start with; and 3)to dropping the subsumption of a classes under propositional functions, since surely class α was determined by the function ‘ ε α’.
ε α’.
An amusing review was produced for the Journal of philosophy by Harry Costello, who had started off Russell’s Harvard logic course in 1914 before he arrived (§8.3.1). Harking back to that time, Costello 1928a recalled the publication of the first edition of PM, with ‘its pages that look something like hen-tracks on the barnyard snow of a winter morning’, and also Royce’s emphasis on the importance of foundational studies. Following a tradition which Russell was trying to replace, Costello wondered if the system should be called ‘logic’ since it was not concerned with reasoning. Like his compatriots, he was not happy with the changes; for example, that type theory was now held to be about symbols whereas paradoxes such as the liar dealt with things (of some kind), or that atomic propositions were as general as claimed (pp. 442–445).
8.5.4 Groping towards metalogic. Bernstein’s review 1926a of PM ended thus:
As a mathematical system, the logic of propositions is amenable to the postulational treatment applicable to any other branch of mathematics. As a language, this logic has all its symbols outside the system which it expresses. This distinction between the propositional logic as a mathematical system and as a language must be made, if serious errors are to be avoided; this distinction the Principia does not make.
This distinction is close to that between logic and metalogic; we also saw Sheffer wanting for it with his ‘predicament’. Several other American authors approached it at this time, as we shall soon see.
At Cornell University Harold Smart presented much of his Ph.D. as a short book on The philosophical presuppositions of mathematical logic. Reviewing the recent development of the subject, with Russell and Royce as principal figures, he judged it to be ‘a complete failure’ (Smart 1925a, 97) for misunderstanding the vision of hero Leibniz, for not using part-whole theory, and for ignoring the creative aspects of mathematics; curiously he hardly mentioned algebraic logic, which was innocent of the first two criticisms. Lewis 1926a was cool in his review for the Journal of philosophy, criticising the author for muddling ‘what is essential’ with ‘what is accidental’, especially an excessive emphasis on extensionality, which MacColl and Lewis himself had shown could be avoided. In reply Smart decreed that ‘formal or abstract truths’ were incompatible with extensionality (1926a, 297). Later he broadened his treatment into a book on the ‘logic’ (philosophy) of the sciences: two chapters were devoted to mathematics. A rather disappointing survey, perhaps the most interesting feature was his appeal to Russell 1914d on ‘the scientific method in philosophy’ (§8.3.1) to stress the need of showing the validity of logical principles (Smart 1931a, 98).
Two American commentators on logicism discussed the theory of types in Mind. Firstly, Suzanne Langer 1926a was understandably concerned by the ‘Confusion of symbols and confusion of logical types’, and wondered if the ban on ϕ (ϕ  ) by the vicious circle principle might also exclude cases of ϕ(ϕ, x) which could be harmless. Perplexed by the linguistic rendering of ϕ
) by the vicious circle principle might also exclude cases of ϕ(ϕ, x) which could be harmless. Perplexed by the linguistic rendering of ϕ  (‘is a cat’ ‘The being-a cat-ness of)..: p. 225), she carried over her doubts to the status of truth-values (p. 229); for the ϕx ‘this proposition is a lie’,
(‘is a cat’ ‘The being-a cat-ness of)..: p. 225), she carried over her doubts to the status of truth-values (p. 229); for the ϕx ‘this proposition is a lie’,
our proposition, now ϕ(ϕx), becomes: ‘“This proposition is a lie” is a lie’, which is no longer—this proposition. ‘This proposition is a lie’ and ‘“This proposition is a lie” is a lie’ are, as a matter of fact, two discrete propositions, and cannot be denoted by the same symbol in the same complex.
Secondly, Paul Weiss 1928a queried the epistemological status of type theory in view of its apparent inability to appraise itself; in the same spirit he analysed the liar and ‘Weyl’s’ heterological paradoxes. In a companion piece in The monist he proposed ‘Relativity in logic’ based upon various interpretations of implication, including Lewis’s, with some emphasis given to entailment; he used a large truth-table to represent the various cases (1928b, 545). He deployed these features also in a lengthy sketch of logical and mathematical ‘systems’, and means of comparing them; following Wittgenstein, he took logical systems to be tautological but mathematical ones not (1929a, 440).
Publishing with the AMS, Church 1928a considered discarding the law of excluded middle without necessarily making an alternative assumption; he doubted that a contradiction could be obtained, and felt it to be ‘meaningless to ask about the truth’ of the law. In reply Langford held that ‘logical facts’ were analytic and that ‘logical principles’ were based upon them; hence no alternative logics were possible; further, ‘π is transcendental’ was allegedly ‘just as much a logical principle’ as the law (1928a, 581).
The next year the philosopher Kurt Rosinger published in The monist a study of ‘The formalization of implication’. Taking the contrast between the central concern of ‘traditional logic’ with inference and the modern interest in implication, he saw Boole as a herald of the change, and noted also the importance of quantification of the predicate (§2.4.6), where ‘logic and mathematics are joined’ (Rosinger 1929a, 277). The symbolic traditions had led to the normalisation; he cited Johnson 1922a on ‘functional deduction’ as a source, although he saw neither PM nor Lewis as giving ‘the real meaning’ of implication, if indeed one existed. In a succeeding note Rosinger 1930a followed Langer in puzzling over the difference between ‘ϕ ’ and ‘ϕx’, deciding that in terms of Frege 1891a (§4.5.5) they were respectively ‘belongingness’ (‘Zusammengehörigkeit’) and ‘necessity of completion’ (‘Ergänzungsbedürftigkeit’). He mentioned, correctly, that Russell had sometimes used ‘propositional function’ to refer to both; but usually it was clear that the former was the function as such and the latter the template for its values, as with mathematical functions.
’ and ‘ϕx’, deciding that in terms of Frege 1891a (§4.5.5) they were respectively ‘belongingness’ (‘Zusammengehörigkeit’) and ‘necessity of completion’ (‘Ergänzungsbedürftigkeit’). He mentioned, correctly, that Russell had sometimes used ‘propositional function’ to refer to both; but usually it was clear that the former was the function as such and the latter the template for its values, as with mathematical functions.
8.5.5 Reactions in and around Columbia. These American sensitivities were partly stimulated by their tradition of postulate theory. We recall from §4.7.3 that John Dewey had suggested the adjective ‘categorical’ to student Veblen in the early 1900s; while he did not study postulate theory, he worked on logic from time to time. His philosophy was a type of pragmatism more comprehensive than that of his mentor Peirce in that he saw all aspects of thought, including (a)logic, as influenced by human activity: this member of the older generation had arrived at alternative logics long ago. In particular, in 1916, when in his mid fifties and at Columbia University, he published a volume of Essays in experimental logic, including his own pieces in the Studies of 1903 (§7.5.4). His title would have puzzled many logicians, but he made his position quite clear: claiming that logic was based upon action (Dewey 1916a, ch. 6) and, for example, warning against Locke’s mistaking ‘logical determinations’ for ‘facts of psychology’ (pp. 404–405). He made a delightful analogy of the difference between idealists and realists as that between ‘eaterists’ and ‘foodists’ (pp. 270–271). Applying his view to epistemology, especially in ch. 11 to Russell’s recently published Our knowledge of the external world, he found the priorities there the wrong way round: world first, patches of colour (or whatever) afterwards, not constructions from the latter to the former (Sleeper 1986a, ch. 4).
In a long review for the Journal of philosophy, written in his temporary Brixton residence (§8.3.7), Russell 1919a agreed with many of Dewey’s points but clashed over the role and place of logic, which Dewey had spread far too widely. Anxious to keep time out of its remit, Russell distinguished temporally from logically primitive notions. He also defended his recent book by explaining the different referents which he and Dewey assigned to the word ‘data’, and protesting at the end that indeed ‘it was not I who made the world’.
Dewey’s Columbia colleague Keyser produced a large book 1922a on Mathematical philosophy as he entered his sixties. He rambled agreeably though without much penetration around a good range of topics, including chapters on invariance, group and postulate theories, the ‘psychology of mathematics’ and the ‘mathematics of psychology’, and even engineering. Logic did not gain a chapter, though PM was praised and some of its concerns appeared in the chapters on limits, variables and infinitude. The next year he wrote a rave review 1923a of Wittgenstein’s Tractatus for the New York evening post, estimating the author as ‘a really great genius of the philosophic order’, a ‘logical mystic’ like Spinoza and Pascal with a ‘deep and beautiful’ theory of inference, who however ‘has not taken sufficient pains to be clear’ on all matters. To give the book more publicity, he abridged his review for the AMS in 1924.
Dewey sustained a large correspondence in addition to prolific publication.24 One regular contact was with Scudder Klyce (1869–1952), a naval officer whose passion lay in rather eccentric metaphysical writings based on a concern with ‘the One and the Many’. He applied it to mathematics in an article 1924a in The monist on the ‘Foundations of mathematics’; there he praised Keyser 1922a, like Keyser judged Wittgenstein to be ‘a mathematical star of the first magnitude’ (p. 622), and felt that there was no real foundation for mathematics. In 1932 he expanded in similar style in a short and self-published Outline of basic mathematics, in which he preferred a postulary approach and found logicism useless: the notion of class of classes confused the One with the Many, for example, and the defining number in terms of them was confused since a number was ‘a word pointing towards an element’ (Klyce 1932a, 19, 68). The book is deservedly obscure.
One of Dewey’s most intense correspondents was another amateur, Arthur Bentley (1870–1957), who made enough money to retire in early middle age and devote himself to philosophy. He was an enthusiastic letter-writer himself, continuing many extensive exchanges. His publications were less impressive; in particular, an essay 1931a on ‘mathematical consistency’, published in Ogden’s journal Psyche, contained an obviously mistaken proof of the denumerability of the real numbers, as Black 1931a pointed out. Next year Bentley put out a book-length Linguistic analysis of mathematics, in which he concentrated on current foundational movements, especially their use of words. An interesting chapter dealt with ‘Word-clusters lacking consistency’, including German examples such as ‘Menge’, ‘Auswahl’ and ‘Zahl’ (1932a, ch. 5). He did not evaluate logicism as such, but PM was praised (the frontispiece marked out the sentence in *54.43 where ‘1+1 =2’ was proved.; he also noted Russell’s stress on bivalency and on the role of operation. As with Keyser’s book, the range was refreshingly wide, but a price was paid in shallowness.25
We have seen a considerable body of American commentary, with the informed students far outweighing the nonentities and eccentrics. Now we switch to Continental Europe for the rest of the chapter, starting with two countries of minor importance.
 niewski. Finally, §8.9 describes the emergence in Vienna of a circle of mathematicians and philosophers, among whom logic was a major concern. The two dominant figures are Carnap and Gödel; the chapter stops with the latter’s completeness theorem of 1930. The next chapter starts with its successor on incompleteness published in the following year, and then concentrates upon the place of logicism in the 1930s, with only summary note taken of parallel developments.
niewski. Finally, §8.9 describes the emergence in Vienna of a circle of mathematicians and philosophers, among whom logic was a major concern. The two dominant figures are Carnap and Gödel; the chapter stops with the latter’s completeness theorem of 1930. The next chapter starts with its successor on incompleteness published in the following year, and then concentrates upon the place of logicism in the 1930s, with only summary note taken of parallel developments.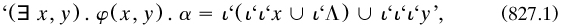
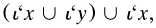 as Kuratowski 1921a was to show later.
as Kuratowski 1921a was to show later.
 months in Brixton, with six weeks’ remission for good conduct; the privileged status of Category A allowed him time for much reading and writing (Papers 8, 312–328). Some of the book on mind was prepared there, but the most substantial outcome was the book on logic. Upon release Russell’s manuscript was typed up by one Mrs. Kyle; on the verso of one of her bills he later recalled her as ‘an admirable typist but very fat. We all agreed that she was worth her weight in gold, though that was saying a great deal’ (RA).
months in Brixton, with six weeks’ remission for good conduct; the privileged status of Category A allowed him time for much reading and writing (Papers 8, 312–328). Some of the book on mind was prepared there, but the most substantial outcome was the book on logic. Upon release Russell’s manuscript was typed up by one Mrs. Kyle; on the verso of one of her bills he later recalled her as ‘an admirable typist but very fat. We all agreed that she was worth her weight in gold, though that was saying a great deal’ (RA).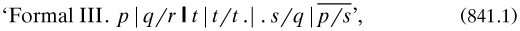
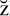 ka 1999a, ch. 10), he took probability to measure the logical relevance between a premise and a conclusion: a notable consequence was a ‘definition of inference distinct from implication, as defined by Mr. Russell’, with the latter placed within probability theory (Keynes 1921a, 117–119).
ka 1999a, ch. 10), he took probability to measure the logical relevance between a premise and a conclusion: a notable consequence was a ‘definition of inference distinct from implication, as defined by Mr. Russell’, with the latter placed within probability theory (Keynes 1921a, 117–119).
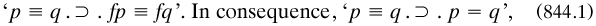
 .(p). fp” we have “
.(p). fp” we have “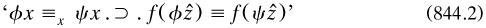
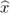 = ψ
= ψ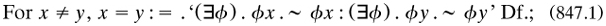
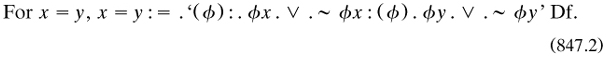
 0 or even
0 or even  ε α’.
ε α’.