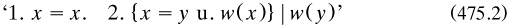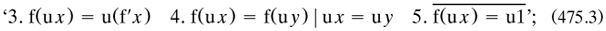4.5 FREGE: ARITHMETIC AS LOGIC
The aim of scientific work is truth. While we internally recognise something as true, we judge, and while we utter judgements, we assert.
Frege, after 1879 (Frege Manuscripts, 2.)
4.5.1 Frege and Frege′. The position of Frege in this story is rather strange, and often misrepresented; so, unusually, we have to begin after his end. Much commentary is available on an analytic philosopher of language writing in English about meaning and its meaning(s), and putting forward some attendant philosophy of mathematics. The historical record, however, reveals a different figure: Gottlob Frege (1848–1925), a mathematician who wrote in German, in a markedly Platonic spirit, principally on the foundations of arithmetic and on a formal calculus in which it could be expressed. Some features (for example, on definitions and axioms) were applicable to all mathematics, and indeed to well-formed languages in general; but even the titles of two of his books make clear that he developed a logicistic philosophy of only arithmetic, with an (unclear) measure of extension to mathematical analysis. His views on geometry were explicitly different (§4.7.4), and he did not attempt the philosophies of (say) probability theory, algebra or mechanics. Further, his highly Platonic concern with objective ‘thoughts’ (‘Gedanken’) and centrally preoccupied with the (possible) ‘reference’ (‘Bedeutung’) of well-formed phrases or propositions, especially with naming abstract objects such as truth, rules him out as a founder of the Anglo-Saxon tradition of analytic philosophy of this century.
During his lifetime the reaction to Frege’s work was modest though, as we shall see, not as minute as is routinely asserted: Russell’s claim to be his first reader after publicising him in 1903 (§6.7.8) is ridiculous. However, after that exposure the audience was not notably greater or more sympathetic, seemingly because his calculus had been shown by Russell to be inconsistent and because he chose then to pursue childish polemics (§4.5.9). Only in his last years and soon afterwards were his merits publicised; but usually they fell upon the consequences of his contributions to formal logic and to language (§8.7—§9 passim). Hence was born that philosopher of language and founder of the Anglo-Saxon analytic tradition; most of the massive Frege industry, especially in English, is devoted to him and his development.28 To distinguish him from the logician rather neglected in Frege’s lifetime, I shall name him as ‘Frege′’, with the prime used in the spirit of the derived function ‘f′(x)’ in Lagrange’s version of the calculus (§2.2.2). This book is concerned with Frege.
As a more welcome consequence of the creation of Frege′, all of Frege’s books have been reprinted, and an edition prepared of most of his papers and pamphlets (Frege Writings: it is cited by page number below when necessary). The surviving manuscript sources have also been published. He corresponded quite extensively, and in 1919 prepared quite a lot of the letters received to give to the chemist and bibliographer of chemistry Ludwig Darmstaedter (1846–1927), who was building up a massive collection of contemporary and historical manuscripts. (Frege’s covering description m1919a is a nice draft summary of much of his work, which the recipient would not have understood!) After Frege’s death in 1925 his Nachlass was inherited by his recently adopted son Alfred, who sent those letters to Darmstaedter and retained all the rest until he gave it in 1935 to the logician and historian of logic Heinrich Scholz (1884–1956) at Münster University (Bernays Papers, 975: 247). With his assistant Hans Hermes, Scholz transcribed many (but not all. documents before the War, and luckily had a transcript at home when the originals were destroyed by bombing of the University on 25 March 1945. But the editions were not completed until the mid 1970s by Scholz’s successors (Frege Letters and Manuscripts, the latter cited from the second edition of 1983). Readers of Frege′ have available much inferior partial editions, not used here.
Let us review Frege’s career, such as it was (Kreiser and Grosche 1983a, Gabriel and Kienzler 1997a). After training in mathematics in Jena in Saxony, Frege prepared his Dissertation at Göttingen in 1873 on complex numbers in geometry. The next year he wrote his Habilitation back in Jena, allowing him to work there as Privatdozent. To his intense disappointment he stayed at this second-ranking university for his entire career, rising to ausserordentlicher Professor in mathematics in 1879 through the support of the physics Professor Ernst Abbe. In that year Johannes Thomae (1840–1921), an analyst and function theorist (and also a former colleague and close friend of Cantor), was appointed ordentlicher Professor. Frege’s relations with him declined later (§4.5.9), perhaps because he himself became only Honorarprofessor, a level between ordentlicher and ausserordentlicher Professor, in 1896. He retired in 1918.
Frege published quite steadily: four books and a few pamphlets, about 20 papers and some reviews (including lengthy ones). At first the papers and reviews appeared with local Jena organisations, and probably found audiences to match; but from the mid 1880s he used nationally recognised philosophical journals, and in the 1900s the Jahresbericht of the DMV, which he joined in 1897 and served (with fellow arithmetician Thomae!) as accounts auditor between 1899 and 1901. The treasurer, and editor of the Jahresbericht, was August Gutzmer (1860–1924); he came to Jena from Halle as a second ausserordentlicher Professor in 1899 and was promoted the next year, but moved back to Halle in 1905.
Given Frege’s sadly modest place in our history, the account in this section is restricted. In some atonement, further features will be described in connection with his exchanges with Husserl (§4.6.3), Hilbert (§4.7.4) and Peano (§5.4.4), and his late writings and revised position of the early 1920s are noted in §8.7.3. Among surveys of his work (as opposed to Frege′’s), the collections Demopoulos 1995a and Schirn 1996a are recommended. Unless otherwise stated, the translations from Frege are mine; I quote many of his original technical terms, the word ‘notion’ being as usual my umbrella word for any of them.
4.5.2 The ‘concept-script’ calculus of Frege’s ‘pure thought’, 1879. (Demopoulos 1995a, pt. 2)
The number of means of inference will be reduced as much as possible and these will be put forward as rules of this new language. This is the fundamental thought of my concept script.
Frege 1896a, 222
In his Habilitation Frege 1874a described a variety of ‘methods of calculation’ to help ‘an extension of the concept of quantity’; they included functional equations (with an application to Fibonacci series, called the ‘Schimper sequence’) and integration techniques using determinants for functions of several variables. No references were given and little seems to be original; so the bearing upon the generality of quantity is not evident. But it shows the early tendency of his interests, which were to flower in his first book, published in Halle in 1879, his 31st year (Frege 1879a).29
In just under 100 pages Frege outlined his ‘concept-script’ (‘Begriffsschrift’) for ‘pure thought’. That is, he sought an objective basis of ‘thoughts’ independent of mental acts, belief structures, or psychological assumptions: this imperative was always to govern his work. But the rest of this title, ‘modelled upon arithmetic’, was unfortunate, for it suggests analogies, and in various places he emphasised extending normal theories of magnitudes; and the last section had a marked mathematical tinge. However, analogies were explicitly avoided, precisely because he wished to build up a symbolic calculus from basic notions; indeed, very few symbols show kinship with either arithmetic or algebra.
After stating his aims in a preface and making the customary nod of the time towards Leibniz’s ‘calculus ratiocinator’, Frege laid out his principal notions in the first of the three sections. A ‘proposition’ (‘Satz’) was regarded as a unified whole if prefaced by the ‘content sign’ ‘—’, and its affirmation or negation judged if the sign 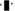 was placed contiguously to the left (arts. 1–4). Truth-values played no role: an affirmed ‘judgement’ (‘Urtheil’) meant that the content ‘occurred’, referring to a ‘fact’. The notion bears some similarity to our highlighting of meta-theory as against object theory, but Frege himself was not thinking in such a framework; his signs expressing the content act more like tokens than like names.
was placed contiguously to the left (arts. 1–4). Truth-values played no role: an affirmed ‘judgement’ (‘Urtheil’) meant that the content ‘occurred’, referring to a ‘fact’. The notion bears some similarity to our highlighting of meta-theory as against object theory, but Frege himself was not thinking in such a framework; his signs expressing the content act more like tokens than like names.
Like Peirce (§4.4.9), ‘The distinction between hypothetical, categorical and disjunctive propositions appears to me to have only grammatical significance’ (art. 4). The conditional judgement between antecedent proposition B and consequent A was displayed in a simple tree layout 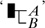 . where the vertical line was ‘the conditional stroke’; but Frege’s account of the various pertinent combinations of affirming or denying A or B was rather ponderous (art. 5). Negation of A was marked by a small vertical line placed such that in ‘A’ it divided the application of the content sign into A to its right and not-A to its left (art. 7). These were the two primitive logical connectives, chosen ‘because deduction seems to me to be expressed more simply that way’ than with other selections (art. 7). Among various rules of inference available he chose for convenience modus ponens (not so named), symbolised by a thick horizontal line between premises and consequent (art. 6). ‘Identity of content’ was presented as the property that two symbols ‘A’ and ‘B’, not their referents, had the same content ‘(A ≡ B)’ (art. 8); this view was not to endure.
. where the vertical line was ‘the conditional stroke’; but Frege’s account of the various pertinent combinations of affirming or denying A or B was rather ponderous (art. 5). Negation of A was marked by a small vertical line placed such that in ‘A’ it divided the application of the content sign into A to its right and not-A to its left (art. 7). These were the two primitive logical connectives, chosen ‘because deduction seems to me to be expressed more simply that way’ than with other selections (art. 7). Among various rules of inference available he chose for convenience modus ponens (not so named), symbolised by a thick horizontal line between premises and consequent (art. 6). ‘Identity of content’ was presented as the property that two symbols ‘A’ and ‘B’, not their referents, had the same content ‘(A ≡ B)’ (art. 8); this view was not to endure.
Next Frege decomposed a proposition into an ‘indeterminate function of the argument A’ (this symbol yet again!), written ‘ϕ(A)’; if two arguments were involved, ‘Ψ(A, B)’ (arts. 9–10). He could have added that this dissection replaced the tradition of subject and predicate. It was a pity that he used the word ‘function’ without adjectival qualification; for, as he emphasised at the end of art. 10, this type of function was quite different from those used in mathematical analysis. The ‘judgement that the function is a fact whatever we may take as its argument  ’ was called ‘generality’ (‘Allgemeinheit’) and symbolised
’ was called ‘generality’ (‘Allgemeinheit’) and symbolised 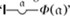 (art. 11): he stressed the independence of this calculus from the propositional by introducing German letters such as ‘
(art. 11): he stressed the independence of this calculus from the propositional by introducing German letters such as ‘ ’ over the ‘cavity’ (‘Höhlung’). This brought in universal quantification; the existential case was defined from it as ‘not for all not …’ by placing negation signs to left and right of the cavity (art. 12).
’ over the ‘cavity’ (‘Höhlung’). This brought in universal quantification; the existential case was defined from it as ‘not for all not …’ by placing negation signs to left and right of the cavity (art. 12).
Frege’s presentation was usually quite clear; for example, while not axiomatic, he made clear his assumptions. However, he was curiously reticent about his choice of them: (apparent) self-evidence seems to have been a factor. In the second section of his book he gave various examples of well-formed (and numbered) formulae in the two calculi (arts. 13–22); again the account is clear and easy to follow, with a sequence of nesting trees of steadily greater complication. The symbolism uses up a lot of space, but it is easy to read and reduces the need for brackets. If Frege were left-handed, then it might have been natural for him to write that way.
While not explicitly stating the rule, Frege substituted symbols quite carefully, warning about not doubling the use of letters in a formula or swapping German and Latin letters. (His treatment of quantification seems to be substitutional rather than objectual, although probably he did not then recognise the distinction.) To make explicit details of a derivation, he often placed to its left a scheme of the form ‘(n): a|b’, which informed that ‘b’ had been substituted for ‘a’ (either or both possibly a tree) in a previous formula (n) (art. 15).
But Frege opened his third section with a mysterious design; I present it schematically as follows:
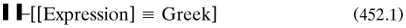
(art. 24). Apart from the two words all the symbols are his, and several were explained only afterwards. The double bar indicated that it was both a judgement and a nominal definition; the array of Greek letters abbreviated the Expression, which came from the predicate calculus with quantification. The Greek letters had ‘no independent content’ but served as place markers in which referring letters (in this case, German ones. could be sited—another substitution technique, in fact, and of an original kind. The verbal counterpart of the Expression read: ‘if from the proposition that  has the property F, whatever
has the property F, whatever  may be, it can always be inferred that each result of an application of the procedure f to
may be, it can always be inferred that each result of an application of the procedure f to 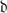 has the property F’ (end of art. 24). The use of ‘procedure’ to describe the function f(
has the property F’ (end of art. 24). The use of ‘procedure’ to describe the function f(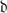 ,
,  ) which permitted the inference of F(
) which permitted the inference of F( ) F(
) F(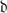 ) for all
) for all  and
and 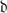 was hardly helpful, but clearly ‘hereditary’ (his word) situations were at hand in this section on ‘the general theory of sequences’, whether in ordinary talk such as the son of a human being human, or in mathematical induction. The latter type of case was his main concern, and he presented three kinds: the version of the above form (formula 81); the second-order kind involving also quantified F, as it now had to be written (91); and that case where the sequence started with the initial member (100).
was hardly helpful, but clearly ‘hereditary’ (his word) situations were at hand in this section on ‘the general theory of sequences’, whether in ordinary talk such as the son of a human being human, or in mathematical induction. The latter type of case was his main concern, and he presented three kinds: the version of the above form (formula 81); the second-order kind involving also quantified F, as it now had to be written (91); and that case where the sequence started with the initial member (100).
Later the names ‘first-order’ and ‘second-order’ would become attached to the kinds, without or with functional quantification, and the relation be known as ‘(proper) ancestral’ according as it did (not. include the first member. Curiously, Frege omitted the first-order proper ancestral; further, the presence of function f of two variables did not inspire him to develop a general logic of relations, either here or later.
Three cases of priority arise. Firstly, MacColl 1877b had anticipated Frege with the propositional calculus, using a broadly Boolean framework (§2.6.4); but Frege seems not to have read him. Secondly and conversely, he preceded by four years Peirce’s group over the predicate calculus and quantification (§4.3.7). Now Ladd’s paper ended with a literature list, including the Begriffsschrift (1883a, 70–71); but she cited Schröder’s review with it and seems to have known of it only that way, so they had been working independently. Finally, Frege’s theory of heredity contains the essentials of Dedekind’s theory of chains in his booklet on integers, already drafted (§3.4.1) but unknown to any one else; Dedekind stated in his preface 1893a to the second edition that he had read Frege only in 1888. Thus none of these similarities suggests influence.
Frege published his first book in the year 1879 of his promotion, and its existence in manuscript had been a factor; but after it appeared his colleagues were apparently disappointed by his preoccupation with a topic of seemingly marginal significance for mathematics. To make his aim clearer, he published a short paper 1879b with the local Jena scientific society immediately after the book was completed, symbolising two mathematical theorems: that three points are collinear, and that any positive integer can be expressed as the sum of four squares. But nobody got excited; in particular, none of the several reviewers.
For example, in the Jahrbuch Michaelis 1881a noted the generality of Frege’s theory but judged that ‘it seems doubtful, that mathematicians would much use of Frege’s concept-script’. In a longer review in a philosophical journal he expressed scepticism over the record of mathematics interacting with philosophy and saw no revolution here, since the ‘concept-script has only a limited scope’ (Michaelis 1880a, 213). He also doubted that the theory of ‘ordering-in-a-sequence’ could be reduced to logic because it was ‘dependent upon the concept of time’ (a true Kantian speaking, as in §4.3.6!), while number was ‘primarily mathematical’ (p. 217). But he admired the calculus itself, and gave a good prosodic description of it.
A long review in a mathematical journal came from Schröder. Like Frege, he paid for his main books and rarely taught their content; but there was little intersection between their logics. In the bibliography of the first volume of his lectures (§4.4.3) Schröder was to mark Frege’s book with an asterisk, indicating special importance; but in his review he was critical of the tree symbolism, pointing out as an example how clumsily inclusive disjunction read: four branches and three negations (Frege’s art. 7), as opposed to his own Boolean ‘(ab + a1b1)’ (Schröder 1880a, 227). He also found the use of various letters ‘only detracts from the perspicuity and rather offends good taste’ (p. 226). The first point relates to utility, but the second is a matter of logic and bears more upon the reviewer than the author.
Behind these and some other criticisms lies the role of analogy: strong in Schröder, absent in Frege. In a paper on the ‘purpose of the concept-script’ written soon afterwards as a reply to Schröder and published by the local scientific society in Jena, Frege 1882a stressed that judgements rather than concepts were his prime category. He also introduced without definition ‘the extension of the concept’ (‘der Umfang des Begriffes’), which seems to be his version of the set of objects satisfying it (p. 2). He also pointed out ‘the falling of an individual under a concept, which is quite different from the subordination of one concept to another’ (pp. 2–3), a distinction corresponding to that for Cantor between membership and proper inclusion for sets; he criticised Boole for conflating this distinction, a point to be repeated many times by mathematical logicians against their algebraic competitors. Reviewing some of Boole’s procedures (and also citing MacColl), he rejected as confusing the multiple uses of signs such as ‘+’; as for his space-consuming version of disjunction, he retorted that formulae in algebraic logic could be very long.
This paper drew on a long manuscript in which Frege m1880a had compared his calculus with Boole, especially the versions of a propositional calculus (§2.5.6). After a survey of Leibniz’s contributions (as then known), he then described his own calculus in detail, symbolising several examples of implications in arithmetic, including mathematical induction. But he revealed little knowledge of Boole’s system, not even discussing the merits of their quite different aims (for example, Boole “burying” the proofs, Frege wanting to expose them in full detail); so not surprisingly his paper was rejected, by three editors. Klein was one of them, for the Mathematische Annalen; in his letter of August 1881 he pointed out Frege’s ignorance of the Grassmanns (Frege Letters, 134–135). A succeeding essay m1882b, refused by a fourth journal, is better in being much shorter. The reputation of young Frege among mathematicians must have been mixed.
4.5.3 Frege’s arguments for logicising arithmetic, 1884. Frege’s next book 1884b, published in his 36th year, devoted its 130 pages to ‘the foundations of arithmetic’ (‘Die Grundlagen der Arithmetik’). The contrast with the Begriffsschrift was marked. Instead of producing symbolic wall-paper, he wrote almost entirely in prose, possibly following an encouraging suggestion made in September 1882 by the psychologist Carl Stumpf (1848–1936) (Frege Letters, 256–257). Instead of ignoring others’ views, he discussed them extensively, often critically. Instead of treating sequences in terms of heredity with no particular numbers used, he put forward his logicist philosophy, that arithmetic could be obtained from his logic alone.30
In his introduction Frege announced his three guiding principles: 1) to ‘keep apart the psychological from the logical, and the subjective from the objective’; 2) ‘the reference of words must be asked in the context of a proposition, not in its isolation’; and 3. to distinguish concept from object. (The second assumption is now called his ‘context principle’ or—very unhappily—his ‘holism’; given its wide remit, his presentation was rather offhand). He began his main text by urging the need in the introduction to definite numbers in the new age of mathematical rigour (art. 1); he must have had the Weierstrassians in mind as one example, although he never attended a course and commented later on the difficulty in procuring copies of the lecture notes (1903a, 149). After some preliminaries, the rest of the book divided into two equal halves.
In the first half Frege reviewed a wide range of philosophers of number taken from British or German authors, and found them all wanting (Bolzano was unknown to him). For example, Mill’s empirical approach (§2.5.8) could not distinguish the arithmetic involved in two pairs of boots from that for one pair of them (art. 25), and confused arithmetic with its applications (art. 17: Mill might not have accepted the distinction). Among Frege’s compatriots and perhaps with certain recent events in mind, Schröder’s textbook 1873a on arithmetic (§4.2.2) was a favourite target. The main failure was to take numbers as composed of repetition of units (Frege 1884b, arts. 29 and 34), which was no better than taking ‘colour and shape’ as basic ‘properties of things’ (art. 21); in consequence numbers were muddled with numerals (art. 43 and 83). He also objected to Schröder’s use of isomorphism between collections, on the grounds that this technique was used elsewhere in mathematics (art. 63). Idealism was attacked for requiring ‘my two, your two, a two, all twos’; in one of his best one-liners, ‘it would be wonderful, if the most exact of all the sciences had to be supported by psychology, which is still groping uncertainly’ (art. 27). Dependency upon space and time was also thrown out (art. 40., and just distinguishing objects would not do (art. 41)—a striking opinion in view of Kempe’s contemporary meditations on multisets, for a different purpose (§4.2.8).
In a profound discussion of ‘one’ Frege criticised predecessors of all ilks for confusing the number with the indefinite article (art. 29–33), although some of his points rested on word-plays with ‘ein’ and ‘Einheit’ (English is better served by ‘one and ‘a’). This was the first lesson that Russell was to learn from him (§6.7.7).
After these failures Frege presented his own theory ‘of the concept of number’. The epistemological election lay between the synthetic a priori and the analytic. The first choice was the Kantian one, and therefore subject to criticism: facile invocations of intuition (of 100,000, for example), and dependence upon physical situations which should not bear upon arithmetic (art. 12). So the vote went to Leibniz: analyticity with logic, both construed objectively (art. 15).
One motive for Frege’s choice was again generality (art. 14):
Does not the ground of arithmetic lie deeper than that of all empirical knowledge, deeper even than that of geometry? The arithmetical truths govern the domain of the numerable. This is the widest; for not only the actual and the intuitive but also all that is thinkable belong to it. Should not the laws of numbers have the most intimate connection with those of thought?
Another piece of common ground lay in equality (‘Gleichheit’: also identity?), which was taken in Leibniz’s form: ‘things are the same as each other, of which one can be substituted for the other without loss of truth’ (‘salva veritate’: art. 65).
The definitions of numbers within logic seem to have been inspired by the following insight. A decent theory should cover both 0 and 1 and not accept the tradition since antiquity (for example, in Euclid. of ignoring the former and treating the latter as something special; for Frege 0 is not nothing, but it has to do with non-existence in some sense; existence had long been recognised as a predicate of an unusual kind; so let all numbers be of that kind.
In this way Frege’s logicism for arithmetic was born; numbers ‘attach’ (‘zukommen’) to concepts F via nominal definitions by ‘falling under’ (‘fallen unter’) them in the way that existence does, as a second-order notion. But an important distinction was presented, rather briefly, in arts. 52–53: between ‘properties’ (‘Eigenschaften’) of a concept and its ‘marks’ (‘Merkmale’), which were properties of objects which fell under it. Thus in the expression ‘four thoroughbred horses’ the adjective was a mark of the concept and a property of each horse, while ‘four’ was the number attached to it: in Cantorian language, properties of a set were marks of its members. This fruitful passage ended with the situation where ‘a concept falls under a higher concept, so to say [one] of second order’ (art. 53), a repeat from 1882a on subordination.
With these notions in place, Frege proceeded to his own theory of Numbers (‘Anzahleri) with a heuristic argument in art. 55, followed later by formal definitions (for which I use ‘ ’):
’):
0) the starter: 0 to concept F if the proposition ‘a does not fall under F’ was true for all objects (‘Gegenstände’) a; thus 0  attached to the concept ‘not equal to itself (art. 74);
attached to the concept ‘not equal to itself (art. 74);
1) the unit: 1 to F if the true propositions ‘a does not fall under F’ and ‘b does not fall under F’ required that a and b had to be the same object; thus 1  attached to the concept ‘equal to 0’ (art. 77);
attached to the concept ‘equal to 0’ (art. 77);
n) the sequence move: (n + 1) to F if there were an object a falling under F and n was attached to the concept ‘falling under F, and not [the same as] a’; thus (n + 1)  attached to the concept ‘n belongs to the sequence of natural Numbers beginning with 0’ (art. 83, after a detailed account of mathematical induction).
attached to the concept ‘n belongs to the sequence of natural Numbers beginning with 0’ (art. 83, after a detailed account of mathematical induction).
Arithmetic was based upon (Leibnizian) equality between Numbers. After a lengthy discussion, with examples taken from various parts of mathematics, Frege described more amply than before the ‘extension of the concept’ (‘Umfang des Begriffes’), a special kind of object comprising the collection of objects which fell under the concept (Parsons 1976a). Then he defined the ‘Number’ attached to F as the extension of the concept ‘equinumerous [‘gleichzahlig’] with F’. Thus the proposition asserting the equality of the extensions of concepts F and G was logically equivalent to that stating that the same Number attached to each concept (arts. 68–69).
Two important notions have crept in. Firstly, Frege invoked the truth-values of propositions, first in the definition of equinumerousness just quoted; but he did not discuss his change from the reliance on facts in the Begriffsschrift, nor did he present any definition of truth. Secondly, in a footnote to art. 68 ‘I believe that for “extension of the concept” we could simply write “concept”’; and while he pointed to objections, he did not seem to realise what a mess the move would cause (Schirn 1983a). The end of the footnote is his limpest sentence anywhere: ‘I assume that one knows what the extension of the concept is’. Russell’s paradox was to show that he did not know it sufficiently well himself, but the notion is already enigmatic. It amounts to a Cantorian set, containing members rather than parts: Frege seems to have invented this set theory for himself, although he had read at least Cantor’s Grundlagen of the previous year (§3.2.7) and even praised the theory of transfinite numbers (arts. 85–86), while criticising the use of isomorphisms (art. 63). Further, how can the truth-values of propositions using equinumerousness be assessed if one or both of the concepts are not explicitly numerical? While he touched on this point (art. 56, for example), he did not resolve it: a vicious circle seems present, and his complaint about Schröder and Cantor using isomorphism rings hollow.
For some unknown reason Frege’s book provoked very few reviews; it did not even receive one in the Jahrbuch, although his Breslau publisher was known there for other books. Part of the small attention paid was a short review by Cantor. He approved of the general aim and the avoidance of space, time and psychology (this from him!); but he criticised details, regarding ‘extension of the concept’ as ‘in general something completely indeterminate’, disagreeing that his own notion of ‘power’ (cardinality. was the same as Frege’s Number, and briefly rehearsing his theory of cardinals and ordinals (Cantor 1885c). His second point was a mistake, perhaps caused by the fact that for him ‘Anzahl’ referred to an ordinal (§3.2.7), a difference which Frege had observed in his remarks on Cantor. In a brief reply Frege 1885b explained the blunder, noting that Cantor had misunderstood Number as related to a concept F instead of to the concept of equinumerousness to it. He was polite; but resentments may have been excited, and an opportunity for their release was provided several years later (§4.5.5).
One might have expected Cantor and Frege to be close; but this is true only geographically, Halle and Jena being 40 miles apart. There is no evidence that they even met, although this presumably happened at some annual gatherings of the DMV.
4.5.4 Kerry’s conception of Fregean concepts in the mid 1880s. In a short paper ‘On formal theories of arithmetic’ Frege 1885a contrasted two kinds: a nice one based upon grounding arithmetic in logic, and a boring one based upon viewing arithmetic as composed of ‘empty signs’, leading to ‘no truth, no science’ such as knowing that 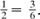 This paper and the book, together with the Begriffsschrift, inspired a substantial and rather negative reaction from Benno Kerry. We met him in §3.3.4 as an acute commentator on Cantor in his 1885a; his comments on Frege occurred within an eight-part suite of articles ‘On intuition and its psychic propagation’, which appeared in the same journal, Vierteljahrsschrift fur wissenschaftliche Philosophie, from 1885 until posthumously in 1891. Based upon his Habilitation at Strasbourg University (Peckhaus 1994a), he included Frege in a wide survey of the literature: he had even read Bolzano. Most of his remarks on Frege are contained in the second and especially the fourth parts (Picardi 1994a); the examples below are taken from the latter.
This paper and the book, together with the Begriffsschrift, inspired a substantial and rather negative reaction from Benno Kerry. We met him in §3.3.4 as an acute commentator on Cantor in his 1885a; his comments on Frege occurred within an eight-part suite of articles ‘On intuition and its psychic propagation’, which appeared in the same journal, Vierteljahrsschrift fur wissenschaftliche Philosophie, from 1885 until posthumously in 1891. Based upon his Habilitation at Strasbourg University (Peckhaus 1994a), he included Frege in a wide survey of the literature: he had even read Bolzano. Most of his remarks on Frege are contained in the second and especially the fourth parts (Picardi 1994a); the examples below are taken from the latter.
Kerry had studied with the philosopher and psychologist Franz Brentano (1838–1917) for a time, and so was well aware of subtle psychological issues in philosophy. He rehearsed various concerns of ‘psychic works’ on ‘inner perceptions’, and so on (Kerry 1887a, 305–307), matters which Frege wished to avoid considering. More pertinently, Kerry wished to rescue arithmetic for the synthetic a priori from ‘the F[regean] logification [‘Logificirung’] of the general concept of Number’ (p. 275), and included a nine-page footnote on affirming or denying analytic and synthetic judgements (pp. 251–260). Some of his criticisms of Frege were based upon his own misunderstandings: for example, the senses of ‘one’ beyond the arithmetical (pp. 276–278), and the (apparent) impossibility of setting up an isomorphism between empty extensions, thus blocking Frege’s definition of 0 (pp. 270–273). But he enquired carefully into Frege’s enigmatic notion of extension of the concept, and the status of that notion (p. 274):
[...] that the judgement ‘the concept “horse” is a simply graspable concept’ of the concept ‘horse’ is also an object, and indeed one of the objects which falls under the concept ‘simply graspable concept’.
He did not claim this situation to be paradoxical, but it was distant from Kantian territory.
4.5.5 Important new distinctions in the early 1890s. Kerry was the first serious student of Frege’s theory. A reply did come, though tardily: perhaps discouraged by the continuing non-impact, Frege published nothing for some years, although he seems to have developed his logicism and symbolism. Early in the new decade he put out two papers (one inspired by Kerry) and a pamphlet; each work carried a title of the form ‘X and Y’ and explained the distinction between the pair of notions involved. The trio seems to have been written or at least thought out together, in an intensive refinement of his theory. I start with the paper which contained the most far-reaching distinction.
Frege began the paper ‘On sense and reference’ (1892a) by stating that now ‘Gleichheit’ carried ‘the sense of identity’, thus marking a change of previous normal practice, or at least indicating a new precision. Claiming that in the Begriffsschrift he had taken identity as a relation between names, he announced a second change by introducing the distinction for ‘signs’ (‘Zeichen’), be they single letters, or one or more words: between their ‘sense’ (‘Sinn’) and their ‘reference’ (‘Bedeutung’) to some object. He gave examples from mathematics, science and ordinary life of signs with different senses but the same referent, such as ‘the point of intersection of [lines] a and b’ and ‘the point of intersection of [lines] b and c’ for three coincident lines; and of signs with no referent at all, such as ‘the least rapidly convergent series’ (pp. 143–145), and presumably ‘Odysseus’ (p. 148). ‘A proper name (word, sign, combination of signs, expression) expresses [drückt aus’] its sense, denotes or designates [‘bedeutet oder bezeichnet’] its reference’ (p. 147). Conversely, an object had these signs as its ‘designation’ (p. 144). Distinct from both notions was the subjective ‘connected idea’ (‘verknupfte Vorstellung’) of the referent pertaining to a thinker (p. 145).
Such distinctions had long been recognised by philosophers and logicians, with names such as ‘signification’ and ‘application’ (to quote the very recent example Jones 1890a); Frege’s novelty lay in the range of use. For example, he re-oriented his view of propositions by placing centre stage truth-values, two only: ‘There are no further truth-values. I call the one the True, the other the False’ (‘das Wahre, das Falsche’: p. 149). This latter pair of notions served as the sole reference of true or of false propositions, as Leibniz’s definition of identity taught (p. 150). In particular, all arithmetical propositions became names of the True—hence his frequent use of noun clauses rather than propositional forms (for example from §4.5.2, ‘the falling of an individual under a concept’ not ‘the individual falls under the concept’). He then described the way in which the reference of a compound proposition was to be determined via its connectives (pp. 152-157)—not unlike testing by truth-tables but perhaps closer to using a valuation functor.
This paper was one of Frege’s most influential contributions, not least upon its author (Thiel 1965a); in his later writings he was much more systematic in deploying or avoiding quotation marks, and in distinguishing a word from its reference. He used its proposals in the pamphlet, which contained a lecture given to the local scientific society (but not published in their journal, unlike his 1879a or 1882a. This time he dealt with the distinction between ‘Function and concept’ (Frege 1891a). He regarded a function as ‘unsaturated (‘ungesättigt’), which became ‘saturated’ when a value for the variable was inserted (pp. 127–129). Perhaps he chose this surprising analogy from chemistry to suit his audience: it would have helped them if he had stated explicitly that he was replacing the traditional distinction between subject and predicate. He also stressed more clearly than before that all possible values of the argument were admitted, so that values which might have been better construed as inadmissible sent the resulting proposition to the False. Presumably his context principle (§4.5.3) inspired this strategy.
Frege defined a new object relative to a function F(x., corresponding to the curve specified by y = f(x): its ‘value-range’ (‘Wertverlauf’), the set of ordered pairs of values of its arguments x and of its ‘values’ (sic) F(x). For symbols he invoked Greek letters and drew upon the diacritical apostrophe to write ‘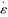 F(ε)’ (pp. 129–131). In the important special case of the concept, a function which took only truth-values for its values, its value-range was named ‘extension of the concept’ (p. 133). He introduced this notion casually, and did not mention his earlier use of the phrase (§4.5.3) where it seemed to name a set of objects rather than ordered pairs of them. Indeed, this author of a paper 1884a on ‘the point-pair in the plane’ did not mention ordered pairs at all here. He could also have clarified the relationship between the two types of function; that (for example. the zeroes of the mathematical function f(x), x variable, give the values of x when the propositional function (or concept) f(x) = 0) refers to the True (and otherwise to the False).
F(ε)’ (pp. 129–131). In the important special case of the concept, a function which took only truth-values for its values, its value-range was named ‘extension of the concept’ (p. 133). He introduced this notion casually, and did not mention his earlier use of the phrase (§4.5.3) where it seemed to name a set of objects rather than ordered pairs of them. Indeed, this author of a paper 1884a on ‘the point-pair in the plane’ did not mention ordered pairs at all here. He could also have clarified the relationship between the two types of function; that (for example. the zeroes of the mathematical function f(x), x variable, give the values of x when the propositional function (or concept) f(x) = 0) refers to the True (and otherwise to the False).
Frege reworked the basic notions of the concept-script in terms of truth-values of asserted contents (1891a, 136–141). He finished with an explanation of functions more marked by brevity than clarity of functions of the second ‘level (‘Stufe’); either functions of functions, or functions of two variables like ‘f’ involved in (452.1) (pp. 141–142). A short review appeared in the Jahrbuch: Michaelis 1894a judged that ‘As with all Frege’s work, the reviewer also has the impression that it gets lost in subtleties’.
In his pamphlet Frege deployed sense and reference in all sorts of contexts, such as
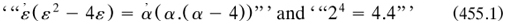
(1891a, 130, 132); he also identified (as it were) mathematical equality such as here with identity, and maintained this position in later writings. He also introduced the technical term ‘thought’ (‘Gedanke’) when stating that the propositions ‘24 = 42’ and ‘4.4 = 4’ express different ones; but its role was explained only in the other paper, 1892a. Published in the journal that had taken Kerry’s suite, it served partly as a reply to Kerry, whose comments had motivated several parts of the draft version (Frege Manuscripts, 96–127).
Frege’s main concern was to tackle the distinction between ‘Concept and object’. He accepted Kerry’s puzzled reading as correct: ‘the concept “horse”’ was indeed no concept but designated an object (Frege 1892b, 170–171). But the reply is glib; some major questions of a paradoxical kind arise concerning the different ways in which a horse is named by ‘horse’ and by ‘the concept “horse”’ (de Rouilhan 1988a, ch. 4).
Frege addressed more completely other of Kerry’s concerns; for example, the senses of ‘is’ beyond that of the copula (1892b, 168–169). Of his own theory he confessed that ‘I did not want to define, but only give hints while I appealed besides to the general sense of language’ (p. 170)—a phrase which suggests that he saw his aim, especially with his concept-script, of capturing Leibniz’s characteristica universalis as an ideal language.
Frege repeated his criticism of the failure, this time by Schröder, to distinguish an object ‘falling under’ a concept from a concept subordinated to another one (p. 168). He also applied to propositions his distinction of sense from reference, which ‘I now designate with the words “thought” and “truth-value”’ (p. 172). Even here he was cryptic; the clearest and most detailed presentation of these distinctions was given in a letter of May 1891 to Husserl, rendered here as Figure 455.1 (Frege Letters, 96: the context is explained in §4.6.3). In contrast to subjective ‘ideas’ (‘Vorstellungen’), ‘thought’ was intended in an objective sense, rather like state of affairs, sharable among thinkers and indeed independent of anyone thinking them. Presumably but regrettably, he came to this schema only after his two papers and pamphlet had been accepted for publication. In a later manuscript he noted that a proposition need not contain any proper names (m1906c, 208).
In another paper from this period Frege reversed previous roles with Cantor when he reviewed Cantor’s pamphlet 1890a reprinting recent articles on the philosophy of the actual infinite (§3.4.4). Perhaps in unhappy memory of last time, his barbs were sharp. After again praising his enterprise, ‘Mr. Cantor is less lucky where he defines’ (Frege 1892c, 163); but he chose Cantor’s use of ‘variable finite’ to definite finitude, which could have been better conveyed in terms of indefiniteness rather than variability but was hardly a failure. Again, ‘If Mr. Cantor had not only reviewed my “Grundlagen der Arithmetik” but also had read it with reflection, then he would have avoided many mistakes’, such as ‘impossible abstractions’ (p. 164). He also recalled Cantor’s error over ‘extension of the concept’, and attacked his epistemological dependence upon abstraction in definitions of cardinal and ordinal numbers (p. 165). In a draft version of the review (Manuscripts, 76–80) Frege was even more sour, especially on this last matter (Dauben 1979a, 220–226). Cantor did not reply to the published version.

FIGURE 455.1. Frege’s schema of sense and reference.
4.5.6 The ‘fundamental laws’ of logicised arithmetic, 1893. (Demopoulos 1995a, pt. 3)
Frege has the merit of [...] finding a third assertion by recognising the world of logic, which is neither mental nor physical.
Russell 1914c, 206
Armed with his new distinctions, Frege could now work out in detail ‘the fundamental laws of arithmetic’ (‘Grundgesetze der Arithmetik’) in his calculus. The first volume, containing 285 pages, appeared, apparently at his own expense, from a Jena house as Frege 1893a, 31 when Frege was in his mid forties. In a long foreword he began by stating his mathematical aims and scope, and lamenting the silence over the Grundlagen: then mathematicians, ‘who give up false routes of philosophy unwillingly’ (p. xiv), were allowed to leave the classroom while he waxed philosophical. Criticising at length the empiricist version of logic 1892a recently published by Benno Erdmann (1851–1921), Frege stressed that ‘I recognise a domain of what is objective, non-real [‘Nichtwirklichen’], while the psychological logicians [such as Erdmann] take the non-real without further ado as subjective’ (p. xviii)—the third realm which Russell was to spot.
The first part of the volume was devoted to the ‘Development of the concept-script’. In the opening articles Frege crisply laid out his basic notions and signs: function (including of two variables) and concept, (un)saturation, thought and truth-values, sense and reference, course-of-values, generality, negation and the connectives, identity (‘Gleichheit’), and the three types of letters. The content-sign ‘—’ of the Begriffsschrift, now named ‘the horizontal’ (art. 5), was presented as a special function-name which mapped true propositions to the True and anything else (for example (his), 2) to the False. When combined with the vertical judgement sign ‘|’ it became the judgement sign ‘|-’, which denoted the ‘assertion’ of a proposition (arts. 5–6). There was a newcomer: ‘the function \ξ’ which ‘replace[d] the definite article’ by taking as value the object falling under the concept represented by ‘ξ’ if unique (such as the positive square root of 2 for the concept ‘positive square root of 2’) and otherwise the extension of that concept (art. 11). This notion grounded his theory of definite descriptions—which was motivated, as with Russell after him (§7.3.4), by the need for mathematical functions to be single-valued.
This time Frege presented three rules of inference: modus ponens, transitivity of implication, and a complicated one for compound propositions with some parts in common; he included various ‘transition signs’ (‘Zwischenzeichen’), mostly horizontal lines, which showed how a formula below it was derived from those above (arts. 14–16). Rules of various kinds were summarised in art. 48, immediately after a listing of the eight ‘basic laws’, with three for the propositional calculus (including negation), three for universal quantification over functions, and one for the extension of the concept. The other rule, introduced in art. 20, replaced equinumerousness in the Grundlagen by the assumption that the equality/identity of two value-ranges was logically equivalent to the equivalence of the quantified corresponding functions:
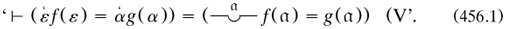
This is Law V, which Russell was to find to be susceptible to paradox (§6.7.7). Although a principle for extensionality, it is now called his ‘comprehension principle’. He used no names for any of his laws; and once again he was silent on their choice, seeming to use self-evidence as a criterion.
After presenting the double-bar sign (452.1). (art. 27), Frege gave much attention to forms of definition. Perhaps by reflecting upon the dubious definition of equinumerousness in the Grundlagen, he favoured only nominal ones (art. 33). One of them, concerned functions of functions ‘X(ϕ(ξ))’; since only objects could be arguments for functions, ‘ϕ’ would have to be replaced by its value-range (art. 21). To improve upon (455.1) he used a new function, ‘ϕ∩ζ’ (I follow his unhelpful choice of Greek letters) which replaced the value ‘ϕ(Δ)’ of the function for argument ‘Δ by the combination ‘Δ ∩ ‘εϕ(ε)’; as usual, he extended the definition to cover all kinds of arguments (arts. 34–35). He used this function frequently in later exegesis: the chief property for a mathematical function was
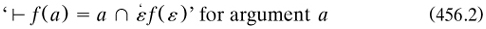
(arts. 54–55, 91). He also stratified functions into ‘levels’ (‘Stufen’) by the kinds of quantification, if any; for example the function in (456.1) was of second level, and quantification of f was third level, and so on (art. 31).
Self-membership being excluded, a theory of types was embodied. However, the logic of relations remained rudimentary, especially when compared with Peirce’s, which Frege seems not to have known. For example, in defining a ‘double value-range’ of a function of two variables, and the associated ‘extension of the Relationship’ (‘Beziehung’) when it took only truth-values, he did not stress the role of ordered pairs of objects (art. 36), with ‘ξ + ζ’ used as illustration). He also defined the extension of the converse of a Relationship (art. 39). Later he dealt with compounding Relationships ‘p’ and ‘q’, and for once a schematic representation of the process (art. 54, formula (B):
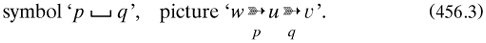
These last notions were introduced in the opening of the second part of the volume, in which Frege worked out the ‘Proofs of the fundamental laws of the Number’ in great symbolic detail; Frege′ and even Frege scholarship is usually silent about it, but see Heck 1993a. The spatial symbolism works very nicely, but Frege chose some ghastly symbols for his various notions, presumably wishing to avoid analogy but often losing both sense and reference for the reader. For example, almost all the numerals refer to pages, articles or theorems! The perplexity could have been reduced by an index of symbols, though several appear in those for laws and definitions at the end of the volume. The text switched regularly between articles talking about the plan in ‘analysis’ (‘Zerlegung’) and those effecting the ‘construction’ (‘Aufbau’); correspondingly, quotation marks around formulae were alternately present or absent.
In the first part Frege had sketched out the theory of defining ‘Numbers’ as the sequence stated verbally in the Grundlagen, launched with  (using ‘T”ε = ε’ to refer to the True), then
(using ‘T”ε = ε’ to refer to the True), then  (via ‘ε =
(via ‘ε = 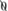 ’) and the relation ‘f’ of ‘successor of (‘Folge’: arts. 41–43). The detailed exegesis included properties such as the uniqueness of the successor and (its converse. of the predecessor of a Number (arts. 66–77, 88–91. and basic features of ‘
’) and the relation ‘f’ of ‘successor of (‘Folge’: arts. 41–43). The detailed exegesis included properties such as the uniqueness of the successor and (its converse. of the predecessor of a Number (arts. 66–77, 88–91. and basic features of ‘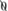 ’ and ‘
’ and ‘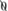 ’ (arts. 96–109). Then attention switched to many properties of ‘endless’ (‘Endlos’) sequences of Numbers with no final member (Cantor’s well-order, not mentioned), including a definition of the concept ‘Indefinite’ which corresponded to Cantor’s
’ (arts. 96–109). Then attention switched to many properties of ‘endless’ (‘Endlos’) sequences of Numbers with no final member (Cantor’s well-order, not mentioned), including a definition of the concept ‘Indefinite’ which corresponded to Cantor’s  0 (art. 122, Cantor not mentioned). He also treated ‘finite’ (‘endlich’) sequences which did stop (arts. 108–121). In art. 144 he at last formally defined an ordered pair:
0 (art. 122, Cantor not mentioned). He also treated ‘finite’ (‘endlich’) sequences which did stop (arts. 108–121). In art. 144 he at last formally defined an ordered pair:
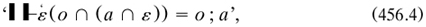
where ‘the semi-colon herewith is [a] two-sided function-sign’. His theorems included versions, stated in terms of indefinite sequences, of Dedekind’s validation (§3.4.2. of mathematical induction and the isomorphism of such sequences (art. 157, Dedekind not mentioned though noted in the introduction to the volume).
Despite much acute precision, some unclarities remain. A significant one concerns the balance between intensional and extensional notions, and even the specification of some of them. Names such as ‘extension of the concept’ suggest that concept itself is an intensional notion of some kind, as indeed is corroborated in various places. In particular, in a letter probably written around this time (Frege Letters, 177) he opined to Peano that
one may freely regard as that which constitutes the class not the objects (individui, enti) which belong to it; for then these objects would be annulled with the class which exists out of them. However, one must regard the marks that are the properties which an object must have, as that which constitutes the class in order to belong to it.
He wrote in similar vein when discussing Husserl (Frege 1894a, 455: the contexts are explained in §5.4.5 and §4.6.3 respectively). In addition, one can hardly conceive extensionally of an empty course of values, so close to the important Number 0. On the other hand, he required that a function-name be always saturated when completed by a proper name, which carried an extensional ring (Furth 1964a, xxvii-xliv). Maybe he had not fully thought out this distinction across his calculus.
The volume received very few reviews. Peano’s, the most important, will be noted in §5.4.5. Michaelis 1896a wrote one paragraph in the Jahrbuch, mentioning as new notions the diacritical apostrophe (he had obviously forgotten reading about it in ‘Function and concept’) and the description functor. After a brief hint of Frege’s logicist programme, he referred to the summary of results at the end of the book, ‘which in its peculiar form may put off many readers’.
4.5.7 Frege’s reactions to others in the later 1890s. After publication of this volume Frege continued work on its successor(s). Various manuscripts show new considerations, such as the sense and reference of concept-words (Manuscripts, 130–136). They seem to relate to critiques of two contemporary logicians which he published in philosophical journals in the mid 1890s. His views on Husserl will be aired in §4.6.3; we note here his ‘critical elucidation’ 1895a of Schröder’s first volume.
One major issue was Schröder’s subsumption relation, which conflated Frege’s ‘falling under’ and ‘falling within’ (membership and improper inclusion). Frege proposed to distinguish them as ‘subter’ and ‘sub’ respectively, and to solve Schröder’s paradox of 0 and 1 (§4.4.2). by invoking the intransitivity of the former relation (pp. 198–199). But he showed again his poor knowledge of Boole in claiming Boole’s universe of discourse was ‘all-embracing’ (‘allumfassend’: p. 197), which is true only for the first book (§2.5.4). He also made play with Schröder’s various uses of ‘0’ and ‘1’, and of mixing concepts with objects. There was no reply in the posthumous part of Schröder’s second volume. Given their fundamental differences, it is amusing to see that each man had seen himself as fulfilling the vision of a ‘calculus ratiocinator’ made by that necessarily Good Thing, Leibniz (for example, Frege in the preface to the Begriffsschrift, and Schröder in the introduction of his first volume)!
Comments of a similar kind were inspired by an article 1894a on integers in the Revue de métaphysique et de morale by the school-teacher Eugene Ballue (1863–1938). Frege’s reply 1895b, his only publication in a foreign language, criticised Ballue’s focus on numerals rather than on numbers, or at least mixing the notions, and also for defining one as a ‘unité’ (‘unite′’) and larger numbers as ‘pluralities’ of it. Ballue did not reply in print, but he corresponded with Frege for a couple of years thereafter (Frege Letters, 2–8), admitting some ‘lack of precision in the [technical] terms’ of his article. He also reported correspondence with Peano (even transcribing one letter), and noted that Peano had not yet treated Frege’s work; this lacuna was soon to be filled (§5.4.5).
A more sarcastic version of the same line was inspired in Frege by the opening article in the Encyklopädie der mathematischen Wissenschaften (§4.2.4), a survey of ‘the foundations of arithmetic’ by Hermann Schubert (1848–1911). Largely concerned with the historical and cultural aspects, Schubert 1898a did not launch this great project well; starting with counting processes, he advanced little further in a routine survey of arithmetical laws and operations, and some algebraic aspects such as the principle of permanence of forms (§2.3.2). Frege’s theory was not discussed, although the Grundlagen was listed in a footnote (p. 3). Doubtless Frege had thought of a more suitable author for the article, and he replied to this product with witty savagery: for example, ‘the numbers as product of counting. Really! Is not the weight of a body the outcome of the weighing as well?’, and would a collection of peas lose its peaness after being abstracted? (Frege 1899a, 241, 244). He also doubted the legitimacy of the principle of permanence (§2.3.2) as a source for proofs (p. 255). Schubert did not reply to this attack, and may not have seen it; for it appeared only as a pamphlet, from Frege’s Jena publisher.
4.5.8 More ‘fundamental laws’ of arithmetic, 1903. For four years Frege did not publish again, until the second volume of the Grundgesetze appeared near the end of 1903, when he was in his mid fifties. A small delay was caused by the need to respond to Russell’s paradox in an appendix; we note that in §6.7.7 and treat here the volume as originally conceived. Exactly the same length as its predecessor, it contained the same mixture of symbolic wallpaper (hardly read) and prosodic discussion (overly read).
Without explanation for the pause of a decade since the first volume, Frege continued the second part of the book on the ‘construction of sequences’ by dealing with topics such as the isomorphic comparison of sequences (arts. 1–5)and the summation of numbers (arts. 33–36). He ended by using again the concept ‘endless’ (‘Endlos’) to distinguish indefinite from finite Numbers (arts. 53–54).
The rest of the volume contained (not all of) the third part of the book, dealing with real numbers. After rehearsing again his stipulations of well-formed nominal definitions of concepts and functions (arts. 55–65), Frege attacked various theories of real numbers recently proposed by contemporaries. Cantor was taken to task on various matters, such as (indeed) sloppily associating the existence of a real number with a fundamental sequence (323.2) of rational numbers (arts. 68–69); however, the basic strategy, similar to definition by equivalence classes, was hardly as hopeless as Frege wished to convey. Among other authors, while praising aspects of Dedekind’s theory of cuts, Frege noted that it contained no investigation of the possibility of constructing the irrational number from the cut (arts. 138–140). Indeed, Dedekind had put the move forward as an axiom (§3.2.4).
Frege’s other main target was the opening pages of Thomae 1898a, the second edition of a textbook on complex-variable analysis. The situation in the Mathematischer Seminar at Jena around that time had deteriorated to such an extent that the course in logic was given by Professor Thomae while Honorarprofessor Frege handled topics such as remedial geometry. Perhaps in revenge, Frege obsessively denounced his senior colleague for talking about numerals instead of numbers, muddling symbols with their referents, allowing ‘=’ to cover both arithmetical and definitional equality without explanation, and regarding zero as a ‘purely formal structure’ (arts. 88–103). Thomae had also compared arithmetic with chess as games; Frege pointed out that chess included moves as well as rules (that is, different categories), and so did arithmetic (arts. 88; 96, 107–123).
The whole passage in the volume, over 80 pages long, is the main source of ‘Frege against the formalists’, as it is now often called. However, while Thomae’s presentation is sloppy,32 it is doubtful any formalist intended to hold so absurd a position as that which Frege criticised. And when Frege denounced another favourite butt, Heine 1872a, for saying that a sequence of numbers continued to infinity by sarcastically claiming that ‘In order to produce it, we would need however an infinitely long blackboard, infinitely much chalk and an infinitely long time’ (art. 124), the stupidity lies with Frege.
The last part of the volume is by far the most important, for it contained Frege’s own theory of real numbers (Simons 1987a). He conceived these objects to be ratios of magnitudes of any kind, from which itself the theory should be independent. To set up the required machinery he drew upon the concept of Relationship and on its extension, which was now also called ‘Relation’ (‘Relation’), without mention of Schröder’s logic of relations; ‘extension of the concept’ became ‘class’ (‘Klasse’: arts. 161–162). Then real numbers formed a class of Relationships, and each one was defined as a Relationship of Relationships. To specify these he drew upon the bicimal expansion of a real number a, of any kind:
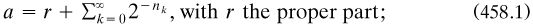
then a could be captured by taking the sequence {r, n1, n2, …} (art. 164: he ignored the ambiguity of expansions ending with non-stop 1s, but it can be dealt with). This sequence could be infinite, finite—or empty in the case of integers, which were notated ‘1’ in contrast to the Number 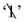 . The negative of any number was defined from the converse of its Relationship, and ‘0’ by compounding any Relationship with its converse since (458.1) was not available (art. 162).
. The negative of any number was defined from the converse of its Relationship, and ‘0’ by compounding any Relationship with its converse since (458.1) was not available (art. 162).
In the rest of the volume Frege established the properties required of Relationships to allow the constructions to be effected, drawing heavily upon functions of functions and compounding. After proving commutativity and associativity (arts. 165–172), he defined the ‘positival class’ of magnitudes from which, among other things, the least upper and greatest lower bounds of a collection of real numbers could be defined (arts. 173–186); the special case of the ‘positive class’ comprised members which satisfied Archimedes’s axiom and thereby avoided infinitesimals (art. 197). He ended by promising more details about this class (art. 245), maybe on using the proper ancestral to generate the sequences of numbers specified by (458.1) and passing to further properties such as upper and lower limits. Presumably he also intended to exhibit the basic arithmetical operations, properties and relations in terms of the sequences defined from (458.1) or from notions derived from them, and proceed to related topic such as upper and lower limits. However, before he could start saving up to publish the third volume Russell’s paradox arrived (§6.7.7).
Why did Frege take a decade to publish this volume? The second part was presumably completed by 1893; and apart from the passage on Thomae most of the rest could have been ready then also. Had he needed several years to pay for it? If so, the return on investment was small. As last time, there were very few reviews; in particular, in the Jahrbuch the school-teacher Carl Färber 1905a wrote one paragraph, solely on the prosodic middle, and found ‘many replies of Frege as pedantic or nit-picking’—harshly phrased, but not unfair. However, a more considered reaction was also published in that year.
4.5.9 Frege, Korselt and Thomae on the foundations of arithmetic. Korselt placed in the Jahresbericht of the DMV a commentary 1905a on Frege’s second volume, in the form of an exchange between ‘F.’ and ‘K.’. First K. appealed to Bolzano33 to argue that F.’s rules for ‘sharp definitions’ were too strong and indeed not achievable in principle; he doubted whether the ‘inner nature’ of, for example, ‘point’ could be captured in the way that F. sought for ‘number’ (p. 372). Cantor’s theory of real numbers seemed to be such a case; while suggesting improvements in presentation, he wondered if doubter F. had ‘either not understood Cantor’s definition or it goes with him like an absent-minded rider, who looked for his horse and sat upon it’ (p. 376). Again, while Thomae’s enterprise was ‘to be considered as failed’ K. wondered ‘how should one otherwise know, that one has come across the “essence” of an object?’ (pp. 379–380). He also defended the practice of abstraction in mathematics since it was executed only on ‘certain conditions’ (but F. rightly wanted to know which ones, and why?). Again, K. (naively) queried the merits of worrying about definitions since only ‘one indicates an uncomfortably long expression or an arbitrary figure of known conditions with a short name, which itself is a figure of the theory?’ (p.381). Dedekind’s creation (323.2) of irrational numbers seemed reasonable to K., since ‘cannot also thoughts, concepts and theorems be created?’ (p.386).
Overall K. gave an intelligent appraisal of all current theories. For whatever reason F. did not answer (their swords had already crossed over geometry in §4.7.4), but instead went for Thomae’s reply 1906a to him in the same journal: a ‘holiday chatter’ on ‘thoughtless thinkers’ such as, apparently, the chess player. Thomae had concluded from his alleged attachment to numerals that ‘for instance one might let the number three grow in the following figures

but then there are the doom-laden little dots’, which under Frege’s characterisation denoted ‘four more threes’ (p. 437). In other words, he rightly rejected the kind of formalism attributed to him by Frege, as treating mathematics as instances of signs, sizes included, instead of the ideographical form of each sign. Thomae’s ironic conclusion was that
Mathematics is the most unclear of all sciences.
Written in the dog-days of the year 1906.
In reply Frege 1906b felt sure that he ‘had destroyed Thomae’s formal arithmetic for ever’ and the recent chatter ‘only strengthened […] this conviction’. Thomae 1906b began his ironic and witty answer; ‘22 years ago Mr. Frege let me know unequivocally in conversation, that he held me as incapable of understanding his deeper deductions. Now he pronounces the same urbi et orbi’. The Honorarprofessor replied with a new account 1908a of the ‘impossibility’ of Thomae’s approach. The editor of the Jahresbericht, Gutzmer, then back at Halle, may have felt pressure from his contact with these two fomer colleagues at Jena (§4.5.1) to accept all this stuff.
This last scratch at Thomae’s eyes was Frege’s final publication before his retirement in 1918, although he continued to lecture on his theory and may have been writing a textbook on it (Manuscripts, 189–190). We note his last period in §8.7.3.
It is not surprising that Frege had a poor reception in general. Intemperate polemics, partly based upon silly criticisms, are not the only reasons; unattractive are seemingly excessive fussing about names, the use of normal words like ‘function’ in unfamiliar ways, highly forgettable symbols in the technical accounts (although not, I hope, the nice if impractical spatial layout), and, after 1903, the presence of Russell’s paradox in his system. Indeed, his logic remains rather mysterious; the logicism is easier to grasp. His failure to acknowledge sources does not help either (and helps the Frege′ers to know that he thought up everything for himself) In particular, Kreiser 1995a has shown recently that Frege’s father Karl-Alexander (b. 1809) published a grammar-book 1862a for schoolchildren which just happens to emphasise a context principle on the primacy of propositions, the role in them of logical connectives, their expression of ‘thoughts’, the distinction between objects, propositions and names, and the designation of an object of a concept by adding ‘the’, and even a spatial layout of symbols (but without lines) to symbolise the subordination of adverbs to verbs. Well, fancy that.
Two serious concerns of Frege have not yet been noted. One was his lack of respect for Hilbert’s way with the foundations of geometry, due in §4.7.4; the other is his response to Husserl, to whom we now turn.
4.6 HUSSERL: LOGIC AS PHENOMENOLOGY
4.6.1 A follower of Weierstrass and Cantor. (Schuhmann 1977a) An unusual member of the Weierstrass school (§2.7.4) was Edmund Husserl (1859–1938), who took courses with The Master in 1878 and 1879 (when Klein, Max Planck, Otto Hölder and Aurel Voss were also around) His special interest was in the calculus of variations, and his version of the course given in 1879 was so good that it was used in the Weierstrass edition (see the editorial remarks in Weierstrass Works 7 (1927)). Husserl then wrote a Dissertation m1882a on the subject at Vienna University under the supervision of Weierstrass’s follower Leo Königsberger (1837–1921. (Biermann 1969a).
But thereafter Husserl devoted his career to philosophy, hoping to achieve there standards of rigour comparable to those in mathematics exhibited by Weierstrass’s lectures, and by similar means of exposing clearly the basic principles and building up the exegesis in a rational manner. While in Vienna he had also studied with Brentano, from whom he learnt that the act of perception was directed towards (more than) one object (in the general sense of that word), which therefore inhered with the act itself, and that psychology was to be understood primarily as the analysis of acts of consciousness (Gilson 1955a). Husserl was to call this brand of philosophy ‘phenomenology’, the philosophical analysis of reasoning with especially reference to consciousness. Brentano was more an inspirer than practitioner of it, partly because he did not focus upon philosophical issues beyond supporting positivism whenever possible.
Husserl was also perhaps the first philosopher outside Bohemia to be influenced significantly by Bolzano; he discovered him first through the article Stolz 1882a (§2.8.2), and then especially via the enthusiasm of Brentano. One point of attraction was the notion of presentations in themselves beyond any particular instances of them; another was pure, objective logic itself, which grew in importance in his philosophy. Thus he was no simple idealist: on the contrary, he sought objective contents independent of any thinker’s (ap)perception of them. Rigour and rationality coupled to perception and inherence: the elaboration of these insights was to dominate his philosophical endeavours life-long.34
The opportunity to launch them came in 1886, when Husserl moved to Halle University as a Privatdozent and wrote his Habilitation 1887a ‘On the concept of number. Psychological analyses’.35 The main supervisors were Erdmann (§4.5.6) and Stumpf (a former student of Brentano); but he also came in contact with mathematicians, especially Cantor (who also told him about Bolzano) and Hermann Grassmann’s son, also Hermann. He expanded the work into his first book, Philosophie der Arithmetik (1891a).
Husserl’s next book was two volumes of Logische Untersuchungen (1900a, 1901a). Partly because of it, he was promoted in 1901 to ausserordentlicher Professor, and moreover at the more prestigious Göttingen University, where Hilbert was one of his new colleagues. Five years later he received a personal full chair. In 1916 he obtained a full chair at Freiburg im Breisgau; he retired in 1928, two years after Zermelo joined the faculty. He wrote incessantly throughout his life, and also corresponded extensively (Husserl Works, Letters); but much of his philosophy has no specific mathematical concern, and he never attempted a logicism. Thus the treatment of his work here will be brief, and confined almost entirely to the main publications of his Halle period. Most of his other publications then were long reviews of books in German on non-symbolic logic; he also wrote many manuscripts on arithmetic and on geometry (Works 12 and 1994a). Some later work and followers appear in §8.7.8.
4.6.2 The phenomenological ‘philosophy of arithmetic’, 1891. (Willard 1984a, chs. 2–3) Although Cantor was mentioned only twice in Husserl’s Habilitation, his influence seems to be quite marked: the choice of the number concept as his topic (Weierstrass may also be detected), and the distinction of cardinal and ordinal by ‘Zahl’ and ‘Anzahl’ (§3.2.7). Focusing on ‘our grasp of the concept of number’, not the number as such, he highlighted the intentional act of ‘abstraction’ from maybe disparate or heterogeneous somethings to form ‘embodiments’ (‘Inbegriffe’: pp. 318–322). His phenomenology refined Cantor’s naive idealism, and indeed may have been a motivation for it (Hill 1997a). For example (an important one), he applied ‘specialisation’ (Cantor’s word, after (323.3) and in §3.6.1) to the counting process to specify numbers out of sequences as successions of ones from ‘something’ (‘Etwas’: 1887a, 336). Two bases furnished ‘the psychological foundation of the number-concept’: ‘1) the concept of collective unification; 2) the concept of Something’ (pp. 337–338).
Husserl soon expanded his Habilitation of 64 pages into a book of five times the length; but it appeared after delay (or hesitation?) as Philosophie der Arithmetik. Logische und psychologische Untersuchungen (1891a). It was dedicated to Brentano, despite his friendly protests, and a lack of interest which took him 13 years to spot the dedication!36 Husserl followed the line of his Habilitation, to near repetition of text in the first three chapters; they comprised about half of the first part, which was devoted to ‘the concepts of multiplicity, unity and Number’ (‘Anzahl’). Much of the second part, on the symbolisation of Number and its logical roots’ was new in text though not in context. Husserl began by claiming that ‘numbers are no abstracta’ and distinguished, say, ‘3’ from ‘the concept 3’: ‘the arithmetician does not operate with the number concepts as such at all, but with the generally presented objects of this concept’ (p. 181); again, ‘Is it not clear, that “number” and the “presentation of counting” is not the same?’ (p.33). Similarly, on ‘Presentations of multiplicities’ (‘Vielheitsvorstellungen’), ‘We enter a room full of people; an instant suffices, and we judge: a set of people’, though he stressed that ‘an instant’ was an over-simple phrase in ‘the explanation of the momental conception of sets’ (pp. 196–197). More generally, he noted ‘figural moments’, acts of perception which create out of a collection ‘e.g. a row of soldiers, a heap of apples, a road of trees, a line of chickens, a flock of birds, a line of geese etc’ (p. 203). But he did not contrast Cantor’s Mengenlehre with the part-whole tradition (a brief waffle about ‘infinite sets’ occurs on pp. 218–222), and he seems not to have known Kempe’s recent theory of multisets (§4.2.8).
This concern with perception bore centrally upon Husserl’s philosophy of arithmetic, in which he saw Numbers as ‘multiplicities’ (‘Vielheiten’) of units; in rather sloppy disregard of the tradition of distinguishing extensions from intensions, he used ‘Menge’ and ‘Inbegriff’ as synonyms. Since his philosophy also drew upon counting members of multiplicities, the grasp of numbers involved numeral systems, which he discussed at length in ch. 12. He developed X-ary arithmetic for any integer X in a rather ponderous imitation of Cantor’s principles (326.2) of generation of ordinals: ‘1, 2,…,X’, with successors ‘X + 1, X + 1 + 1’ through multiples to polynomials in X (pp. 226–233). X was always finite; he was not following Cantor into the transfinite ordinals, maybe because of their dubious perceptibility. Further, the central place of counting in his philosophy of arithmetic casts doubt upon the primacy of cardinals stated in the preface (p. 10).
Husserl’s number system was prominent in his final chapter, which treated ‘The logical sources of arithmetic’ (not ‘foundations’, note); for again ‘the method of sensed [‘sinnliche’] signs is thus the logical method’ (p. 257). Thus, despite the mention of ‘logic’ in the sub-title of his book, its role was linked only to relationships between numbers, not the numbers themselves: ‘from the development of a general arithmetic in the sense of a general theory of operations’, as he put it in his final words (p. 283). The status of 0 and 1 was also not clear: ‘One and None—they are the only ‘beiden’] possible negative answers to the How many. […]But logical this is not’ (p. 131), in a passage where unit and unity were rather mixed together.
This attitude makes a great contrast with Frege, whose Grundlagen Husserl had read since completing his Habilitation. The difference is beautifully captured by their reactions to exactly the same passage from Jevons: ‘Number is but another name for diversity. Exact identity is unity, and with difference arises plurality’ (1883a, 156). For Husserl in both Habilitation and book this procedure was satisfactory, although Jevons’s following remarks on abstraction were psychologically naive (1887a, 319–321; 1891a, 50–53). By contrast, in the Grundlagen Frege had found the whole approach to be indefensible, in its use of successions and especially in assumptions about units (1884b, art. 36).
Husserl was also critical of Frege, partly for avoiding psychological issues which for him were central (Husserl 1891a, 118–119) but also on other matters. The most important was the equivalence of extensions of concepts: ‘I cannot see, that this method marks an enrichment of logic’ since it worked with ‘ranges’ (‘Umfänge’: p. 122). In particular, he did not find convincing Frege’s Leibnizian definition of ‘equality’ (§4.5.3) because ‘it defines identity instead of equality’, reversing the correct relationship because ‘Each same characteristic grounds the same judgements, but to ground the same judgements does not ground the same characteristics’ (p. 97; compare p. 144). Given the paradox that Russell was to find in Frege’s comprehension law (456.1), Husserl’s intuition was very sharp; Frege’s own modification of his calculus was to involve modifying identity (§6.7.7). Less clear is Husserl’s claim that ‘More difficult [than counting] is it, correctly to characterise psychologically the role which the relations of equality are assigned by the number-presentations’ (p. 142).
Husserl completed his book in April 1891 by writing a short preface; in the same month he prepared a long review of Schröder’s first volume 1890a, which appeared later in the year as Husserl 1891b. It shows further moves towards objectivity, perhaps inspired in part by reaction against Schröder. For example, having appraised Schröder’s calculus as an ‘algorithmic logic of extensions’ (‘Umfangslogik’: p. 7), he stressed more strongly than in the book the ‘ideal content of concepts’, which ‘no person possesses’ as Schröder seemed to assume (p. 17). Schröder’s failure to handle this distinction led to ‘all confusion’, and Husserl expended upon various examples and consequences. One of these was Schröder’s paradox of 0 and 1 after (444.6), where for once Husserl noted the merits of the membership relation in the Mengenlehre (pp. 35–36). He also disliked some technical features; for example, since subsumption incorporated equality as well as inclusion, the definition (444.3) of ‘identical equality’ using it was ‘an obvious circle-definition’ (p. 30). But he seemed to misunderstand Schröder’s use of ‘Principle’ to denote an axiom when criticising Schröder’s new one for distributivity (pp. 37–38). Another change was bibliographical: for the first time in print Husserl mentioned the Peirceans (p. 3).
Schröder referred little to Husserl in the posthumous part of his lectures, and only once to this review (1905a, 484). Meanwhile, others had reacted to Husserl’s book.
4.6.3 Reviews by Frege and others. One of the first reviews of Husserl’s Arithmetik came from Jules Tannery; although writing in the Bulletin des sciences mathématiques, he concentrated on the philosophy. Warming to the book in general and Husserl’s doubts over Leibnizian identity, he declared that ‘axioms are conditions imposed upon definitions’ (1892a, 240), a kind of conventionalism which his younger compatriot Henri Poincaré was to expound later (§6.2.3, §7.4.3, 5). In the Jahrbuch Michaelis 1894a was still more positive; perhaps recalling Frege (§4.5.2), he concluded that Husserl’s book ‘may be considered by far the best that has been written on the foundations of arithmetic for a long time’. However, neither reviewer much penetrated the philosophy or the psychology: for that a sterner piece, in a philosophical journal, came from Frege.
Frege mainly just contrasted his philosophy with Husserl’s. For example, he attacked the mixture of logic and psychology (Frege 1894a, 181), which for Husserl was intentional. Maybe deliberately, he misunderstood as a ‘naive opinion’ Husserl’s remarks on heaps and swarms in connection with numbers, diagnosing as cause ‘because he seeks in words and combinations of words specific presentations as their references’ (pp. 186–187) without allowing that heapness or swarmhood could be part of that reference. Indeed, he seems not have realised that for Husserl ‘presentation’ had an objective ring, maybe following Bolzano, not his own subjective connotation. But he also rightly detected some confusion between multiplicities and Numbers (p. 179), and he could have been more critical than pp. 188–189 on the handling of 0 and 1.
Doubtless Frege’s review nudged Husserl further along the path towards objectivity; but the extent of its impact needs careful appraisal (Hill 1994a). The Frege′ industry routinely informs us that the review quite transformed poor Husserl’s philosophy; but elementary attention to chronology and sources (Hill 1991a, pt. 1) shows that this claim refers far more to the False than to the True. We noted Husserl’s use of ‘ideal content of concepts’ in his review of Schröder, so that he was already shifting his position even while his book was in press; later (1900a, 179) he retracted only a few pages of censure of Frege (including the comments on equivalence, which were worth retaining!), and left intact his basic approach and other reservations of Frege’s theory (on identity, for example).
One of these concerned sense and reference: instead of Frege’s distinction for proper names, recently introduced (§4.5.5), Husserl worked in Arithmetik with ‘a two-fold reference’ of an ‘abstract name’, both ‘as name for the abstract concept as such’ and ‘as name for any object falling under this concept’ (1891a, 136). In recognition of this difference, Frege explained his own position in the beautiful schema given in §4.5.5. His letter was a response to Husserl sending both his book and the review of Schröder; when reviewing the former, Frege seems not to have noted the changes evident in the latter. In reply Husserl politely pointed out several similarities between them; for example, observing the distinction between a logic as such and its calculus (Frege Letters, 100).
4.6.4 Husserl’s ‘logical investigations’, 1900–1901. During the 1890s logic moved to centre stage in his phenomenological concerns as he sought his version of the objective. Bolzano’s work made its full impact during this period. The principal outcome was one of his major publications, the Logische Untersuchungen, published in two volumes and dedicated to Stumpf (Husserl 1900a, 1901a). A lightly revised second edition appeared in 1913 and 1921; I use it here, as it is much more accessible (but not always the English translation 1970a). Here a few features of his view of logic and its relationship to mathematics are noted.
The first volume contained Husserl’s ‘Prolegomena to pure logic’, a long essay on psychologism, where, perhaps unhappily, he enjoined both German idealism and the sociological reductionism of Mill (1900a, art. 13). Of his various criticisms, one concerned the unavoidably limited horizons of human experience, which surely prevented delivery of the generality required by a philosophy of mathematics. A relatively well-known passage used a mathematical example (art. 46):
All products of arithmetical operations go back to certain psychic acts of arithmetical operating. […]Quite other is arithmetic. Its domain of research is known, it is completely and exhaustively determined by the familiar series of ideal species 1,2,3,… […] The number Five is not my own or anyone else’s counting of five, it is also not my presentation or anyone else’s presentation of five. It is in the latter regard a possible object of acts of presentation […].
The passage was inspired by one in Cantor using ‘five’ (1887–1888a, 418–419).
The ‘pure logic’ which Husserl sought was a normative science of objective contents, requiring ‘the fixing of the pure categories of meaning’ (‘Bedeutung’), objects, their relationships and laws, and ‘the possible forms of theories or the pure theory of manifolds’ (1900a, arts. 67–70). The application of mathematics to logic recalls Boole, though the details were quite different; for under ‘pure manifold’, whose laws determine ‘the theory’s form’, he included Riemann’s theory, Hermann Grassmann’s calculus and Cantor’s Mengenlehre (art. 70). Finally, he drew in probability theory, though without clear intent (art. 72).
The larger second volume contained six investigations of the title. Husserl discussed others’ work in some detail; after Brentano the author most cited was Bolzano, mainly for his Wissenschaftslehre. His own exegesis sought to articulate the pure logic from the main notions of his descriptive psychology: expression, meaning, attention, objects, experiences, contents, and so on. Of greatest mathematical interest is the third investigation, where he extended the part-whole theory in Arithmetik into an elaborate classification of kinds of part, such as (not) spatio-temporal and (in)dependent, and their relationships to aspects such as redness of objects (Smith and Mulligan 1982a). The discussion shows that phenomenology deserves a much better place among the philosophies of mathematics than it normally gains. But Husserl’s pure logic itself seems to be rather fugitive (with ‘pure’ being passed from one notion to another!); for example, he did not discuss logical connectives or quantification theory, which surely should come into a logic influenced by mathematics. His silence over Peirce and Schröder is loud.
4.6.5 Husserl’s early talks in Göttingen, 1901. The next stage of Husserl’s development is rather surprising. At the end of his Habilitation one of his six ‘theses’ stated that irrational numbers needed ‘logical justification’ (1887a, 339). Perhaps in fulfilment, he had announced in the preface of Arithmetik a second volume to deal with negative, rational, irrational and complex numbers; indeed, apparently it was ‘largely ready’ (1891a, 8, 7). But his philosophical uncertainties prevented the volume from being completed (the surviving manuscripts are published in Works 12, 340–429).
However, when he moved to Göttingen in 1901, the year of publication of the second volume of the Untersuchungen, Husserl gave two lectures to the Göttinge Mathematische Gesellschaft in November and December on ‘the imaginary in mathematics’. The word ‘imaginary’ covered all these types of number (m1901b, 432–433); but instead of trying (and failing) to grasp them by phenomenological means, the ‘way through’ was now provided by specifying a consistent axiom system and the manifold or domain (‘Gebiet’) of objects determined by it. One of the main properties was defined thus (p. 443):
A formal axiom system, which contains no inessentially included axiom, is called definite, when each theorem which decidedly has a sense through the axiom system, thereby falls under the axiom system, be it as consequent, be it as contradiction, and that will apply overall, where it can be shown on the basis of the axioms that each object of the domain is reduced to the group of numerical objects, for which each relationship fulfils the true identically and every other is therefore false.
Thus Husserl’s notion of definiteness was oriented around arithmetic (‘group’ above carries no technical meaning), but was related to propositions which were not derivable from any axiom system. To us it sounds very close to Hilbert on axiomatics: so it did to Husserl, who distinguished between definiteness ‘relative’ to a particular domain and the unrestricted absolute version which ‘= complete in the Hilbertian sense’ (p. 440); the Club minutes of the lectures use ‘vollständig’ for the first sense and ‘definit’ for the second.37 Now Hilbert had recently spoken to the Club on axiomatics (§4.7.3), with Husserl present; but Husserl seems to have formulated his own approach independently before arriving in Göttingen, in connection with his treatment of manifolds in the Untersuchungen (Hill 1995a, Majer 1997a). The converse is also true; Hilbert had found his own way to axiomatics during the 1890s, as we shall now see.
4.7 HILBERT: EARLY PROOF AND MODEL THEORY, 1899–1905
4.7.1 Hilbert’s growing concern with axiomatics. Husserl’s use of axioms was a sign of the mathematical times, for their role grew quite noticeably during the last 30 years of the 19th century. Two branches of mathematics were largely responsible (Cavaillès 1938b): abstract algebras, mostly group theory (Wussing 1984a, pt. 3) but also other structures (some traces were seen in §4.4 with Dedekind and Schröder); and geometries, now various with the acceptance of the non-Euclidean versions. As a mathematician, Hilbert was an algebraist; his earliest work dealt with invariants and algebraic number theory. The latter also brought him to axiomatics; but his first detailed exercise was in geometry.
Hilbert was concerned with geometries throughout the 1890s (Toepell 1986a). While still at Königsberg he gave a course on projective geometry in 1891, followed three years later by one on foundational questions such as the independence of axioms and particular ones such as connection and continuity (called ‘Archimedes’s axiom’). Some wider publicity came in a short note 1894a in Mathematische Annalen on defining from certain axioms ‘the straight line as the shortest connection between two points’.
After his move to Göttingen in 1895 Hilbert continued working on the projective side, becoming especially interested in the proof in Isaac Schur 1898a of Pascal’s famous theorem on the collinearity of the three points of intersection of the opposite sides of a hexagon inscribed in a conic, which did not use continuity. He treated this theorem in a special short course at Easter 1898 ‘On the concept of the infinite’, which dealt with geometrical spaces and continuity rather than Cantor’s Mengenlehre. This brought him to a course in the winter semester of 1898–1899 on ‘the foundations of Euclidean geometry’, of which several dozen copies were made; it led to one of his most famous publications. He was then in his late thirties.
As part of the growing interest in axiomatics, it had become clear that Euclid had not specified all the assumptions that he needed; so some of the gaps were filled (Contro 1976a), especially by Moritz Pasch (1843–1930) with an emphasis on the ordering of points, and then by Peano with a treatment also using lines and planes (§5.2.4). Hilbert decided to fill all the remaining gaps. An unusual occasion for publicity arose in June 1899, when a statue was unveiled to celebrate the work of Gauss and the physicist Wilhelm Weber. Klein thought that some accounts of scientific work related to their interests should be prepared, and so two booklets were written. Physics professor Emil Wiechert described electrodynamics, in honour of the heroes’ creation of the Magnetische Verein; and Hilbert drew on his lecture course to present the ‘Foundations of geometry’, with especial reference to the Euclidean version (Geometry1 (1899)). The essays were published together as a book by Teubner, Hilbert receiving 235 Reichsmarks for his part (Hilbert Papers, 403/6).
Over the decades Hilbert’s essay expanded from its original 92 pages to over 320 pages in the seventh edition (1930). Some of this extra material arose from additions or changes to the text, even to the axiom system; but most of it was reprints of articles on geometry or the foundations of mathematics written in the interim (Cassina 1948–1949a), for the book inspired him to a general study of the foundations of geometry and also arithmetic. The words ‘formalism’ and ‘metamathematics’ became attached to his philosophy and techniques during his second phase, which ran from the late 1910s to the early 1930s (§8.7.4); he gave it no special name during the first one, which ran until 1905, but ‘axiomatics with proof and model theory’ is a reasonable characterisation.
4.7.2 Hilbert’s different axiom systems for Euclidean geometry, 1899–1902. In his first edition Hilbert presented 20 axioms: I 1–7 on ‘Connection’ (‘Verknüpfung’), II 1–5 on ‘Ordering’ (‘Anordnung’), III for the parallel axiom (in a Euclidean version rather than one of the equivalents found since), IV 1–6 on ‘Congruence’, and V on ‘Continuity’. Then he proved various elementary properties of points, lines and planes; angle was defined from IV 3 as the ‘system’ of two intersecting half-lines. The second chapter dealt with the independence of the axioms, which he demonstrated by working with a corresponding co-ordinate geometry and assuming the consistency of the real numbers which it used. While the independence of each group of axioms seems well shown, that within a group was not fully handled, and some redundancy was soon found (§4.7.3). Then he handled planar areas, and proved Pascal’s theorem and a similar one due to Desargues. In the final chapter he made some straight-edge constructions in the plane, assuming congruence; they led to remarkable links to number theory which may have been a little out of place and contrasted sharply with the regular use of diagrams in the earlier chapters. In the Jahrbuch Friedrich Engel 1901a summarised the book in some detail and judged that ‘it gives a satisfactory, nay definitive answer to many pertinent questions for the first time’.
Hilbert’s stress on the consistency and independence of axioms, and on the axioms (not) needed to prove particular theorems, characterised his philosophy of mathematics at this time. Concerning a lecture by Hermann Wiener 1892a to the DMV on proving Pascal’s and Desargues’s theorems, he had stated that ‘one must be able to say “tables, chairs, beer-mugs” each time in place of “points, lines, planes”’ (Blumenthal 1935a, 402–403); but this famous remark is normally misunderstood and Hilbert may not have thought it through at the time.
Firstly, Hilbert was advocating model theory for the axioms (intuitively at this early stage), not the mere use of words nor the marks-on-paper formalism that Frege detected in the symbol-loving arithmeticians (§4.5.8); intuitive knowledge of Euclidean geometry motivated the axiomatising enterprise in the first place. Unfortunately he did not make this point in the book, although the lecture course had contained consideration of ‘intuition’ (‘Anschauung’: Toepell 1986a, 144–147): one obvious consequence is that intuitive knowledge of beer-mugs is different. Secondly, he treated concepts such as ‘point’ as implicitly defined via axioms. Thirdly, the same versatility could not be demanded of the logical connectives used to form and connect his propositions; for example, ‘and’ cannot become ‘wine-glass’.
Typically of mathematicians’ casual attitude, Hilbert took logic for granted in his book; but he soon began to attend to it (§4.7.4). The Paris lecture of 1900 on mathematical problems (§4.2.6) showed him already to be aware of the consistency of an axiom system. He continued to develop his approach to geometries, in papers and also before the Göttinge Mathematische Gesellschaft. The talk on 18 February 1902 may have surprised the audience, for he presented a quite different axiomatic treatment using groups of continuous motions, the latter defined in terms of mappings;38 the details appeared in a long paper 1902b in Mathematische Annalen, curiously given the same title as the book. He cited Lie for the algebra and Riemann and Helmholtz for the geometry, but not his colleague Klein for either. This axiom system was much simpler than its predecessor, so that the proof-theoretic task was reduced. The number system was used to definite a ‘number plane’ of co-ordinates, and set theory was prominently used. These features led the young American mathematician E. B. Wilson (1879–1964) to conclude an acute and sceptical commentary 1903a on the paper that a better title for it would be ‘Geometric analogues of ensembles’, on the grounds that its reliance upon numbers and sets could not capture geometry itself.
Despite the difference of approach in this paper, Hilbert reprinted it in later editions of his book. The second edition (1903) won for him in the following year the third Lobachevsky prize, awarded by Kazan University for contributions to geometrical knowledge; as a member of the jury, Poincaré wrote a long and admiring report 1904a. The changes in this edition included not only misprints; for the text was also altered, at one point in a very important way.
4.7.3 From German completeness to American model theory. Hilbert soon imitated for arithmetic his success with geometry in a short paper 1900a for the DMV ‘On the concept of number’. This time axioms I 1–6 covered ‘connection’ by addition and multiplication, II 1–6 for ‘calculation’ via the equality relation, III 1–4 for ‘ordering’ by inequalities, and IV 1–2 for ‘continuity’. The first axiom of this last group was Archimedes’s, as usual; it guaranteed the existence of the real numbers and thereby the real line, hence underpinning geometry. The other axiom was a significant innovation:
IV 2. (Axiom of completeness). It is not possible to add another system of things, so that the system of numbers resulting from the composition of the axioms I, II, III, IV 1 will be thoroughly filled; or briefly: the numbers form a system of things, which due to the maintenance of the collective axioms is not capable of further extension.
This use of ‘completeness’ is not that to which we have become accustomed from Hilbert’s second phase, but follows Dedekind, perhaps consciously. To us it is a kind of meta-axiom about sets or manifolds, like Husserl’s absolute definiteness (§4.6.5) but independent of it: the other axioms are assumed to have captured all the objects required by the theory. He ended the paper by reporting Cantor’s conclusion (§3.5.3) that the set of all alephs was ‘inconsistent (unready)’. In similar vein, he told members of the Göttinge Mathematische Gesellschaft (including Husserl. on 29 October 1901 of one consequence: admit the completeness axiom but omit Archimedes’s, and the system is contradictory.39
Clearly this kind of assumption was not confined to arithmetic, so Hilbert added the corresponding axiom in the second (1903) edition of his book; in a review for the Jahrbuch Max Dehn 1905a described it as a ‘“between” axiom’, a ‘second continuity axiom’ equivalent to Dedekind’s cut principle. Hilbert must have found it very soon after publishing the first edition, for it was directly added to the French translation 1900a; it also entered the English one 1902a. That translation, published by Open Court, was reviewed in the Company journal The monist by Veblen 1903a, who mentioned a recent American contribution to the axiomatisation. It had been made by E. H. Moore, who had received an honorary doctorate from Göttingen University at the statue ceremony in 1899, at the relatively early age of 38 years. (Hadamard, three years younger still, was also given one.) He soon published a paper 1902a in his Transactions of the American Mathematical Society showing the redundancy of Hilbert’s axioms II 4 in the group on ordering (a claim concerning I 4 on connections was soon withdrawn).
This was the reference made in his review by Oswald Veblen (1880–1960), then a student of Moore at the University of Chicago, writing a thesis on the axioms of Euclidean geometry but based upon Pasch’s use of ‘order’ between ‘points’ (the only two primitives). He published his doctorate as a paper 1904a in the Transactions, presenting a system of 12 axioms for the purpose. Inspired by Hilbert’s notion of completeness, he defined an axiom system to be ‘categorical’ if ‘there is essentially only one class’ of objects satisfying the axiom system, so that any two classes would be isomorphic; otherwise, it was ‘disjunctive’ if further axioms could be added. These terms were not his own; he acknowledged them (p. 346) as due to the Professor of Philosophy at Chicago, John Dewey, no less (but no mathematician). The second term has not endured, but the first, and its attendant noun ‘categoricity’, became standard; probably Dewey thought of it in rough mathematical analogy with ‘categorical’ in logic (his reaction to symbolic logic will be noted in §7.5.4 and §8.5.5). The notion may have stimulated Moore to devise the similar methodology of analogous theories in his general analysis (§4.2.7).
Veblen’s thesis helped launch ‘postulate theory’, important in the rise of American mathematics (Scanlan 1991a): the name ‘model theory’ has become more common. The notion of modelling was not new: non-Euclidean geometries had used it, and Boole’s reading of his algebra of logic as in terms of elective symbols or of classes (§2.5.3) is another example. But the theory was treated much more systematically from now on, not least for the recognition of (non-)categoricity. Benjamin Peirce’s work on linear associative algebras (§4.3.2) also played a role in showing how various systems of postulates could be handled; indeed, Moore’s Chicago colleague L. E. Dickson (1874–1954) exposed closer links in a paper 1903a in the Transactions.
In 1907 Veblen himself co-authored a textbook in mathematical analysis. Although categoricity was not represented, it was a pioneer work in the (dubious) educational practise of using axioms from the start (Veblen and Lennes 1907a, ch. 1). The authors took the axioms from the other major American postulationalist, E. V. Huntington (1874–1952). He passed his entire career at Harvard University, except to write a Dissertation 1901a on the geometrical interpretation of real numbers and vector algebra at Strasbourg University under the direction of Dedekind’s friend Heinrich Weber. On his return he studied the former kind of quantities by means of postulate theory; indeed, he started a little before Veblen and was more prolific. His main mathematical interest was finding axiom systems for various mathematical theories and studying their consistency, independence, completeness and ‘equivalence’ (his word for categoricity). He published most of his studies in the Transactions: the early cases included 1902a for ‘absolute continuous magnitudes’, 1902b for positive integers and rational numbers, and 1903a for real numbers; a later long study of the continuum (in another journal) will be noted in §7.5.6.
In addition, Huntington 1904a examined Schröder’s algebraic calculus, and so brought model theory to logic. By such means the central place of interpretation in Hilbert’s conception of axiomatics flowered naturally into model theory in American hands.
4.7.4 Frege, Hilbert and Korselt on the foundations of geometries. (Boos 1985a) Frege saw both Hilbert’s lecture course and the book in the winter of 1899–1900 and sent objections by letter (Letters, 147–152, 60–79). His logicism was not an issue, since it did not include geometry: the main point concerned the use of axioms rather than definitions to determine or specify objects (Demopoulos 1994a). Typically for Frege, in Hilbert’s groups I and III of axioms ‘the referents of the words “point”, “straight line”, “between” have not been given, but will be assumed as known’ (Letters, 61): typically in Hilbert’s reply, ‘The complete definition of the concept point is given first by the finished construction of the system of axioms. […] point in the Euclidean[,] non-Euclidean, Archimedean, non-Arch[imedean] geometry is something different each time’(pp. 68–69).
Frege left the matter for a time, presumably while he finished the second volume of the Grundgesetze. But then he sent a short two-part paper 1903b to the DMV in which he rehearsed again his view that axioms rather than definitions gave precision. He repeated his doubts about axioms by comparing some of Hilbert’s second group, on connection, with a group of his own for congruence in arithmetic (pp. 267–268); but since his first axiom could be false, the point was poorly made.
Among other parleys, Frege rejected Hilbert’s assumption that consistency guaranteed existence, since the latter rested for him on criteria of reference. For example (p. 269), Hilbert’s axiom I 7, that ‘On each straight line there exists at least two points’, was no better than considering
‘Explanation. We think to ourselves of objects, which we name gods.
Axiom 1. Each god is all-powerful.
Axiom 2. There exists at least one god.’
Since Hilbert allowed geometrical axioms to be interpreted in terms of beer-mugs, he might not have objected to this satire. He did not reply to the paper, but Korselt responded with his first printed comments on Frege. Among other matters, he treated ironically Frege’s own account of reference (Korselt 1903a, 402):
Should one not finally be able to agree over the ‘meaning’ of an expression, then this is only an indication [‘Zeichen’] that one or more [disagreeing persons] must make more sentences about this sign [‘Zeichen’] or with this sign. ‘The sign has no meaning’ will thus name: ‘No sentences are known to us, which rule the use of these signs in general or in a given domain’.
Rather pointedly, he recommended that mathematicians read Bolzano’s Wissenschaftslehre in order to avoid falling into contradiction (p. 405). In the Jahrbuch Dehn 1905b wrote a brief review of this exchange, judging that Korselt’s reply showed in an ‘enlightening way, the objections [of Frege] as untenable’.
Frege replied at great length to both Korselt and Hilbert in a three-part paper. Some of his comments (1906a, 282–284) sunk to the level of polemic then being directed at Thomae (§4.5.9). Otherwise, he ran again through his preference for definitions. He also launched a long attack on axiomatics based on proposing in nonsense language that ‘Each Anej bazes [‘bazet’] at least two Ellah’, and wondered what it might mean (p. 285). Covertly it seems to say that Frege at Jena is at least equal to Cantor and Gutzmer at Halle; in any case it reduces the issue to the choice of words, not to definitions versus axioms.
More importantly, perhaps confronted by the novelty of several geometries rather than the one and only arithmetic, Frege seems to have confused sense and reference himself several times. In particular, he corroborated Korselt’s irony, for he construed it as denying that the parallel axiom ‘might have the same or similar wording in all geometries, as if nothing were to depend on the sense’ (‘Sinn’: p. 293), whereas surely reference is involved.
Frege’s performance is variable in quality; in any case, by 1906 his authority in this area had been compromised by the failure of his law (456.1) of comprehension. This time Dehn 1909a was even briefer in the Jahrbuch, merely recording Frege’s main points without comment. Korselt’s reply 1908a was oblique, in that he presented his own view of logic, based as usual on Bolzano (for example, the important account of logical consequence in Bolzano 1837a, art. 155). A proposition-in-itself, Korselt’s ‘proposition’, corresponded to Frege’s ‘thought’; it contained ‘presentations’ (‘Vorstellungen’) as parts, either with classes or individuals. Also needed were relations of various types and numbers of places, rather like some of Cantor’s order-types (not cited); he used them in a partly symbolic listing of the axioms of geometry from Hilbert’s second edition.
Hilbert was perhaps too enchanted with representing geometrical axioms by beer-mugs to think through the consequences for concepts and for logic, and did not sufficiently stress the place of intuitive theory prior to its axiomatisation; but Frege was equally blind to model theory, in any form (Hintikka 1988a). In a manuscript of the time (Manuscripts, 183. although mercifully not in print, he even declared that
Nobody can serve two masters. One cannot serve truth and untruth. If Euclidean geometry is true, then non-Euclidean geometry is false, and if non-Euclidean geometry is true, then Euclidean geometry is false.
A main issue behind the non-discussion with Hilbert, and also Korselt’s contribution, was Frege’s adherence to the correspondence theory of truth, in contrast to Hilbert’s preference for consistency of axiom systems. Another theme was definitional equivalence between systems, a topic crossing the boundaries of mathematics, logic and philosophy which was only being born at this time (Corcoran 1980a), precisely because of Hilbert’s work on axiomatics and the American launch of model theory. Meanwhile Hilbert was forging links between logic and proof theory.
4.7.5 Hilbert’s logic and proof theory, 1904–1905. (Peckhaus 1990a, chs. 2–3, 5. Hilbert chose to talk about ‘the foundations of arithmetic’ at the next International Congress of Mathematicians, which took place at Heidelberg in August 1904. After surveying various positions of the topic, including those of Kronecker, Frege and Dedekind, he outlined his own approach, ‘unfortunately too short, because of the limited time accorded to each communication’ (Fehr 1904a, 386). Cantor and Jules König took part in the discussion; the broader context will be explained in §7.2.2.
The published version, Hilbert 1905a, carried the interestingly different title ‘On the foundations of logic und arithmetic’, although the basic content may have been the same. He began his own treatment by positing the existence of two ‘thought-objects’, ‘1 (one)’ and ‘= (equals)’ and forming combinations of them by concatenation: for example,
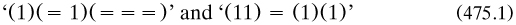
(the brackets seem to be primitive also). The formulae which we call ‘well-formed’ belonged to the ‘class of beings [‘Seienden’], with its associated ‘correct proposition’ (‘richtige Aussage’) a; the rest went to the complementary ‘class of non-beings’, with  . The other logical connectives were ‘u.’ for conjunction, ‘o.’ for disjunction, ‘|’ for implication, and the rather clumsy symbols ‘A(x(o))’ and ‘A(x(u))’ for first-order existential and universal quantification over proposition A containing the ‘arbitrary’ x. The axioms were
. The other logical connectives were ‘u.’ for conjunction, ‘o.’ for disjunction, ‘|’ for implication, and the rather clumsy symbols ‘A(x(o))’ and ‘A(x(u))’ for first-order existential and universal quantification over proposition A containing the ‘arbitrary’ x. The axioms were
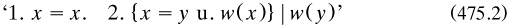
for some (unexplained) propositional function w.
To this machinery Hilbert added ‘three further thought-objects u (infinite set, infinity), f (successor), f′ (accompanying operation)’, and developed arithmetic based upon the axioms of Dedekind and Peano (not cited):
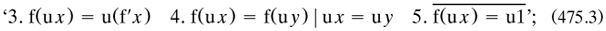
he did not make clear the need for quantifiers, and introduced rules of inference only later. But he argued for consistency of the system in a novel way: propositions provable from them have the same number of thought-objects on either side of the equality sign, whereas candidate contradictories do not.
The paper is very suggestive though not too clear; arithmetic and logic are somewhat intertwined, with logic primarily used to make proofs more explicit, not for a deeper purpose such as Frege intended. Hilbert reads somewhat like the formalists whom Frege attacked, although the use of ‘thought-object’ showed that he was working with the referents of his symbols. This aspect came out more clearly in a superb lecture course m1905a on the ‘Logical principles of mathematical thought’ given at Göttingen in the summer semester of 1905.40 For he began by contrasting three ways of presenting arithmetic. In the ‘geometrical’ way appeal was made to diagrams (fols. 3–9). The ‘genetic’ way was somewhat more formal, in which rational numbers were treated as ordered pairs and irrational numbers treated from their decimal expansions; he cited as examples the textbooks Pasch 1882a (§6.4.7) and Frege’s favourite (§4.5.8) Thomae 1898a. Finally came the ‘axiomatic’ way, his preference; the first two chapters of the first part contained axioms for arithmetic and geometry. On the whole he followed respectively his paper and the second edition of his book, but the treatment of consistency and independence was rather more elaborate. A long third chapter gave axioms for ‘science’: specifically, mechanics, probability theory and physics.
More original was the second part (fols. 122–188), on ‘the logical principles’. In the first chapter Hilbert ran though many aspects of set theory, especially (non)denumerability and power-sets; interestingly, he did not attempt an axiomatisation. Then followed the ‘logical calculus’, whose symbols for connectives were ‘≡’ for identity, ‘|’ again for implication, and in a reverse from normal, ‘+’ for conjunction and ‘·’ for disjunction; they linked ‘beings’ (‘Seienden’), not necessarily propositions, therefore. An axiom system was given for them and for the special beings ‘0’ and ‘1’ (fols. 143–152); the consequences included two ‘normal forms’ for logical expansions (fols. 160–163). In this and other details he seems to have drawn upon Schröder, who was not named.
The existence of these beings was guaranteed by a remarkable ‘axiom of thought’ or ‘of the existence of an intelligence’, no less: ‘I have the capacity to think of things, and to indicate them by simple signs (a, b,…, x, y,…) in such a perfectly characteristic way, that I can always recognise them unequivocally’ (fol. 143).41 Again Hilbert cited no sources, but he was aware of the Fries circle of neo-Kantian philosophers mentioned in §4.2.5; indeed, he held in high esteem its young member Leonard Nelson (1882–1927), who sought the a priori by analysing a theory into its components, a procedure quite congenial with axiomatics. One recalls also the power of the mind as advocated by Dedekind (§3.4.3), whom Hilbert mentioned as a pioneer logical arithmetician. Frege was also cited, for the ‘very interesting resource of a concept-script’ (fol. 138); but he was no source for an axiom of this kind.
Hilbert ended his course with his own philosophical considerations. After acknowledging Cantor and Dedekind and referring to ‘Weierstrassian rigour’ in proofs, he urged that ‘the proof, that there can be no “Ignorabimus” in mathematics, must remain the ultimate aim’ (fol. 168), echoing an optimism put forward in his Paris lecture 1900c (§4.2.6). His fervour was stimulated by awareness of paradoxes in set theory which he had mentioned earlier in his course. One of them arose from the class of all power-classes, which we recognise as a version of the paradox of the greatest cardinal (fol. 136). We shall see in §6.6.1 that it was to lead Russell in 1901 to discover his own paradox, that the class of all classes not belonging to themselves belongs to itself if and only if it does not. Remarkable, then, is Hilbert’s other main example—this paradox itself, apparently already known to his younger colleague Zermelo (fol. 137). How had he come to set theory?
4.7.6 Zermelo’s logic and set theory, 1904–1909. (Peckhaus 1990a, ch. 4) Like Husserl, Ernst Zermelo (1871–1953) began his mathematical career with a Dissertation on the Weierstrassian calculus of variations, at Berlin in 1894. He became Privatdozent at Göttingen in 1899, staying until accepting a chair at Zürich in 1910. Leaving in 1916,42 he lived privately until becoming in 1926 Honorarprofessor at Freiburg am Breisgau, where Husserl was soon to be a colleague.
Soon after arriving in Göttingen, Zermelo’s main interest switched from applied mathematics to set theory, and remained so for the rest of his career; Hilbert was probably the main influence.43 The discovery of the paradox seems to have been one of his earliest findings, but largely unknown because for some reason he did not publish it, and only mentioned it in print once (1908a, 116–117). Hilbert made no special fuss either; when Frege told him in 1903 of Russell’s discovery, he merely replied that Zermelo had priority of three or four years by then (Frege Letters, 80). Although Hilbert’s lecture course had always been available in Göttingen, specific knowledge of Zermelo’s priority came to light only in the 1970s, in connection with Husserl. While preparing a volume of Husserl’s Works, the editors found at the page of his own copy of the review 1891b of Schröder discussing the paradox (444.6) of 0 and 1 a note recording a communication of April 1902 from Zermelo (maybe a letter now lost., laying out the paradox in the form ‘the set of all sets which do not contain themselves as elements [...] does not contain itself as element’.44 Husserl did not add that the paradox is (presumably) constructible within his own theory of manifolds, of which Mengenlehre was a case (§4.6.4), and he seems never to have pursued the matter.
Zermelo did publish on Mengenlehre at this time, especially in Mathematische Annalen. One paper introduced the axiom of choice in 1904; discussion is postponed until §7.2.6 when we note Russell’s independent detection at around the same time. Another was the full-scale axiomatisation of set theory in 1908b. Primarily intended to block out the paradoxes, his axioms included extensionality, the basic construction of sets, power-set, union, infinity and choice. Several of them captured the concerns of Cantor and Dedekind, especially their exchange of 1899, although Zermelo seems not to have been privy to it (G. H. Moore 1978a); maybe Hilbert had told him about the letters that he had received from Cantor at that time, which give some hints (§3.5.3). Like Cantor, he followed an approach which Russell had recently called (§7.4.4) ‘limitation of size’ (Hallett 1984a, ch.7). He did not attempt to define the notion of set; maybe he followed Hilbert’s penchant for intuition of some kind.
Zermelo also left the logic implicit; and this decision disfigured his system, in that another axiom, of separation, declared that a set could be formed of the objects satisfying any propositional function which was ‘definite’ for some overall set. Russell noticed this defect at once (see his letter of 8 March 1908 to Jourdain in my 1977b, 109); Weyl 1910a had to make clear that this vague adjective meant that the function was constructed by only a finite number of logical connectives and quantifiers and set-theoretic operations. Zermelo’s paper contained a rather odd recipe of Peano’s symbols mixed with Fregean notions such as assertion and the use of truth-values, with a side-salad of Schröder for first-order quantification (Peckhaus 1994b). These features are rather surprising, because he was paid to teach a logic course in 1906 and 1907 (though poor health delayed him until the summers of 1908 and 1909), and in 1907 he had been appointed Honorarprofessor for mathematical logic. This was the first such post in Germany (Peckhaus 1992a); Frege’s title a decade earlier (§4.5.1) had been in mathematics.
In his paper Zermelo proved various basic theorems; his proof of Schröder-Bernstein was cited in §4.2.5. At the same time he wrote another paper, which appeared as 1909a in Acta mathematica, on the related theme of the role of mathematical induction in handling finite sets. He used Dedekind’s notion of the chain (§3.4.2), but he defined infinitude inductively instead of reflexively, and so was able to avoid using an axiom of infinity.
This concern to show that an axiom may not be needed in a given situation is typical of Hilbertian proof theory, as we have seen above. The influence of Hilbert on Zermelo extended not only to consider set theory but also to treat it axiomatically; and the latter aspect makes them both thoroughly modern mathematicians (Mehrtens 1990a, ch. 2). Zermelo’s approach contrasts starkly with that of Schönflies, whom we saw practise Mengenlehre in Cantor’s non-axiomatic way early on in this chapter on parallel processes, in which set theory has been the main linking thread.
 was placed contiguously to the left (arts. 1–4). Truth-values played no role: an affirmed ‘judgement’ (‘Urtheil’) meant that the content ‘occurred’, referring to a ‘fact’. The notion bears some similarity to our highlighting of meta-theory as against object theory, but Frege himself was not thinking in such a framework; his signs expressing the content act more like tokens than like names.
was placed contiguously to the left (arts. 1–4). Truth-values played no role: an affirmed ‘judgement’ (‘Urtheil’) meant that the content ‘occurred’, referring to a ‘fact’. The notion bears some similarity to our highlighting of meta-theory as against object theory, but Frege himself was not thinking in such a framework; his signs expressing the content act more like tokens than like names. . where the vertical line was ‘the conditional stroke’; but Frege’s account of the various pertinent combinations of affirming or denying A or B was rather ponderous (art. 5). Negation of A was marked by a small vertical line placed such that in ‘A’ it divided the application of the content sign into A to its right and not-A to its left (art. 7). These were the two primitive logical connectives, chosen ‘because deduction seems to me to be expressed more simply that way’ than with other selections (art. 7). Among various rules of inference available he chose for convenience modus ponens (not so named), symbolised by a thick horizontal line between premises and consequent (art. 6). ‘Identity of content’ was presented as the property that two symbols ‘A’ and ‘B’, not their referents, had the same content ‘(A ≡ B)’ (art. 8); this view was not to endure.
. where the vertical line was ‘the conditional stroke’; but Frege’s account of the various pertinent combinations of affirming or denying A or B was rather ponderous (art. 5). Negation of A was marked by a small vertical line placed such that in ‘A’ it divided the application of the content sign into A to its right and not-A to its left (art. 7). These were the two primitive logical connectives, chosen ‘because deduction seems to me to be expressed more simply that way’ than with other selections (art. 7). Among various rules of inference available he chose for convenience modus ponens (not so named), symbolised by a thick horizontal line between premises and consequent (art. 6). ‘Identity of content’ was presented as the property that two symbols ‘A’ and ‘B’, not their referents, had the same content ‘(A ≡ B)’ (art. 8); this view was not to endure. ’ was called ‘generality’ (‘Allgemeinheit’) and symbolised
’ was called ‘generality’ (‘Allgemeinheit’) and symbolised 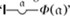 (art. 11): he stressed the independence of this calculus from the propositional by introducing German letters such as ‘
(art. 11): he stressed the independence of this calculus from the propositional by introducing German letters such as ‘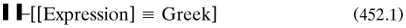
 has the property F, whatever
has the property F, whatever  ’):
’): This paper and the book, together with the Begriffsschrift, inspired a substantial and rather negative reaction from Benno Kerry. We met him in
This paper and the book, together with the Begriffsschrift, inspired a substantial and rather negative reaction from Benno Kerry. We met him in 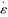 F(ε)’ (pp. 129–131). In the important special case of the concept, a function which took only truth-values for its values, its value-range was named ‘extension of the concept’ (p. 133). He introduced this notion casually, and did not mention his earlier use of the phrase (
F(ε)’ (pp. 129–131). In the important special case of the concept, a function which took only truth-values for its values, its value-range was named ‘extension of the concept’ (p. 133). He introduced this notion casually, and did not mention his earlier use of the phrase (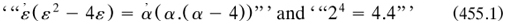

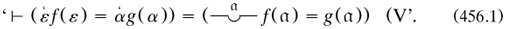
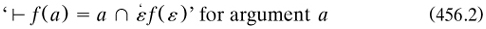
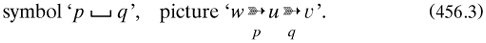
 (using ‘T”ε = ε’ to refer to the True), then
(using ‘T”ε = ε’ to refer to the True), then  (via ‘ε =
(via ‘ε =  0 (art. 122, Cantor not mentioned). He also treated ‘finite’ (‘endlich’) sequences which did stop (arts. 108–121). In art. 144 he at last formally defined an ordered pair:
0 (art. 122, Cantor not mentioned). He also treated ‘finite’ (‘endlich’) sequences which did stop (arts. 108–121). In art. 144 he at last formally defined an ordered pair: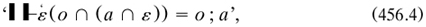
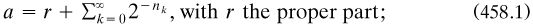
 . The negative of any number was defined from the converse of its Relationship, and ‘0’ by compounding any Relationship with its converse since (458.1) was not available (art. 162).
. The negative of any number was defined from the converse of its Relationship, and ‘0’ by compounding any Relationship with its converse since (458.1) was not available (art. 162).
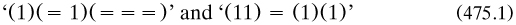
 . The other logical connectives were ‘u.’ for conjunction, ‘o.’ for disjunction, ‘|’ for implication, and the rather clumsy symbols ‘A(x(o))’ and ‘A(x(u))’ for first-order existential and universal quantification over proposition A containing the ‘arbitrary’ x. The axioms were
. The other logical connectives were ‘u.’ for conjunction, ‘o.’ for disjunction, ‘|’ for implication, and the rather clumsy symbols ‘A(x(o))’ and ‘A(x(u))’ for first-order existential and universal quantification over proposition A containing the ‘arbitrary’ x. The axioms were