’. When volume and page numbers are needed, they come from the second printing of the 1920s (§8.4.4).
I hoped sooner or later to arrive at a perfected mathematics which should leave no room for doubts, and bit by bit to extend the sphere of certainty from mathematics to other sciences.
Russell 1959a, 36
6.1.1 Plans for two chapters. This chapter and its successor treat Russell’s career in logic from 1897 to 1913. The point of division lies in 1903, when he published the book The principles of mathematics, where he expounded in detail the first version of his logicist thesis. This chapter traces the origins of that enterprise in his student ambitions at Cambridge University from 1890 to 1894 followed by six years of research under a Prize Fellowship at Trinity College and then a lectureship there; The principles was the principal product.
In addition to the birth of logicism, we shall record the growing positive role of Cantor’s Mengenlehre, the influence on Russell of Whitehead from 1898, and especially their discovery of the Peano school two years later. But we also find his paradox of set theory (1901), which compromised the logic of the new foundations. Convinced of the seriousness of the result, he then collected all paradoxes that he could find (§7.2.1–2), in the hopes of diagnosing the underlying common illness. The next chapter covers the years of collaboration with Whitehead which was to lead to the revised version of logicism presented in the three volumes of Principia mathematica (1910–1913) (hereafter, ‘PM’).
The use of some technical terms needs to be explained. Throughout the period Russell and Whitehead referred to ‘class(es)’, both in their early phase when they were using the part-whole theory and also when referring to Cantorian sets after converting to Cantor and the Peanists: ‘set’ was then a neutral word, referring to a collection, such as ‘sets of entities’ in The principles (1903a, 114–115). I have followed the same practise, which of course is converse to modern parlance: however, I use ‘set theory’ to refer to the theory in general, reserving ‘Mengenlehre’ for cases where Cantor’s own conception is involved. Technical distinctions between classes and sets date only from later developments of axiomatic set theory.
While I quote Russell and Whitehead writing of ‘contradictions’, I have preferred to use the word ‘paradoxes’. Both words have a variety of different meanings (Quine 1962a), and it was sloppy of Russell not to make any distinction between results such as his own paradox of set theory and correct but surprising theorems or constructions that turn up in mathematics. I shall also write about ‘the propositional and predicate calculi’ and of ‘quantification’, where he spoke Peanese about ‘free’ and ‘apparent variables’. Finally, I am using ‘logicism’ to describe his philosophical position, though this now common word was introduced with this sense only in the late 1920s (§8.7.6, §8.9.2).
Finally, Russell used ‘analysis’ in two different ways which he did not clearly distinguish and which therefore have misled many commentators. In its narrow sense it means breaking down a theory or body of knowledge into its basic units; its more general sense includes this one together with the companion synthetic process of construction of complexes from these units (Hager 1994a, ch. 4). ‘The business of philosophy, as I see it’, he wrote later but seems to have thought from early on, ‘is essentially that of logical analysis, followed by logical synthesis’ (1924a, 176). Cauchy’s ‘mathematical analysis’ has this general sense in its unfortunate name (§2.7.2), and Russell seems to have been following this tradition.
6.1.2 Principal sources. In addition to the original texts and historical surveys, some general sources are available. Of Russell’s own reminiscences, his My philosophical development (1959a) and the first volume of his autobiography (1967a) are the most significant; but they are not reliable. He had a strong memory, and so relied on it more than was warranted (as often happens with people so gifted). Sometimes the errors are just of dating (not trivial in history, of course), but others are more serious. For example, a main theme of this chapter is that he massively over-simplified the story of writing The principles. Again, he claimed that one day he dictated to a secretary ‘in a completely orderly sequence’ the ideas which became the book Our knowledge of the external world (1967a, 210), and the tale has been much cited as evidence of the human capacity for mental preparation; however, letters of the time show that he struggled hard with the manuscript for months (§8.3.2).
In addition, the collections of letters that were added to the chapters of Russell’s autobiography were not always well chosen or explained. For example, it includes a long string of letters to one Lucy Donnelly, who was never mentioned in the text (pp. 163–184); she was an American friend of a cousin of Russell’s first wife Alys and later a patron of his last wife Edith, and met him when he lectured at her college, Bryn Mawr, in 1896 (§6.2.1).1 Other victims of silence include G. H. Hardy, with whom Russell actually enjoyed a long and varied friendship (my 1992a).
Russell published his life story in the 1960s to gain funds for the various world-significant enterprises that were then operating under his name. For the same reason he sold his Nachlass to McMaster University in Hamilton in Ontario, Canada where it forms the basis of the splendid Russell Archives (hereafter, ‘RA’). After his death in 1970 the rest of his unpublished materials went there, and when Edith died eight years later his library of books, offprints and journals was transferred also. When his second wife Dora died in 1986, some more of his manuscripts were found and transferred to the Archives; they are cited as ‘(RA, Dora Russell Papers)’.
Manuscripts until 1903 cause tricky problems of dating; for up to and including The principles of that year Russell often transferred folios of a rejected draft to its successors, so that several of them, including that book, are chronologically mixed. In addition, he used the new public facility of typing bureaux from time to time,2 so that some items exist in both holograph and typed forms, often differently incomplete. Many of these manuscripts are now appearing alongside his published papers, essays and book reviews in an edition of his Collected papers edited by a team based at McMaster. Cited as ‘Russell Papers’, it is planned in 30 volumes: his logic and philosophy will occupy volumes 2–11, following the initial volume published in 1983, which covered his years at Cambridge to 1899. The mass of manuscripts on and around logic are surveyed in my 1985b.
The edition excludes Russell’s books, and most of his notes on others’ writings on logic and mathematics, which survive in two large notebooks and several files of loose sheets. It also deliberately omits the masses of unpublished correspondence, though letters are used in the editorial matter. Further, the first volume of a selection of his letters has appeared (Russell Letters 1). His most important correspondents during his years as a logician were Couturat (Schmid 1983a), Frege, Hardy, Whitehead; and Philip Jourdain, who took a lecture course with him in 1901–1902 at Cambridge (§6.8.2) and later wrote to him at length on logic, Mengenlehre and their histories (my 1977b).
PM is normally cited by theorem number, as ‘(PM, *41·351)’, with the modern six-pointed star; following Peano, the original text used the eight-pointed ‘’. When volume and page numbers are needed, they come from the second printing of the 1920s (§8.4.4).
Russell’s massive bibliography is magisterially catalogued in Blackwell and Ruja 1994a. Any item, published or manuscript, will be cited by article or formula number if possible, but page numbers in the edition will be used when necessary, and also references to other material there. Russell published several papers on logic in French; they appear in the edition also, but I cite, and normally quote, the English translations that are provided. Finally, manuscripts are usually cited by page number in the edition; several are cited as, say, ‘m1904c’, in which case I recall that no published work is named ‘1904c’.
Finally, since 1971 the Archives has published a journal entitled ‘Russell’, which is the single principal source of information of Russell studies in general. This activity has grown enormously especially from the 1980s, with his philosophy prominently featured and logic appearing from time to time (my 1990b surveys work in these areas). But the mathematical background and indeed foreground of logic is often not well treated: the commentary on Russell’s philosophy usually lacks serious attention to Peano, Cantor, or the last 1,600 of the 1,800 pages of PM.
In these two chapters we see one of the two lives that Russell lived at that time, that of a philosopher-scholar working quietly and often on his own in the country; from 1905 to 1911 he lived at Bagley Wood near Oxford (Plate 3), in a house then the only one in the area, designed for him by a college friend (my 1974a). For the rest of his time he was The Honourable Bertrand Russell, in London and other Important Places, knowing everybody and throwing himself into major social issues of the time such as Free Trade in the mid 1900s (Papers 12, 181–235). As a young member of the British aristocracy, he felt deeply the responsibility of his class at that time; Inheriting The Earth and so obligated to tend it carefully. Indeed, in this respect the philosopher Russell was of the same cast; this late Victorian (as he thought of himself) set up a logicist empire of mathematics and philosophy, and devoted much energy to its meticulous construction, especially after discovering its infection by paradoxes. Let us consider now the origins.
6.1.3 Russell as a Cambridge undergraduate, 1891–1894. (Griffin and Lewis 1990a) Russell’s parents died when he was an infant, and he passed a lonely childhood educated by tutors. His interest in mathematics developed quite quickly, especially for Euclidean geometry. By his teens he was proving things himself, for in 1890 he sent in to the Educational times a solution of a non-trivial problem set there about a property of a parabola touching all sides of a triangle (my 1991a).
PLATE 3. Russell outside his house at Bagley Wood with his friend Goldsworthy Lowes Dickinson, maybe in 1905 (RA). The picture appeared in my 1977b, at which time the other figure had not been identified. It features also as the frontispiece of Russell Papers 4 (1994), with identification.
Going up to Trinity College Cambridge as a minor scholar in mathematics in October 1890, Russell took the Part 1 Mathematics Tripos after three academic years. Immediately he sold his mathematical books—an action which suggests little enthusiasm for the experience. In his reminiscences he gave very few details; by contrast, his predecessor by one year, Grace Chisholm (1868–1944) at Girton College, was eloquent on the matter: ‘At Cambridge the pursuit of pure learning was impossible. There was no mathematician—or more properly no mathematical thinker—in the place’ (my 1972a, 131). But this does not conform with the situation in applied mathematics, with figures of the calibre of J. J. Thomson, J. J. Larmor and Lord Rayleigh in and around town; indeed, the enrolment of Trinity in the year after Russell’s included E. T. Whittaker, who soon became one of their distinguished successors. In addition, her judgement was harsh on Whitehead, although he had published very little by that time (his early thirties); Russell liked him as a teacher.
The disillusion seems to be more justified in pure mathematics, and at the undergraduate level, where, in Chisholm’s view, Arthur Cayley ‘sat, like a figure of Buddha on its pedestal, dead-weight on the mathematical school of Cambridge’ (p. 115). Russell himself recalled that he never heard of Weierstrass while a student (1926a, 242); yet Cambridge gave Weierstrass an honorary doctorate in 1893. The initiative may have been taken by E. W. Hobson and A. R. Forsyth, the analysts at the University at the time; both knew Weierstrass’s work, especially Forsyth 1893a on complex analysis.3
The main defect with the Part 1 Tripos seems to have been the system of crammer-training; it reduced education to rehearsing techniques for answering Tripos questions, and replaced academic nourishment by aspiration for a high place on the list of Wranglers (the curious name for the mathematics graduates). ‘Everything pointed to examinations, everything was judged by examination standards, progress stopped at the Tripos’, recalled Chisholm, ‘There was no interchange of ideas, there was no encouragement, there was no generosity’ (p. 115). She left Cambridge to discover real mathematics at Göttingen where she wrote a Dissertation under the direction of Felix Klein in 1895, and after returning to England married one of the coaches, W. H. Young (1863–1942) (§4.2.4). Russell also travelled away, but in the mind.
6.1.4 Cambridge philosophy in the 1890s. (Griffin 1991a, chs. 2–3) After passing the Part 1 Mathematical Tripos as joint 7th Wrangler, Russell turned to philosophy for Part 2. After some resistance, around the time of the examination he fell in with the dominating doctrines of Kantian and especially neo-Hegelian philosophy. The most prominent representative at Cambridge was J. M. E. McTaggart (1866–1925), but the leading British figure was F. H. Bradley (1846–1924) at Oxford. Since Russell practised this philosophy with some enthusiasm for the rest of the decade and held Bradley in high regard, some main features need to be noted, with Bradley’s The principles of logic as the main source (1883a, cited from the second edition of 1922, which is almost unaltered and much more accessible; the ‘Additional notes’ to many chapters and new material at the end are not used).
Both kinds of philosophy stressed the importance of mental constructions and the objects thereby produced; in the neo-Hegelian form, they were the only items for analysis, with facts treated on a par with propositions. Bradley emphasised judgement of the existence, content and meaning of ideas. Logic was an important handmaiden, for it distinguished categorical from hypothetical propositions and supplied basic notions like negation and principles such as identity, contradiction, excluded middle and double negation (Book 1, ch. 5). But his attention to matters symbolical was restricted to a short chapter on Jevons’s system (§2.6.2), where he lamented its limitation to syllogistic logic and also showed himself not only resolutely but also triumphantly unmathematical (pp. 386–387).
Proof by contradiction was used frequently to produce sceptical conclusions from the given premises. In particular, taking a ‘thesis’ and its conflicting ‘antithesis’, a resolution was effected in the form of a ‘synthesis’ in some higher level of theorising (Book 3, pt. 2, chs. 4–6). In Appearance and reality, which appeared just before young Russell joined the faith, the ultimate goal was ‘the Absolute’, the realm of everything including itself (Bradley 1893a, esp. chs. 14 and 26).
Bradley concluded that a relation was internal to the objects related (quite opposite to Peirce, whose work he did not seem to know): ‘Relations, such as those of space and time, presuppose a common character in the things that they conjoin’ (1883a, 253). Continuity and the continuum of space and time were fruitful source of contradictions, such as the same body in different places (p. 293). Among arithmetical examples, one and one only made two if they were manipulated in some way; otherwise they remained as one and one (p. 401). These kinds of cases were to attract Russell strongly, as we shall soon see.
[...] I don’t know how other people philosophize, but what happens with me is, first, a logical instinct that the truth must lie in a certain region, and then an attempt to find its exact whereabouts in that region. I trust the instinct absolutely, tho’ it is blind and dumb; but I know no words vague enough to express it. If I do not hit the exact point in the region, contradictions and difficulties still beset me; but tho’ I know I must be more or less wrong, I don’t think I am in the wrong region. The only thing I should ever, in my inmost thoughts, claim for any view of mine, would be that it is in a direction along which one can reach truth—never that it is truth.
Russell to Bradley, 30 January 1914 (RA)
Russell effected a sort of synthesis out of his education, in that he applied this philosophy to study foundational aspects of mathematics over the rest of the decade. He started out with some issues in dynamics (Papers 2, 29–34); they drew him to geometry, upon which he then concentrated. He also gradually took more interest in arithmetic and Mengenlehre. The selected survey in this section follows the order of these main concerns: the choice is partly guided by his later interests, which tended to focus upon arithmetic, Mengenlehre, continuity, infinity and geometries.
6.2.1 Russell’s idealist axiomatic geometries. (Griffin 1991a, ch. 4) In 1895 Russell won a Fellowship at Trinity with a study of geometry; this success led him to a career as a philosopher rather than as an economist or politician (1948a). His dissertation was examined by Whitehead and the philosopher James Ward: the manuscript has disappeared, but a chapter appeared in Mind as 1896a; by oversight he left the word ‘chapter’ on p. 23 (regrettably changed to ‘paper’ in Papers 2, 285). Later that year he lectured on the topic in the U.S.A., at Bryn Mawr College and Johns Hopkins University, and after his return he published with Cambridge University Press a revised version of the dissertation as An essay on the foundations of geometry (1897c). Appearing in June in a run of 750 copies, it contained a few diagrams in its 200 pages; dedicated to McTaggart, effusive thanks were offered to Whitehead in the preface. He also wrote some other papers and manuscripts, now all gathered together in Papers 2. From the first essay up to 1899 Russell’s position was basically unchanged; I shall usually quote from the book, and concentrate on his attention to axioms.
After a 50-page ‘Short history of metageometry’, using the word to cover all non-Euclidean geometries (§3.6.2), various philosophies of geometry were analysed. Two of them were found especially wanting. Firstly, Riemann’s theory of manifolds (§2.7.3) was criticised for failing to stipulate the space in which they were to be found (Russell 1897c, 64–65); to readers of Riemann who understood him better, his ability to formulate all properties of the manifold without recourse to any embedding space (‘intrinsically’, we now say) is precisely one of his virtues. Secondly, the recently deceased Hermann von Helmholtz, who for Russell ‘was more of a philosopher than a mathematician’ (p. xii), had moved too much the other way in advocating a totally empiricist philosophy of geometry, especially the claim that it could be deduced from mechanics (Helmholtz 1878a (§3.6.2) was one of Russell’s main sources). He concluded a long discussion thus with this typically Victorian flourish of capital letters (p. 81):
But to make Geometry await the perfection of Physics, is to make Physics, which depends throughout on Geometry, forever impossible. As well might we leave the formation of numbers until we had counted the houses in Piccadilly.
His views on these German predecessors were held still more strongly by the German neo-Kantian philosopher Paul Natorp (§8.7.1) in a commentary on his book (Natorp 1901a, art 3).
Russell’s own position was guided by the neo-Hegelian philosophy that he had imbued. Instead of distinguishing between Euclidean and non-Euclidean geometries, he divided geometry into its ‘projective’ and ‘metrical’ branches by the criterion that the former involved only order but the latter also ‘introduces the new idea of motion’ (1897c, xvii) in order to effect measurement. These geometries were human constructions given space and time as an ‘externality’, and in this sense they were applied mathematics; however, synthetic a priori knowledge was present, and the main aim was to locate its place and role—central for projective geometry but only in parts of the metrical branch.
Russell did not present his position very clearly. For example, he found three a priori axioms for projective geometry, but presented them twice in somewhat imprecise and different ways, even in different orders (pp. 52, 132). The second account assumed that
P1) The ‘parts of space’ are distinguished only by lying ‘outside one another’, although they are all ‘qualitatively similar’;
P2) ‘Space is continuous and infinitely divisible’, finally arriving at a point, ‘the zero of extension’;
P3) ‘Any two points determine a unique figure, called a straight line’, three points a plane, four a solid, and so on finitely many times.
For the ‘very different’ (p. 146) metrical geometry Russell also proposed three a priori axioms, which he correlated with the ‘equivalents’ in the projective trio (p. 52). Nevertheless his order was different again; I shall mimic the one above:
M1) ‘The Axiom of Dimensions’, that ‘Space must have a finite integral number of Dimensions’ (p. 161);
M2) ‘The Axiom of Free Mobility’, that ‘Spatial magnitudes can be moved from place to place without distortion’ (p. 150), thus permitting the possible congruence between two figures to be examined;
M3) ‘The Axiom of Distance’, that ‘two points must determine a unique spatial quantity, distance’ (p. 164), which was zero only when the two points coincided.
6.2.2 The importance of axioms and relations. In his book Russell tried to grant axioms M1)–M3) a priori status also. Concerning M1), the fact that we live in a world of three dimensions was ‘wholly the work of experience’ although ‘not liable to the inaccuracy and uncertainty which usually belong to empirical knowledge’ (pp. 162, 163). Together with Euclid’s parallel postulate and straight line axiom (that two straight lines cannot enclose a space), they were ‘empirical laws, obtained’ by investigating ‘experienced space’ (pp. 175–176). M2) and M3) were a priori in the double sense of being ‘presupposed in all spatial measurement’ and ‘a necessary property of any form of externality’ (p. 161; see also pp. 173–174).
Most ambitious, however, was Russell’s claim that M1)–M3) were also sufficient for metrical geometry. The reason was that the ‘metageometers’ have constructed other ‘metrical systems, logically as unassailable as Euclid’s […] without the help of any other axioms’ (p. 175). However, he overlooked the possibility that some other geometry might be constructed in which other axioms were needed: this was exactly the option allowed for by Riemann’s approach, under which all geometries, Euclidean or non-Euclidean, were placed on the same epistemological level.
In his final chapter Russell considered the consequences of his position with regard to Kantian and Bradlean understanding of space and time. While the treatment is uncertain, with philosophical vicious circles spinning, it is striking that he relied upon axioms: we have seen already that mathematical theories were very often not axiomatised, Peano and Hilbert standing out among the exceptions of the time (and giving a very different treatment of geometries from Russell’s: §5.2.4, §4.7.2). As part of his childhood interest in mathematics Russell had been profoundly puzzled when learning that in his Elements Euclid was forced to assume something to prove his theorems with such impressive rigour (1967a, 36). He must also have been drawn to axioms by his exposure from schooldays to that work, which was given great emphasis in English education; indeed, national controversies had raged over its manner of teaching in the Association for the Improvement of Geometrical Teaching (from 1897, the Mathematical Association: Price 1994a.) Although he saw the limitations of Euclid’s rigour (as he related in an essay 1902b in the Association’s Mathematical gazette), the place of axioms remained important with him, and grew during his logicist phase. Certainly he did not learn it from neo-Hegelian philosophy where, as Bradley put it in the opening sentence of his Logic, ‘It is impossible, before we have studied Logic, to know at what point our study should begin. And, after we have studied it, our uncertainty may remain’.
Among the axioms, M2) had two philosophical consequences. Russell also formulated it as ‘Shapes do not in any way depend upon absolute position in space’ (1897c, 150), which not only imposed the opinion that space was relative but also focused his attention upon relations in general. ‘All elements—points, lines, planes—have to be regarded as relations between other elements’, he is reported to have told his Bryn Mawr audience in November 1896, in connection with projective geometry, ‘thus space is simply an aggregate of relations’ between points, lines and planes (Papers 1, 342). In the book, ‘Position is not an intrinsic, but a purely relative, property of things in space’, indeed, even externality itself was ‘an essentially relative conception’ (1897c, 160); hence ‘points are wholly constituted by relations, and have no intrinsic nature of their own’ (p. 166). Thus, the relation of distance between two points was unique: by the Axiom of Distance, ‘A straight line, then, is not the shortest distance, but is simply the distance between two points’ (p. 168). In a manuscript ‘Note on order’ he considered in detail relation(ships) between points for projective geometry and even laid out collections of axioms specific to them (m1898c, 345–347).
Russell’s interests in axioms and in relations, which remained strong throughout his mathematical career, took part of their common origin from geometry, especially its projective part. As a neo-Hegelian he saw relations themselves as internal to the objects related, but surely they could not share all the same properties; for example, the property ‘being a factor of’ between integers is not itself a factor. Such difficulties may have led him to reject the position held in a paper in Mind ‘On the relations of number and quantity’, where he treated them as different categories (Michell 1997a); ‘number’ was ‘applied’ to produce ‘measure’, while ‘quantity’, some ‘portion’ of the ‘continuum of matter’, yielded a ‘magnitude’ (1897b, 72–73). Soon afterwards he also dropped his advocacy of the relativism of space (§6.3.1).
6.2.3 A pair of pas de deux with Paris: Couturat and Poincaré on geometries. (Sanzo 1976a) Russell’s book does not seem to have excited the mathematicians; for example, Arthur Schönflies told the Göttinge Mathematische Gesellschaft on 18 June 1897 that ‘the author is a philosopher, the picture thus philosophically presented. For mathematicians it offers no interest’.4 However, it inspired a letter to Russell from Couturat, then entering his thirties, which initiated an extensive correspondence. Couturat also reviewed the book in two papers in the Revue de métaphysique et de morale, as part of his survey of foundational studies in mathematics mentioned in §4.2.3; Russell wrote a reply. This trio seems to have provoked Henri Poincaré (1854–1912) into print, with similar results in the same venue. The list of six papers is
Couturat 1898a (May), Couturat 1898b (July), Russell 1898d (November);
Poincaré 1899a (May), Russell 1899c (November), Poincaré 1900a (January).
Couturat also soon became involved in a French translation of Russell’s book, to which both he and Russell made some revisions and additions; it appeared from Gauthier-Villars as Russell 1901f.5
While remembered as a critic, Couturat was not a very critical one. The main features of his long review 1898a included some Kantian antinomies of space (not discussed above) and the empirical status of Euclid’s axioms; in the follow-up 1898b he treated the concepts of magnitude and quantity, where he wandered off into some group theory. Russell’s rather unimpressive response 1898d concentrated on axioms. He proposed that if a penny were rolled exactly one revolution on a horizontal surface and the length of this line compared with that of the radius, then the closeness of the ratio to π would give information on the ‘space-constant’ of empirical space (p. 326). But he also used his relativism to argue for ‘the à priori character of Euclidean space’ on the grounds that no absolute magnitude existed (pp. 327–328); but this does not easily fit with his empiricism. At the end he even went for a conventionalist view, that Euclid’s axioms ‘constitute the simplest hypothesis for explaining the facts’ (p. 338).
This last argument, quite uncharacteristic of Russell, was the preference of Poincaré. Then 45 years old, he was drawn into action by Russell’s rejection in the reply to Couturat of his own view that axioms were conventions, so that their truth-value need not be considered (p. 325; compare 1897c, 30–38). Finding Couturat’s review to be a ‘very banal eloge’, Poincaré 1899a really was critical, on several issues. He rightly savaged Russell’s sloppy formulation of projective geometry by P1)–P3), pointing out that P1) should have said that a straight line was determined by two points rather than the other way round; that the plane was specified as containing all three lines determined by pairs of three given points; and that a plane and a line always meet, possibly at the point of infinity, an important concept which Russell had not discussed at all (pp. 252–253). Among several other issues, he felt that Russell had exaggerated the similarities between projective and metrical geometries; in particular, the former was not necessary for experience (pp. 263–269), and qualitative aspects of geometry lay largely in topology (which he was then developing in a remarkable way: Bollinger 1972a).
In this and his second piece Poincaré criticised Russell’s talk of externality, and especially of the truth or falsehood of axioms on empirical grounds involving space; for him axioms were only convenient conventions, as was the fact that we live in three dimensions (1900a, 72–73). Further, Russell’s proposed experiments to (dis)prove Euclid’s axioms were actually exercises in mechanics or optics, whatever the geometry (pp. 78, 83–85).
In his reply to Poincaré’s first paper, Russell 1899c bowed suitably low over the failure of his axiomatisation, and gave a strikingly detailed and symbolised formulation of a new system of axioms.6 But he stood firmer against conventionalism. As in his reply to Couturat, he saw essential and indeed welcome aspects of empiricism in metrical Euclidean geometry; he found no difficulty in seeking the truth-value of propositions such as ‘There exist bodies (e.g. the earth) whose volume exceeds one cubic millimetre’ (p. 398), and held out for isolating the notion of distance. But he may not have realised that Poincaré’s conventionalism involved a sharp distinction between physical space and material bodies existing and moving in that space, and thus between a body and the portion of space which it occupies (O’Gorman 1977a). The choice of geometry for space, and properties such as its continuity and congruence between figures, were conventional, and so had no causal effect on bodies. Russell’s statement about the size of the earth concerns a body (including a convention about the unit of measurement), not geometry as such.
The exchange did not seem to leave any major mark on the positions of the opponents. In any case, Russell’s interest in geometries decreased thereafter; his last major essay was an article, apparently written early in 1900 and entitled ‘Geometry, non-Euclidean’ when it appeared as 1902c in the tenth edition of the Encyclopaedia Britannica. The first part was historical, largely following his geometry book with the division into three periods and his three axioms; he provided more details about non-Euclidean metrics. But the short philosophical part was naturally a long way from 1897, especially on the a priori nature of Euclidean geometry; in his final paragraphs on the ‘Philosophical value of non-Euclidean Geometry’ he now concluded that ‘There is thus a complete divorce between Geometry and the study of actual space’ (p. 503). But he also emphasised here the merit of considering ‘different sets of axioms, and the resulting logical analysis of geometrical results’, and this philosophy was to remain durable.
6.2.4 The emergence of Whitehead, 1898. In the exchanges with his Paris confrères Russell admitted to changes of expression and even mind on several aspects since the publication of his book; for example, to Couturat he corrected his remark on Helmholtz quoted in §6.2.1 to ‘the possibility of Geometry cannot depend upon Physics’ (1898b, 327). The exchange with Poincaré had also reinforced some growing doubts about the relativity of space, but he went public on the issue only in 1900, especially at the Paris Congress of Philosophy (§6.3.2).
Russell also kept a set of critical annotations about the Essay in his own copy of it (RA). Against a remark on p. 120 about points specifiable only by means of properties such as the straight line between them, he judged that ‘This is a mistake. Pts., like str. lines, must be supposed to differ qual[itative]ly’. And of a quotation on p. 171 from William James’s The principles of psychology (1890) that ‘relations are facts of the same order with the facts they relate’, such as ‘the sensation of the line that joins the two points together’, he confessed to himself that ‘I have nowhere in my book grasped the meaning of this remark. Wh. gives a truer view than mine; everything spatial is both a relation and an object’.
Russell was alluding to a large volume 1898a of more than 600 pages by Whitehead, entitled A treatise on universal algebra with applications and published by Cambridge University Press. Then in his 38th year, Whitehead had been a Fellow of Trinity College since 1884 thanks to a (lost) dissertation on Clark Maxwell’s theory of electromagnetism; he had taken about seven years to write this his first book. This time it was Whitehead to thank Russell in the preface, for help over non-Euclidean geometry, a topic on which he himself was about to publish a paper (to add to two on hydrodynamics).
The title suggests a marked change of interest from those two papers, but it was ill-chosen, apparently at a very late stage. Whitehead had taken it from a paper by J. J. Sylvester 1884a which only treated matrices, an algebra which he did not treat extensively in his book though he often deployed determinants. His book contained no all-embracing algebra, but instead a collection of newish algebras with applications mainly to geometries and a few aspects of mechanics. The chief inspiration came from the Ausdehnungslehre of Hermann Grassmann, whose work was beginning to gain general attention at last (§4.4.1). The British had taken little interest so far, however, so Whitehead ended with a bibliography of Grassmann’s main writings as one of the historical notes appended to some chapters.
In the preface Whitehead saw symbolic logic both as pure ‘systems of symbolism’ valuable for ‘the light thereby thrown on the general theory of symbolic reasoning’ and in application as ‘engines for the investigation of the possibilities of thought and reasoning connected with the abstract general idea of space’ (p. v). Further, perhaps under the influence of Benjamin Peirce (§4.3.2), he defined mathematics ‘in its widest signification’ as ‘the development of all types of formal, necessary, deductive reasoning’, so that ‘the sole concern of mathematics is the inference of proposition from proposition’ (p. vi). He did not furnish any extended philosophical discussions; but he had obviously not washed in neo-Hegelianism, and Russell’s note to himself above shows the superiority of interpreting points as members of a manifold.
In a short Book 1 on ‘Principles of algebraic symbolism’, Whitehead mentioned both Grassmann’s and Riemann’s theories of manifolds, cited Boole on (un)interpretability (§2.5.3), and emphasised general algebraic operations and their various laws. Then followed a Book on ‘The algebra of symbolic logic’, based upon Boole but using ‘+’ without restriction and acknowledging MacColl (§2.6.4) for the propositional calculus. Like most contemporaries of all nationalities, he seems not to have read Hermann’s brother Robert, who had explored the links between that calculus and algebraic logic more explicitly (§4.4.1). And in any case this Book played no essential role in the remaining five. Reviews of the book concentrated on this algebra and logic: a 40-page description Couturat 1900d in the Revue; a rather discursive survey, also of Grassmann’s work, in Natorp 1901a, arts. 1–2; and a feeble notice MacColl 1899a only of Book 2 in Mind.
Book 3, on ‘Positional manifolds’, ran through principal features of projective geometry in n dimensions, but in a largely algebraic manner expressing a point as a linear combination Σrαrer of some basis {er}; Whitehead covered (hyper)planes and quadrics. Grassmann came to the fore in the 100-page Book 4 on the ‘Calculus of extension’, where Whitehead’s coverage included not only the basic means of combination but also some aspects of matrix theory. Applications arrived in Book 5 on ‘Extensive manifolds of three dimensions’; the main one was to systems of ‘forces’, but these were treated kinematically and the theory was virtually vector algebra. Measurement was introduced in the longest and most interesting Book, 6 on ‘The theory of metrics’ (156 pages), where he followed Cayley for axioms and worked through the theory in some detail for elliptic and hyperbolic geometries, adding some applications to mechanics and kinematics.
In the final Book 7, ‘Applications of the calculus of extension to geometry’, Whitehead treated vector algebra and analysis, including the vector and scalar products (‘Vector area’ and ‘Flux’ on pp. 509 and 527 respectively). He also handled some standard partial differential equations and elements of potential theory.
Overall the volume gives an unclear impression, resoundingly belying its title; Whitehead had mixed logic, algebra and geometry together, but the fusion had eluded him. While it marked an important stage in the development of his philosophy in general (Lowe 1962a, ch. 6), he seems not to have seen ahead clearly. His next major mathematical foray was a long paper of 1899 on aspects of group theory, which he submitted to the Royal Society but then withdrew after finding many of his results in recent work by the German mathematician Georg Frobenius (my 1986a). He intended to write a successor to this ‘Volume 1’, treating quaternions, matrices and Peirce’s algebras (1898a, v); but he never fulfilled it, for the contact with Russell was gradually to develop into a formal collaboration (§6.8.2) which was to embody his philosophical aspirations, or at least several of them (§8.1.1–2). It has enjoyed no substantial influence (or detailed historical appraisal), although Russell reported on 16 August 1900 after the Paris Congress that ‘Whitehead has a great reputation; all the foreigners who knew Mathematics had read and admired his book’ (Letters 1, 202).
6.2.5 The impact of G. E. Moore, 1899. Russell communicated this news about Whitehead to his special philosophical friend G. E. Moore (1873–1958). ‘It was towards the end of 1898 that Moore and I rebelled against both Kant and Hegel’ (Russell 1959a, 54). A year junior to Russell at Trinity and trained in the same neo-Hegelian philosophy, Moore came the more rapidly to regard it as dangerous to mental health. He announced his revolt mainly in a paper 1899a in Mind on ‘The nature of judgement’, where he proposed in anti-idealist vein:
1) facts are independent of our experience of them;
2) judgements (or propositions) deal primarily with concepts and relationships between them rather than with mental acts;
3) existence is a concept in its own right; so that
4) truth is specifiable relative to these various existents.
Instead of an all-embracing monism of the Absolute, he advocated pluralities, and moreover Out There rather than in the mind: for example, the truth or falsehood of existential judgements such as ‘the chimera has three heads’ was determined by relationship between the concepts chimera, three, head and existence. If ‘the judgement is false, that is not because my ideas do not correspond to reality, but because such a conjunction of concepts is not to be found among existents’ (p. 179). His new position also held no sympathy for phenomenology, where the act of perception of an object inhered with the object perceived (§4.6).
In the same vein, and volume of Mind, Moore 1899b also published a review of Russell’s Essay on geometry. While unable to tackle its mathematical side, he attacked the use of psychology and psychologism to identify the genesis of knowledge with knowledge in general, for example for failing to show that time was necessary for diversity of content (p. 401). He also queried the status of ‘ideal motion’ to move a figure onto another one as allowed by the Axiom of Free Mobility, for it surely assumed the congruence to be appraised (p. 403). Russell had already moved on from the position in his book towards a Moorean stance; this review, especially concerning the theory of judgement, nudged him along further.
6.2.6 Three attempted books, 1898–1899. Fitted out with Whitehead’s geometric and logical algebras and Moore’s external reality, Russell drafted a monograph on the foundation of mathematics during the summer of 1898. Its long title shows evidence of the new influences: ‘An analysis of Mathematical Reasoning Being an Enquiry into the Subject-Matter, the Fundamental Conceptions, and the Necessary Postulates of Mathematics’. Much of it is lost or was transferred into later drafts; the surviving holograph and typescript m1898a show that a substantial text had been prepared (Griffin 1991a, ch. 7).
The philosophical ground was still traditional: judgements prominent, subject-predicate logic and the part-whole theory of collections. But the place of Whitehead is evident in the title of the first of Russell’s four Books: ‘The Manifold’. He took the word as synonymous with ‘Class’, denoting a collection of ‘terms’ construed intensionally under some predicate; an extensional collection formed an ‘assemblage’ (pp. 179–180). The last chapter of the Book treated ‘the branch of Mathematics called the Logical Calculus’ (p. 190), exhibiting a “mathematicism” in tune with Boole, say, but converse to the logicism soon to come. It encompassed a fragment of Whitehead’s Boole/Grassmann way of treating predicates a, b,… and their complements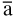 
,
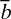,… relative to the Whiteheadian universe i. In ‘Book II Number’ the formula
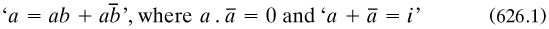
was used to interpret judgements of adding the integers associated with a and b (pp. 201, 193). Development of the algebra convinced him in his holograph that ‘the relation of whole and part underlies addition, and hence all Mathematics’ (p. 205).
Whitehead’s approach was evident also the discussion of number in Book 1. Cardinal integers were extensional manifolds (p. 196), but the connection between the two notions remained obscure. In the chapter on ‘Ratio’ Russell mooted the strategy of taking it as primitive and treating an integer as a special case of ratio: ‘20 would mean that the thing of which it is predicated has to the unit the relation 20:1’; similarly, 1/20 was construed as 1:20 (p. 207).
Among the fragments of ‘Book III Quantity’, the chapter ‘On the Distinction of Sign’ is notable for the immediate emphasis on the ‘connection with order, and the two senses in which a series may be ordered’ (p. 216); the link pervaded the chapter, and spilled into others. In particular, in connection with ‘position in space or time’ Russell indicated converse relationships such as ‘A’s adjective of being east of B, and B’s adjective of being west of A’ leading to the contradiction of space mentioned in §6.1.4 (p. 225). The consequences were fundamental for this young idealist: ‘relations of this type pervade almost the whole of Mathematics, since they are involved in number, in order, in quantity, and in space and time’ (p. 226).
The role of Moore came through in the greater place now accorded by Russell to concepts, and to more detailed examination of kinds of judgement. He referred quite frequently to ‘existents’, terms possessing the (primitive) property of existence. His examination of predication drew much on the pertaining classes. Partly in connection with such needs, numbers no longer had their old idealist home: ‘Anything of which a cardinal integer can be asserted must be the extension of some concept—must be, in fact, a manifold’ (p. 196).
Soon after setting aside this book, Russell tried another one, ‘On the Principles of Arithmetic’. Two chapters survive, on cardinal and ordinal integers, largely following the predecessor as taking manifolds as basic and emphasising relations between terms; he thought that cardinals were epistemologically prior to ordinals (m1898b, 251).
The next book-to-be, on ‘The Fundamental Ideas and Axioms of Mathematics’ followed broadly the same approach but returned to the previous scale of ambition. An apparently complete ‘Synoptic Table of Contents’ shows that eight Parts were involved: on ‘Number’, ‘Whole and Part’, ‘Order’, ‘Quantity’, ‘Extensive Continuity’, ‘Space and Time’, ‘Matter and Motion’ and ‘Motion and Causality’ (Russell m1899b, 265–271). ‘I find Order & Series a most fruitful & important topic’, he told Moore on 18 July 1899, ‘which philosophers have almost entirely neglected’ (G. E. Moore Papers, 8R/33/14). An intensional approach is evident in the course of cogitating about 1, one and allied terms: ‘A class may be defined as all terms having a given relation to a given term’ (m1899b, 276). A lengthy discussion of inference stressed the logical order of propositions involved (pp. 291–294).
These forays show Russell in an enthusiastic state of mind but with neither the basic notions nor the mathematical range fully under control. For example, in the last text he simply added truth ‘to the list of predicates’ with the hiccup that ‘To define truth is impossible, since the definition must be true’ (p. 285).
Noticeably absent from all these drafts was Cantor’s Mengenlehre; but Russell had come across it in 1896 and found it steadily more interesting. Let us now examine this parallel process.
6.2.7 Russell’s progress with Cantor’s Mengenlehre, 1896–1899. The initial contact came not from Cambridge mathematics or the principal existing commentaries, but from Ward, who gave him perhaps in 1895 the pamphlet version 1883c of Cantor’s Grundlagen (Russell 1967a, 68: he also received Frege’s Begriffsschrift, but could make nothing of it). He may have started to read Cantor then; but the principal initiation came later that year when he was asked to review for Mind a book on atomism by the French philosopher Artur Hannequin. It contained over 20 pages on Cantor, drawing on the French translations 1883d (1895a, 48–69), and on this evidence Russell found against Cantor in the review, mainly on the simple grounds that since the first number-class ‘has no upper limit, it is hard to see how the second class is ever to begin’ (Russell 1896b, 37).
Later in 1896 a more substantial French volume on this new subject came Russell’s way, and for the same reason: Mind asked him for a piece on Couturat’s De l’infini mathématique (1896a.) As we saw in §4.2.3, this book played a notable role in diffusing Mengenlehre and the foundations of arithmetic to a wider public than the mathematicians; Russell’s review 1897a must have helped to inform English-speaking philosophers, for he both surveyed many of Couturat’s themes and showed their philosophical richness. But he was still not convinced by the rehearsal of Cantor’s arguments for the existence of actually infinite numbers; and he also demurred against ‘the axiom of continuity’, as expressed by the Dedekind cut principle (p. 64, not so named). He also found ‘mathematical zero’ to be ‘grossly contradictory’, although ‘quantitative zero is a limit necessarily arising out of the infinite divisibility of extensive quantities’ (p. 64). At least he had advanced beyond the idealism run riot in an incomprehensible manuscript inference of the previous year that ‘In reality, 0 sheep means so many cows’ (Papers 2, 17); but much rethinking was still needed.
Russell applied himself to Mengenlehre with ardour in the winter of 1896–1897. A notebook called ‘What shall I read?’, kept between 1891 and 1902, shows that the French translations of Cantor were on the menu then, together with Dedekind’s booklet on continuity (Papers 1, 357, 358).7 He started to transcribe and comment upon Cantor’s work at length in the right hand pages of a large black notebook (transcribed in Papers 2, 463–481); the opposite pages were left blank for later comments, such as bewilderment at the laws of combination of transfinite ordinals. But Mengenlehre seems to have dropped away while he had his Whitehead and Moore experiences; it came back to his reading list only in April 1898 with Dedekind’s booklet on integers (which he had just bought), and in July 1899 with Cantor’s main suite of papers (§3.2.6), including the full Grundlagen received from Ward some years earlier (Papers 1, 360, 362). He started a second large notebook on some of these works, which was to run into the 1900s and cover many other writings past and present (RA, Dora Russell Papers).
Russell’s progress with Cantor’s Mengenlehre grew with his understanding. In 1896 he had found it mistaken for failing to obey the normal rules (about infinities, for example). When he passed from (competent) commentators to the Master, he found it to be a rich source of both mathematical ideas and a solution to some idealist contradictions. By 1899 it was moving more centre stage, especially for the bearing of Cantor’s theory of different order-types upon relations and order. But the full impact was still to come, and amidst other changes of philosophical import.
6.3.1 Changing relations. One central tenet issue of idealism was that relations were internal to the terms related. Russell had already found against this view, especially in concerning asymmetrical relations such as ‘greater than’ between terms; for example, it was surely necessary to pick out the ‘>’ in ‘A > B’ to distinguish it from ‘B > A’ (Papers 2, 121, of 1898). Such doubts were reinforced during the winter of 1898–1899 when he prepared a course of lectures on the philosophy of Leibniz, delivering them in the following Lent (that is, spring) Term at Cambridge.8 When he wrote up his lectures in book form he opposed Leibniz’s internalist opinion that a proposition necessarily contained a subject and a predicate; he cited ones containing ‘mathematical ideas’ such as ‘There are three men’, which could not be construed as a sum of subject-predicate propositions, ‘since the number only results from the singleness of the proposition’ (1900b, 12); we may also sense here a philosopher primed to find the quantifier. He concluded, against Leibniz, that ‘relation is something distinct from and independent of subject and accident’ (p. 13), a change that must have dented his idealism considerably.
TABLE 631.1. Russell’s Classification of Relations
Symmetrical (631.1) |
ArB ⊃ BrA (ArB and BrC) ⊃ ArC |
equality, simultaneity, ‘identity of content generally’ |
Reciprocal (631.2) |
ArB ⊃ BrA (ArB and BrC) not ⊃ BrC |
inequality, separation in space or time, ‘diversity of content generally’ |
Transitive (631.3) |
(ArB and BrC) ⊃ BrC and ArB ⊃ not BrA |
whole, part, before, after, greater, less, cause, effect |
One-sided |
None of the above |
predication, occupancy of space or time |
During this period of preparation Russell considered in detail ‘The classification of relations’ in an essay m1899a read in January to the Cambridge Moral Sciences Club in which he described three main kinds together with a residual category. He used the names and examples as in Table 631.1; he seems to have adopted from Gilman 1892a (§4.3.9) the notation ‘ArB’ for a relation r between terms A and B.9 To save space I use ‘⊃’ for Russell’s ‘if … then’.
From various examples, Russell decided that ‘diversity is a relation, and the precondition of all other relations’ (p. 142). Curiously, he did not consider the converse of a relation in general, although they arose in two of his kinds: he was still a long way behind Peirce and Schröder. But he maintained his move towards the externalist interpretation with this poser at the end of his manuscript: ‘When two terms have a relation, is the relation related to each?’.
6.3.2 Space and time, absolutely. Closely connected to the status of relations was the relativity of space, time and motion. Russell’s unease about relativism became in the spring of 1899 a switch to the absolutist positions, first for space and then also for time—two more voltes faces of the retiring idealist. Of his various writings of this period (Papers 3, 215–282) I take his lecture 1901g to the International Congress of Philosophy in Paris. This was the first occasion that he addressed an international audience of this calibre.
Russell wrote with the polemical conviction of a convert, citing Moore for his current philosophical line (pp. 252, 257). ‘Since the arguments against absolute position have convinced almost the entire philosophical world’, which included himself until rather recently, ‘it would perhaps be well to respond to them one by one’ (p. 249). He then mentioned Leibniz as one culprit, but he chose as standard target the Metaphysik (1879) by the German phenomenologist Hermann Lotze (1817–1881), who apparently was ‘full of confusions’ over senses of being (p. 253). Indeed, some criticisms seemed to be directed more against idealism as such rather than relativism; for example, that the view that a proposition in geometry had to be linked to time (pp. 248, 253), and that propositions had to have a subject-predicate form (p. 251).
Russell’s main argument for absolutism was that each event then had its own location, so that for example, the simultaneity of two different events can be appraised (pp. 241–243). He started his exegesis with new definitions of symmetrical and transitive relations (631.1, 3), but stipulating only the respective first conditions of his classification manuscript (p. 241). ‘Following Schröder’ with the notation ‘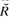
’ (after (446.4)) for the converse of R, he noted that the terms of such a relation lay in a series and doubted that when R denoted posterity relativism could properly express such a series of events in time, since the relation itself was supposed to be “absorbed” in the events (p. 242). He also noted similarities between his theory and that presented by Schröder 1901a at the Congress on ‘an extension of the idea of order’ beyond Cantor’s range to cases where several members of a collection could take the same rank; this was the only time that the theories of the two men converged.
6.3.3 ‘Principles of Mathematics’, 1899–1900. Russell added to the proofs of his book on Leibniz a footnote approving Leibniz’s opinion that ‘infinite aggregates have no number’ as ‘perhaps one of the best ways of escaping from the antinomy of infinite number’ (1900b, 117). So even in 1900 Cantor’s theory was not accepted. Indeed, given his idealist concern with continuity, Russell’s reaction to Cantor’s formulation of it had been surprisingly slight.
But after reading Cantor’s Grundlagen in July 1899 (§6.2.7), Mengenlehre featured more prominently in Russell’s next attempt to write a book on the foundations of mathematics. As its quoted title above shows, he was moving towards a more definitive conception; indeed, in contrast to its predecessors with their many discarded or transferred parts, this manuscript is pretty complete, about 170 pages in print in Papers 2 (m1899–1900a). Further, its division into Books was to be followed fairly closely in The principles of 1903 (Table 643.1 below); indeed, in his habit of transferring manuscripts in well-ordered series, he took into it several portions of ‘Analysis of Mathematical Reasoning’, including much of Part 3 on quantity and the chapter on distinction of sign.
Cantor featured mainly in Part 5, ‘Continuity and Infinity’, where Russell discussed his formulation of continuity (pp. 110–115) and the generation of transfinite numbers, chiefly ordinals (pp. 116–125); however, in an earlier chapter on ‘Infinite collections’ he rehearsed again his doubts from the footnote in the Leibniz book (pp. 33–34). He still did not appreciate Cantor’s general theory of order-types (§3.3.3), for it did not feature as much as it deserved in his Part 4 on ‘Order’. However, he emphasised strongly the underlying importance of order: the logical order of propositions in inference, whole and part itself, ordinal numbers, and space and time. He gave a comparable status to the various kinds of relations and the series which they generated.
Elsewhere the Whitehead approach was again strong. In particular, manifolds were now collections, with the part-whole relation given Part 2 to itself. A chapter on ‘Totality’ concentrated upon ‘all’ or ‘any’ members of a whole which might share a predicate; but the quantifiers, already well known to Peirce and Schröder, were still absent. Integers remained difficult to define from collections and might have to be indefinable, though Russell mooted again from the ‘Reasoning’ manuscript the idea of defining integers as special cases of ratios (§6.2.6). Part 3 on ‘Quantity’, taken over from that manuscript, attempted a very general theory; some of his difficulties with infinity (and also with zero) arose from efforts to make them quantities. In places his ideas resembled those of Bettazzi’s monograph 1890a (§5.2.6), of which however he was still unaware.
Russell also wrote at some length on the calculus, seemingly using De Morgan’s old textbook (§2.4.2), on which he had made notes in 1896 (Papers 2, 519–520); he even adopted the antiquated name ‘differential coefficient’ as the title of a chapter (m1899–1900a, 131). It opened with such a lamentable summary of Leibniz’s approach that one must conclude that his recent reading of that philosopher had omitted the calculus entirely. His account of limits concluded that ‘dy/dx is the limit of a ratio, not a ratio of limits’ (p. 135), which is Cauchy’s approach (272.1), which he did not mention at all. So his principles of mathematics were still somewhat scattered, and also scrappy; no Part was devoted to geometries, although various aspects arose in the discussions of space and time, and of mechanics.
Russell seems to have worked on this manuscript until June 1900. In that month he also completed a draft of his Congress offering on the absoluteness of space and time and sent it off to Couturat. A month later, in the company of Alys and the Whiteheads, he followed it to Paris.
I am obliged to you that you gave me the sad announcement of the death of Peano. He indeed is the man whom I much admired, from the moment when I came to know him, for the first time, in 1900, at a Philosophical Congress, which he dominated on account of the exactness of his mind.
Russell 1932a, to Sylvia Pankhurst
6.4.1 The Paris Congress of Philosophy, August 1900: Schröder versus Peano on ‘the’. As was described in §5.5.1, this event, unprecedented in scale, generated considerable interest; the products included four volumes of proceedings, and three lengthy reports on the logical and mathematical sessions, two from organiser Couturat 1900e and 1900f, and Lovett 1900a for the U.S.A. In addition to presenting his own paper 1901g on absolute order in space and time—which received a tepid discussion—Russell also read for W. E. Johnson an abstract on ‘logical equations’. Presuming that they attended, he and Whitehead will have heard, among others, Poincaré (on mechanics), MacColl and Schröder, and abstracts read from MacFarlane and Poretsky. But the magic time was the morning of Friday 3 August, when the Peanists gave their concert (§5.5); Peano and Padoa in person, Burali-Forti and Pieri in summaries read out by Couturat.
As we recall, Peano had spoken on definitions in mathematics. An ensuing discussion, presumably around 10 o’clock, first stimulated Russell’s excitement in him. Peano 1901a rejected definitions such as
on the grounds that ‘a’ could not be allowed to float free. Schröder objected to this ban, citing as an example his own specification (445.3) of the contradiction 0 as (a and not-a) for any proposition a (Lovett 1900a, 169–170). But Peano stood his ground; as Russell recalled to Norbert Wiener in 1913, Schröder’s proposed definition (446.1)1 of his empty domain 0 was ill-formed (my 1975b, 110):
There is need of a notation for ‘the’. What is alleged does not enable you to put ‘0 = etc. Df.’. It was a discussion on this very point between Schröder and Peano in 1900 at Paris that first led me to think Peano superior.
This personal contact with Peano was the crucial factor for Russell (and Whitehead); first the ‘the’ question, and then reflection about the Peanists in general from Friday lunch-time onwards. Russell had received one offprint from them, Pieri 1898a on geometry, in 1898 (§5.5.5); and he had seen the paper Couturat 1899a in the Revue on Peano, for he mentioned it in a letter to its author on 9 October 1899 (copy in RA). But these texts had not been enough.
After the Congress Russell stayed abroad for a few days before returning to England. Later he stated that he received and read Peano’s works at the Congress (1959a, 65); but in fact Peano had with him for sale only the current issue (volume 7, number 1) of his Rivista di matematica (my 1977b, 133), and Russell had to wait until the end of August before the earlier numbers and other material came in the post. He was busy enough, however, since the proofs of the Leibniz book had been around since June. Moore read these, and Russell also told him on 16 August of an ‘admirable’ gathering, with ‘much first-rate discussion of mathematical philosophy. I am persuaded that Peano and his school are the best people of the present time in that line’ (Russell Letters 1, 202).
Russell received from Peano the first two editions of the compilation Formulaire des mathématiques, the first six volumes of the Rivista (now trading under the title ‘Revue de mathématiques’) , and the short book 1889b on geometry. He read again Cantor’s Grundlagen, and by November he had also consumed Pieri’s offprint, Dedekind’s booklet on integers again, Bolzano’s book on paradoxes, Bettazzi’s monograph on quantities, Pasch’s lectures on geometry, and at last Cantor’s final pair of papers 1895b and 1897a on general sets (the first in the Italian translation 1895c in the Rivista); next Febuary’s reading included Hilbert’s book on the foundations of geometry (Papers 1, 363–364). Among other works, he bought in September a set of Schröder’s lectures then published (RA). Late in 1900 he also looked at the first (and then only) volume of Frege’s Grundgesetze, but made little of it (letter to Jourdain in my 1977a, 133); this was a pity, for he had told Moore in August that the meaning of ‘any’ had been of special interest in Paris, and here Frege was perceptive.
6.4.2 Annotating and popularising in the autumn. One of Russell’s first reactions to the Peanist experience was to add comments and references to the several folios of the current manuscript on ‘Principles of Mathematics’ (§6.3.3). The most striking addition, dated October, filled most of the space surrounding his titling of Part 2, on ‘Meaning of whole and part’.10 To the left he put:
I have been wrong in regarding the Logical Calculus as having specially to do with whole and part. Whole is distinct from Class, and occurs nowhere in the Logical Calculus, which depends on these notions: (1)implication (2) and (3) negation.
His word ‘class’ referred to Cantorian sets, centre stage in Peano’s logic; he cited Bettazzi’s book for whole-part theory. To the right he resolved that ‘I must preface Arithmetic, as Peano does, by the true Logical Calculus, to be called Book I, The Individual’.
Also in the autumn Russell wrote two papers for Mind. The first, 1901a ‘On the notion of order’, drew much on Part 4 of the current ‘Principles’ manuscript: definitions of (in)transitive and (a)symmetrical relations, series generated by them, and a lengthy discussion of logical order before turning to examples in integers, space and time. But in the text he cited Peanists several times (including Pieri’s offprint), Bolzano’s book, and De Morgan’s paper 1860a on relations. The second paper was based upon the English draft of his Paris talk on absolute order, and so was largely pre-Peanist in content; but he cited the new master twice on matters of geometry (1901e, 265, 269), and for the first time in print he mentioned Frege, on the objectivity of cardinals (p. 278).
Russell also proposed to editor G. F. Stout a more popular essay for Mind on the Peanists, an idea which Stout welcomed. He produced in the autumn an excellent survey, starting out with Weierstrass’s emphasis on rigour and not only emphasising distinctions such as between a term and its unit class but also indicating the Peanists’ mathematical range, of which ‘the theory of Arithmetic [... is] I think Peano’s masterpiece’ (m1900c, 358). He also took note of some German work, such as Schröder and writings (not Hilbert’s) on the foundations of geometry. Unfortunately the essay was not published; maybe Stout changed his mind, but then the Mathematical gazette would have been a suitable venue. At all events, British readers never saw a most timely and competent piece of enlightenment.
6.4.3 Dating the origins of Russell’s logicism. In his reminiscences Russell tells us that during the rest of 1900 he wrote yet another book manuscript at great speed, which formed the substance of The principles of mathematics (Russell 1903a); in the intervening period some revision was carried out, especially on the two opening Parts and the last one (1959a, 72–73; 1967a, 145). But he told Jourdain a different story in April 1910 (my 1977b, 133):
During September 1900 I invented my Logic of Relations; early in October I wrote the article that appeared in RdM VII 2–3 [Russell 1901b in Peano’s Rivista (§6.5.2)]; during the rest of the year I wrote Parts III-VI of my Principles (Part VII is largely earlier, Parts I and II wholly later, May 1902) [... ]
Russell received back the manuscript from the Press after publication, and kept it in his files. Like this letter, it suggests a different story from the well-known recollection (my 1997b); a very heterogeneous text, not only because of transferral of folios from ‘Principles’ but especially for the chronology of the writing, which follows the order of Parts 3-4-5-6-1-2-1again-7. Further, Parts 1 and 2 were referred to only in general ways in the later ones; in particular, a mention in Part 5 that ‘irrationals could not be treated in Part II’ (p. 278) refers to ‘I or II’ in the manuscript, and in a similar remark four pages later ‘I’ was altered to ‘II’ for publication. In addition, unlike the other three Parts, in the manuscript of Parts 3–6 the chapters are numbered from 1 onwards in each Part instead of the consecutive system that was printed (numbers 19–52); the texts are not divided into the numbered articles printed (149–436); and there are no printers’ markings. It seems likely that another version of them was prepared (probably a typescript), which he and the printer used.
These elements of evidence suggest two surprises: that Parts 1 and 2 did not exist at all in 1900, at least not beyond sketch form; and that the book conceived in 1900 did not advocate logicism. These hypotheses, and study of the manuscript of the book and pertinent letters and diaries, suggest this scenario:
1) In the autumn of 1900 Russell was sure that Peano’s programme was important for him, with its logic and the central role given to Cantor’s set theory, and so could provide Parts 1 and 2 with the grounding that he had been seeking; however, a logic of relations had to be introduced. He also followed the Peanists in maintaining some distinction between mathematics and logic, although he was not sure what or where it was, especially regarding set theory. So he re-wrote Parts 3–6 of ‘Principles’: Part 5, on infinity and continuity, was especially pertinent.
2) In the new year (and century), Russell decided that the distinction did not exist: instead, pure mathematics was contained in Peanist logic. (His special sense of ‘pure’ will be explained in §6.5.1.) However, he did not yet have a detailed conception of this logic, apart from the need for relations, which he quickly sketched out; still awaiting clarity were the constants and indefinables, and the status of set theory.
3) In January, and definitively in May, he rethought a discussion in Part 5 of Cantor’s diagonal argument, and thereby found his paradox.
4) Around the same time Russell thought out more clearly the basic notions of his logic, and thereby refined logicism. The notion of variable was now crucial, for Part 1 carried ‘The Variable’ as its new title (§6.7.1). However, propositional functions and quantification still remained rather in the shadows. Part 2 on ‘Number’ was also written, including the definition of cardinal integers as classes of similar classes, basic for arithmetic and therefore for logicism.
5) By the spring of 1902 Part 1 could be developed further; the prominence of the variable was tempered by deeper consideration of propositional functions, so that the Part was now called ‘The indefinables of mathematics’. Despite the presence of the paradox, logicism could still be stated, in more detail, and the book readied for publication by further referencing and changes and two new appendices.
This proposed chronology, outlined in more detail in Table 643.1, guides the design of the rest of this chapter. After a preface and an elaborate analytical table of contents, the main text of the latter was divided into seven Parts with 59 chapters and 474 numbered articles, 498 pages in all. By intention, the text was largely prosodic, with a modest use of symbols and rather few formulae or diagrams; the formal version was planned for a sequel volume (p. xvi).
TABLE 643.1. Russell’s Progress with The principles, August 1900–February 1903. ProM = ‘Principles of mathematics’ m1899–1900a. Pr = The principles of mathematics. Papers entry gives the first page(s) of the text(s).
TABLE 643.2. Summary by Parts of Russell’s ‘Principles of mathematics’ (1899–1900) (‘ProM’) and The principles of mathematics (1903) (‘Pr’).
The Summaries of Pr use many chapter titles but do not always follow the order of chapters.
The length and range of both book and its own manuscript could generate an historical analysis of comparable length, ‘with an appendix of leading passages’ (to quote the sub-title of his book on Leibniz). Quite a few folios came from ‘Principles’ (Table 643.2 compares the book with this manuscript), and some even earlier (King m1984a). A few were discarded but kept—for example and not only, the folio heralding his paradox (§6.6.2). Later, many changes and additions were made in proof.
Despite its fame, a book never out of print since its re-issue in 1937 (§9.5.4), no comprehensive survey of its contents seems to have been written (Vuillemin 1968a is one of the best studies); indeed, many commentators seem unable to get much beyond Parts 1–2 and the two appendices. Both published and written versions are noted here, along with several associated manuscripts and published papers which are now gathered together in Papers 3.
6.4.4 Drafting the logic of relations, October 1900. Russell was bowled over by reading the Peanists; mathematical range combined with logical power, especially the use of predicates and quantification, and especially the overthrow of subject-predicate logic with the distinction between membership and inclusion. But he soon found fault with them; in particular, they had failed to develop a logic of relations. Thinking out many of the required details in September, he wrote out a draft manuscript m1900c of a paper for Peano the next month, in which he affirmed his belief in the central importance of relations for logic and mathematics. I note here some main features, reserving some details for the final version in §6.5.2.
Russell wrote fully in Peanese, with all the notations, ‘Pp’ for both axioms and rules of inference, ‘=Df’, the numbering of propositions, wallpaper look, the lot. His opening flourish criticised Schröder and Peirce; like the Peanists, he did not appreciate their achievements, or De Morgan’s before them. Again he used, with acknowledgement, only Schröder’s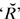 
for the converse of relation R, and also ‘1’ and ‘0’ in (446.6) for identity and diversity respectively. As he told Jourdain in April 1910, ‘I read Schröder on Relations in September 1900, and found his methods hopeless, but Peano gave just what I wanted’ (my 1977b, 134). Thus much of the logic which he developed repeated details of the structure which the algebraists had already furnished. (This was the major issue between Russell and Wiener (§8.2.7), which stimulated the reminiscence quoted in §6.4.1). But the differences were substantial: in particular, he construed relations as intensions defined by some property external to the objects related.11 He denoted the ‘domain’ and ‘converse domain’ of a relation by using whenever possible the corresponding lower case Greek letter, such as ‘ρ’ and 
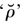for relation R (m1900c, 590).
Among other preliminaries Russell distinguished between the compound ‘R1R2’ of relations R1 and R2, and the class ‘R1 ∩ R2’ of ordered pairs in common between them (p. 591). Padoa’s symbol ‘Elm’ for the class of unit classes (§5.4.6) was frequently used, for it was easier in Peanese to handle unit classes than their individual members. In an interesting paragraph he floated the idea that diversity might replace identity as a ‘logical indefinable’ (pp. 593–594).
A striking pair of symbol-strings occurred within a few lines on pp. 591–592:
The second formula simply used Peanese to say that x belongs to the class of classes y (because there exists a class z belonging to y and containing x as member), while the first stated that membership was itself a relation and so belonged to the class of them. However, has the symbolism slipped into a formalism? Is not the first ‘ε’ a noun while the second is a verb? This conflation of use and mention is an early case of many to be found in Russell’s logic.
Between these two lines occurs a hiccup when Russell defined the class of individuals by the property of belonging to a class. However, since a class can belong to a class of classes, then this definition or that of Cls (not given here. needs refinement. The status of individuals was to remain a considerable difficulty in Russell’s logic (§7.8.3).
The mathematical exercises concentrated on arithmetic. After defining the similarity of two classes by the existence of a one-one relation taking one class for its domain and the other for converse domain, Russell defined the class of cardinal numbers as the converse domain of the one-one compound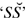 
of any many-one relation S, so that two similar classes had the same cardinal (pp. 595–596)—and Peano’s principle of abstraction (536.1) now became a theorem. He also rehearsed various basic definitions and properties of ordinal numbers, including transfinite ones, where he introduced the name ‘progression’ for an infinite well-ordered series (p. 597). I leave the details to the more ample presentation in the published version (§6.5.2).
In addition to material which would become very familiar in Russell’s later logical writings, the draft included articles on ‘groups’ with applications to ‘distance’ and ‘angles’ (pp. 594–595, 609–612). The mathematics came from Cayley and Klein, and his interest in it harked back to his geometry book (1897c, 28–38). ‘Group’ for Russell was basically a permutation group composed of a class of one-one relations which contained the converse of each member (the identity relation ‘1” was assumed present) and the compound of any two members which had equal domains): in Peanese (m1900c, 594),
(with ‘Df’ serving double duty). The motivation came from Whitehead, as we shall see in §6.5.3. Unfortunately, although Russell’s contact with Whitehead had increased by the time of his final version, he left out these articles—an early sign of his narrowing conception of mathematics, which unfortunately was to continue through the decade.
After this exercise Russell then rewrote Parts 3–5 of his previous ‘Principles’ into a new book during November, and Part 6 the month afterwards. The concluding article of each Part was a general summary; we shall use it for guidance, together with the table of contents.
6.4.5 Part 3 of The principles, November 1900: quantity and magnitude. (Manuscript, Byrd 1996a; summary, art. 186. This Part, ‘Quantity’, largely followed the previous version (§6.3.3): ‘Magnitudes are more abstract than quantities: when two quantities are equal, they have the same magnitude’ (p. 159) as defined via transitive and symmetrical relations (p. 163). He stressed that both notions were general, dependent upon order (to be analysed in the next Part), but not upon divisibility and so not necessarily restricted to continuous or discrete ranges. Among derived notions, an important one in connection with measurement was ‘the terms intermediate between any two’ a0 and an in a series, which ‘may be called the stretch from a0 and an’. A ‘whole composed of these terms is a quantity, and has a divisibility measured by the number of terms, provided their number is finite’ (p. 181).
In places this Part was less pithy than its predecessor, but one main extension lay in ch. 22 on the ‘quantitative zero’; it had ‘a certain connection both with the number 0 and the null-class in Logic, but it is not (I think. definable in terms of either’ (p. 184). He considered but rejected various other possible definitions; for example, identity would not do because ‘zero distance is not actually the same concept as identity’ (p. 186). He finally plumped for defining a zero for each kind of magnitude rather than some “universal” type, and used as defining expression ‘the denial of the defining concept’ of its kind, such as ‘no pleasure’ for the zero magnitude of pleasure. It was a special relation, holding ‘between no pleasure and pleasure, or between no distance and distance’, say; it was ‘not obtained by the logical denial of pleasure, and is not the same as the logical notion of not pleasure’ (p. 187).
6.4.6 Part 4, November 1900: order and ordinals. (Manuscript, Byrd 1996a; summary, art. 248) This Part, ‘Order’, elaborated in prose many of the ideas of the draft paper on relations together with applications to measurement; but continuity and infinity were postponed as much as possible until the next Part. Russell explained at length the generation of series as domains and/or converse domains of relations of various kinds (chs. 34–35), with special emphasis on transitive asymmetrical relations (hereafter, ‘TAR’) in ch. 26 for producing order in general (ch. 36) and progressions in particular (ch. 38). This led him to define ordinal numbers, with negative ones generated by the converse of a relation (p. 244). He then gave in ch. 30 an account of Dedekind’s definition of integers (§3.4.1), with the transformation theory reworked in terms of relations. Although he appreciated the significance of the theorem which guaranteed mathematical induction, nevertheless he concluded that Dedekind produced ‘not the numbers, but any progression’ (p. 249).
One assumption in Dedekind’s treatment was that ordinals were prior to cardinals. Russell noted this also, but sided with Cantor’s opposite viewpoint (pp. 241–242). The issue was to recur as logicism developed.
As in his draft for Peano, Russell’s account of TAR included a criticism of Peano’s principle of abstraction which he restated as defining a concept such as the number of a class by such relations. He noted its assumption of an entity satisfying this relation, which he cast as an axiom, ‘my principle of abstraction’ (p. 220). This principle was to play quite an important role in Russell’s drive for nominal definitions in mathematics, although he tended to replace it by talk of the corresponding classes of classes or relations in order to avoid the charge of ambiguous definition (Rodriguez-Consuegra 1991a, 189–205).
Another major use of TAR was in defining the concept of distance, which Russell handled in a rather peculiar ch. 31 to end the Part. Seeking a definition more general than that used in mathematics itself, he presented it as a one-one TAR between two terms of the generated series; thus the sum of two distances came from compounding the corresponding relations. If the second distance was the reverse of the first, then zero distance was produced: symmetry was abandoned, and the relations were mutually converse (1903a, 253). While somewhat obscure, the treatment played a significant role in the Part following.
6.4.7 Part 5, November 1900: the transfinite and the continuous. (Manuscript, Byrd 1994a; summary, art. 350) At 112 pages ‘Infinity and Continuity’ was the longest Part of the book. Deeply influenced by set theory—not just order but also the theory of transfinite numbers and the real number system—it was the first extended account in English of this material. Russell showed a good mastery of the current situation; on the transfinite cardinals, for example, he emphasised the Schröder-Bernstein Theorem 425.1 (cited from Borel 1898a, 108–109 and Zermelo 1901a) and doubted that trichotomy could be proved (p. 306).
Russell began his own way of handling the theorems with one of his major innovations: ‘The correlation of series’ (ch. 32) by means of order-isomorphic relations, so that ‘when one series is given’ as generated by relation P, ‘others may be generated’ by applying a one-one ‘generating relation’ R and its converse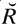 
so as to product PR; it was a TAR if P was also (p. 261). In the next March he was to develop the method further in his second paper for Peano, and sometime to add three important new articles to the book (§6.5.4).
One main innovation in this Part was Russell’s definition of irrational numbers. He took the class of rational numbers, an ‘everywhere dense set’ for Cantor (§3.2.3), as a ‘compact series’ (not the sense of this adjective which has endured), and defined an irrational number as a ‘segment’, that is, the class of rational numbers less than some given one. ‘My contention is, that a segment of rationals is a real number’ (p. 272), or more precisely after much discussion of limits, ‘a segment of rationals which does not have a limit’ (p. 286). His approach resembled Dedekind’s cut (§3.2.4), which he had analysed in the interim (pp. 278–284.; but instead of positing a number corresponding to a cut Russell gave another nominal definition in terms of classes of classes.
For Russell the advantage of his procedure was that the existence of these numbers was guaranteed only this way, and he criticised at some length the theories of Dedekind, Cantor and Weierstrass on this issue (pp. 280–285). However, his Peanist enthusiasm had rather led him astray. He used the word ‘existence’ here in Peano’s sense (541.3), defined of a class that it be non-empty. But for mathematical purposes existence has to be understood far more generally, and none of his victims can be accused of error in principle merely for not defining non-empty classes even if one may criticise them on other grounds. A further irony is that he had been anticipated in this definition by Moritz Pasch—not in the textbook 1882b on geometry which had much pleased him in earlier work and also in Part 6 to come here, but in the contemporary one 1882a on the calculus; he learnt of his predecessor only in 1910 from Jourdain (my 1977b, 139).
The ‘infinitesimal calculus’ received in this Part a rare, and short, exposition from Russell (ch. 39). Although he cited Leibniz several times, his appraisal of Leibniz’s methods as ‘extremely crude’ (p. 325) shows that he had still not carefully read the mathematics. His account naturally followed the dictates of Weierstrass, whose approach he had learnt from the textbook literature, especially Stolz 1885a, Dini 1892a and C. Jordan 1893a (pp. 328–329); in particular, ‘dy/dx [...] is not a fraction, and dx and dy are nothing but typographical parts of one symbol’ (p. 342), quite opposed to Leibniz’s own reading of it as the ratio dy ÷ dx of differentials (§2.7.1).
Russell’s main concern was with the status of infinitesimals and the continuum, to which he devoted three chapters (40–42). Again in line with the Cantorian Diktat (§3.6.3), he concluded that ‘infinitesimals as explaining continuity must be regarded as unnecessary, erroneous, and self-contradictory’ (p. 345). On this last calumny he considered Zeno’s famous paradoxes, giving the usual but irrelevant solution of Achilles and the tortoise in terms of limits (pp. 350, 358-360).12 When he came to write Part 1, this paradox would play a different role (§6.7.4); for now, as November 1900 drew to an end, he reverted to his old subject.
6.4.8 Part 6, December 1900: geometries in space. (Manuscript, Byrd 1999a; summary, art. 436) For mathematical directions in this Part, on ‘Space’, Russell drew upon Pasch and Whitehead. Hilbert’s book was cited only for three details (pp. 384, 405, 415); a foundational approach allowing interpretations as beer-mugs would have seemed alien to Russell. He organised this Part along the lines of his book on geometry, specifying separately the projective, descriptive and metrical branches in terms of appropriate relations between points and then examining the relationships between them (chs. 45–47, 48). Point itself was an indefinable class-concept for each geometry (p. 382, with Pieri 1898a highly praised); its existence was defended against the relativistic critics by appeal to absolute space (ch. 51).
Russell’s affirmation of absolutism was not the only philosophical change since the days of the geometry book: Moorean empiricism having replaced idealism, principles had to be changed. In particular, instead of assuming space to be an a priori externality (§6.2.1), he provided ‘Definitions of various spaces’ (ch. 49); each one was a class of terms (or entities. endowed with relations between them appropriate to the axioms of the associated geometry, and its continuity could be formulated entirely by Cantorian means (ch. 50). The number n of dimensions of a space was defined from the series of series of .). (n – 1 times) of terms, each one generated by a TAR (pp. 374–376). Cantor’s proof of the equi-cardinality of line and plane (§3.2.5), and its extension to more dimensions, showed for Russell that his definition could be extended to dimensions, thus making clear that the numbers themselves were ordinals (p. 376).
Russell did not confine himself to the various axioms but also considered appropriate metrics, drawing on discussions of distance and measurement in earlier Parts, and related notions. For example, in metrical geometry ‘An angle is a stretch of rays [from its vertex], not a class of points’ (p. xxxv in the table of contents, summarising p. 416).
So Russell finished the old century with a fine reworking of geometry. However, the basis of the philosophy was still not fully thought out; Parts 1 and 2, on basic logical notions and definitions of cardinals, were still not down on paper. As always throughout his years of studying the foundations of mathematics, the weak part was the foundations themselves; the mathematical roots lay tangled in the ground. Let us leave him at the end of the century with this productive four-Part draft, and catch up with the activities since Paris of his friend Whitehead, work which was already beginning to intersect with his own.
6.4.9 Whitehead on ‘the algebra of symbolic logic’, 1900. Whitehead’s reaction to the Paris Congresses was different from Russell’s, for he continued in a largely algebraic style with an examination of Cantor’s theory of finite and infinite cardinals, spiced up with the new Peano/Russell logic. Maybe the combination of the Peanists with the philosophers and Hilbert announcing Cantor’s continuum hypothesis as the first of his problems to the mathematicians sparked this interest. At all events, he produced three papers and an addendum within two years, publishing them all in the American journal of mathematics, slightly over 100 pages in total length. The venue may seem surprising; but, in addition to its reputation it was edited by Frank Morley (1860–1937), who had been a fellow student with Whitehead in the mid 1880s but had emigrated to the U.S.A. and was then professor at Johns Hopkins University.13 In patriotic U.S.A. style, Whitehead’s Peanist eight-point asterisks used to number the theorems were printed as five-pointed stars ‘
’!
Whitehead’s first paper 1901a, written in 1900 and proof-read the following February, dealt with ‘the algebra of symbolic logic’. Finding algebraic logic to be ‘like argon in relation to the other chemical elements, inert and without intrinsic activities’, he sought to inject it with the juices of the theory of equations: factorising Boolean expansions into ‘prime’ linear terms in its predicate variables x, y,... and their complements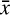 
, 
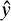,... relative to some universe i, with coefficients a, b,... 
, 
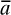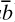,...; finding a necessary and sufficient condition that such an expansion admits a unique solution; extending theory to cases where these quantities were denumerably infinite in number; forming symmetric functions of these quantities; examining the groups of substitutions and of transformations of the variables (hence Russell’s awareness of groups in (644.2)); and seeking invariants under these transformations. In the third paper, finished in July 1901 according to a February footnote added to its predecessor, he calculated the ‘order’ (meaning the cardinality) of some of the classes of groups that he had found; he did not confine himself to finite group theory, for he interpreted answers such as 24n as ‘equal to the power of the continuum at least’ if the size n of the group was infinite (Whitehead 1903a, 171). In such ways he brought algebra into transfinite arithmetic; his treatment of the finite cardinals is described in §6.5.3.
6.5.1 Logicism as generalised metageometry, January 1901. Unlike his book on geometry, Russell did not use the word ‘metageometry’ in Part 6 of The principles. But the plurality of geometries was prominent: the theorems of a geometry depend hypothetically upon the axioms and other assumptions required (Nagel 1939a). One passage in the manuscript is especially striking: ‘In this way, Geometry has become (what it was formerly mistakenly called) a branch of pure mathematics, that is to say, a subject in which the assertions are that such and such consequences follow from such and such premisses, not that entities such as the premisses describe actually exist’ (also printed thus, at p. 373). This passage, or at least the thoughts in it, may well have solved for Russell his demarcation problem between logic and mathematics; generalising this conception of metageometry, he envisioned logicism as the philosophy which defined all pure mathematics as hypothetical, and that the Peanist line between mathematics and logic did not exist. All mathematics, or at least those branches handled in this book, could be obtained from mathematical logic as an all-embracing implication, for this new category of ‘pure mathematics’; the propositional and predicate calculi (including relations) with quantification provided the means of deduction, while the set theory furnished the “stuff”: terms or individuals, and classes or relations (of classes or relations …) of them. Maybe a trace memory of this origin of logicism came to him when he introduced the reprinting of the book many years later: ‘I was originally led to emphasis this [implicational] form by the consideration of Geometry’ (1937a, vii).
Later on in Part 6 occurs a similar passage: ‘And when it is realized that all mathematical ideas, except those of Logic, can be defined, it is seen that there are no primitive propositions in mathematics except those of Logic’ (1903a, 430). Unfortunately, unlike the passage from page 373 just cited, this one belongs to a sector of the manuscript which is lost,14 so we cannot tell if it was so written in December 1900; my guess is that it does contain some rewriting. But it also shows other features of the developing logicism, such as an emphatic discussion of the need for nominal definitions (p. 429):
[... ]a definition is no part of mathematics at all, and does not make any statement concerning the entities dealt with by mathematics, but is simply and solely a statement of a symbolic abbreviation; it is a proposition concerning symbols, not concerning what is symbolized. I do not mean, of course, to affirm that the word definition has no other meaning, but only that this is its true mathematical meaning.
The details of the logicistic vision were still not clear, but Russell made his first public statement of it in a popular essay ‘On recent work on the principles of mathematics’. Written in January 1901 (my 1977b, 133), it was published in the July number of a ‘most contemptible’ (Russell in Papers 3, 363) American journal called International monthly, nevertheless selling over 6,000 copies.15 This essay has become one of his best known works of this genre, largely because he included it in the anthology volume Mysticism and logic in 1918. His announcement took the form of an aphorism which soon became very well known: ‘mathematics may be defined as the subject in which we never know what we are talking about, nor whether what we are saying is true’ (1901d, 365). Its kernel is the hypothetical character given to mathematics; but its import as the birth announcement of logicism has understandably escaped readers. One early example was a ramble Vailati 1904a around this ‘most recent definition of mathematics’ by one of the Peanists, who taught Russell’s logicism at the University of Turin then (see his letter of 26 July to Giovanni Vacca in Letters, 235). Another hint came a little later with the unfortunate identity thesis that ‘formal logic, which has thus at last shown itself to be identical to mathematics’ (Russell 1901d, 367), although it lacks elaboration to clarify its seemingly whimsical tone: ‘those who wish to know the nature of these things need only read the works of such men as Peano and Georg Cantor’ (p. 369). We return to this matter in §6.7.3.
Also regrettable is Russell’s equally famous aphorism in the essay: the howler, often quoted by fellow misinterpreters, that ‘Pure mathematics was discovered by Boole, in a work which he called the Laws of thought (1854)’. It launched a whole paragraph of incomprehension (p. 365), typical of the way in which one kind of symbolic logician did not at all understand the work of the other tradition. Presumably he used here the adjective ‘pure’ in its traditional sense rather than his new one, in which case earlier examples can be found (for example, Diophantos in the +4th century); but either way he misunderstood Boole’s use of uninterpretable formulae (§2.5.3), although Whitehead had clearly explained it in Universal algebra (1898a, 10–12 and elsewhere). Again, he did not convey the central fact that Boole always saw his work as mathematics applied to logic (§2.5.8). Furthermore, like the algebraic logicians to follow him, Boole’s logic was only qualitative: Russell’s vision was of a logic both qualitative and quantitative, with constructions of real numbers, continuity and geometry to be made.
This remark on Boole is not the only hiccup in the essay: in the 1918 reprint Russell had to add some footnotes to correct mistaken opinions made about Cantor (pp. 374, 375); the second one will be handled in §6.6.2. But logicism was emerging, as Russell absorbed the logic that he had recently learnt and then developed it in two important papers for Peano’s journal.
6.5.2 The first paper for Peano, February 1901: relations and numbers. The final version of Russell’s paper on relations, prepared by February in French, was sent to Peano in March. Peano’s letter of thanks and acceptance contained the extensionalist statement that ‘The classes of couples correspond to relations’ (Kennedy 1975a, 214), explaining the absence of such a theory from his programme but doubtless also confirming to Russell the need for his paper! (compare §7.4.1). It appeared later in the year in two consecutive issues of the Rivista as Russell 1901b.
In the first article of the paper Russell ran through in somewhat more detail than in his draft (§6.4.4) the criticism of Schroder and Peirce, notations such as ‘R’ and 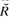, and basic properties such as compounds and converses. Among many other passages repeated here were the ungram-matical proposition ‘ε ε Rel’ (644.1.; but the idea of diversity as indefinable was surprisingly dropped, as were the articles on groups, distance and angles.
The next article, elaborating art. 3 of the draft, treated ‘Cardinal numbers’ on the basis of similarity between two classes u and v:
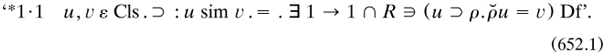
He added nervously, that ‘If we wish to define a cardinal number by abstraction, we can only define it as a class of classes, of which each has a one-one correspondence with the class “cardinal number” and to which belong every class that has such a correspondence’ (p. 321). These nominal definitions took him that one crucial step beyond the Peanists, but he wrote hypothetically, and also only in words. Perhaps as a concession to non-logicist Peano or maybe in shared doubt, his surrounding theorems dealt with ‘the number of a class’ in the Peanist tradition (§5.3.3) rather than numbers themselves. But the passage reads oddly for another reason: art. 1 had ended with the categorical statement that ‘the cardinal number of a class u will be the class of classes similar to u’ (p. 320)! However, that remark was added only on the proofs, as the end product of a tortuous analysis, through the draft and final versions to these proofs, of the similarity relation and its domain and converse domain (Rodriguez-Con-suegra 1987a, 143–150).
In art. 3 Russell reworked from the draft ‘Progressions’, his name for denumerable series, as well-ordered classes. His first presentation of a symbolic definition of a number seemed again nervous: ‘ω, or rather, if one wishes, a definition of the class of denumerable series. The ordinal numbers are, in effect, classes of series’ (p. 325: the original French, ‘si l’on veut’, is perhaps less weighty). The uncertainty was justified, however, albeit unintentionally; for (already in the draft. he forgot to use u in series form and so had actually defined 
0. He acknowledged and corrected this error in the second paper for Peano (1902a, 391). Here he went on to prove results which corresponded to the basic operations of arithmetic; for example (1901b, 328):
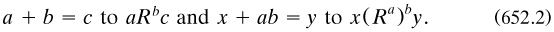
Then multiplication could be defined by associating a relation B with each muliplicand (p. 331):
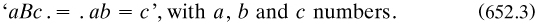
The notion of ratio lost more status, for division was effected by using the corresponding relations: b/c was linked to B (p. 332).
Perhaps the most important novelty relative to the draft was art. 4, on ‘finite and infinite’. Perhaps building upon Cantor and especially Dedekind (§3.4.2), Russell defined a finite and an infinite class by the respective properties of not being, or being, similar to the class created by removing one member. In an interesting following paragraph he noted the alternative definition of finite numbers by mathematical induction, and confessed himself unable to deduce either definition from the other one (p. 335). He had come across an issue which was to help him to recognise an axiom of choice three years later (§7.1.6), and grudgingly to adopt an axiom of infinity two years after that (§7.6.1).
The last two articles of the paper were largely rewritings in Peanese of Cantor’s theories of everywhere dense sets (now ‘compact series’), and of progressions and their inverse order-type ‘regressions’ within them. Russell reworked in detail many results in Cantor’s recent paper 1895b, including the construction of compact sub-classes and properties of limit members. His treatment relied on the existence for each series u of a one-one ‘generating relation’ R whose domain contained u and converse domain included all relata of members of u (forming themselves a sub-class of u) together with further properties to ensure well-order (p. 341).
6.5.3 Cardinal arithmetic with Whitehead and Russell, June 1901. Despite some slips and unclarities, this paper was a brilliant début in Peanese, one of the best in the Rivista to date. But absent from it were Russell’s nominal definitions of cardinals; they were given in the middle of Whitehead’s second paper, which was completed by June and published in the American journal of mathematics as 1902a. Whitehead began by introducing Peano’s symbolism and Russell’s logic of relations; on Cls (also written ‘cls’), ‘a class whose extension is formed by all classes’, he included the proposition
(p. 372), which was to raise Jourdain’s eyebrows in the Rivista, for one (1906a, 134–135).
Whitehead also introduced the important notion ‘cls2 excl’, the class of mutually exclusive (or disjoint. class, whose cardinality was the product of those of the given classes. The ‘multiplicative class’ ‘dx’ of a class d was defined on p.383 as
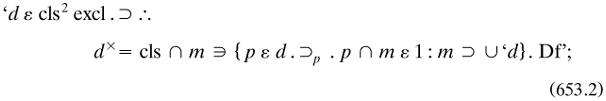
it was to be crucial in the development of logicist arithmetic. The applications centred on proving in as general manner as possible theorems on the addition and multiplication of cardinals, especially 0, and extending the binomial theorem to infinite indices. In a small addendum paper Whitehead 1904a proved that strict inequality of cardinals was preserved under addition.
Russell was credited by Whitehead with adapting into Peanese Cantor’s proof by diagonal argument (§3.4.6) that the cardinality of a class was less than that of its power-class (1902a, 392–394). But his main contribution was art. 3, listed separately as Russell 1902d, in which he gave the nominal definition of cardinals as classes of classes. 0 was the class ‘iΛ’ of the empty class Λ; 1 the class of all unit classes, thus allowing him to replace Padoa’s ‘Elm’ by ‘1’; and so on, with the defining expressions formulated to avoid the vicious circle implicit in my chatty formulation above. After defining the class ‘Nc’ of cardinal numbers as the class of classes of classes z for which there exists a class having z as its cardinal, Russell unfortunately slipped up in his definitions from 1 upwards (p. 435); he pointed out the mistake to Frege December 1902 (Frege Letters, 251) and the following November to Couturat (RA), but not in The principles. I give both definitions, in chronological order:
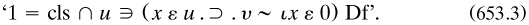
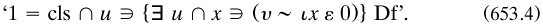
The first definition fails because it allows the class 0 ε 1.
After defining the class ‘Nc fin’ of finite cardinal numbers by the property of mathematical induction—which he took as known rather than primitive—Russell worked through the basic operations and (in)equations of finite arithmetic. However, his construction was incomplete, in that he used multiplication but did not define it. After defining the class of infinite cardinals as the complement of Nc fin relative to Nc, he also proved various results of its different arithmetic, finishing off with the Schröder-Bernstein Theorem 425.1 to establish trichotomy (p. 430, citing Borel 1898a, as in §6.4.7).
6.5.4 The second paper for Peano, March-August 1901: set theory with series. A draft of Whitehead’s paper seems to have inspired Russell to treat ordinals with comparable detail. A second paper for Peano was apparently drafted in the spring of 1901, and revised into French during July and August (Papers 3, 630–673); like the first, it also appeared the following year in two consecutive issues, as Russell 1902a. He provided a ‘General theory of well-ordered series’, largely as presented in Cantor’s recent two-part paper (§3.4.7). It enriched Russell’s budding logicism by expressing in Peanese his conviction of the importance of order for logic and mathematics.
Although much material was reorganised between draft and published version, there were no major changes of content and far less hesitancy than in the first paper. Presumably for reasons of diplomacy, Russell discarded the draft remark that the Peanists’ ‘endeavour to dispense with relation altogether as a fundamental logical notion’ (Papers 3, 632). The major theme of this paper was the class ‘of relations generating well-ordered series’, defined from the appropriate kind of transitive relation P, with domain π (1902a, 390). The class λP of relations order-isomorphic to P launched a lasting concern with ‘the relation likeness [L] between two relations’ P and P′ with common domain π under the generating relation (§6.4.7) S with domain σ:
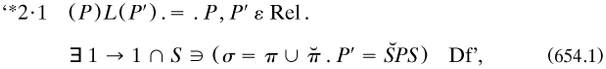
together with the class λP of relations order-isomorphic to P (p. 392). ‘As the properties of likeness are important, I shall develop some of them’, especially concerning order-isomorphism and terms in the generated series (pp. 393–395, 407–409). Likeness led via the class Ω ‘of relations generating well-ordered series’ (p. 390) to
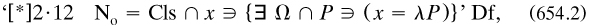
where this time without doubt ‘No is the class of ordinal numbers. An ordinal number is a class of well-ordered similar relations’, although the status of (654.2) as definition was not mentioned (p. 393, ‘No’ misprinted). After a previous, and this time correct, definition of ω (p.391), he advanced up to ω1 (p. 416), the starter of Cantor’s third number-class; he even proved results such as ω1 = ωω1 (p. 420). He also established Cantor’s theorem that the series of ordinals less than any given one was well-ordered, but he confessed that ‘We do not know how to demonstrate that the class of all ordinals forms a well-ordered series’ (p. 405), and later that ‘There is no reason, so far as I know, to believe that every class can be well-ordered’ (p. 410).
Russell worked out many features of ordinal arithmetic. In contrast to his definition of mathematical induction in the first paper, he now had in *6.1 ‘a generalized form of complete induction. In a well-ordered series, if s be a class to which belong the first term of the series and the successor of any part of the series contained in s, then the whole series is contained in s’ thanks to the transitive and asymmetric relation which generated the terms of s as its field (pp. 404–405). Maybe there was influence from Burali-Forti (§5.3.8) as well as Peano in this reduction of assumptions.
While trying later in this article to show that the ordinals were associative under multiplication (*6.47), Russell confessed that ‘I do not know how to extend the method of Prop 6.47 to a product of an infinite number of ordinals’ (p. 408). Further thoughts on precisely this technique would make him a pioneer of the axioms of choice three years later (§7.1.6).
In addition, Russell considered the transfinite cardinals, starting out from a definition of 0:
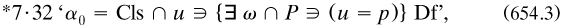
where ‘I have replaced Cantor’s aleph by α, since this letter is more convenient’ (p. 410); ‘p’ was the ‘range’ of P, that is, the union of its domain and converse domain (p. 390). In a short manuscript on ‘continuous series’ produced probably later in 1901 (Papers 3, 431–436), he went further by trying to produce Peanist definitions of rational and real numbers in imitation of Cantor’s way of producing continuous order-types (§3.4.6).
In a ‘Note’ within the paper Russell extended the definitions to cases where P and P′ might not be well-ordered, thus creating relation-arithmetic’ instead of Cantorian ordinals (1902a, 407–408). He developed the theory during the winter in various notes (Papers 3, 437–451). Perhaps around this time and certainly under the influence of the content of this paper, he added three important articles (299–301. to Part 5 of The principles. In the first he outlined the basic principles of likeness between relations, and relation-arithmetic, presaging his most original contribution to PM (§7.8.5). In the second he recalled Cantor’s two principles of generating finite and then transfinite ordinals (§3.2.6); but he felt that Cantor’s well-ordering principle ‘seems to be unwarranted’, giving the absence of a proof of the well-ordering of the continuum as an example. The third one took the special case of ‘the type of the whole series of all ordinal numbers’—where talk of the greatest one led to a ‘contradiction’ of Burali-Forti (p. 323). Logicism had seemed to be going wonderfully well; however, just at this sunny time the roof fell in. As he recalled later (1959a, 73), ‘after an intellectual honeymoon such as I have never experienced before or since’ in writing The principles in the autumn of 1900, ‘early in the following year intellectual sorrow descended upon me in full measure’.
A paradox is properly something which is contrary to general opinion: but it is frequently used to signify something self-contradictory [...] Paralogism, by its etymology, is best fitted to signify an offence against the formal rules of inference.
De Morgan (1847a, 238, 239.
6.6.1 Russell on Cantor’s ‘fallacy’, November 1900. In the essay in the International monthly Russell described as a ‘very subtle fallacy’ Cantor’s belief (§3.5.3) that there is no greatest cardinal (1901a, 375). He was following a passage in the manuscript of The principles written in November 1900 on ‘The philosophy of the infinite’ where, with his usual enthusiasm for faulting Cantor before reading him carefully, he found two supposed errors:
1) there was such a number, namely that of the class ‘Cls’ of all classes, so that
2) the diagonal argument (346.1) could not be applied to it to create a class of still greater cardinality.
Applying that argument to Cls by setting up a mapping to its power-class in which each class of classes was related to itself and every other class to its own power-class, he thought that ‘Cantor’s method has not given a new term, and has therefore failed to give the requisite proof that there are numbers greater than that of classes’ (Coffa 1979a, 35).
But at some time in the ensuing months Russell thought over this argument, and diagnosed a different illness. Maybe he had read Cantor’s paper 1890a introducing the diagonal argument, perhaps in the Italian translation 1892b in Peano’s Rivista, which he now possessed. Or maybe he had told his result to Whitehead, who was then working on Cantor’s theory of cardinals (§6.5.3) and who would doubtless have found unbelievable the deduction above. In a letter to Jourdain now lost, Russell reported that ‘In January he had only found that there must be something wrong’ concerning this argument (Jourdain 1913e, 146). He now found fault neither in the idea of no greatest cardinal nor in the diagonal argument but in the new class thrown by up the mapping—and the new news was very serious.
6.6.2 Russell’s switch to a ‘contradiction’. We recall from §3.4.6 that Cantor’s diagonal argument showed that the cardinality of any class α; was less than that of its power-class P(α) by attempting to set up an isomorphism between the classes but finding a member of P(α)—that is, a class—to which there was no corresponding member of α. After noting that some classes belonged to themselves while the rest did not do so, Russell now took his deduction to show that the class of all classes which did not belong to themselves belonged to itself if and only if did not do so—and, by a repetition of the argument, vice versa also. This is his paradox.
The passage in The principles was withdrawn (but Russell kept the folio), and in May 1901 the revised argument was expressed in terms of predicates in the chapter on ‘Classes and Relations’ of an attempted ‘Book 1 The Variable’ (§6.7.1) (m1901c, 195):
We saw that some predicates [for example, ‘unity’] can be predicated of themselves. Consider now those (and they are the vast majority) of which this is not the case. [...] But there is no predicate which attaches to all of them and to no other terms. For this predicate will either be predicable or not predicable of itself. If it is predicable of itself, it is one of those referents by relation to which it was defined, and therefore, in virtue of their definition, it is not predicable of itself. Conversely, if it is not predicable of itself, then again it is one of the said referents, of all of which (by hypotheses) it is predicable, and therefore again it is predicable of itself. This is a contradiction, which shows that all the referents considered have no common predicate, and therefore do not form a class.
He was to summarise this deduction on 24 June 1902 in his second letter to Frege (Frege Letters, 215–217). In May 1905 he outlined it to Jourdain (my 1977b, 52), and a few weeks later he gave a much more detailed account to Hardy (my 1978a).
This result was a true paradox, a double contradiction, not another neo-Hegelian puzzle to be resolved by synthesis. Although Russell always called it simply ‘The Contradiction’, he surely realised its significance quickly; if he ever thought otherwise, then Whitehead, Hardy or Jourdain would have soon set him straight. But no doubt his neo-Hegelian habit of seeking contradictions helped him to find it, and early on in his Peanist phase. There is a striking contrast here with Frege, who had been in the same area of work for over 20 years but had not found it. We recall from §4.7.6 that Zermelo had found the paradox in 1899; but he seems to have told nobody outside the Gottingen circle, so that it was new to both Frege and Russell.
The change of interpretation, occurring at some time over a period of intense work, may explain Russell’s uncertainty over its date. In his autobiography he gave May 1901 (1967a, 147); but in earlier reminiscence he stated Spring (1959a, 75–76), and twice—surely wrongly—June (1944a, 13; 1956a, 26). Even nearer the time he was no better, giving Jourdain the June date in the recollection of 1910 noted in §6.6.1 but Spring in 1915 (my 1977b, 133, 144).
Whenever the change occurred, something had gone wrong. Where was the error: in the set theory, or the logic, or both? Maybe somewhere else? And could the paradox be Solved, or only avoided?
6.6.3 Other paradoxes: three too large numbers. (Garciadiego 1992a, ch. 4. There should have been further consequences of the new interpretation of Cantor’s argument; for Cantor’s claim that there was no greatest cardinal was perhaps another paradox—or maybe two of them. Russell’s deduction had drawn upon the diagonal argument, which itself leads to a paradox concerning the exponentiation of cardinals. Writing again his ‘Cls’ for the class of all classes and using Cantor’s overbar notation, it takes forms such as
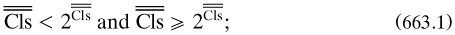
the first property follows from the power-class argument while the second relies upon the definitions of Cls. On the track of this paradox, Russell was diverted from it by his switch of thinking, and it has rarely been mentioned in the discussion of paradoxes (my 1981a). Instead, the usual paradox of the greatest cardinal is a different one based just on the sequence of cardinal without exponentiation; in the above notation, it could read
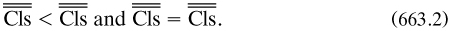
Russell never mentioned (663.2) at all, and (663.1) only in one of his papers (1906a, 31) and in his popular book on logicism (1919b, 135–136), naming it after Cantor. (By contrast, more modern accounts of the paradoxes usually present (663.2) and ignore (663.1.).) The most relevant passage in The principles occurs in a discussion of the diagonal argument (p. 362), fairly heavily rewritten at some stage and occurring shortly before the passage on Cantor’s ‘fallacy’ which he was to replace.
In his lists of paradoxes Russell stressed much more strongly that of the greatest ordinal number, which takes forms such as (663.2) with one overbar instead of two and inequality read in ordinal terms. Presumably he gave it greater publicity because of its intimate connection with order and thereby with relations, two staples of his philosophy. The two paradoxes are closely linked; for if the Cantorian cardinal β generates a paradox, then ordinal β must be pretty large also. He learned of trouble with ordinals in January 1901 in correspondence with Couturat (Papers 3, 385), from whom he borrowed the paper Burali-Forti 1897a. After defining a ‘perfectly ordered class’, explicitly different from Cantorian well-order, Burali-Forti had shown that the trichotomy law did not apply to its members; thus its order-type Ω could satisfy the order-inequalities
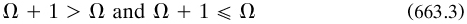
without logical qualms. But he had also confused the situation by repeating, from an earlier paper 1894a on simply ordered classes, a mistaken definition of well-order; he corrected himself only in an addendum 1897a. Thus the possibility of paradox was mixed in with different kinds of order and with mistakes (as the Youngs 1929a were to point out rather heavy-handedly, quoting Cantor’s sarcasm from a letter to them).
Russell’s reaction to Burali-Forti’s deduction was to apply it to Cantor’s well-order-type, obtain the result analogous to (663.2), and award it also the status of paradox. He named it after Burali-Forti first in a note added at the end of his second paper in the Rivista, where he wished to deny the property of well-ordering to the inequality relation (1902a, 421); and later in The principles in the new article 301 noted in §6.5.4 (G. H. Moore and Garciadiego 1981a).
Cantor had known this result already, and followed his policy of avoiding the absolute infinite, as with the paradox of the greatest cardinal (§3.5.3). So did E. H. Moore, who found it a little later than Burali-Forti and took it to be really paradoxical; but, despite his strong interest in Mengenlehre (§4.2.7), he only wrote about it in a letter of September 1898 to Cantor.16 So Russell was unaware of that predecessor.
Whatever the historical situation about these three strange results, Russell did see them as paradoxes. They were very much his creations, including the names.
