This chapter covers the period during which Whitehead and Russell collaborated to work out their logicistic programme in detail. Mostly they prepared Principia mathematica at their respective homes at Grantchester near Cambridge and Bagley Wood near Oxford; thus much discussion was executed in letters, of which several survive at Russell’s end.
This chapter divides into two halves around 1906 and 1907 because of their change of strategy. After accumulating more paradoxes and axioms, and much work on denoting (§7.2–§7.4.5), Russell developed intensively a logical system which he called ‘the substitutional theory’ (§7.4.6–8); but then he abandoned it and switched to the one which was to appear in PM (§7.7-9). At the division point are noted some of the reactions of others to logicism and related topics, especially set theory, and the independent activities of Whitehead (§7.5–6).
Another difference between the two halves concerns access to Russell’s writings: the first one is comprehensively covered in Russell’s Papers 4, but the succeeding volume will not be ready for the second half until after the completion of this book. In some compensation, two compilations of papers by Russell and others are available: Russell Analysis (1973) and Heinzmann 1986a.
7.2.1 Uniting the paradoxes of sets and numbers. The task was to find a logical system of propositions and propositional functions, with quantification over them and also over individuals, using set theory as fuel, in which as much mathematics as possible could be expressed but the paradoxes avoided and indeed Solved. ‘Four days ago I solved the Contradiction’, Russell had told himself in his journal on 23 May 1903, while finishing The principles, ‘the relief of this is unspeakable’ (Papers 12, 24). But, like stopping smoking (which Russell himself never attempted), it was easy to do, lots of times. ‘Heartiest congratulations Aristotles [sic] secundus’, wrote Whitehead in a telegram the following 12 October after another solution; however, Russell wrote on it later: ‘But the solution was wrong’ (RA, reproduced in Garciadiego 1992a, 187).
Before publishing The principles, Russell had found that his own paradox could be expressed in terms of relations. He showed Frege on 8 August 1902 that if relations ‘R and S are identical, a[nd] the relation R does not hold between R a[nd] S. One sets this equal to (R)T(S), where T should be a relation. With R = T one then obtains a contradiction’ (Frege Letters, 226–227). He published this version in a paper of 1906, where he also generalised it to cover all three paradoxes of classes in terms of any relation f between classes u (1906a, 35):
Given a property ϕ and a function f, such that, if ϕ belongs to all the members of u, f‘u always exists, has the property ϕ, and is not a member of u; then the supposition that there is a class w of all terms having the property ϕ and that f‘w exists leads to the conclusion that f‘w both has and has not the property ϕ.
The paradoxes arise as shown in Table 721.1.
7.2.2 New paradoxes, mostly of naming. (Garciadiego 1992a, ch. 5) New paradoxes soon arrived, mostly concerning naming and definability. At the International Congress of Mathematicians at Heidelberg in August 1904, the Hungarian mathematician Julius König (1849–1913) proposed a refutation 1905a of Cantor’s continuum hypothesis by claiming to show that the continuum was not well-ordered. Cantor was present, and after the lecture took part in a discussion with Hilbert and Schönflies: ‘only simple remarks were made and not objections to the proof, according to a report (Fehr 1904a, 385), ‘However, Mr. Cantor reserved for himself the right to a more considered examination of the problem’, and indeed emotionally urged colleagues to locate the mistake. Hausdorff 1904a quickly found it, in the use of a theorem about cardinal exponentiation under invalid conditions (Kowalevski 1950a, 198–203, wrongly credits Zermelo). The discussion continued at a gathering of mathematicians at Wengen in the Bernese Overland: König’s failure ‘is a great triumph for Cantor who spoke of nothing else in Wengen’, Hilbert told Klein in a letter.1
However, the following year König came back with a different refutation 1905b; like the first, it appeared in Mathematische Annalen. The non-de-numerable cardinality of the continuum entailed that not all real numbers could be defined in a finite verbal expression; hence there must be a smallest such number—but this property itself was stated in a finite verbal expression. He concluded that Cantor’s well-ordering principle was false (this claim related to the controversy over the axioms of choice to be described in §7.2.5), and by consequence the continuum hypothesis also.
Around the same time, the French school-teacher Jules Richard (1862–1956) published a similar paradox, in a note 1905a in a general science journal; it was reprinted the following year in Acta mathematica. He also considered the set F of finitely definable numbers and wondered about a number definable by applying Cantor’s diagonal argument to the members of F; a different number was produced, but the argument itself furnished it by a finite definition. His version was independent of König’s; it grew partly out of some consideration of his own recent book on the philosophy of mathematics (Richard 1903a, 107–113), and he had been led to write his note by reading of the Heidelberg contretemps.
Russell heard of these paradoxes from the publications or from correspondents such as Couturat and Jourdain. But another version arrived directly, from a resident in Summertown in north Oxford, not far from him at Bagley Wood: G. G. Berry (1867–1928), a junior librarian at the Bodleian Library and in Russell’s opinion ‘a man of very considerable ability in mathematical logic’. Stimulated by reading The principles, he wrote ten letters to Russell between 1904 and 1910 (published in Garciadiego 1992a, 166–184): his only known writings on logic, which also reveal an impressive familiarity with Cantor’s theory of transfinite numbers. The paradox which he gave to Russell came in the first letter of 21 December 1904, in which he also considered the class of ordinals not finitely definable: ‘This least member of the class is then the least ordinal which is not definable in a finite number of words. But this is absurd, for I have just defined it in thirteen words’ (p. 168). Russell’s reply is unfortunately lost, but he published the paradox (first in 1906h, 645).
According to a note left by Russell, Berry also brought him a paradox to his front door (Garciadiego 1992a, 166):
The first time he came to see me at Bagley Wood he was bearing, as if it were a visiting card, a piece of paper on which I perceived the words: ‘the statement on the other side of this paper is false’. I turned it over & found the words: ‘the statement on the other side of this paper is false’. We then proceeded to polite conversation.
This recollection seems incorrect: doubtless Berry had written ‘false’ on one side of the paper and ‘true’ on the other one. But it is the origin of ‘the visiting card paradox’, as it has become known.2 Surprisingly, Russell never included it in his lists of paradoxes; publicity was to be brought by Jourdain, especially in a paper 1913f. Presumably Russell regarded it only as a variant on the classical Greek paradox of the liar, which arises from pondering upon the truth-value of the proposition ‘This proposition is false’.3 He did list that paradox, first in 1906h, 632; he might have been encouraged to do so by this nice version sent to him in January 1905 by his friend Oliver Strachey (RA):
David said, (in a moment of wrath):—‘All my remarks between the hours of 2 and 3, are, have been, or will be lies’. All his other observations in this period were palpable falsehoods, and this one was made at 2.30. Was it true or false? In my present state of mind this seems to be another edition of the damnable Contradiction,—probably soluble by what you call the harsh and highly artificial suggestion of various types of propositions. [...] Any sign of lunacy in this letter please put down to your Appendix B and blame yourself (like suicides or the heroes of Smiles’ Self-Help).
Down the side of the letter he questioned: ‘What I mean is Can a proposition be its own subject?’. Russell wrote on it: ‘Answered more or less’ (but now lost., and he repeated this version to Jourdain the following April (my 1977b, 44, 50). Berry found it independently, and told Russell in November 1906 (Garciadiego 1992a, 179–180).
7.2.3 The paradox that got away: heterology. One paradox which never seems to have come to Russell’s attention is that named after the German philosopher Kurt Grelling (1886–1942), who published it in a paper written with his friend Leonard Nelson (1882–1927) (1908a, art. 4). Some words can be predicated of themselves: in English, ‘word’ is a word, ‘noun’ a noun, and so on. This property is called ‘autological’, and is obviously itself autological. Others English words are not autological; ‘German’, say, or ‘verb’. They are called ‘heterological’—but this word is heterological if and only if it is not so.
Grelling and Nelson both belonged to the Fries school of philosophers (§4.2.5); their paper appeared in its Abhandlungen. Close to David Hilbert in Göttingen, they came to paradoxes partly through his interest in them (Peckhaus 1995b). Their own is an interesting one, not least for endangering the law of excluded middle (which kind of word is ‘gracious’, say?), as they noted in a survey of candidate ‘solutions’ and ‘corrections’ (arts. 6–7), in which they sought to avoid ‘circular definitions’ and propositions (arts. 13–15). It suggests extensions to phrases and propositions, such as ‘I kan spel verry acurratly’. Strangely, Russell never mentioned it, although he corresponded with Grelling in 1909 on a possible translation of The principles, and in the following year on type theory (RA). The translation was not done, but later Grelling translated some of Russell’s philosophical books; so the contact must have continued.4 In his Dissertation written at Göttingen under Hilbert’s direction, Grelling 1910a reviewed the development of finite arithmetic without using an axiom of infinity, relying much on Zermelo’s recent investigation 1909a (§4.7.1) and working out from Russell’s definition of cardinal numbers as classes of similar classes.
Another member of the Fries school was the mathematician and philosopher Gerhard Hessenberg (1874–1925). As we saw in §4.2.5, he published in the Abhandlungen a long article 1906a on ‘Basic concepts of Mengenlehre’, which was also sold in book form. As a Kantian, Hessenberg was prone to see paradoxes everywhere and came only to the naming paradoxes in the 23rd of his 30 chapters—a rather dull treatment which however may have inspired Grelling and Nelson two years later. The next chapter treated the ‘ultrafinite paradoxes’ such as Russell’s, which he appraised as ‘not especially mathematical, from that also comprehensible to lay people, but at the same time not dangerous for mathematicians, who have nothing to do with the class of all things’. His solution followed from assuming that ‘a class is to be distinguished from each one of its elements’ (art. 97, together with praise for Poincaré 1906b (§7.4.5)). He took Burali-Forti’s paradox more seriously, since it related to his extensive discussion of order-types; in fact, he found it to be ‘completely unsolved’, and tried to sketch a solution in terms of theorems claiming it impossible to adjoin elements to the class of all ordinals (arts. 98–99).
7.2.4 Russell as cataloguer of the paradoxes. Apart from Grelling’s, Russell collected or created all the ‘paradoxes of logic’, as he came to call them (the title of his paper 1906h, for example). His motive was not only a practical one, the doctor seeking out all occurrences of the virus in the body logic, whether in classes, names, propositional functions, propositions or truth-values; he also wanted to Solve them in some philosophical sense, and not merely avoid them. This desire for a “global” remedy may have prevented him from wondering if the paradoxes differed in any basic way. Thus he made no reaction to another of Peano’s flash (but typically undeveloped. insights at the end of a miscellany paper 1906b in his Rivista: after formalising Richard’s definition of the troublesome number N, Peano noted that it was partly symbolic and partly verbal, so that ‘the example of Richard does not pertain to Mathematics, but to Linguistics; an element, fundamental in the definition of N, cannot be defined in an exact manner (according to the rules of Mathematics)’. This line of attack, and the distinction of paradoxes which it excited, was not to be taken up until the 1920s (§8.4.6); Russell was not one of the instigators, although Peano mentioned the remark to him in a letter of September 1906 (Kennedy 1975a, 218). Cantor was close to it also; in a letter of 8 August 1906 to Hilbert he pointed out the difference between definitions as such, always finite, and the concepts which they define (Hilbert Papers, 54/29).
Russell also did not much consider the logical forms of the paradoxes. In Cantor’s and Burali-Forti’s results, given the premise p that there exists a greatest cardinal or ordinal respectively, opposing conclusions (c and ~c) are deduced about it:
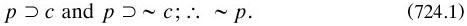
Reductio ad absurdum proofs can have this logical structure, sometimes in the condensed form given by c = p:
(This is the version called ‘reductio’ in PM, *2·01, although without distinction of ‘⊃’ from ‘∴’—or of reductio from the method of indirect proof, which is effected by deducing contradictory consequences from ~p). But with Russell’s paradox, from the premise r that his class exists, we deduce the following about the proposition b that it belongs to itself:
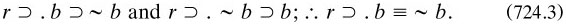
The differences may be reconciled via reductio, so no basic issue arises; in its terms, the paradoxes of the greatest numbers and of naming exemplify the first form while Russell’s, the liar and Grelling’s take the second.
Questions of form should be distinguished from those concerning the existence assumptions that have to be abandoned in each case (my 1998b). For example, there is no barber who shaves those and only those who do not shave themselves, thus there is no barber (seemingly Russell’s reaction in 1918–1919a, 261); by contrast, eliminating Russell’s paradoxical class affects set theory and logic quite fundamentally, as he was to find for several years to come.
7.2.5 Controversies over axioms of choice, 1904. In other letters of 1906 Peano expressed to Russell his opinions on the current discussion of the axioms of choice (Kennedy 1975a, 216–217). It bore strongly upon logicism; indeed, Russell deserves greater credit for its recognition than is generally realised. Luckily, it has been well examined by historians, especially in the early 1980s.5 Thus the summary here is brief; some general points now, and Russell’s role in the next sub-section.
As part of his investigations of set theory (§4.7.6), Ernst Zermelo published at the end of 1904, his 34th year, a short paper 1904a in Mathematische Annalen in which he proved Cantor’s well-ordering principle (§3.5.1). His proof rested upon admitting a new axiom proposed with his friend Erhard Schmidt (1876–1959); in his axiomatisation of set theory Zermelo 1908b called it ‘the axiom of choice’, which soon became the standard name. Given a non-empty class M, assume the existence of a functional covering to associate with each non-empty subclass M′ one of its members as ‘distinguished’; then the collection of them may be treated as a class on a par with its parent classes. The proof followed by associating any member of any well-ordered subclass of M with its complementary subclass.
The assumption of infinite selections had been made before by many authors, including Weierstrass, Dedekind and Cantor (§3.5.2), but its status had rarely been questioned. But Peano was one who did: in the above letter to Russell he recalled that he had stated it as a principle in his paper on differential equations described in §5.2.5 (1890b, 150). However and typically, he had not developed his insight, and serious attention dates only from Zermelo’s paper.
A sharp controversy quickly developed over the legitimacy of the axiom. Soon after publishing 1904a, Zermelo surveyed it himself before the Göttinge Mathematische Gesellschaft on 15 November 1904.6 Running for several years, it was an exceptionally rich source of controversy among mathematicians and philosophers (though Hessenberg was rather agnostic in 1906a, ch. 25). The following questions attracted especial attention:
1) Different forms of the axiom were found; for this reason I use the plural ‘axioms’. Were they in fact logically equivalent, and were some philosophically more acceptable than others? One important issue was whether the choices were made simultaneously or successively; another concerned denumerably versus non-denumerably many choices.
2) Which theorems were logically equivalent to the axioms, and so became candidate axioms themselves? In a sequel paper Zermelo 1908a showed that the well-ordering principle was one; over the decades more and more results were found to be either equivalent to, or necessary or sufficient for them (G. H. Moore 1982a, app. 2).
3) Was the infinitude of independent choices a legitimate mathematical procedure? If so, was the choice class defined, or merely constructed? The French school of analysts became much exercised with this matter, especially in mutual correspondence which I cite as ‘Letters 1905a’. Emile Borel, subscribing to a constructivist view of mathematics similar to Kronecker’s (§3.6.4), worked only with classes put together by at most a denumerable number of unions and complementations of classes (§4.2.3); thus to him all forms of the axiom were unacceptable. At first Henri Lebesgue was chary of its use, for example in his analysis 1905a of René Baire’s classification of functions (§4.2.2) he strove hard (but unsuccessfully. to avoid it; but he let it slip into his later work (G. H. Moore 1983a).
4) If acceptable at all, where in mathematics were the axioms needed? Very many places were found in set theory and mathematical analysis, and also in other branches of mathematics; the gold-digging went on for quite a time.
5) Could proofs using the axioms be reworked without them? Sometimes this was clearly so, often apparently not—and on occasion the matter was unclear. An interesting example is the Bolzano-Weierstrass theorem (§3.2.6), where both answers seemed to apply. Eventually it was realised that four different theorems lay under this title, depending upon the way in which definition of infinitude was used and what kind of point was claimed to exist. The following version of the theorem does need an axiom: an inductively infinite bounded class of points possesses at least one limit point (Sierpinski 1918a, 122).
6) Do they lead to paradoxes of their own? After all, Zermelo’s paper came out shortly before the appearance of the naming paradoxes, which could be applied to ordered classes. Certain consequences took the same logical form. In particular, the Italian mathematician Giuseppe Vitali (1875–1932) published a little pamphlet 1905a related to the new theories of integration and measure of the time (§4.2); assuming available the required properties of a measure such as infinite additivity, he used an axiom to construct a class whose measure was both zero and greater than 1 (an example of (724.1)), and conclude that it was not measurable.
7.2.6 Uncovering Russell’s ‘multiplicative axiom’, 1904. Among works published before 1904 which showed implicit use of infinite selections, Russell’s The principles is a prominent example. Various passages on, for example, definitions of the infinite, the well-ordering principle, and the multiplication of cardinals, show him on the brink of its discovery. In May 1905, in his second letter to Russell (Garciadiego 1992a, 170), Berry pointed to this last context (a passage on p. 118.; presumably in his reply he learnt that Russell had in fact found the axiom exactly there the previous summer. As Russell was to recall to Jourdain in March 1906 (my 1977b, 80),
As for the multiplicative axiom, I came on it so to speak by chance. Whitehead and I make alternate recensions of the various parts of our book, each correcting the last recension made by the other. In going over one of his recensions, which contained a proof of the multiplicative axiom, I found that the previous proposition used in the proof had surreptitiously assumed the axiom. This happened in the summer of 1904. At first I thought probably a proof could easily be found; but gradually I saw that, if there is a proof, it must be very recondite.
Note that his dating of the discovery places it slightly before the conception and writing of Zermelo’s paper, so reversing the priority over finding Russell’s paradox (§4.7.6).
We saw that Whitehead had stressed the importance of defining infinite multiplication logicistically via the definition (653.2) of the multiplicative class dx of a class d: pursuing this line, Russell found this surprising need, using the name ‘multiplicative axiom’ because of this context. In contrast to Zermelo’s assumption of a covering functional, he accepted the need for the class involved. At first he thought that he assumed less than Zermelo had because of its restriction to mutually disjoint classes (my 1977b, 63), but in March 1906 Jourdain gave him a rather loose argument for their equivalence (pp. 81–83); a tighter proof appeared in PM, *258·32–37.
Like his contemporaries, Russell realised that the proofs of many theorems were now puzzling or maybe defective; but logicism faced a special extra difficulty. Whatever form his logic were to take, it had to be finite, both horizontally in the lengths of expression and formulae and vertically in the lengths of proofs. But the first constraint was now threatened: how could he find in his logic a propositional function to express an infinitude of independent selections of members from classes?
Spotting this quandary in January 1906, Jourdain wondered if the axioms might be stated in terms of the possibility of splitting a many-many relation into an infinite class of many-one relations in some appropriate way. Russell agreed, proposing an alternative version about the existence of a class which had only one member in common with each class in a class of mutually disjoint classes (my 1977b, 67–69); but, quite apart from the state of logicism at the time, especially the relationship between classes and propositional functions in general, the place of the axiom was not clear. He corresponded with Jourdain, and also Hardy, on examples of its use; and he worked on it from time to time, most notably in a manuscript m1906h of 31 folios, in which he compared a variety of forms expressed in terms of classes, relations or substitutions (the latter his logical system at that time, as we shall see in §7.4.6). He was to remain very sceptical about this axiom, and looked forward to a proof of it from standard procedures and notions of set theory (§7.8.7); but he never dealt with the quandary spotted by Jourdain.
7.2.7 Keyser versus Russell over infinite classes, 1903–1905. Another axiom for set theory confronted Russell, this time sent from the U.S.A. In the early 1900s the mathematician and philosopher Cassius Keyser (1862–1947) became interested in mathematical induction (hereafter, ‘MI’), especially in connection with definitions of infinity. After a survey paper 1901a on the finite and the reflexive infinite published by the American Mathematical Society, he presented his main conclusion in a lecture to them; that the existence of an infinite class was assumed as an ‘axiom of infinity’. He considered Poincaré’s view argued in 1894a, that much of ‘the nature of mathematical reasoning’ rested upon MI as a primitive procedure, and saw the axiom buried in Poincaré’s metaphysical belief that ‘the affirmation of the power of the mind which knows itself capable of conceiving of the indefinite repetition of the same act as soon as it is possible once’ (Keyser 1903a, 427, translating Poincaré. Similarly, Dedekind’s theory of chains to generate the cardinals (§3.4.2) included the ‘theorem on the definition by induction’ which assumed the axiom in the ψ transformation, and again in Dedekind’s (and also Bolzano’s) claimed proof of the existence of an infinite class by taking an object, the thought of it, the thought of the thought of it, and so on—but how? (pp. 429–434).
A committed Christian, Keyser rehearsed his views in an aroma of theology in a paper 1904a in the April issue of The Hibbert journal, a ‘quarterly review of religion, theology and philosophy’ recently founded from funds established 50 years earlier by the Victorian philanthropist Robert Hibbert (1770–1849). Among texts criticised by Keyser was Russell’s The principles, which had appeared in the interim; so Russell quickly wrote a short reply 1904f in the next issue. Following his line in his book (1903a, 357–358), he asserted that Dedekind’s theory implied the actual infinite but did not presuppose it, so that the axiom was not needed. However, in a retort Keyser did not budge, on the grounds that ‘trying to prove that proof is a possible thing’ involved an unavoidable vicious circle (1905a, 382). At this time Russell still regarded propositions as objects, which bolstered his defence; but in 1906 he changed to Keyser’s position (without the theology. after further work on his logical system (§7.7.2).
Frege and Russell are not ordinary language philosophers, but ideal language philosophers.
Jan Dejno
ka (1996a, 222)
7.3.1 First attempts at a general system, 1903–1905. (Russell Papers 4, Parts 1–2) Russell wrote some thousands of folios in and around logic between 1903 and 1907. Among those that he kept, many form fairly connected essays on specific topics; but some long ones read like logical experiments, in which he started out from one possibility or issue but then wandered around a whole range of options, producing partly developed and mutually inconsistent forays. Numerous nice features adorn the corpus; the coverage in this chapter is perforce limited.
Some manuscripts were versions of ‘Volume II’. In one group, cited collectively as Russell m1903c, the treatment was systematic enough to use Peano’s numbering of propositions by asterisked digit strings and method of dots for brackets, as well as various of his notations; Whitehead was especially fertile in inventing new ones. They used ‘ϕ|x’ for the ‘value’ of a propositional function ϕ of one argument, with ‘|’ specified as an indefinable, before switching for a time to ‘ϕ‘(x)’. For abstraction they moved away from Peano’s symbol ‘∋’ for ‘such that’ either to existential quantification or to the right apostrophe as in ‘x(X)’ for the ‘form’ of the well-formed formulae (or ‘expression’. X in which x was a constituent. The form X was not necessarily a propositional function ϕ; but in such a case, the two notions were assumed to be inverse (p. 53):
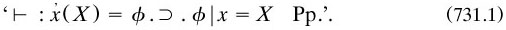
Here, and throughout these manuscripts, Russell used Frege’s assertion sign (§4.5.6), and seemingly in a similar way. In March 1908 he explained the need for this sign to the writer Horace M. Kallen thus (copy in RA):
In common language, the effect aimed at is produced by the use of a verb instead of a verbal noun, e.g. ‘Caesar died’ instead of ‘Caesar’s dying’. But when you are using symbols, this is impossible, and therefore a special symbol is required. Thus I should say, in words,
‘The proposition “x = x” is true’ or “is the law of identity” or etc.
But if I wish to assert ‘x = x’, I write
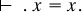
Russell also tried out Frege’s modification to Law 5 to solve his paradox (§6.7.7), and a variant idea involving two kinds of membership to a class; but without success in both cases (pp. 3–15; see also Papers 4, 611–619). He essayed a few adventurous definitions, such as this one for the empty class (p. 30):
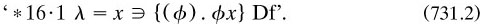
He also gave outlines of the theories of propositional functions and relations, again trying modifications to avoid the paradoxes without being close to any Solution (pp. 38–72).
A long and important manuscript is a collection of sheets marked ‘FN’ in the top left-hand corners, and dating from the autumn of 1904 (Russell m1904d). The first page has not survived, but we may surmise that the title was something like ‘Fundamental Notions’. The pagination goes up to 888, but he seems to have left gaps for possible later insertions. At all events, the 304 surviving folios show that he stopped around every 50 or so and wrote out the main assumptions or axioms tried since the last pause. In one particularly good folio, reproduced as Plate 4, he went over the batch of principles proposed to allow the proof of Cantor’s power-class theorem and then assessed them in pencil under the four-valued calculus ‘True’, ‘False’, ‘Probably true’ and ‘Doubtful’.
By June 1904 Russell was able to answer a request for information from Couturat (the context is explained in §7.4.1) with a collection of notes m1904a on the ‘Outlines of symbolic logic’ for these topics. Assertion was included among the indefinables; so was abstraction from ϕ, which was written ‘ϕ‘(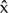
)’ (and remained so far apart from the latter omission of the apostrophe while the associated class abstraction was symbolised ‘x(ϕ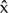)’. A passage in ‘FN’ written soon afterwards contains a plan for ‘Part I. Symbolic Logic’ in five Sections and articles up to *28 (m1904a, 149–150).
7.3.2 Propositional functions, reducible and identical. In addition, some durable notions were taking shape. One of these, explained to Russell by Whitehead in a letter of 23 April 1904, was the ‘reducibility’ of a function ‘ϕ!x’ (with exclamation mark), propositional or not, meaning that ‘an equivalent expression is x ∈ u’ for some class u (Papers 4, xxiv). While they had not yet attempted to impose any type theory on the predicate calculus, the aim of associating a function with a “simpler” one was similar. Russell wrote out axioms for ‘Reduc’ and some allied notions in his notes for Couturat (Russell m1904a, 84), and in an essay for himself at the time he included the sufficient condition that the truth-value of a reducible function was not affected if it were contained among its own values, and likewise for its negation function (pp. 89–90). In FN, which included a section on reducibility in the plan for the Part (p. 149), he referred to this condition as ‘the “vicious-circle” principle’ (m1904d, 138). This marks the début of another important idea in PM (§7.4.5), although here not adjoined to a type theory.
Russell also thought of the converse situation: a function ϕ was ‘irreducible’ if it were satisfied by some but not all members of any class u and also of its complementary class not-u. Moving the other way, ‘Irreducible sets [sic] are got by a zigzag’ which found terms satisfying some ϕ and then not-ϕ (written ‘-ϕ’: pp. 120–121). This procedure, which may have its origins in one of his late revisions to The principles, 103–105, gave birth to a ‘zigzag’ theory of solving the paradoxes by discarding from logicism such “complicated” propositional functions and their classes; the name may have been inspired by the alternation between functions and their negatives. However, although he entertained the theory for some time (§7.4.4), he never found a criterion of complication sufficiently simple to be practical.
PLATE 4. A striking folio from Russell’s working text ‘FN’ of 1904 (RA). He reviewed the efforts of the previous 40 folios to solve his paradox, with especial reference to Cantor’s (correct) power-set theorem. The sheet is shown also as Russell Papers 4 (1994), Plate 6.
Another important notion arising from these considerations was the relation of identity. Using Schröder’s symbol ‘1’’, Russell first used it for classes with this assumption (not definition) from equivalent propositions:
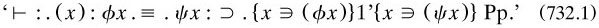
(m1903c, 5: the equivalence came out as a theorem on p. 15). The feeling here is intensional: equality of classes a and b came out extensionally on p. 17 as
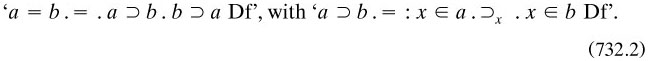
By the time of writing to Couturat the identity relation was defined
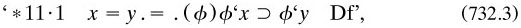
where apparently x and y were terms (m1904a, 81). This (Leibnizian. form of definition was to be adopted hereafter, although changes of theory altered the range of entities over which ϕ was quantified. One relevant factor here was the (lack of. restriction to propositional functions; for he was well aware that mathematical functions were different in kind, which needed to be treated with great care.
7.3.3 The mathematical importance of definite denoting functions. (Russell Papers 4, Part 3)
When we are speaking of an Individual, it is usually an abstraction that we form; e.g. suppose that we are speaking of the present King of France; he must actually be either at Paris or elsewhere [...]
Whately Logic9 (1848), 84 (from the third edition (1829) onwards.
We saw in §6.7.4 that Russell was much engaged with six little words, such as ‘a’, ‘any’ and ‘some’. Among them ‘the’ rose to prominence, partly for its intrinsic interest but also for its central place in mathematical analysis and set theory. In particular, Cauchy’s insistence that mathematical functions had to be single-valued (§2.7.2) was upheld by all successors, including the Weierstrassians; thus Russell had to be able to express them within his logical system. They were an especially important case of ‘denoting functions’, which he defined as any function which, unlike a propositional function, did not take a proposition as its value; others included, for example, the class of all arguments satisfying a propositional function. A good theory of these functions should also help to explain the use of such phrases in natural languages as well as in mathematics.
Russell occupied himself not only with the referentiability of denoting functions but also with allied issues such as their relationships with propositional functions and in turn to propositions, sentences and statements; the status and occurrence of universals and particulars; the ontological consequences of quantification; the effect of the paradoxes upon the generality of logic by imposing restrictions in the ranges of variables; and the place of truth-values. The intricacy of the resulting systems, and the intensity of Russell’s endeavours both published and unpublished, allow for much interpretation:7 this section picks out some principal features which bear most closely upon logicism.
‘If I say “I met a man,” the proposition is not about a man’, wrote Russell in The principles, ‘this is a concept which does not walk the streets, but lives in the shadowy limbo of the logic-books’ such as his own (1903a, 53). In a suite of manuscripts he tried to disentangle the relationships between concepts, proper names, and phrases and especially between propositional functions and denoting. In an early one, written in the summer of 1903, he reflected ‘On the meaning and denotation of phrases’ by noting of the current Prime Minister that ‘A proper name, such as Arthur Balfour, is destitute of meaning, but denotes an individual. On the other hand, verbs and adjectives have meaning but no denotation’; and soon he considered the case of ‘the present King of France’ (m1903d, 284–285). Whether or not Russell took the case of Monsieur le Roi from Whately, he treated Him differently; instead of pondering upon the current Royal Residence, he found a phrase with meaning but no denotation.
The relationship between names and descriptions was a very important issue, since truth values could change. A very nice arithmetical example came from the proposition, assumed true, that ‘the number of people at the meeting was greater than any one expected’; 5,432 came, but ‘5,432 was greater than any one expected’ is false (p. 317). Whitehead and Russell discussed this case in more detail the letters of the following April (RA).
With such examples Russell entered the labyrinth of reference, and wandered around it looking for a credible exit. As guide he worked with ‘complexes’, well-formed formulae in the predicate calculus including functions of functions, relations and quantification (m1904c, a summary written in October to enlighten Whitehead). One source was the philosophy of reference of the Austrian psychologist Alexius Meinong (1853–1920), especially a theory of complexes and ‘assumptions’ which Russell popularised in Britain with a long essay 1904e in Mind (J. F. Smith 1985a). Meinong granted reference to ‘the present King of France’ and even oxymorons such as ‘round square’, and permitted them to refute the law of contradiction by existing and not existing at the same time—both too luxuriant and illogical for Russell. However, in other respects, such as the notion of complexes, Russell received Meinong’s ideas positively, though he did not use them in his logicism (see the mixed reception of Meinong on zero in ch. 42 of The principles). The later, converse, influence is noted in §8.7.2.
In June 1905 an escape route began to appear when Russell laid down a list of principles in an experimental text ‘On fundamentals’. ‘A complex C has both being and meaning’, he decided (m1905a, 369), importing the former property from The principles as ‘that which belongs to every conceivable term, to every possible object of thought’ (1903a, 449). Being occurred with the assertion of C, while meaning was linked to its truth; similarly, each component of C had a corresponding ‘entity-position’ or ‘meaning-position’ (m1905a, 361). However, ‘The manner of occurrence of “the author of Waverley”’ in ‘People were surprised that Scott was the author of Waverley’ was ‘peculiar’, for the kinds of reason pertaining to the arithmetical substitution above (p. 370).
Russell analysed at length types of occurrences of components in complexes and propositions in compound propositions, and especially the difference between denoting and propositional functions. For notation ‘We may use (C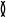 
x) for a general complex’ (p. 366); the unusual symbol was possibly taken from Arthur Cayley’s sign for polynomial forms in his theory of invariants. On identity, the form (732.1) was preserved, but ϕ ‘may be a denoting function, or a propositional function, or a propositional function of a denoting function, or a denoting function of a propositional function, but must not be a propositional function of a propositional function’ (p. 371).
7.3.4 ‘On denoting’ and the complex, 1905. Russell later wrote at the head of this manuscript that the list of its principles contained ‘the reasons for the new theory of denoting’ (Papers 4, 358). This was written in the next month, July 1905, as the paper ‘On denoting’, which appeared in Mind the following October (1905d). Perhaps his most famous essay, it was written in difficult personal circumstances, especially the death of a close friend, which must have contributed to the poor exposition (Urquhart 1995a). Understandably, editor G. F. Stout had been very reluctant to publish it (Russell 1959a, 83); but Russell never placed a major philosophical paper there again.
Russell began by stressing ‘the distinction between acquaintance and knowledge about’, of which the latter came through denoting. In a later paper he expressed this distinction in terms of ‘knowledge by acquaintance and knowledge by description’, and introduced the name ‘definite descriptions’ for his theory (1911c, 151–154). Working here with his six little words, he covered some of the corresponding complexes, such as ‘C (a man)’ as ‘It is false that “C(x) and x is human” is always false’. But the bulk of his analysis fell upon phrases using ‘the’, which led to ‘by far the most interesting and difficult of denoting phrases’ (1905d, 417). After a succinct and organised resumé of the June list of principles, with Scott and Monsieur le Roi again as main examples, he came up with these criteria under which a definite denoting phrase actually denoted, within the context of a proposition (p. 423):
[... T]he proposition ‘Scott was the author of Waverley’ (i.e., ‘Scott was identical with the author of Waverley’) becomes the proposition ‘One and only one entity wrote Waverley, and Scott was identical with that one’; or, reverting to the wholly explicit form: ‘It is not always false of x that x wrote Waverley, that it is always true of y that if y wrote Waverley y is identical with x, and that Scott was identical with x’.
Russell did not point out that his trio of criteria for the existence of a referent for a denoting phrase were exactly those which Peano 1897b had proposed (§5.4.3) in the special context of a single-valued mathematical function. Presumably Russell had forgotten Peano’s text, which he must have read in 1900; the first paragraph of the section is line-marked in the margin of his copy (RA). But he never referred to it, or to Peano at all, in the manuscripts preceding this paper.
Another difference is that Peano’s criterion was given nominally whereas Russell’s came contextually within a proposition. This basic feature was not emphasised in the paper, and is often overlooked; but Russell made it quite clear to Jourdain on 13 January 1906 (my 1977b, 70):
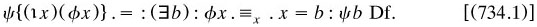
We put [for existence]
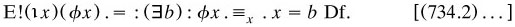
If u is a class, we write ι‘u for (ιx)(x ∈ u), that is,
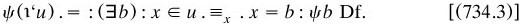
Contextual definitions were to be centrally important in PM, as we shall see in §7.8.4–5. They show one reason for distinguishing descriptions from names: the former, but not the latter, involve the scope within the defining formula.
Connected to contextual definition was ‘denoting complex’, a phrase composed of more than one word and working via the denotations of its constituent words, which Russell also emphasised in his paper. But later he played down its importance; when Ronald Jager 1960a argued plausibly that this complex denoted a meaning, as opposed to a ‘denoting phrase’ which expressed it, Russell wrote to him on 28 April 1960 (RA) that he had seen his paper as a ‘reductio ad absurdum of the view that a denoting complex has a meaning as well as (sometimes) a denotation’, was ‘surprised by your view that the concept of a denoting complex seems to you an essential part of my theory’ and judged that ‘I came later to think all that stuff about denoting complexes is unnecessary and in no degree essential to my argument’.
This self-criticism of the paper reflects the small reaction to it at the time. But G. E. Moore welcomed it in a letter of 23 October 1905 (RA); the ontological parsimony of Russell’s criteria would have warmed him. However, he acutely queried Russell’s claim that ‘all the constituents of propositions we apprehended are entities with which we have immediate acquaintance’ (italicising in a clause near the end of Russell’s paper., and wondered if the variable permitted such acquaintanceship. In his rapid reply Russell claimed that this was the case, but he admitted himself uncertain as to whether the variable was an entity or not (Papers 4, xxxv). The philosophy was still wanting; indeed, the feature highlighted by Moore was to concern Russell deeply after PM.
7.3.5 Denoting, quantification and the mysteries of existence. Russell’s account above to Jourdain involves a rather muddling aspect of his logic, which becomes noticeable from 1905 onwards: his multiple uses of the word ‘existence’, and the symbols that went with them (my 1977b, 71–74). There were two senses for individuals (‘I’ in Table 735.1), and three for classes (‘C’):
On individuals, the two senses do not necessarily interact; for example, the present King of England would not have been ignominiously placed at the bottom level in the type theory of PM. However, proved there is
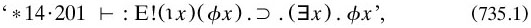
with a comparable proposition involving relations at *53·3.
TABLE 735.1. Russell’s congeries of existences
Case |
Notation (s) |
Sense of existence |
I1 |
∃x (∃x) |
As in existential quantification |
I2 |
E!(ιx)(ϕx) |
Of a referent of a denoting phrase |
C1 |
∃u (∃u) |
As in existential quantification |
C2 |
Eu |
Abstractable from a propositional function |
C3 |
∃‘u ∃u ∃!u |
Non-emptiness (Peano’s (541.3)) |
The relationship between the senses for classes is harder to determine, especially as Russell used C2 and C3 rather informally; but, for example, the empty class exists (or may do so) in senses C1 and C2 but not C3 while conversely the class which generates Russell’s paradox exists only in C3. In some theories existence was allowed under conditions; in particular, C2 obtained in PM only within contextual definition (734.2). The zigzag theory tried to deny C2 to classes when the propositional function was too complicated.
In addition, some relationships obtained between the I and C senses. I1 might permit any of the Cs, while I2 implied C3 thus:
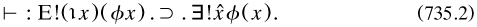
Russell did not prove this proposition in PM because by then he had largely dropped C3.
Russell did not always have these different senses of ‘existence’ under control. We saw his exaggerated claim in 1900 that only his definition of irrational numbers delivered the existence theorem (§6.4.7); thus he granted Peano’s sense C3 a primacy which it did not deserve. It appeared in another round of exchanges at this time.
7.3.6 Russell versus MacColl on the possible, 1904–1908. (Bibliography, Rahman 1997a) We saw in §2.6.4 that Hugh MacColl had proposed in 1877a that Boole’s algebra could be used to formulate the propositional calculus. Over the years he had continued with his researches, and with a paper 1897a of a series on ‘Symbolic reasoning’, published in Mind as he entered his sixties, he made an innovation for which he is now best remembered: modal logic (not his name), in which ‘possible’ and ‘impossible’ were basic notions.
Russell was one of MacColl’s principal targets for discussion. Already in a long letter of 6 October 1901 MacColl had queried a passage in Russell’s recent paper on order in Mind (§6.4.2) on the relationships of implication between various theorems in Book 1 of Euclid’s Elements (Russell 1901a, 296). The issue for MacColl was not geometry but implication itself; for propositions A and B ‘A implies B’ meant for him ‘It is impossible that A can be true and at the same time B false’; while ‘A does not imply B’ meant ‘It is possible that A can be true and at the same time B false’. He gave further examples from arithmetic, and from modal relations such as the certainty ‘a whale can swallow a herring’;8 he gave variants on this example in 1902a, 357–358. For him a proposition was ‘certain’ if it followed from the pertaining assumptions and rules, and ‘impossible’ if not. While Russell’s reply to MacColl’s letter is not extant, he probably did not warm to these suggestions; indeed, it may have helped prompt his note 1902b on ‘the teaching of Euclid’ (§6.2.2), when he stressed the lack of rigour in Euclid’s Elements.
Their published exchanges date from 1904. MacColl had another string of (short) papers on ‘Symbolic logic’ running in The Athenaeum, and in a pair 1904a he raised similar doubts about the logic of non-Euclidean geometry, as presented in Russell’s book 1897c on geometry. In his reply in the October issue, Russell 1904g detached questions of our ignorance, such as whether or not ‘our actual space may be non-Euclidean’, from logic, where ‘all propositions are merely true or false. I should not now divide true propositions into necessary and contingent, or false propositions into impossible and possible’. He also stressed ‘the difference between geometry as the science of actual space, and geometry as a branch of pure mathematics’. His logicism asserted that ‘In pure mathematics, as such, we do not consider actual objects existing in the actual world, but hypothetical objects endowed by definition with certain properties’; however, this was a not a proper reply in that MacColl had been discussing Russell’s pre-logicist book on geometry.
MacColl pursued his line in his Mind series, especially in 1905a in the January issue with a short April addendum 1905b on ‘Existential import’. Russell’s reply 1905b was again short but instructive, for it shows that he saw existence in logic only in the Peano sense C3 above: ‘To say that A exists means that A is a class which has at least one member’. He made this point in order to confront MacColl’s unsatisfactory definition of the empty class as ‘our universe of non-existences’. Russell opposed this admission of possible objects with his own theory of denoting; but in May 1907 Jourdain was to reprove him for not having explained also existence in the I2 sense, and Russell accepted the criticism (my 1977b, 102).
Russell sent MacColl a proof of his reply, and MacColl added a paragraph 1905c pleading for a broader philosophy in which ‘Symbolic Logic has a right to occupy itself with any question whatever on which it can throw any light’, especially existence. In a book 1906a on Symbolic logic and its applications, based upon several of his articles, MacColl presented his modal system in detail (including a range of rather unhelpful notations, not reproduced here). In a review in the April 1906 issue of Mind Russell noted that he dealt ‘always with whole statements or propositions, not, like most writers, with classes’, so that ‘he is primarily concerned with implication, not with inclusion’ either in part-whole theory or in Russell’s preferred Cantorian way (Russell 1906c, 255). He also repeated his disagreements about possibilities and existence, and in another review 1908a of the book for The Athenaeum he rejected MaColl’s empty class of unreal members in a witty remark on ‘the present king of France’: ‘Thus republics have kings, who only differ from the kings of monarchies by being unreal’.
Perhaps motivated by MacColl’s work, Russell surveyed the various senses of possibility and necessity used in logic and epistemology, in a lecture m1905f delivered to the Oxford Philosophical Club in October. However, finding none of them to be definitive, he recommended ‘that the subject of modality ought to be banished from logic, since propositions are simply true or false’—a hostile non sequitur followed by a declaration which for MacColl begged the question. He also misinterpreted his adversary as linking possibility and necessity respectively with existential and universal quantification of a propositional function; later he promoted this sense of modality himself.9
In this lecture (p. 518), the Mind review and elsewhere Russell also deplored MacColl’s failure to distinguish a proposition from a propositional function. As MacColl had pointed out to Russell in a letter of 24 February 1906 (RA), back in his early days he had interpreted the universally affirmed proposition ‘All X is Y’ as ‘if an individual belongs to the class X it belongs to the class Y’ (1877a, 181). However, he treated propositions not as designators but as forms of words, sometimes true and sometimes false; for example, ‘Mrs. Brown is not at home’ (1906a; 18–19). In a longer reply in Mind to Russell, he insisted that a propositional function, which ‘I should prefer calling a functional proposition [,...] must, from my point of view, be classed as a proposition’ (MacColl 1907a, 470).
The last exchange ran through the 1908 volume of Mind. Starting out from A. T. Shearman’s review 1907a there of The principles (§6.8.1), MacColl concentrated this time on implication (1908a and 1908b, with Russell 1908b in between). Again the principal divide was the status of propositional functions; for example (due to MacColl) ‘he is a man’ was a proposition that could possibly be true, while for Russell it was a propositional function if ‘he’ was indeterminate.
MacColl deserves great credit for his innovations. Both in his work from the late 1870s and now, he emphasised propositions in logic over and above classes or terms. He also made a good distinction between the senses of truth-values attributable to, say, ‘3 > 2’ or ‘3 < 2’ and to ‘Mrs. Brown is not at home’. His stress on knowledge rather than truthhood is good, as is his claim that we need logics, as (though not just as) we need algebras and need geometries. But the modal brands received an unclear start here, with his views on propositional functions and variables, absurd conceptions of empty classes and of infinitude, and unintuitive notations. So their later development had to wait some years for C. I. Lewis (§8.3.3), and in many respects far longer than that (Rescher 1969a, ch. 1).
7.4.1 Couturat’s Russellian principles. While Russell was searching for solutions and axioms, and puzzling over denoting, his publications were gaining attention in Paris. As in the late 1890s (§6.2.3), the main venue was the Revue de métaphysique et de morale, with Couturat and Poincaré among the authors.
The news started well for Russell. Up to the appearance of The principles, Couturat’s interest in logic had been dominated by the algebraic tradition; for example, in an article on ‘Symbolic logic or algebra of logic’, written with C. S. Peirce’s former student Christine Ladd-Franklin at her request10 for an American dictionary of philosophy and psychology, they gave merely two passing mentions to Peano and none to Russell (Couturat and Ladd-Franklin 1902a). But we saw in §6.8.1 that Couturat published a lengthy review 1904a of The principles, and the book then inspired him to write in the Revue a series of five long articles 1904–1905a with the same title in French. The publisher of the journal quickly put out a lightly revised version, together with some other material, as a book 1905b. Citations are to this version; a German translation 1908a soon appeared.
Although Couturat’s book was less than half the length of Russell’s, he presented logicism pretty comprehensively, and for the first time in French. As usual, he did not criticise Russell much, rendering not only the title but much of the content of The principles: the basic logic and set theory; the finite and transfinite numbers; order and continuity; real numbers and magnitudes; and finally dimensions and the three branches of geometry. But he ignored mechanics without explanation, and did not dwell on the underlying philosophical issues. He cited a wide range of literature, with a notable enthusiasm for the recent work on axioms and models (§4.7.3) by Oswald Veblen and E. V. Huntington (pp. 168–174); he even added a postscript on p. 308 on Huntington 1905a-b on the continuum (§7.5.6), and wrote warmly about it to Russell on 21 October (RA). Among recent developments, he sided with Keyser (§7.2.7) on the need for an axiom of infinity (p. 60).
The other material included two new notes, on set theory and group theory; perhaps aware of Russell’s (644.2) or Whitehead (§6.4.9), Couturat had subsumed the latter under the logic of relations as ‘a branch of the science of order’ (p. 208). Finally, an appendix reprinted a long piece 1904b from the Revue on Kant’s philosophy of mathematics: he doubted the legitimacy of synthetic a priori judgements and the formulation of hypothetical ones, and concluded that ‘the progress of Logic and of Mathematics in the 19th century has invalidated the Kantian theory and given right to Leibniz’ (p. 303).
Later that year Couturat published with Gauthier-Villars a short complementary guidebook 1905a to L’algèbre de la logique—a much older subject but still little known in France. In 1914 Open Court published an English translation, with a preface by Jourdain: a Polish translation is noted in §8.8.2. He ran through the theories in their classial and propositional forms roughly at the level of Schröder’s first volume, though unfortunately with only a mention at the end of the logic of relations. There and in art. 11 he cited, as a work in preparation, a ‘Manual of logistic’; it had arisen from a course given at the Collège de France where he was substituting for Henri Bergson. For some reason this piece of vulgarisation never left his busy study (§8.6.2);11 but in his inaugural lecture 1906b for the course, on ‘logic and contemporary philosophy’, he aired his oppositions to psychological and to sociological foundations for logic. With Russell, and maybe Poincaré also, he was at one here. However, his advocacy of logic earned derision in a reply Borel 1907a in the Revue stressing the need for intuition in mathematics—which doubtless Couturat did not deny.
7.4.2 A second pas de deux with Paris: Boutroux and Poincaré on logicism. (Sanzo 1976a) Borel is typical of the reception of Couturat’s writings in France; indeed, on 18 December 1904 Couturat had written to Russell about his failure to interest Borel and Lebesgue in Peanese (text in §11.1). The hostility soon became public: from Poincaré once again, and his nephew Pierre Boutroux (1880–1922), a mathematician and philosopher. ‘Poincaré is an oracle for the readers of the Revue de métaphysique et de morale, and Boutroux also’, Couturat told Russell on 11 February 1904;12 the high reputation of the nephew in his lifetime is difficult to explain at this historical distance. The sequence in the Revue this time is as follows:
Boutroux 1904a (November) and 1905a (July), Russell 1905g (November);
Poincaré 1905c (November) and 1906a (January), Couturat 1906a (March);
Poincaré 1906b (May), Russell 1906h (September), Poincaré 1906c (November).
We can deal with Boutroux quickly. His two papers were devoted to showing that the notion of correspondence between elements under a function could not be expressed by a theory of relations, as the logicists claimed, since it was not a ‘logical notion’ but ‘an intuitive fact analogous to physical law’ (1905a, 620–621). The two views are in fact not contradictory: in his reply Russell 1905g contented himself with a tutorial on relations as propositional functions of two independent variables, and on distinguishing a class as such from a listing of its members. Boutroux’s second paper elaborated upon a lecture 1905b given at the International Congress of Philosophy at Geneva in August 1904 (§7.5.1). He wrote the text at Cambridge in the following December, when he visited Whitehead; the chats may not have been too fruitful, for Whitehead had to add two paragraphs 1905a to Russell’s reply denying that he thought that functions did not belong to logicism but that the symbolism ‘is not practically useful in the development of Analysis’. He was also sorry that a remark on functions ‘made in the course of a conversation would be presented as a carefully considered definition’!
7.4.3 Poincaré on the status of mathematical induction. (Schmid 1978a, ch. 6) The collision between Russell and Poincaré started from a collection of partly reworked articles on the philosophy of mathematics and science which Poincaré had published as the book La science et la hypothèse (1902a). An English translation 1905a came out three years later, which Russell reviewed in the July issue of Mind. He found fault with Poincaré’s position that MI was ‘a means of passing from the particular to the general: it is merely a means of passing from one general proposition to another’ (Russell 1905c, 590). We saw in §6.5.3 that his logic of relations, partly enhanced by Frege’s ancestral relation, demoted MI from the prime place which Poincaré assigned to it. In addition, as during the last dance, he rejected again the view that a geometry is not entirely conventional. Editor Stout invited Poincaré to reply, which he duly did in a short letter 1905b, repeating his own stances on both issues and announcing that an essay on MI was soon to appear in the Revue.
Poincaré had been motivated by Couturat’s Russellian essays, perhaps by two of the three references to himself; for one found against him on MI and another only partially accepted conventionalism in geometry (Couturat 1905a, 62–63, 205). Called ‘Mathematics and logic’, Poincaré’s paper appeared in the Revue in two parts; then he added a third part in response to new work from Russell. Later he reworked the trio in his next popular book, Science et méthode (Poincaré 1908b). They formed less of an advance over nephew Boutroux than one might expect.
The first part, Poincaré 1905c, comprised a survey of mathematical logic as he understood it, which was not very deeply: for example, a propositional function ‘ϕ(x), x being the variable. The proposition ϕ(x) can be true or false’ (p. 827), like MacColl but probably inspired by deliberate obtuseness. Again, he was amused that Couturat’s presentation ‘contains numeral adjectives, cardinal as well as ordinal’, such as ‘“A relation holds between two terms”’ (p. 830); he might as well have criticised the use of page numbers in the Revue. Some reading of, say, Dedekind on Zahl and Anzahl (§3.4.2) would have helped him.
Poincaré treated MI better; indeed, ‘Thus it is only here that the true debate commences’ (p. 832). For him specifying the integers by the Peano axioms or some equivalent procedure has to be primitive because any effort to justify or prove it assumed the integers in the first place (pp. 832–835). In his second part 1906b he treated David Hilbert’s work on the foundations of arithmetic (§4.7.5) with much greater warmth, but still found the definition of MI to be wanting since the talk of finite and infinite numbers embodied it (p. 23).
Couturat’s long reply to these two papers also reads somewhat like a tutorial; for example, on the different senses of number (1906a, 216). He also ridiculed the implication that Russell was the first to (claim to) advance logic beyond Aristotle. He ended by hoping that Poincaré ‘will come to a more just and more favourable appreciation of Logistic when he will have studied it’ (p. 250). However, in one important respect he was on the same limited ground as Russell (§7.3.5); he spoke of the existence of a class only in Peano’s sense of its non-emptiness (pp. 232–233).
7.4.4 Russell’s position paper, 1905. (Moss 1972a) The next stage of Russell’s progress was motivated not by Paris follies but by a paper recently published in the Proceedings of the London Mathematical Society (hereafter, ‘LMS’) by the Cambridge mathematician E. W. Hobson (1856–1933). In his attempt to solve especially Burali-Forti’s paradox, and also to appraise Zermelo’s introduction of the axiom of choice, he had proposed ‘a law, or set of laws, forming the norm by which the aggregate [class] is defined’ (Hobson 1905a, 173). He seems to have intended a constructive approach in building up these norms, although without using propositional functions. After mutual discussions and correspondence, critical replies came in from Hardy, Jourdain and Russell; we are concerned with the last, which was submitted to the LMS in November 1905 and published the next March as his 1906a.
Reformulating Hobson’s norm as a propositional function, Russell separated issues surrounding the paradoxes from those related to Zermelo’s axiom. He compared the latter with the multiplicative axiom (which he still thought less general), and gave theorems from set theory when needed. He also published for the first time his charming illustration about the need for infinite selections to show that 
0 boots divide into pairs as any reasonable owner would desire (pp. 47–48).13
Most of Russell’s paper was devoted to the paradoxes of classes. He gave his first extended listing of them, including the general relational version described in §7.2.1, and showed that Hobson’s norm was not sufficiently restrictive to avoid them. Curiously, he did not reinforce his point by mentioning also the paradoxes of naming (§7.2.2), although he thanked Berry for another detail (p. 36).
Russell also surveyed three candidate Solutions, all based on abandoning class comprehension in some way. He treated first ‘The zigzag theory’, which came closest in form to Hobson’s own approach; ‘we define a predicative propositional function as one which determines a class (or relation if it contains two [or more] variables.’ (p. 38). But he warned that in this theory the ‘axioms as to what functions are predicative have to be exceedingly complicated’, and that he had not found them (p. 39). Next, ‘The theory of limitation of size’ was inspired by the greatest number paradoxes, but seemed less convincing under his functional generalisation (pp. 43–44). He might have added that the class producing his own paradox was not that large; as he had put it excellently to Jourdain in June 1904, it is ‘only half way up’ (my 1977b, 35), for if a class did not belong to itself then its complement did.
In the final candidate, ‘The no-classes theory’, ‘classes and relations are banished altogether’, and propositional functions avoided, leaving only propositions p and their constituents a. When x was substituted for a in p, the resulting proposition was written ‘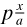
’, and the theory rested largely on these objects, which replaced classes (Russell 1906a, 45–47). (Relative to the type theory to come in PM, this one was not ramified. He noted their single-valuedness, and confessed to difficulties in defining some transfinite numbers. Meanwhile Poincaré got wound up again.
7.4.5 Poincaré and Russell on the vicious circle principle, 1906. Poincaré’s addition 1906b to his paper on ‘mathematics and logic’ was partly provoked by Couturat’s reply 1906a, and also by a treatment by Peano’s follower Mario Pieri in the Revue of the consistency of the axioms of arithmetic (Pieri 1906a). But Russell’s new paper also fell within his sights. Poincaré fixed upon the naming paradoxes (which Russell had not treated), especially the version due to his countryman Richard (§7.2.2); he diagnosed the illness as lying in the impredicative manner of defining a number by a condition which itself involved naming. Therefore his ‘TRUE SOLUTION’ lay in avoiding such a ‘vicious circle’, and he wondered if Russell’s ‘zigzaginess’ had the same aim (1906b, 307–308).
Poincaré also returned to MI, but in the new spirit. In a discussion of the axioms of choice Russell had mentioned in his paper their need for proving the equivalence of the inductive and reflexive definitions of cardinal finitude (1906a, 49); Poincaré now regarded as Russell’s first defining clause (‘a cardinal number which obeys mathematical induction starting from 0’) as impredicative, and so the former treatment of finite and infinite numbers in Russell 1902 (§6.5.3) as ‘vicious’ (1906b, 310, attributed to Whitehead). After attacks on the axiom of choice for its lack of obviousness (pp. 311–315) he came to radical conclusions: ‘logistic is no longer sterile, it engenders antinomy’, and even more generally, ‘there is no actual infinity; the Cantorians forgot that, and they have fallen into contradiction’ (p. 316).
Russell could not let pass such dismissals sous silence; so a muse by him on ‘The paradoxes of logic’ appeared in the Revue four months later, in September. As usual, there were errors to correct; for example, the liar paradox had nothing to do with the infinite (Russell 1906h, 633). But he responded to the naming paradoxes positively by taking seriously the vicious circle principle (hereafter, ‘VCP’) as a key to a solution, while pointing out that it too had no intrinsic link to the infinite (p. 634). He expressed it in Peanese as ‘All that contains an apparent variable must not be one of possible values of that variable’ (p. 634), and he began to think out how the ‘universe of discourse’ (p. 641) would have to be divided up into different sorts of things (pp. 640–646).
On MI, Russell recalled that his remark on equivalent definitions had been directed towards the need of the axiom of choice, not a confession that finitude was indemonstrable (pp. 646–648). Poincaré’s brief rejoinder 1906c dwelt mainly on this last point, including a new and succinct statement of the basic issues involved:
Definition A. A finite number is a cardinal number n such that n < n + 1.
Definition B. An inductive number is a number which is part of all the recurrent classes [of numbers, that is, which contained 0 and also (n + 1) if they contained n].
Proposition C. Any finite number is inductive.
For him MI was C; for Russell it was B, with C as an alleged theorem.
The dispute lay largely upon philosophical differences. Poincaré compared it as the Kantians (himself and his nephew) against the Leibnizians; Couturat dismissed the analogy in his reply 1906a to Poincaré, but there were evident cross-purposes of a similar kind. The Kantian in Poincaré distinguished mathematical from logical knowledge and saw the role of the mind as unavoidable; the logicist in Russell/Couturat located mathematical within logical knowledge and sought to leave out the mind (Detlefsen 1993a). Further, Poincaré seems to have been loyal to syllogistic logic, which Russell had recently described in his lecture on modalities (§7.3.6) as ‘a subject scarcely more useful or less amusing than heraldry’ (m1905f, 516).
The place of intuition in mathematical thought was another issue: Poincaré stressed it, while logicists wanted to avoid it in their foundations although presumably they would admit intuition in the creation of mathematics, and surely it played a role in choosing indefinables. In a review of the exchange for the American Journal of philosophy W. H. Sheldon 1906a made such points; and indeed Russell had some creation of his own to do, for he thought that at last he had constructed a general logical system to Solve the paradoxes.
7.4.6 The rise of the substitutional theory, 1905–1906. In his reply to Poincaré Russell also announced that the no-classes theory was ‘the most satisfying’ Solution (1906h, 636), and he gave some details of its apparatus. The presence of the ‘constituent’ a in proposition p was the basic ‘matrix’ of the substitution, written ‘p/a’; the result of substituting b for a in p to produce proposition q was symbolised ‘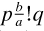
’. Simultaneous substitutions were used, to replace relations, as in ‘
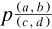’ (pp. 636–638). The existence of an infinite class was proved on p. 639 by inductively generating from two distinct ‘constituents’ a and u the sequence of (true or false) different propositions
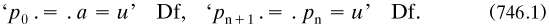
Russell worked intensively on this theory from the autumn of 1905 and through 1906. Early in February 1906 he added a note to the proofs of his LMS paper 1906a that ‘the no-classes theory affords the complete solution of all the difficulties’ about the paradoxes. He prepared a successor m1906d, which he submitted to the LMS on 24 April; it was accepted, but he withdrew it during the autumn, for he was losing faith in the theory. Hundreds of folios on it survive, though none saw print;14 m1906d was published in the collection Russell Analysis (1973). The funeral is recorded in the next sub-section; here I summarise the theory, using that manuscript and a shorter one m1905e which he had written out in December for Hardy’s benefit.
‘We must distinguish between substitution and determination’, Russell began to Hardy. Variables in the usual sense having disappeared, the proposition ‘Plato is a man’ was obtained by substituting ‘Plato’ for (say) ‘Socrates’ in ‘Socrates is a man’ instead of determining constituent x with the value ‘Socrates’. Thus ‘ϕ!x’ was now an ‘expression’ (proposition?) containing x rather than a propositional function, and one of the axioms was
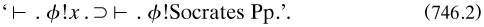
Universal quantification was understood thus: ‘(x). ϕ!x is the proposition ‘any value of ϕ!x is true”’.
The result of substitution had always to be unique; so Russell stressed that definite denoting phrases played a central role in the theory. After quoting their contextual definition (734.1) from ‘On denoting’ for the expression ψ!x, he gave the corresponding sense I2 of existence (fol. 4):
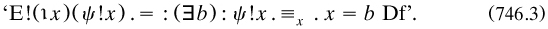
Russell then gave a string of definitions concerning the presence or absence of a from p (fol. 6), with substitution now also written ‘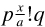
’, where they were based upon
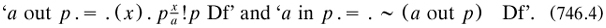
At this stage negation was an indefinable in Russell’s theory; by the time of the manuscript m1906d for the LMS it was defined on p. 169 for proposition q as
Although this proposition was not presented as a formal definition, it rendered a profound difference, for now the truth and falsehood of propositions were admitted as indefinables in the theory. Further, and more explicitly than before, propositions themselves were objects as much as were entities (the new word for ‘constituents’); ‘p should be the name of a genuine entity, and not a mere phrase like “the King of France” or “the King of England”’ (p. 168).
Russell did not stress differences between propositions and entities; for example (an important one), he defined identity between x and y simply as
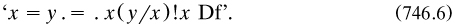
without discussing any relationship between them (p. 169). It is hard to understand what the former property might describe, since this was decidedly not a theory about names (or about universals); however, he allowed propositional and non-propositional substitutions together (p. 175).
This theory solved the paradoxes by splitting matrices into ‘types’, starting with p/a and then moving to p/(a, b) for the substitution of two individuals, q/(p/a) which ‘gives rise to classes of classes’ (or rather to their analogue), ‘q/{p/(a, b)}’ ‘which is a matrix of the third type’, and so on (pp. 176–177). Here was another profound change of policy; for the first time in a major theory Russell had stratified his logical universe. After writing his reply to Poincaré a few months later, he was to strengthen this approach by adopting the VCP (§7.7.1).
The construction of mathematics began naturally enough with the cardinal integers, to be defined as the analogue to classes of similar classes. For the lowest type
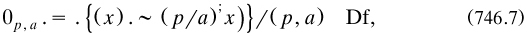
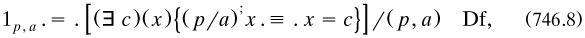
and so on (my symbolic version of a rather unclear informal discussion on pp. 175–177). The procedure went up to the transfinite numbers, which were defined by imitating Cantor’s principles of generation (§3.2.6). Then he set in well-order a sequence of entities by inductively defining a sequence of two-place relations from propositions; the proof (746.1) that infinitely many objects existed, in the later reply to Poincaré, was to be a simplified version. The resulting numbers ω and 0 were respectively ‘entity-ordinals’ and ‘-cardinals’, ω1 and 1 ‘ordinal-ordinals’ and ‘-cardinals’, and so on (pp. 180–183). But the continuation created only a finite number of these types (p. 177), which would not allow ωω or ω to be reached: thus Cantor’s and Burali-Forti’s paradoxes were brutally solved in that many numbers prior to the offending ones could not be reached anyway. Similarly, for the naming paradoxes, ‘definable is relative to some given set of fundamental notions’ I, and ‘“definable in terms of I”’ is never itself definable in terms of I’ (p. 185); and his own paradox was solved by banning a matrix from being substituted within itself (pp. 171–172). The liar paradox seemed to be banished by distinguishing a proposition from its truth-value.
7.4.7 The fall of the substitutional theory, 1906–1907. Russell’s manuscript was refereed for the LMS by A. B. Kempe (§4.2.9). In his report he was generally praising, but he did not understand the reductionist flavour, either concerning the senses in which classes no longer existed or the meaninglessness of ‘the present King of England’ (Kempe Papers, Packet 39; copy in RA). Sending this report to Russell, the editor of the Proceedings, A. E. H. Love, wrote to him on 12 October 1906 saying that another referee was quite critical but that nevertheless the paper was accepted, and suggesting that some revision might be effected (RA). Russell’s response was immediate; he withdrew the paper. The reasons were probably not due to Kempe’s criticisms, which largely concerned presentation and unfamiliarity with his philosophical procedures. A few days later he reported the withdrawal to Jourdain as effected because ‘there was much in it that wanted correction, and I preferred to wait till I had got things into a more final shape’ (my 1977b, 93).
It seems that during the year Russell saw the various difficulties, mathematical and philosophical, grow to unacceptable levels; at all events, late in 1906 he abandoned the substitutional theory, although not the notion of substitution. The status of entities as ‘constituents’ of propositions was in any case vague; the best move is to make them individuals, but their place in logic still needed clarification (§7.9.3). In addition, the technical difficulties of the theory were formidable. Could it really provide sufficient apparatus to deliver the mathematics envisaged, especially something to imitate the functional hierarchy? The outer regions of Cantor’s empire, such as ωω, were out of reach anyway.
A philosophical difficulty concerned the status of propositions and their truth-values, especially concerning falsehoods; for what sort of object could correspond to a false proposition? Russell prepared a short manuscript m1906e on ‘Logic in which propositions are not entities’, where he converted propositional quantification ‘(p).p’ into functional and individual quantification ‘(ϕx).ϕx’; but it is hard to see how meaning could be preserved.
Russell tackled this question in two philosophical papers: 1906g in the October issue of Mind, and especially in a lecture read on 3 December to the Aristotelian Society and published as 1906j. His target was the monistic theory of truth as advocated by his relative Harold Joachim in The nature of truth (1906); one of his main criticisms was based upon rejecting the internalist construal of relations (§6.3.1). In developing his own reductionist position he held that beliefs held of some thing such as a fact; but then ‘objective falsehoods’ had no referent. For some reason he did not then entertain the alternative option that there was not a fact to that which a false proposition corresponded, rather than a non-fact to which it did. But, as he told Jourdain the next June, ‘Consideration of the paradox of the liar and its analogies has led me to be chary of treating propositions as entities’ (my 1977b, 105); so ‘p is false’ in (746.5), to take one example from the substitutional theory, had to go.
A further fear was that ‘some contradiction should be found to result from the assumption that propositions are entities’, as Russell put it in his LMS paper, though he had not found one (m1906d, 188). But it soon arrived (m1906a, fol. 7): I express it in terms of the propositions
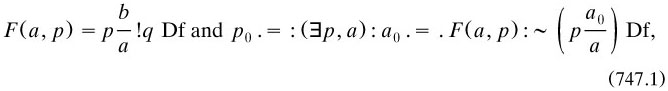
where apparently all letters symbolise propositions. The negation in the last clause exhibits kinship with the liar paradox, and indeed he showed that essentially
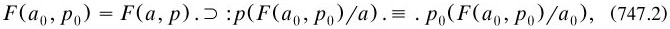
an unacceptable equivalence in the consequent. He communicated it on 22 January 1907 to Ralph Hawtrey (text in §11.3), a former student who was reading the manuscript of PM (§7.8.1). He did not consider his paradox stated at the end of The principles, based upon associating a proposition with the proposition ‘every member of a class m of propositions is true’ (§6.7.9); but it may also be constructed within the theory.15 It is a pity that he seems to have forgotten about this paradox, both at this time and later (§7.9.1–2). He also did not react to the observation in Grelling and Nelson (§7.2.3), that the theory assumed the self-contradictory proposition ‘A class may not be subject of a sentence’ (1908a, art. 9).
Despite being abandoned, the theory left a noteworthy mark upon Russell’s logical career, and not only for its prime place in his thought for well over a year. A close link between his theory of definite descriptions and his logicism, in the succeeding theories substitution was used—for example, in a published paper on a basic feature of logic, which we now consider.
7.4.8 Russell’s substitutional propositional calculus. Soon after publishing ‘On denoting’ Russell wrote a paper on ‘the theory of implication’. On 23 July 1905 he sent it to Frank Morley (RA), who accepted it for the American journal of mathematics, where it appeared in the following April as a 44-page paper. He concentrated upon ‘material implication’ between propositions, construed as ‘the theory of how one proposition can be inferred from another’ (1906b, 159). Thus he jumbled together implication and inference Peano-style; in particular, the theorem
was ‘an important principle of inference, which I shall call the “principle of assertion”’ (p. 180) and often used as the modus ponens rule of inference.
In other respects, however, ‘the ideas are more those of Frege’ (p. 160), with a reference to the Grundgesetze. Russell noted four features. Firstly, he continued to use the notion of assertion of a proposition p and the sign ‘
. p’, here with the “explanation” that ‘it may be read “it is true that” (although philosophically this is not what it means)’ (p. 161). Secondly, ‘The essential property that we require of implication is this: “What is implied by a true proposition is true”’ (p. 161), which is not a tidy reading of Frege. Thirdly, he distinguished implication between (variable) propositions and over quantification, as in ‘the formula
where ‘(q) . q’ was ‘an absolute constant, meaning “everything is true”’ (p. 193). Finally, he defined his logical connectives from ‘implication and negation as our primitive ideas’ (p. 160); for example (p. 176),
Russell also used his notation ‘(C x)’ from denoting (§7.3.3); but, in a ghastly choice of name, he called it a ‘propositional function’, where, for example, ‘“p ⊃ q” is a propositional function of p and q’ (p. 163), not the usual denotation!
Substitutional influence was evident not only in the prominent place of truth-values and propositional quantification but also in the ‘principle of substitution’ and the fraction symbol to separate substituent from substituand (p. 165). However, perhaps because that theory was at an early stage, Russell allowed variables to vary, and quantification to occur over them, in normal ways. These procedures formed the second of his ten ‘primitive propositions’ for the calculus (pp. 164–168, with no *2·4 for some reason), fairly similar to the ten presented in The principles, 16–18. There he had warned that ‘the method of supposing an axiom false, and deducing the consequences of this assumption’ as in normal independence proofs ‘is here not universally available’ (p. 15); now he stressed that that caveat ‘concerning primitive propositions applies with even greater force to primitive ideas’ (1906b, 160). He compared his treatment of formal rules with that of the ‘algebra of logic’ presented in Huntington 1904a (§4.7.3); but he showed no American sensibility to model theory (pp. 183–192).
For propositional quantification Russell added the ‘primitive idea’, written ‘(x).(C x)’, meaning ‘the truth of (C x) for all values of x’ (p. 194). This introduced ‘formal implication’ with quantification over x; but now the reference of ‘propositional function’ seemed to revert to normal, or maybe covered functions of propositions also. The three new assumptions did not enlighten: two of them stated rather Biblically that ‘What is true of all is true of any’ and its converse, while the third announced that ‘If it is true, for all values of x, that p implies (C x), then p implies that (C x) is true for all values of x’ (pp. 194–195). He ended by noting that the paradoxes required limitations on the ranges of the quantifiers, but sensibly suspended consideration of the matter.
Russell introduced his paper as ‘the first chapter of the deduction of pure mathematics from its logical foundations’ (p. 159), with doubtless a large substitutional text in mind. This was not to be; before examining his next phase, however, in the next section we review others’ reactions to his and Whitehead’s mathematical logic in the mid 1900s, and in §7.6 Whitehead’s concurrent researches.
