The story begins in French mathematics and philosophy in the late 18th century: specifically the semiotic ‘logique’ of Condillac and Condorcet and the connections with the algebraic theories, especially the calculus, developed by Lagrange (§2.2). Then it moves to England, for both topics: the adoption of Lagrangian mathematics by Babbage and Herschel, and the revival of logic (although not after the French model) in the 1820s (§2.3). Next come the two principal first founders of algebraic logic, De Morgan and Boole (§2.4–5). The main initial reactions to Boole are described in §2.6.
In a change of topic, §2.7 also starts with the French, but charts a rival tradition in the calculus: that of Cauchy, who inaugurated mathematical analysis, based upon the theory of limits and including a radical reformulation of the calculus. Then the refinements brought about from the 1860s by Weierstrass and his followers are noted; the inspiration drawn from a doctoral thesis by Riemann is stressed. Thereby the scene is set for Cantor in §3.
While two important philosophers, Bolzano and Kant, are noted (§2.8.2), the chapter does not attempt to cover the variety of approaches adopted in logic in general during the period under study. For a valuable survey of the teaching of logic internationally, see Blakey 1851a, chs. 14–22. A pioneering revision of the history of linguistics for this period and later is given in Aarsleff 1982a.
2.2.1 The ‘logique’ and clarity of ‘idéologie’. Supporters of the doctrine of ‘ideology’ became engaged in the political life of France in the mid 1790s, including collision with the young General Napoléon Bonaparte; and the word ‘ideology’ has carried a political connotation ever since. However, when Antoine Destutt de Tracy introduced the word ‘idéologie’ in 1796, it referred not to a political standpoint but to an epistemological position: namely, to ideas, their reference and the sign used to represent them. It exemplified the strongly semiotic character of much French philosophy of the time, especially following certain traits of the Enlightenment.
This was already marked in the hands of the Abbé Condillac, the father-figure of the Idéologues. His treatise La logique was published in 1780, soon after his death in that year.1 The ‘logic’ that it espoused was the method of ‘analysis’ of our ideas as originating in simple sensory experiences, followed by the process of ‘synthesis’ in which the ideas were reconstructed in such a way that the relations between them were clearly revealed (Rider 1990a). To us the book reads more like a work in semiotics than logic: both words had been used by Condillac’s father-figure, John Locke (1632–1704), in his Essay concerning human understanding, and he took them as synonyms because words were the most common kind of sign (Locke 1690a, book 4, ch. 21: this seems to be the origin of the word ‘semiotics’). For Condillac the procedure of analysis and synthesis followed nature: ‘the origin and generation both of ideas and of the faculties of the soul are explained according to this method’ (Condillac 1780a, title of pt. 1). When the Ecole Normale was opened in Paris in 1795 for its short run of four months as a teacher training college,2 a copy of this book was given to every student.
Condillac did not present logical rules in his doctrine: instead, broadly following views established in Port-Royal logic and Enlightenment philosophy, he laid great emphasis on language. In order that the ideas could indeed be clearly stated and expressed, the language of which the signs were elements had to be well made, so that indeed ‘the art of reasoning is reduced’ to it (title of pt. 2, ch. 5). He did not discuss syllogistic logic, where the rules were assumed to apply to reasoning independently of the language in which it was expressed. In showing this degree of uninterest in tradition, his approach was rather novel. But he gained attention from savants in various fields of French science. For example, the chemist Antoine-Laurent Lavoisier was influenced by Condillac to improve the notation of his subject, even to the extent of writing down chemical equations. Similarities between logics and chemistry were to recur at times later (Picardi 1994b).
2.2.2 Lagrange’s algebraic philosophy. Obviously mathematics was the apotheosis of a clear science, and within mathematics algebra gained a preferred place. Condillac himself wrote a treatise on algebra entitled ‘The language of calculation’ which was published posthumously as his 1798a, in which the formal rules of ordinary arithmetic and algebra were explained, the legitimacy of the negative numbers as numbers was stressed (§2.4.2), and so on.
Some mathematicians of the time were drawn to the doctrine. The most prominent was the Marquis de Condorcet (1743–1794), although his emphasis on the mathematical rather than the linguistic features inevitably made his position less well appreciated. Much of his work in probability and the calculus was heavily algebraic in character (for example, he esteemed closed-form solutions to differential equations over any other kind). But the master of algebras of the time was Joseph Louis Lagrange (1736–1813), who had come to Paris from Berlin in 1787. He popularised his position in teaching both at the Ecole Normale and especially at the Ecole Polytechnique. This latter was a preparatory engineering school which opened in 1794 (the year of Condorcet’s suicide, incidentally); in contrast to the failure of the other school, it ran successfully.
Lagrange had formed his preferences for algebraic mathematical theories in his youth in the late 1750s, quite independently of Condillac or the Idéologues (indeed, rather prior to them). But he found a congenial philosophical climate within which his views could be propounded. He tried (unsuccessfully, but that is another matter) to ground all mechanics in principles such as that of least action, which could be stated entirely in algebraic terms, without resource to either geometrical theories or the intuition of experience: ‘One will not find Figures in this work’ is a famous quotation from his Méchanique analitique (1788a, preface).
The algebras involved are not the common ones of Condillac but the differential and integral calculus and the calculus of variations, of which Lagrange had proposed algebraic versions (see Dickstein 1899a and Fraser 1985a respectively). As the former calculus is of some importance for our story, a little detail is in order.
According to Lagrange, every mathematical function f(x + h) could be expanded in a power series in the increment variable h on the argument variable x; and the ‘derived functions’ f′(x),f″(x),… (these were his terms and notations) were definable in terms of the coefficients of the appropriate powers of h. These definitions, and the manner of their determination, were held by him to be obtainable by purely algebraic means, without resource to limits or infinitesimals, common procedures of the time but unrigorous in his view. The integral was also defined algebraically, as the inverse of the derived function. The whole approach was extended to cover functions of several independent variables. The only exceptions to be allowed for were ‘singular values’ of x, where f(x) was undefined or took infinite values; even multi-valued functions were allowed. Other theories, such as the manipulation of functions and of finite and infinite series, were also to be handled only by algebraic means.
Lagrange gave his theory much publicity in connection with the courses which he taught in some of the early years of the Ecole Polytechnique, and his textbook Théorie des fonctions analytiques (1797a) was widely read both in France and abroad. The next section contains a few of the new results to which it led. However, the standpoint lacked a measure of conviction; was it actually possible to define the derived function and the integral in every case, or even to produce the Taylor-series expansion of a function in the first place, or to manipulate series and functions, without admitting the dreaded limits or infinitesimals? These alternative approaches, particularly the latter, continued to maintain a healthy life; and we shall see in §2.7.3 that in the 1820s Cauchy was to give the former its golden age.
2.2.3 The many senses of ‘analysis’. One further link between ‘logique’ and mathematics merits attention here: the use in both fields of the word ‘analysis’. We saw it in Condillac’s philosophy, and it occurred also in the titles of both of Lagrange’s books. In both cases the method of reducing a compound to its constituent parts was involved: however, one should not otherwise emphasise the common factor too strongly, for the word was over-used in both disciplines. Among mathematicians the word carried not only this sense but also the ‘analytic’ type of proof known to the Greeks, where a result was proved by regressing from it until apparently indubitable principles were found; the converse method, of starting from those principles and deriving the result, was ‘synthetic’. Neither type of proof is necessarily analytic or synthetic in the senses of decomposition or composition. Further, during the 17th and 18th centuries ‘analytic’ proofs were associated with algebra while ‘synthetic’ ones were linked with geometry (Otte and Panza 1997a). However, developments in both these branches of mathematics made such associations questionable; for example, precisely around 1800 the subject called ‘analytic geometry’ began to receive text book treatment.
Thus the uses of these terms were confusing, and some of the more philosophically sensitive mathematicians were aware of it. One of these was Sylvestre-François Lacroix (1765–1843), disciple of Condorcet and the most eminent textbook writer of his day. In an essay 1799a written in his mid thirties, he tried to clarify the uses to which these two words should be put in mathematics and to warn against the two associations with branches of mathematics. However, his battle was a losing one, as Joseph-Diez Gergonne (1771–1859) pointed out in a most witty article in his journal Annales de mathématiques pures egt appliquées; for example, ‘an author who wants to draw the regards and the attention of the public to his opus, hardly neglects to write at its head: “Analytical treatise”’ (1817a, 369)! His joke was to be fulfilled within a few years, as we see in §2.7.2.
2.2.4 Two Lagrangian algebras: functional equations and differential operators. Lagrange did not invent either theory, but each one gained new levels of importance under the algebraic regime which he encouraged, and was to find a link with logic in De Morgan and Boole. On their histories, see respectively Dhombres 1986a and Koppelman 1971a; and for both Panteki 1992a, chs. 2–5.
Functional equations can be explained by an example from Lagrange himself. To find the derived function of xm for any real value of m he assumed it to be some unknown function F(x) and showed from the assumed expansion
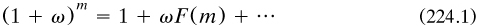
that F satisfied the functional equation
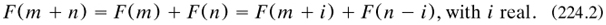
By assuming the Taylor expansions of F about m and n respectively for the last two terms (and thus bringing the derived functions of F into the story) and then equating coefficients of i, he found that
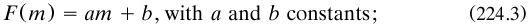
and from the cases m = 0 and 1 it turned out that b = 1 and a = 0. Thus putting in (224.1)
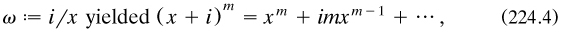
so that the derived function of xm was shown to be mxm–1 by using only the Taylor expansion and algebraic means (Lagrange 1806a, lecture 3: see also lectures 4–6).
Differential operators arise when the quotient dy/dx is interpreted not as the ratio dy ÷ dx (§2.7.1) but as the operator (d/dx) upon y. The result of this operation was also written ‘Dy’ in order to emphasise the operational feature. In this reading, orders and powers of differentials were identified:

The most important application was to Taylor’s series itself, which now took a form concisely relating D to the forward difference operator Δ:
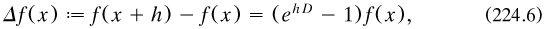
where ‘1’ denoted the identity operator. From results such as this, and summation interpreted as the (algebraically) inverse operator to differencing, Lagrange and others found a mass of general and special results, most of which could be verified (that is, reproved) by orthodox means.
2.2.5 Autonomy for the new algebras. However, some people regarded these methods as legitimate in themselves, not requiring foundations from elsewhere: it was permitted to remove the function from (224.6) and work with

A prominent author was the mathematician François-Joseph Servois (1767–1847), who wrote an important paper 1814a in Gergonne’s Annales on the foundations of both these algebras. Seeking the primary properties that functions and operators did or did not obey, when used either on themselves or on each other, he proposed names for two properties which have remained in use until today. If a function f satisfied the property
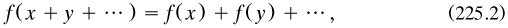
then f ‘will be called distributive’; and if f and another function g satisfied the property

then they ‘will be called commutative between each other’ (p. 98).
Had Servois been working with axioms—which in contrast to the late 19th century (§4.7), was not a normal procedure at the time—then he would have put forward two axioms for a general algebra. As it is, he knew the importance of the properties involved, and they gradually became diffused (by De Morgan and Boole among others, as we shall see in §2.4.7 and §2.5.2–3). These two algebras are important for reasons beyond their technical details; for they were among the first ones in which the objects studied were not numbers or geometrical magnitudes.3 This feature was reflected in the practise of several authors to use the word ‘characteristic’ to refer to the letters of the algebra, not to the functions or operators to which they referred. Lacroix was such an author, and an example is given in his account of Servois’s paper, where ‘the characteristics [f and g] are subjected only to the sole condition to give the same result’ in order to refer to ‘commutative functions’ (Lacroix 1819a, 728).
2.3.1 A Cambridge revival: the ‘Analytical Society’, Lacroix, and the professing of algebras. While French mathematics was in a state of rapid development after the Revolution, most other countries slept pretty soundly. However, by the 1810s some movements were detectable, partly in reaction to the massive French achievements. Various reforms took place in the countries of the British Isles: we consider here the best known (although not the first of them), namely, the creation of the ‘Analytical Society’ by a group of undergraduates at Cambridge University in the early 1810s (Enros 1983a). Its name exemplified the association of analysis with algebra mentioned in §2.2.3. While the Society ran only from 1812 to 1817, its enthusiasm for algebras was continued in the activities of its most prominent members. In particular, Charles Babbage, John Herschel and George Peacock published in 1816 their English translation of the second (1806) edition of Lacroix’s textbook on the calculus (Lacroix 1816a: the large treatise was cited above).
In order to clarify the philosophy of the new English mathematicians, a contrast with Lacroix would be in order here. As was noted in §2.2.3, he was under the strong influence of Condorcet, and thereby back to encyclopaedistic philosophy. Following their advocacy of plurality of theories and even its classification, Lacroix himself had presented all the three main traditions of the calculus, especially in his large treatise but also in the shorter textbook version. Initially he had shown a strong adherence to Lagrange’s position; but over the years he had moved gradually towards a preference for the theory of limits, while still presenting the other approaches. By contrast, the young men at Cambridge voted unequivocally and uniquely in favour of Lagrange’s approach, and in their editorial preface they even reproached Lacroix for his preference for limits over ‘the correct and natural method of Lagrange’ (Lacroix 1816a, iii).
2.3.2 The advocacy of algebras by Babbage, Herschel and Peacock
Since it leads to truth, it must have a logic.
Robert Woodhouse on complex numbers
(De Morgan 1866a, 179; compare 1849b, 47)
This love of algebra(s) was evident already in their senior (and presumably influential) Cambridge figure Robert Woodhouse (1773–1827), who even criticised Lagrange for not being algebraic enough; he wrote an essay 1801a ‘On the necessary truth’ obtainable from complex numbers in exactly the spirit of the quotation above, which De Morgan seems to have recalled from his student days in the 1820s. The reliance upon algebra had prevailed with Babbage and Peacock in the 1810s, and continue in various forms in England throughout the century.4 Indeed, Babbage and Herschel had already begun to produce such research while members of the Analytical Society, and they published several papers over a decade. Functional equations (then called ‘the calculus of functions’) was the main concern, together with related types such as difference equations: their formation and solution (partial and general), the determination of inverse functions, the calculation of coefficients in power-series expansions, applications to various branches of mathematics, and so on. The methods were algorithmic, rather wildly deployed with little concern over conditions for their legitimacy.5
The influence of French mathematics was quite clear, and various works, even earlier than Lagrange’s writings, were cited. In return, Gergonne 1821a wrote a summary of some of Babbage’s results in his Annales. However, the philosophy of ‘logique’ did not enjoy the same influence: even in a paper ‘On the influence of signs in mathematical reasoning’ Babbage 1827a only cited in passing (although in praise) one of the French semiotic texts, and otherwise set ‘logique’ aside. English logic was to gained inspiration from other sources, as we shall see in §2.4–5. First, however, another aspect of English algebra calls for attention.
While his friends were rapidly producing their research mathematics, Peacock was much occupied with the reform of mathematics teaching at Cambridge University. But in the early 1830s he produced a textbook 1830a on the principles of algebra, which gave definitive expression to the philosophical position underlying the English ambitions for algebra. He recapitulated some of these ideas in a long report on mathematical analysis (1834a, 188–207).
A principal question was the status of negative numbers, and of the common algebra with which arithmetic was associated; complex numbers fell under a comparable spotlight (Nagel 1935b). English mathematicians (and also some French ones) had long been concerned with questions such as the definability of (a – b) when a < b. Peacock’s solution was to distinguish between ‘universal arithmetic’ (otherwise known as ‘arithmetical algebra’) in which subtraction was defined only if a > b, and ‘symbolical algebra’, where no restrictions were imposed. The generalisation from the first to the second type of algebra was to be achieved via ‘the principle of the permanence of equivalent forms’, according to which ‘Whatever form is Algebraically equivalent to another, when expressed in general symbols, must be true, whatever these symbols denote’ (Peacock 1830a, 104; on p. 105 the principle was mistakenly called ‘algebraical forms’). This hardly limpid language states that a form such as, say anam = an + m in the first type of algebra for positive values n and m maintained its truth when interpreted in the broader canvas of the second type, which seems to be a version of the marks-on-paper algebra later known as ‘formalism’ often but mistakenly associated with Hilbert’s proof theory (§4.7).
While the same laws applied in each algebra, this change in generality led to some change in emphasis: arithmetical algebra stressed the legitimacy of signs, while symbolical algebra gave precedence to the operations under which the elements of the algebra were combined. From this point of view Peacock was moving towards the modern conception of abstract algebras which were distinguished from their interpretations; but instead of adopting axioms he stressed the (supposed) truths of the theorems (validly) derivable in symbolical algebra.
In this way Peacock’s philosophy of algebra involved an issue pertaining to logic, although its links to logic were developed by others. He did not take much interest in recent or contemporary developments in logic at his time. For example, he did not relate his symbolical algebra to Condillac’s standpoint, where negative numbers were granted full status within the number realm on the grounds of an analogy with negation (1798a, 278–288), or his universal arithmetic to Lazare Carnot’s opposition to negative numbers for their alleged non-interpretability in geometrical terms (1803a, 7–11). Neither did he react to the rather sudden revival of interest in logic in England in the 1820s, to which we now turn.
2.3.3 An Oxford movement: Whately and the professing of logic. While Cambridge began to come alive in mathematics during the 1810s and 1820s, Oxford executed a reform of the teaching of humanities students by introducing a course in logic. The study of logic in Britain was then in a peculiar state. The classical tradition, based upon inference in syllogistic logic, was still in place. But for a long time an alternative tradition had been developing, inspired by Locke and continued in some ways by the Scottish Common-Sense philosophers of the late 18th century. Critical of syllogistic logic, especially for the narrow concern with inference, its adherents sought a broader foundation for logic in the facultative capacity of reasoning in man, and included topics such as truth and induction which we might now assign to the philosophy of science. Showing more sympathy to the role of language in logic than had normally been advocated by the syllogists, they laid emphasis on signs as keys to logical knowledge (Buickerood 1985a). At the cost of some simplification, this approach will be called ‘the sign tradition’.
As has been noted, French ‘logique’ did not enjoy much British following; further, Kantian and Hegelian philosophies were only just starting to gain ground, and in any case logic as such was not very prominent in these traditions. Again, although the contributions of Leibniz had gained some attention in Germany (Peckhaus 1997a, ch. 4), the news had not been received in Britain to any significant extent.
The leading figure in this reform was Richard Whately (1787–1863), who graduated at Oxford in 1808 in classics and mathematics and took a college Fellowship for a few years before receiving a rectorship in Suffolk. While there he wrote articles on logic and on rhetoric for the Encyclopaedia metropolitana, a grandiose survey of the humanities and the sciences conceived by the poet Samuel Taylor Coleridge. Several of the articles that appeared over the years until its completion in 1845 were of major importance; but none matched Whately’s in popularity, especially the logic article, which first appeared in the encyclopaedia as his 1823a and then, in a somewhat extended form, as a book in 1826 (Whately Logic1). The year before he had moved back to Oxford; he left Oxford in 1831 to become Archbishop of Dublin, where he remained for the rest of his life.
The impact of the book both encouraged the Oxford reform and helped to stimulate it. Commentaries and discussions by other authors rapidly began to appear. Whately put out revised editions every year or so for the next decade (and also later ones), and many further ones appeared in Britain and the U.S.A. until the early 20th century. From its first edition of 1826 it carried the sub-title ‘Comprising the substance of the article in the Encyclopaedia metropolitana: with additions, etc.’. Its first three Books comprised an introduction and five chapters, and a fourth Book presented a separate ‘Dissertation on the province of reasoning’, with its own five chapters. The ‘additions etc’ mainly constituted an ‘Appendix’ of two items; and from the third edition of 1829 there was a third item and a new supplement to the chapter ‘On the operations of the mind’. Later, the structure of the book was altered to four Books and the Appendix. Comparison of the first and the ninth (1848) editions shows that the changes of phrasing and small-scale structure throughout the work, and the additions, sometimes substantial, are far too numerous to record here. Instead I cite by page number the first edition, of which a photographic reprint appeared in 1988 under the editorial care of Paola Dessì. Further, I do not explore the influence upon Whately of the theologian Edward Copleston: according to Whately’s dedication of the volume, it seems to have been quite considerable.
The great popularity of Whately’s book is rather strange, as at first glance his treatment seems to be rather traditional: indeed, its original appearance in the Encyclopaedia metropolitana gained so little attention that even the date of its publication there became forgotten. He began the main text of the book by repeating the line about logic as ‘the Science, and also as the Art, of Reasoning’ (p. 1), and in the technical exegesis he stressed that logic should be reduced to its syllogistic forms. However, there were passages on religious questions which doubtless caused some of the attention (several of the extensive revisions mentioned above were also in these areas) and in other respects he put forward new views which were to be taken up by his successors (Van Evra 1984a). For example, contrary to the normal tradition in England, he claimed that ‘logic is entirely conversant about language’ (p. 56: interestingly, in a footnote). His definition of a syllogism was formulated thus: ‘since Logic is wholly concerned in the use of language, it follows that a Syllogism (which is an argument stated in a regular logical form) must be an “argument so expressed, that the conclusiveness of it is manifest from the mere form of the expression,” i.e. without considering the meaning of the terms’ (p. 88).6 (The various French traditions sympathetic to this view were not mentioned in the historical sketch given in his introduction). Again, in his analogy between logic and science he compared it with sciences such as chemistry and mechanics, and sought for it foundational principles and autonomy such as they enjoyed.
Among these sciences Whately claimed ‘a striking analogy’ between logic and arithmetic. Just as ‘Numbers (which are the subject of arithmetic) must be numbers of some things’, so ‘Logic pronounce[s] on the validity of a regularly-constructed argument, equally well, though arbitrary symbols may have been substituted for the terms’ (pp. 13, 14). However, he did not press the analogy with mathematics any further than this, and he did not introduce any mathematical techniques in his presentation (or indulge in any sophisticated assessment of sets or collections of things). Although ‘Mathematical Discoveries […] must always be of the description to which we have given the name of “Logical Discoveries” […] It is not, however, meant to be implied, that Mathematical Discoveries are effected by pure Reasoning, and by that singly’ (pp. 238–239). Similarly, in the reform at Oxford the logic course was offered as an alternative to one on Euclid; despite giving his book such a Euclidean title as ‘Elements’, he did not anticipate the insight to be made later that Euclid himself could be put under logical scrutiny (§2.4.3, §4.7.2).
One point of difference for Whately between logic and mathematics lay in the theory of truth. ‘TRUTH, in the strict logical sense, applies to propositions, and to nothing else; and consists in the conformity of the declaration made to the actual state of the case’ (p. 301); by contrast with this (correspondence. theory, ‘Mathematical propositions are not properly true or false in the same sense as any proposition respecting real fact is so called; and hence the truth (such as it is) of such propositions is necessary and eternal’ (the rather woolly p. 221).
We turn now to an important successor of Whately. However, he came to logic largely by other routes.
2.4.1 Summary of his life. Born in 1806 in India, Augustus De Morgan studied at Cambridge University in the early 1820s, and was one of the first important undergraduates to profit from the renaissance of mathematics there. However, as a ‘Christian unattached’ (as he described himself) he could not take a position, and so in 1828 he became founder Professor of Mathematics at London University, then newly founded as a secular institution of higher learning (Rice 1997a). Resigning in 1831, he resumed his chair in 1836, at which time the institution was renamed ‘University College London’ after the founding of King’s College London in 1829, and the ‘University of London’ was created as the body for examining and conferring degrees. He resigned again in 1866, over the issue of religious freedom for staff, and died five years later.
De Morgan was prolific from his early twenties; his research interests lay mainly in algebras, logic and aspects of mathematical analysis, but he also wrote extensively on the history and philosophy of mathematics and on mathematical education. This section is devoted, in turn, to his views an algebra, his contributions to logic, and relationships between logic and mathematics.
2.4.2 De Morgan’s philosophies of algebra. De Morgan’s views on the foundations of algebra vacillated over the years, and are hard to summarise.7 In his first writings on the subject, including an early educational book On the study and difficulties of mathematics, he adopted a rather empirical position, in that algebraic theories were true and based upon clear principles; negative numbers were to be explained (away) by rephrasing the results in which they appeared or justified by the truths of the conclusions drawn from the reasonings in which they were employed (1831a, esp. ch. 9). But, like most English mathematicians of his time, he was influenced by Peacock’s work on the foundations of algebra (§2.3.2). In a long review of Peacock’s treatise he showed more sympathy than hitherto to the abstract and symbolic interpretation, allowing algebra to be ‘a science of investigation without any rules except those under which we may please to lay ourselves for the sake of attaining any desirable object’ (De Morgan 1835a, 99).
However, in the same passage and elsewhere in the review De Morgan referred to truth in the context of algebra, an imperative which informed all of his further thoughts on the subject. Thus he did not try to formulate the modern abstract position based upon axioms; for these axioms would have a status corresponding to hypotheses in science. With regard to Peacock, for example, while De Morgan also advocated the generality of algebra he did not wish to have recourse to the principle of the permanence of equivalent forms but relied upon truth and the interpretation of the symbols and of the theories of which they were components.
Instead, De Morgan used other language, which was also found in connection with logic: the distinction between ‘algebra as an art’, where it functioned merely as a symbolism, and ‘algebra as a science’, where the interpretation of the system was of prime concern. Interestingly, in the first of a series of articles ‘on the foundations of algebra’ he called the art a ‘technical algebra’ and the science a ‘logical algebra, which investigates the method of giving meaning to the primary symbols, and of interpreting all subsequent symbolic results’ (1842b, 173–174): although he soon confessed that ‘logical’ was a ‘very bad’ term (p. 177), there were certain links with logic which will be noted in §2.4.4. When in the next article he stated that x and ÷ were ‘distributive’ over + and – (1849a, 288, with a reference to Servois), he did not grant these laws axiomatic status in a sense which we would recognise; and he did not even mention the instances of commutativity in the system.
In the first paper De Morgan noted some analogies which held between the common algebras and functional equations (1842b, 179). He could speak with authority, as a few years earlier he had written the first systematic account of this young algebra, as a long article 1836a on ‘the calculus of functions’ published in the Encyclopaedia metropolitana. The presentation was technical more than philosophical, concerned with solutions to the equations (for one and for several independent variables), the inverse function, and so on; but this topic was to bear upon one of his main contributions to logic, as we shall see in §2.4.7.8
2.4.3 De Morgan’s logical career. De Morgan was well aware of the changes taking place at Oxford: one of his early educational writings was a survey 1832a of ‘the state of the mathematical and physical sciences’ there. He was partly inspired by Whately’s book to take up logic, but his initial motivation was one which Whately had set aside: the logic involved in Euclidean geometry. The volume on ‘studies and difficulties’ contained a chapter ‘On geometrical reasoning’, in which he laid out the valid syllogistic forms, using ‘ ’, ‘
’, ‘ ’ and ‘Δ’ for the terms, and outlined the syllogistic form of Pythagoras’s theorem (1831a, ch. 14). For background acquaintance with logic he cited there a passage from Whately’s book, in its third edition of 1829, as ‘a work which should be read by all mathematical students’.9
’ and ‘Δ’ for the terms, and outlined the syllogistic form of Pythagoras’s theorem (1831a, ch. 14). For background acquaintance with logic he cited there a passage from Whately’s book, in its third edition of 1829, as ‘a work which should be read by all mathematical students’.9
De Morgan again advocated studying the logic of geometry in another educational article 1833a, and he took his own advice in a pamphlet 1839a on the ‘First notions of geometry (preparatory to the study of geometry)’. Here he laid out the logic which, as he stated in the preamble, ‘he found, from experience, to be much wanted by students who are commencing with Euclid’; however, he did not then apply this logic to the ancient text. Most of the pamphlet was reprinted with little change as the first chapter of his main book on the subject, Formal logic (1847a). By then he had launched his principal researches, which appeared as a series of five papers ‘On the syllogism’ published between 1846 and 1862 in the Proceedings of the Cambridge Philosophical Society. There were some articles and book reviews elsewhere, especially a short book 1860a proposing a ‘syllabus’ for logic; the total corpus is quite large.10
2.4.4 De Morgan’s contributions to the foundations of logic
The law is good if one makes legal use of it.
De Morgan, motto (in Greek) on the
title page of Formal logic
De Morgan was not a clear-thinking philosopher, and his views are scattered in different places: also, they changed somewhat over time, although he did not always seem to be aware of the fact (different definitions of a term given in different places, for example). He worked largely within the syllogistic tradition, but he was much more aware than his contemporaries of its limitations, and extended both its range and scope: the preface of Formal logic began with the statement that ‘The system given in this work extends beyond that commonly received, in several directions’. We shall note some principal extensions in the next three sub-sections.
As with all logicians of his time and long after, De Morgan did not systematically distinguish logic from metalogic. The long chapter ‘On fallacies’ of his book made almost every other distinction but this one (see pp. 242–243 for some tantalising cases); and a particularly striking later example is his assertion that ‘a syllogism is a proposition; for it affirms that a certain proposition is the necessary consequence of certain others’ (1860b, 318).
De Morgan offered views on the character of logical knowledge in general; and we shall take his use of ‘necessary’ quoted just now to start with this theme. In the opening chapter of his book, on ‘First notions’, he stressed that logic was exclusively concerned with valid inference; truth was a secondary concept, dependent ‘upon the structure of the sentence’ (1847a, 1). The more formal treatment began in the second chapter with a specification of logic as ‘the branch of inquiry (be it called science or not), in which the act of the mind in reasoning is considered, particularly with reference to the connection of thought and language’ (p. 26).
Many of the forms of inference which De Morgan then investigated were dependent upon language; in particular, scientific induction, where he drew on probability theory to justify universal propositions rather than inference from particulars to particulars (chs. 9–11). The sub-title of his book is worth noting here: ‘or, the calculus of inference, necessary and probable’—not the ‘necessary and possible’ of modern modal logic. There is also a link between logic and quantity, if the connection with probability is held to be that logic deals with the quantities 0 and 1. We shall meet the notion of quantity later in his work at §§2.4.6–7.
However, De Morgan did not wish to dwell upon ‘the science of the mind, usually called metaphysics’ (p. 27):
I would not dissuade a student from a metaphysical inquiry; on the contrary, I would rather endeavour to promote the desire of entering upon such subjects; but I would warn him, when he tries to look down his own throat with a candle in his hand, to take care that he does not set his head on fire.
De Morgan’s title ‘Formal logic’ may show influence from a recent Outline of the laws of thought, anonymously published by the Oxford scholar William Thomson (1819–1890); for he defined ‘logic to be the science of the necessary laws of thinking, or, in more obscure phrase, a science of the form of thought’ (1842a, 7) and then examined in detail the various forms that the notion of form could take. However, De Morgan did not handle too well the distinction between form and matter; Mansel 1851a was to point this out in a thoughtful review of the book and of the second edition (1849) of Thomson (Merrill 1990a, ch. 4). In his papers on the syllogism De Morgan somewhat changed his position on the nature of logic, or at least on his manner of expressing it. ‘Logic inquires into the form of thought, as separable from and independent of the matter thought on’, he opined in the third paper (1858, 75), in a manner reminiscent of his distinctions in algebra. However, later he claimed that mathematics has never ‘wanted a palpable separation of form and matter’ (p. 77); so now logic ‘must be […] an unexclusive reflex of thought, and not merely an arbitrary selection,—a series of elegant extracts,—out of the forms of thinking’ (pp. 78–79). This is a kind of completeness assertion for logic: all aspects of thinking and inference should be brought out.
In revising the distinction between form and matter, De Morgan cast the copula in a very general form. In the second paper he recalled that in his book ‘I followed the hint given by algebra, and separated the essential from the accidental characteristics of the copula’ (1850a, 50, referring to 1847a, ch. 3). The essentials led to the ‘abstract copula’, ‘a formal mode joining two terms which carries no meaning’ (p. 51). He laid down three laws that it should satisfy, giving them symbolic forms:
1) ‘transitiveness’ between terms X, Y and Z, ‘symbolized in

where ‘—’ was ‘the abstract copular symbol’ and ‘=’ was informally adopted as an equivalence relation between terms or propositions;
2) ‘convertibility’ between X and Y (which we would call ‘commutativity’: as we saw in §2.4.2, he did not use Servois’s adjective); and
3) a completeness (meta)property of bivalent logic which he called ‘contrariety: in X—Y and [its negation] X--Y it is supposed that one or the other must be’ (p. 51). Since reflexivity (X—X) was taken for granted, he had in effect defined the abstract copula as an equivalence relation; but his sensitivity to relations and the state of algebra of his day did not allow him to take this step (that is, to see its significance). However, in effecting his abstraction and specifying the main pertaining properties he may well have recalled the abstraction applied to functions in forming functional equations.
These remarks […] caution the reader against too ardent an admiration of the syllogistic mode of reasoning, as if it were fitted to render him a comprehensive and candid reader. The whole history of literature furnishes incontestable evidence of the insufficiency of the Aristotelian logic to produce, of itself, either acuteness of mind, or logical dexterity.
Blakey 1847a, 162
In his book, which appeared in the same year as Blakey’s caution (in an essay on logic), De Morgan pointed to some forms of inference which lay outside the syllogistic ambit. ‘For example’, a well-remembered one, ‘“man is animal, therefore the head of a man is the head of an animal” is an inference, but not syllogistic. And it is not mere substitution of identity’ (1847a, 114). To cover such cases he offered the additional rule ‘For every term used universally less may be substituted, and for every term used particularly, more’ (p. 115). While his treatment was not fully satisfactory, his modifications can be cast in a sound form (Sanchez Valeria 1997a).
De Morgan also noted the case ‘X)P + X)Q = X)PQ’, which in his notation (p. 60) stated that if every X was both P and Q, then it was also ‘the compound name’ P and Q, and which ‘is not a syllogism, nor even an inference, but only the assertion of our right to use at our pleasure either one of two ways of saying the same thing instead of the other’ (1847a, 117). This remark occurred in a section in which he tried to formulate syllogistic logic in terms of ‘names’: that is, terms and the corresponding classes (the rather unclear pp. 115–126).
Partly in the context of this extension, De Morgan discussed at some length in ch. 7 limitations of the Aristotelian tradition. For example, on existence he noted the assumption that terms be non-empty, and criticised the medieval ‘dictum de omni et nullo’, where in universal affirmative propositions ‘All Xs are Ys’ all objects satisfying X must also satisfy Y, and in universal negative propositions ‘No Xs are Ys’ no object satisfying X may also satisfy Y.
These ideas show that De Morgan tried to push out the province of logic beyond syllogisms. In the next two sub-sections I note his two main extensions of its methods, and even of its province.
2.4.6 Contretemps over ‘the quantification of the predicate’. This phrase referred to the cases in which the middle term of a syllogism was made susceptible to ‘all’ and ‘some’. Thus, in addition to ‘all Xs are Ys’ and the other standard forms, there were admitted also the octet of new forms ‘All/Some X is all/some/not any Y’ (where ‘some’ must exclude the case ‘all’), and the repertoire of valid and invalid syllogistic forms was greatly increased. The extended theory uses the word ‘quantification’ in the way to which we are now accustomed; and, while we shall see in §4.3.7 that that use has closer origins in Peirce’s circle, the content here is similar.
The name was introduced by the Scottish philosopher William Hamilton (1788–1856). A student at Oxford University during the same period as Whately, Hamilton passed his career in his native country of Scotland, for many years at the University of Edinburgh. He seems to have introduced his new theory around 1840, and developed it in his teaching. De Morgan came across a similar form of the theory in 1846, in which he considered propositions of forms such as ‘Most/Some of the Ys are Zs’, and he described it in the first paper on the syllogism (1846a, 8–10). In an addition to this paper he discussed them in more detail, taking the collections associated with the quantified predicates to be of known sizes, as in ‘Each one of 50 Xs is one or other of 70 Ys’ (pp. 17–21). In his book he called these syllogisms ‘numerically definite’ and extended the notion further, in that he specified only numerical lower bounds of subjects possessing the predicated properties (‘m or more Xs are Ys’). In his book he found the numbers associated with the predicates involved in the conclusion of valid syllogisms (1847a, ch. 8). His second paper contained a treatment of these forms of proposition different from Hamilton’s in exhibiting an algebraist’s concern for symmetries of structure between a form and its contrary forms (1850a, 38–42: see also the fifth paper 1862a).
Hamilton responded to De Morgan’s basic idea of quantification with accusations of plagiarism, and a row began which continued for the remaining decade of Hamilton’s life (Laita 1979a). De Morgan claimed, doubtless with justice, that his invention was independent of Hamilton (see especially the appendix to his book.; and in fact priority for the innovation belongs to neither of the two contestants but to the botanist George Bentham (1800–1884), in a book on logic which was an extended commentary upon the first edition of Whately’s book. Bentham had outlined his treatment of propositions, and then applied it to the analysis of some of the traditional forms of valid syllogism, stressing quite explicitly that his approach was superior to the normal classification (1827a, esp. pp. 130–136, 150–161). George was the nephew of Jeremy Bentham, and indeed acknowledged the influence of some manuscripts of his uncle; so maybe the idea goes back further!11
Now in 1833 Hamilton harshly reviewed the third edition of Whately’s Logic for the stress on language among other things; perhaps they had suffered poor relations at Oxford University. (He claimed that logic was better taught in Scotland than in England). He also noted here several other books (Hamilton 1833a, 199–200., and one of them was Bentham’s. So he can be fairly accused at least of cryptomnesia (forgotten and maybe unnoticed access). Bentham’s book sold very poorly, his publisher going bankrupt soon after its launch; he himself was presumably too deeply involved in botany to complain, and nobody noticed his work until 1850, when attention was drawn in The Athenaeum (Warlow 1850a). Even such a bibliophile as De Morgan did not come across Bentham’s book until his 1858a, 140 where Warlow and an ensuing discussion were cited.12
These extensions of the syllogism need careful exposition (which Hamilton did not provide), for the relationship between the eight cases needs careful examination since they are not all independent. In fact, there is little in the theory beyond the ‘Gergonne relations’, which Gergonne 1816a had presented in a paper in the same volume of his Annales as his paper on ‘analysis’ cited in §2.2.5, in order to clarify the (intuitive) use of Euler diagrams (my 1977a). The paper exercised little influence, the Annales gaining only a small circulation even in France:13 De Morgan was one of the first to cite this paper, in his first reply to Hamilton cited above (1847a, 324), although he did not appreciate the significance of Gergonne’s classification. However, he made other useful extensions to syllogistic logic in his Syllabus by adding to the list of categorical propositions forms such as ‘Every X is Y’, ‘everything is either X or Y’, ‘some things are neither X s nor Ys’, and so on (most clearly in 1860b, 190–199, with exotic names).
A related extension was presented in the appendix of De Morgan’s fourth paper, which treated ‘syllogisms of transposed quantity’. Here ‘the whole quantity of one concluding term, or of its contrary, is applied in a premise to the other concluding term, or to its contrary’, as in ‘Some Xs are not Ys; for every X there is a Y which is Z: from which it follows, to those who can see it, that some Zs (the some of the first premise) are not Xs’ (1860a, 242–246; he referred to his earlier (and briefer) mentions of this type of syllogism). The most interesting feature, which Peirce was to grasp (§4.3.6) but seemed to elude De Morgan himself, is that it is valid only for predicates satisfied by finite classes.
The episode of the quantification of the predicate may not seem now to be of great importance. However, at the time it brought publicity to logic; in particular, it stimulated Boole into print on the subject, as we shall see in §2.5.3.
2.4.7 The logic of two-place relations, 1860. (Merrill 1990a, chs. 5–6)It is a curious feature of the history of philosophy that, while there had been awareness since Greek antiquity of roles for relations (Weinberg 1965a, ch. 2), nobody seems to have taken seriously the fact that relational propositions, such as ‘John is taller than Jeremy’, cannot fall within the compass of syllogistic logic. De Morgan opened up this part of logic in arguably his most important contribution.
De Morgan touched upon relations from time to time. He contributed an article 1841a on ‘Relation (mathematical)’ to the Penny cyclopaedia, restricting himself to cases in arithmetic and algebra though including the operator form (225.1).14 In his book he recalled the uses of the term in older writers on logic (1847a, 229). Within logic, we saw his abstract copula in §2.4.4, and will note his part-whole theory of class inclusion in §2.4.9, both of which embodied relations; and he even used the notion of a relation as a predicate in orthodox syllogistic logic, when pointing out that
If I can see that
Every X has a relation to some Y
and Every Y has a relation to some Z,
it follows that every X has a compound relation to some Z
(1850a, 55). Again, properties of the product of functions, akin to properties such as (224.3) in functional equations, were included in his discussion of the abstract copula in the context of relations and their compounding (p. 56):
The algebraic equation y = ϕx has the copula =, relatively to y and ϕx: but relatively to y and x the copula is = ϕ.[…]. The deduction of y = ϕψz from y = ϕx, x = ψz is the formation of the composite copula = ϕψ. And thus may be seen the analogy by which the instrumental part of inference may be described as the elimination of a term by composition of relations.
He also commented on relations elsewhere; for example, whole and part, ‘with its concomitants, I call onymatic relations’ (1858a, 96). Indeed, relations were even granted priority over classes: ‘When two objects, qualities, classes, or attributes, viewed together by the mind, are seen under some connexion, that connexion is called a relation’ (p. 119).
However, not until the late 1850s, his own mid fifties, did De Morgan study the logic of relations, in his fourth paper 1860a on the syllogism. Beginning by referring to the above two quotations as instances of the ‘composition of relations’, he then treated relations (but only between two terms. in general. The paper is a ramble even by his standards, but there are two key passages.
‘Just as in ordinary logic existence is implicitly predicated for all the terms’ (p. 220), so relations were taken here to be likewise endowed; however, for some reason De Morgan did not mention appropriate universes of discourse. Symbolised by ‘L’, ‘M’ and ‘N’, the corresponding lower case letters denoted the contraries; and periods were used to distinguish a relation from its contrary; thus, for example,
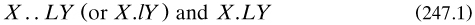
respectively expressed that X was/was not ‘some one of the objects of thought which stand to Y in the relation L’ (p. 220). Compound relations were indicated by the concatenation ‘LM’, and quantification over relations by primes such that LM′ ‘signify an L of every M’ and L, M ‘an L of none but Ms’. The converse to L was written ‘L–1’, or ‘Lv’ for ‘Those who dislike the mathematical symbol’;15 further, ‘L–1X may be read “L-verse of X”’ (p. 222). He also proved that ‘if a compound relation be contained in another relation, […] the same may be said when either component is converted, and the contrary of the other component and of the compound change places’ (p. 224), a result of significance:
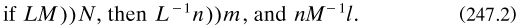
Next De Morgan mentioned some main desirable properties of a relation, similar to those for the abstract copula (although he made no use of ‘=’ in the paper). One was convertibility, ‘when it is its own inverse’, and where ‘So far as I can see, every convertible relation can be reduced to the form LL–1’ (p. 225). With transitivity, ‘when a relative of a relative is a relative of the same kind’, ‘L signifies ancestor and L–1 descendant’, and he mentioned a ‘chain of successive relatives, whether the relation be transitive or not’, like the sequence of functional operations ϕnx for positive and negative integers n (p. 227).
De Morgan now applied this apparatus to syllogistic logic, with little concern for the extensions discussed in the previous sub-sections. All three propositions of a syllogism were cast in relational form and the various valid figures laid out (pp. 227–237). He mentioned in passing the syllogisms expressible in terms of onymatic relations, and did not (trouble to) present the pertaining numerically definite syllogisms; and his paper faded away in its final pages (the appendix dealt with the ‘syllogisms of transposed quantity’ noted in §2.4.6). But he noted in places the generality of his new concern: for example, that ‘quantification itself only expresses a relation’ between the quantified predicates (p. 234); or that ‘The whole system of relations of quantity remains undisturbed if for the common copula “is” be substituted any other relation’ (p. 235), so that some structure-similarity obtained between the calculi of relations and of classes.
2.4.8 Analogies between logic and mathematics
But, as now we invent algebras by abstracting the forms and laws of operation, and fitting new meanings to them, so we have power to invent new meanings for all the forms of inference, in every way in which we have power to make meanings of is and is not which satisfy the above conditions.
De Morgan 1847a, 51
It is clear that De Morgan drew upon a number of similarities between logic and algebra: however, in one respect logic had to remain more fundamental. For even in the most abstract approach to algebra one is constrained by the need for the axioms to form a consistent system; but then a logical notion is underlying the algebra. He recognised this point in connection with the distinction between the ‘form’ and the ‘matter’ of an argument when he stated that ‘logic deals with the pure form of thought, divested of every possible distinction of matter’, including those pertaining to algebra and arithmetic (1860c, 248–249; see also 1858a, 82).
However, De Morgan also pointed out many analogies between logic and algebra, and to a lesser extent with arithmetic. The quotation above belongs to the discussion of the abstract copula just described. Among other examples, he claimed (incorrectly) that elimination between algebraic equations functioned like inference in logic (1850a, 27). Similarities of property were sometimes reflected in the use of the same symbol. For example, he expressed the disjunction of propositions ‘by writing + between their letters’ (1847a, 67: unexplained in 1846a, 11). Again, for ‘the convertible propositions’ ‘no P is Q’ and ‘some Ps are Qs’ involving two terms P and Q he chose ‘the symbols P.Q and PQ, which the algebraist is accustomed to consider as identical with Q.P and QP’ (1846a, 4: no such point made at 1847a, 60). Indeed, as we saw around (247.1–2), he used algebra-like notations deploying ‘=‘,’–’ and/or brackets of various kinds to distinguish and classify types of proposition and valid forms of syllogistic inference (see, for example, 1850a, 37–41). The procedures included rules for rewriting terms P, … in terms of their contraries p, …; for example, ‘All P are not q’, symbolised ‘P))q’, was convertible salva veritate to ‘No P are Q’, symbolised ‘P).(Q’. As a result no real distinction remained between subject and predicate from the symbolic point of view. The account in his Syllabus even included a ‘zodiac’ circle of 12 bracket-dot notations for valid syllogisms grouped in threes by logical opposition and placed at the corners of equilateral triangles (1860b, 163). His status in the history of semiotics should be raised.
Some of these collections of notations displayed duality properties, although De Morgan did not emphasise the feature. However, in using the symbol ‘x’ to represent the contrary term of a term X he deployed a symmetry of roles for X and x, and combinations of them using the dots and brackets of (247.1), which was rather akin to duality (see, for example, 1846a, arts. 1–2 for the definition and an initial deployment).
Although De Morgan once opined that ‘It is to algebra that we must look for the most habitual use of logical forms’ (1860a, 241), he did not restrict himself to similarities with algebra and with arithmetic, but tried to encompass mathematics as a whole. Indeed, he introduced the expression ‘mathematical logic’ in his third paper on the syllogism, as ‘a logic [which] will grow up among the mathematicians, distinguished from the logic of the logicians by having the mathematical element properly subordinated to the rest’ (1858, 78). Of course he was referring to mathematical presence in general, not the specific doctrine of mathematical logic which will be the subject of several later chapters. However, he did use the word ‘mathematical’ in general contexts in his logic, often in connection with his discussion of collections, which we now note.
2.4.9 De Morgan’s theory of collections. If an algebra admits ‘some’ or ‘all’ into its brief, then stuff of some kind enters its concerns, be it of terms, individuals, properties or whatever; and it will form itself into collections, with associated properties of inclusion. Like all the logicians covered in this chapter, collections of things were handled by De Morgan part-whole (§1.2.2), not with the set theory to come from Georg Cantor (§3.2).
In his first paper on the syllogism, De Morgan soon stressed an important idea: ‘Writers on logic, it is true, do not find elbow-room enough in anything less than the universe of possible conceptions: but the universe of a particular assertion or argument may be limited in any matter expressed or understood’ (1846a, 2). Throughout these papers, and to a lesser extent in his book (1847a, 110, 149), he deployed the idea of a universe of discourse/objects/names with good effect. For example, he divided a universe U into (some) class A and its complement a, and for a pair of such ‘contraries or contradictories (I make no distinction between these words)’, he noted that ‘The contrary of an aggregate is the compound of the contraries of the aggregants; the contrary of a compound is the aggregate of the contraries of the components’ (1858a, 119; compare 1860b, 192). This is the form in which he gave the laws which are now known after his name.
Like most of his contemporaries, De Morgan did not systematically present all the properties that his collections satisfied; but here are a few cases. The earliest example occurs in his 1839 pamphlet, to be repeated in his book: if ‘All the Xs make up part (and part only) of the Ys’ and Ys similarly with Zs, then ‘All the Xs make up part of part (only) of the Zs’ (1839a, 26; 1847a, 22). He associated the conclusion drawn with a fortiori reasoning.
Later in his book De Morgan specified identity as a property of objects: if X)Y and Y)X, then ‘The names X and Y are then identical, not as names, but as subjects of application’ (1847a, 66): unfortunately he immediately gave ‘equilateral’ and ‘equiangular’ in plane geometry as examples of identical names, having forgotten about figures such as rectangles. When the referent (not his term) of X was part of that of Y he described the terms X and Y respectively as ‘subidentical’ and ‘superidentical’ (p. 67).
Were these versions of identity to be interpreted intensionally or extensionally? In his third paper on the syllogism De Morgan gave his most detailed (though rather unclear) discussion. He distinguished between three senses of whole and part, ‘giving rise into three logical wholes’. Firstly, ‘arithmetical’ was an extensional version with ‘the class as an aggregate of individuals’, where the aggregate was the extensional union of the parts of the class; or it was ‘the attribute as an aggregate of qualities of individuals’, where ‘attribute’ was a quality of the class as a whole. Secondly, ‘mathematical’ was used ‘most frequently, of class aggregated of classes; less frequently, rarely in comparison, of class compounded of classes’, where ‘compound’, in contrast to ‘aggregate’ and in some kinship with ‘attribute’, referred to a property adhering to every member of an aggregate. Finally, ‘metaphysical’ was ‘almost always, of attribute compounded of attributes: sometimes, but very rarely, of attribute aggregated of attributes’.
To clarify this none too clear classification (‘rarely’? ‘frequently’?), De Morgan added: ‘Extension, then, predominates in the mathematical whole; intension in the metaphysical’ (1858, 120–121, with some help from pp. 96–100 and from 1860b, 178–181). However, he did not pursue the major question of how much actual mathematics could be encompassed within the extensional realm; his use of the word ‘mathematical’ is rhetorical. A regrettable tradition was launched.
This issue exemplifies De Morgan’s strengths and weakness as a logician. He had made major insights in this paper, and elsewhere in his writings he presented novelties to logic and suggested new connections, or at least analogies, with mathematics, especially algebra. However, he surrounded his fine passages with much discursive chatter, fun to read but inessential to any logical purpose. He did not gain the full credit that he deserves; but the reader has to turn prospector to find the nuggets. Much of his argument rested upon examples rather than general theorems or properties—which constitutes another similarity with his essay on functional equations. Furthermore, his contributions were to be somewhat eclipsed by the more radical innovations made by his younger contemporary and friend, George Boole.
2.5.1 Summary of his career. Boole must be among the most frequently mentioned mathematicians today, because of the bearing of his logic upon computing. In 1989 I saw the ultimate compliment, in Lima (Peru): a computer company displaying its name ‘George Boole’ in large letters on the side of its building. However, Boole himself did not relate his theory even to the computing of his day: on the contrary (1847a, 2),
To supersede the employment of common reason, or to subject it to the rigour of technical forms, would be the last desire of one who knows the value of that intellectual toil and warfare which imparts to the mind an athletic vigour, and teaches it to contend with difficulties and to rely upon itself in emergencies.
In fact, many of the details of Boole’s “famous” theory are not well known. While not a detailed account,16 enough is given here to indicate later the differences between the tradition that he launched and the mathematical logic which was largely to supplant it.
Born in Lincoln in 1815, Boole passed the first 35 years of his life in and around that city. He had to maintain himself and even his family as a school-teacher, and was largely self-taught in mathematics; but nevertheless he began publishing research papers in 1841, in the recently founded Cambridge mathematical journal. His main interest lay in differential equations. His work in logic, our main concern, reached the public first as a short book entitled The mathematical analysis of logic (1847a, hereafter ‘MAL’), followed by a paper 1848a in the Journal.
In the following year Boole moved to Cork in Ireland, as founder Professor of Mathematics in Queen’s College, a constituent of the new Queen’s University of Ireland. He stayed there for the remaining 15 years of his life, and wrote the definitive version of his logic, as the book An investigation of the laws of thought (1854a, hereafter ‘LT’). Reception of his ideas was rather slow; even his correspondence with De Morgan, while substantial (Boole–De Morgan Letters), did not focus strongly on the details of either man’s system (Corcoran 1986a).17 In fact, as we shall see, their contributions to logic, while both mathematical and even algebraic in type, differed fundamentally in content. He seems to have had little contact even with William Rowan Hamilton in Ireland, although they had algebra and time as common matters of concern.
The year after his second book was published, Boole married, and produced five daughters at regular two-year intervals. His wife Mary, a woman of considerable intelligence, helped him with the preparation of textbooks on differential and on difference equations, which appeared as Boole 1859a and 1860a respectively. He began work on the first one soon after publishing LT;18 they made much more impact at the time than those on logic. During these years he also wrote extensively on the application of his logical system to probability theory. He also attempted a more popular account of that system which, however, was never completed; a selection of these and other manuscripts on logic has appeared recently as Boole Manuscripts.19 There is no edition of his works, although all his four books have been reprinted. In addition, MAL appeared in 1952 in an edition of many of his writings and some manuscripts on logic and probability theory (Boole Studies).
2.5.2 Boole’s ‘general method in analysis’, 1844. As was remarked briefly in §2.4.2, English mathematics became greatly concerned with operator methods of solving differential equations. One of the leading workers was D. F. Gregory (1813–1844), Scottish by birth but very English in his researches. In a monograph on these methods he laid out the basic laws of differential operators ‘a’ and ‘b’ operating on functions u and v. Citing Servois for terms (§2.3.2), he wrote (Gregory 1841a, 233–234):
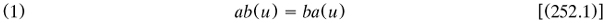
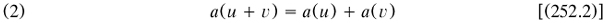
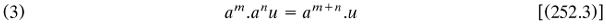
The first of these laws is called the commutative law […] The second law is called distributive […The third] may conveniently be called the law of repetition […].
By this time Gregory, the editor of the Cambridge mathematical journal, was encouraging new talent and taking Boole’s first papers. In 1843 Boole had prepared enough material to write a large paper on this subject, which he submitted to the Royal Society, with Gregory’s and De Morgan’s encouragement. After difficulties with the referees, he had it accepted for the Philosophical transactions, where it appeared as 1844a and later even won one of the Society’s gold medals, the first occasion for a mathematical paper.
Boole’s essay, entitled ‘On a general method in analysis’, treated ‘symbols apart from their subjects’. Working out from the symbolic version (224.6) of Taylor’s theorem, he produced a wide range of solutions of differential and difference equations and also summation of series and the use of generating functions. He started his account with the same three laws for differential operators to obey as were proposed by Gregory (whom he cited); he also used Servois’s adjectives for the first two. However, he called the third ‘the index law’; and he placed the laws at the head of the presentation, whereas Gregory’s had appeared well into his book. After stating these laws, he noted at once that commutativity (252.3) applied only to differential equations with constant coefficients. Much of the paper was devoted to finding solutions to equations involving both commutative and non-commutative operators.
2.5.3 The mathematical analysis of logic, 1847: ‘elective symbols’ and laws. By the time of that paper De Morgan and William Hamilton were quarrelling over the quantification of the predicate (§2.4.6), prompting Boole to write up his own views about logic, in the short book MAL of 1847. While its content was substantially different from the subject matter of the two contestants—he ignored quantification of the predicate, in fact—some of their other issues were reflected (Laita 1979a).
In a tradition of his time, Boole treated logic as a normative science of thought allied to psychology; indeed, it was fundamental to his operational theory (Hailperin 1984a). In his introduction he spoke of ‘mental operations’ at some length (1847a, 5–7), and formulated his basic principles in the following way (pp. 15–16). Symbolising by ‘1’ a ‘Universe’ which
comprehend[s] every conceivable class of objects whether existing or not […] Let us employ the letters X, Y, Z, to represent the individual members of classes. […] The symbol x operating upon any subject comprehending individuals or classes, shall be supposed to select from that subject all the Xs that it contains. […] the product xy will represent, in succession, the selection of the class Y, and the selection from the class Y of such individuals of the class X as are contained in it, the result being the class whose members are both Xs and Ys.
Although for some reason he did not mention his 1844a or cite Gregory, Boole set down the basic ‘laws with these mental acts [x] obeyed in a form closely similar with those for the differential operators (pp. 17–18). Given an ‘undivided subject’ u + v, with u and v ‘the component parts of it’, then the ‘acts of election’ x and y obeyed the laws



[…] From the first of these, it appears that elective symbols are distributive, from the second that they are commutative; properties which they possess in common with symbols of quantity […]
The third law (3) we shall denominate the index law. It is peculiar to elective symbols, and will be found of great importance in enabling us to reduce our results to forms meet for interpretation.
The formulation of (253.3) in terms of xn rather than x2 is very striking; in a footnote he compared it with the law +n = +, another consideration of Gregory (this time, 1839a on ‘algebraic symbols in geometry’) which again he did not cite.
As normal for his time, Boole was not axiomatising a theory in any manner that we would practise today; rather he was laying down laws for his elective symbols to obey, in the algebraic tradition. He stated rather few of the laws and properties that his system required; (253.1) as the only distributivity law (over subjects u, v,…), and no associativity laws (with consequent sloppiness over bracketing). He reserved the word ‘axiom’ for a property stated in the space occupied above by my second string of ellipsis dots: ‘The one and sufficient axiom involved in this application is that equivalent operations performed upon equivalent subjects produce equivalent results’. We would regard this axiom as a metatheoretic principle.
Boole stressed interpretation. His introduction began with the statement that in ‘Symbolical Algebra […] the validity of the processes of analysis does not depend upon the interpretation of the symbols which are employed, but solely upon the laws of their combination’ (p. 3), and we saw him mention interpretability at the head of this sub-section. However, some commentators were less familiar with this issue. For example, in December 1847 Arthur Cayley (1821–1895) wondered if it was true in this calculus that ‘ x has any meaning’, and Boole explained ‘that this question is equivalent to whether √–1 × √–1= –1 in a system of pure quantity for although you may interpret √–1 in geometry you cannot in arithmetic’. In his reply Cayley disliked this analogy, but Boole insisted that √–1 should be treated ‘as a symbol (i) which satisfies particular laws and especially this
x has any meaning’, and Boole explained ‘that this question is equivalent to whether √–1 × √–1= –1 in a system of pure quantity for although you may interpret √–1 in geometry you cannot in arithmetic’. In his reply Cayley disliked this analogy, but Boole insisted that √–1 should be treated ‘as a symbol (i) which satisfies particular laws and especially this

(Boole Manuscripts, 191–195).
In Boole’s algebra the cancellation law did not hold for multiplication: zx = zy did not imply that x = y. Thus he needed the notion, novel for its time, of the ‘indefinite symbol’ v (or class), as it let him render as equations many relationships which otherwise would have had to appear as (some analogue of) inequalities. For example (p. 21), ‘If some Xs are Ys, there are some terms common to the classes X and Y. Let those terms constitute a separate class V, to which there shall correspond a separate elective symbol v, then

However, he offered no laws which v should satisfy, and he did not distinguish between traditional forms of proposition and those involved in quantification of the predicate; for example, ‘vx = vy’ could cover both ‘Some Xs are Ys’ and ‘Some Xs are some Ys’ (pp. 21–22).
Like De Morgan (§2.4.9), Boole’s theory of classes was an extensional version of part-whole analyses of collections. Inclusion was the only relation, with proper or improper not always distinguished: ‘The equation y = z implies that the classes Y and Z are equivalent, member for member’ (p. 19; see also p. 24). But again little information was given about ‘–’ or ‘+’; for example, he left rather implicit that ‘+’ linked only disjoint classes.
2.5.4 ‘Nothing’ and the ‘Universe’. The symbol ‘0’ first appeared on p. 21 when Boole rendered the categorical proposition ‘All Xs are Ys’ as
Obviously ‘0’ symbolised the mental act complementary to the elective symbol 1, but he gave it no formal definition nor stated its laws (of addition to any x, for example).
For the universe (p. 20),
The class X and the class not-X together make the Universe. But the Universe is 1, and the class X is determined by the symbol x, therefore the class not-X will be determined by the symbol 1 – x.
So ‘1’ was serving double duty for elective symbols and for classes. The idea of an identity operator (or entity or whatever) in this world of expanding algebras was a novelty which took time to be understood, although it was already present in the Lagrangian (224.6): Cayley was to be another pioneer, in his paper 1854a on matrix multiplication.
Another example of the conceptual difficulties arises later: ‘To the symbols representative of Propositions […] The hypothetical Universe, 1, shall comprehend all conceivable cases and conjunctures of circumstances’, and x ‘shall select all cases in which the Proposition X is true’ (pp. 48–49). Boole offered no further explanation of this hypothetical Universe, which sounds the same as the “absolute” Universe presented before (253.1); but to have “everything” in that way is to have nothing at all, since non-part-ship of such a Universe is impossible. More importantly, within this Universe true propositions cannot be distinguished from tautological ones, or false propositions from self-contradictory ones (Prior 1949a). Further, it led him to claim that a disjunction of particular propositions, but not a disjunction of universal ones, could be split into disjunctions; the (alleged) grounds were that the disjunction was hypothetical whereas the components were categorical (p. 59). On the role of universes he lagged behind De Morgan in insight.
Boole clearly thought that 0 ≠ 1, but the status of this proposition is not clear; since he had no symbol for ‘not’, it has to be an additional assumption. The closest that he came to the issue occurred when he mooted in MAL ‘the nonexistence of a class: it may even happen that it may lead to a final result of the form

which would indicate the nonexistence of the logical Universe’ (1847a, 65). But he did not extend his discussion to propositions such as

we shall note at (445.1) that Schröder was to consider them. Naturally, Boole did not assert anything like ‘x ≠ 0 (or 1) implies that x = 1 (or 0)’, as the classial interpretation would have been lost. A. J. Ellis 1873a made this point in contrasting Boole’s treatment of propositions with that of classes; however, he formulated the contrast as being between algebra and propositions.
Boole also read ‘0’ and ‘1’ as two different states or situations. In the symbolisation of a proposition, ‘0’ referred to ‘no such cases in the hypothetical Universe’ (p. 51). The paper 1848a was still less clear; ‘0’ took the stage, as an elective symbol, without cue, after the statement that ‘There may be but one individual in a class, or there may be a thousand’ but apparently not none (p. 127).
But Boole also interpreted ‘0’ and ‘1’ as numerical quantities. For example, on connections of logic with probability, after noting that ‘every elective symbol […] admits only of the values 0 and 1, which are the only quantitative forms of an elective symbol’, he compared a manner of expressing hypothetical propositions with some unstated means using probability theory ‘(which is purely quantitative)’, and added that ‘the two systems of elective symbols and quantity osculate, if I may use the expression, in the points 0 and 1’ (p. 82).
2.5.5 Propositions, expansion theorems, and solutions. Boole did not treat propositions X, Y,… as “atomic” entities, but presented his interpretation as propositions only when specifying the hypothetical type, ‘defined to be two or more categoricals united by a copula (or conjunction)’ (p. 48). But even now the constituent propositions did not stand alone but were encased in their truth-values: for example, ‘(1 – x)y’ corresponded to ‘X false, Y true’ (p. 50). A few lines later he did interpret three propositions without reference to truthhood; but since he made no comment on the change, it was probably unintentional.
The truth-value of a combination of propositions was defined in (the appropriate. terms of the truth-values of its components. In particular, the truths of the conjunction and of the inclusive disjunction of X and Y were rendered on p. 51 respectively as
The procedure was to sum all mutually exclusive cases ‘which fill up the Universe of the Proposition’ given (p. 52). An interesting example was ‘Either X is true, or Y is true’ when X and Y were ‘exclusive’; then only two cases (X true and Y false, and Y true and X false. had to be summed, yielding on p. 53

This equation was presumably rendered uninterpretable by the presence of –2; but it was soluble by applying the index law to convert it into a quadratic in x and y and then taking factors (p. 56).
Boole was not primarily concerned with laying out deductions from his premises in the meticulous way that Frege, Russell and the mathematical logicians have accustomed us to expect, but rather to find their consequences by means of algebraic manipulations. So with these tools he “solved” collections of logical premises; for syllogisms, by rendering their premises in forms such as (255.1–2) and eliminating, in an algebraic sense, the middle term represented by y, thereby obtaining the conclusion concerning x and z. For example, ‘All Ys are Xs, No Zs are Ys, ∴ Some Xs are not Zs’ became
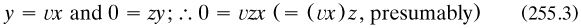
by multiplying together each side of the premising equations (p. 35).
The book was completed by a key feature of Boole’s method of solution: the expansion of functions of elective symbols. He drew on the differential calculus in an extraordinary way. ‘Since elective symbols combine according to the laws of quantity, we may, by MacLaurin’s theorem, expand a given function ϕ(x), in ascending powers of x’ (p. 60), just like that: deployment of (224.6) (in its orthodox form) and imposition upon x of the index law (253.3) gave on p. 61, after manipulation,
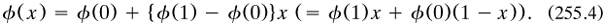
He called ‘moduli’ the values ϕ(0) and ϕ(1), and showed that they characterised the function; in particular, it satisfied the index law if and only if its moduli did (rather briefly on p. 64).
The expansions of functions of two variables in series of terms xy, x(1 – y), y(1 – x) and (1 – x)(1 – y), of functions of three variables in xyz, xy(1 – z),… were effected by iteration on these variables rather than the corresponding versions of MacLaurin’s theorem. These expansions resemble the representation of a vector in a vector space with a normalised basis, in that, by the index law, the product of any two different terms is zero; indeed, he expressed the theorem as the general linear combination
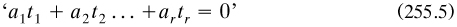
for base terms {tj} with coefficients {aj} 4 (p. 64). This property led to another major result, that if the function was expanded in such a series, then any term which took a non-zero modulus was itself equal to zero (pp. 64–65).
The purpose of (255.4) was to extend beyond the special forms appropriate to syllogisms the deduction of consequences from premises. Without explanation—or interpretation as a process of thought—Boole allowed division into his algebra, initially on pp. 72–73 with the example

(The form of notation ‘10’ for the arguments is unfortunate, since it already has the interpretation as a product). Since the moduli obeyed the index law, these quotients could take the exotic values 0/0 and 1/0. He showed the consequences on pp. 74–75 with the example
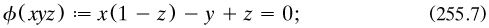
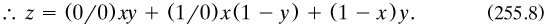
He replaced 0/0 ‘by an arbitrary elective symbol’ v (without comment on the change of category from number to mental act of election); and ‘the term, which is multiplied by a factor 1/0 (or by any numerical constant except 1), must be separately equated to 0’ by the major result stated above. Thus (255.8. became
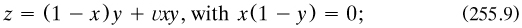
in words, ‘the class Z consists of all the Ys which are not Xs, and an indefinite remainder of Ys which are Xs’, together with ‘All Xs are Ys’ (pp. 74–75). He concluded the book with another technique from algebra, by showing how to use indeterminate multipliers to handle several general elective equations simultaneously (pp. 78–81).
Some sleight of hand seems to be evident here. Since neither 0/0 nor 1/0 is 0 or 1, why should only the first be replaceable by a symbol v which obeys the index law; or alternatively, why should only the second demand that its term be set to zero? One can, of course see reasons for Boole’s distinction in the consequences for logic, but what are they in the algebra? One can surely argue as good a case for the conversion of 1/0 as for 0/0, on the possible grounds that the index law was satisfied:

2.5.6 The laws of thought, 1854: modified principles and extended methods. Boole later recorded that MAL had been written in haste, and that he regretted its publication (1851a, 252). He never specified the sources of his regret, but the points just discussed may have been among them. In addition, some casualness in presentation is evident: concerning 0, +, – and division, for example. The paper 1848a was not much clearer, and even introduced the new obscurity ‘x 1 or x = [sic] the class X’ (p. 126). Further, in contrast to (253.1) but without comment, he now presented the distributivity law for elective symbols themselves rather than over their subjects; presumably this change was a slip, for in his system he really needed, and used, both laws.
Two copies of MAL contain extensive hand-written additions (see G. C. Smith 1983a, and Boole Studies, 119–124), and a manuscript of around 1850 (pp. 141–166) constitutes more substantial a study than its title ‘Sketch’ suggests. Among the novelties Boole moved away from syllogistic logic towards the sign tradition inspired by Locke and others (§2.3.3). In a manuscript of the late 1840s he asserted that ‘In general we reason by signs. Words are the signs most usually employed for this purpose’ (Manuscripts, 14). These words may echo Whately: that signs are primary, and that ‘language affords the signs by which these operations of the mind are expressed and communicated’ (1826a, 55). They contrast with Boole’s neutral remark in MAL that ‘The theory of Logic is thus intimately connected with that of Language’ (1847a, 5).
The next outcome was the second book, 1854a on The laws of thought; Van Evra 1977a contains a general survey of its logical contents. The title (but not the contents. closely follows that of Thomson 1842a (§2.4.4). While basically the same algebra and expansion theorems as in MAL were presented and greater clarity was evident in general, various new results appeared, and also certain changes of emphasis and interest were manifest. The most substantial one is that over 150 pages were devoted to probability theory, which linked to logic via belief vis-à-vis certainty and the interpretation of compound events as logical combinations (in his sense) of simple ones (Hailperin 1986a).
Among the main changes, the psychology was less prominent than before, although Boole began by repeating his intention of ‘investigat[ing] the fundamental laws of those operations by which reasoning is performed’ (p. 1) and ‘x, y, & c., representing things as subjects of our conceptions’ (p. 27). Semiotics was much more to the fore, starting with ch. 2 on ‘signs and their laws’, where both words and symbols were so embraced. The story itself was worked largely as a theory of classes: ‘If the name is “men,” for instance, let x represent “all men,” or the class “men”’ (p. 8). The distributivity law took the 1848 form over symbols rather than (253.1) of MAL over subjects (p. 33).
The index law (253.3. was now framed as

rather than the previous xn = x: Boole showed that x3 = x was not interpretable since factorisation included either the uninterpretable term (1 + x) or the term (–1 – x) of which the component –1 did not satisfy the corollary to (256.1)

(p. 50: presumably similar points were to apply to xn = x for all n). Boole renamed the index law ‘the law of duality’, as a symmetric function of x and (1 – x), and he used this important algebraic property at various later places in the book.
On connectives, ‘Speaking generally, the symbol + is the equivalent of the conjunctions “and,” “or,” and the symbol –, the equivalent of the preposition “except”’ (p. 55). However, mutual exclusivity was still imposed upon ‘+’ (p. 66), so that the union of ‘things which are either x’s or y’s’ was represented in terms of inclusive and exclusive forms (p. 56): respectively,
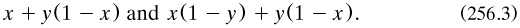
Similarly, for interpretation (x – y) required that the class of ys was included within that of the xs (p. 77). The axiom of §2.5.3 concerning ‘equivalent operations performed upon equivalent subjects’ now became two ‘axioms’, which stated that when ‘equal things’ were added to or taken from equal things, the results were equals (p. 36).
1 was still the ‘Universe’, but it was specified within ‘every discourse’, where ‘there is an assumed or expressed limit with which the subjects of its operation are confined’ (p. 42): a recognition of the priority of De Morgan (§2.4.9) would not have been amiss. 0 was the class for which ‘the class represented by 0y may be identical with the class represented by 0, whatever the class y may be. A little consideration will show that this condition is satisfied if the symbol 0 represent Nothing’ (p. 47). Thus, while he had clearly grasped the extensional aspect of class, he seemed not to wonder if the empty class was literally no thing (compare p. 88).
In between 0 and 1, the indefinite ‘class’ v again usually ranged from 0 to 1 inclusive (pp. 61–63); for example, when 0/0 was converted (this time, by analogy) to the class v, ‘all, some, or none of the class to whose expression it is affixed must be taken’ (pp. 89–90). However, when reducing ‘Some Xs are Ys’ to ‘vX = vY’, v was ‘the representative of some, which, although it may include in its meaning all, does not include none’ (p. 124). Boole’s unclarity is disappointing, for it had long been known in logic that certain inferences may fail if the antecedent or consequent involves empty predicates, especially with particular propositions (Hailperin 1986a, 152–155).
Still no symbol was employed in LT for ‘not’, presumably for the symmetry inherent in the fact that ‘we can employ the symbol y to represent either “All Y’s” or “All not-Y’s”’ (p. 232). From the index law Boole claimed to prove ‘the principle of contradiction’, which took the symbolic form (256.2) (pp. 49–51); however, as his friend R. L. Ellis m1863a remarked, the absence of ‘not’ renders the law independent of the principle, which was interpreted by the law rather than expressed via it. But (256.2) was given other sorts of work to do, in particular, to distinguish the cases of 0/0 and 1/0; for the latter was ‘the algebraic symbol of infinity’ and ‘the nearer any number approaches to infinity (allowing such an expression., the more does it depart’ from (256.2) rather than from the index law which might admit (255.10) (p. 91).
Among results or remarks which made their débuts in LT, in the footnote in which he disproved the possibility of x3 = x after (256.1), Boole perceived—with no enthusiasm—the possibility of non-bivalent logics, in which ‘the law of thought might have been different from what it is’ (p. 50). Once again he ignored De Morgan, who had touched on the point in his own book (1847a, 149) and had raised it in a letter to him in 1849 (Boole-De Morgan Letters, 31).
The expansion theorem (255.4) duly appeared, proved by assumption of form and calculation of the coefficients, with MacLaurin’s theorem now in a footnote (pp. 72–73). But it was supplemented by this important result for any equation f(x) = 0; that

‘independently of the interpretation of x’ (p. 101), with analogues for several variables (p. 103). Several different proofs were given, usually drawing on (255.4) (pp. 101–104); as Harley 1871a pointed out, it follows from the theory of roots of equations adapted to two-valued variables.
The importance of this result lay in its role in eliminating x from an equation ϕ(xyz…) = 0 containing x and other variables. This move greatly enriched his method of deduction, which was presented in chs. 7–8 with some nice short-cuts executed in ch. 9. One new extension was a theorem concerning ‘any system of equations’ Vr = 0; that ‘the combined interpretation of the system will be involved in the single equation,

(pp. 120–121). The purpose of squaring was to avoid the loss of terms by cancellation across the equations if simple addition were practised; the index law reduced the equation itself to linear form.
Boole solved class equations basically as in MAL (255.8–10), though now in a more general framework (pp. 90–98). Take as subject the class z from a given collection of given classes u, v,…, form every combination uv, u(1 – v), (1 – u)v, … of the remaining classes, express the logical premises as equations, and use the appropriate expansion and elimination theorems with z as subject to determine from the equations the coefficients c attached to each such combination m. If c = 1, then m was part of z; if c = 0, then not so; if c = 0/0, then any part vm of m was part of z; if c took any other value, then the proposition m = 0 imposed sufficient conditions for any class z to be found at all. Further, several equations could be reduced to a single linear combination of them (ch. 8).
One final feature, arising in Boole’s treatment of probability theory, contrasts him with the philosophies of arithmetic of Frege and Russell. As we shall see in §4.5.3 and §6.5.4, they were to define cardinal numbers as sets of similar sets; for Boole, ‘let the symbol n, prefixed to the expression of any class, represent the number of individuals contained in that class’ and he treated ‘n’ as an operator, noting that it ‘is distributive in its operation’ over classes. He then read the frequentist interpretation of probability as the appropriate ratio n(x)/n(1) for a class x (pp. 295–297). His further development of these ideas led him to some work on inequalities, in a context which we recognise today as linear programming (Hailperin 1986a, 36–43, 338–350).
2.5.7 Boole’s new theory of propositions. Boole proposed in LT a new distinction of propositions: instead of the categorical and hypothetical categories, he now worked with ‘primary or concrete’ and ‘secondary or abstract’ types. The second names clarified the distinction; the former type of proposition related ‘to things’ and the latter ‘to propositions’. Primary propositions were categorical, but once again they were not treated as “atomic” entities; instead, they were components of secondary ones, which included hypothetical propositions such as ‘If the sun shines the earth is warmed’ (p. 53).
To us Boole’s characterisation of this type of proposition places them in the metatheory, with his example wanting of interior quotation marks. However, lacking such a conception but desirous of giving the primary components objectual status, he replaced his hypothetical universe of the previous sub-section with time, as a location for propositions to consign their truth-value (and thereby become “things”). ‘X’, ‘Y’, and so on now denoted ‘the elementary propositions concerning which we desire to make some assertion concerning their truth or falsehood’, while x ‘represent[s] an act of the mind by which we fix our regard upon that portion of time for which the proposition X is true’ (pp. 164–165). Further, ‘1’ now ‘denotes the whole duration of time, and x that portion of it for which the proposition X is true’, so that ‘1 – x will denote that portion of time for which the proposition X is false’; hence ‘The propositions X is true/false’ were rendered respectively by ‘x = 1’ and ‘x = 0’ (pp. 168–169). The basic laws, and the means of combination, applied once more (with the usual restrictions on ‘+’ and ‘–’ in place again); the ‘time indefinite’ v seems to have been non-empty, although if v and x had no common period of truthhood, then vx = 0 (p. 171). This theory resembles a Boolean algebra of propositions, which however was to come only with Hugh MacColl (§2.6.4).
It is curious that Boole did not claim here to derive the law of excluded middle for propositions, which would take the form

for he did state the law of duality (256.2) in this context (p. 166). A “proof” is compromised by the absence of ‘not’ from his language; (257.1) is best seen as embodying a necessary assumption about truth and falsehood. Earlier in the book he had produced the rather similar result, that (x + 1 – x) was the expansion of the function 1 via the expansion theorem (255.4) (p. 76).
While Boole noted that ‘this notion of time (essential, as I believe it to be, to the above end [of explicating the theory of secondary propositions]) may practically be dispensed with’ (p. 164), this was obviously not his personal wont. Indeed, he recalled his previous approach in MAL involving ‘the Universe of “cases” or “conjunction of circumstances”’, but found it far less clear than his new formulation (p. 176). This judgement followed a remarkable passage in which he speculated on the possibility of placing primary propositions in space but rejected it on the ground that ‘the formal processes of reasoning in primary propositions do not require, as an essential condition, the manifestation in space of the things about which we reason’, and that ‘if attention were paid to the processes of solution [in certain stated problems in mechanics] alone, no reason could be discovered why space should not exist in four or in any greater number of dimensions’ (pp. 174–175).
2.5.8 The character of Boole’s system
All sciences communicate with each other [that which] they have in common. By common I mean that of which they make use in order to show something; but not that to which their proof refers, nor the [final] outcome of what they show. Boole, motto on the title page of MAL
(in Greek, taken from Aristotle, Posterior analytics)
The logic which Boole offered was to be understood as a normative theory of the products of mental processes (descriptive psychology was, of course, not his brief). In LT it was grounded in the belief of ‘the ability inherent in our nature to appreciate Order’ and thereby produce ‘general propositions’ which ‘are made manifest in all their generality from the study of particular instances’ (1854a, 403, 404). Thus in the underlying philosophy of logic Boole stood at the opposite pole from the empiricism of John Stuart Mill, for whom even the principles of logic, if true, were formed by induction from experience (John Richards 1980a).
Boole devoted ch. 5 of LT to ‘the fundamental principles of symbolical reasoning’, where he began by arguing for his various principles from instances, but the case was not overwhelmingly put. Even in his final chapter on ‘The constitution of the intellect’ he rested his case on the assertion that ‘The laws of thought, in all its processes of conception and of reasoning, in all those operations of which language is the expression or the instrument, are of the same kind as are the laws of the acknowledged processes of Mathematics’ (1854a, 422).
Boole’s system fulfilled some of the ambitions for a characteristica universalis of Leibniz, who had even formulated the index law in the form xy = x for x and y as propositions (not his symbols). However, Boole learnt of Leibniz’s proposal (as then known) only in 1855 (Harley 1867a), after LT appeared; the informant was R. L. Ellis, who was helping to bring Leibniz’s logic and philosophy to British attention (Peckhaus 1997a, ch. 5).
There was also an important religious connotation in Boole’s position. A Disssenter, he adhered to ecumenical Christianity, aloof from the xs and (1 – x)s of the disputing Christian factions. He implicitly exhibited his position in LT by devoting ch. 13 to sophisticated logical analyses of propositions due to Samuel Clarke and Benedict Spinoza concerning the necessary existence of ‘Some one unchangeable and independent Being’ (p. 192). He also cited Greek authorities, and also Hegel, as sources for the importance of unity among diversities (pp. 410–416). He alluded to his stand a few lines from the end of the book by mentioning ‘the Father of Lights’, and finished off with some enigmatic lines about the bearing of religious belief upon his logic.
In his final years Boole enthused over the presentation of logic by the French theologian A. J. A. Gratry 1855a, in which claims such as God as truth gained prominence, in addition to topics such as nullity versus unity, universal laws of thought, and the exercise of the human mind. He held in awe the theologian Frederick Denison Maurice, who advocated ecumenical Christianity and was therefore dismissed from his Professorship of Divinity at King’s College London, part of the established Trinitarian Church of England; Boole had a portrait of Maurice set by his bed as he lay dying (my 1982a, 39–41).
MAL related heavily to syllogistic logic; the book contains passages on it set in smaller type, often taken from Whately’s Logic, as Boole hinted on p. 20. But in LT he showed the revolutionary implications of his work; the details of syllogistic logic was demoted to the last of the 15 chapters strictly devoted to logic, and with quantification of the predicate again left out.
As logic, Boole’s principal aim was consequences of premises rather than detailed deductions from them. The theory was always algebraic, with a strong kinship to differential operators: equations were the principal mode of working, facilitated in formation and manipulation by the indefinite symbol (or class) v. It was interpreted in terms of classes and propositions, and later to probability theory. (Non-)interpretability was a major feature, both of functions and of equations.
Differential operators were not the only link with mathematics. In MAL Boole noted ‘the analogy which exists between the solutions of elective equations and those of the corresponding order of linear differential equations’ (1847a, 72). In addition, he was enchanted by singular solutions of differential equations, since they had the character of unity from opposites required by the index law that he liked so much also in Maurice: as he put it, on the one hand, the ‘positive mark’ of solving the equation, but also ‘the negative mark’ of lying outside the general solution (1859a, 140). However, as a result of ignoring quantification of the predicate, Boole’s treatment of syllogisms was corrigible, partly for want of clarity over ‘−’ and ‘+’, but especially for failing to detect singular solutions (Corcoran and Wood 1980a). For example, for the universal affirmative proposition ‘All Xs are Ys’, symbolised as
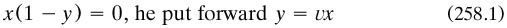
as ‘the most general solution’ (1847a, 25); but he should have noticed that x = 0 was missing from it, and also that it did not hold if x = 0 and v was a class such that vy ≠ 0. Thus some solutions of his equations were not logical consequences of the premises under his system. The difference between necessary and sufficient conditions was again not under control; but this mathematician with a strong interest in singular solutions should have noticed analogous situations in his logic.
Collections were handled in normal part-whole style of the time; but Boole’s reading of (x +y) only for disjoint classes x and y (p. 66) was very take-it-or-leave-it. In a manuscript of 1856 he offered the following “deduction” of his definition:
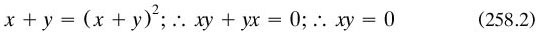
(Manuscripts, 91–92). It seems strange for a logician to have confused a sufficient condition with a necessary one: maybe he asserted this version of ‘+’ to avoid having to read the intersection of the classes as a multiset, to which an object may belong more than once (such as the collection 3, 3 and 8 of roots of a cubic equation). If so, then he was in a strong tradition; for when multisets arrived in the 1870s and 1880s they gained little attention at first (§4.3.4, §4.2.8). But from a modern point of view, his theory can be read in terms of signed multisets, where an object can belong to a collection any finite number of times, positive or negative (Hailperin 1986a, ch. 2).
Absent from Boole’s theory were the quantifier as such (although v did some of the work); any logic of relations (even after the publication of De Morgan 1860a he seems not to have taken them up); or any use of counter-arguments to establish results, or presentation of fallacies. In addition, his adherence to algebra prevented him from using pictorial representations such as Euler diagrams to depict an argument, although the untutored reader might thereby have been helped.
2.5.9 Boole’s search for mathematical roots
De Morgan develops the old logic, Boole converted the forms of algebra into exponents of the forms of thought in general.
Neil 1872a, 15
In various manuscripts, especially from 1856 onwards, Boole sought a foundation for his logic in the philosophical framework used by other logicians of his time, such as Whately. More insistent than they on distinguishing between mental acts and their products, he proposed this scenario. The mind effects ‘Conceptions’ or ‘Apprehensions’ by the extensional processes of addition and subtraction of classes. The products were ‘Concepts’ which were subject to ‘Judgement’ as to their agreement or not. The products were ‘Propositions’, which were then subject to ‘Reasoning’ by inference among them to yield the ‘Conclusion’ (Manuscripts, ch. 5).
However, these procedures left Boole’s philosophy incomplete. For, unlike other logicians apart from De Morgan, his logic used mathematics, so that a rich philosophy of mathematics was required—and this he never found, the relevant manuscripts being restricted to particular aspects such as axioms and definitions (Manuscripts, ch. 14). In particular, he did not break the following vicious circle, and may not have realised its existence. Whatever mathematical theory grounded his logic, it had to be consistent to fulfil its office; but consistency is already a concept taken from logic.... Thus did the mathematical roots of his logic elude him.
Boole’s logic was applied algebra, the ‘mathematical analysis of logic’. He remarked en passant but interestingly on this aspect when he followed an appraisal of a general treatment of logical equations with the comment in LT that ‘The progress of applied mathematics has presented other and signal examples’ of such unification of methods (1854a, 157, italics inserted). However, features such as the use of MacLaaurin’s theorem to prove the expansion theorem (255.4) suggesr that an orthodox application of one theory to another may be too straightforward. Inspired by the proposal of Laita 1977a that a universal calculus of symbols underlies both his mathematics and his logic, I offer in Figure 259.1 this represntation of his system. It has a Boolean structure, as is indicated on the right hand side. This feature is important; for since Boole offered laws of thoughts, his system should apply to itself.
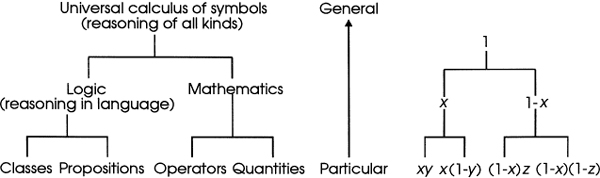
FIGURE 259.1. Schematic conjecture about Boole’s system.
2.6.1 Some initial reactions to Boole’s theory
Mr. Boole began with a short account, which was read: he then published his larger work which is much less read, and would not have been read all but for the shorter one.
De Morgan to Jevons, letter of 15 September 1863
(Jevons Papers, File JA6/2/114)
This information may surprise us, for whom LT is the main source on Boole. In fact it seems to begin to supersede MAL from around the time of this letter; in particular, as we shall see in the next sub-section, Jevons himself dealt with it alone. But even then the reception was modest; for example, for all his recent caution against syllogistic logic (§2.4.5.), Blakey showed no understanding of Boole in his history of logic (1851a, 481–482).
Let us start with Boole’s most fervent follower: his widow Mary (1832–1916), who prosecuted his ideas, mainly in philosophical and educational contexts and oriented around the alleged power of the mind, for the fifty years of her widowhood. While she became well known as an eccentric advocate, she had a good understanding of his ideas, and her testimony about him can be taken as basically reliable (Laita 1980a). She also referred to his religious stimuli and to his praise of Gratry thus: ‘Babbage, Gratry and Boole [...] published their books. Then finding themselves confronted with dishonest folly, they left the world to come to its senses at its leisure’ (M. E. Boole 1890a, 424.. However, by then these aspects of his system had been set aside completely by his successors, even though Victorian science in general was rather infatuated with connections with Christianity. One important link was to Spiritualism and related topics; several logicians were interested in psychical research.20
Although De Morgan’s theory had little in common with Boole’s, he was appreciative of his friend’s achievements; ‘by far the boldest and most original’ generalisation of ‘the forms of logic’, he opined in an encyclopaedia article, making algebra ‘appear like a sectional model of the whole form of thought’ (1860c, 255). Interestingly, he misrepresented ‘+’ as creating multisets, ‘with all the common part, if any, counted twice’ (pp. 255–256); and he did not use Boole’s logical system in his own work.
Soon after Boole’s death an interesting development occurred when the British chemist Benjamin Brodie (1817–1880) published in 1866 a Boolelike algebra for chemistry, as an alternative to the prevailing atomic theory. The main idea was that of chemical operations on a litre of substance-space, yielding a certain ‘weight’, such as x converting the litre into a litre of hydrogen, which had a certain weight. Succeeding operations x and y gave a ‘compound weight’ which was represented as xy and assumed to be commutative; joint operation was written ‘(xy)’, equal to xy; collective operation was (x + y) and separate operation was x + y. Since the result for a two-part compound was the same weight, the basic laws were
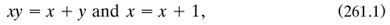
where ‘1’ denoted the litre with no weight in it.
Since it followed that 0 = 1, Brodie’s system did not enjoy a warm reception; but of historical interest is his correspondence with mathematicians (published in Brock 1967a), partly inspired by a vigorous discussion at the 1867 meeting of the British Association for the Advancement of Science. De Morgan wrote several letters, stressing the functional aspects of operations and so criticising (261.1)1 for equating ‘symbols of aggregation]egation_ & comb]ination_’, and noting that ‘though Water = Oxygen × Hydrogen is certainly Oxygen + Hydrogen yet Oxygen + Hydrogen is not necessarily Water’. (Compare him already on this sort of point in 1847a, 48–49 and 1858a, 120). He preferred the alternative form

to (261.1), for it ‘is not only analytically perfect, but is also interpretable’ (Brock 1967a, 103, 109–110). Herschel doubted the utility of other notations that Brodie proposed pp. 122–124..
2.6.2 The reformulation by Jevons. Brodie’s strongest critic was Stanley Jevons (1835–1882), who even wrote a piece for the Philosophical magazine but withdrew it after receiving criticism from the physicist W. F. Donkin (Brock 1967a, 114–118). He was the first to work seriously on Boole’s system, initially in a short book entitled Pure logic (Jevons 1864a), to which the account below is largely confined. Then in his thirtieth year, he had recently been appointed tutor at Owens’s College, Manchester.
Although he had taken courses in mathematics from De Morgan at University College London, Jevons concerned himself solely with Boole’s system, and only as presented in LT. Subtitling his own book ‘the logic of quality’, Jevons followed Boole in detaching logic from the study of quantity, and gave several admiring references to Boole’s work. However, he made some basic criticisms of Boole’s system; while he presented them as his last chapter, it is best to take them now, as they obviously guided the construction of his alternative system.
Four ‘Objections’ were made. Firstly, Boole’s ‘logic is not the logic of common thought’, even within its normative brief (art. 177). His reading of ‘+’ was singled out for especial criticism, and entered into Jevons’s second claim, that ‘There are no such operations as addition and subtraction in pure logic’ (art. 184), and also the third, that the system ‘is inconsistent with the self-evident law of thought’ that A or A is A (art. 193). Finally, ‘the symbols 1/1, 0/0, 0/1, 1/0, establish for themselves no logical meaning’ (art. 197).
Jevons worked with ‘terms’, which covered ‘name, or any combination of names and words describing the qualities and circumstances of a thing’ (art. 13). Without attribution, he used De Morgan’s notations ‘A’ and ‘a’ for a term and its negation, and implicitly drew on the same symmetry of role between A and a which was noted in §2.4.8. A principal connective was ‘+’, which stood ‘for the conjunctions and, either, or, &c., of common language’ and did not suffer the Boolean restriction to disjointness of its components (art. 16); however, he avoided the evident ambiguity of his explanation by using it only as ‘or’. His account of ‘+’ seemed to allow for both inclusive and exclusive disjunction of terms (arts. 64–72); but his examples in art. 179 used the inclusive sense, as in ‘academic graduates are either bachelors, masters, or doctors’. He represented ‘and’ by ‘combining’ terms A and B in a Boolean manner to produce AB (art. 41). The other main connective was ‘the copula is’, symbolised ‘=’, which registered ‘the sameness of meaning of the terms on the two sides of a proposition’ (art. 21).
All and nothing appeared in Jevons’s system. He defined ‘the term or mark 0’ rather thoughtlessly as ‘excluded from thought’ (art. 94, where however he did state the basic laws 0.0 = 0 and 0 + 0 = 0); and he introduced a ‘Universe of Thought’ specified like De Morgan’s relative to a logical argument. art. 122, well into the text, and reflecting its subsidiary role in his system. But he also proposed the ‘Law of infinity, that ‘Whatever quality we treat as present we may also treat as absent’, so that ‘There is no boundary to the universe of logic’ U; in particular, its negation ‘u is not included in U’. Jevons was on the border of possible paradox here, but he made proposals in a footnote (to art. 159., which ended: ‘this subject needs more consideration’.
Jevons also used ‘U’ to render ‘some’ as a term; but he denied U the property U = U and replaced it by an appropriate constituent terms in an argument: for example, ‘A = UB, meaning that A is some kind of B [sic] is much better written as A = AB’ (art. 144). However, this principle seems to infringe his ‘Condition’ that ‘the same term have the same meaning throughout any one piece of reasoning’ (art. 14). (Boole had required his class v to satisfy normal properties (1854a, 96), but he used more than one such class when necessary). Further, as with Boole, Jevons left unclear some questions of existential import of particular propositions.
Jevons was somewhat more conscientious than Boole in stating the basic laws of his system; but it is often less clear whether a proposition is a principle or a theorem, and, if the latter, how it was proved. For example, again like Boole he had no separate symbol for ‘not’ (not even in his ch. 7 on ‘Negative propositions’). He gathered most of his principles together in art. 109; some were Boolean but others not, and the reference of the name ‘Duality’ was changed. His names and formulations, sometimes cryptic, are given here:
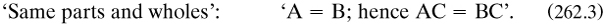
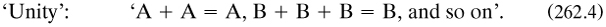
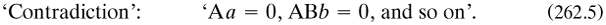
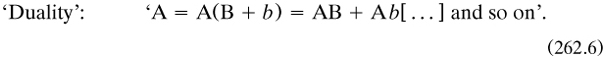
In addition, a ‘law of difference’ had been stated in art. 77 but omitted here, presumably for a lack of ‘not’; making temporary use of ‘≠’, it would read
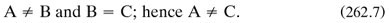
Among his theorems, one on ‘superfluous terms’ (art. 70) became quite well known as ‘absorption’ for terms B and C:

Jevons’s method was to set up the premise(s) in equational form, to characterise logic itself as the ‘science of science’ (art. 37):
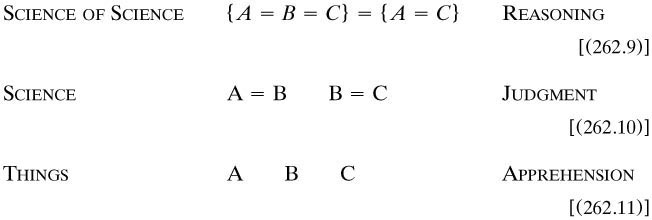
Then he used two modes of ‘inference’, both modelled on Boole’s. In the ‘direct’ mode the premises were combined in suitable ways to cancel out middle terms; for example, the syllogism ‘No A is B, Every A is C, ∴Some C is not B’ came out as
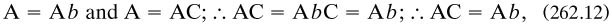
as required (art. 148). In the more general ‘indirect inference’ (ch. 11) all possible combinations of the terms in the premis(es) were listed, and combined with each of their terms, as a sum of products. Then each combination was appraised as an ‘included subject’ if it did not contradict either side of at least one of the premises, as a ‘contradiction’ if it contradicted one side of a premise, or as an ‘excluded subject’ if it contradicted both sides of every premise. The second type was to be deleted, leaving the other two as ‘possible subjects’, and their sum (in his sense of ‘+’) as the consequences.21 Thus the consequences pertaining to a (simple or compound. term t were found by equating it (in his sense of ‘=’) to the sum of the consequences of which it was part; in other words, he found the term to which t was ‘equal’ given the premises. Various means of simplification and basic or derived laws such as (262.1–7) were found.
For example, from the premise A = BC, the three categories of consequence were ABC; ABc, AbC, Abc and Abc; and aBc, abC and abc. Selecting (say) b for the four possible subjects, two options arose. Thus (arts. 116–117)
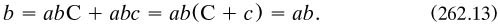
Many of Jevons’s examples were oriented around syllogisms, but in ch. 14 he reworked one of Boole’s general cases and obtained the same consequences.
Jevons’s procedures avoided Boole’s expansion theorems, and dispensed with subtraction, division, 0 and 1, and most of the attendant methods; but his indirect mode of inference was rather tedious to operate, though more powerful. So in a paper 1866a he announced his ‘logical abacus’, in which slips of paper containing between them all combinations of terms and their negations were prepared; the ones required for the given premises were selected and the consequences read off. He realised that the selection and appraisal could be better effected non-manually, and for the purpose he introduced in the paper 1870a his ‘logical machine’, which produced the required inferences by mechanical means (Mays and Henry 1953a). His procedure has some structural similarity with the truth-table method for determining the truth-values of propositions (§8.3.2).
Over and above these technicalities is the question of the relationship between mathematics and logic after these modifications. Jevons may not have fully considered it. In the introduction of Pure logic he stated that
The forms of my system may, in fact, be reached by divesting his system of a mathematical dress, which, to say the least, is not essential to it [...] it may be inferred, not that Logic is a part of Mathematics, as is almost [sic] implied in Prof. Boole’s writings, but that the Mathematics are rather derivatives of Logic.
(1864a, art. 6: compare his 1874a, 191–192). This reads like a presage of Frege’s or of Russell’s logicisms, but is more of a preliminary speculation, and did not influence them.22
2.6.3 Jevons versus Boole. While his Pure logic was in press, Jevons sent Boole some proofs and corresponded with him; but the clash of position, especially concerning ‘+’, was irreconcilable. For Jevons, (262.4) stated that any (finite) number of inclusive self-alternatives to A could be reduced to one instance without change of meaning: thus logical ‘addition’ differed from mathematical addition. For Boole,
[... ] it is not true that in Logic x + x = x, though it is true that x + x = 0 is equivalent to x = 0. You seem to me to employ your law of unity [(262.4)] in two different ways. In the one it is true, in the other it is not. If I do not write more it is not from any unwillingness to discuss the subject with you, but simply because if we differ on this fundamental point it is impossible that we should agree in others.23
The difference between the two men may be summarised as follows. Like many of the pioneers of new algebras in the 19th century, Boole was consciously extending the realm of algebras; but nevertheless he was still mindful of the properties of common algebra, which was formed as a generalisation of arithmetic. Thus he defined operations of addition, subtraction, multiplication and division, giving them these names because they satisfied laws (fairly) similar to those of the traditional versions. Jevons objected to this influence, and sought to reduce its measure in his version of Boole’s system. However, he seemed to have confused the more general conception of algebras (of which Boole was a practitioner. with the bearing of Boole’s algebra upon quantity (which, as we saw at the end of §2.5.6, was very modest). This distinction can be related to that between universal arithmetic and symbolical algebra, and the use of the principle of the permanence of equivalent forms (§2.3.2).
2.6.4 Followers of Boole and/or Jevons. Despite their differences, Jevons appreciated the novelties of Boole’s system; in 1869 he opined to Macmillan, the publisher of all his books after Pure logic, that ‘it must I am afraid be a long time before the old syllogism is driven out, and symbols of the nature of Boole’s substituted in the ordinary course of instruction’.24 Yet he did not encourage change: for example, his popular primer 1876a on logic never mentioned Boole once, and his later books were largely restricted to syllogistic concerns. They were reprinted quite frequently, whereas of Boole’s only LT received a reprint, in 1916, before recent times.
Some advocates of the new algebra of logic preferred Boole’s version to Jevons’s. For example, G. B. Halsted 1878b wrote from the U.S.A. to Mind defending Boole’s system, especially for its ability to express both the inclusive and exclusive kinds of disjunction via (256.3); he also rejected Jevons’s association of Boole’s mathematical approach with an algebra of quantity.
Boole’s stoutest defender was John Venn, who concentrated on LT in his book Symbolic logic (the origin of this term. of 1881. For him Jevons’s reforms meant ‘that nearly everything which is most characteristic and attractive in [Boole’s] system is thrown away’ (Venn 1881c, xxvii). He also defended Boole’s definition of ‘+’ on the grounds that both senses of ‘or’ could be expressed by means of (256.3).25 ‘I have done my best to make out in what relation [Jevons] himself considers that his exposition of the subject stands to that of Boole; but so far without success’ (p. xxviii.; but he was certain that Jevons’s adherence to intensions led to various ‘evils’, such as ‘the catastrophe’ of not reading particular propositions extensionally (p. 36). However, in staying largely around the syllogistic tradition he was closer to MAL than to LT. In a lengthy review for Mind C. J. Monro 1881a shared Venn’s adhesion to Boole’s principles, including over (x + x) and the need for ‘0/0’.
Among other aspects of the book, Venn did not use De Morgan much, and on the ‘Logic of Relatives’ he commented: ‘the reader must understand that I am here only making a few remarks upon a subject which […] would need a separate work for its adequate discussion’ (pp. 400–404), but which he did not then write. The best remembered feature of the book is the diagrammatic representation of logical relationships, now misnamed ‘Venn diagrams’. The method so named is in fact usually Euler’s procedure based upon the Gergonne relations (§2.4.6). His own way, which he published first in a paper 1880a in the Philosophical magazine, was to draw closed convex curves in such a way as to exhibit all their possible intersections, and marking those which were empty in a given logical situation. It amounts to a pictorial representation of Jevons’s method of taking the logical disjunction of all pertinent conjunctions.26
A significant newcomer was the Scotsman Hugh McColl (1837–1909), as he then called himself; I shall use his later version ‘MacColl’. In a paper 1880a on ‘Symbolic reasoning’ in Mind, and in related papers of the time, he offered himself as a ‘peacemaker’ (p. 47. between logic and mathematics. He divided the former field in the manner similar to Jevons: ‘pure logic’ covered ‘the general science of reasoning understood in its most exact sense’ (not Jevons’s sense, as he noted., while ‘applied logic’ took this knowledge to ‘special subjects’, such as mathematics. For symbolism he offered (pp. 51–53.:

The latter two notions were unclearly indicated, ‘= 1’ and ‘= 0’ seeming to be the notions intended. While his treatment was oriented around syllogisms, he accepted the main lines of Boole’s work; but in 1877a he proposed that the propositional calculus be treated as a Boolean algebra, not done by either Boole or Jevons. Further, he read implication A:B between propositions A and B as equivalent to A = A × B (Rahman and Christen 1997a). He also subsumed quantification under this implication; for example, ‘all X is Y’ became ‘an individual has attribute X: this individual has attribute Y’. MacColl’s contributions of the 1900s to logic, better remembered, will be described in §7.3.6.
By contrast with these developments, De Morgan’s contributions lay eclipsed, even his logic of relations.27 Independently of De Morgan, R. L. Ellis m1863a had perceived the need for such a logic, but he did not fulfil it (Harley 1871a). However, some effort was made by the young Scottish mathematician Alexander MacFarlane (1851–1913), in a three-part paper 1879–1881a published by the Royal Society of Edinburgh, with a summary version 1881a in Philosophical magazine. Using family relationships for his example, he wrote out the members related in equations such as

for ‘the sons of A are B, and C, and D’, and developed quite an elaborate system for compounding relations and universes.
MacFarlane’s paper followed a short book 1879a on Boole’s system. He kept most of it, including the expansion theorems, coefficients such as 0/0, and the application to probability theory; but he used ‘−’ and ‘+’ without restrictions. He used separate symbols for nouns and adjectives, lamenting Boole’s failure to do so. Although Venn 1879a reviewed the book at some length in Mind, none of MacFarlane’s work was influential; but it is of interest in treating both De Morgan and Boole.
Jevons’s version of Boole’s system gradually gained preference over Boole’s own version. For example, when the Cambridge logician W. E. Johnson (1858–1931) wrote at length on ‘The logical calculus’ in Mind, he emulated Jevons in reducing the mathematical link; for example, with Johnson ‘1’ and ‘0’ became ‘Truism’ and ‘Falsism’ (1892a, 342–343). This work was noted by Venn, in the second edition 1894a of his book, for which Johnson read the proofs. While the basic purpose and design of the chapters was largely unchanged about 20% new material was added, raising the length to 540 pages. Some examples of the updating will be noted in §4.3.9 and §4.4.5.
The same change occurred abroad, especially regarding technical derivations, when the systems were studied by figures such as F. Kozloffsky and P. S. Poretsky in Russia, Ventura Reyes y Prósper in Spain (§4.4.4) and Hermann Ulrici in Germany (§4.4.1). We shall also see a rise in De Morgan’s reputation when the fusion envisioned by MacFarlane was accomplished, and also Jevons’s changes were adopted, by the two new major figures in algebraic logic: C. S. Peirce and Ernst Schroder (§4.3–4). For now, we turn to something entirely different.
2.7.1 Different traditions in the calculus
To the mathematician I assert that from the time when logical study was neglected by his class, the accuracy of mathematical reasoning declined. An inverse process seems likely to restore logic to its old place. The present school of mathematicians is far more rigorous in demonstration than that of the early part of the century: and it may be expected that this revival will be followed by a period of logical study, as the only sure preservative against relapse.
De Morgan 1860b, 337
De Morgan concluded the main part of his last completed paper on the syllogism with this accurate prophecy. While he did not specify any branch of mathematics, undoubtedly mathematical analysis was one of the prime examples. The remainder of this chapter is devoted to a summary of the development of this discipline during the 19th century up to around 1870 (just before De Morgan’s death, incidentally). While the main innovations took place in France and Germany, some notice was taken in Britain, and he was one of the first to encourage interest in his home country, as we shall note in §2.7.3.
Lagrange’s approach to the calculus (§2.2.2), reducing it to algebraic principles, was the third and newest tradition (my 1987a). It competed with theories stemming from Newton based in limits (but not pursued with the refinement that Cauchy was to deploy), and with the differential and integral calculus as established by Leibniz, the Bernoullis and Euler. Here the ‘differential’ of a variable x was an infinitesimal increment dx on x and of the same dimension as x, while ∫x was similarly an infinitely large variable of that dimension. The rate of change of y with respect to x, the slope of the tangent to the curve relating x and y, was written ‘dy/dx’, and was to be read literally as the ratio dy + dx of differentials, itself normally finite in value. The integral was written ‘∫y dx’, which was to be understood again literally, as the sum (‘∫’ was a special forms of ‘s’ adopted by Leibniz. of the product of y with dx: as the area between the curve and the x-axis, it was seen as the sum of infinitesimally narrow rectangles
This tradition was by far the most important one of the 18th century, which led the establishment of the calculus as a major branch of mathematics. Limits also gained some favour, although on the Continent they were presented without the kinematic elements present in Newton’s ‘fluxional’ version in isolated Britain. So Lagrange had to meet stiff competition when selling his alternative approach; and it was mentioned in §2.2.2 that some of his contemporaries were not convinced of its legitimacy or practicability. We turn now to its most formidable opponent in the early part of the 19th century: Cauchy.
2.7.2 Cauchy and the Ecole Polytechnique. Born in 1789, Augustin-Louis Cauchy studied at this school in the mid 1800s (after Lagrange had finished teaching there., then entered the Ecole des Ponts et Chaussées in Paris and worked for a few years in the corresponding Corps. But his research interests developed strongly, and when Napoléon fell and the Bourbon Catholic monarchy was restored, Bourbon Catholic fanatic Cauchy was given in 1816 great and even artificial boosts to his career: appointment to the restored Académie des Sciences without election, and a chair in analysis and mechanics at his old school. During the Bourbon period (which ended with the revolution of 1830., he was in his element, and produced an amazing range and mass of top-class mathematics (my 1990a, esp. chs. 10–11, 15). Our concern here is with his teaching of analysis at the Ecole Polytechnique, in which he set up many essential features of mathematical analysis as they have been understood ever since, especially the unification, in a quite new way, of the calculus, the theory of functions, and the convergence of infinite series. Most of the main ideas appeared in two textbooks—the Cours d’analyse (1821a) and a Résumé of the calculus lectures (1823a)—though some other results were published in research papers and later textbooks. A major inspiration and feature was his extension of the theory to complex variables; but I shall not need to treat it here, because it did not bear on the development of logic as such.27
The underlying link was provided by the theory of limits, in which the basic definitions and properties were presented to a measure of generality and degree of precision that had not been attempted before: ‘When the values successively attributed to the same variable approach indefinitely a fixed value, so as to differ from it as little as one might wish, this latter is called the limit of all the others’ (Cauchy 1821a, 19). He stressed, in a way then novel, that passage to this limit need be neither monotonic nor one-sided. He also represented orders of ‘infinitely small’ and ‘infinitely large’ by monotonic decrease of sequences of integers to zero. His choice of terms was unfortunate, as these infinitesimals did not at all correspond to the types such as dx mentioned in the previous sub-section. Nor did his infinities presage any Cantorian lore in this regard; on the contrary, elsewhere he explicitly denied the legitimacy of the completed infinite.
In terms of limits Cauchy cast many basic components of mathematical analysis, in the forms that have been broadly followed ever since. The convergence of the infinite series Σjuj was defined by the property that the remainder term rn after n terms passed to (the limiting value. zero as n approached infinity; in this case the n th partial sum sn of the series approached the sum s (pp. 115–120: he popularised the use of these notations). The exegesis following in ch. 6 included the first batch of tests for convergence of infinite series.
The continuity of a function ƒ(x) at a value x was defined in a sequential manner: that ƒ(x) ‘will remain continuous with respect to the given limits, if, between these limits, an infinitely small increase of the variable always produces an infinitely small increase of the function itself’ (p. 43). Cauchy also re-expressed it for continuity ‘in the vicinity of a particular value of the variable x’, and proved in ch. 2 various theorems on continuous functions, of both one and several variables. Other material appearing in the Cours, ch. 5 included a study of functional equations, although his treatment was oriented more around conditions for the solution (especially for continuous functions. of simple equations, and the derivation of the binomial series, rather than Babbage-like manipulations (§2.4.2. to solve complicated ones. On functions in general, he insisted that they always be single-valued, so that even √x (x > 0) had to be split into its positive and negative parts. This restriction became standard in mathematical analysis, with fundamental consequences for Russell (§7.3.4).
The calculus appeared two years later in Cauchy’s Résumé of 1823. There he defined the derivative and the integral of a function respectively as the limiting values (if they existed. of the difference quotient and of sequences of partition sums:
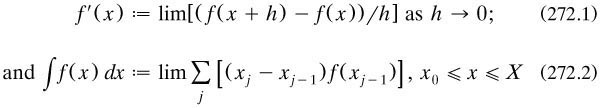
as the partition of chosen points {xj} within the finite interval [x0, X] became ever finer (lectures 3, 21). The great novelty of his approach lay not particularly in the forms of the defining expressions, for they had appeared before (usually in vague forms); it was the fact that the definitions were independent of each other, so that the ‘fundamental theorem of the calculus’, asserting that the differential and the integral calculi were inversedly related branches, could now really be a theorem, requiring sufficient conditions on the function for its truth, rather than the automatic switch from one to the other branch which had normally been the assumption made in the other versions of the calculus.29 In his case his proof required the function to be continuous (in his sense) over the interval of definition of the integral (lecture 26).
In his exegesis of the calculus Cauchy proved versions of many of the standard results and procedures of the calculus: properties of derivatives and partial derivatives of all orders, differentials (though, as with infinitesimals he presented a new kind of definition bearing no resemblance to traditional versions) and total differentials, mean value theorems, term-by-term integration of infinite series, multiple integrals, differentiation and integration under the integral sign, integrals of simple functions, and so on. Four points need emphasis here, the first mathematical, the last two logical, and the second both at once.
Firstly, one of the main theorems was Taylor’s, for which Cauchy provided forms for the remainder term and thereby imposed conditions for its convergence (lectures 36–37 and second addition). Lagrange’s faith in the series, described in §2.2.2, was rejected; indeed, Cauchy went further, for in lecture 38 of the Résumé, and in more detail in a paper 1822a, he refuted the assumption that a function can always be expanded in a series in the first place by providing counter-examples such as exp(—1/x2) at x = 0.
Secondly, Cauchy’s statements of the convergence of that series, and of the fundamental theorem, in terms of broad definitions of basic concepts and sufficient conditions for the (claimed) truth of the stated theorem, characterise the novel kind of rigour with which he invested his new doctrine; for he always presented theorems in terms of sufficient and/or necessary conditions laid upon functions, integrals, or whatever. Indeed, one must credit him for even thinking of stating conditions at all for the validity of several of the standard processes mentioned in the above exegesis.
Thirdly, Cauchy raised the status of logic precisely by stressing such conditions, and their weakening or strengthening when modifying theorems. However, he did not adopt any theory of logic known at the time—least of all the ‘logique’ of Condillac (§2.2.2), with its associations with algebra which his new discipline was intended to supplant.
Finally, while Cauchy called his subject ‘mathematical analysis’, his proofs were almost always synthetic in the traditional sense of the term explained in §2.2.3; that is, he started from basic concepts and built up his proof with the theorem as its last line. This confusing use of the word ‘analysis’ flourishes throughout the rest of our story!
2.7.3 The gradual adoption and adaptation of Cauchy’s new tradition. The reception was quite complicated in all countries, and is not well studied. The new approach was detested at the Ecole Polytechnique by both staff and students, as being far too refined for the students at an engineering school and remote from their concerns; the superior strength for heuristic purposes of the Leibniz-Euler tradition of differentials and integrals were preferred for applied mathematics, world-wide. However, when Cauchy left France in 1830 to follow the deposed Bourbon king into exile after the revolution in July of that year, many aspects of his doctrine were retained by his successors who taught the course in analysis at the school over the years (Navier, Sturm, Liouville and Duhamel), although in some cases it was diluted in precision and mixed in with elements of the other traditions.
In Britain De Morgan produced a large textbook on The differential and integral calculus. In a Cauchyan spirit he began with an outline of the theory of limits and gave versions of (272.1–2) as basic definitions; but he made no mention of Cauchy in these places (De Morgan 1842a, 1–34, 47–58 (where he even used Euler’s name ‘differential coefficient’ for the derivative!. and 99–105). He even devoted some later sections to topics consistent with his philosophy of algebra (§2.4.2) but which Cauchy did not tolerate, such as pp. 328–340 on Arbogast’s calculus of ‘derivations’ (an extension of Lagrange’s approach to the calculus which influenced Servois in §2.2.5), and ch. 19 on ‘divergent developments’ of infinite series. He did not even rehearse in this book the treatment of continuity of functions which he had given in 1835 in an algebra textbook: ‘“let me make x as small as I please, and I can make 7 + x as near to 7 as you please”’ (1835b, 154–155). This is the first occurrence of the usual form of continuity which is used today and called the ‘(ε, δ)’ form (G. C. Smith 1980a). Cauchy had introduced these Greek letters into mathematical analysis; but they did not underlie his definitions of continuity, which we saw in the last sub-section to be sequential. De Morgan’s definition appeared in a book on algebra because, in another difference of view from Cauchy’s, he regarded the theory of limits as algebraic since it handled mathematical objects and properties such as √2 and √8 = 2√2 (see, for example, 1836a, 20).
At the research level two of Cauchy’s most important first followers were young foreigners, who took up prominent problems in analysis and even refined his approach. N. H. Abel 1826a studied the convergence and summation of the binomial series for both real and complex values of the arguments. J. P. G. Dirichlet 1829a examined the sufficient conditions that a function should exhibit in order that its Fourier series could converge to it, and found that a finite number of discontinuities and turning values were required. At the end he threw off the characteristic function of the irrational numbers (as we now call it), as an example of a function which could not take an integral.
Abel was also one of the founders of elliptic functions in the 1820s, and his work and the independent contributions of Jacobi helped to spread Cauchy’s approach in this important topic. Dirichlet’s study was also influential, since Fourier series had become an important technique for applied mathematics, especially as a form of solution of differential equations (my 1990a, esp. chs. 9, 15, 17–18). Further, he discussed some of the ensuing issues with the young Bernhard Riemann (1826–1866), who was inspired in 1854 to draft out a doctoral thesis at Göttingen University on these series. In fact a thesis on the foundations of geometry was chosen by examiner Gauss. Both texts appeared only posthumously, under the editorial care of Dedekind, apparently in 1867.
In his thesis 1867b on geometry Riemann provided a philosophical study of space informed by mathematical insights (Ferreirós 1999a, ch. 2). The chief idea was ‘n-fold extended magnitude’ (space in general. upon which ‘Mass-relationships’ obtained; an important example was physical ‘space’ whose relations were studied in geometry, but discrete cases were also admitted (art. 1, para. 1). It is not necessary for us to pursue his line of thought, which is just as well given his cryptic style (Novak 1989a.; he admitted both continuous and discrete ‘manifolds’ (‘Mannigfalthigkeiten’) of objects falling under general concepts, with a part-whole relation implicitly adopted.
Riemann’s thesis 1867a on analysis contained a more direct use of set-theoretic notions (following Cauchy and Dirichlet), again formulated in cryptic but extraordinarily suggestive terms. Its appearance was a seminal event in the history of real-variable analysis: immediately several mathematicians started to explore and clarify various of its ideas. One part of the thesis tried to refine Cauchy’s definition (273.2) of the integral by defining upper and lower bounds on the sequence-sums in terms of the maximal and minimal values of the function over each sub-interval defined by the partition: a clearer version of this idea using upper and lower sums is due to Gaston Darboux 1875a. The main part dealt with various consequences of Dirichlet’s conditions for convergence of Fourier series: we shall pick these up in §3.2.3, as they provided the origins of Cantor’s creation of set theory.
2.7.4 The refinements of Weierstrass and his followers. Riemann’s paper was a wonderful source of problems for mathematicians; the main originator of techniques by means of which these and other problems in real-variable analysis could be tackled was Karl Weierstrass (1815–1897), who rose to great prominence in world mathematics from the late 1850s, especially with his lecture courses given at Berlin University. He accepted Cauchy’s basic approach to real-variable analysis (and, like Cauchy himself, used limits and equivalent definitions of continuity and convergence also in complex-variable analysis30); but he came to see that in various ways its definitions and procedures did not match the aspirations for rigour which Cauchy had uttered.
Over the years Weierstrass and his disciples followed Cauchy’s basic ideas on giving broad definitions and seeking sufficient and/or necessary conditions for theorems, working with limits, continuity, convergence, and so on, and producing detailed synthetic proofs; but they introduced several refinements. From the 1870s German figures dominated, such as Cantor, Paul du Bois Reymond, Hermann Hankel, Axel Harnack, Eduard Heine and Hermann Amandus Schwarz; but some other nationalities provided important contributors during the 1870s and 1880s, such as Darboux, Charles Hermite and Camille Jordan in France, Ulisse Dini and Giuseppe Peano in Italy, and Gösta Mittag-Leffler and Ivar Bendixson in Sweden. The most pertinent innovations are grouped below as five inter-related issues;31 some will be described in more detail in §3.2 and §4.2.
Firstly, while Cauchy had a completely clear grasp of the basic definitions and use of limits, he was hazy on the distinction between what we now call the least upper bound and the upper limit of a sequence of values. For example, he used the latter notion in his Cours d’analyse when presenting the first batch of tests of convergence of infinite series, but he specified it with rather vague phrases such as ‘the limit towards which the greatest values converge’ (1821a, 129). The distinction had to be sorted out, and the different contexts for their respective use.
Secondly, theorems involving limits, and considerations of functions with infinitely many discontinuities and/or turning values and the definability of their integrals, focused attention on collections of points (or values) possessing certain properties. They were to be construed as sets, and were the main stimuli for the growth of point set topology, especially within Cantor’s theory. Riemann’s draft thesis was particularly fruitful in this context, for he constructed several examples of the type of function just mentioned and found their Fourier series; further, his definition of the integral worked in effect with sets of measure of zero without explicitly mentioning either set or measure.
Thirdly, and sometimes as examples of the last issue, the relationship between rational and irrational numbers needed closer examination. It was well known that each type of number could be construed as the limit of a sequence of numbers of the other type; but it became clear that, especially in connection with theorems asserting the existence of some limit, the proof might require irrational numbers to be defined in terms of rational ones in order to avoid begging the question of existence involved in the theorem. Cauchy had faltered in his Cours when, for example, he drew on the real line structure when claiming to establish necessary and sufficient conditions for the convergence of an infinite series (1821a, 116: compare pp. 337, 341).
Fourthly, Cauchy and his successors tended to move fairly freely between properties of continuity and convergence defined at a point, in its neighbourhood, and over an interval of values. While the distinction between these different types of context was obvious, the consequences for mathematical analysis only began to be grasped in the Weierstrassian era. Then there were introduced modes of continuity and especially convergence: uniform, non-uniform, quasi-uniform. The need for these distinctions was increased when the ‘(ε,δ)’ form of continuity came to be preferred over Cauchy’s sequential form. The contexts included the convergence and term-by-term differentiation or integration of infinite series of functions, differentiation under the integral sign, double and multiple limits taken simultaneously or in sequence, and many aspects of handling functions of several variables. Quite a few variables could be present together: for example, in the series of functions  not only were x and n at work but quite possibly also incremental variables on both of them (x + h and n + m, say). Working out careful forms of definition and proof here, and keeping modes distinct from each other, required very meticulous scrutiny (Hardy 1918a).
not only were x and n at work but quite possibly also incremental variables on both of them (x + h and n + m, say). Working out careful forms of definition and proof here, and keeping modes distinct from each other, required very meticulous scrutiny (Hardy 1918a).
Finally, and notably in connection with the first and the fourth issues, the use of symbolism had to be increased in both considerable measure and a systematic manner. One type of case is of particular interest here: some nascent quantification theory, to express and indeed clarify the functional relationships between the different variables operating in a problem: in particular, to distinguish ‘For all x there is a y such that …’ from ‘There is a y such that for all x …’.
2.8.1 Mathematical analysis versus algebraic logic. The major place has been given to algebra and algebraic logic because during the period covered it emerged in this chapter as a group of (differing) uses of algebras to represent procedures in logic. By contrast, in the last section we saw no explicit logic, although ideas were born which will be taken up in the succeeding chapters on mathematical logic. No explicit clash between the two lines of work was in operation; however, some conflict in purpose and philosophy is evident.
In a famous and influential passage in the preface to Cours d’analyse, Cauchy wrote: ‘as for methods, I have sought to give them all the rigour that one requires in geometry, so as never to have recourse to the reasons drawn from the generality of algebra’ (1821a, ii). The key word is ‘rigour’, which he conceived in terms of the broad definitions and deductive lines of reasoning to prove in detail theorems which usually incorporated necessary and/or sufficient conditions upon the mathematical components involved. His allusion to geometry concerned the strict rigour which proofs of Euclidean geometry were then held to exhibit: exposure of Euclid’s lacunae and flaws was not to occur for several decades (§4.7.1–3). But Cauchy was not appealing to intuition: on the contrary, as with Lagrange, no diagrams adorned his writings. Further, his disparagement of ‘the generality of algebra’ was directed especially against the Lagrangian tradition. However, it was precisely that tradition to which the English mathematicians adhered, from Babbage and Herschel to De Morgan and Boole; and the last two men found major sources of analogy and technique to guide and inspire their mathematicisations of logic. This clash will provide points of contrast during our examination of the further refinements and extensions of Weierstrass’s version of mathematical analysis, which form a main theme of the rest of this book. First, however, we must briefly locate two “background” philosophers.
2.8.2 The places of Kant and Bolzano. The thought of Immanuel Kant (1724–1804) bears somewhat upon our story regarding both logic and mathematics. He wrote little explicitly on logic, and the 1800 edition of his logic lectures is of somewhat doubtful authenticity (Boswell 1988a). Regarding logic as providing ‘the general rules for understanding relationships between bodies of knowledge’, he largely followed the syllogistic tradition; in particular, he defined ‘analytic’ propositions as those cast in syllogistic form and in which the subject was contained within the predicate, and ‘synthetic’ simply as not analytic. His philosophy of mathematics was based upon the premise that mathematical propositions were ‘synthetic a priori’; that is, they were neither analytic nor dependent upon our experience for their truthhood. Space and time were granted the same status; one consequence was the claim that Euclidean geometry was the only possible one (§4.7.4), a view which was to gain him a bad press by the late 19th century. In addition, his use of the traditional part-whole theory of collections, embodied in the containment property above, was to be challenged by Cantor’s set theory. A survey of Kant’s position and its relationship to some modern philosophies of mathematics is provided in Posy 1992a.
The reception of Kant’s epistemology among mathematicians and logicians was more mixed. The main assumption was the role of active ‘thinking’, which allowed the agent to use his power of ‘intuition’ to make ‘judgements’ about relationships between individual ‘objects’ and/or more general ‘concepts’. Positivists usually dismissed such talk as mere ‘idealism’; however, in all versions of logic some role was usually assigned to judgements.
Kant also discussed at length certain ‘antinomies’ of knowledge, such as the existence and also non-existence of a first moment in time. This dichotomy was heightened by Kant’s semi-follower G. W. F. Hegel (1770–1831) into a methodology of ‘thesis’ and ‘antithesis’ resolved in a ‘synthesis’: it formed a central feature of the ‘neo-Hegelian’ movement in philosophy which became dominant at the end of the century, especially in the England of the young Russell (§6.1.3). However, it was not much used for solving the paradoxes which came to infect mathematical logic and Cantorian Mengenlehre in the 1900s.
This avoidance of Kantian principles was fairly typical of the reception of Kantian philosophy by Russell and followers; as a philosopher of both logic and mathematics he was found generally wanting (and Hegel even more so., especially for allowing synthetic a priori judgements, relying upon syllogistic proofs, and maintaining links between logic and psychology. Conversely, some thinkers of a generally Kantian persuasion were to criticise mathematical logics, disagreeing over the conception of analysis and wishing to see a greater role assigned to intuition, and in some cases doubting the legitimacy of the Cantorian actual infinite.
The situation was complicated by the rise to importance from the 1870s of various schools of ‘neo-Kantian’ philosophy, which remained active throughout our period. The most relevant change was to reject the Master’s claim that space and time were a priori forms of perception or pure intuition and to treat them as constructions affected by pure thought in which logic played some role (Friedman 1996a). Among the schools, the one associated with Marburg University is the most relevant, since they favoured thought and method(ology) over, say, sense-experience, or psychology. Among their members Ernst Cassirer considered logicism most closely (§7.5.2, §8.7.8). A further untidiness arises over the use of the word ‘intuition’: whether in some fairly strict Kantian sense (as often with philosophers. or in a looser sense of initial formulations of theories (as often with mathematicians).
These philosophical traditions were enormously influential during the 19th century, especially but not only in German speaking cultures; I have not attempted to do them justice here. By contrast, the work of the Bohemian philosopher and mathematician Bernard Bolzano (1781–1848) was then little-known. He achieved much in mathematics, logic and philosophy but gained little influence outside his immediate circle during his lifetime or afterwards; so he gains only this short review and a few mentions hereafter.
Bolzano’s career falls into three phases. After training in philosophy, physics and mathematics at Prague University he joined the Theological Faculty but pursued mathematics as his main research interest. Two books and three booklets came out between 1804 and 1817; the most important item, 1817a, contained a newly rigorous proof of the intermediate value theorem drawing upon formulations of the notions of limit, continuity of functions and convergence of infinite series strikingly similar to those found soon afterwards in Cauchy’s Cours (1821) and thus making him a co-pioneer of mathematical analysis. He must have realised that this booklet was significant, for in 1818 he placed it also as a number in the Abhandlungen of the Böhmische Gesellschaft der Wissenschaften; thus, uniquely among these works, it is not rare.
For his living Bolzano taught religion at the Faculty, and drew from it, and from considerations of contemporary life, a Utopian socialist philosophy. This was Very Naughty, and as a result he was sacked in 1819. The second phase sees him living much in Southern Bohemia with a family called ‘Hoffmann’, where his major production was a four-volume epistemological work, Wissenschaftslehre (Bolzano 1837a). Many of his ideas on logic were formulated here, of which two are particularly notable: his concern with ‘deducibility’, formulated in a manner general enough to individuate logical consequence (see esp. arts. 154–162); and his stress on objective truths as opposed to (though intimately linked with) judgements, as expressed in propositions (arts. 122–143, 198–218, 290–316). While not algebraic in the English sense, his logic used a relatively large amount of symbolism, and also the part-whole theory of collections (indeed, rather more substantially than with most contemporaries).
The political atmosphere seems to have calmed down enough for Bolzano to return in 1842 to Prague, where he continued to work until his death in 1848. During this phase mathematics was back on his agenda, producing especially a remarkable survey of the ‘Paradoxien des Unendlichen’ which was published as a posthumous book 1851a. The editor, Franz P ihonský, was one of a group of devoted followers who tried to sustain and spread his work, but with little success. There was also a huge collection of manuscripts to be edited, but little was done. Even a twelve-volume edition of his main philosophical and religious publications (including the Wissenschaftslehre), put out by a Vienna house in 1882(Bolzano Writings), failed to capture the imagination.
ihonský, was one of a group of devoted followers who tried to sustain and spread his work, but with little success. There was also a huge collection of manuscripts to be edited, but little was done. Even a twelve-volume edition of his main philosophical and religious publications (including the Wissenschaftslehre), put out by a Vienna house in 1882(Bolzano Writings), failed to capture the imagination.
But just around that time some of Bolzano’s logic and mathematics began to receive attention. In an encyclopaedia article on the concept of limit Hankel 1871a had mentioned the analysis booklet; maybe he had seen it listed in the entry for Bolzano in the first volume (1867) of the Royal Society catalogue of scientific papers. At all events, publicity now slowly increased: Otto Stolz wrote an article 1882a in Mathematische Annalen on the analysis booklet and one of the early books. The book on paradoxes was reprinted in 1889, and the booklet in 1894 and 1905. During this century Bolzano’s reputation has steadily risen, especially as more anticipations have come to light in the manuscripts; further editions and also translations have been made, dominated now by a Gesamtausgabe of both publications and (chosen versions of. manuscripts.32 But in most contexts his successors have found only premonitions of now known notions and theories, albeit astonishing, rather than novelties directly to stimulate new work: the first figure of note to be significantly influenced was the philosopher Edmund Husserl (§4.6.1). More normally, Bolzano’s meditations on the infinite(s) brought him to the edge of the results, already achieved, of an early admirer of the 1880s: Georg Cantor, whose own feats are chronicled in the next chapter.
1 On the political significance of Condillac’s thought, see Albury 1986a; his edition/translation of the Logique has a very useful introduction. On the general background in Port-Royal logic and Enlightenment philosophy, see Auroux 1973a and 1982a.
2 Bad planning and poor financing caused the early demise of the Ecole Normale. The current institution carrying this name was founded in 1810 as the elite establishment of the new Université Impériale, which despite its name was basically the school-teaching organisation for the Empire. On the French educational structure of the time, see my 1988a.
3 On these and many related developments in post-Lagrangian algebras, see my 1990a, chs. 3 and 4. Unfortunately, none of the histories of algebra has recognised the importance of these theories for the development of algebra in general.
Associativity had already been stressed by Legendre in connection with number theory, without name; this one is due to W. R. Hamilton.
4 On the algebras to be discussed here, see especially Nagel 1935b, Joan Richards 1980a and Pycior 1981a. There were other interests in English mathematics, in which algebras were not necessarily marked: for example, the philosophy of geometry (Joan Richards 1988a). On Cambridge mathematics in general in the early 19th century, see Becher 1980a and my 1985a.
5 This algorithmic character is a common factor between Babbage’s mathematics and his later work in computing (my 1992b). On his work on algebra see Panteki 1992a, ch. 2.
6 In this quotation I have put form for Whately’s word ‘force’, which seems to be a misprint although it appears in every edition that I have seen, including the original encyclopaedia appearance (1823a, 209). Boole made the same change when paraphrasing this passage in a manuscript of 1856 (Manuscripts, 109). De Morgan was to take the word ‘force’ to refer intensionally to a term (for example, 1858a, 105–106, 129–130). See also footnote 21 on Jevons.
Whately was also well known in his lifetime for a wry and witty commentary on observation and testimony entitled Historic doubts relative to Napoleon Buonaparte (1819, and numerous later editions).
7 See Joan Richards 1980a and Pycior 1983a. I do not treat the influence upon De Morgan of the work of the Irish mathematician William Rowan Hamilton, or of the philosophical writings of Herschel and William Whewell.
8 De Morgan’s article is merely noted in Dhombres’s extensive study 1986a of the history of functional equations, because equations of functions in one variable are largely omitted; however, it has an extensive section on functions of two variables (De Morgan 1836a, 372–391).
9 De Morgan 1831a, 212. Why, then, did he write on one of the front pages of his copy of this edition of Whately’s book: ‘This is all I had seen of Whately’s logic up to Aug. 7, 1850’? Like his whole library, the copy is held in the University of London Library.
10 Most of De Morgan’s five papers on logic, together with the summary of an unpublished sixth paper and some other writings, are conveniently collected in De Morgan Logic (1966), edited with a good introduction by Peter Heath; its page numbers are used here. See also his correspondence with Boole, edited by G. C. Smith (Boole-De Morgan Letters); but note the cautions on the edition expressed in Corcoran 1986a. Merrill 1990a is a survey of his logic, especially that of relations; but for the connections with mathematics, largely missing (ch. 7), see Panteki 1992a, ch. 6.
11 Previously George Bentham had published a short treatise 1823a in French, exposing a classification of ‘art-and-science’ based upon Jeremy’s philosophy of science. However, he explicitly set aside French logique in the preface of his 1827a. For an advocacy of his originality, see Jevons 1873a; and on predecessors to Bentham, see Venn 1881a, 8–9.
12 There is no copy of Bentham’s book in De Morgan’s personal library (on which see footnote 9). On them and Hamilton see Liard 1878a, chs. 3–4.
13 The extent of Gergonne’s influence on mathematicians and logicians seems to have been far less than his philosophical writings merited. For another example, he published a perceptive article 1818a on forms of definition which gained little recognition. However, the young J. S. Mill took a course with Gergonne in 1820 at the Faculté des Sciences of the Université Royale de France at Montpellier, and might have heard some of the same material.
14 All the articles in this encyclopaedia were unsigned; but the British Library contains a copy with all the authors named in the margin, and De Morgan’s name is given here. His widow’s biography 1882a includes a list of his (many) contributions, drawing also on his own copy; I have not traced it, but I share her doubts about the attribution to him of ‘Syllogism’ (in 23 (1842), 437–440). A more likely author is J. Long, the chief editor of the encyclopaedia; he wrote the general article on logic, which is interestingly entitled ‘Organon’ (17 (1840), 2–11: De Morgan’s pamphlet 1839a is praised on p. 7 as a study of ‘a purely formal logic’).
15 This type of notation for inverse functions had been introduced by Herschel in the 1820s, in connection with his work on functional equations (§2.3.1).
16 Various rather trivial accounts of Boole’s life and work, and some mistaken ones, can be found. MacHale 1985a is the best biography, to be supplemented by two exceptional obituaries: the well-known Harley 1866a, and the forgotten Neil 1865a. Items concerned with specific aspects of his work will be cited in situ. Especially recommended is Panteki 1992a, chs. 5 and 7; her 1993a provides further little-known background. Jourdain 1910a includes an important survey, using manuscripts which Harley had owned but which are now lost (see also footnote 21). Styazhkin 1969a has a useful survey in ch. 5.
17 De Morgan’s obituary 1865a of Boole shows the limitation of their relationship. Short, and as nearly concerned with his own work as with Boole’s, it states that ‘Of his early life we know nothing’ and that he died ‘at some age, we suppose, between fifty and sixty’ (in fact, he was 49). The piece is anonymous, and I attribute it to De Morgan only because he is listed as a contributor to the volume of the journal (Macmillan’s magazine) in which it appeared, and no other person named there could possibly have been the author.
18 See Boole’s letters to MacMillan s of 30 August and 7 September 1855 in Reading University Archives, MacMillan’s Papers, file 224/10.
19 The Boole Papers have recently been put in some order, maintaining the original call-marks. Some years ago a smaller collection was acquired by Cork University; it includes an unpublished biography by his sister Mary Ann.
20 On this theme see my 1983a. Mrs. De Morgan published in 1866 the first extended study of physical mediumship, to which he contributed a superb preface. When the Society for Psychical Research was founded in 1882, Mrs. Boole herself was a founder member of Council (although she resigned at once, feeling improperly placed as the only woman …). Venn and Lewis Carroll were members; and Johnson sometimes helped his sister Alice, who was the first Research Officer, over mathematical matters.
21 Later Jevons developed this idea of contradiction with a proposition to form the notion of the ‘logical force’ of a proposition, the number of propositions which it negated (1880a, ch. 24). However, I do not think that this idea bears on the use of ‘force’ noted in footnote 6.
22 Russell seems not to have drawn on Jevons at all; Frege’s criticism of Jevons’s definitions of numbers in terms of diversity is noted in §4.6.2.
23 The correspondence is published in my 1991b (p. 30 here); parts of some of them are in Jourdain 1913d, which was hitherto the only available source for some letters (p. 117 here). Otherwise on Jevons see, for example, Liard 1878a, ch. 6.
The recent edition of Jevons’s correspondence (1972–1981. extols his (important. contributions to economics uncluttered by his (important. contributions to logic. For example, his letters with Boole, Venn and De Morgan have been systematically omitted; a very few are included in his widow’s edition (Jevons Letters (1886)).
24 Jevons to Macmillan, 16 February 1869. The file of letters is held at the British Library (London), Add. Ms. 55173; this one is also excluded from the edition of Jevons mentioned in the previous footnote.
25 This point comes out especially clearly in Venn’s correspondence with Jevons in March 1876 (letters in Jevons Papers, and Venn Papers, File C45).
26 Later MacFarlane 1885a outlined an alternative ‘logical spectrum’ based upon representing all of the candidate classes by a sequence of contiguous rectangles and half-rectangles. Convex curves cannot treat more than four classes; many modifications were proposed (for example, in Anderson and Cleaver 1965a) before A. W. F. Edwards 1989a found an indefinitely iterable algorithm. Venn 1881b surveyed the history of logic diagrams in a piece for the Cambridge Philosophical Society, and in a companion survey 1881a of notational systems he recorded over a score! Shin 1994a analyses mostly Venn diagrams in terms of mathematical logic.
27 For example, on 15 September 1863, in connection with Jevons s correspondence with Boole, De Morgan wrote to Jevons and offered to send him an offprint of his 1860a on relations (Jevons Papers, Letter JA6/2/114); but Jevons appears not to have responded.
28 Among commentaries on Cauchy’s analysis and its prehistory, see Bottazzini 1986a, and my 1970a (esp. chs. 2–4 and appendix. and 1990a (esp. chs. 10 and 11). See also footnote 30.
29 Lagrange’s allowance of exceptional values x or the unction (§2.2.2) was the best kind of awareness expressed hitherto. Between him and Cauchy, Ampére had essayed some ideas in this direction.
30 However, Weierstrass s founding of complex-variable analysis in power series was different from Cauchy’s, and also from another approach due to Riemann (Bottazzini 1986a, chs. 4, 6, 7).
31 Among general secondary sources, see Pringsheim 1898a and 1899a, T. W. Hawkins 1970a, my 1970a (ch. 6 and appendix), and Dugac 1973a.
32 This edition, Bolzano Works, was launched with the splended biography E. Winter 1969a, written by a leading Bolzano scholar; the manuscripts, which are held in the Vienna and Prague Academies, are being distributed among its various series and sub-series. The five early mathematical works were photo-reprinted in 1981 as Bolzano Mathematics. Several items have been translated into various languages: the trio mentioned in the text are available in English (only parts of the Wissenschaftslehre). His work has been subject to much commentary, variable in quality; of the general studies, Sebestik 1992a is recommended. On the status of the principle of contradiction in Bolzano, Kant and many other figures, see Raspa 1999a.