CHAPTER 10
The Fate of the Search
A STORY as rich and interconnected as this one could generate masses of meta-consideration; but I avoid the temptation, especially as various “local” conclusions have been drawn and summaries made en route. After a general comparison of algebraic and mathematical logics, the focus falls mainly upon Russell, and is mainly organised before, during and after PM; it ends with several appraisals of logic(ism. in the U.S.A. in the early 1940s. The chapters ends with a flow-chart for the whole story and some notes on formalism and intuitionism,1 before locating symbolic logic in mathematics and philosophy in general, and emphasising the continuing lack of a definitive philosophy of mathematics.
10.1 INFLUENCES ON RUSSELL, NEGATIVE AND POSITIVE
10.1.1 Symbolic logics: living together and living apart. (My 1988b.)
Boole, Schröder, etc., have made the Algebra of Logic, while Mr. Peano and his school have made the Logic of Algebra.
Itelson (Couturat 1904c, 1042.)
While algebraic logic has not been a main theme of this book, its main thrusts have been conveyed: the separate initiatives from de Morgan and Boole (§2.4–5. and their fusion by Peirce and Schröder (§4.3–4). The many differences from mathematical logic also emerged: mathematics applied to logic rather than the other way round, as Gregorius Itelson nicely put it at the Congress of Philosophy at Geneva (though his remit to algebra was too narrow.; laws rather than axioms, and algebraists’ exploitation of duality; rapid derivation of consequences, not the detailed exposure of proofs; part-whole rather than set theory; the language of nouns and adjectives rather than of particles; and some algebraists’ concern with model theory, especially with Boole on (un.interpretability. The roots of the differences go back to the 1820s, when Cauchy grounded mathematical analysis on the theory of limits and rejected Lagrange’s foundation of the differential and integral calculus in power series (§2.7.2). The later mutual lack of sympathy is especially clear when Russell virtually ignored the algebraists when developing his mathematical logic of relations (§6.4.4., and Peirce dismissed The principles in a few lines (§6.8.1).2 Reactions to Kempe are another good contrast: Peirce’s enthusiasm (§4.2.9. came through to Royce’s reworking 1905a; (§7.5.4); Russell received an offprint of that paper, but his marginal notes consist of rewriting various results in Peanese (RA)
Despite the (sporadic. advocacy of Peirce’s work by Ladd-Franklin (§8.3.4. and the approval of Schröder by Löwenheim and Skolem (§8.7.5), the algebraic tradition was heavily eclipsed by mathematical logic, especially after PM appeared (Anellis and Houser 1991a). One reason was its seeming lack of purpose: we may admire the insights of Peirce and check the catalogues of Schröder, but where are they going? (Similarly, the initial influence of Grassmann upon Schröder, Peano and Whitehead diminished). The aims of Peano and Russell, and of Frege when noted, were much more specific: directional rather than postulational logic, as Stebbing put it (§9.5.1). This difference seems to have underlain the change of allegiance for Whitehead: publishing Universal algebra in 1898 (§6.2.4. but then collaborating with Russell on logicism. When algebraic logic began to revive in the 1940s (due to Tarski among others., Boolean algebra remained prominent; but otherwise it was a much altered subject, concerned with metalogic and model theory, and deploying abstract algebras and set theory.
The incompatibility between the two traditions came back to tax Russell in the 1960s, when G. Spencer Brown sought his support for an unorthodox manuscript with the Boolean title The laws of form. It contained in effect the propositional calculus based upon the Sheffer stroke but without brackets, a great simplification of the procedures of PM (compare Hoernlé on Sheffer in §8.3.3). The theory of types was discarded, although the predicate calculus was not developed sufficiently to refound logicism. However, the anti-logicistic cast of the theory was clear, as Russell realised when praising ‘a new calculus of great power and simplicity’ for Allen and Unwin, with whom it first appeared as Spencer Brown 1969a, in the first of many printings.3
10.1.2 The timing and origins of Russell’s logicism. We have just noted negative influences; now for positive ones. Although Russell could be amazingly in error in his recollections (§6.1.2), there is no doubt over his repeated assertions of the three most important forces: G. E. Moore, for a turn from neo-Hegelianism to empiricism; Cantor, for envisioning a foundation for mathematics in Mengenlehre; and above all Peano, for providing logical and mathematical techniques for such a vision to be effected. Thus armed, Russell came to his conception of an empiricist philosophy of mathematics grounded in Peanist logic enhanced with relations and expressed in set theory (§6.5.1).
The timing of Russell’s creation of logicism in 1901 is striking. Not merely did an ambitious and intelligent young man in his late twenties set out a programme, but also an ambitious and intelligent member of the British aristocracy, whose Inheritance Of The World Was A Large Responsibility, sought an empire of his own, colonising (pure. mathematics within mathematical logic. The consonance of situations is worth noting; for example, recall from §6.1.2 his concurrent work in the mid 1900s on logic and on the Free Trade question. Hilbert’s proof theory of that time also has similar global aspirations, and there are other cases for the period (Stump 1997a); for example, International Congresses in various disciplines, especially those in connection with the ‘Universal Exhibition’ held in Paris in 1900 (§6.4.1). The word ‘universal’ then had a cachet often granted today to ‘international’; Peano is a nice example, with his ‘universal’ class V (§5.2.3) and his advocacy of ‘universal’ languages, especially his own Latin without inflexion. This interest was shown by some other logicians: Couturat for Esperanto (which Carnap was also to learn.and then Ido (which also attracted Ladd-Franklin).
On the paradoxes, when recognised they played a large role in all foundational theories, as “mistakes” to be avoided or even Solved; flaws of thought, as it were. However, the well-known story that they promoted the ‘foundational crisis’ (following Weyl’s dubious phrase in §8.7.7.has been heavily undermined by historical research of recent decades, and has gained no support here. Indeed, it is doubtful that, with the possible exception of Zermelo (§4.7.6), set theory motivated anybody to take up foundational studies; in particular, Cantor created Mengenlehre to tackle technical problems in mathematical analysis (§3.2), the foundational side only coming later (§3.4). ‘Away with the myth of the crisis!’, to paraphrase the title of a recent historical survey of foundational studies (Borga and Palladino 1997a).
10.1.3 (Why) was Frege (so) little read in his lifetime? It is also clear, and correct, from Russell’s recollections that Frege’s influence on him began to assert itself (as it were. only when his main lines had been formed from Cantor and Peano. Sadly, it is “common knowledge” among many philosophers that Frege was Russell’s main source; their writings point to the close similarities between the systems of the two men, and often marginalise or even ignore completely all other figures. However, historians who have mastered enough logic to distinguish conjunction from implication know that the similarity of some B to an earlier A does not necessarily entail influence from A to B, and Frege-to-Russell is a clear case in many respects. The first known influences of Frege were recorded in §6.7.7, and further examples were given later; but in scale they do not at all match those from Cantor and Peano. It is a great pity that Russell did not digest Frege earlier; at the very least, his logical calculus and logicism could have been more clearly stated. But even then, Frege’s logic was notably Platonic while Russell’s tried to be empirical; and Frege’s logicism was explicitly confined to arithmetic and (some) mathematical analysis, whereas Russell’s ambitions extended to much more (pure) mathematics.
How well was Frege’s work known before Russell’s publicity? His claim to be the ‘first reader’ of the Begriffsschrift has been shown to be absurd (§4.5.2). Further early readers of Frege included Kerry (an excellent start in §4.5.4), Cantor, Schröder, Peano, Husserl and Hilbert, and reviews in the Jahrbuch by Michaelis; among others not recorded here are Brentano and some of his followers (Linke 1946a). Russell’s appendix in The principles spread the news considerably; but the book also reported the paradox to which Frege’s system was susceptible, and he reduced his publishing afterwards, an embittered victim (§8.7.3). Thus, unlike PM, the reception of his logic was not separated from that of his logicism. After applause in the 1910s from figures such as Jourdain (§8.2.3) and Ziehen (§8.7.2), the revival of interest in the 1920s led by Wittgenstein and then Carnap tended to focus on the linguistic and semantic aspects of Frege′s system and lead to the invention of Frege’ (§4.5.1), a philosopher of language and of all mathematics, who has not been a concern here.
Thus, while the reception of Frege was far from the silence which Russell imagined, it never attained a deserved level. The usual reason given for repelling readers is the strange notations; but in §4.5.9 additional sources were sought in Frege’s unfortunate use of standard terms such as ‘function’, and especially in the level of foundation proposed, extreme even in a country where in general such studies were favoured. Furthermore, his claim in the 1900s that the Euclidean was the only geometry was not good advertising (§4.7.4). This last factor will return soon, as Russell’s own influence is considered.
10.2 THE CONTENT AND IMPACT OF LOGICISM
Logical and mathematical judgements are true only in the world of ideal entities. We shall probably never know whether these entities have any counterparts in any real objects.
Łukasiewicz 1912a, 12
10.2.1 Russell’s obsession with reductionist logic and epistemology. A major motivation for Russell was the improvement of rigour, especially in mathematical analysis already before Cantor. One of its main features was reduction: not only of real numbers to rationals and thence to integers, but also of other branches of mathematics to arithmetic. Whitehead and Russell effected these reductions in their logicistic construction of (some) mathematical analysis, but went deeper down to classes and then to propositional functions and relations.
These mathematical reductions were twinned with the philosophical empiricism which Russell adopted from G. E. Moore. As he recalled later, in the 1900s ‘my universe became less luxuriant. [... ] Gradually, Occam’s razor gave me a more clean-shaven picture of reality’ (1959a, 62). Logicism was his first detailed foray into reduction; not just the mathematical and logical cases just mentioned but also of mathematical logic to its ‘primitive propositions’, and of many philosophical categories to relations. A related term was ‘meaningless’, which however came close to self-reference with his many uses: denoting phrases without referents, classes or names or propositions which generate paradoxes, non-membership of an empty class, and ill-formed phrases or formulae (my 1977b, chs. 13–17 passim).
Russell’s desire to eliminate abstract objects also led him to construe individuals as basic elements of the physical world (§7.9.3). But then his logic became a posteriori, and he was forced to assertions such as ‘Logic, I should maintain, must no more admit a unicorn than zoology can; for logic is concerned with the real world just as truly as zoology, though with its more abstract and general features’ (1919b, 169). But one does not have to follow Leibniz, or Scholz for that matter (§9.6.3), on logic holding in all possible worlds to wonder why it should worry about unicorns, or bullocks either: Russell’s conflations of various senses of existence (§7.3.5) has reared its ugly head (or horn) again, and his word ‘concerned’ above is hopelessly ambiguous. Logic is not so much an exact science as a subtle science.
Further, reification slips back into this threadbare empire, especially when quantification is applied: then propositions have surely to be taken as abstract objects, propositional functions seem to be ‘attributes’ (to use the term of Quine 1969a, ch. 11), and the relationship between the predicate calculi and set theory is unclear (G. H. Moore 1980a). Russell’s gradual change from intensionality to extensionality, especially in the second edition of PM, was also reductionst; it raises similar doubts (§8.4.4), and Ramsey’s extreme version (§8.4.7) still more. Later Russell queried the measure of extensionality deployed by Carnap (Russell 1940a, ch. 19), and Carnap himself became doubtful (1967a, ix).
These last cases concern reductionist epistemology. During Russell’s logicist phase he was doubtful about the utility of his logical techniques in philosophy in general. For example, while making a point on 6 February 1905 to his philosopher relative Joachim about how a complex is not wholly determined by its constituents, he made clear both his indebtedness to Moore and the limited philosophical scope of logicism:
Mathematical pre-occupations can hardly be the cause of my views, since they are derived from Moore, who only crammed up enough Mathematics to get through the Little-Go [entrance examination]. As a matter of fact, it was mainly through Ethics that Moore reached his views. As for me, I admit that the philosophy of Arithmetic seemed to me to require something like the theory of entities. But I consider Aesthetics or Ethics or Theory of Knowledge just as good a field for proving the necessity of my views. […] My Symbolic Logic is only intended to apply within a certain sphere. I hold it to be absolute truth, but not all truth. But I never apply it to properly philosophical problems. As to ‘man is mortal’, I am aware that there are dozens of other valid interpretations besides ‘if x is a man, x is a mortal’; but this is for me the most convenient.4
But by the early 1910s Russell was applying his logical techniques and principles to reductionist epistemology; prominent were the logic of relations, the avoidance of abstract objects, and the tying of true propositions to facts by correspondence. In the late 1910s he came to call his position ‘logical positivism’ (§8.3.6); but the earlier Our knowledge of the external world as a field for scientific method in philosophy (1914), to quote its title in its important full, made perhaps the greatest impact, especially on the VC. The enthusiastic conversion of Schlick was noted in §8.9.1. The major effect on Carnap has been recorded in detail, and personal evidence is also available. When in London in July 1965 Carnap gave Russell a copy of Schilpp 1963a on his philosophy, and wrote in it: ‘To Bertrand Russell, from whom I learnt the scientific method in philosophy, I give this token of my admiration and gratitude’; he also marked the passage in his autobiography mentioning Russell’s book (RA).
The word ‘scientific’ hides another reduction, made by Russell and his followers: of science to mathematics and physics. This narrowing has blighted much philosophy of science ever since, by retarding the philosophies of the life sciences and medicine, and also of technology. The effort of Woodger to logify biology (§9.5.3.) was most ingenious but mistakenly conceived or at least very limited in scope.
The policy of reduction continued when Russell’s (and Frege’s. philosophies were mutated by others, especially philosophers of language, to ‘analytic philosophy’, an umbrella term which became popular in the late 1940s; it embraced especially Moore’s and also parts of Wittgenstein’s later philosophy, and helped to invent Frege′.5 But it often degraded into language games, to Russell’s disgust: ‘Bad philosophy is an Oxford speciality’, he exclaimed in 1956, ‘and bad philosophy is still philosophy!’ (Logic, 322).
Finally, to resume a theme from §1.2.4, despite the stress laid on the links between mathematical logic and language during our period, its impact upon linguistics was very limited. The adherence to bivalency was one reason, but take even the case, say, of classical negation: what is the positive counterpart to ‘I have not eaten even an apple today’?
10.2.2 The logic and its metalogic
It has been a great misfortune to logic that universities have considered the necessary training of a logician to consist of a knowledge of Greek rather than of science.
Russell to J. O. Wisdom, 18 August 1959 (RA)
We have found the foundations of all systems studied here to be somewhat obscure. One reason was the lack of recognition of axioms as schemata; in particular, in PM schematic letters were conflated with real variables, and quantifier words such as ‘all’ and ‘some’ were used multiply. This unclarity is especially marked because both the propositional and the predicate calculi incorporated quantification in the normal sense. Frege had made some distinctions by using different kinds of letter (§4.5.2); but even his ordinary words can be ambiguous.
Another feature of logic was its universality, which was upheld by most adherents to all versions into the 20th century: one, and only one kind. Itelson used the word ‘metalogic’ at Geneva in 1904, but he rejected the notion involved (Couturat 1904c, 1041); Stammler acted similarly much later (§8.7.9).6
Russell always held to logical monism; he took it first came from Peano, along with the term ‘primitive proposition’ to cover both axioms and rules of inference (§6.4.4). It prevented both men from clarifying the foundations of their logic: Russell’s seems to have been inductive, in the scientific sense (§7.8.3). But the simple claim that he muddled logic with metalogic needs some refinement. The theory of definite descriptions shows that he knew the difference between a phrase and the object which it may be denoting (if any); and, like any one else, he wrote about a symbol if necessary. But some important demarcations are lacking; for example, whether type theory classified symbols or their referents (§7.9.2).
A very serious case is implication. While Russell identified it with 
p ⊃ q between propositions p and q and inference with p ⊃ q, often he did not separate them, or individuate logical consequence or entailment; laws such as excluded middle and contradiction were placed in the logic rather than stated of it (§7.8.3). Ponder his reaction in a letter of 15 May 1919 to Lewis upon receiving the Survey (§8.3.3): ‘I have never felt that there was any very vital difference between you and me on this subject, since I fully recognize that there is such a thing as “strict implication”, and have only doubted its practical importance in logistic’ (RA).
It is not even clear whether the logicism of PM was implicational or inferential. But its logic became viciously encircled by its logicism, in that (some) mathematics came out of mathematical logic, which itself was taken to be whatever was required to deliver this mathematics—an ironic feature of a calculus supposedly based upon the vicious circle principle.
While the logical calculi of PM became well established (including the logic of relations for more advanced readers), the universalist conception behind it became a growingly negative influence from the late 1910s. Rules of inference were gradually recognised as distinct in status from axioms. Brouwer admitted ‘mathematics of the second order’ by 1907, although giving it little publicity (§8.7.7). Later, Wittgenstein and Ramsey defined logic without involving logicism, and for the second edition of PM Russell made some changes under Wittgenstein’s influence; however, he did not use the hierarchy of languages which he had proposed in 1922 in reaction to the Tractatus (§8.4.3). Frege also spotted it at that time (§8.7.3), but kept it to himself. Several Americans groped towards metalogic and metalanguage (§8.5.3–5), while Hilbert’s coterie developed metamathematics (§8.7.4). But the full distinctions were effected principally by Gödel (§9.2.3) and Tarski (§9.6.7), insights which mark the logic of the 1930s most clearly from that of the 1920s. This point leads us to the next topic.
10.2.3 The fate of logicism. While not exhaustive, the survey in the preceding two chapters shows clearly that a far greater variety of positions was held and uses made of mathematical logic than is conveyed by the traditional history about three competing philosophies of logicism, formalism and intuitionism. This feature belongs to a full study of the development of logics and epistemologies between the wars—a fine topic not yet explored comprehensively, which deserves a book the size of this one.
Logicism competed not only with formalism and intuitionism but also with (neo-)Kantian philosophy, phenomenology, conventionalism, and axiomatic set theory. It maintained a fairly good status in Britain, the U.S.A. and Italy, and even picked up a little from the mid 1920s among the French. But then it became overshadowed, especially by formalism and the attendant techniques of metamathematics and model theory; Russell, and also Whitehead and Frege, were blind to the latter, and so misinterpreted formalism as marks-on-paper philosophy (a mistake which has been made endlessly ever since). PM is replete with proof theory in all its details; but it lacked proof theory in the sense which Hilbert and his colleagues were individuating, thus helping the eclipse to occur.
There was also a difficulty of discipline: logicism, whether in Russell’s or Frege’s version, was too mathematical for philosophers to understand and too philosophical for mathematicians to appreciate. Even E. H. Moore opined to the historian Florian Cajori on 17 November 1926 that ‘Certainly the extreme tendencies of Peano, Schröder, and Whitehead and Russell are beyond the approval, or at least the adoption, of working mathematicians’ (Moore Papers, Box 1, Folder 16). In consequence, many nice mathematical features of PM were largely unnoticed, especially the axiomatic set theory embodied within the logical calculi, and the point-set topology and especially transfinite arithmetic developed in its latter Sections. Other features were taken for granted; for example, the tri-distinction (already with Frege. between zero, the empty class and nothing (§6.7.2), which cleared away much ambiguity.7 The point can be generalised: mathematicians are usually dismissive of logic and philosophy, and thereby correspondingly careless from logical and philosophical points of view (Corcoran 1973a).
For the same reason, while Stebbing and especially Ramsey and Carnap were distinguished followers, neither Whitehead nor Russell had doctoral students in Hilbertian quantity, nor corps of successors. Neither man seemed to have such aspirations; and in any case logicism was only part of Whitehead’s philosophy of mathematics, and after abandoning the fourth volume of PM (§8.2.2.) he went in other philosophical directions, apart from his strange recasting of PM in 1934 (§9.4.3). Thus he is often demoted in the history of logicism—an understandable but unfortunate situation which I have tried to repair with the information available.
As part of the modest reception of logicism, there was little discussion of the limited range of mathematics covered in PM (Table 782.1): only set theory, finite and transfinite arithmetic, and some mathematical analysis and (had the last volume been completed. geometry. Russell had put forward a broader vision in The principles, even if the exposition was incomplete: onwards to the differential and integral calculus, then through geometries to handle space, and thus to some mechanics; the indefinables ‘alone form the subject-matter of the whole of mathematics; no others [...] occur anywhere in Arithmetic, Geometry or rational Dynamics’ (1903a, 11). However, the range of mathematics to be unified was not mentioned in PM; seemingly the authors had become so bogged down in the details of the early segments that they lost sight of the rest. In addition, potential followers would have been discouraged from attempting the trek by the recognised presence of the three doubtful axioms (infinity, choice, reducibility).
This point can be related to a general feature of implication which is often misunderstood. In A ⊃ B, proposition A is sufficient for proposition A, and A is necessary for B; so an implication moves from the less general to the more so, with the conclusion B embodying less knowledge than the premise A. From ‘Socrates is a man’ it follows that ‘Socrates is mortal’; but the conclusion follows also from, for example, ‘Socrates is a cat’. Similarly, logicism takes a relatively narrow base of mathematical logic and seeks (pure) mathematics as conclusion; but it fails, not only because of Gödel’s incompletability theorem and corollary but also in the many branches of mathematics that slipped through the net anyway.
Gödel’s results caused the logicist aim to be reformulated, especially by Quine (§9.4.4), in terms of possible relationships between mathematical logic, set theory and (some) mathematics. We noticed that, except for a few figures like Carnap and Dubislav, the reception of the results after publication in 1931 was rather slow; and Russell never absorbed them. At some stage he acquired the offprint of Gödel’s paper previously owned by Countess Zeppelin, the translator of Carnap’s Syntax (§9.3.7); but he marked only footnote 19, on the class of elementary formulae (RA). It is highly ironic that he had proposed the notion of a hierarchy of languages, essential for Gödel, for he never properly understood it (§9.5.4); for example, in a survey of logical positivism he mentioned his hierarchy and within a few lines said that Gödel’s theorem applied to ‘any formal system’ (1950a, 371), while in his philosophical recollections he judged that the hierarchy merely ‘disposes of Wittgenstein’s mysticism and, I think, also of the newer puzzles presented by Gödel’ (1959a, 114, italics inserted). In his last decade he was still wondering about the significance of the theorem (text in §11.9).
The balance between PM and metamathematics in the early 1940s is well exemplified by Church. Then in his early forties, he published as 1944a some of his undergraduate course on mathematical logic given at Princeton University: due to war conditions, the book is not well known, at least not in Europe. While he covered the same logic as in PM, the treatment was much closer to Hilbert-Bernays (§9.6.2), from the separation of the first- and higher-order ‘functional’ calculi to the stress on consistency, completeness, deduction theorems, normal forms and decidability. PM was not much mentioned, and of its ingredients only type theory was presented in detail, and then with the ‘ramified’ theory omitted (pp. 109–112). Later Church greatly revised the parts of the book up to the second-order predicate calculus into a new edition 1956a. Whitehead and Russell were mentioned dozens of times in the many new historical footnotes, but always on details. Although a type theory was constructed, logicism was not discussed: apparently it would have appeared in a second volume (p. 332), which was never published.
Similarly, when in the mid 1960s the Polish logician Andrzej Mostowski (1913-1975. delivered 16 lectures on ‘thirty years of foundational studies’ from 1930, he covered axiomatic set theory, intuitionism, formalism and model theory, but not logicism. In the introduction he mentioned its conversion into ‘a reduction of mathematics to set theory’, which was ‘unsatisfactory’ because of the difficulties facing the latter subject (1966a, 7); Quine appeared only for the stratification used in his book Mathematical logic (p. 143). However, the silence rebounds in part on Mostowski; for Quine and others were keeping alive the relationship between logic and set theories (Quine 1969a., and in recent years various aspects of PM have been freshly studied.8
10.2.4 Educational aspects, especially Piaget. As with all philosophical schools, logicism paid no attention within arithmetic to ‘goes-into’ integers. They arise in contexts such as the Euclidean algorithm: for example, 7 goes into 23 thrice, with 2 over. Words like ‘thrice’ show that a special vocabulary applies to these integers, which are neither cardinals nor ordinals; and the mention of Euclid shows that their history is long. Yet they usually escape the attention of mathematicians and philosophers—and, despite their heuristic utility, educators also.
The Swiss educational psychologist Jean Piaget (1896–1982) came eventually to the borders of logicism. An early book 1923a in his studies of the child dealt with reasoning, with syllogistic logic providing the main basis to the extent that in ch. 3 he examined understanding of the ‘logic of relations’ without resource to any recent authors on the topic. However, by the late 1930s, while deploring Russell’s separation of logic from psychology, he was imitating PM in giving prominence to (order-)isomorphism between classes, and even their ‘additive composition’, when studying the child’s supposed ‘conception of number’ (1941a, chs. 3–6, 7). But not only did he ignore negative and (ir.rational numbers (and goes-into numbers., but more broadly he seems not to have grasped the distinction between creating or appreciating mathematics and justifying it epistemologically. These two books, and others, appeared in English in Ogden’s series.
Piaget next wrote a volume 1942a on ‘numbers, classes and relations’, a plod through the algebra of classes and relations with a touch of type theory on pp. 76–79. Publication of the book during the War greatly limited its impact, though the author sent Russell a copy in 1946 (RA). The influence of PM came through Piaget’s belief that rationality resembles mathematical reasoning, which in turn was captured by (mathematical) logic. But such a position is hardly credible, especially for the creative sides of mathematics itself. Later his work played a role in the ‘new mathematics’ educational idiocy of the 1960s onwards.9
10.2.5 The role of the U.S.A.: judgements in the Schilpp series. The importance of Americans in this story, only partly recognised, deserves separate consideration. The initial stimulus did not come from C. S. Peirce, although both he and his father helped to foster an interest in algebras. The key mathematician was E. H. Moore, with his own interest in set theory and the development of postulate theory by his student Veblen, and also by Huntington; and from philosophy came Royce, who publicised Kempe and especially stimulated mathematical logic through his students, especially Lewis, Sheffer and Wiener, and also Cohen and Eaton. Thereafter interest continued steadily to the emergence of Veblen’s student Church and Whitehead’s sort-of student Quine, and the immigration of Carnap and Gödel in the 1930s.
Then Royce’s influence arose again. The founding of Journal of symbolic logic (§9.4.5) owes much to C. J. Ducasse (1881-1969), who was the founder President of the sponsoring Association. Although mainly an analytic philosopher, he was deeply interested in logic—because, like Sheffer, Lewis and Eaton, he took Royce’s courses around 1910 (Ducasse and Curry 1962a).
Soon after the founding, opportunities to appraise Whitehead and Russell were provided by a major new American enterprise. We recall from §9.5.4, in connection with Dewey, that Schilpp launched in 1939 a series of volumes entitled ‘Library of living philosophers’, where extended articles on a philosopher were published together with his replies. In 1941 Whitehead was the third philosopher to be treated (though he was not well enough to reply). His principal follower, Victor Lowe (1907–1988), provided a long survey 1941a of his philosophy to the mid 1920s, including the Universal algebra and the construction of space in 1905 (§7.6.1). Lowe deliberately left the mathematical logic to Quine who, then in his early thirties, contributed a piece 1941b on ‘Whitehead and the rise of modern logic’. Reviewing briefly but comprehensively the entire contents of PM, he drew upon his recent Mathematical logic and other work (§9.4.4) to point out imprecisions caused by conflating theory with metatheory; for example, the conditional and implication (pp. 140–141), and propositional functions as abstract attributes and as linguistic expressions (pp. 144–146). He also noted the excess multiplicity of notations in the logic of relations, and Whitehead’s return to logicism in 1934, both with ennui (pp. 152-153; compare 1985a, 113).
Quine did not try to distinguish Whitehead’s contributions to PM from those of Russell, who was Schilpped three years later (after G. E. Moore, incidentally). Three authors considered mathematical logic. Reichenbach reviewed it pleasantly, but inaccurately when attributing to Russell the notion of propositional function (1944a, 25). His most thrusting query concerned the status of intuitionistic and three-valued logics, which he cautiously supported (pp. 40-44, including also a mention of Gödel). Russell replied that ‘I agree, of course, that a three-valued logic is possible’, as to Lewis in 10.2.2; but he argued for bivalency on the ground that it ‘embraces unverifiable truths’, with non-true encompassing both false and unknown (1944b, 682).
In response to Russell’s introduction 1937a to the reprint of The principles (§9.5.4), James Feibleman (1904–1987) felt that ‘the old Russell is to be defended against the new Russell’ by advocating ‘modified realism’ for logic; for example, disjunction ‘is logical because it can neither be successfully contradicted nor shown to involve self-contradiction’, while definite descriptions and classes were justified on the grounds that ‘real existence means possibility of actualization, expressed in propositional functions’ (1944a, 158–159, 161). Defending his current position, Russell merely stressed preferring ‘minimum vocabularies’ in formal systems (1944b, 687).
Logicism was reviewed by Gödel, then in his late thirties, in an article which has become well known in its own right. Like Quine on Whitehead, he noted the imprecisions of PM, ‘in this respect a considerable step backwards as compared with Frege’ (1944a, 126), and he deployed metatheory thereafter. Focusing upon the vicious circle principle, he pondered various senses of ‘applied to itself, and found that when applied to itself a contradiction arises; so he concluded that it was false (pp. 132–133: we saw Behmann’s priority in §9.3.4). The Platonist in Gödel emerged in doubting the location of logicism in the extensional logic of the second edition of PM (pp. 143–146); he also pointed out that the reconstruction of mathematical induction effected there (§8.4.4) was unsuccessful. Curiously, he did not drive home the consequences for PM of his theorem (p. 139). As usual, he struggled to produce the final version of his contribution (Dawson 1997a, 162–166), so it came to Schilpp too late for Russell to write a reply—a great pity.
The appearance of the volume in 1944 motivated Weyl 1946a to meditate in the American mathematical monthly on the relationship between mathematics and logic. In 1935 he had opposed the founding of the Association for Symbolic Logic, on the grounds that the subject was part of mathematics anyway;10 now he addressed Russell’s opposite view, that mathematics was part of logic. He reviewed the three main schools (including a detailed outline of type theory., and also his own position in Das Kontinuum (1918. (§8.7.7). While noting that the distinction between classes and predicates, so important to logicians, ‘leaves the mathematician cool’ (p. 268., he concluded (p. 279. that
we are less certain than ever about the ultimate foundations of (logic and. mathematics [...]we have our ‘crisis’. We have had it for nearly fifty years. Outwardly it does not seem to hamper our daily work, and yet I for one confess that it has had a considerable practical influence on my mathematical life [...].
10.3 THE PANOPLY OF FOUNDATIONS
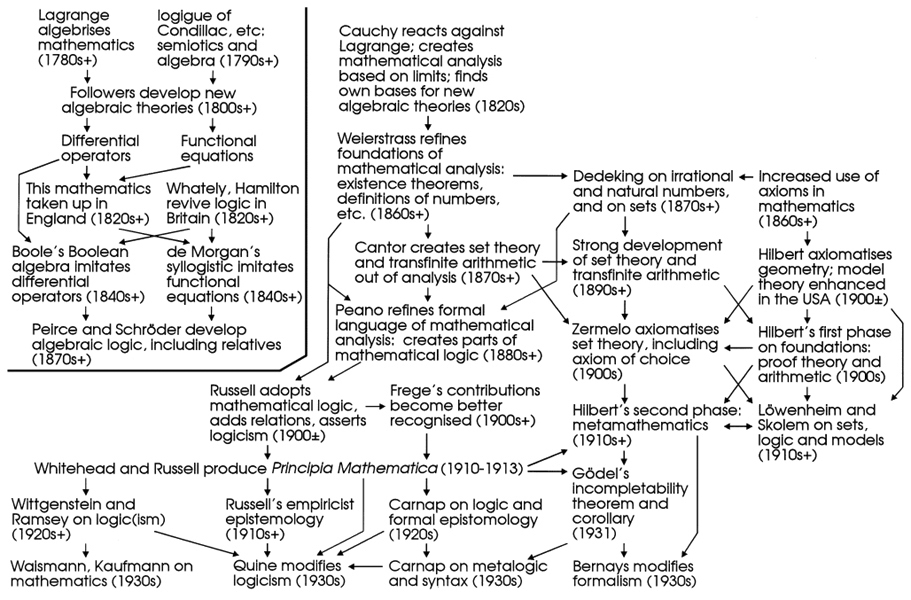
Figure 103.1 is a summary flow-chart for the principal and largely positive influences of branches of mathematics upon algebraic logic, mathematical logic, formalism with model theory, and axiomatic set theory. The emphasis on influence means that achievements which did not make much impact for some time are omitted (principally Bolzano, the Grassmanns and Frege’s creative phase). The main traditions or schools left out are intuitionism, phenomenology, Polish logic (too varied in range to be captured here., and (neo-)Kantian philosophies. The thick black line separating algebraic and mathematical logics largely concerns the predicate calculi and theories of collections; in other respects, such as the propositional calculi, there was more common ground.
Also not explicitly indicated are national differences. Having created most of the elements of algebraic logic, Britain showed some interest in the mathematical version in the new century. But much suspicion of symbolic logics remained (my 1986c.; for example, J. S. Mill (§2.5.8. and the neo-Hegelian tradition were taught at Oxford University until after the Second World War. The U.S.A. was far more sympathetic, as we have just seen. German mathematics and philosophy were both concerned with foundations, especially via axioms or assumptions; but mathematicians preferred formalism and/or axiomatic set theory, while many philosophers maintained the (neo-)Kantian or phenomenological traditions, which involved factors such as intuition and judgement which logicism hoped to avoid or re-interpret. The VC became an important force in Central Europe and to some extent in Britain, and then in the U.S.A. after emigration of key members; so logic and Russellian epistemology gained considerable currency there. Poland rapidly became an important country after its creation in 1920, and PM was a major source for Lesniewski and Chwistek, and quite significant for Łukasiewicz and Tarski. France was hostile and then mildly interested, but Italian vigour was located almost entirely with the Peanists. None of these interests seems to manifest nationalism, although the growth of Polish logic with its new country is striking.
Among the philosophies, intuitionism created much publicity in various countries but gained few converts; however, one was Weyl. As he judged above, the search for mathematical roots had not produced any internationally accepted position. One reason was the continuing failure to find a definitive solution (or Solution) of the paradoxes of logic and set theory; for at least some of them should fall within any philosophy of mathematics.11 Similarly, the concern with form persisted from De Morgan’s distinction of form from matter (§2.4.4) through Russell’s attempt to define mathematical logic as ‘the study of forms of complexes’ (§8.2.4) to Carnap’s structuralisms (§8.9.3, §9.3.2) and Stebbing on ‘the ideal of form’ (§9.5.1); but no version was definitive even for bivalent logic. Again, De Morgan also pioneered the logic of relations, which both traditions developed considerably; but it cannot carry a philosophy of mathematics on its own.
Weyl’s judgement is still valid: the following half century has still not produced a victor. On the contrary, many more logics have been developed (Mangione and Bozzi 1993a); and variant or new philosophies of mathematics have appeared (Tymoczko 1986a), including anti-foundationalism, which incidentally Neurath pioneered from the 1920s for the philosophy of science. The variety of these developments underlined an observation made long before by Condillac in his Logique (§2.2.7) that ‘the study of a well-treated science is reduced to the study of a well-made language’ (1780a, pt. 2, ch. 9); for the science of logic needed self-study—Sheffer’s predicament, from which hierarchies rescue the enlightened.
In the same spirit of pluralities, the writing of this book was inspired by the historical importance of the matters described, especially for their lovely mixture of logic, mathematics, set theory and philosophy. No philosophical defence of either logicism or logical positivism is offered or intended; for, if done properly, history is metatheoretic, looking at the situations of its historical figures and of the past without having to affirm or deny any stance found there.
The place of symbolic logic in mathematics and philosophy may be broadly described as follows. Algebraic logic came from a readiness in mathematics to entertain new algebras; it gave back especially Boole’s algebra of logic, a sophisticated logic of relations with quantification based upon part-whole theory, and Schröder’s logicising catalogue of mathematical theories. Mathematical logic grew out of the desire in mathematical analysis for rigour, and came back with a sophisticated logic of predicates and relations with quantification based upon set theory, and a detailed method of framing definitions and working out proofs. It also took Cantor’s vision of Mengenlehre as a foundation for mathematics, and handed back a detailed logicistic exposition of the links between set theory, finite and transfinite arithmetic, and some mathematical analysis and geometry. But it also led to surprising news about the limitations of axiomatisation with Gödel’s theorem and corollary.
Both traditions took from logic and philosophy a long concern with valid and invalid arguments, and came back with clear indications of the limitation of syllogistic logic. They also provided new insights about the connection between relations (including predicates) and collections, part-whole theory in one case, set theory in the other. Eventually mathematical logic helped to give to philosophy the centrality of the distinction between theory and metatheory—its most precious gift to knowledge of this century. But it also warned about the central place of paradoxes of various kinds, and failed to provide a definitive solution of them.
In this general context, Russell’s aspirations show one main negative and one main feature. Both are independent of Gödel’s incompletability theorem while reinforced by it:
–)A leading motivation for Russell’s logic and philosophy, but also a source of his difficulties, was his quest for certainty in (mathematical) knowledge. But maybe he was mistaken to ground fairly clear objects like 1, 2 and even (
0 + 371) in the uncertainty of classes, especially when he found paradoxes at their centre. His search for the logicist roots of mathematics was unsuccessful; moreover, the logical roots which he proffered were enigmatic. Logic(s) and mathematics are overlapping disciplines, with (axiomatic) set theory in the intersection, where the Peanists had (unclearly) located it. Hence logicism founders: logic may clothe the body mathematic, but it cannot provide the body itself, at least not all of its many limbs. Not only is there far more to logic than mathematics (as a logicist would affirm), but also there is far more to mathematics than logic, even the mathematical brand. Mathematics exhibits an amazing range of interconnections within and between its branches, and some of them inspire quite large-scale reductions, among which PM was one of the most extensive. But even there most mathematics ‘gets away’; many links, yes, but no unifier of the whole lot.
+) While PM failed in its main objective, theories were developed and insights made in the prosecution of this great enterprise which endured long after the original vision had become clouded. In Russell’s hands it also inspired an influential tradition in empiricist epistemology. All the traditions and schools described in this book greatly deepened understanding of the (meta-)theoretic questions posed; by 1940 the foundations of mathematics enjoyed a far richer range of treatments than ever before, and the searches of Whitehead and of Russell had played major roles in the progress.
10.4 SALLIES
It was long before I got the maxim, that in reading an old mathematician you will not read his riddle unless you plough with his heifer; you must see with his light, if you want to know how much he saw.
De Morgan to W. R. Hamilton, 1853 (Graves 1889a, 438)
Symbolic logic [...] has been dismissed by many logicians on the plea that its interest is mathematical, and by many mathematicians on the plea that its interest is logical.
Whitehead 1898a, vi
[...] philosophers subsequent to Kant, in writing on mathematics, have thought it unnecessary to become acquainted with the subject they were discussing, and have therefore left to the painful and often crude efforts of mathematicians every genuine advance in mathematical philosophy.
Russell, close of 1900a
Accordingly, we can say that the algebra of logic is a mathematical logic by its form and by its method, but it must not be mistaken for the logic of mathematics.
Couturat, close of 1905a
Historians whose purpose is simply to understand the meaning and drift of mathematics will do better to leave [Principia mathematica] alone.
Sarton 1936a, 54