1.1 Four generations of the Sierpiński triangle evolution3
1.2 Convex and concave functions11
2.1 Complete graphs K
4 and K
5
20
2.2 Arc betweenness22
2.3 Network motifs23
2.4 Closing in on the target27
2.5 Regular lattice with N = 16 and k = 428
2.6 Commellas and Sampels first construction for N = 6 and k = 431
2.7 Preferential attachment35
2.8 IP alias resolution38
2.9 ATM cloud38
3.1 Length of the coast of Britain44
3.2 Three generations of the Cantor set46
3.3 IFS for the Sierpiński triangle52
3.4 Another IFS for the Sierpiński triangle53
3.5 The L
1, L
2, and L
∞ metrics55
3.6 Illustration of Hausdorff distance56
4.1 A set that is open, and a set that is not open63
4.2 Covering of a square by six open sets64
4.3 Line segment has d
T = 165
4.4 Topological dimension of a square65
4.5 Covering a square by 4 sets66
4.6 Box counting for a line and for a square67
4.7 3E boxes cover the set69
4.8 Starfish box counting71
4.9 Six iterations of the Hilbert curve73
4.10 Two generations of the Sierpiński carpet74
4.11 Randomized Sierpiński carpet75
4.12 Cantor dust76
4.13 Minkowski sausage in two dimensions79
4.14 astrocytes82
5.1 Self-similarity with K = 8 and α = 1∕490
5.2 Three generations of a self-similar fractal90
5.3 Sierpiński triangle95
5.4 The Open Set Condition for the Sierpiński gasket95
5.5 Sinuosity generator 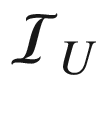 based on the Koch fractal96
based on the Koch fractal96
5.6 Topology generator 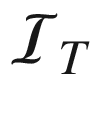 97
97
5.7 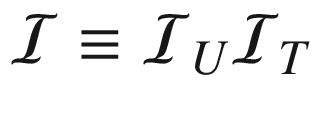 applied to a straight line initiator97
applied to a straight line initiator97
5.8 IFS for goose down98
5.9 Packing the diamond region with four balls100
5.10 Packing a square with long skinny rectangles100
5.11 Constructing the Lévy curve104
5.12 The Lévy curve after 12 iterations105
5.13 Pythagoras tree after 15 iterations105
6.1 Maximal box size for the Sierpiński carpet110
6.2 s
max is reached when B(s
max) = 1110
6.3 Python code for binary search114
6.4 % error in s
min for N = 1000 and 𝜖 = 0.001, for 1 ≤ d
B ≤ 2114
6.5 s
min for N = 1000 and for three values of 𝜖, for 1 ≤ d
B ≤ 2115
6.6 Coarse-grained and fine-grained images of clover116
6.7 Spiral (left) and spiral and line (right)119
6.8 Spiral radius for J = 4120
6.9 Clothoid double spiral122
7.1 A node 3-covering (i) and an arc 3-covering (ii)133
7.2 Arc s-coverings for s = 2, 3, 4134
7.3 A node covering which is not an arc covering134
7.4 An arc covering which is not a node covering134
7.5 Comparing B
N(2) and B
A(2)135
7.6 Optimal B
D (3) box (left), and optimal B
D (5) and B
D (7) boxes (right)136
7.7 Diameter-based versus radius-based boxes137
7.8 Frequent associations among 62 dolphins138
7.9 Node degrees for the dolphins network139
7.10 Diameter-based box counting results for the dolphins network139
7.11 Chain network140
7.12 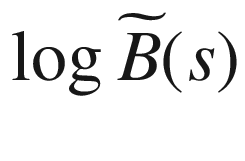 versus
versus 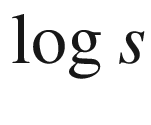 using wide boxes140
using wide boxes140
7.13 Radius-based box141
7.14 Covering a 6 × 6 grid142
7.15 Fractal versus non-fractal scaling143
8.1 Example network for node coloring146
8.2 (i) Auxiliary graph with s=3, and (ii) its coloring146
8.3 Minimal covering for s = 3147
8.4 (i) Auxiliary graph with s=4, and (ii) minimalcovering for s=4147
8.5 A weighted network148
8.6 Auxiliary graph for box size s
1 = 0.85149
8.7 Two boxes are required for box size s
1
149
8.8 USAir97 network150
8.9 Random Sequential Node Burning
151
8.10 Covering using Random Sequential Node Burning
152
8.11 Random Sequential Node Burning applied to a hub and spoke network153
8.12 Double ring hub and spoke network153
8.13 Network with 7 nodes and 8 arcs154
8.14 Maximum Excluded Mass Burning
156
8.15 Box Burning
157
8.16 Network for illustrating box burning158
8.17 Box burning 2-covering and a minimal 2-covering158
8.18 Disconnected boxes in a minimal covering159
8.19 Compact Box Burning
160
8.20 Adjacent nodes only connected through a hub162
8.21 Overlapping boxes163
8.22 Example network with 7 nodes and 8 arcs166
8.23 Increasing u
i to 1 blocks other dual variable increases169
8.24 Results of applying Dual Ascent to Zachary’s Karate Club network169
8.25 Closing nodes in Zachary’s Karate Club network172
8.26 Linear program results for Lada Adamic’s social network
174
8.27 BCLP is infeasible for C. elegans
174
10.1 Embedding dimension202
10.2 Packing of powder particles207
10.3 Radius of gyration216
11.1 1-dimensional grid with 8 nodes224
11.2 1-dimensional grid with K = 100225
11.3 Three examples of a Voronoi tessellation229
11.4 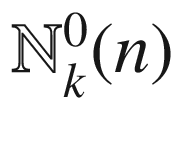 for k = 0, 1, 2231
for k = 0, 1, 2231
11.5 A hub and spoke network233
11.6 Non-truncated and truncated boxes in a 2-dimensional grid235
11.7 Neighbors in a 6 × 6 grid236
11.8 Correlation dimension of K × K grid versus K
239
11.9 Correlation dimension of K × K × K grid versus log10K
242
11.10 Triangulated hexagon243
12.1 Constructing 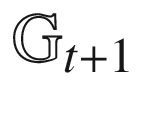 from
from 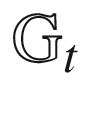 249
249
12.2 Three generations with p = 1250
12.3 Three generations with p = 0250
12.4 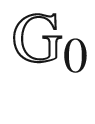 and
and 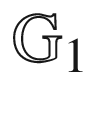 for x = 2 and m = 3252
for x = 2 and m = 3252
12.5 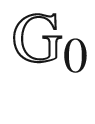 and
and 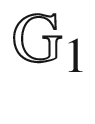 and
and 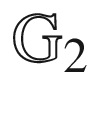 for α = 0 and x = 2 and m = 2253
for α = 0 and x = 2 and m = 2253
12.6 Three generations of a (1, 3)-flower254
12.7 Construction of a conical graph for which d
V(n
⋆) = 5∕3263
13.1 A network (i) and two ways to interconnect K copies (ii)268
13.2 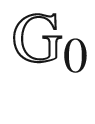 has four border nodes268
has four border nodes268
13.3 Constructing 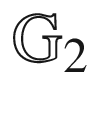 from
from 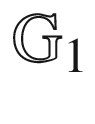 269
269
13.4 Generating a network from the Maltese cross fractal270
13.5 A network satisfying Assumption 13.2 but not Assumption 13.3272
13.6 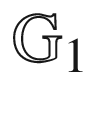 and
and 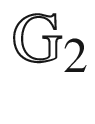 for a chain network273
for a chain network273
13.7 Another example of 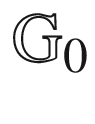 and
and 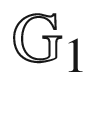 274
274
13.8 Ω
0 and 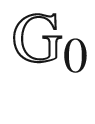 for the Maltese cross274
for the Maltese cross274
13.9 Two invalid choices of Ω
0
275
13.10 Example for which 2R
0 + 1≠1∕α
275
13.11 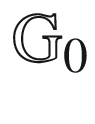 has no center node277
has no center node277
13.12 Network generator 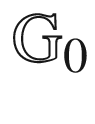 (left) and
(left) and 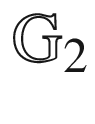 (right)278
(right)278
14.1 Shannon entropy for the distribution (p, 1 − p)282
14.2 Farmer’s shades of grey example290
14.3 H
q versus q for four values of p
298
15.1 Networks (i) and (ii)308
15.2 Networks (iii) and (iv)308
15.3 Hub and spoke with a tail network314
15.4 Coverings for K = 6, for s = 3 and s = 5314
15.5 Results for the hub and spoke with a tail network316
15.6 Three hubs connected to a superhub316
15.7 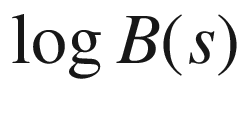 and H(s) for the hub and spoke with a tail network317
and H(s) for the hub and spoke with a tail network317
15.8 Network for which d
I > d
B: minimal coverings for s = 2 and s = 3318
15.9 Maximal entropy minimal 3-covering319
15.10 Erdős–Rényi network320
15.11 Results for the Erdős–Rényi network321
15.12 Results for the jazz network322
15.13 Results for Lada Adamic’s social network
322
15.14 Communications network323
15.15 Results for the communications network323
16.1 Two generations in a multifractal construction326
16.2 Generation 1 of the multifractal Cantor set327
16.3 Four generations of the multifractal Cantor set for p
1 = 0.2328
16.4 Logarithm of generation 4 probabilities for p
1 = 0.2329
16.5 Generalized dimensions of the multifractal Cantor set332
16.6 f
q versus p
1 for the multifractal Cantor set336
16.7 f(α) spectrum for the multifractal Cantor set337
16.8 Geometry of the Legendre transform of f(α)344
16.9 The six points in the unit square349
16.10 Specifying to which box the boundaries belong350
16.11 Nine points covered by two boxes354
16.12 Two generations of the Tél-Viscek multifractal359
17.1 Two minimal 3-coverings and a minimal 2-covering for the chair network367
17.2 D
∞ for three networks372
17.3 Two plots of the generalized dimensions of the chair network374
17.4 Box counting and 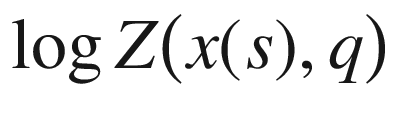 versus
versus 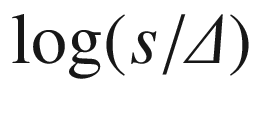 for the dolphins network375
for the dolphins network375
17.5 Secant estimate of D
q for the dolphins network for different L and U
376
17.6 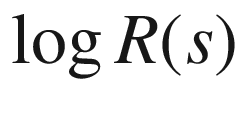 versus
versus 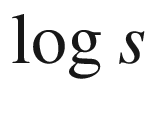 for the dolphins network381
for the dolphins network381
17.7 jazz box counting (left) and D
q versus q for variousL, U (right)381
17.8 Local minimum and maximum of D
q for the jazz network and L = 4, U = 5382
17.9 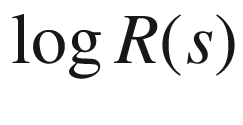 versus
versus 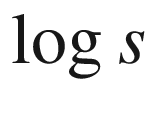 for the jazz network382
for the jazz network382
17.10 C. elegans box counting (left) and D
q(L, U) versus q for various L, U (right)382
17.11 Generation-1 (left) and generation-2 (right) rectangles and their probabilities384
17.12 The second generation probabilities 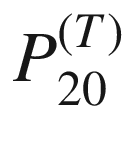 385
385
18.1 Two minimal 3-coverings of a 7 node chain394
18.2 chair network (left) and d
H calculation (right)397
18.3 Two 7 node networks with the same d
B but different d
H
397
18.4 Box counting results for s = 2 (left) and s = 3 (right)398
18.5 Box of radius r = 1 in a 6 × 6 rectilinear grid399
18.6 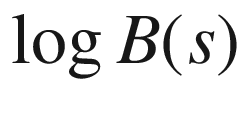 versus
versus 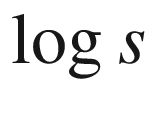 for the dolphins network400
for the dolphins network400
18.7 B(s)[s∕(Δ + 1)]d versus d for  (left) and
(left) and 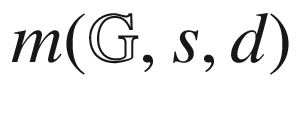 versus d (right) for dolphins
400
versus d (right) for dolphins
400
18.8 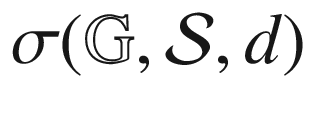 versus d for dolphins for d ∈ [0, 3] (left) and d ∈ [2.26, 2.40] (right)401
versus d for dolphins for d ∈ [0, 3] (left) and d ∈ [2.26, 2.40] (right)401
18.9 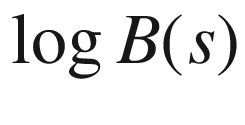 versus
versus 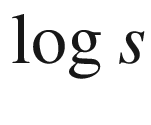 for the USAir97 network402
for the USAir97 network402
18.10 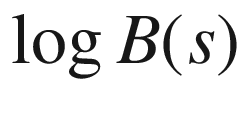 versus
versus 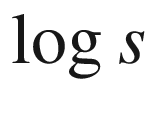 (left) and
(left) and 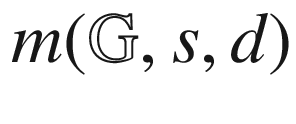 versus d (right) for the jazz network402
versus d (right) for the jazz network402
18.11 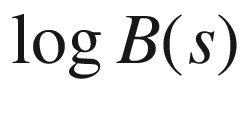 versus
versus 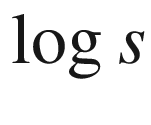 (left) and
(left) and 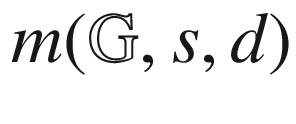 versus d (right) for the C. elegans network403
versus d (right) for the C. elegans network403
18.12 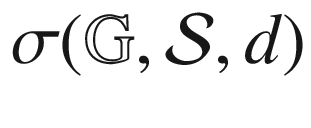 versus d for C. elegans for d ∈ [0, 5] (left) and d ∈ [2.26, 2.40] (right)404
versus d for C. elegans for d ∈ [0, 5] (left) and d ∈ [2.26, 2.40] (right)404
18.13 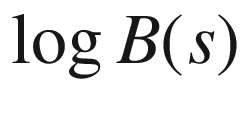 versus
versus 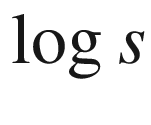 for s ∈ [4, 14] for the protein network404
for s ∈ [4, 14] for the protein network404
18.14 Summary of d
B and d
H computations405
18.15 Perturbations of the jazz network406
18.16 d
B and d
H of a network growing with preferential attachment406
18.17 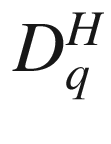 versus q for the network
versus q for the network  of Fig. 18.3409
of Fig. 18.3409
18.18 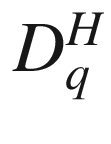 versus q for the dolphins network409
versus q for the dolphins network409
18.19 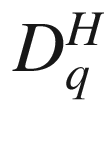 versus q for the jazz network410
versus q for the jazz network410
18.20 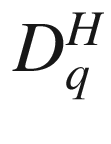 versus q for the C. elegans network410
versus q for the C. elegans network410
19.1 Cantor dust lacunarity414
19.2 Lacunarity for a Cantor set414
19.3 Gliding box method for the top row416
19.4 Gliding box example continued416
19.5 Three degrees of lacunarity417
19.6 Lacunarity with three hierarchy levels418
19.7 A covering of Ω by balls420
19.8 Ω is partitioned into 16 identical smaller pieces424
20.1 Lyapunov numbers427
20.2 F maps a square to a parallelogram428
20.3 Cell structure432
21.1 Kadanoff’s block renormalization441
21.2 Renormalizing the small-world model for k = 1443
21.3 Two-site scaling446
21.4 Two different minimal 3-coverings of the same network447
21.5 Procedure Network Renormalization
447
21.6 Network renormalization with diameter-based boxes448
22.1 Horton’s ordering of streams455
22.2 Metric dimension example458
22.3 Tetrahedron and cube460
22.4 Wheel network and complete bicolored graph460
22.5 Computing 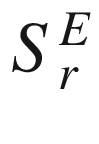 by summing over cross sections463
by summing over cross sections463
22.6 Two-dimensional triangular lattice  465
465
22.7 A finite graph  embedded in
embedded in  466
466
22.8 1-dimensional (left) and 2-dimensional (right) graphs466
22.9 A tree whose nodes have degree 1 or 3469
23.1 Rectifiable Arc472
23.2 Computing the length of a rectifiable arc472
23.3 A differentiable convex function lies above each tangent line477
23.4 Two supporting hyperplanes of a convex function477
23.5 The Legendre transform G of F
478
23.6 The conjugate F
⋆ of F
479
23.7 Small network to illustrate Hall’s method481
23.8 Small hub and spoke network483
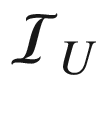 based on the Koch fractal96
based on the Koch fractal96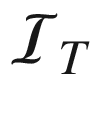 97
97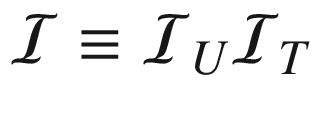 applied to a straight line initiator97
applied to a straight line initiator97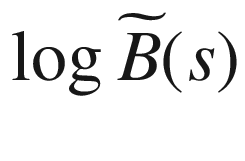 versus
versus 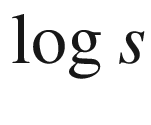 using wide boxes140
using wide boxes140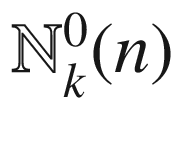 for k = 0, 1, 2231
for k = 0, 1, 2231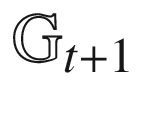 from
from 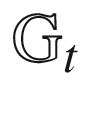 249
249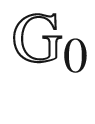 and
and 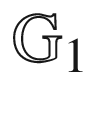 for x = 2 and m = 3252
for x = 2 and m = 3252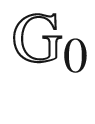 and
and 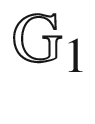 and
and 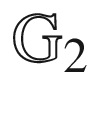 for α = 0 and x = 2 and m = 2253
for α = 0 and x = 2 and m = 2253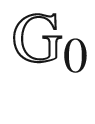 has four border nodes268
has four border nodes268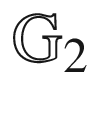 from
from 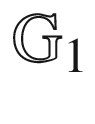 269
269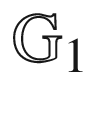 and
and 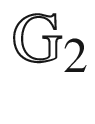 for a chain network273
for a chain network273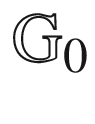 and
and 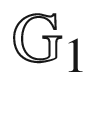 274
274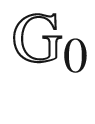 for the Maltese cross274
for the Maltese cross274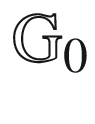 has no center node277
has no center node277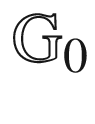 (left) and
(left) and 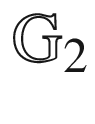 (right)278
(right)278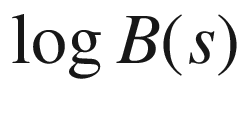 and H(s) for the hub and spoke with a tail network317
and H(s) for the hub and spoke with a tail network317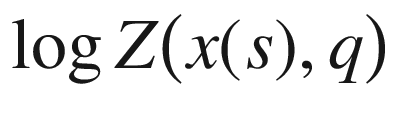 versus
versus 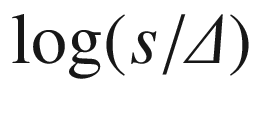 for the dolphins network375
for the dolphins network375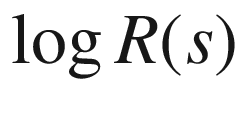 versus
versus 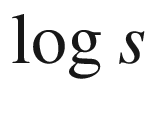 for the dolphins network381
for the dolphins network381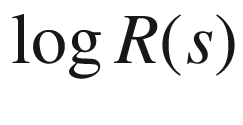 versus
versus 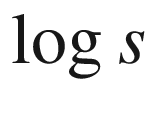 for the jazz network382
for the jazz network382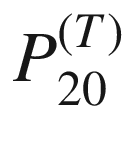 385
385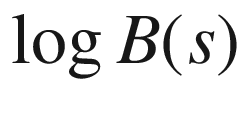 versus
versus 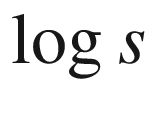 for the dolphins network400
for the dolphins network400 (left) and
(left) and  versus d (right) for dolphins
400
versus d (right) for dolphins
400 versus d for dolphins for d ∈ [0, 3] (left) and d ∈ [2.26, 2.40] (right)401
versus d for dolphins for d ∈ [0, 3] (left) and d ∈ [2.26, 2.40] (right)401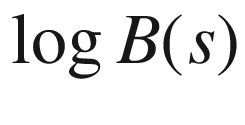 versus
versus 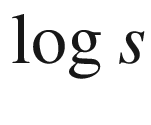 for the USAir97 network402
for the USAir97 network402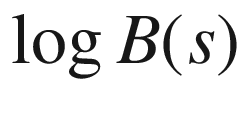 versus
versus 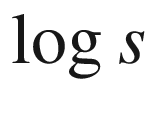 (left) and
(left) and 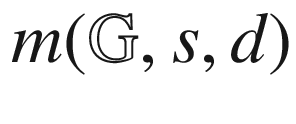 versus d (right) for the jazz network402
versus d (right) for the jazz network402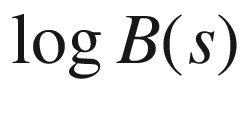 versus
versus 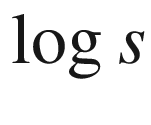 (left) and
(left) and  versus d (right) for the C. elegans network403
versus d (right) for the C. elegans network403 versus d for C. elegans for d ∈ [0, 5] (left) and d ∈ [2.26, 2.40] (right)404
versus d for C. elegans for d ∈ [0, 5] (left) and d ∈ [2.26, 2.40] (right)404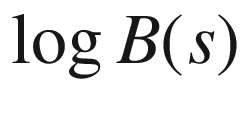 versus
versus 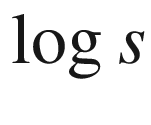 for s ∈ [4, 14] for the protein network404
for s ∈ [4, 14] for the protein network404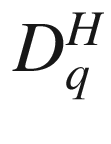 versus q for the network
versus q for the network  of Fig. 18.3409
of Fig. 18.3409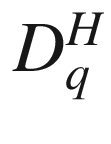 versus q for the dolphins network409
versus q for the dolphins network409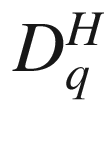 versus q for the jazz network410
versus q for the jazz network410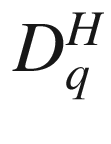 versus q for the C. elegans network410
versus q for the C. elegans network410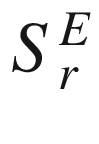 by summing over cross sections463
by summing over cross sections463 465
465 embedded in
embedded in  466
466