Preface

There has been a strong resurgence of interest in the fractional calculus over the last two or three decades. This expansion of the classical calculus to derivatives and integrals of fractional order has given rise to the hope of a new understanding of the behavior of the physical world. The hope is that problems that have resisted solution by the integer-order calculus will yield to this greatly expanded capability. As a result of our work in the fractional calculus, and more particularly, in functions for the solutions of fractional differential equations, an interest was fostered in the behavior of generalized exponential functions for this application. Our work with the fundamental fractional differential equation had developed a function we named the F-function. This function, which had previously been mentioned in a footnote by Oldham and Spanier, acts as the fractional exponential function. It was a natural step from there to an interest in a fractional trigonometry. At that time, only a few pages of work were available in the literature and were based on the Mittag-Leffler function. These are shown in Appendix A.

This book brings together our research in this area over the past 15 years and adds much new unpublished material.

The classical trigonometry plays a very important role relative to the integer-order calculus; that is, it, together with the common exponential function, provides solutions for linear differential equations. We will find that the fractional trigonometry plays an analogous role relative to the fractional calculus by providing solutions to linear fractional differential equations. The importance of the classical trigonometry goes far beyond the solutions of triangles. Its use in Fourier integrals, Fourier series, signal processing, harmonic analysis, and more provided great motivation for the development of a fractional trigonometry to expand application to the fractional calculus domain.

Because we are engineers, this book has been written in the style of the engineering mathematical books rather than the more rigorous and compact style of definition, theorem, and proof, found in most mathematical texts. We, of course, have made every effort to assure the derivations to be correct and are hopeful that the style has made the material accessible to a larger audience. We are also hopeful that this will not detract the interest of the mathematical community in the area since their skills will be needed to develop this important new area. Most of the materials of this book should be accessible to an undergraduate student with a background in Laplace transforms.

After an introductory chapter, which offers a brief insight into the fractional calculus, the book is organized in two major parts. In Chapters 2–11, the definitions and theory of the fractional exponential and the fractional trigonometry are developed. Chapters 12–19 provide insight into various areas of potential application.

Chapter 2 develops the F-function from consideration of the fundamental fractional differential equation. It generalizes the common exponential function for application in the fractional calculus. The F-function, the fractional eigenfunction, together with its generalization, the R-function (Chapter 3), will later form the theoretical basis of the fractional trigonometry. Properties of these functions are developed in these two chapters. Their relationship to other functions for the fractional calculus is presented. An important characteristic of the R-function is that it contains the F-function as a special case and also contains its derivatives and integrals. In later chapters, it is shown that many of the newly defined fractional trigonometric functions inherit this important property. Chapter 4 further develops properties of the R-function that expose the character of this fractional exponential function.

In Chapter 5, the R-function, 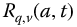, with real arguments for a and t, is used to define the fractional hyperbolic functions. These functions generalize the classical hyperbolic functions. Fractional exponential forms of the hyperbolic functions are derived as well as their Laplace transforms. Furthermore, fractional differintegrals of the functions are determined. An example demonstrates the use of the Laplace transform in the solution of fractional hyperbolic differential equations. The fractional hyperbolic functions are found to be closely related to the R₁-trigonometric functions defined in Chapter 6.

Chapters 6–8 present three fractional trigonometries. We have tried to make each of these chapters as stand-alone developments, at the expense of minor repetition. Chapter 6 develops the R₁-trigonometry. It is based on the R-function with imaginary parameter a, namely 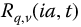. Multiplication of the parameter by i toggles the R₁-hyperbolic functions to the R₁-trigonometric functions, and so on.

A fractional trigonometry, the R₂-trigonometry based on an imaginary time variable, 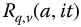, is developed in Chapter 7. It is found that these functions are characterized by their attraction to circles when plotted in phase plane format.

The obvious extension of these two trigonometries, the R₃-trigonometry of Chapter 8, sets both the a parameter and the t variable to be imaginary, 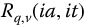. It was thought at the time that this trigonometry would behave as an hyperbolic analog to the R₂-trigonometry. However, such simple relationships between the two were not found.

Chapter 9 presents the heart of the fractional trigonometry, namely the fractional meta-trigonometry. Here, both a and t are allowed to be fully complex, by choosing as the basis . This chapter generalizes the results of the previous four chapters. Laplace transforms for the generalized functions are determined along with their fractional differintegrals. Fractional exponential forms for the functions are also determined.

In Chapter 10, the ratio and reciprocal functions associated with the generalized fractional sines and cosines of Chapter 9, that is, 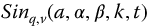and 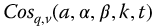, as well as the generalized parity functions are considered. The parity functions represent a new set of fractional trigonometric functions with no counterpart in the classical trigonometry. Because of the large number of possible ratio and reciprocal functions, the treatment in this chapter is cursory.

Because of the newness of this material, we have tried to be generous with the graphic forms of the functions. In spite of this attitude, we have found that because of different behavior over various domains of the functions and the number of parameters in the functions that complete coverage in this regard to be impossible and the reader is encouraged to program some of the functions and to experiment for themselves.

In Chapter 3, two new functions, the G- and H-functions, are introduced. These functions are generalizations of the R-function with multiple real and complex roots in the denominators of their Laplace transforms. Because of the great generality of these functions, consideration of these functions as the basis for further generalization of the fractional trigonometry is discussed in Chapter 11. In Chapter 12, these functions are needed for the solution of linear fractional differential equations with repeated roots.

Part II of the book is largely dedicated to applications and potential application of the fractional trigonometry.

The most important application is the use of the fractional trigonometry for the solution of linear constant-coefficient commensurate-order fractional differential equations. In Chapter 12, specialized Laplace transforms for the meta-trigonometric functions are developed and applied to the solution of these linear fractional differential equations. Examples showing the solution of fractional differential equations with unrepeated roots and with repeated real and complex roots are given.

Chapter 13 studies the time- and frequency-domain responses for linear fractional systems based on the R-function and the meta-trigonometric functions. The stability of the basic fractional elements is also considered.

Unlike the classical trigonometric functions, the fractional counterparts do not generally share the periodicity property. As a practical result, we are limited to evaluation of the defining infinite series for function evaluation. This presents numerical difficulties as the time and/or order variables increase. Chapter 14 discusses this problem and establishes series convergence.

Phase plane plots of pairs of the fractional trigonometric functions define a new and unique family of spirals, the fractional spirals. Chapter 15 studies these spirals and their relationship to some of the classical spirals.

Linear oscillators are often used in the study of ordinary differential equations and in the modeling of physical systems. Chapter 16 identifies those linear fractional trigonometric oscillators that are neutrally stable. This chapter also explores possible application of coupled fractional trigonometric oscillators.

Chapters 17–19 study the possible application of the fractional spirals and thus the fractional trigonometry and fractional differential equations. The potential applications include sea shell growth and morphology, mathematical classification of spiral galaxy morphology, and various weather phenomena such as hurricanes and tornados.

Finally, Chapter 20 looks at some of the many remaining challenges and opportunities relative to the fractional exponential function and the fractional trigonometry, in particular, the need for a fractional field equation as it relates to spatial fractional spiral morphology.

For the professional with a background in the fractional calculus, a quick coverage of the essence of the book may be had from Chapters 2, 3, 9, and 12, with selected attention to the applications of interest contained in Chapters 15–19.

Carl F. Lorenzo
Tom T. Hartley
Cleveland OH,
July 2016