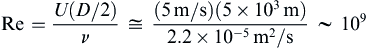Chapter 13

Geophysical Fluid Dynamics

Abstract

Geophysical fluid dynamics deals with flows of air and water in the atmosphere and ocean. Here fluid velocities are subsonic, the medium is stratified, and the rotation rate of the earth is important. The latter two phenomena suppress vertical motions so horizontal velocities predominate, especially at large scales, even when the flow is turbulent. In fact, the length scales of the motion are often so large that the advective acceleration is small compared to the Coriolis acceleration (small Rossby number), and the fluid's horizontal velocity is perpendicular (not parallel) to the horizontal pressure gradient. Near surfaces where friction is important, the direction of the flow in a boundary layer depends on the distance from the surface. Coriolis effects also cause surface-wave motions to include particle deflections in both horizontal directions, and for surface waves to be trapped near vertical boundaries. Coriolis effects modify internal waves, too. At even larger scales where the curvature of the earth leads to nontrivial variations in the Coriolis frequency, Rossby waves spanning a significant range of latitude may be subject to barotropic and/or baroclinc instabilities.

Keywords

Coriolis acceleration; Stratification; Buoyancy frequency; Boussinesq approximation; Geostrophic flow; Ekman layer; Gravity waves; Kelvin waves; Potential vorticity; Internal waves; Rossby waves; Barotropic instability; Baroclinic instability; Geostrophic turbulence
Chapter Objectives

13.1. Introduction

Together the atmosphere and ocean have a large and consequential impact on humanity. The combined dynamics of the atmosphere and ocean are leading contributors to global climate. We all live within the atmosphere and are almost helplessly affected by the weather and its rather chaotic behavior that modulates agricultural success. Ocean currents effect navigation, fisheries, and pollution disposal. Populations that occupy coastlines can do little to prevent hurricanes, typhoons, or tsunamis. Thus, understanding and reliably predicting geophysical fluid dynamic events and trends are scientific, economic, humanitarian, and even political priorities. This chapter provides the basic elements necessary for developing an understanding of geophysical fluid dynamics.
The two features that distinguish geophysical fluid dynamics from other areas of fluid dynamics are the rotation of the earth and vertical density stratification of the media. These two effects dominate the dynamics to such an extent that entirely new classes of phenomena arise, which have no counterpart in the laboratory-scale flows emphasized in the preceding chapters. (For example, the dominant mode of flow in the atmosphere and the ocean is along the lines of constant pressure, not from high to low pressures.) The motion of the atmosphere and the ocean is naturally studied in a coordinate frame rotating with the earth. This gives rise to the Coriolis acceleration (see Section 4.7). The density stratification gives rise to buoyancy forces (Section 4.11 and Chapter 8). In addition, important relevant material includes vorticity, boundary layers, instability, and turbulence (Chapters 5, 10, 11, and 12). The reader should be familiar with these topics before proceeding further with the present chapter.
Because the Coriolis acceleration and fluid stratification play dominating roles in both the atmosphere and the ocean, there is a great deal of similarity between the dynamics of these two media; this makes it possible to study them together. There are also significant differences, however. For example the effects of lateral boundaries, due to the presence of continents, are important in the ocean but less so in the atmosphere. The intense currents (like the Gulf Stream and the Kuroshio) along the western ocean boundaries have no atmospheric analog. On the other hand phenomena like cloud formation and latent heat release due to moisture condensation are solely atmospheric phenomena. Plus, processes are generally slower in the ocean, in which a typical horizontal velocity is 0.1 m/s, although velocities of the order of 1–2 m/s are found within the intense western boundary currents. In contrast, typical velocities in the atmosphere are 10–20 m/s. The nomenclature can also be different in the two fields. Meteorologists refer to a flow directed to the west as an “easterly wind” (i.e., from the east), while oceanographers refer to such a flow as a “westward current.” Atmospheric scientists refer to vertical positions by heights measured upward from the earth’s surface, while oceanographers refer to depths measured downward from the sea surface. In this chapter, the vertical coordinate z increases upward, following the atmospheric science convention.
The rotational effects arising from the Coriolis acceleration have opposite signs in the two hemispheres. Note that all figures and descriptions given here are valid for the northern hemisphere. In some cases the sense of the rotational effect for the southern hemisphere has been explicitly mentioned. When the sense of the rotational effect is left unspecified for the southern hemisphere, it should be assumed as opposite to that in the northern hemisphere.
Example 13.1
Solution
For the thunderstorm, the Reynolds number should be computed using the radius of the rising column of air and a mid-troposphere (z ≈ 5 km) value of the kinematic viscosity since such storms may span the troposphere:

Re=U(D/2)ν≅(5m/s)(5×103m)2.2×10−5m2/s∼109

image

 
This is a free shear flow driven by buoyancy and it has some of the character of a buoyant plume, so at this high Reynolds number it is most-definitely turbulent.
For the water wave, the characteristic fluid velocity within the wave, ωA, is set by the wave's frequency from (8.28), ω2 = 2πg/λ, and the wave's amplitude A. This leads to:

Re=ωAλν=[2πg/λ]1/2Aλν=[2πgλ]1/2Aν=[2π(9.81m/s2)100m]1/2(4m)1.×10−6m2/s∼3×108.

image