Additional Answers and Solutions for
MATHEMATICS FOR THE NONMATHEMATICIAN
The following chapter contains the complete text of the Instructor’s Manual originally published for use with this work. It contains additional solutions and answers to the problems in the text.
PART I. PLANS OF COURSES BASED ON THIS TEXT
PART II. SUGGESTIONS FOR PRESENTING INDIVIDUAL CHAPTERS
PART III. SOLUTIONS AND ANSWERS
4. Number: the Fundamental Concept
5. Algebra, the Higher Arithmetic
6. The Nature and Uses of Euclidean Geometry
7. Charting the Earth and the Heavens
8. The Mathematical Order of Nature
10. Mathematics and Painting in the Renaissance
13. The Simplest Formulas in Action
14. Parametric Equations and Curvilinear Motion
15. The Application of Formulas to Gravitation
18. Trigonometric Functions and Oscillatory Motion
19. The Trigonometric Analysis of Musical Sounds
20. Non-Euclidean Geometries and Their Significance
21. Arithmetics and Their Algebras
22. The Statistical Approach to the Social and Biological Sciences
24. The Nature and Values of Mathematics
This text is addressed to liberal arts students and to other students who do not intend to major in mathematics or science. The audience then may consist of liberal arts students who take mathematics as part of their cultural preparation for work in the social sciences, the arts and the humanities; prospective elementary school teachers who should have a broader background on which to base their teaching of arithmetic and simpler facts of geometry; and prospective high school teachers in nonscientific subjects.
For the general liberal arts student and the prospective teacher a course based on the material as arranged in this text would seem to the author to be most suitable, for the book presents mathematics as an integral component of western culture. From a purely pedagogical standpoint, the presentation of mathematics as a development intimately involved with other branches of our culture may awaken interest in a subject which has failed notoriously to attract the nonscientist.
Even for a broad liberal arts mathematics course this text may contain more material than can be covered in the time allotted. However, many of the chapters as well as sections in chapters are not essential to the logical continuity. These chapters and sections have been starred. Thus Chapter 10 on painting shows historically how mathematicians were led to projective geometry (Chapter 11), but from a logical standpoint, Chapter 10 is not needed in order to understand the succeeding chapter. Chapter 19 on musical sounds is an application of the material on the trigonometric functions in Chapter 18 but is not essential to the continuity. The two chapters on the calculus are not used in the succeeding chapters. Desirable as it may be to give students some idea of what the calculus is about, it may still be necessary in some classes to omit these chapters. The same can be said of the chapters on statistics (Chapter 22) and probability (Chapter 23).
There is also the possibility of covering most or all of the chapters by omitting certain sections within chapters. Chapter 6 on Euclidean geometry may well serve as an illustration. The mathematical material of this chapter is intended as a review of some basic ideas and theorems of Euclidean geometry and as an introduction to the conic sections. Some of the familiar applications are given in Section 6-3 (see the Table of Contents) and probably should be taken up. However, the applications to light in Sections 6-4 and 6-6 and the discussion of cultural influences in Section 6-7 can be omitted.
Some of the material, whether or not included in the recommendations for particular groups, can be left to student reading. In fact, the first two chapters were deliberately fashioned so that they could be read by students. The objective here, in addition to presenting intrinsically important ideas, was to induce students to read a mathematics book, to give them the confidence to do so, and to get them into the habit of doing so. It seems necessary to counter the students′ impression, resulting no doubt from elementary and high school instruction in mathematics, that whereas history texts are to be read, mathematics texts are essentially reference books for formulas and homework exercises.
For a one-semester liberal arts course, the basic content can be as follows:
on a historical orientation, |
|
on logic and mathematics, |
|
Chapters 4 and 5 |
on the number system and elementary algebra, |
through Section 6-5, on Euclidean geometry, |
|
through Section 7-3, on trigonometry, |
|
on coordinate geometry, |
|
on functions and their uses, |
|
through Section 14-4, on parametric equations, |
|
through Section 15-10, on the further use of functions in science, |
|
on non-Euclidean geometry, |
|
on different algebras. |
Any additional material would enrich the course but would not be needed for continuity.
Colleges concerned primarily with the training of prospective elementary school teachers may feel that they must give preference to topics that these students will soon be obliged to teach. It is possible to choose material that will meet such objectives.
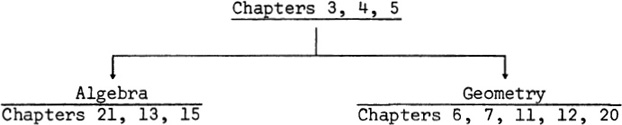
For courses emphasizing the number concept and its extension to algebra, one can take advantage of the logical independence of numerous chapters and use Chapters 3 through 5 on reasoning, arithmetic, and algebra and Chapter 21 on different algebras. To pursue the development of this theme into the area of functions one can include Chapters 13 and 15.
Courses emphasizing geometry can utilize Chapters 6, 7, 11, 12, and 20 on Euclidean geometry, trigonometry, projective geometry, coordinate geometry, and non-Euclidean geometry respectively. Some algebra, that reviewed in Chapter 5, is involved in Chapters 7 and 12. If knowledge of the material of Chapter 5 cannot be presupposed, this chapter must precede the treatment of geometry.
The essence of the two preceding suggestions may be diagramed thus:
Of course, starred sections in these chapters are optional. If the essential material is covered, other chapters can, of course, be included.
There is rather little that one should teach, in the formal sense of teaching, of the contents of this chapter. The purpose of the chapter (and to a large extent of the next one) is to combat and hopefully eradicate dislike and fear of mathematics which many students have acquired in their elementary and high school experiences. By openly debating the question of whether mathematics is worth studying and by offering material that the student can read easily there is the possibility that he will find the approach at least disarming and perhaps refreshing and inviting.
Moreover, because he can read and understand the material he may be encouraged to tackle the later chapters with equal success and so overcome the psychological handicap which hinders many college students.
There is some effort to at least name the values of mathematics, the material benefits of mathematics to engineering, the value in aiding man to understand natural phenomena, the uses in the social sciences, the importance for philosophy as, for example, in finding truths, the uses in the arts of painting and music, and the values of mathematics proper. The latter are mathematics as an art and as an intellectual challenge. Puzzles are a good example of an intellectual challenge on a low level.
Though, as already noted, this chapter too may serve to encourage the student that he can master mathematics because he finds that he can read the material, there is more positive content to be advanced than in Chapter 1. The student should learn that mathematics was not created once and for all in some ancient time but that there have been successive periods of development and these have been tied to and stimulated by problems and movements of various civilizations. The civilizations which should be discussed are the Egyptian and Babylonian, the classical Greek, the Alexandrian Greek, the Roman, the Hindu and Arabic, the medieval, and Western European since about 1400. The Roman and medieval civilizations are singular because despite achievements in other areas, they were nonproductive in mathematics. These exceptional cases could provoke a discussion of what factors in a civilization promote mathematical activity. The question cannot be answered at this stage but students might be asked to keep this in mind and to note that the answer is important because it would tell us what we must do in our civilization to foster mathematics.
Though this chapter does emphasize that mathematics is distinguished from other fields by its insistence on deductive proof, the teacher should make sure that the students see that the creation of mathematics is not deductive. The important implication for the learning of mathematics is that students should be encouraged to guess, conjecture, experiment and pursue ideas even though they see no immediate prospect of success. They must be assured that even the greatest mathematicians were baffled for years in their efforts to solve problems.
This chapter is largely a review of arithmetic. It is the author's contention that students should learn to operate with numbers on the basis of the physical meanings of numbers. Thus –2+(–5) is –7 because two debts of 2 dollars and 5 dollars amount to a debt of 7 dollars. Moreover these operations must ultimately become automatic and the mind freed for thinking about more advanced and more complicated mathematics. The axiomatic approach is presented in order to assure students that mathematics does live up to the standard of ultimately proving all its results deductively. But in the case of numbers we know so surely what is correct on intuitive grounds that we do not need to cite axioms to argue that 3+5=5+3.
There are three distinct applications of numbers in Section 4-6. These are not essential to the continuity but they may be intriguing and they may convince students that even a knowledge of numbers is significant for applications. One of these applications deals with the subject of other bases for the number system, a topic receiving much emphasis today.
This chapter is largely a review of algebra. Most students have forgotten (or never really learned) their high school algebra and for them it is important to review. The topics covered suffice for all uses of algebra in later chapters. If the course were to be devoted to elementary algebra the author would use a different organization and presentation. But to help students recall earlier work it seems necessary to use the presentation to which they are accustomed. The method of obtaining the quadratic formula is novel but the reason for using it is that it is possible to motivate its discovery. To keep the notion of proof in algebra before the students, they should be asked to cite axioms on equalities, such as equals added to equals.
This chapter is also largely review work. However, there is a decided effort to show that Euclidean geometry can be useful in solving practical as well as scientific problems. The high school geometry courses are usually purely mathematical, and students do not see why the many theorems should be learned. The starred sections can of course be omitted but some applications should be taken up. The emptiness and pointlessness of mathematics, as far as the student is concerned, must be combated and one can do so here with rather simple applications. Moreover, the major thesis that mathematics is vital to the study of nature can already be supported substantially.
Though many students now take trigonometry in high school, this chapter undertakes to treat the subject as new to the student and the presentation is more detailed. That is, the review goals of Chapters 4, 5, and 6 are now dropped. Here too some applications should be included. Many of these, such as finding the distance to the moon and the radius of the moon, demonstrate the remarkable power of even simple mathematics.
This chapter supplies historical continuity. It also puts together the evidence which the Greeks acquired for concluding that nature is mathematically designed. In addition the chapter serves as a breather. Students who fear mathematics and are scared of symbolism may find once again that there is something here they can grasp. The chapter can be left to student reading.
This chapter sets the stage for the appearance of mathematics in Western Europe. It is remarkable that though civilization in Europe (apart from Greece and Rome) can be said to date from Roman times and certainly from the fifth century of our era, no mathematics of consequence was developed in Europe until about 1400 A.D. What trifles were known prior to that time were taken from the poor Roman texts. The Europeans became interested in mathematics when they learned, through a series of historical events which are related in the chapter, of the Greek works. Other events in Europe, for example, the geographical explorations and the breakdown of the totally religious outlook, encouraged the study and development of mathematics in Europe. This chapter can be read by the students and need not be discussed in class if the time does not permit it.
This chapter on painting, though of course intrinsically important as a major example of how mathematics has been applied to and determines painting styles, is also intended to stimulate interest in mathematics by students who like the arts and fail to see values in mathematics. The use of mathematical perspective is basic in the Renaissance paintings and one who would appreciate these creations must know something about the mathematical structure. The relationship then of the two fields is not incidental but fundamental. The chapter can, of course, be recommended as just interesting reading and not made part of the course.
Since the entire text cannot be covered in the usual 6-point course, this chapter on projective geome try could be omitted for prospective elementary school teachers. It can be of interest to liberal arts students in that it shows how some mathematical problems arise from ideas that were first explored in behalf of realistic painting. The chapter is descriptive and so does not call upon any detailed prior knowledge of geometry.
Coordinate geometry is fundamental in mathematics and should be included in almost any course. The graphing of simple equations and the relationship between curve and equation is used in later chapters. The application of this chapter's material is made in later chapters.
Here is an introduction to functions and a treatment of simple linear and quadratic functions. The study of functions as a topic of pure mathematics is rather pointless. Hence the attempt has been made to introduce these functions in connection with definite and concrete physical situations. Historically the physical phenomena considered were precisely the ones which led to the introduction of functions.
This chapter on parametric equations makes further use of functions and also introduces another idea of coordinate geometry, namely, the representation of a curve by two parametric equations instead of one direct relationship between x and y. The motion of projectiles was studied intensively in the sixteenth and seventeenth centuries (it still is today) and, as the next chapter will show, suggested to Newton how to unify in one theory the motions that take place on earth and the motions of the heavenly bodies.
This chapter, on the mathematical side, is still concerned with functions, notably the inverse square function. However, as noted in connection with Chapter 13, the study of mathematical functions appears empty to young people and so the chapter shows how functions can be used to determine the mass of the earth and the mass of the sun, to establish Kepler's laws, and in other applications. These few examples given in the chapter are necessarily simple but they are taken from the greatest mathematical and scientific work of our era - the work of Newton in establishing the laws of our solar system. This work gave enormous prestige to mathematics and stimulated the most important mathematical developments of the eighteenth century. A few physical concepts are utilized in the applications but these are fully discussed in the chapter. No prior knowledge of science is presupposed.
The two chapters on the calculus can do no more than give students an inkling of what the calculus is about. To some the mere thought that they can study ideas of the famous calculus is thrilling. Others will not get the ideas in this brief treatment and the attempt to present them will fail.
These two chapters present trigonometric functions. Again to relieve the boredom of studying functions as an end in themselves, Chapter 18 tries to motivate the topic by seeking to learn about the motion of a bob on a spring. This physical motivation is, from the student's standpoint, not an exciting one, though at least it is concrete. The application that is scientifically important and that appeals to many students is the analysis of musical sounds. The latter can be approached on the basis of what is done with the bob on the spring. The introduction of the subject of musical sounds is another effort to show students that seemingly bare and uninviting mathematical functions enable man to understand another extensive area of our physical world, the area of musical sounds.
Non-Euclidean geometry does attract students because it challenges ideas they understand and are convinced of. In the intellectual development of Western man it is, next to the very founding of mathematics itself, the most significant and portentous development. This creation forced the realization that mathematics is not portraying laws inherent in the design of the universe but is merely providing man-made schemes or models which we can use to deduce conclusions about our world only to the extent that the model is a good idealization.
The realization that geometry does not offer truths forced the realization that arithmetic likewise fails to do so. Mathematicians were obliged to recognize that there are many arithmetics and the corresponding algebras. This chapter, too, arouses interest because it challenges ideas the students had thought unquestionable.
Though a few applications to social phenomena appear earlier in the text, there is little opportunity to consider such applications until one takes up the mathematical topics of statistics and probability. These topics are important in the modern world and, though the chapters have been starred because they are not essential for the mathematical continuity, they are valuable in giving students some idea of how social and biological phenomena are approached.
This is a summarizing chapter. It is possible at the end of the course to characterize mathematics, its values for science, and the limitations of mathematics meaningfully because the students now have some experience with the subject on which to draw. One can refer to earlier material to illustrate what one means by a deductive structure, mathematical models, and so on.
1. The oarsman takes the goat across (the wolf does not eat cabbage). He comes back and takes the wolf across and takes the goat back. He leaves the goat on the original shore and takes the cabbage across. Then he goes back and brings the goat over.
2. The man fills the 5-pt jar and then fills the 3-pt jar from the 5-pt one. He empties the 3-pt jar, and then pours the 2 pt remaining in the 5-pt jar into the 3-pt jar. He now fills the 5-pt jar and pours enough into the 3-pt jar to fill it. Since there were 2 pt in the 3-pt jar, one pint is drawn out of the 5-pt jar, leaving 4 pt in it.
3. Refer to the two couples as Mr. and Mrs. A and Mr. and Mrs. B. Mr. A takes Mrs. A across. He comes back and takes Mr. B across. Mrs. A now goes back and brings Mrs. B across.
1. Egyptian, Babylonian, classical Greek, Alexandrian Greek, Hindu, Arab and Western European (from 1500 on)
2. The methods and formulas gave results which worked; that is, the results were correct as far as experience showed. Thus if they calculated the area of a rectangular field by using length times width, a larger rectangular area would grow more crops.
3. The pre-Greek Egyptian and Babylonian civilizations thought in physical terms. A rectangle was a piece of land. Even in the case of whole numbers and fractions, though these civilizations did work with pure numbers, they did not consciously think of numbers as entities in themselves and seek to understand them as such. The Greeks thought of numbers and geometrical forms as ideas existing as such and even superior to the concrete interpretations of numbers and geometrical figures.
4. To start with assured premises and to establish to conclusions deductively
5. They preserved the Greek works and took over ideas from the Hindus. The Europeans learned Greek and Hindu mathematics from Arabic works (though later the Europeans also acquired Greek manuscripts).
6. The Greeks were the first to think of mathematics as an independent discipline, and to formulate standards for obtaining mathematical conclusions. They also built up a large body of geometry.
7. We see from the survey in the chapter that far more was created after Greek times than during that period.
1. Arithmetic tells us only that 4 · 5 = 20. Whether the answer is to be interpreted as 20 men or 20 trucks depends entirely on the physical situation to which the numbers are applied.
2. One cannot multiply a number of pennies by a number of pennies whether in the form of 25¢ or 0.25 dollar. One can multiply 25 by 25 or 0.25 by 0.25. Whether the answer makes physical sense depends on whether there is any physical sense in the original problem. There is no physical point to 25C by 25¢. There is physical point in asking, for example, how much money will 25 times 25¢ amount to. This problem cannot be reformulated as 0.25 times 0.25 because the first 25 is a number of times and not 0.25 dollar.
3. Justice, liberty, democracy, good and evil
4. One cannot divide 30 books by 5 people. One can divide 30 by 5. Whether the answer is 6 books can be decided only on physical grounds.
5. As in Exercise 2, one cannot multiply dollars by dollars or cents by cents. One can multiply 6 by 1 or 600 by 100. The correct mathematics in this situation is 6 times 1 where physically the 6 means 6 repetitions and the 1 means 1 dollar. For this physical interpretation the 6 cannot be replaced by 600.
6. Mathematics deals with the concepts themselves and not the physical interpretations or realizations. Thus mathematics can deal with 3 · 5 but not with 3 people times 5 books. Likewise mathematics deals with the concept of a triangle but not with a triangularly shaped piece of land.
7. The abstract concepts are general and the reasoning about them can be applied to hundreds of situations. Furthermore, it is easier to work with abstractions, at least to the extent that irrelevant details are ignored. The Greeks also thought that the abstract con cepts were the essence of knowledge.
1. Abstraction refers to selecting the key or basic properties of some physical object, as the rectangular shape of a piece of land. The fact that the boundary and surface are formed by particles of earth is ignored. In idealization we ignore some significant fact for the sake of a simpler model. Thus regarding the earth as a point in astronomical work is contrary to the fact that the earth is an extended body but the idealization is good enough for some scientific work.
2. For some purposes it is correct to regard the lines to the sun as parallel. Thus two shadows of two nearby objects may be regarded as formed (outlined) by parallel lines of light from the sun. However, if A and B are far apart on the earth′s surface then the lines to the sun may usually not be taken as parallel. The direction of the sun will differ and this difference may be important (as in calculating the distance of the sun from the earth).
3. Yes. The thickness would not usually matter. If it did one might have to regard the pole as a cylinder or as a tapering cylinder (cone).
1. That the coin will always fall heads
2. Deductive reasoning consists of those ways or modes of combining premises so that the conclusion is necessary or indubitable.
3. It can often be done more readily, less expensively; and in some cases it is the only method available. Above all the conclusions are certain, whereas they are not in induction and analogy.
4. No. One may not have the premises with which to reason.
5. One could do this by adopting suitable premises. (It is interesting to get students to suggest premises.) However, not all people would agree to the premises.
6. The answers are in the answer section of the textbook. In each case, drawing circles to represent the classes of objects or people involved will show whether or not the conclusion must hold. Only if it must is the reasoning valid.
7. At least one of the premises must be false.
8. The reasoning may be correct but the conclusion untrue because at least one of the premises may be untrue.
1. The Egyptians and Babylonians relied on the usefulness of the result to accept the mathematical procedure or formula. The Greeks insisted on deductive proof.
2. The scientist uses induction from observations or experiments and reasoning by analogy as well as deductive reasoning. The mathematician uses only deductive reasoning to prove his conclusions.
3. The Egyptian and Babylonian reliance upon adopting formulas and procedures if they were good enough for daily use is an empirical basis. The Greeks started with axioms and reasoned deductively. Hence they were sure of their conclusions without having to test them at all.
4. (a) The argument is valid. However, the first premise is not true,
(b) Valid and in this case also true
5. No. From the information given, the square of an even number could also be odd.
6. The argument relies on induction, which is not acceptable in mathematics. It is not obvious that the square of any larger number is even.
7. Yes. If the square of a number is even and the number itself were odd, then by the first premise the square of the number would be odd. But we are given that the square is even.
8. Primarily because they wished to be sure that the conclusions were correct
9. If the sides are a, b, c and the opposite angles are A, B, C then because a = b, A = B. Because b = c, B = C. Then A = B = C because things equal to the same things are equal to each other.
10. By reasoning deductively from the known truths. Since conclusions established deductively are indubitable, there would be new truths.
1. The Greeks believed the axioms were truths.
2. They adopted abstract mathematical concepts; they insisted on deductive proof; and they chose axioms which they believed were truths.
3. Yes. The insistence on obtaining truths, as opposed to useful or approximate results, is the position of philosophers. Historically the early Greek mathematicians were philosophers and these were the men who set the standards for mathematics. One could argue that mathematics began with the Egyptians and Babylonians, who were not philosophers. But the distinguishing features of mathematics were imposed by philosophers.
1. It seems as though the triangles should be congruent.
2. It seems as though EFGH should be a parallelogram. (It is. EF joins the midpoints of two sides of triangle ABC. Hence EF is parallel to and equal to one half of AC. Likewise GH is parallel to and equal to one half of AC as a side of triangle ADC. Hence EF is parallel to GH and equal to GH.)
3. No. The proof is inductive and as a matter of fact the conclusion is not true. When n = 41, the formula yields 412 and this is not prime.
4. If corresponding sides are equal and if one angle of one equals the corresponding angle of the other, the quadrilaterals are congruent.
5. 13 + 23 + . . . + n3 = (1 + 2 + . . . + n)2.
1. The results were useful.
2. On the whole the Egyptians and the Babylonians thought in terms of the physical meanings of the mathematical concepts. The Greeks thought of the abstract concepts as objects in themselves.
3. To start with truths (the axioms) and to deduce further truths
4. The distinguishing features of mathematics as we understand the subject today were imposed or set by the Greeks.
5. (a) and (b) follow necessarily from the premises.
6. No one of the conclusions stated necessarily follows.
7. No. All quadrilaterals need not be parallelograms.
8. John will not be successful.
9. Nothing. Smith might go to the movies even when it does not rain.
10. The statement “I go to the movies only if it rains” means that “if I go to the movies, it must rain.” Since Smith went to the movies, it must have rained.
1. The position of a digit in a number determines the quantity represented by the digit.
2. Because otherwise we would not be able to distinguish the meaning of 5, say, in 507 and 57
3. We can operate with it as we operate with all other numbers. There is one exceptional fact: We cannot divide by 0.
4. As a quotient of integers or as decimals
5. The definitions must give results which agree with experience.
1. Any even number can be written as 2m, where m is an integer. Then (2m)2 = 4m2 = 2 · 2m2. Since the (2m)2 contains 2 as a factor, (2m)2 is even.
2. If we multiply any number ending in 1, 3, 5, 7, or 9 by itself, the product ends in 1, 3, 5, 7, or 9 and so must be odd.
3. If a were odd, then by Exercise 2, a2 would be odd. But a2 is given as even. Hence a cannot be odd.
4. The assertion is false because, for example, 22 + 32 = 13 and 13 is not a square.
1. The answers are given in the answer section of the textbook.
2. The answers are given in the answer section of the textbook.
3. The argument is false. It is true that no irrational can be expressed with a finite number of decimal places. But there may be and there are other numbers which cannot be expressed with a finite number of decimal places.
1 to 5. The answers are given in the answer section of the textbook.
1. The only basis for belief other than actual calculation in this case is that the principle holds for small numbers where actual calculation shows it is correct.
2. We can prove that the principle is correct. a (b − c) = a[b + (−c)] = ab + a(−c) by the distributive axiom (Axiom 9). Then ab + a(−c) = ab + (−ac) because the product of a positive and a negative quantity is negative. Then ab + (−ac) = ab − ac because to add a negative quantity is equivalent to subtracting the corresponding positive quantity.
3. The answers are given in the answer section of the textbook.
4. (a + 3)(a + 2) = (a + 3)a + (a + 3)2 = a2 + 3a + 2a + 6 = a2 + 5a + 6.
5. (n + l)(n + 1) = (n + l)n + (n + 1)1 = n2 + n + n + 1 = n2 + 2n + 1.
6. Equals divided by equals give equals.
7. Subtract 2 from both sides; equals subtracted from equals give equals.
8. Yes, by the distributive axiom
9. No. To show that it is false for all a, b and c we have but to find one case where it is false. Let a = 2, b = 3, c = 4.
1. The average speed is the speed that would enable him to do the entire trip in the same time as under the actual speeds. One tends to think that the speed upstream and the speed downstream can be averaged. But these speeds are used for different periods of time, 3 hr on the way up and 1 1/2 hr on the way down. Hence they cannot be averaged to obtain the average speed.
2. The correct average price should be that which produces the same money as if the apples and oranges were sold separately. The correct average price will depend upon how many of each are sold. Thus if he sells 12 apples and 12 oranges at 5 pieces for 10¢, he receives (24/5)(10) or 48¢. But if he sells 12 apples at 2 for 5¢ he receives 30¢ and for 12 oranges at 3 for 5¢ he receives 20¢ or a total of 50¢. Hence the average of 5 pieces for 10¢ is wrong.
3. As noted in Exercise 2, the correct average price depends on how many of each are sold, a apples should bring a(5/2). b oranges should bring in b(5/3). Hence the total income should be (5a/2) + (5b/3). Then the average price should be [(5a/2) + (5b/3)]/(a + b).
4. As the answer to Exercise 3 shows, the average price depends on a and b. It is not possible to simplify the average price so as to eliminate a and b.
5. The first man digs 1/2 of the ditch per day and the second 1/3 of the ditch per day. It is correct to say that together they dig 5/6 of the ditch in one day. Then the average per man is 5/12 because the 2 men would dig twice this much in one day.
1. Each ace can be paired with any one of 4 kings. Hence 16 pairs in all.
2. Each choice of color can be made with each choice on the heater and with each choice on the radio. Thus 3 · 2 · 2.
3. The reasoning is the same as in Exercise 2.
4. Each of 6 numbers on one die can be paired with 6 on the other. Hence 6 · 6.
1. When the sums are 6 or more one must convert them to base six. Thus 3 + 2 = 5 in base 6. 3 + 4 = 11 in base 6. 5 + 5 = 14 in base six; etc.
2. When the products are 6 or more one must convert them to base 6. Thus 3 · 4 = 20 in base six.
3. 0 + 0 = 0, 0 + 1 = 1, 1 + 1 = 10. 0 · 0 = 0, 0 · 1 = 0, 1 · 1 = 1.
4-7. These are answered in the answer section of the textbook.
8. Let the base be b. Then 1 · b2 + 0 · b + 1 = 10. Then b = 3.
9. To express any number from 0 to 63, we can use base 2, base 3, etc. If we use base 2 and have separate weights for 1, 2, 22, 23, 24, and 25 we shall need six weights and we know that we can handle all weights in question because all numbers from 0 to 63 can be expressed with 0 or 1 in the six places a, b, c, d, e, f. If we use base 3 or some higher base we need multiples of the separate powers. Thus to represent 53 in base 3 we write 1 · 33 + 2 · 32 + 2 · 3 + 2. Thus we would need a weight for 33, 2 weights of 3, etc. This in itself requires 7 weights. Thus to use base 3 or a higher base we need more weights. If we seek to build up a set of weights which do not correspond to writing numbers in any base, we find that we must have 1, 2, 4 or 2 two′s, 8, etc. and end up with more weights.
The answers to follow complete the set of answers given in the back of the textbook.
1. (d) 
(e) 
(i) 
(j) 
(k) 
2. (a) 
(d)
(f) 
(g) 1
(h) 
(j) 
(l) 2
(m) 
(o) 4
3. (c) 6ab
(e) 24xyz
4. (c) a + 2b
(d) 2x + 4y
5. (c) 7
(b) 11
(d) 
(g) 
6. (b) 
(b) 
(e) 
(g) 
7. (a) 
(b) 
(c) 
(d) 
(b) 2.2
(c) 2.5
9. (a) Correct
(c) Correct
(g) Correct
(i) False
10. (a) 1
(d) 111
(f) 10,000
11. (a) 1
(c) 6
(e) 9
1. Symbols are used to secure brevity and generality as in the case of ax + b and often to avoid ambiguity by using different symbols for different meanings of a word as in the use of = and ≡ for the word equal. The symbol = is to be used in x + 4 = 7 whereas the symbol ≡ is to be used in (x + l)(x − 1) = x2 − 1.
2. The statement is vague. Equal in what respects? In intelligence? In physical characteristics? In political rights?
3. As an example of the use of words, consider (c). We must say: The product of some number times the sum of that number multiplied by itself and the product of that number and another number.
4. Yes
5. (a) 3x + 4
(b) 3x2 + 4
1. the answers to those parts not in the back of the text are:
(b) 610
(c) 109
(f) 103
(h) 1/103
2. Yes. We have but to remember the meaning of positive integral exponents to see that the statement is correct.
3. (a) False
(b) Correct
(c) False
(d) Correct
(e) False
1. (a) 312
(b) 312
(c) 58
(d) 10b
(e) 1012
(f) 104
(g) 310
(h) 304
2. (a) 105 or 100,000
(b) 64/63 or 6
(c) 85/86 or 1/8
(d) a3b3/a2 or ab3
(e) a3b3/a2b2 or ab.
(b) Correct
(c) False
(d) Correct
(e) False
(f) False
1. The answers are given in the answer section of the textbook.
2. The answers are given in the answer section of the textbook.
3. Use the distributive axiom and the theorems on exponents.
4. Try numbers for x and y. If for these numbers the left side does not equal the right side, the equality is false. But if for specific numbers the left side does equal the right, the statement is merely verified but not proved.
6. The answer is correct but the reasoning is not.
7. The flaw lies in the step of dividing both sides by a-b. Since a = b, the divisor is 0.
1. Let x be the length of the rod. Then (x/1100) − (x/16,850) = 1. Solving for x gives 1177 ft.
2. By the Pythagorean theorem x2 + (2640)2 = (2641)2. Thus x2 = (2641)2 − (2640)2 = (2641 − 2640)(2641 + 2640) = 5281. 
ft
3. 800/(200 + x) = 640/(200 − x). Multiply both sides by (200 + x)(200 − x). Then x = 22 mi/hr.
4. Let x be the number of years. Then 10,000 + 600x = 20.000 + 400x. Solving for x gives x = 50 years.
5. Let x be the height of the staff. Then (x + 2)2 = x2 + (18)2. Solving for x gives x = 80 ft.
6. Let x be the number of copies. Then 5000 + x = 5x. Solving for x gives x = 1250 copies.
7. The mathematical equation must relate numbers only. Hence as a mathematical equation 1/4 = 25 is incorrect.
8. The same reason as in Exercise 7
1. (a) (x − 6)(x − 2) = 0
(b) (x + 9)(x − 2) = 0
2. (a) Since the sum of the roots is −8 we form a new equation in y where y = x − 4. Then x = y + 4. Substitute in the original equation. (y + 4)2 − 8(y + 4) + 12 = 0 or y2 − 4 = 0. Hence y = +2 and −2 and x = 6,2.
(b) Let y = x + (7/2). Then x = y − (7/2). Substituting in the given equation yields y2 − (121/4) = 0. Then y = 11/2, −11/2 and x = 2,−9.
3. (a) Let y = x + 6. Then x = y − 6. Substituting in the original equation gives y2 − 27 = 0. Then 
. Then 
, 
. Of course 
.
(b) Let y = x − 6. Then x = y + 6. Substituting in the original equation gives 
. Then 
, 
.
1. In each case we first make sure that the coefficient of x2 is 1. If it is not, as in (a), we divide through by that coefficient. We then substitute the values of p and q in (30). The answers are in the back of the text.
1. The answers not given in the answer section of the textbook are: (a) 6x + 18, (d) x2 − 9, (g) x2 − y2.
2. The answers not given in the answer section of the textbook are:
(b) (x − 4)(x + 4),
(c) (x − a)(x + a),
(d) (a − b)(a + b),
(g) (x + 1)(x + 4),
(h) (x − 3)2,
(k) (x − 3)(x − 4).
3. 2x = −2; x = −1.
4. The answers not given in the answer section of the textbook are:
(a) x = 3/2,
(b) x = −3/2,
(f) x = 1/6,
(i) x = (c + b)/a.
5. Let x = number of grams of acid to be added. The number of grams of water in the 50 grams is 0.75(50) = 37.5 gr. Then 37.5/(50 + x) = 0.60. Clear of fractions and solve for x. x = 12 1/2 gr
6. Let x be the unknown grade. Then (60 + 70 + x)/3 = 75. Then x = 95.
7. (a) (x − 5)(x − 1) = 0
(b) (x − 7)(x + 1) = 0
(c) (x − 6)(x − 1) = 0
(d) (x + 9)(x − 3) = 0
(e) (x − 4)(x − 3) = 0
(f) (x − 7)(x + 2) = 0
8. (a) Let y = x + 5. Answer: −9 and −1.
(b) Let y = x − 5. Answer: 9 and 1.
(c) Let y = x + 5. Answer: 
(d) Let y = x − 5. Answer: 
.
(f) Let y = x + 6. Answer: 
9. The answers not given in the answer section of the textbook are:
(a) 
,
(b) 
,
(d) 
,
(f) 
(g) 
.
10. Let t be the number of hours both ships travel until they meet. Then the ship at B travels 2t miles in t hours. The ship at A travels 5t miles in t hours. Then by the Pythagorean theorem 25t2 = 102 + 4t2 or 21t2 = 100 and 
. This is the time it takes the two ships to meet. In the text, x was the distance BC. But BC = 2t. Hence 
. Thus we get the same answer.
1. Axioms are statements whose truth we accept as evident. Theorems are proven on the basis of the axioms.
2. Because they seemed to be self-evident truths
3. Using the construction suggested in the text we have 
A = AC′B, because they are base angles of the isosceles triangle AC′B. Now AC′B is an exterior angle of triangle ACC′. Hence AC′B > C. Then A > C. But angle A is given equal to C. Hence BC is not greater than BA. Likewise if we assume BC less than BA we can obtain the same contradiction by laying off BC on BA.
4. Use the figure and the suggestion in the text. If we draw GH so that 1′ = 2 then GH is parallel to CD by Theorem 2. But AB is given parallel to CD. By Axiom 5 there can be just one line through the point where AB and GH intersect which is parallel to CD. Hence 1 cannot be greater than 2. If we assume 1 is less than 2 we can repeat the argument by drawing a line through the intersection of CD and EF so as to introduce an angle 2′ equal to 1.
5. Referring to Fig. 3–7, we have that 1 = 2 because they are alternate interior angles of parallel lines. Likewise 3 = 4. But l + A + 3 = 180° because they form a straight angle. Then 2 + A + 4 = 180° because we have replaced 1 and 3 by equal angles.
6. If two adjacent sides and the included angle of one equal the corresponding sides in the other
7. If the ratio of two adjacent sides in one equals the ratio of the corresponding sides in the other
8. Let x be the other arm. Then x2 + (5280)2 = (5281)2 or x2 = (5281)2 − (5280)2 = 1(5281 + 5280). Then x = 103 ft.
9. The areas of two similar triangles are to each other as the square of the ratio of any two corresponding sides. In the present case the ratio of corresponding sides is 3. Hence the ratio of the areas is 9 or one area is 9 times the other. But the price of the larger plot is only 5 times that of the smaller one. Hence the larger plot is the better buy.
10. The circumference of the roadway is 2π(21,120,000 + 1) = 2π (21,120,000) + 2π. Hence the circumference of the roadway exceeds the circumference of the earth by 2π ft.
11. Parallel lines do not meet by the very definition of parallel lines. Euclid′s assumption is Axiom 5 which is a quite different statement.
1. If we draw the lines AE and BE we have two triangles ACE and BCE. These are congruent by s · a · s = s · a · s. Hence AE = BE.
2. We have similar triangles and AD/OD = A′D′/OD′. We know that OD = 93,000,000 mi, 0D′ = 1 ft, and D′D′ = 0.0045 ft. Then we can calculate AD. One must convert the miles to feet. AD = 418,500 mi.
3. By the argument in the text the rectangle of maximum area should be a square. Hence the dimensions are 100 by 100.
4. The rectangle must be a square. Hence p/4 by p/4
5. Use the idea that is discussed on p. 134. Suppose the farmer had to enclose a rectangular area on both sides of the lake edge with 200 ft. of fencing. This rectangle must be a square with dimensions of 50 ft by 50 ft. Then the half which lies on one side of the edge has dimensions 25 by 50.
6. Think of a rectangle with dimensions a and b which add up to 12. The perimeter is 24. This rectangle is largest when a = b = 6.
7. By the Pythagorean theorem, (R+h)2 = R2 + x2. Hence 
.
8. Since h is small compared to R, we can drop h2 compared to 2Rh.
9. We can use the result of Ex. 8. 
miles, approx.
10. Suppose A and B are two rectangles with the same area and A is a square. If the perimeter of A is not less than B, replace A by a square A′ which has the same perimeter as B does. Then the area of A′ will be greater than that of B. Since A and B have the same area, A′ has more area than A. But A has more perimeter than B, and A′ has the same perimeter as B. Hence A has more perimeter than A′ but less area. This is impossible because if p is the perimeter of a square the area is p2/16.
1. The mirror image of A is on a perpendicular from A to the mirror and as far behind the mirror as A is in front.
2. The physical problem can be translated into light rays. If a light ray goes from A to point P on m to A′, the shortest path is the one for which AP and A′P make equal angles with m. As pointed out on page 141, this is a geometrical fact. Hence it applies to the location of the pier also.
3. He should aim at the point P on m for which AP and A′P make equal angles with m.
4. Since billiard balls behave like lights rays, the final direction will be parallel to the original one.
5. As the text suggests, if 
, then pick P′ so that there 
. Then AP′ + P′A′ is the shortest path from A to the mirror to A′. But APA is given as the shortest path. Hence 1 must equal 2.
1. The circle is an ellipse for which the two foci coincide. Then PF = PF′ and this is the radius.
2. Since PF + PF′ = 10 and PF′ = PF + FF′ = 6, PF + PF + 6 = 10. Hence PF = 2.
3. Because PF + PF′ is the sum of two sides of the triangle PFF′. This sum must always be greater than the third side.
4. The point on the axis must be equidistant from focus and directrix. Hence it is 5 units from the focus (and directrix).
1. QP + QF1, > PF1, because the sum of 2 sides of a triangle is greater than the third side. Hence QP + PF2 + QF1 > PF2 + PF1. Now QF2 = QP + PF2. Hence QF2 + QF1 > PF2 + PF1 = a.
2. If Q is any point on t other than P, then by Exercise 1, QF2 + QF1 > PF2 + PF1. Hence the shortest path from F2 to t to F1 is F2P + PF1. By Exercise 5 of Section 6–4, F2P and F1P must make equal angles with t.
3. Each light ray will strike some point P on the ellipse, such as P in Fig. 6–32 and be reflected to F1, because, as proven in Exercise 2, F2P and F1P make equal angles with t, and light is reflected in accordance with just this equality of angles.
4. The lengths F1P and F2P become coincident radii. Then since both F1P and F2P make equal angles with t and the total angle is 180°, the radii are perpendicular to the tangent.
1. Consider Δ ACD and Δ ABE. AC = AB; A is common; and AD = AE. Hence the triangles are congruent and so BE = DC. Then triangles CBD and BCE are congruent, so that DBC = BCE. From this, the base angles of ABC are equal because they are supplements of equal angles.
2. (a) 3 = l because they are vertical angles. Then because 3 = 2, 1 = 2 and so we have alternate interior angles equal.
(b) Since 1 is also supplementary to 4, 1 = 2 because supplements of the same angle are equal. But then we have equal alternate interior angles.
3. The theorem on p. 141 applies here.
4. It should take the path of a parabola whose focus is at A and directrix is m. Then the ship is as far as it can get from any gun at A or on the shore (simultaneusly).
5. Let P be the center of any circle T and let us use C′ and D′ to denote the centers of circles C and D. Then if we draw a radius from C to the common point E of tangency of circles C and T, this line must pass through P because CE and PE must both be perpendicular to the common tangent at E. Then if r is the radius of T, C′P = c − r, Similarly the lines from P and D′ to the common point F of tangency of T and D must form one straight line because PF and D′F are both perpendicular to the common tangent. Then PD′ = r + d. Now PC′ + PD′ = c − r + r + d = c + d. This quantity is the same no matter where T is. Hence the points P satisfy the definition of an ellipse.
1. 
, 
, 
2. (b) sin 70° = 0.9397
(d) cos 55° = 0.5736
(f) tan 80° = 5.6713
3. cos A varies from 1 to 0.
4. tan A varies from 0 to unlimitedly large values.
5. sin A = BC/AB, cos B = BC/AB, etc.
6. 90°-A is the other acute angle B. Hence we are back to Exercise 5.
7. sin2 A = BC2/AB2; cos2 A = AC2/AB2. Then sin2 A + cos2 A = (BC2 + AC2)/AB2. But by Pythagorean theorem the numerator equals the denominator. If we know sin A, we can compute cos A or vice versa.
8. sin D = FE/FD, cos D = ED/FD, tan D = FE/ED
1. Use tan A = BC/AC. Then A = 56° and AC = 300. Answer: 445 ft
2. Let x = distance from the observer to the bldg. Then tan 5° = 1248/x or x = 1248/tan 5°. Answer: 14,265 ft
3. Let x = the length. Then sin 5° = 1000/x or x = 1000/sin 5°. x = 11,500 ft.
4. tan 50° = 380/x. Then x = 380/tan 50°. x = 319 ft. Hence the ship is 19 feet beyond the rocks.
5. tan A = 75/100 and tan B = 100/75.
6. From the given equation we have (r + 3) sin 87°46′ = r or (r + 3) (0.99924) = r. Then 0.99924r + 2.99772 = r. Hence 0.00076r = 2.99972. Then r = 3944 mi.
1. The angle POV equals the measured angle of 30°. To see this, drop a perpendicular from P to OV. Hence the latitude is 30°.
2. From 90° south latitude to 0° at the equator and then from 0 to 90° north latitude at the North Pole
3. The longitude increases from 0° to 180° west longitude. Then he crosses the 180° longitude line and the longitude becomes east longitude and decreases from 180° to 0°.
4. The 30° circle
5. He travels 2/360 of the earth′s circumference or (2/360)(25,000) or 139 miles, approximately.
6. The radius of the 41° latitude circle is computed on p. 168 and is 3019 miles. Then the man travels 5/360 of the circumference or (5/360) 2π(3019) which is 263 miles, approximately.
7. He travels the full circumference of the 41° latitude circle. Since (Exercise 6) the radius is 3019, the circumference is 18,960 mi.
1. cos E = 4000/ES. Then ES = 4000/cos E = 4000/0.000043 = 93,000,000 mi.
2. sin 16° = RS/ES. RS = ES sin 16′ = 93,000,000 (0.0046) = 428,000 mi
3. From the given equation we have (241,000 + r)sin 15′ = r or (241,000 + r)(0.0044) = r. Solve for r. r = 1065 mi
4. Using Fig. 7–23(b) with M replacing V, we have sin E = MS/ES. Then MS = ES sin E = 93,000,000 sin 23° = 36,000,000 mi.
1. sin 45°/sin r = 4/3. Then sin r = (3/4) sin 45°. r = 32°
2. sin i/sin r = 2/3. Then sin i = (2/3)sin r. The largest value possible for r is 90°. Then sin r = 1 and the largest value for sin i = 2/3 = 0.6666. Then the largest i value is about 42°.
3. Let i and r be the angles of incidence and refraction at the air-to-glass boundary. Then sin i/sin r = v1/v2 where v1 and v2 are the velocities of light in air and glass. Now the angle of incidence at the glass-to-air boundary is r. Call the angle of refraction r′. Then sin r/sin r′ = v2/v1. If we multiply this equation by the preceding we have sin i/sin r′ = 1 or sin i = sin r′ or i = r′. Then the initial and final rays are parallel.
4. sin 50/sin 45 = v1/v2. v1 is 186,000. Solve for v2 which proves to be 172,000 mi/sec.
1. (a) 19°
(b) 28°
(c) 71°
(d) 62°
2. The hypotenuse is 2. Then 
, 
, 
.
3. The answers not given in the back of the textbook are:
(b) 12/13; 5/13; 12/5
(e) 
4. 4/5; 3/4
5. 
; 
6 
; 
7. tan 40° = AB/100; AB = 100 tan 40° = 83.91 ft
8. Let x = height of the pole. Then tan 20° = x/15 or x = 15 tan 20° = 5.46 ft.
9. Let the angle be denoted by A. Then cos A = 40/60. Then A = 48°.
10. Let x be the distance. Then tan 35° = x/60 or x = 60 tan 35° = 42 ft.
11. Let x be the distance from target to gun. Then tan 50° = x/2000. x = 2000 · tan 50° = 2384 ft.
12. Following the method on p. 168 we have cos 23° = O′P/OP. Then O′P = OP cos 23° = 4000(0.9205) = 3682 mi. This is the radius. The circumference is 2(3682)π.
13. In Exercise 12 we have the circumference of the 23° latitude circle. Then the man travels (5/360) 2π · 3682 = 107 miles, approximately.
14. Again following the method of p. 168 we have cos 67° = O′P/OP. Then O′P = OP cos 67° = 4000(0.3907) = 1,560 miles.
15. sin i/sin r = 4/3. Angle i = 45°. Then r = 32° approximately.
16. sin i/sin r = 3/4. Then sin r = (4/3) sin i. Here i = 30°. Then sin r = 4/6 and r = 42° approximately.
1. The pre-Greek views were unscientific. The planets were associated with gods who ruled the affairs of men. The Greek views offer mathematical schemes which show regular patterns of planetary motion.
2. All reality reduces to numbers and relationships among numbers.
3. All motions take place about a fixed earth.
4. Deferent and epicycle (see p. 191)
5. If the planet moves clockwise on the epicycle while the epicycle moves anticlockwise on the deferent, the path is practically an ellipse.
6. Nature follows a rational pattern, a pattern obtained by human reasoning. With the Greeks each of the several domains of nature which they studied had a mathematical pattern.
7. The planets follow a plan or pattern which is described by mathematics. Presumably the universe was designed so that the planets would follow this pattern.
8. The properties of space and of objects in space were found to be described by Euclidean geometry. Again the presumption is that space and the objects were designed to possess the properties which follow from the axioms of geometry.
1. Mathematics seems to flourish in civilizations that are interested in the physical world.
2. The rediscovery of the Greek works; a revived interest in the physical world stimulated by the Greek works; the geographical explorations; the employers′ and laborers′ interest in materials; a freer intellectual atmosphere brought about by the Reformation; new inventions such as gunpowder and lenses which led to mathematical problems.
3. God designed the universe mathematically.
1. The artists were impelled to portray nature as human beings saw it. To do so they had to create a mathematical system of perspective.
2. A conceptual system uses principles and conventions which may have very definite meaning but which are not what one actually sees in the real world. Thus the use of a gold background on which angels are portrayed is intended to suggest that the angels live in heaven. An optical system portrays what the eye actually sees in real scenes.
3. Alberti, Uccello, Piero della Francesca, and Leonardo da Vinci
4. The eye sees what a section of the projection actually contains.
5. See the italicized statements on pp. 220 and 221. A fourth theorem (p. 222) is that horizontal lines making a 45° angle with the canvas must be drawn so as to pass through a diagonal vanishing point.
1. (a) It will be a triangle.
(b) It will be a quadrilateral.
2. Because the figure and the section look alike to the eye
3. (a) The two triangles lie in one plane.
(c) Desargues′ theorem holds for any two triangles whether they lie in different planes or the same plane.
4. 5/4
5. The geometrical property which holds for some figure will also hold for the figure obtained by a section of a projection of that figure from some point.
6. DA and DB become infinite and so their ratio approaches 1. Then C becomes the midpoint of AB.
2. The three points of intersection lie on one line.
1. Four lines, no three of which pass through the same point
2. We can interchange the words point and line in a theorem about figures lying in one plane and obtain a new theorem.
3. Four lines all passing through one point.
4. Interchange point and line and draw the figure.
5. If one dualizes a theorem then, according to the principle of duality, he automatically obtains a new theorem.
1. To discover geometrical properties common to a figure and a section of a projection of that figure, or common to two different sections of the same projection of that figure, or two sections of two different projections
2. Projective geometry is concerned with properties that are invariant or remain the same under any projection and section. These properties usually deal with intersections of points and lines, points lying on a line, and the property of being a conic section. Euclidean geometry is concerned with congruence and similarity of figures. These properties hold only under special projections and sections.
3. The theme is that projective geometry arose from the work on realistic painting.
1. He took over the axiomatic, deductive method of mathematics.
2. See the middle paragraph of p. 252.
3. The Europeans needed some efficient and more effective methods, especially for new and more complicated curves coming into mathematics.
4. The new astronomy, the design of a clock, paths on maps, the design of lenses, projectile motion
1. Two numbers which locate the position of the point with respect to two perpendicular lines
2. It is an equation in x and y which is satisfied by the coordinates of any points on the curve and only these points.
3. See answer section of textbook.
4. (a) For example, x = 51, y = 10.
(b) For example, x = 0, y = 6.
5. Yes, because (−3)2 + 2(5)2 = 59.
6. Since (3)2 + (−2)2 = 4 · 3 + 1, the answer is yes.
7. (a) A straight line with a slope of 3, cutting the y-axis at (0,7)
(b) A circle with center at the origin and radius of 7
(c) A circle with center at the origin and radius of 
(d) Write the equation as y = −(x/2) + 3. Hence a straight line with slope of −1/2, cutting the y-axis at (0,3)
(e) Same as (c)
8. Yes. These coordinates have a different geometrical meaning but serve to locate points with respect to the equator and the 0° −longitude (half) circle.
9. Yes. If its position with respect to the coordinate axes is different, the same curve will have a different equation.
10. Yes, the slope is m.
11. (0,7)
12. (0,b)
13. Slope of m; (0,b)
14. There are no values of x and y which belong to both equations. Hence it is meaningless to subtract one equation from the other. The x′s and y′s of one are not the same as the x′s and y′s of the other.
Exercises 3 to 7 are answered in the answer section of the textbook.
2. Write the given equation as y + 25 = (x − 5)2 and introduce x′ and y′ such that x′ = x − 5 and y′ = y + 25. Follow the text procedure on pp. 269–270.
3. The curve of y = −x2 + 6x is the same as the curve of −y = x2 − 6x. The latter curve differs from y = x2 − 6x in that for the same x-value, each y-value is the negative of the other y-value. Hence the curve is reversed with respect to the x-axis, or one can say the curve is the reflection in the x-axis of the curve of y = x2 − 6x which is shown in Fig. 12–16.
5. Each point on y = x2 − 6x + 9 is 9 units higher than the point on y = x2 − 6x with the same x-value.
6. One can always find the pairs of x- and y-values which satisfy the equation, and the points having these pairs of values form a curve. (One could point out that in odd cases the curve may consist of one point, e.g., x2 + y2 = 0, or there may be no curve, e.g., x2 + y2 = −9.
7. (c) This is one form of the hyperbola.
3. The length in question is determined by letting y = 0. Then x = ±5. Hence the total length is 10.
4. Equation (18) becomes 
. This represents a circle.
5. We calculated in Exercise 3 the coordinates of the point where the path crosses the positive x-axis. These are (5,0). Hence the distance from (3,0) is 2. Likewise the point where the path crosses the negative x-axis has coordinates (−5,0). The distance of this point from (3,0) is 8.
The answers are given in the answer section of the textbook.
1. We can write equations in four letters and speak about them as though they represented figures in a four-dimensional space. But there is no implication that a real four-dimensional space exists.
2. A hyperplane
3. Yes. They introduced the idea of representing a curve by an equation in x and y and applying algebra to the equation to deduce facts about the curve.
4. To an extent. We still need the older, purely geometric Euclidean geometry for basic facts about simple figures such as lines, triangles, and circles. Beyond that we can use either geometric proofs or coordinate geometry to establish other geometrical facts. Sometimes one approach is simpler than the other.
1. 0
2. 0
3. The x-coordinates are the same.
4 and
5. See answers in back of text.
6. Because 
, the point lies on the circle.
7. These curves are all parabolas. See Section 12–4.
8. These curves are all parabolas but displaced from the standard position. See Section 12–5.
9. See Eq. (19) and Fig. 12–17.
10. The curve is a hyperbola.
11. Given ax2 + bx + c = 0, graph y = ax2 + bx + c and find where the graph cuts the x-axis.
1. Shapes and sizes of objects and motion
2. A qualitative explanation is one which deals with physical concepts such as heaviness, rising, falling, motion, heat, cold, natural place, force, attraction, and the like. A quantitative explanation relates the measures of varying quantities. It is really a description rather than an explanation.
3. To isolate the primary qualities and not try to treat both primary and secondary ones; to idealize a physical phenomenon, as in neglecting the friction of air in studying motion, rather than to tackle the full physical problem with all factors included; to obtain basic physical principles from observation and experiment rather than to accept those which the human mind thinks must hold; and to seek quantitative description rather than physical explanation.
4. The Greeks sought to understand the workings of nature. Bacon and Descartes sought to use scientific knowledge to help men secure the necessities of life, maintain health, and even secure comforts.
5. Galileo sought quantitative description. The description would use mathematical formulas. Moreover, he planned to deduce other formulas from known ones by mathematical means.
1. A relationship between variables
2. A formula is a symbolic representation of a function by an equation involving the variables.
5. r is the independent variable and A, the dependent one.
6 and
7. See answer section of textbook.
8. t = ±3. The negative value does not have physical significance if the formula represents the distance a dropped body falls in t seconds.
9. When C = 0, F = 32. This is the freezing temperature of water. When C = 100, F = 212. This is the temperature at which water boils.
1. No. A force is needed to overcome the friction of air.
2. With no gravity, the man would stay in the same place. With gravity, he is accelerated downward.
3. In 59 min it travels (59/60)10. In 1 min it travels (1/60)50. The total distance is 64/6 mi in 1 hr and so the average speed is 10 2/3 mi/hr.
4. From v = 32t we have v = 128. The average speed is (0 + 128)/2 or 64 ft/sec. This is the actual speed at t = 2.
5. Acceleration is the rate of change of speed.
6. The graph is a straight line through the origin with a slope of 32.
7. 400; 676; 1600 ft
8. The graph is a parabola.
9. The parabola opens downward.
10. He falls according to the formula d = 16t2.
11. 
approximately
12. They would attain larger velocities as they fell (when d is greater than 1).
13. v = 5.3t; d = (5.3/2)t2
14. v = at; d = (1/2)at2
15. Square both sides in (6). Then v2 = 64d. Hence d = v2/64. When v = 88, d = 121 ft.
16. We can, following the suggestion, use v = 32t and ask what is t when v = 88. Answer: 2 3/4 sec
17. 32 is replaced by 11. Hence d = v2/22.
18. We have d = v2/22. This is the distance traveled when the velocity starts from 0 and the acceleration is 11 ft/sec2. When v = 88, d = 352. If the object starts with 88 ft/sec and decelerates at 11 ft/sec2, it will travel 352 ft before reaching 0 velocity. In one second the automobile travels 88 ft.
19. Let d be the depth of the well (to the water). Then d = 16t2 relates the time and distance of fall. 
is the time for the stone to fall. d/1152 is the time it takes the sound to reach the man. Then 
. To solve this for d, write 
. Now square both sides and we obtain a quadratic equation in d. However, the coefficients are large. A simpler solution is obtained by letting t1 be the time it takes the stone to reach the water. Then 
is the distance to the water and 
is the time it takes the sound to come back. Consequently 
. This quadratic in t1 is easy to solve it we first replace 16/1152 by 1/72. Then t1 = 6.
1. The speed and distance will be greater because the ball has the speed of 128 ft/sec in addition to the speed acquired by the action of gravity.
2. v = 128 + 32t; d = 128t + 16t2.
3. Substitute the t values in (7) and v = 192 and 240 ft/sec. Substitute the t-values in (8) and d = 432 and 756 ft.
4. The curve is a parabola opening upward.
5. Write d = 16(t2 + 6t). Now complete the square. Then d + 144 = 16(t2 + 6t + 9) = 16(t + 3)2. Let t′ = t + 3 and d′ = d + 144.
1. Cf. (10); d = 128t − 16t2.
2. (a) When t = 4, d = 384 ft;
(b) When t = 4, v = 32 ft/sec.
(c) We must first find t when v = 0. This t-value is 5. When t = 5, d = 400 ft.
3. d = 0. This means the ball has just returned to the ground.
4. The height of 512 ft is reached on the way up and 4 sec later on the way down.
5. v = 1000 − 32t; d = 1000t − 16t2. v = 0 when t = 1000/32. Substitute this value of t in the formula for d. d = 15,625 ft
7. v = 96 − 5.3t, d = 96t − (5.3/2)t2, v = 0 when t = 96/5.3 = 18.1 sec, approximately. Substitute this value of t in the formula for d. d = 870 ft, approximately.
8. d = Vt − 16t, where V is the initial speed. We know that d = 0 when t = 60. Hence 0 = 60V − 16 · 602. Then V = 960 ft/sec.
9. The initial velocity at the suggested origin is 300 mi/hr or 300 · 5280 ft/hr. Then d = 300 · 5280t − 16t2.
10. v = 96 − 32t; d = 96t − 16t2.
11. Since the origin in Exercise 10 is at the roof, when the ball returns to the ground, d = −112. Substitute this value of d in d = 96t − 16t2 and solve for t. t = 7 sec
1. (a) 224
(b) 80
(c) 112
(d) 155
(e) 288
2. (a)
(b) 5
(c) 12 1/2
(d) 1/2
3. (a) (0 + 160)/2 or 80
(b) (0 + 256)/2 = 128
4. Yes. At t = 7, v = 224; at t = 8, v = 256. The average speed during the eighth second is (224 + 256)/2 = 240 ft/sec.
5. v = gt; d = gt2/2.
6. (a) Average v = gt/2
(b) d = gt2/2
7. (a) 256
(b) 784
(c) 196
(d) 225
(e) 441
8. (a) 2
(b) 
(c) 3
(d) 
(e) 13/4
9. (a) 160
(b) 176
(c) 224
(d) 332
(e) 288
10. (a) 1
(b) 9/8
(c) 7 3/8
(d) 2 11/16
11. v = 100 + gt; d = 100t + gt2/2.
12. In each case we let d be the given distance and solve the resulting quadratic equation in t.
(a) 2
(b) 4
(c) 1.9 sec, approximately
(d) 1.1 approximately
13. (a) v = 128 − gt
(b) d = 128t − (gt2/2)
14. (a) 144
(b) 140
(c) 80
(d) 44
16. See answers in back of text.
17. Yes. The only change would be that the acceleration due to gravity, which is 32 ft/sec2 on the earth, would have to be replaced be the value that fits the particular body. Thus on the moon, 32 is replaced by 5.3.
1. Since t = x/2, y = 3x/2. This represents a straight line.
2. Since t = x/4, y = 5x2/16. This represents a parabola.
3. Since t = x/2, y = 5x + x2. This represents a parabola.
4. Give values to t and calculate the corresponding x and y. Plot the x and y. The graph is a straight line.
1. The object would have the horizontal speed of the airplane in any case. Without gravity the object would move horizontally at the velocity (speed) of 100 mi/hr and stay alongside the plane. (This is similar to the astronaut′s walk in space except that the motion there is not in a straight line.)
2. The time required will be the same because the vertical motion is given by y = 16t2 in both cases.
3. The equations x = 100t and y = 16t2 describe the motion. When y = 500, 
. This is the time to reach the ground. When 
, 
ft, approximately.
4. The bullet has the speed of the plane plus the speed with which it is fired or 3000 ft/sec.
5. The equations describing the motion are x = Vt, and y = 16t2 when x and y are measured from the point of fire and y is positive downward. We know that x = 300 and y = 1 are correct values. Hence 300 = Vt and 1 = 16t2. Then t = 1/4 and V = 1200 ft/sec.
6. The bomb falls 5280 ft. The vertical motion is given by y = 16t2. When y = 5280, 
. In this time the bomb travels 
ft. Hence it should be released ft before the plane reaches the target. 
ft, approximately.
7. The plane is directly over the place where the bomb strikes the ground because both have the same horizontal motion.
1. Horizontal velocity = 300 cos 40° = 230 ft/sec; vertical velocity = 300 sin 40° = 193 ft/sec.
2. Since t = x/20, y = (−x2/25) + (3x/2). It is a parabola opening downward.
3. Make a table of values by letting t = 0, 1, 2, etc.
4. When the projectile strikes the ground y = 0. The t = 30/16. Hence x = 20(30/16) = 37.5 ft.
5. At the maximum height the vertical velocity is 0. The vertical velocity is given by v = 32t + 30. (The 30 which appears in y = − 16t2 + 30t is the vertical velocity. Compare (7) and (8).) v = 0 when t = 30/32. At this value of t, y = 14.1 ft, approximately.
6. When the shell strikes the ground, y in (8) is 0. Then t = 500/16. The vertical velocity at this value of t is given by (7). At t = 500/16, v = −500. The horizontal velocity is always the same and is 866 ft/sec. We see that the terminal velocity is the same as the initial velocity except that the vertical component is directed downward. The magnitude of the terminal velocity is 
. See Fig. 14-4, where 
.
1. From (20) we have t = x/V cos A. If we substitute this in (22), we obtain y = −(16x2/V2 cos2 A) + x(sin A/cos A).
2. From (21), when vy = 0, we have time = V sin A/32.
3. We substitute the value of t obtained in Exercise 2 in (22). Then max y = V2 sin2 A/64.
4. When the projectile reaches the ground, y = 0. From (22), the time equals V sin A/16. If we look at the time to reach maximum height (see Exercise 2) we see that it takes twice as long to reach the ground again.
5. We must use (25), where now A = 40° and V = 2000. Then x1 = 123,000 ft.
6. We can use the result on p. 322. Max x1 = V2/32 = (800)2/32 = 20,000 ft
7. The maximum range is given by max x1 = V2/32 = (2000)2/32. The angle of fire must be 45°. Now for any x and t, x = Vt cos A [see Eq. (20)]. Hence let x = (2000)2/32, A = 45°, V = 2000 and solve for 
sec
8. In Exercise 3 we found that the max y for any angle of fire is V2 sin2 A/64. For fixed V, this quantity is a maximum when A = 90°.
1. The sketches are made by making a table of values. One can find the direct equation and check.
2. See answers at the back of the text for (a), (b), and (c). As for (d), t = (x − 7)/3 and y = 5[(x − 7)/3] + 9 = (5x/3) − (8/3).
3. (a) x = 240 · 5280t, y = 16t2
(b) Let y = 5280 and solve for 
sec
(c) Same time as in (b) because the vertical motion is the same
(d) Let y = 2 · 5280 in y = 16t2 and solve for 
sec
(e) Since it takes 
sec to fall, the bomb will travel 
ft.
4. (a) 
and
(b) 
(c) Use (25) or since the 45° angle of fire gives maximum range, use V2/32. Answer: 125,000 ft
(d) In Exercise 3 of the preceding list we found that the maximum height is given by V2 sin2 A/64. Here V = 2000 and A = 45°. Answer: 31,250 ft
1. In a geocentric system the earth is fixed and the motions of the other bodies are described as they appear from the earth. In a heliocentric system the sun is regarded as fixed and the motions are described in relation to the sun.
2. No. He continued to use the deferent and epicycle scheme.
3. The sun is at one focus of each ellipse.
4. His main innovation was to replace each system of deferent and epicycles for any one planet by an ellipse. He also gave three new laws of motion.
5. If the planet moves counterclockwise while the epicycle moves clockwise, the path is a crude ellipse. The main point is that a single curve, if reasonably simple, say an ellipse, is easier to comprehend and work with than a combination of curves.
7. Because the scheme was mathematically simpler
8. The student would have to admit that he accepts it because he was taught to do so.
11. Let D be the given distance and calculate T from T2 = D3. Then T = 165 yr.
1. Because one is a constant times the other so that a large mass feels heavy
2. The man's mass is also 160 pounds (of mass). His weight on the moon is 5.3 times his mass or 5.3(160) = 848 poundals. This is also 848/32 pounds of weight.
3. The man's mass is 160 lb. His weight on the sun is 27 · 32 · 160 poundals or 27 · 160 pounds of weight.
2. The acceleration is a = GM/(5000 · 5280)2. We do know that 32 = GM/(4000 · 5280)2. If we divide the first equation by the second, we have a/32 = (4000 · 5280)2/(5000 · 5280)2 = 16/25. Than a = (16/25(32) = 20.5 ft/sec2 approximately.
3. Strictly speaking, no, because the formula d = 16t2 was derived on the assumption that the acceleration is 32 ft/sec2 all along the path.
4. 150 lb (of mass)
5. The mass of the automobile is 3000 lb. Then, by (3), F = 3000 · 12 = 36,000 poundals = 36000/32 lb (of force).
1. The weight or force of gravity is given by (6). Then F = GM · 150/(8000 · 5280)2. We know that 150 · 32 = GM · 150/(4000 · 5280)2. Then F/150 · 32 = (4000 · 5280)2/(8000 · 5280)2 = 16/64 = 1/4. Hence F = 150 · 32(1/4) poundals or 150(1/4) pounds of weight.
2. The law shows how the same mass m has a weight which varies with distance from the center of the earth.
3. Let the two masses be m and 2m. Then the two forces are GMm/r2 and GM · 2m/r2. The latter is twice the former.
4. The man's weight is given by F = GMm/r2 where M is the mass of the earth. If M were one tenth as much, then F would be one tenth as much or 15 lb.
5. By (5) the acceleration would be twice as much. The body would acquire more velocity each second and reach the ground sooner.
6. By (5) the acceleration of the body higher up would be less.
7. In place of F = GMm/(4000 · 5280)2 we would have F2 = GMm/(1000 · 5280)2. Since F = 150, we have F2/150 = (4000 · 5280)2/ (1000 · 5280)2 = 16. Hence F2 = 16 · 150 lb.
8. In the case of F = GMmr/R3, the force increases linearly with r. In the case of F = GMm/r2, the force decreases as the square of r.
9. The weight would still decrease as the distance from the center of the earth increased but it would not decrease so much.
10. Yes. By (6), F/m = GM/r2 and for a fixed r, this ratio is the same for any mass m and its weight F.
1. Yes. According to Newton's first law of motion, if no force acts on an object, the object remains at rest if it is at rest or it moves at a constant speed in a straight line if it is in motion. If an object does not move in a straight line, a force must act on it and this force, by Newton's second law, causes an acceleration.
2. No. We have but to review the derivation to see that it does not.
3. By (24), a = (50)2/5 = 500 ft/sec2. The force is exerted by the hand.
4. The moon's velocity is given by 2π · 240000 · 5280/(26/3) · 24 · 60 · 60 in ft/sec. We now compute v2/r where v is the value just given and r = 240,000 · 5280. The result is a = 0.00897 ft/sec2approximately.
5. The mass of the sun is 4.40 · 1030 lb. The volume of the sun is (4/3)(432,000 · 5280)3. The ratio of mass to volume is about 90.
1. We cannot consider the formula for the variation of mg with latitude. All we can say is that as the latitude increases, more centripetal force is required to keep an object rotating with the earth. Hence less gravitational force is available to supply the weight, and weight decreases as one moves from either pole to the equator.
2. By (30), v2 = GM/r. If the satellite is close to the earth r = R. Also GM = 14 · 1015. Then v2 = 14 · 1015/4000 · 5280. Then v = 26000 ft/sec, approximately.
3. By (30), v2 = GM/240,000 · 5280 = 14 · 1015/240,000 · 5280. Then v = 3300 ft/sec, approximately.
4. The circumference of the moon's path is 2π · 240,000 · 5280. The velocity, by Exercise 3, is 3300 ft/sec. Then the time is the distance divided by the velocity or approximately 27.8 days.
5. We use (30), in which r = 4500 · 5280 ft and GM = 14 · 105. Then v = 24,000 ft/sec, approximately.
1. It applies to all masses in the universe insofar as all uses of it show. The calculations based on it agree with experience.
2. He derived them mathematically from his laws of motion and gravitation.
3. Since Kepler's laws proved to be mathematical consequences of the laws of motion and gravitation -- laws that applied to all other motions -- it was more likely that the heliocentric view, which gives rise to Kepler's laws, is correct.
4. A check on the correctness of physical principles is that one can derive from them conclusions which agree with experience. Since Newton's principles lead to Kepler's laws and the latter are known to be observationally correct, Newton's principles are likely to be correct
1. See answers in answer section of textbook.
2. See answers in answer section of textbook for (a), (b), (c), and (e). (d) 4.675 · 10 (f) 7.4/103
3. See answers in answer section of textbook for (a), (b), (c), and (d). (e) 2.8/103 (f) 6
4, 5, and 6. Answers are given in the answer section of the textbook.
7. (a) By (5), a = GM/(6000 · 5280)2. We know that 32 = GM/(4000 · 5280)2. Hence a/32 = (4000 · 5280)2/(6000 · 5280)2 = 16/36. Then a = 32(16/36) = 14.2 ft/sec2.
(b) The reasoning is the same except that 14,000 replaces 6000. Then a = 2.6 ft/sec2.
8. (a) A man who weighs 200 lb at the surface has 200 lb of mass. When he is 2000 miles above the surface of the earth, then GM/(6000 · 5280)2 = 14.2. Hence the pull of gravity F is m times this latter amount or F = 14.2(200) = 2840 poundals or 2840/32 lb.
(b) Use 7(b) and argue as in 8(a). Answer: 520 poundals
9. The man's mass is 200 lb. On the moon a = GM/r2, where M is the mass of the moon and r its radius. Now a = 5.3. Hence F = 200(5.3) = 1060 poundals = 1060/32 lb.
1. The rate of change of distance compared to time is the change in the distance divided by the interval of time in which that change takes place.
2. Average speed is the average over some interval of time or the distance traveled in that interval divided by the interval of time. Instantaneous speed is the speed at an instant of time as opposed to the average over an interval of time.
3. The notion of limit
4. The distance fallen in 5 seconds is 16 · 52 or 400 ft. The average speed is 400/5 or 80 ft/sec. After 4 sec the body falls 16 · 42 or 256 ft. Hence during the fifth second the body falls 400 − 256 or 144 ft. The average speed during this second is 144/1 ft/sec.
5. Repeat the process on pp. 371–372 with t = 5 instead of t = 4. In step (6) we obtain k/h = 160 + 16h. The limit of k/h as h approaches 0 is 160.
6. At t = 3, d3 = 128 · 3 − 16 · 32. At t = 3 + h, d3 + k = 128(3 + h) − 16(3 + h)2 = 128 · 3 + 128h − 16 · 9 − 16 · 6h − 16h2. Then k = 128h − 96h − 16h2. k/h = 32 − 16h. As h approaches 0, k/h approaches 32.
1. (a) y1 = bx1; y1 + k = b(x1 + h). Then k = bh and k/h = b. Since b is constant, the limit of k/h or 
.
(b) 
Then 
and 
. As h approaches 0, 3ax1h and ah2 approach 0 and k/h approaches 
. Hence 
and since this holds for any x, 
= 3ax2.
(c) y1 = c, y1, + k = c; k = 0; hence k/h = 0 and the limit of k/h = 0. That is, = 0.
2. 
. Then k = 2x1 h + h2 and k/h = 2x1 + h. The limit of k/h as h approaches 0 is 2x1 or = 2x1. The example suggests that the constant in the original function makes no contribution to the derivative.
3. The answers are given in the answer section of the textbook.
4. If we apply (25), we get 
= 100 + 32t. At t = 4, = 228 ft/sec.
5. (a) The instantaneous rate of change of the volume with respect to the radius is the surface of the sphere.
(b) If V = (4/3)πr3, then by (23), 
= 4πr2 and this is the expression for the area of the surface of the sphere.
6. should be 4ax3.
7. If A = x2, then 
= 2x. The result is intuitively reasonable because if we think of a square and think of a slightly larger one (see figure alongside) then the rate at which the area increases depends on the length of 2 adjacent sides AB and BC or we could say that the actual increase for an increase h in x is 2xh + h2 and the rate for the increase h in x is 2x + h. For very small h the rate of increase in area is 2x.
8. = l. Geometrically, for a small change h in w, the increase in area is l/h. Then the average rate is l and in this case l is also the instantaneous rate.
1. (a) = (1/100)2x. At x = 3, = 6/100. This is the slope.
(b) At x = 5, = 10/100. The slope is steeper at x = 5.
(c) At x = 0, = 0. The tangent to the curve is horizontal at x = 0.
2. (a) = 4 − 2x. At x = 1, = 2. The direction is that of the tangent which has a slope of 2.
(b) We must find when = 0. Since = 4 − 2x, = 0 when x = 2.
3. At A the slope and therefore the derivative is some positive number. The slope and therefore the derivative decreases to 0 at the peak then the derivative becomes more and more negative. About halfway toward the lowest point the derivative becomes less negative and then becomes 0 at the lowest point. After that it becomes more and more positive.
4. y = x2 and y = x2 + 5 have the same graph except that the latter is 5 units higher. Then at any given value of x, the slopes are the same. Hence the derivatives must be the same.
1. = 128 − 32t. At t = 4, or v is 0. This means physically that the body has reached the highest point of its motion. Geometrically it means that the graph of d = 128t − 16t2 has the slope 0 at t = 4 or the tangent is horizontal there.
2. A = xy. y = (p/2) − x. Then A = x[(p/2) − x] = (px/2) − x2. Then = (p/2) − 2x. When = 0, x = p/4. Then y = p/4. The rectangle is a square. The calculus method is direct. We know how to proceed. It would take more fumbling to find the geometrical proof.
3. A = xy. y + 2x = 100 or y = 100 − 2x. Then A = x(100 − 2x) = 100x − 2x2. Hence = 100 − 4x. When = 0, x = 25. Then y = 50. Here too, the calculus method is more direct.
4. Let y be the vertical dimension and x, the horizontal one. Then A = xy. But 3y + 2x = 100 or y = (100 − 2x)/3. Then A = x(100 − 2x)/3 = (100/3)x − (2/3)x2. = (100/3) − (4/3)x. When = 0, x = 25. Then y = 50/3.
5. As the text shows, V = 50r − πr3. Then = 50 − 3πr2. When 
. If we substitute this value of r in h = (50 − πr2)/πr we get 
.
1. (a) When t = 6, d = 576. Hence the average speed is 576/6 or 96 ft/sec.
(b) When t = 5, d = 400. Hence during the sixth second the average speed is (576 - 400)/1 = 176 ft/sec.
(c) = 32t. At t = 6, = v = 192 ft/sec.
2. Calculate the instantaneous speed at t = 6. This, by Exercise 1 (c), is 192 ft/sec. This value must be close to the average speed in the interval from 5.9 to 6.
3. = 20x. Hence:
(a) 40
(b) 60
(c) 20a
4. v = = 32t. Hence a = 
= 32.
5. The answers are given in the answer section of the textbook.
6. = 2x + 2 and at x = 2, = 6.
7. = 2x + 2. When = 0, x = −1.
8. (a) = 2x + 10. When = 0, x = −5 and y = −25. A minimum
(b) = 2x − 10. When = 0, x = 5 and y = −25. A minimum
(c) = −2x + 10. When = 0, x = 5 and y = 25. A maximum
(d) = −2x + 6. When = 0, x = 3 and y = 9. A maximum
(e) = −2x + 6. When = 0, x = 3 and y = 11. A maximum
9. = 3x2. At x = 0, = 0. The function does not have a minimum or a maximum at x = 0.
10. 
= 144 − 32t. When = 0, t = 9/2 sec. and h = 324 ft.
11. Let x = a side of the base and y, the height. Then V = x2y. But x2 + 4xy = 400 or y = (400 − x2)/4x. Then V = 100x − (x3/4). Hence = 100 − (3x2/4). When = 0, 
. Then y = 10/
.
12. Using x and y as in Exercise 11, we have V = x2y and 2x2 + 4xy = 400 or x2 + 2xy = 200. Then y = (200 − x2)/2x. V = 100x − (x3/2). Then = 100 - (3x2/2). When = 0, 
. Then 
. Hence the box is a cube.
1. See answer section of textbook.
1. = −32. Thus v = −32t + C. When t = 0, v = 150. Hence v = −32t + 150. Now d = −16t2 + 150t + C. But d = 0 when t = 0. Then C = 0 and d = −16t2 + 150t.
2. Let distance be measured downward from the point 50 ft above where the object is dropped. = 32 and so v = 32t + C. When t = 0, v = 0. Then C = 0 and v = 32t. Hence d = 16t2 + C. When t = 0, d = 50. Then C = 50 and d = 16t2 + 50.
3. Since the distance is measured upward from the ground, = −32 and v = −32t + C. Now v = 0 when t = 0. Then C = 0 and v = −32t. Hence d = −16t2 + C. When t = 0, d = 75. Then C = 75 and d = −16t2 + 75.
4. Since distance is measured upward from the ground, = −32; v = −32t + C. When t = 0, v = 100. Then C = 100 and v = −32t + 100. Next, d = −16t2 + 100t + C. When t = 0, d = 50. Hence C = 50 and d = −16t2 + 100t + 50.
5. Distance is measured upward from the ground. Then = −32 and v = −32t + C. When t = 0, v = −100. Hence C = −100 and v = −32t −100. Then d = −16t2 − 100t + C. When t = 0, d = 50. Then C = 50 and d = −16t2 − 100t + 50.
1. = x2. Then A = (x3/3) + C. When x = 2, A = 0. Then C = −8/3. Hence A = (x3/3) −8/3. When x = 6, A = (63/3) −(8/3) = 69 1/3.
2. As in Exercise 1, A = (x3/3) + C. When x = 4, A = 0. Then A = (x3/3) − (64/3). When x = 6, A = (216/3) − (64/3) = 50 2/3.
3. = x. Then A = (x2/2) + C. When x = 4, A = 0. Then C = −8 and A = (x2/2) − 8. When x = 6, A = 10.
4. = x2 + 9. Then A = (x3/3) + 9x + C. When x = 3, A = 0. Then C = −36. Hence A = (x3/3) + 9x − 36. When x = 6, A = 90.
1. We may use (29). The 500-lb weight has a mass of 500 lb. Hence 
. If we neglect the factor 32, the answer in ft-lb is about 257,000,000.
2. If the gravitational force were always what it is at the surface of the earth it would be GMm/R2 [see Eq. (23)]. However (p. 400), GM = 32R2. Hence the force would be 32m. Hence the work would be 32 · 500 · 100 · 5280. If we neglect the 32 to keep the answer in ft-lb, the result is 264,000,000.
3. From k = [300 + 2(100 − 
)]h we have that k/h = 300 + 2(100 − ). When h approaches 0, k/h approaches 
and approaches x. Hence = 300 + 2(100 − x) = 500 − 2x. Then W = 500x - x2 + C. When x = 0, W = 0. Hence W = 500x − x2. To raise the tool completely x = 100. Then W = 40,000 ft-lb.
4. W1 = c/r1. W1 + k = c/(r1 + h). Then k = [c/(r1 + h)] - [c/r1] = −ch/(r1 + h)r1 = 
. Hence 
. When h approaches 0, 
or for any r, = −c/r2.
1. Use (33) with R = 4000 · 5280 and d = 240,000 · 5280. Then V = 36,500 ft/sec, approximately.
2. The derivation of (34) applies to escape velocity from the earth. However, the only place in which we used a value which applies specifically to the earth was in deriving (29) where we used the fact that GM = 32R2. For M the mass of the moon, GM = 5.3R2 where R is the radius of the moon. Then (34) becomes, for the moon, 
.
1. The basic new idea is the limit concept.
2. The history of the calculus shows that mathematicians go through a period of thinking and fumbling before they arrive at the correct logical approach.
1. (a) Starting with = −32, we have v = −32t + C and since v = 200 when t = 0, v = −32t + 200. Then d = −16t2 + 200 + C. But d = 0 when t = 0. Hence d = −16t2 + 200t.
(b) At the maximum point or v = 0. Hence t = 200/32 and d = −16(200/32)2 + 200(200/32) = 625 ft.
(c) When the object hits the ground, d = 0. Then t = 200/16. Substitute this value of t in v = −32t + 200 and we obtain −200 ft/sec.
2. (a) The height above the roof is obtained exactly as in (a) of Exercise 1. Then d = −16t2 + 200t.
(b) The height above the ground is d = −16t2 + 200t + 100.
3. (a) = −5.3. Hence v = −5.3t + C. When t = 0, v = 200. Hence C = 200 and v = −5.3t + 200. Then d = −(5.3/2)t2 + 200t + C. When t = 0, d = 0. Then d = −(5.3/2)t2 + 200t.
(b) The maximum height is attained when or v is 0. Then t = 200/5.3. Substitute this value of t in the formula for d and we obtain d = 3585 ft.
(c) The object loses less velocity per second as it rises because the downward acceleration is only 5.3 ft/sec2 on the moon and 32 ft/sec2 on the earth. Hence it takes longer for the velocity to become 0.
4. (a) = 3x. Then A = (3x2/2) + C. When x = 0, A = 0. Hence C = 0 and A = 3x2/2. When x = 4, A = 24.
(b) The triangle is a right triangle with arms of 4 and 12. Hence the area is (1/2)(4)(12) = 24.
5. (a) = 2x + 7. Then A = x2 + 7x + C. When x = 4, A = 0. Then C = −44. Hence A = x2 + 7x − 44. When x = 6, A = 34.
(b) The area of the trapezoid is (1/2)(2)(15 + 19) = 34.
6. Use (29) with m = 200, R = 4000 · 5280 and r = 4100 · 5280. Then W = 3297 · 106 poundals.
7. Use (33) with R = 4000 · 5280 and d = 100 · 5280. Then V = 5700 ft/sec, approximately.
1. Answers are given in the answer section of the textbook.
2 and 3. Answers are given in the answer section of the textbook.
4. Because every 360° the function repeats the values it takes on in the preceding 360° interval
5. It describes the height of Q above or below 0.
6. The function y = sin A first of all emphasizes the relation between two variables, A and y. Moreover, the function is defined for all values of A.
7. It starts from 0, rises to 1 at 90°, falls to 0 at 180°, falls farther to −1 at 270° and then rises to 0 at 360°. Thereafter it repeats this behavior every 360°.
8. Two values.
9. The period is 360°. The cycle refers to the set of y-values going from 0 to 1 to −1 to 0.
1, 2, and 3. The answers are given in the answer section of the textbook.
4. The variation of A from 0 to 2π produces the same variation in sin A as when A goes from 0 to 360°. Hence see Exercise 7 of the preceding list.
1, 2, 3, and 4. See the answer section of the textbook.
5. The shape is the same as when t varies from 0 to 1. See Fig. 18-12.
6. The shape is similar to that of Fig. 18-12 except that there are 3 full cycles of y-values in the interval from t = 0 to t = 1.
7. The shape is that of Fig. 18-12 except that all y-values are twice as large (or as small when y is negative).
8. Comparing with (7), we see that f = 10.
9. See the back of the textbook.
1. From (15) we have 32 · 2 = (l/2)k or k = 128.
2. Use (22). 
3. T = 1/f = 0.01 sec
4. By (21), y = sin 2πft provided the amplitude or maximum displacement is 1. If it is D, then y = D sin 2πft. [Cf. Eq. (24)]. In our case f = 50 and D = 3 in.
5. Use (24). D = 3 in. = 1/4 ft. k = 75 and m = 3. Hence y = 3 sin 5t or, in feet, y = (1/4) sin 5t.
6. In (25), T = 1 and k = 50. Hence m = 50/4π2 lb.
7. (a) The mass makes 5 oscillations or has a frequency f of 5 and it moves 4 units above and below its equilibrium position.
(b) 2πf = 10. Hence f = 5π. The amplitude is again 4.
8. By (22), 
. Make m larger to decrease f.
9. Compare a = −(GM/R3)r with (18) where a = −(k/m)y. In each case the acceleration is a constant times the displacement. Now (18) leads to (24). Hence by the very same steps, except that r replaces y and GM/R3 replaces k/m, we get r = D sin 
t. Thus the man oscillates back and forth in the tunnel. Since D is the initial displacement, the man will go from one end of the tunnel to the other and back again repeatedly.
1. y = D sin 2πft. Here the D is the amplitude or the maximum. displacement which a typical air molecule undergoes. f is the number of times per second that the typical molecule makes a complete oscillation or a complete back-and-forth motion about its mean or rest position.
2. y = 0.0005 sin 2π · 300t.
3. The frequency is 540 and the amplitude is 0.002 in.
4. 400/20 or 20 cycles/sec
1. (a) y = sin 2πt has a frequency of 1 in one second along the t-axis and y = sin 6πt has a frequency of 3. Both have an amplitude of 1. Sketch both on the same axes and add ordinates as is done in Fig. 19-5.
(b) y = sin 2πt has a frequency of 1 in one second along the t-axis and an amplitude of 1. y = (1/2)sin 4πt has a frequency of 2 and an amplitude of 1/2. Sketch both on the same set of axes and add ordinates as is done in Fig. 19-5.
(c) y = sin 2πt has a frequency of 1 in one second, y = sin 3πt has a frequency of 1 1/2. This means that the graph will go through 1 1/2 cycles in one second. The amplitude is 1. Graph both on the same set of axes and add ordinates as is done in Figure 19-5.
2. (2) y = sin 8πt repeats its behavior 4 times in one second. Hence the entire function will repeat when y = sin 2πt repeats, that is, after one second. The frequency of the entire function is 1.
(b) The frequency of y = 2 sin 2πt is 1 and that of y = sin 4πt is 2. Hence the two together will repeat when the first one does; that is, the frequency of the entire function is 1.
(c) As in (b), all three functions will repeat when the first one does. Hence the frequency of the entire function is 1.
(d) The respective frequencies of the three terms are 100, 200, and 300. The entire function repeats when the first one does, that is, after 1/100 of a second. The frequency of the entire function is 100.
1. See p. 446, lines 11 to 13.
2. The frequency of the entire sound is 240. The amplitude of the third harmonic is 0.01.
3. See answer section of textbook.
4. The third harmonic has a frequency three times that of the fundamental or 3 · 720.
5. The harmonics beyond the first one (the fundamental tone) repeat their behavior many times in each cycle of the first harmonic. Hence the entire sound repeats when the first harmonic does. If this one repeats itself, say 100 times a second or has a frequency of 100, then the others certainly repeat themselves each time the first one does; so the entire sound repeats when the first one does.
1. The first has a larger amplitude and so is louder. The second one has a larger frequency and so is higher pitched.
2. A simple sound is one in which the motion of a typical air molecule can be represented by y = D sin 2πft.
3. A musical sound repeats its behavior many times a second or is periodic. Noise is aperiodic or irregular. Hence the musical sound can be represented by a sum of sine functions according to Fourier's theorem.
4. The pitch of a complex sound is set by the frequency of the first harmonic. The quality depends on which harmonics are present and their amplitudes.
5. Musical sounds can be represented mathematically but music appeals to the ear, and the physiological processes and individual reactions are not contained in the mathematics.
1. See p. 453, line 8.
2. Euclid's parallel axiom is a somewhat complicated statement, and therefore was not as self-evident a truth as axioms were supposed to be.
3. The alternative axioms such as Playfair's made assertions about what happens far out in space beyond man's experience. As mathematicians began to appreciate this fact, they became dissatisfied with such assertions as axioms.
4. Saccheri proposed to take the two alternative possibilities -- no parallel lines to a given line and more than one parallel line to a given line -- and show that when each of these is used as an axiom in conjunction with Euclid's other axioms (of course, aside from Euclid's parallel axiom), then a contradiction can be deduced. Thus the only remaining possible state of affairs, the existence of one and only one line parallel to a given line, would have to be true.
5. No. Saccheri did not arrive at a contradiction when he assumed that there could be more than one parallel line to a given line, but he did deduce such strange theorems that he, nevertheless, decided that such a geometry was impossible. He did arrive at a contradiction by assuming that no parallel lines exist. His conclusion was that Euclid's geometry is the only possible geometry.
6. They realized that an alternative geometry was possible (there was no contradiction in it) and that such an alternative geometry could apply to physical space.
1. See p. 458, middle.
2. In Euclid's geometry, parallel lines are lines (in the same plane) which have no point in common. In Gauss's geometry, the term parallel lines is reserved for the two lines (m and n on p. 458) which separate those lines through point P which do meet a given line l from those which do not.
3. See p. 459, the next-to-the-last paragraph.
4. See p. 459, the last paragraph.
5. The triangle with angle sum of 170°.
6. Both triangles have an angle sum of 170°. Their areas must be equal because, if one area were smaller than the other, the triangle of smaller area would have to have an angle sum closer to 180°.
7. The triangles are similar.
1. Riemann pointed out that experience tells us only that a line is endless, not that it is infinite.
2. There are no parallel lines.
3. Theorems which can be derived from those axioms which are alike in Gauss's, Euclid's and Riemann's geometries will be the same.
4. Gauss's geometry is more like Euclid's because only one axiom is changed -- the axiom on parallel lines.
5. In Euclid's geometry the sum is 180°; in Gauss's, the sum is always less than 180°; and in Riemann's geometry the sum is always more than 180°.
6. See p. 461, last paragraph.
7. A geometry whose axioms differ from Euclid's and, consequently, whose theorems differ from Euclid's
8. It is obliterated. Similar triangles must be congruent.
1. Not if one uses figures of ordinary or small size.
2. Yes, because all agree to within possible measurements
3. Because the sum of 179° 59' 58" was subject to experimental error so that the true sum could be more, equal to, or less than 180°
1. The concept of line in Euclidean geometry is undefined and must merely possess the properties stated in the axioms. This is true of the "lines" on a cylindrical surface.
2. Definitions presuppose other concepts in terms of which the definitions are made. Hence one must start with undefined concepts.
3. If we interpret line to be great circle on the sphere.
4. Yes. The geometries created by mathematicians are intended to fit or describe physical space and do so rather well, but no one of them may be the precise description of the geometrical properties of physical space.
5. In some instances, yes. Builders and carpenters often do, but surveyors and astronomers use light rays.
6. The character of the geometry would almost certainly be some kind of non-Euclidean geometry.
1. Since several geometries which differ from one another all fit physical space, we can no longer decide which is the true one. We are forced to conclude that mathematics is not necessarily a body of truths.
2. The mathematical space merely has some correspondence with physical space. The former is constructed by human beings; the latter is fixed in the real world and independent of human beings.
3. Yes, in the sense that the applicability of its results must be checked. Yet mathematics differs primarily in the concepts with which it deals and in its insistence on deductive proof.
1. That mathematics is not a body of truths about the physical world
2. It caused scientists to face the fact that scientific theories are not truths and that science cannot seek truths because these may be unattainable. Scientists can construct useful theories.
3. In both cases, law and mathematics, fundamental axioms or principles are assumed and consequences are deduced. But the principles of two different legal systems will differ, and so will the consequences. This is the case in geometry also.
4. Yes. If one recognizes that all science can do is provide a theory which agrees with experience, the existence of non-Euclidean geometries gives more latitude in the formation of useful theories.
1. No. From the standpoint of what happens physically, 10 + 10 does not give 20.
2. No. We may to the best of our ability to measure decide that the smaller bags each contain 10 lb. But when we put them together, we may be able to measure the error and find that the total weight is more or less than 20 lb.
3. If we assume that the 5-lb weights are very accurate, the scale will still balance. The axiom involved is that equals added to equals give equals.
4. If we assume that the 100-ft/sec velocity and the 32t-ft/sec velocity are precise figures, then the two velocities add.
5. No. The frequencies do not add. The readers who covered Chapter 18 would recognize that the combination of the two sound waves would have a frequency of 50 cycles/sec.
6. The mixture has a temperature of 45°.
1. No. We have seen (p. 483, bottom) that in adding batting averages, we cannot replace 2/3 by 4/6 or 8/12.
2. We must show that
or
or
or
3. Any fraction whose numerator is −1. Thus 1/2 + −1/2 = 0/4 = 0.
4. Yes.
1. As examples of entries in the addition table, we have 5 + 4 ≡ 2, 6 + 1 ≡ 0, 6 + 2 ≡ 1, 6 + 3 ≡ 2, etc.
2. As examples of entries in the multiplication table we have 5 · 4 ≡ 6, 5 · 5 ≡ 4, 6 · 1 ≡ 6, 6 · 2 ≡ 5, 6 · 3 ≡ 4, etc.
3. Yes.
4. To divide 4 by 2 we need some number x such that 4 ≡ 2x, modulo 6. The possible values of x are 0,1,2,3,4, and 5. For x = 2, we have 4 ≡ 4, modulo 6 and this is correct. Hence one answer is 2.
To divide 3 by 2 we need an x such that 3 ≡ 2x, modulo 6. Again the possible values are 0,1,2,3,4, and 5. No one of these numbers serves as an answer.
5. To find an x such that 4 ≡ 2x, modulo 7, we have x = 2. To find an x such that 3 ≡ 2x, modulo 7, we have x = 5. If the modulus is a prime number, we can always divide one number by another in that modular arithmetic.
6. 9 or 9 ± any multiple of 12
7. a ≡ b, modulo m, means a = b + pm and c ≡ d, modulo m, means c = d + qm. Then a − c = b − d + (p - q)m. Since (p - q)m is a multiple of m, a − c ≡ b − d, modulo m.
8. a = b + pm; c = d + qm. Then ac = bd + bqm + dpm + pqm2 = bd + (bq + dp + pqm)m. We see that ac − bd is a multiple of m. Hence ac ≡ bd, modulo m.
9. We cannot always divide one congruence by another.
10. Two numbers each congruent to a third, modulo m, are congruent to each other, modulo m.
11. The sum is 1220. The sum of the digits in this sum is 5. The sum of the digits in 578 is 20 or 2, modulo 9. The sum of the digits in 642 is 12 or 3, modulo 9. We see that the sum of the sums of the digits, that is, 2 + 3, is congruent to the sum of the digits in 1220.
12. The product is 371,076. The sum of the digits in this product is 24 or 6, modulo 9. The sum of the digits in 578 is 2, modulo 9, and the sum of the digits in 642 is 3, modulo 9. The product of these sums, that is, 2 · 3, equals the sum of the digits in the original product.
13. (a) Yes. (a + b) − (b + a) = 0 and 0 is a multiple of m.
(b) Yes. a + (b + c) ≡ (a + b) + c, modulo m, because a + (b + c) = (a + b) + c.
(c) Yes. a(b + c) ≡ ab + ac, modulo m, because a(b + c) = ab + ac.
14. (a) 5
(b) 3
(c) 6
(d) 2
(e) 4
(f) 3
15. (a) 1, 4
(b) 0, 2, 4
(c) 1, 3, 5
1. Since the union is B, all the objects in A are in B.
2. All the objects in A must also be in B.
3. Because many of the properties of addition, e.g., the commutative and associative properties, hold for union as well as ordinary addition
4. A ∩ A = A and A ∪ A = A.
5. The objects common to A and B ∪ A are just those in A. Hence the answer is A.
6. Let A be the set of all professors, B the set of all intelligent persons, and C the set of all students. The premise that all professors are intelligent becomes A ∩ B = A. The premise that no students are intelligent becomes B ∩ C = 0. Then by "multiplying" the two equations (see p. 496, Step 14) we have (A ∩ B) ∩ (B ∩ C) = A ∩ 0 or A ∩ B ∩ C = 0 or, since A ∩ B = A, A ∩ C = 0. This conclusion means that no professors are students.
7. An object is in A ∩ (B ∪ C) if it is in A and in B or C. Such an object is then in A ∩ B or in A ∩ C. Hence it is in (A ∩ B) ∪ (A ∩ C). Conversely, if an object is in (A ∩ B) ∪ (A ∪ C), it must be in A ∩ B or A ∩ C or both. If it is in A ∩ B, it is in A and in B. Hence it will be in B ∪ C and in A ∩ (B ∪ C). Thus, any object in one side of the given equation is in the other and the two sides must be co-extensive.
8. (a) A ∩ B can contain no more than is in A. Then A ∪ (A ∩ B) is A.
(b) A ∪ B surely contains all the objects in A. Then A ∩ (A ∪ B) is A.
(c) A − B contains all the objects in A that are not in B. Then (A − B) ∪ B contains what is in A but not B and what is in B, the latter also containing the rest of A. Then (A − B) ∪ B = A ∪ B.
9. We have to show that for at least some A's and B's there is no X such that A = B ∩ X. Suppose B is contained in A. No matter what X is, B ∩ X cannot be greater than B. Hence B ∩ X cannot equal A because A contains objects not in B.
1. See p. 502.
2. 8113; 1200.
3. 6.1; 5; 10. The mean is the best representative because it takes into account that 6 students got a grade of 10. If only 1 has a grade of 10 and 6 a grade of 8, the median would be the same but the mean would change.
4. 31; 35; 40. Here it is more difficult to say which average best represents the data. The mean or median would be a reasonable choice.
5. If the word average means median than the statement is automatically correct by the definition of median and so affirms nothing. If the word average means mean or mode (assuming there is some measure of intelligence), then it need not be true.
6. No, because the depth may be 10 ft in one area and still there may be a mean depth of 4 ft.
1. 3.24
2. 3
3. 12.8
4. The variations from the mean height are greater in the city where the standard deviation is 3 in.
5. A grade of 75 where the standard deviation is 5 means that the student did much better than most of the students because most grades were grouped more closely about 65 in this case.
6. The standard deviation is a measure of how closely the data are grouped about the mean or how much they depart from the mean.
1. It is a graph or table which shows a set of data (scores, grades, wages) and how many people, for example, are associated with each one of the data.
2. See p. 508.
3. 95.4%
4. 47.7%; 99.8%
5. The graph is a normal frequency curve with the portion to the left of one o to the left of the mean chopped off.
6. The modal income is 95. The mean would lie to the left because the number of people earning salaries that are smaller than 95 is much larger than the number of people earning larger salaries.
7. There are two different species, each with its own mean and variations from that mean.
1 and 6. See answer section of textbook.
7. The formula is a concise representation of the data. Moreover, we can use the formula to calculate values of the dependent variable for given values of the independent variable (these values may not be in the given data). Of course, to do so assumes the formula has a validity beyond that in the given data.
8. He would know a good deal about what types of equations fit curves of given shapes and so be able to select the form of the equation to fit a given curve.
1. One would expect high ability in mathematics.
1. The deductive approach starts with axioms that seem to apply to the field and then deduces conclusions. The statistical approach starts with data and uses techniques to obtain more or less reliable information from the data.
2. The phenomena of economics are so complex that one cannot find basic axioms.
3. No. The population may be increasing and the percentage of unemployed may actually be decreasing. Or, if women lose jobs, their husbands may be earning more and so the families can be better off.
4. No. The records of what deaths are due to cancer may be more accurate or the identification of cancer as the cause of death may be surer.
5. Bo. The cause may be some physiological or neurological factor which prompts men possessing it to smoke.
6. No. The intelligence of the children may be due to the greater intelligence of the parents. More intelligent parents may marry late because they enter professions requiring a lot of schooling. Hence it may not be the age of the parents but their intelligence.
7. No. The people who live longer may have better physical constitutions, but because they live so long get to need false teeth.
1. One. It means the event is certain to happen.
2. Zero. It means the event is impossible.
3. The probability of a 2 is 2/6. The probability of a 3 is 3/6. The probability of 3 or more is 4/6.
4. No. The two possible outcomes, living or dying, are not equally likely.
5. 6/10
6. 13/52
7. Distinguish the coins as, say, penny, nickel, dime, quarter. There are 16 possible ways in which they can fall. Four of these would be 3 heads and a tail. Hence 4/16
8. 1 − (5/32) or 27/32
9. 3/6
10. It is improbable but not impossible.
11. 6 · 6 or 36 in all
12. 4 and 1; 1 and 4; 2 and 3; and 3 and 2. Hence 4
13. 4/36 in view of Exercises 11 and 12.
14. 1/248.
15. On p. 525 we find that the probability of 2 heads and a tail on a single throw of three coins is 3/8. But, as pointed out on p. 525, to throw one coin 3 times is the same as throwing three coins simultaneously.
16. During the five-minute interval from 8 to 8:05, say, there are four minutes for which the first train will be southbound and only one minute for which the first train will be northbound. If the young man enters the station at any time during the five-minute interval he will be 4 times as likely to get there between 8 and 8:04 as between 8:04 and 8:05. Hence the probability of getting a southbound train is 4/5.
17. 
or 1
18. The probability of two tails is 1/4; the probability of at least one head is 3/4. Hence the odds are 
.
1. Take the number of people alive at age 40 and divide it into the number of people alive at age 60.
2. 85/100; 58/85.
3. The problem is the same as the probability of 3 heads in a throw of three coins. Hence 1/8.
4. The probability that all four will recover without any treatment is the same as the probability of 4 heads in one throw of four coins. This is 1/16. This is not very unlikely. Hence it is not clear that the treatment is really the reason that all four recovered.
1. The probability of a height falling within 3a to the right of the mean is 0.499. The probability of a height falling within 2a on either side of the mean is 0.954.
2. The probability of a bulb falling beyond la to the left of the mean is 0.159.
3. The probability of falling beyond 2a to the right of the mean is 0.023.
4. The probability of falling within lσ to the right of the mean is 0.341.
5. The probability of falling between lσ and 2σ to the right of the mean is 0.136.
1. The eighth row is 1, 7, 21, 35, 35, 21, 7, 1. The sum is 128. The probability of 4 heads and 3 tails is 35/128.
2. From the seventh row of Pascal's triangle we obtain 15/64.
3. The probability of two heads (Exercise 2) is 15/64. Hence (15/64)2000.
4. The mean number of heads is 10,000/2 or 5000. The standard deviation of the frequency distribution of heads is 
or 50, To get 5100 heads or more, one must get a number of heads which lies more than 2σ to the right of the mean. This probability is 0.023.
5. The mean number of those who normally survive out of 100 is 50. The standard deviation of the probability curve which shows the probability of 1, 2, . . . , 100 surviving is 
, The chance of 65 or more surviving is the probability of a number more than 3a to the right of the mean, and this is 0.001. The likelihood of 65 or more surviving without treatment is very small. Hence the likelihood that the treatment is effective is high.
6. Here the mean is 500 and the standard deviation of the probability curve of 1, 2, . . . , 1000 people surviving is 
, approximately. The probability of 650 people surviving is the probability of something which lies about 10a to the right of the mean. This probability is very small. Since under treatment 650 did survive, the likelihood that the treatment was effective is very great.
7. The mean number of boys, on the hypothesis that boys and girls are equally likely, is 800, and the standard deviation of the probability curve of the various possible number of boys is 
. The number 860 lies 3σ to the right of the mean, and the probability of at least 860 boys is 0.001. Hence the hypothesis is to be discredited.
8. If the coins are unbiased, the mean number of heads is 800 and the standard deviation of the number of heads is 
. The probability of at least 860 heads is 0.001. Hence the hypothesis that the coins are unbiased is very unlikely. However, one must be more cautious in this case because there is, after all, the possibility of 860 heads in a toss of 1600 coins.
9. The mean number of those who should be alive at the age of 70 if the probability of living is 1/2, is 200. The standard deviation of the probability distribution that 1, 2, 3, . . . people will be alive at age 70 is 
. Since only 150 were alive, the number of those alive is 5a below the mean. The probability of an event 5a or more below the mean is very small. Hence under the 50% death rate, the probability that only 150 should be alive at age 70 is very small. One must conclude that the death rate in that industry is not 1/2 but much greater.
1. (a) 1/19
(b) 1/19
(c) 9/38
2. (a) 4/52
(b) 13/52
(c) 16/52
3. 2/6
4. (a) 3/7
(b) 4/7
(c) 1
5. (a) 3/9
(b) 4/9
(c) 7/9
6. (a) 1/36
(b) 1/36
7. (a) 65/100
(b) 65/70
(c) Yes
8. Since 61 inches is 2σ below the mean, the probability of a height 2a or more below the mean is 0.023.
1. Concepts, axioms, and theorems.
2. Yes. The whole numbers are direct abstractions from experience with individual objects. The irrational numbers were created to provide ideally exact lengths. Such numbers are not arrived at by the experience of measurement.
3. We must start with some premises in order to make deductive proofs.
4. The growth of mathematics since Greek times has been enormous. Moreover, our understanding of what the Greeks produced differs radically from what the Greeks took mathematics to be.
5. Algebra, Euclidean geometry, projective geometry, trigonometry, non-Euclidean geometries, etc.
6. A willingness to tackle problems suggested by phenomena of nature. As more phenomena are explored, more problems are suggested. There must be support for men who spend their time in solving such problems, and communication among mathematicians so that all can take advantage of what has been created.
7. The formulation and solution of new problems whether suggested by scientific work or devised by minds speculating about numbers or geometrical figures
8. Reliability of the conclusions; the discovery by reasoning alone of implications of the axioms; prediction of physical events
1. Concepts and rational schemes or theories to represent physical phenomena; comprehension to the extent that such schemes explain; an ordering of physical knowledge; prediction of physical events.
2. Because the concepts embody the essential features and are not encumbered by irrelevant physical properties. Moreover, the same concepts and results apply to many different physical phenomena or situations.
1. The study of nature, the aesthetic values, and intellectual activity
2. The arguments for mathematics as an art are given on pp. 550–552. One could attack the thesis on the ground that an art must appeal to the senses or at least through the senses.
3. Pure mathematics is concerned with ideas and problems that are investigated primarily because they are aesthetically or intellectually attractive. Applied mathematics is concerned with ideas and problems directed to the investigation of nature.
4. Yes. However, to produce worthwhile mathematics they must offer either usefulness to science and engineering or aestheticallly valuable material.
