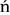ski, Waclaw, 627, 801–2parallel computation, 587, 603
parallel postulate, 42, 84–88, 90, 94
parity function, 588
partial derivative, 33
partial differential equations (PDEs), 34–35, 187, 455–83, 681–82, 993–94; criticality of, 479–80; dispersive, 236, 468, 471; elliptic, 468–71, 681–83; fully nonlinear, 462; homogeneous linear, 457; hyperbolic, 468–70, 490; inhomogeneous linear, 457–58; linear, 51, 458, 471–72; local solvability of, 471; nonlinear, 457; order of, 461; parabolic, 468, 470–71; quasilinear, 462; regular, 480, 482; semilinear, 462; subcritical, 479–80, 482; supercritical, 479–80, 482; symbols of, 682–83
partial differential operators, 239
partition functions, 62, 529, 667, 669
partitions: of natural numbers, 555, 797, 807, 994–95; of sets, 558
Pascal, Blaise, 741–42
Pascal’s triangle, 741
Pasch, Moritz, 137–39
path integral, 38, 526–28, 541, 545
Peano, Giuseppe, 111, 128, 138, 701, 787–88, 795
Peano arithmetic, 138, 151, 154, 258–59, 638, 701, 787, 819; first-order, 259, 638
Pell equations, 98, 255, 315, 317, 706
Penrose, Roger, 829
Penrose staircase, 951
Penrose filings, 829
Penrose’s incompleteness theorem, 492
percolation, 662–66
Perelman, Grigori, 281, 388, 401–3, 406, 440, 461, 714, 970
perfect matchings in a graph, 566, 587, 596
perfect number, 104
perfect phylogeny problem, 846
periodic points, 498–99
permanent of a matrix, 591
permutation matrices, see matrices, permutation
permutations, 174, 259–61, 420, 558
Perron’s formula, 336
perspective, 945–46
perturbation theory, 527–28, 541
phase of a Fourier coefficient, 859
phase problem in crystallography, 829
phase space, 286
phase transitions, 7, 261, 573, 657, 660–64, 667–68, 845
phenomenological equations, 480–81
philosophasters, 935
phylogenetic tree, 846
π, 60, 79, 108–9, 222–23, 261–62, 325, 748; continued fraction for, 192; formula for, 262, 998–99; hexadecimal expansion of, 262, 998–99; transcendence of, 81, 223, 262
Picard iteration method, 465, 470
pigeonhole principle, 167, 567; proof complexity of, 591–94
Pisot number, 828
pivoting in Gaussian elimination, 607
planar graphs, see graphs, planar
Plancherel theorem, the, 207, 212, 261, 427, 453, 686
Plateau problem, 458
Plato, 83–84
Platonic solids, 52, 84, 187, 189
Poincaré, Jules Henri, 42, 93–94, 146–47, 152, 209, 215, 400, 403, 432, 484, 495–96, 690, 714, 722, 727–28, 785–87, 802, 946–48
Poincaré conjecture, 141, 219, 403, 714, 786; in four dimensions, 404; in more than four dimensions, 404–5
Poincaré duality, 189
Poincaré map, 495
Poincaré quantum group, 275
Poincaré transformations, 457, 478
Poincaré’s recurrence theorem, 690–91
point at infinity, 41, 43, 267, 356, 366, 370, 386, 721
Poisson, Siméon-Denis, 757
Poisson bracket, 286, 525–26, 541
Poisson distribution, 264
Poisson equation, 286–87, 457–58, 483, 492
polar convex body, see duality, of convex bodies
polarization identity, 268
Pölya-Redfield enumeration, 559–61, 831
polynomial equations, 49–50
polynomial ring, 24
polynomial time, 169
polynomial-time algorithms, 197–98, 350, 353, 355, 551, 579, 873–74, 880; for primality testing, 353
polynomial-time reducibility, 582–83, 591
polynomials, 284, 326, 328–29, 363–65, 738; approximation by, 253
polytopes, 52
Pontryagin classes, 394
Pontryagin duality, see duality, Pontryagin
position operator, 286
positional system for numbers, 77
posterior distributions, 160, 920, 926–27
postmodernism, 967–69
potentials in complex dynamics, 503–4
Potts model, 669
power series, 38, 122, 126, 144, 201, 308, 368, 752
power-set axiom, 157, 314, 620–21
preconditioning a system of linear equations, 609
presentations of groups, 433–34
primality testing, 351–53, 595; polynomial-time, 352–53; randomized, 351–52, 892
prime factorization, see factorization of integers, into primes
prime number theorem, 63, 338, 346, 356, 714–15, 729, 804
prime numbers, 63, 69–70, 75, 319, 325, 332–36, 338–41, 348–53, 357, 714–15; distribution of, 229, 283–84, 356–59; gaps between, 66, 342–45
primitive polynomials, 888
primitive recursive functions, 111–12
Princet, Maurice, 947
principal ideals, 58, 221, 322–23
Principia Mathematica (Newton), 87, 136, 743, 750
Principia Mathematica (Whitehead and Russell), 147, 149, 781, 795
prior distribution, 160, 920, 926
prisoner’s dilemma, 901
private goods, 901
probabilistic computation, 269–71
probabilistic method, 197, 563, 572
probabilistic proof systems, 596–99
probabilistically checkable proofs, 598–99
probability amplitudes, 269–71
probability distributions, 263–71, 917
probability theory: foundations of, 793, 795, 814–15
probability thresholds, 661–62
Proclus, 85
products, 23–24
projections, 43, 240–41, 295, 422; Mercator, 978; orthogonal, 240–41, 295, 518; stereographic, 169, 401
projective determinacy, axiom of, 632–34
projective geometry, 43, 92, 169, 173, 187, 267, 356, 388, 400
projective orthogonal groups, 688
projective representations, 544
projective spaces, 161, 230, 267, 300, 313, 365
projective special linear groups, 41, 43, 688
projective unitary groups, 688
projective varieties, see varieties, projective
proof complexity, 591–94
proofs, 74, 129–42, 622, 637, 642, 646; by contradiction, 150
propagation of singularities, 467, 469
proper time, 485
propositional logic, see logic, propositional
propositions, 73
protein folding, 841
protein structure, 835
pseudorandomness, 116, 600–602
pseudosphere, 92
PSPACE, see complexity classes
public goods, 901
public-key cryptography, 602, 890–95
pure states, 270
Putnam, Hilary, 50
Pythagorean comma, 936
Pythagorean tuning system, 936
QR factorization, 607–8
quadratic convergence, see convergence, quadratic
quadratic equations, 49, 133, 193, 708
quadratic fields, 254
quadratic forms, 267–69, 317, 319; binary, 320–23, 325; positive definite, 268
quadratic reciprocity, see reciprocity, quadratic
quadratic residues, 104, 317, 325, 327, 339
quadratic sieve method, 354–55
quadratic variation of a martingale, 652
quadratic-like mappings, 508
quadrature, 292, 609, 614; Clenshaw-Curtis, 609; Gaussian, 292, 609
quadric surface, 62
quadrivium, the, 935
quantifiers, 14, 31, 149, 621, 635–36, 638, 640–41; elimination of, 640–44
quantum computation, 269–72
quantum field theories, 528–29, 542–48; topological, 227
quantum groups, 272–75
quantum mechanics, 269, 287, 513, 526, 539; operator formulation of, 526
quartic equations, 99, 101, 326, 709, 737
quasi-conformal mappings, 713
quasi-isometry, 443–45
quasi-Newton methods, 613
quasicrystals, 828–29
quaternions, 82, 105, 276–79, 389, 765
Quechua numeration, 984–85
quintic equations: insolubility of, 50, 101, 327, 708–10
quotients, 24–26, 28, 257, 284; of groups, 26; of rings, 284
radial lines, 504
radical of a positive integer, 361, 681
Ramanujan, Srinivasa, 62, 64, 268, 729, 797, 807–8
Ramanujan conjecture, 729, 732
Ramanujan graphs, 198
Ramanujan-Nagell equation, 254
Ramanujan’s ternary form, 269
Ramanujan’s Lost Notebook, 808
Ramsey theory, 215, 562, 567–68, 573–74, 627, 639, 702
random graphs, 572, 645–46, 660–62
random packing, 836
random restriction method in computational complexity, 588
random trees, 655–57
random variables, 265–67
random walks, 61, 72, 198–99, 648–51, 679
random-cluster model, 669
randomized algorithms, 116, 351, 595, 892
randomness, 115–16, 199, 269, 361
randomness extractors, 599
range of a function, 11
rank, 245; of a set, 621; of a vector bundle, 393
Raphson, Joseph, 110
rational numbers, 17–18, 82, 126–27, 144, 171, 242, 246, 284, 316, 622; approximation by, 192, 222, 315–16, 710
ratios, 79
reaction-diffusion equations, 219, 844
real closed fields, 643
real division algebra, 395
real numbers, 18, 80–82, 102, 123, 127–28, 144, 616, 622–25, 171, 627, 242, 630, 246, 635, 275, 639–40, 643–45, 698, 776
real projective line, 409
reciprocity: Artin’s law of, 720, 812–13; higher, 104, 719–20, 812–13; quadratic, 104, 718–20, 812; quartic, 104, 719
recursive functions, 111–13
recursive sets, 439–40
recursively enumerable sets, 439–40, 638–39
recursively presentable group, 439
reductio ad absurdum, 150
reductive groups, 430
Reed-Solomon codes, 883–86
reflexive relations, 12
refutation systems, 593
regular cardinals, see cardinals, regular
regular polyhedra, 52
regular polytopes, 53
regular primes, 692
regularity of solutions to partial differential equations, 481
relative consistency proofs, 623
relativity, 539; equivalence principle in, 486, 488; general, 164, 172, 483–93; principle of, 484, 487; special, 483–85
repelling orbits, 502
representation ring of a group, 423
representation varieties, 417–18
representations, 207, 274, 279, 420–24, 783–84; decomposable, 427; induced, 424; irreducible, 279, 422–29, 515–16, 561; linear, 234, 279; regular, 423, 516–18, 520; unitary, 313, 514–16
residue mod m, see modular arithmetic
resolution of singularities, 369
resolution rule, 594
restriction mapping problem, 839
retractions, 694
Reuleaux triangle, 978
rhythmic augmentation and diminution, 938
Ribet, Ken, 692
Ricci curvature, see curvature, Ricci
Richard’s paradox, 146
Riemann, Georg Friedrich Bernhard, 36, 91–92, 124–25, 127, 137, 143, 282, 284, 336–37, 356–58, 475, 729, 771, 774–76, 780, 782, 929, 947–48
Riemann curvature tensor, 488
Riemann hypothesis, 63, 68, 229, 337–38, 356–58, 714–15; for curves, 356, 730–31; generalized, 229, 340–41, 348, 729–30
Riemann integration, see integration, Riemann
Riemann mapping theorem, 728, 774–75
Riemann sphere, 282, 370, 389, 412, 500, 723
Riemann surface bundle, 414
Riemann surfaces, 209, 282–83, 300, 408, 411–14, 416, 529–30, 723, 728–29, 775, 805, 816; families of, 413–14, 417
Riemann zeta function, 38, 228–29, 283–84, 336, 344, 356, 359, 685, 715, 775
Riemann-Roch theorem, 683, 724, 775, 820
Riemannian manifolds, 218, 280, 296–97, 394, 444
Riemannian metrics, 46–47, 172, 280, 300, 311, 407, 775
Riesz, Frigyes (Frédéric), 689–90, 798–99
Riesz representation theorems, 185, 791, 798
rigid transformations, 39
rigidity theorems, 442, 444, 703, 711
rigor in mathematics, 117–29, 137, 930–31
rings, 22, 24, 57, 104–5, 108, 221, 254, 284–85, 317–19, 329, 376–77, 391, 776; graded, 391; of polynomials, 108
risk-neutral pricing, 912
road rage, 918
Robbin, Tony, 952–53
Robertson-Seymour theorem, 725
Robinson, Abraham, 128, 822–23
Robinson, Julia, 50
Rodriguez’s formula, 291
Rogers-Ramanujan identities, 557, 807
root systems, 233–34
roots: of polynomials, 66, 101; of unity, 327–28
rotational invariance: of Brownian motion, 650, 653; of normal distribution, 266
rounding errors, 606–7
Ruffini, Paolo, 101
rules of inference, 84, 140, 152, 700
Runge-Kutta method for numerical solution of ordinary differential equations, 610
Russell, Bertrand Arthur William, 128, 145–49, 781, 795–96, 929, 933–34
Russell, John Scott, 234–35, 237
Russell’s paradox, 128, 145, 171, 619, 779, 781, 795, 807
Russell’s theory of descriptions, 933–35
Saccheri, Gerolamo, 87
Saint Petersburg paradox, 747
Salem numbers, 828–29
sample average, 266
sample mean, 916
sample space, 263–65
satisfiable formulas, 582
satisfiable theories, 639
satisfying assignment, 582
scalar curvature, see curvature, scalar, 280, 488
scalar multiplication, 21, 285
scaling properties of partial differential equations, 477
scaling relations between critical exponents, 663
scattering theory, 287–88, 472
Schauder fixed point theorem, 696
schemes, 285, 367, 373, 377–79, 381
Schmidt, Friedrich Karl, 730–32
Schoenberg, Arnold, 940–41
Schottky problem, 418
Schrödinger equation, 216, 285–88, 456, 459, 472, 478, 514, 526, 540, 830
Schramm-Loewner evolution, see stochastic Loewner evolution
Schubert calculus, 62
Schweikart, F. K., 88
“Scottish Book, The” of Banach, 810
search engines, 30, 876–77; ranking problem for, 876
search problems, 577–78, 580–81
second derivative, 34
second largest eigenvalue, 198, 572
second moment method, 573
section of a bundle, 393
seed of a pseudorandom generator, 600
Seiberg-Witten invariants, see invariants, Seiberg-Witten
Seifert-van Kampen theorem, 437, 441
Selberg’s upper bound sieve, see sieves
self-adjoint matrices, see matrices, self-adjoint
self-adjoint operators, see operators, self-adjoint
self-avoiding random walk, 63, 70
self-reference, 701
self-similarity, 183, 502, 509
semi-parametric approach to statistical models, 925–26
semialgebraic sets, 364, 643–44
semidirect product, 24
sensitive dependence on initial conditions, 495–96, 501–2
Serre, Jean-Pierre, 692, 732, 974, 1000, 1001
set of measure zero, 183, 247, 628, 686, 796
set systems, 568–69
set theory, 6, 9–10, 127–28, 143, 145–46, 314, 615–34, 776, 779; naive, 145
sexagesimal place-value system, 77–79
shadow price, 289
Shannon, Claude, 770, 812, 879, 881
Shannon wavelet, 859
Shannon’s theorem, 881–83
Shelah, Saharon, 627, 630, 632–34, 646
Shimura-Taniyama-Weil conjecture, 69, 692
shock formation, 237
shock waves, 481, 775, 809, 818
shortest path, 310
Shuja, Abu Kamil, 133
Sierpi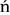ski’s carpet, 801
sieves, 345–46; Brun, 345; combinatorial, 345; number field, 355; of Eratosthenes, 334, 345; Selberg’s upper bound, 346
sigma-algebra, 247
signature of a permutation, 260
signature of a quadratic form, 268
similar matrices, see matrices, similar
simple connectedness, 38, 177, 309, 403, 714
simple groups, see groups, simple
simple harmonic oscillators, 524–27
simplex algorithm, 288–90, 613
simply connected manifolds, see manifolds, simply connected
simulated annealing, 834
simultaneous linear equations, 22, 48, 102
sine function, see trigonometric functions
Singer, Isadore, 683
singular cardinal hypothesis, 630, 633
singular cardinals, see cardinals, singular
singular value decomposition, 608
singularities, 258, 281, 367–69, 415, 476; of an algebraic variety, 723
SIRS model, 845
six-exponentials theorem, 223
skein relation, 225–27
skew-Hermitian matrices, see matrices, skew-Hermitian
Skewes, Stanley, 804
slack variables, 870
smooth functions, 185
smooth manifolds, see manifolds, smooth
smooth solutions, 195–96
smooth structures on manifolds, 397–99, 404, 407
Sobolev embedding theorem, 212, 449
Sobolev inequality, 705–6
Sobolev spaces, 211
social equilibrium, 900–901
solitons, 235–38
Solovay, Robert, 627, 629, 632
solubility by radicals, 102, 213
soluble groups, see groups, solvable
solvable groups, see groups, solvable
solving equations, 48–52
Sophie Germain primes, 892
soundness, 637; of a proof system, 592
space complexity of an algorithm, 114–15
space groups, 828
space-filling curve, 787
spacelike hypersurface, 468–69
spacelike vector, 43, 484, 487
spanning set, 22
spanning tree, 245
special functions, 290–93
special linear groups, 41, 230–31, 429, 688
special orthogonal groups, 39, 230, 425–26, 429
special relativity, see relativity, special
special unitary groups, 277
species, 150
spectral gap, 198
spectral radius formula, 518
spectral theorem, 217, 240, 295, 511–13, 519, 689
spectroscopy, 832
spectrum, 294–95, 472, 512; of a graph, 571
sphere, 53, 208, 215, 244, 282, 390, 400, 403, 670, 714, 728–29, 734; n-dimensional, 386
sphere packing, 58–60
spherical geometry, 40–41, 90, 92, 283, 401
spherical harmonics, 295–97
spherical Radon transform, 297
spherical structure, 401–2
spin configuration, 666
split-stepping, 237
splitting of a prime, 319, 322–23, 325–26, 330
spontaneous magnetization, 667
sporadic examples, 53
sporadic simple groups, 252, 688
spread, 150
square-integrable function, 511
square roots, 80–81, 327; of minus one, 56; of two, 30, 56, 78, 150, 222, 315–16, 710–11
squared error, 918
stability: of Minkowski space, 490–91; of orbits, 495; of the solar system, 728, 786, 815
stable letter, 437–38
stacks, 367
standard deviation, 265–66
state-field correspondence, 544
states, 860; of physical systems, 513, 540; of a quantum computer, 269–70; on a von Neumann algebra, 517
statistical arbitrage, 916
statistical models, 922
statistics, 917–18
Stein’s paradox, 918–20
Steiner triple systems, 173
Steinitz’s exchange lemma, see exchange axiom
Stirling’s formula, 214
stochastic differential equations, 461, 654–55, 838
stochastic integrals, 651–52, 655
stochastic Loewner evolution, 655, 664–65
stochastic matrices, see matrices, stochastic
stock market crashes, 913
Stokes’s theorem, 179–80
Stone-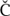
ech compactification, see compactification, Stone-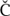ech
stopping time, 653
stress-energy-momentum tensor, 485–86
string theory, 164, 528–29, 538–41
strong cosmic censorship conjecture, 492
strong Fermat congruence, 351–52
strong law of large numbers, 266, 677, 815
strong Markov process, 653, 655
structural stability, 497
Sturm-Liouville equation, 291
Sturm-Liouville theory, 766
subrepresentations, 515
subroutines, 579
subset sum problem, 583
subspace topology, 302
substructures, 23
successive approximation, 31
successor function, 111, 146, 258
successor ordinal, 618
Suite for Piano (Schoenberg), 941
Summa (Luca Pacioli), 99
super-attracting fixed point, 499
supercompact cardinals, see cardinals, supercompact superposition: in quantum mechanics, 269–72; principle of, 457–58
supremum norm, see L∞-norm
surgeries, 281, 400; on links, 403
survival function in medical statistics, 923–24
Suslin’s hypothesis, 624, 627, 632–33
Swinnerton-Dyer, Peter, 685
Sylvester, James Joseph, 103, 768–69
Sylvester’s law of inertia, 768
symbol of a Toeplitz operator, 521
symbols of PDEs, see partial differential equations, symbols of
symmetric groups, 234, 260, 422, 424, 561, 688, 709–10
symmetric polynomials, 329–30
symmetric relations, 12
symmetric space, 713
symmetry, 19, 52, 59–61, 204, 229, 273
symmetry reductions, 480
symplectic geometry, 297–301, 531
symplectic manifolds, see manifolds, symplectic
symplectic space: linear, 297, 300
syntonic comma, 937
Szemerédi’s regularity lemma, 571
Szemerédi’s theorem, 570
Szemerédi-Trotter theorem, 570
tableau, 289
tangent space, 46
Tarski, Alfred, 627, 640–41, 643, 645, 813–14
Tauberian theorems, 803
tautology, 592
Taylor, Richard, 229, 252, 692–93
Taylor series, 38, 119, 122, 124, 200, 205, 282, 304, 541, 745
Teichmüller spaces, 413–14, 416–18
tensor categories, 275
tensor products, 272, 274–75, 301
ternary Goldbach problem, see Goldbach’s conjecture, ternary
Thales of Miletus, 130
theorema aureum, 718
theoretical computer science, 7, 575–604
Théorie Analytique de la Chaleur (Fourier), 755
Théorie Analytique des Probabilités (Laplace), 753
theories, formal, 636–46
Theory of Linear Operations (Banach), 810
thermodynamic limit, 667
theta series, 268
three-body problem, 51, 495–96, 726–28; restricted, 495, 728
three-dimensional manifolds, see manifolds, three-dimensional
Thurston, William, 388, 402–3, 461, 714
Thurston’s geometrization conjecture, see geometrization conjecture
Tits, Jacques, 162
Toeplitz index theorem, 521
Toeplitz operators, see operators, Toeplitz
tomography problem, 307
topological group theory, 441–43
topological manifolds, see manifolds, topological
topological methods in combinatorics, 572
topological spaces, 182, 221, 227, 301–3, 309, 633
topological twisting, 530–31
Torricelli, Evangelista, 135
torus, 26, 45, 53, 208–9, 300, 309, 387–91, 530–33, 536–38, 711–13
total space, 392
totally disconnected set, 504
Tower of Hanoi, 113
trace, 515
trace-class operators, see operators, trace-class
Traité de Dynamique (d’Alembert), 750
transcendence of e, see e, transcendence of
transcendental numbers, 71–72, 81, 222–23, 241, 262, 616, 766, 773
transfinite numbers, 258, 616–19, 778–79
transition functions, 45, 282–83, 300, 396–98
transition matrices, 198
transitive actions, 421
transitive closure, 624
transitive relations, 12
translation invariance, 253, 457
transmission control protocol (TCP) of the Internet, 868
traveling salesman problem (TSP), 567, 583, 872–75
Treatise of Fluxions, A (Maclaurin), 121
triangle inequality, 248, 253, 268, 705, 790
triangulation, 54
trichotomy, law of, 127
trigonometric functions, 204, 220, 262, 295–96, 307–9
trigonometric polynomials, 212, 296, 451
trimmed mean, 916
Trotter product formula, 237
Turán’s theorem, 566
turbo codes, 886
turbulence, 815
Turing, Alan, 50, 113, 219, 358, 577, 638, 701, 707–8, 818, 821–22
Turing machines, 113, 576–78, 818
twelve-tone music, 940
twin prime conjecture, 362, 715, 804; asymptotic version, 343
twisted Chevalley groups, 688
two-dimensional arithmetic progression, 718
two-soliton interaction, 235
Tychonoff’s theorem, 168
types: Russell’s theory of, 147–48
Ulam, Stanislaw, 237, 359, 361, 568–69, 628, 958
umbrella problem, 561
unavoidable configurations, 697
uncertainty principle, see Heisenberg uncertainty principle
uncountable cardinals, see cardinals, uncountable
uncountable sets, 71, 146, 170–72, 183, 223, 247, 616–18, 622, 626–29, 632, 703, 806
undecidability, 622–25, 628–29, 633, 638–39; of first-order logic, 821
underdetermined system of equations, 459
uniform approximation, 253
uniform convergence, see convergence, uniform
uniform distribution, 263–64, 266, 674
uniform family of circuits, 585
uniformization theorem, 209, 281, 283, 416, 460, 728–29, 786
unipotent matrices, see matrices, unipotent
unique factorization, 221, 254–55, 285, 318, 320–25, 327, 692, 719
uniqueness of solutions, 48, 510
unit in a ring, 318–19
unitary groups, 230
unitary matrices, see matrices, unitary
unitary operators, see operators, unitary
unitary representations, see representations, unitary
universal covers, 309–10, 441–42
universal family of marked elliptic curves, 414
universal properties, 166, 301, 433–34, 436–37
universal set, 249
universality, 650, 657–59, 663–66, 669; of the Mandelbrot set, 508–9
universe of all sets, 314, 619–22, 625
unlink, 225–26
upper-triangular matrices, see matrices, upper-triangular
vacuum Einstein equations, see Einstein equations, vacuum
vacuum state, 542
van der Waerden, Bartel, 104–5, 568
van der Waerden’s theorem, 568, 570
vanilla options, 914
van Ceulen, Ludolph, 109
variance, 265–67
varieties, 272, 285, 313, 366, 376–80, 722–23; Abelian, 190, 418; abstract algebraic, 731; affine, 313; exponential, 644; function field of, 723; irreducible, 376; projective, 313; rational, 374
vector bundles, 176–77, 227, 313, 392–94; trivial, 313, 392
vector spaces, 21–22, 27–28, 30, 33, 52, 57, 103, 105, 172, 219, 239, 244–45, 253–54, 275–76, 278–79, 284–85, 294, 314, 419–25; basis of, 21–22, 28, 30, 223; dimension of, 22; direct sum of, 24; infinite dimensional, 22, 29
vertex operator algebra, 60, 541, 544–49
Viète, François, 99, 136, 737–38
Vinogradov, Ivan, 343
Vinogradov’s three-primes theorem, 715–16
Virasoro algebra, 544
Vitali covering lemma, 455
Vizing’s theorem, 565
volatility of a share price, 911–14
volume, 57, 158, 174, 183, 672, 679, 790; in n dimensions, 671
von Neumann, John, 148, 153, 512–13, 515–16, 817–19, 821
von Neumann algebras, 313, 515–17
von Neumann’s ergodic theorem, 512, 689–91
Voronoi diagram, 829
Voronoi surface, 842
Wardrop equilibria, 865–66
Waring’s problem, 715, 717, 751, 803–4
wave equation, 35, 235–36, 456–57, 460, 466, 468, 478, 490
wavelets, 313–14, 848–62; Battle-Lemarié, 854; interval, 855; Mexican hat, 855; Meyer, 854; multiwavelets, 855
weak convergence, see convergence, weak
weak cosmic censorship conjecture, 492
weak law of large numbers, 266, 746
weak solutions to PDEs, 195–96, 313, 476
weakly compact cardinals, see cardinals, weakly compact
wedge product, 179
Weierstrass, Karl, 92, 124–29, 143–44, 476, 758, 770–71, 833
Weierstrass approximation theorem, 253, 452, 771
Weierstrass function, 833
Weierstrass P-function, 724
Weierstrass product expansion of the gamma function, 214
weight enumerators, 552–53
weighted AM-GM inequality, 704
Weil, André, 337, 347, 713, 819–21, 823, 966
Weil’s theorem, 381–82
well-ordered set, 258, 617, 619, 624, 626
well-ordering principle, 108, 147, 158, 619, 621
well-posed problems, 468–69, 473
Well-Tempered Clavier (Bach), 938
Westzynthius, Erik, 66
Weyl, Hermann, 147–49, 151, 490, 521, 788, 805–6
Weyl curvature, see curvature, Weyl
Weyl formula, 219
Weyl group, 233–34
Whitehead link, 225
Whitney trick, 405
Wick rotation, 529
Wiener-Hopf equations, 812
Wiles, Andrew, 69, 229, 252, 359, 380, 381, 692, 693
winding numbers, 386, 410, 521, 532, 683
Woodin, Hugh, 141, 630, 632, 634
Woodin cardinals, see cardinals, Woodin
word hyperbolic groups, 446
word metrics, 443
word problems, 435–36, 440, 445–46; for groups, 708
world lines, 484; length of, 485
World Wide Web, 875
worldsheets, 529–40-41
worst-case complexity, 578
x-ray transform, 307
Yang-Baxter equations, 161
Yang-Mills equations, 490
Yau, Shing-Tung, 163
Yoneda lemma, 417
Zariski topology, 303
Zelmanov, Efim, 438
zeolites, 834
Zermelo, Ernst, 128, 145, 147–48, 619–20, 780
Zermelo-Fraenkel set theory, 619
Zermelo-Russell paradox, 145
zero-one law, 646
zero-knowledge proof systems, 597–98
zeros of the Riemann zeta function, 336–38, 344, 357–58, 715
zeta functions, 284
ZFC axioms, 314, 619–29, 634, 702
Zhu Shijie, 741
Zorn’s lemma, 158